1 Introduction

The purpose of this paper is to explore the application of the conformal mapping technique to a class of steady viscous gravity currents in the presence of non-uniform potential flows. Conformal mapping is a mathematical technique based on transforming a physical domain to a simpler one where angles between intersecting curves are preserved. The conformal mapping technique has been applied to a broad set of problems [1–3]. These include aerofoil theory [4], turbulent dispersion near obstacles [5], spreading in curved 2D geometries [6], viscous sintering [7, 8], diffusion-limited aggregation [9], and strained vortices [10].

In this paper we discuss the application of conformal mapping to viscous gravity currents. This will enable us to understand the spread of viscous gravity currents in situations where their dynamics may be reduced to a non-linear partial differential equation of the form

$$\begin{aligned} \lambda \left( \frac{\partial \phi }{\partial x}\frac{\partial h^{\beta }}{\partial x}+ \frac{\partial \phi }{\partial y}\frac{\partial h^{\beta }}{\partial y}\right) = D\left[ \frac{\partial }{\partial x}\left( h^{\alpha } \frac{\partial h^{\alpha }}{\partial x}\right) + \frac{\partial }{\partial y}\left( h^{\alpha } \frac{\partial h^{\alpha }}{\partial y}\right) \right] , \end{aligned}$$
(1)

where x, y are the coordinates in the horizontal plane, h the gravity current height, \(\phi \) a harmonic function and \(\lambda \), D, \(\alpha \) and \(\beta \) are constants dependent on the ambient flow conditions and type of problem.

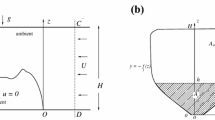
We illustrate this technique by applying it to a class of problems that are realisable in a laboratory, namely viscous gravity currents driven by a Hele–Shaw flow as illustrated in Fig. 1. The physical problem and the viscous gravity current theory are presented in Sect. 2. This is taken from the well-established model presented by Huppert [11]. In Sect. 3 the viscous gravity current theory is transformed using the conformal mapping technique. The results are presented in the form of a known similarity solution that has been used in the case of a uniform ambient flow [12]. In Sect. 4 the application to two complex flows is presented, and the results of the conformal mapping technique are given. In Sect. 5 the experimental study is presented where both the experimental setup is described and the results are analysed. The viscous gravity current profiles are non-dimensionalised, mapped, and then compared with the known similarity solution. The wider applications of this method and the general conclusions from this work are discussed in Sect. 5.1.

Fig. 1
figure 1

Schematic of the Hele–Shaw cell with the saline released from a point source at \((x_\mathrm{S},y_\mathrm{S})\)

Full size image

2 Effect of an ambient laminar flow on a thin viscous gravity current

We consider a steady, thin viscous gravity current (density \(\rho _\mathrm{c}\)) that moves in a viscously dominated ambient flow (density \(\rho _\mathrm{a}\), where \(\rho _\mathrm{c} > \rho _\mathrm{a}\)). The reduced gravity is given as \(g^{\prime } = g\left( \rho _\mathrm{c}-\rho _\mathrm{a}\right) /\rho _\mathrm{a}\), where g is the gravitational acceleration. The kinematic viscosity, of both the ambient fluid and injected fluid, is given as \(\nu \). The flow is confined by two horizontal plates, separated by a vertical distance d. The gravity current is generated by a constant flux \(q_\mathrm{c}\) of fluid, discharged from a localised point source (\(x_\mathrm{S},y_\mathrm{S}\)). The movement with time, t, of a thin viscous gravity current moving over a horizontal plate, in static ambient fluid, is described by Huppert [13] as

$$\begin{aligned} \frac{\partial h}{\partial t} =\frac{g^{\prime }}{3\nu }\left[ \frac{\partial }{\partial x}\left( h^3\frac{\partial h}{\partial x}\right) + \frac{\partial }{\partial y}\left( h^3\frac{\partial h}{\partial y}\right) \right] . \end{aligned}$$
(2)

In the absence of a gravity current, the viscous pressure driven flow within a Hele–Shaw cell is a layerwise potential flow described to leading order as \(\varvec{u}= \varvec{U}(x,y) F(z)\); where \(\varvec{U} = (U_{x},U_{y})\) is the incompressible \(\left( \mathrm{i.e.\ }\partial U_{x} /\partial x+\partial U_{y}/\partial y = 0\right) \) depth-averaged external velocity, \(F(z) = (6z/d)\left( 1-z/d\right) \) and z is the vertical distance from the bottom plate [14]. The ambient laminar flow generates shear stress \((\varvec{\tau })\) on the bottom surface of the Hele–Shaw cell [15]:

$$\begin{aligned} \varvec{\tau } = \left. \mu \frac{\partial \varvec{u}}{\partial z}\right| _{z=0} =\mu \; \varvec{U} F^{\prime }(0). \end{aligned}$$
(3)

For the case when a viscous gravity current is released within an ambient flow, as described above, the shear stress exerted on top of current physically drives it with a depth-averaged velocity of \({\overline{\varvec{u}}}_\mathrm{c} = h \varvec{\tau }/(2\mu )\). When the Hele–Shaw flow is constrained by obstacles or vertical-bounding side walls, the layerwise potential flow description is valid everywhere except with a distance \(\mathcal {O}(d)\) from the boundaries or side walls [16]. When a gravity current spreads in the Hele–Shaw cell, providing the gravity current is thin (i.e. \(h\ll d\)) and the viscosity contrast with the ambient fluid is small, the viscous shear stress drives the gravity current. It drives it so that it becomes parallel to the local flow immediately above the thin viscous gravity current.

When the ambient flow varies spatially, the steady form of the viscous gravity current is described by the non-linear advection–diffusion equation [12] as

$$\begin{aligned} \frac{F^{\prime }(0)}{2} \left( U_x\frac{\partial h^2}{\partial x}+U_y\frac{\partial h^2}{\partial y}\right) = \frac{g^{\prime }}{3\nu }\left[ \frac{\partial }{\partial x}\left( h^3 \frac{\partial h}{\partial x}\right) +\frac{\partial }{\partial y}\left( h^3 \frac{\partial h}{\partial y}\right) \right] , \end{aligned}$$
(4)

the left-hand-side can be written as \(\varvec{\nabla } \cdot \left( h{\overline{\varvec{u}}}_\mathrm{c}\right) \), where \(\varvec{\nabla } = \left( \partial /\partial x, \partial / \partial y\right) \) and \({\overline{\varvec{u}}}_\mathrm{c}\) is the mean velocity of the gravity current. Hence, Eq. (4) is of the form of Eq. (1), where \(\lambda =F^{\prime }(0)/2 = 3/d\), \(D = g^{\prime }/6\nu \), \(\alpha = 2\) and \(\beta = 2\). For the case of uniform ambient flow, where \(U_x\) is a constant and \(U_y=0\), Eames et al. [12] has shown that Eq. (4) characterises the flow accurately.

For a steady current of volume flux \(q_\mathrm{c}\), the mass conservation for a constant flux release requires

$$\begin{aligned} q_\mathrm{c} = \int _\mathrm{c} \left( \frac{F^{\prime }(0)}{2} \varvec{ U} h^2 -\frac{g^{\prime }}{3 \nu } h^3 \varvec{ \nabla } h \right) \cdot {\hat{\varvec{n}}} \;\mathrm{d} S, \end{aligned}$$
(5)

where C is a contour spanning the current width, \({\hat{\varvec{n}}}\) is the unit vector normal to C and \(\mathrm{d} S\) is the line element along the contour C.

3 Conformally mapped steady equations

Transforming Eq. (4) from the \(z = x + iy\) plane to the \(w =\phi +i\psi \) plane [17] gives

$$\begin{aligned} \lambda \frac{\partial h^2}{\partial \phi } = \frac{\partial }{\partial \phi } \left( Dh^3 \frac{\partial h}{\partial \phi } \right) + \frac{\partial }{\partial \psi } \left( Dh^3 \frac{\partial h}{\partial \psi } \right) , \end{aligned}$$
(6)

where \(\psi \) is the streamfunction. Since \(\mathrm{d} \psi = \varvec{U}\cdot {\hat{\varvec{n}}}\; \mathrm{d} S\), the integral, Eq. (5), is transformed to

$$\begin{aligned} q_\mathrm{c} =\int ^{\psi _+}_{\psi _-} \left( \lambda h^{2} - \frac{2Dh^3 \varvec{\nabla } h \cdot {\hat{\varvec{n}}}}{\varvec{U} \cdot {\hat{\varvec{n}}}}\right) \mathrm{d} \psi , \end{aligned}$$
(7)

where \(\psi _\pm \) are the bounding values of the streamfunction. We non-dimensionalise Eqs. (6) and (7) by introducing the characteristic scales \(\varTheta ^*\) for the plane \(w =\phi +i\psi \) and \(H^*\) for the gravity current height h, where

$$\begin{aligned} \varTheta ^*= & {} \left( \frac{Dq_\mathrm{c}}{4\lambda ^2}\right) ^{1/2}, \end{aligned}$$
(8a)
$$\begin{aligned} H^*= & {} \left( \frac{4q_\mathrm{c}}{D}\right) ^{1/4}. \end{aligned}$$
(8b)

Hence, the dimensionless plane \(W =\varPhi + i\Psi \), where \(\varPhi =\phi /\varTheta ^*\), \(\Psi =\psi /\varTheta ^*\), and the dimensionless gravity current height \(H = h/H^*\). We use these non-dimensional parameters to express the dimensionless forms of Eqs. (6) and (7) as

$$\begin{aligned}&\frac{\partial H^2}{\partial \varPhi }= \frac{\partial }{\partial \varPhi } \left( \frac{\partial H^{4}}{\partial \varPhi } \right) + \frac{\partial }{\partial \Psi } \left( \frac{\partial H^{4}}{\partial \Psi } \right) ,\end{aligned}$$
(9a)
$$\begin{aligned}&\int ^{\Psi _-}_{\Psi _+} \left( H^{2}-H^2\frac{\partial H}{\partial {\varPhi }} \right) \mathrm{d} {\Psi }=1. \end{aligned}$$
(9b)

We focus on the limit, when \(|\partial H/\partial {\varPhi }| \ll 1\), where the streamwise flux, due to the hydrostatic pressure gradient, is much weaker than the contribution caused by the viscous shear stress. In this case, it is the viscous shear stress that drives the viscous gravity current with the ambient flow. In addition, we assume that the cross-stream flux is larger than the streamwise flux. Hence, this gives the condition that \(|\partial H^{4}/\partial {\Psi }| \gg |\partial H^{4}/\partial {\varPhi }|\). Together, this simplifies Eqs. (9a, 9b) to give the following approximations

$$\begin{aligned}&\frac{\partial H^2}{\partial {\varPhi }} \simeq \frac{\partial }{\partial {\Psi }} \left( \frac{\partial H^4}{\partial {\Psi }} \right) , \end{aligned}$$
(10a)
$$\begin{aligned}&\int ^{\Psi _-}_{\Psi _+} H^2 \;{\mathrm{d} \Psi } \simeq 1. \end{aligned}$$
(10b)

The similarity solution to Eqs. (10a, 10b) is calculated here by writing \(H^2 = {\tilde{H}}({\varPhi }) \cdot {\hat{H}}({{\hat{\Psi }}})\), where \({\hat{\Psi }} ={\Psi }/\varGamma (\varPhi )\). Substituting into Eqs. (10a, 10b) yields

$$\begin{aligned}&\left( \frac{\varGamma ^2}{{\tilde{H}}^2}\frac{\mathrm{d} {\tilde{H}}}{\mathrm{d} {\varPhi }} \right) {\hat{H}} - \left( \frac{{\Psi }}{{\tilde{H}}}\frac{\mathrm{d} \varGamma }{\mathrm{d} {\varPhi }}\right) \frac{\mathrm{d} {\hat{H}}}{\mathrm{d} {{\tilde{\Psi }}}} \simeq \frac{\mathrm{d}{\hat{H}}^2}{\mathrm{d} {{\hat{\Psi }}}^2}, \end{aligned}$$
(11a)
$$\begin{aligned}&\left( \varGamma {\tilde{H}}\right) \int ^{{\hat{\Psi }}_-}_{{\hat{\Psi }}_+} {\hat{H}} \;{\mathrm{d} {\hat{\Psi }}} \simeq 1, \end{aligned}$$
(11b)

where the expressions in the brackets must be constants for a similarity solution to be constructed. Using this condition, from Eqs. (11a, 11b) we find that \(\varGamma (\varPhi ) \propto \left( \varPhi - \varPhi _\mathrm{s}\right) ^{(-1/3)}\) and \({\tilde{H}}(\varPhi ) \propto \left( \varPhi - \varPhi _\mathrm{s}\right) ^{1/3}\), where \(\left( \varPhi _\mathrm{S}, {\Psi _\mathrm{S}}\right) \) is the mapped origin of the gravity current. The non-dimensional gravity current height is then derived from Eq. (11a) using the given functions for \(\varGamma (\varPhi )\) and \({\tilde{H}}(\varPhi )\). After some manipulations we get

$$\begin{aligned} {\hat{H}} \simeq \frac{1}{12^{1/2}} \left( \varPhi - \varPhi _\mathrm{S}\right) ^{-1/6} \left( 9^{2/3}-\frac{\left( \Psi -\Psi _\mathrm{S}\right) ^2}{\left( \varPhi -\varPhi _\mathrm{S}\right) ^{2/3}}\right) ^{1/2}. \end{aligned}$$
(12)

The edge of the gravity current corresponds to when \(H=0\). Hence, the mapped edge of the gravity current reduces to

$$\begin{aligned} \Psi - \Psi _\mathrm{S} \simeq \pm 9^{1/3}\left( \varPhi -\varPhi _\mathrm{S} \right) ^{1/3}. \end{aligned}$$
(13)

4 Applications to selected problems

We illustrate the conformal mapping technique by applying it to two steady state examples where thin viscous gravity currents are advected by potential flows. These consist of a positive straining flow (Sect. 4.1) and flow around a cylinder (Sect. 4.2). The measured edge of the gravity currents (x, y) are non-dimensionalised by the length scale \(L^*=\varTheta ^*/U_0\). The non-dimensional co-ordinates \((X = x/L^*,Y=y/L^*)\) in the horizontal plane can be written in terms of complex potentials (\(Z = X+iY\)). The complex plane Z is transformed to the plane \(W = (\varPhi + i \Psi )\) using the conformal mapping technique.

4.1 Linear straining flow

For linear straining flows the conformal mapping is

$$\begin{aligned} W= Z + \frac{\varepsilon }{2} Z^2, \end{aligned}$$
(14)

where \(\varepsilon \) is the non-dimensional strain rate (\(\varepsilon = \epsilon L^*\)). The transformed equation (14) can be written as

$$\begin{aligned} \varPhi= & {} X + \frac{\varepsilon }{2} \left( X^2 - Y^2\right) , \end{aligned}$$
(15a)
$$\begin{aligned} \Psi= & {} Y\left( 1+\varepsilon X\right) . \end{aligned}$$
(15b)

The case of a thin viscous gravity current transported by a uniform shearing flow, as studied by Eames et al. [12], corresponds to \(\varepsilon =0\). In this case the gravity current is discharged from a point source and expands radially until the ambient flow takes over and advects the current downstream. We define the far field as a distance downstream of the point source where (\(X^2 \gg Y^2\)). In the far field, the ambient flow dominates and the width of the current remains constant.

The effect of a positive straining flow, \(\varepsilon > 0\), leads to a narrowing of the gravity current when the inflow dominates over the buoyancy driven cross-stream transport mechanism. In the far field, where \(X\gg 1/\varepsilon \), Eqs. (15a, 15b) reduces to \(\varPhi \simeq \varepsilon X^2/2\) and \(\Psi \simeq \varepsilon YX\). Substituting these expressions into Eq. (13), the edge of the gravity current, reduces to \(Y \simeq \pm 9^{1/3}\left( 2X\varepsilon ^2\right) ^{-1/3}\) (where \(\varPhi _\mathrm{S} = 0\) and \(\Psi _\mathrm{S} = 0\)). This analysis shows that the role of the straining flow is to limit the lateral cross-stream spread of the gravity current and then in the far field to cause it to decrease as the flow accelerates. In this case the conformal mapping technique can be used to map both the near and far field effects.

For negatively straining flows (\(\varepsilon <0\)), the exterior ambient flow ultimately slows to such an extent that the streamwise flow, due to gradients in pressure, becomes important (compared to the streamwise advection), the term \(\partial H^{4}/\partial {\varPhi }\) (in Eq. 9a) is no longer negligible. Hence, the similarity solution (Eq. 12) is no longer appropriate. On the centreline (\(Y=0\)) the conformal mapping equations (15a, 15b) reduces to \(\varPhi = X+\frac{\varepsilon }{2}X^2\) and \(\Psi = 0\), hence the change in gravity current height (\(\partial H/\partial \varPhi \)) can be expressed as

$$\begin{aligned} \frac{\partial H}{\partial \varPhi } \sim \left( X +\frac{\varepsilon }{2}X^2\right) ^{-7/6}. \end{aligned}$$
(16)

As \(X \rightarrow -2 \varepsilon ^{-1}\), we see from Eqs. (9a, 9b) and (10a, 10b), that the similarity solution breaks down. Thus, in the interval \(1 \ll X \ll -2\varepsilon ^{-1}\), \(\partial H /\partial \varPhi \ll 1\) and Eqs. (15a, 15b) describes the gravity current.

4.2 Spreading past a rigid body in a uniform flow

For flows around a cylindrical object the conformal mapping is

$$\begin{aligned} W(Z) =Z +\frac{\mathcal {R}^2}{Z}, \end{aligned}$$
(17)

where \(\mathcal {R}\) is the non-dimensional radius (\(\mathcal {R} = r/L^*\)). The transformed equation (17) can be written as

$$\begin{aligned} \varPhi= & {} X \left( 1 + \frac{\mathcal {R}^\mathrm{2}}{X^\mathrm{2}+Y^\mathrm{2}} \right) , \end{aligned}$$
(18a)
$$\begin{aligned} \Psi= & {} Y\left( 1 - \frac{\mathcal {R}^\mathrm{2}}{X^\mathrm{2} +Y^\mathrm{2}}\right) . \end{aligned}$$
(18b)

A rigid planar body in a Hele–Shaw cell imposes a kinematic constraint \(\varvec{U} \cdot \varvec{\hat{n}} = 0\) on the ambient flow and constraint \(\varvec{\nabla } H \cdot \varvec{\hat{n}}=0\) on the gravity current, where \(\varvec{\hat{n}}\) is a unit vector perpendicular to the planar edge of the body. To satisfy the kinematic condition on the surface of the cylinder, we require \(\partial H/ \partial \Psi = 0\) on the boundary streamline \(\Psi = 0\). Obtaining \(\partial H/\partial \Psi \) from Eq. (12), we find that this is only possible when \(\Psi _\mathrm{S} = 0\), thus Eq. (12) is valid only if the source is located on the stagnation streamline or if the gravity current never touches the cylinder (and thus no condition on H needs to be applied).

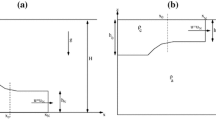
In the W-plane the body is transformed to a flat plate. Hence, the similarity solution, Eq. (12), is valid when the source is located on the stagnation streamline of the body (e.g. see Fig. 2b) or sufficiently off-centre that the gravity current does not strike the body. When the gravity current strikes the rigid body a zero normal flux condition needs to be explicitly applied.

For a cylinder of non-dimensional radius \(\mathcal {R}\), the origin of the gravity current in the \((\varPhi ,\Psi )\) plane is at \(\varPhi _\mathrm{S}= X_\mathrm{S}(1+\mathcal {R}^2/X^2_\mathrm{S})\) upstream. Since \(X_\mathrm{S} > \mathcal {R}\), as the source is outside the cylinder, \(\varPhi _\mathrm{S}\) cannot be larger than \(2X_\mathrm{S}\). However, for physically large cylinders, \(\mathcal {R}\) increases, and hence the distance \(X_\mathrm{S}\) becomes significant. Although the streamwise flux is important in the vicinity of the stagnation points, its global impact on the far field gravity current is weak. In the far field, in this case defined by the condition that \(X \gg \mathcal {R}\), Eqs. (18a, 18b) reduces to \(\varPhi \simeq X\) and \(\Psi \simeq Y\), hence substituting in Eq. (13) the edge of the gravity current is given as \(Y \simeq \pm 9^{1/3}\left( X- X_\mathrm{S} \right) ^{1/3}\) where \(\Psi _\mathrm{S} = 0\).

5 Experimental study

A series of experiments were undertaken to test the results of the conformal mapping techniques described in this paper. A summary of the test conditions are shown in Table 1 where the symbols are used in Fig. 2 to show the different test conditions. The same symbol notation is then used in Fig. 3 for the conformally mapped edge of the viscous gravity currents.

Table 1 The uniform flow case (no strain) is given as \(\mathrm{N}_1\)
Full size table

5.1 Experimental setup

The experimental setup is identical to that used by Eames et al. [12] and consisted of flow in a horizontal Hele–Shaw cell (60 cm wide and 75 cm long), where the upper and lower horizontal glass plates are separated by \(d=0.5\) cm. The flow, per unit width, within the Hele–Shaw cell, q, was controlled using a pin valve and measured with a flow meter. At the gravity current inlet the depth-averaged ambient velocity, \(U_0\), is given as q / d. At relatively low Reynolds numbers (\(\text {Re} = U_0d/\nu \)), the flow within a Hele–Shaw cell agrees well with potential flow theory. In these experiments the Reynolds number was usually below \(\text {Re} \simeq 100\); sufficiently low that the ambient flow was laminar. Although the boundary layer thickness is modified by the spatially varying flow, the wall shear stress is described by Eq. (3).

The intrusive viscous gravity current was fed, via a 0.4 cm diameter point source, through the lower plate at a steady volume flux \(q_\mathrm{c}\) from a gravity driven tank. The density contrast between the gravity current and ambient fluid was created using sodium chloride and the density was measured using a pycnometer. To distinguish the gravity current from the ambient flow, a small quantity of food dye was added to the saline, and a diffused light source was used to provide a white background to the horizontal Hele–Shaw cell.

A positive linear straining flow (Sect. 4.1) was created using plastic formers, which spanned the depth of the Hele–Shaw cell and were fixed to the sides of the channel. The shapes were cut using a computer-navigated cutting machine creating a symmetrical flow contraction with profiles \(y= 30\left( 1+\epsilon x\right) ^{-1}\) cm, where \(\epsilon \) is the strain rate.

For the case of flow past a cylinder (Sect. 4.2) plastic acrylic circular discs were placed on the edge of the gravity current source inlet and the origin \((x_\mathrm{s},y_\mathrm{s})\) was shifted to the centre of the disc. The radius, r, of the cylinder varied from 4.0 to 5.0 cm, which in all cases is less than \(10~\%\) of the channel width.

5.2 Experimental results and analysis

The steady shape of the gravity currents were analysed by manually identifying the edge from digital plan view images of the gravity current, see Fig. 2a, b. The central dark circle is a brass plug fitted flush onto a lower glass plate. The centre of the plug contained the inlet hole. The straining boundary walls and cylinder can be seen by the white plastic formers in Fig. 2a, b. Three cases were examined: uniform flow (\(\mathrm{N}_1\)), positive straining flow (\(\mathrm{P}_{1,2,3}\)), and flow around a cylinder (\(\mathrm{C}_{1,2,3}\)) (see Table 1 for test conditions).

Fig. 2
figure 2

Plan view digital images of the steady form of a thin dense viscous gravity current (\(g^{\prime }=13.8\) cm/s\(^2\), \(q_\mathrm{c}=0.3\) cm\(^3\)/s) generated from a point source discharging in (a) positive straining flow test P\(_3\) and (b) flow around a cylinder test C\(_3\). The half-widths for the positive strain (\(\mathrm{P}_{1,2,3}\)) and cylinder (\(\mathrm{C}_{1,2,3}\)) tests are plotted in (c, d). See Table 1 for ambient flow conditions

Full size image

The results of the leading edge contours of the steady state viscous gravity current shows that the different ambient flow configurations had a significant effect on the lateral dispersion of the viscous gravity current. In all cases the overall width of the current decreased significantly as the ambient velocity increased. This is shown in Fig. 2a, b where the results for different ambient velocities are plotted over a digital image of an experiment. In all cases the gravity currents were symmetrical in the \(y=0\) axis. Hence, in Fig. 2c, d we plot the half-widths of the gravity currents.

For the positive straining case, Fig. 2a, c, the ambient velocity balanced the cross-stream spreading of the gravity current leading to, far downstream, a current with approximately constant width. In addition, due to the increase in ambient flow, as the strain rate (\(\epsilon \)) increased, the lateral spreading of the gravity current decreased significantly. In the far field the gravity current is observed to contract due to the straining flow.

For the flow around a cylinder, Fig. 2b, d, the viscous gravity current widens as it passes around the cylinder. The lateral dispersion is dependent on the ambient flow, for high ambient flow the gravity current remained in proximity to the cylinder. In the far field, the gravity current experienced a significant contraction for the high ambient velocity case. However, the gravity current remained significantly wider than the gravity current propagating in uniform flow.

The non-dimensional contours of the gravity currents, Fig. 2c, d, are transformed, (Eqs. 15a, 15b and 18a, 18b), and compared with the similarity solution, Eq. (13). The results of this conformal mapping are shown in Fig. 3, where the uniform flow case has been included for comparison. In the absence of an external inhomogeneous flow (test \(N_1\), where \(\varepsilon = 0\), \(\varPhi = X\) and \(\Psi = Y\)), the width of the gravity current spreads according to Eq. (13) and the agreement between theory and observation is good (Fig. 3a) and comparable to previous study by Eames et al. [12]. For the non-uniform cases, the conformal mapping equations (14) and (17) provide good characterisation of the viscous gravity current edges for their respective flow configuration. The results for both examples (Fig. 3b, c) follow the trend of the similarity solution (Eq. 13). For these complex external ambient flows there is a greater degree of scatter in the results. It can be seen that for the positive straining flow, Fig. 3b, shows that the similarity solution underestimates the mapped width of the experimental gravity current. And for the flow around a cylinder, Fig. 3c, the mapped experimental data appear to be in good agreement with the similarity solution however with a greater uncertainty than the uniform flow case.

Fig. 3
figure 3

The similarity solution of the gravity current edge Eq. (13), denoted by the solid line, is compared to the measured gravity current profiles for a no strain \((\varepsilon =0)\), b linear positive strain \((0.02<\varepsilon <0.17)\) and c flow around a cylinder \((2.67<\mathcal {R}<6.63)\). For specific test conditions refer to Table 1

Full size image

6 Discussion and conclusion

We have shown how conformal mapping can be applied to analyse steady viscous gravity currents driven by complex ambient potential flows. The theory and laboratory observations show that a spatially varying external velocity fluid has a pronounced effect on how a gravity current spreads. The cross-stream spreading of gravity currents is sensitive to the influence of local straining regions, with a positively straining flow limiting the width of the current and further downstream leading to a thinning of the gravity current as the flow accelerates. We have shown that the conformal mapping technique can be used for gravity currents spreading in straining flows and flows past a rigid body. This technique is limited to cases where the effect of streamwise advection is stronger than the buoyancy driven streamwise component. When this does not hold the conformal mapping method, in its present form, does not offer greater simplification.

The conformal mapping technique may be relevant to understand gravity currents spreading in porous media. For a homogeneous thick porous medium where the flow is \(\varvec{u} = \varvec{U}(x,y)\) and \(F(z) = 1\), the equation describing the steady form of the gravity current [18] is

$$\begin{aligned} \varvec{\nabla } \cdot (\varvec{U} h) = \varvec{\nabla } \cdot \left( D h \varvec{\nabla } h\right) , \end{aligned}$$
(19)

which falls into the class of problems described by Eq. (1) for \(\alpha = \beta = 1\). For a homogeneous porous flow, \(\varvec{U}\), the conformal mapping technique is applicable and may help to understand the influence of a spatially varying flow caused by a boundary induced straining flow on gravity currents.

The last example concerns viscous gravity currents flowing steadily down a shallow hill whose height is \(h_\mathrm{s}(x,y)\). The steady form of a gravity current flowing down an incline is described by (see [19])

$$\begin{aligned} 0 =\frac{g^{\prime }}{3\nu }\left[ \frac{\partial }{\partial x}\left( h^3\frac{\partial h}{\partial x}\right) + \frac{\partial }{\partial y}\left( h^3\frac{\partial h}{\partial y}\right) + \frac{\partial h_\mathrm{s}}{\partial x}\frac{\partial h^3}{\partial x}+ \frac{\partial h_\mathrm{s}}{\partial y}\frac{\partial h^3}{\partial y}\right] , \end{aligned}$$
(20)

for \( \left| \varvec{\nabla } h_\mathrm{s} \right| \ll 1 \). The form of a steady viscous gravity current can be analysed using conformal mapping, when \(h_\mathrm{s}\) satisfies Laplace’s equation (i.e. \(\varvec{\nabla } ^2 h_\mathrm{s} = 0\)), as the equation falls into the class of problems described by Eq. (1).