Skip to main content
SpringerLink
Log in

Induced Stress Fields in Isotropic Elastic Discs Due to Contact Shear Stresses and Their Implications for Brazilian Test Strength Characterization

  • Research
  • Published:
Journal of Elasticity Aims and scope Submit manuscript

Abstract

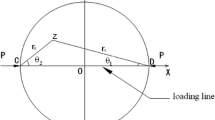
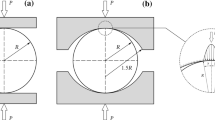
Tensile strength characterization of brittle materials by means of uniaxial tensile tests is often unfeasible, as most samples form chips during specimen preparation, leading to unacceptable geometric deviations. For this reason, the disc specimens used in Brazilian tests to determine indirect tensile strength are preferred. Despite its influence on the induced stress field and the location of the failure initiation point, the actual stress distribution along the contact is still under debate. In the present work, the complex variable method is used to develop a new analytical formulation based on the simplest possible shear stress distribution along the disc boundary that fulfils elastic equilibrium. Based on this formulation, an integration method is used to obtain the stress field generated inside specimens—elastic discs—that are subjected to distributed shear forces on their contact rims. An application of this method to the Brazilian test case is performed, proving that shear and frictional forces can be considered simultaneously. Furthermore, a mathematical procedure to simultaneously consider radial and shear stress distributions along the loaded boundary is developed to determine any possible stress field for relevant practical applications. The results confirm that shearing significantly increases stress in the vicinity of the contact area, which may explain the wedge failure pattern sometimes observed in real test specimens. Additionally, the proposed formulation guarantees that if failure is initiated in the centre of the specimen, the applied shear stress distribution no longer influences the indirect tensile strength of the material, although it influences the final test output if failure is initiated at any other point along the vertical diameter.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

Data Availability

No datasets were generated or analysed during the current study.

References

  1. ISRM: Suggested methods for determining tensile strength of rock materials. Int. J. Rock Mech. Min. Sci. 15, 99–103 (1978)

    Article  Google Scholar 

  2. ASTM D3967-16: Standard Test Method for Splitting Tensile Strength of Intact Rock Core Specimens (2016)

    Google Scholar 

  3. ASTM C496/C496M-17: Standard Test Method for Splitting Tensile Strength of Cylindrical Concrete Specimens (2017). https://doi.org/10.1520/C0496_C0496M-17

  4. Fairbairn, E.M.R.: A tribute to Fernando L. L. B. Carneiro (1913 - 2001) engineer and scientist who invented the Brazilian test. Mater. Struct. 35, 195–196 (2002). https://doi.org/10.1617/13888

    Article  Google Scholar 

  5. Timoshenko, S., Goodier, J.N.: Theory of Elasticity. McGraw-Hill, New York (1951)

    Google Scholar 

  6. Muskhelishvili, N.I.: Some Basic Problems of the Mathematical Theory of Elasticity. Noordhoff, Groningen (1953)

    Google Scholar 

  7. Yu, J., Shang, X.: Analysis of the in fl uence of boundary pressure and friction on determining fracture toughness of shale using cracked Brazilian disc test. Eng. Fract. Mech. 212, 57–69 (2019). https://doi.org/10.1016/j.engfracmech.2019.03.009

    Article  Google Scholar 

  8. Kourkoulis, S.K., Markides, C.F., Chatzistergos, P.E.: The standardized Brazilian disc test as a contact problem. Int. J. Rock Mech. Min. Sci. 57, 132–141 (2013). https://doi.org/10.1016/j.ijrmms.2012.07.016

    Article  Google Scholar 

  9. Kourkoulis, S.K., Markides, C.F., Hemsley, J.A.: Frictional stresses at the disc-jaw interface during the standardized execution of the Brazilian disc test. Acta Mech. 224, 255–268 (2013). https://doi.org/10.1007/s00707-012-0756-3

    Article  Google Scholar 

  10. Guerrero-Miguel, D.J., Álvarez-Fernández, M.I., García-Fernández, C.C., González-Nicieza, C., Menéndez-Fernández, C.: Analytical and numerical stress field solutions in the Brazilian test subjected to radial load distributions and their stress effects at the centre of the disk. J. Eng. Math. 116, 29–48 (2019). https://doi.org/10.1007/s10665-019-10001-1

    Article  MathSciNet  Google Scholar 

  11. Alvarez-Fernandez, M.I., Garcia-Fernandez, C.C., Gonzalez-Nicieza, C., Guerrero-Miguel, D.J.: Effect of the contact angle in the failure pattern in slate under diametral compression. Rock Mech. Rock Eng. 53, 2123–2139 (2020). https://doi.org/10.1007/s00603-020-02044-z

    Article  Google Scholar 

  12. Bahaaddini, M., Serati, M., Masoumi, H., Rahimi, E.: Numerical assessment of rupture mechanisms in Brazilian test of brittle materials. Int. J. Solids Struct. 180–181, 1–12 (2019). https://doi.org/10.1016/j.ijsolstr.2019.07.004

    Article  Google Scholar 

  13. Kim, H.M., Lee, J.W., Yazdani, M., Tohidi, E., Nejati, H.R., Park, E.S.: Coupled viscous fluid flow and joint deformation analysis for grout injection in a rock joint. Rock Mech. Rock Eng. 51, 627–638 (2018). https://doi.org/10.1007/s00603-017-1339-3

    Article  Google Scholar 

  14. Yuan, R., Shen, B.: Numerical modelling of the contact condition of a Brazilian disk test and its influence on the tensile strength of rock. Int. J. Rock Mech. Min. Sci. 93, 54–65 (2017). https://doi.org/10.1016/j.ijrmms.2017.01.010

    Article  Google Scholar 

  15. Japaridze, L.: Stress-deformed state of cylindrical specimens during indirect tensile strength testing. J. Rock Mech. Geotech. Eng. 7, 509–518 (2015). https://doi.org/10.1016/j.jrmge.2015.06.006

    Article  Google Scholar 

  16. Chau, K.T., Wei, X.X.: A three dimensional analytic solution for the Brazilian test. In: Frontiers of Rock Mechanics and Sustainable Development in the 21st Century, pp. 141–143 (2001)

    Google Scholar 

  17. Serati, M., Alehossein, H., Williams, D.J.: 3D elastic solutions for laterally loaded discs: generalised Brazilian and point load tests. Rock Mech. Rock Eng. 47, 1087–1101 (2014). https://doi.org/10.1007/s00603-013-0449-9.

    Article  Google Scholar 

  18. Serati, M., Alehossein, H., Erarslan, N.: The Brazilian disc test under a non-uniform contact pressure along its thickness. Rock Mech. Rock Eng. 49, 1573–1577 (2016). https://doi.org/10.1007/s00603-015-0773-3

    Article  Google Scholar 

  19. Wei, X.X., Chau, K.T.: Finite solid circular cylinders subjected to arbitrary surface load. Part I. Int. J. Solids Struct. 37, 5733–5744 (2000). https://doi.org/10.1016/S0020-7683(99)00290-5

    Article  Google Scholar 

  20. Hondros, G.: The evaluation of Poisson’s ratio and the modulus of materials of a low tenisle resistance by the Brazilian (indirect tensile) test with particular reference to concrete. Aust. J. Basic Appl. Sci. 10, 243–268 (1959)

    Google Scholar 

  21. Markides, C.F., Pazis, D.N., Kourkoulis, S.K.: Closed full-field solutions for stresses and displacements in the Brazilian disk under distributed radial load. Int. J. Rock Mech. Min. Sci. 47, 227–237 (2010). https://doi.org/10.1016/j.ijrmms.2009.11.006

    Article  Google Scholar 

  22. Hung, K.M., Ma, C.C.: Theoretical analysis and digital photoelastic measurement of circular disks subjected to partially distributed compressions. Exp. Mech. 43, 216–224 (2003). https://doi.org/10.1177/0014485103043002011

    Article  Google Scholar 

  23. Ma, C.C., Hung, K.M.: Exact full-field analysis of strain and displacement for circular disks subjected to partially distributed compressions. Int. J. Mech. Sci. 50, 275–292 (2008). https://doi.org/10.1016/j.ijmecsci.2007.06.005

    Article  Google Scholar 

  24. Addinall, E., Hackett, P.: Tensile failure in rock-like materials. In: Spokes, E.M., Christiansen, C.R. (eds.) The 6th U.S Symposium on Rock Mechanics (USRMS), pp. 515–538. American Rock Mechanics Association (1964)

    Google Scholar 

  25. Lavrov, A., Vervoort, A.: Theoretical treatment of tangential loading effects on the Brazilian test stress distribution. Int. J. Rock Mech. Min. Sci. 39, 275–283 (2002). https://doi.org/10.1016/S1365-1609(02)00010-2

    Article  Google Scholar 

  26. Lanaro, F., Sato, T., Stephansson, O.: Microcrack modelling of Brazilian tensile tests with the boundary element method. Int. J. Rock Mech. Min. Sci. 46, 450–461 (2009). https://doi.org/10.1016/j.ijrmms.2008.11.007

    Article  Google Scholar 

  27. Markides, C.F., Pazis, D.N., Kourkoulis, S.K.: Influence of friction on the stress field of the Brazilian tensile test. Rock Mech. Rock Eng. 44, 113–119 (2011). https://doi.org/10.1007/s00603-010-0115-4

    Article  Google Scholar 

  28. Kourkoulis, S.K., Markides, C.F., Bakalis, G.: Elastic contact of smooth cylinders by caustics, pp. 25–27 (2013). https://doi.org/10.1007/s00419-012-0715-4

  29. Markides, C.F., Kourkoulis, S.K.: The influence of jaw’s curvature on the results of the Brazilian disc test. J. Rock Mech. Geotech. Eng. 8, 127–146 (2016). https://doi.org/10.1016/j.jrmge.2015.09.008

    Article  Google Scholar 

  30. Markides, C.F., Kourkoulis, S.K.: Naturally accepted boundary conditions for the Brazilian disc test and the corresponding stress field. Rock Mech. Rock Eng. 46, 959–980 (2013). https://doi.org/10.1007/s00603-012-0351-x

    Article  Google Scholar 

  31. Kourkoulis, S., Markides, C.F., Chatzistergos, P.: A combined numerical and experimental study of the displacement field in the standardized Brazilian disc test. In: 10th HSTAM International Congress on Mechanics, pp. 1–8 (2013)

    Google Scholar 

  32. Lu, A., Wang, S., Cai, H.: Closed-form solution for the stresses in Brazilian disc tests under vertical uniform loads. Rock Mech. Rock Eng. 51, 3489–3503 (2018). https://doi.org/10.1007/s00603-018-1511-4

    Article  Google Scholar 

  33. Sadd, M.H.: Elasticity. Elsevier, Amsterdam (2009)

    Google Scholar 

  34. Barber, J.R.: Elasticity. Springer, Netherlands (2010)

    Book  Google Scholar 

  35. Sokolnikoff, I.S.: Mathematical Theory of Elasticity. McGraw-Hill, New York (1956)

    Google Scholar 

  36. Muskhelishvili, N.I.: Some Basic Problems of the Mathematical Theory of Elasticity. Noordhoff, Groningen (1953)

    Google Scholar 

  37. Kourkoulis, S.K., Markides, C.F., Hemsley, J.A.: Frictional stresses at the disc-jaw interface during the standardized execution of the Brazilian disc test. Acta Mech. 224, 255–268 (2013). https://doi.org/10.1007/s00707-012-0756-3

    Article  Google Scholar 

  38. Markides, C.F., Kourkoulis, S.K.: Naturally accepted boundary conditions for the Brazilian disc test and the corresponding stress field. Rock Mech. Rock Eng. 46, 959–980 (2013). https://doi.org/10.1007/s00603-012-0351-x

    Article  Google Scholar 

  39. Garcia-Fernandez, C.C., Gonzalez-Nicieza, C., Alvarez-Fernandez, M.I., Gutierrez-Moizant, R.A.: Analytical and experimental study of failure onset during a Brazilian test. Int. J. Rock Mech. Min. Sci. 103, 254–265 (2018). https://doi.org/10.1016/j.ijrmms.2018.01.045

    Article  Google Scholar 

  40. Li, D., Li, B., Han, Z., Zhu, Q.: Evaluation on rock tensile failure of the Brazilian discs under different loading configurations by digital image correlation. Appl. Sci. 10, 5513 (2020). https://doi.org/10.3390/app10165513

    Article  Google Scholar 

Download references

Acknowledgements

This research was funded by the Ministry of Science and Innovation of Spain through Grant MCINN-23-PID2022-142015OB-I00 funded by MCIN/AEI/10.13039/501100011033 and by “ERDF A way of making Europe” and by the Regional Foundation for Scientific and Technological Research FICYT through grant SV-PA-21-AYUD/2021/51328.

Author information

Authors and Affiliations

  1. DinRock Group, University of Oviedo, C/ de la Independencia 13, 33004, Oviedo, Asturias, Spain

    Diego-José Guerrero-Miguel, María-Belén Prendes-Gero, Martina-Inmaculada Álvarez-Fernández & Celestino González-Nicieza

Authors
  1. Diego-José Guerrero-Miguel
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. María-Belén Prendes-Gero
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Martina-Inmaculada Álvarez-Fernández
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Celestino González-Nicieza
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

Mathematical development and coding, D.-J.G.-M. and C.G.-N.; visualization, D.-J.G.-M.; writing—original draft preparation, M.-B.P.-G.; writing—review and editing, M.-I.Á.-F.; supervision, C.G.-N.. All authors have read and agreed to the published version of the manuscript.

Corresponding author

Correspondence to Diego-José Guerrero-Miguel.

Ethics declarations

Competing Interests

The authors declare that there is no conflict of interest between the exposed results and the funding detailed in the acknowledgements section.

Additional information

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Guerrero-Miguel, DJ., Prendes-Gero, MB., Álvarez-Fernández, MI. et al. Induced Stress Fields in Isotropic Elastic Discs Due to Contact Shear Stresses and Their Implications for Brazilian Test Strength Characterization. J Elast (2024). https://doi.org/10.1007/s10659-024-10072-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10659-024-10072-x

Keywords

Mathematics Subject Classification

Search

Navigation