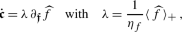Abstract
The paper presents a versatile framework for solids which undergo nonisothermal processes with irreversibly changing microstructure at large strains. It outlines rate-type and incremental variational principles for the full thermomechanical coupling in gradient-extended dissipative materials. It is shown that these principles yield as Euler equations essentially the macro- and micro-balances as well as the energy equation. Starting point is the incorporation of the entropy and entropy rate as canonical arguments into constitutive energy and dissipation functions, which additionally depend on the gradient-extended mechanical state and its rate, respectively. By means of (generalized) Legendre transformations, extended variational principles with thermal as well as mechanical driving forces can be constructed. On the thermal side, a rigorous distinction between the quantity conjugate to the entropy and the quantity conjugate to the entropy rate is essential here. Formulations with mechanical driving forces are especially suitable when considering possibly temperature-dependent threshold mechanisms. With regard to variationally consistent incrementations, we suggest an update scheme which renders the exact form of the intrinsic dissipation and is highly suitable when considering adiabatic processes. It is shown that this proposed numerical algorithm has the structure of an operator split. To underline the broad applicability of the proposed framework, we set up three model problems as applications: Cahn-Hilliard diffusion coupled with temperature evolution, where we propose a new variational principle in terms of the species flux vector, as well as thermomechanics of gradient damage and gradient plasticity. In a numerical example we study the formation of a cross shear band.
Similar content being viewed by others
1 Introduction
In order to model dissipative size effects in solid materials that are, for example, related to the width of shear bands or the grain size in polycrystals, nonstandard continuum theories have to be elaborated that are based on characteristic length scale parameters. The idea is to incorporate at least first-order spatial gradients of micro-structural variables that describe (possibly in a homogenized sense) the irreversibly evolving microstructure. It is of great importance here to account for thermomechanical coupling effects such as thermal softening and temperature increase due to intrinsic dissipation. Practical applications include technological processes like sheet-metal forming or extrusion of metals. Within this work, we present a unified framework for the fully coupled thermomechanics of gradient-extended dissipative solids that is applicable to a wide range of model problems such as diffusion, (crystal) plasticity and damage. The formulation is embedded into the concept of standard dissipative solids that is characterized by energy and dissipation functions, see Biot [7], Ziegler [90] and Halphen & Nguyen [33]. In particular, the strongly coupled multifield problem will exhibit an incremental variational structure which is an extension of the framework of gradient-extended dissipative solids presented in Miehe [49,50] towards nonisothermal processes.
Historically, the consideration of long-range effects via length scales can be traced back to the work of the brothers Cosserat & Cosserat [13]. They investigated a microstructure with rigid particles by introducing an additional microrotation governed by three additional degrees of freedom. Since then, a lot of research has been done on so called micropolar, micromorphic and microstrain continua, i.e., by Eringen [18], see also Leismann & Mahnken [38] for a comparative study. The book of Capriz [11] provides a general setting for materials with microstructure where order parameters are considered as components of elements of an abstract manifold. Here, we also refer to the work of Mariano [44]. In Maugin [45] the standard thermodynamic theory of local internal variables is extended by an additional dependency of the energy function on the first-order spatial gradient of a (not necessarily scalar) internal variable, see also Maugin & Muschik [47] and Frémond [25]. An important ingredient of such theories is a proper energetic treatment of the microstructural processes yielding additional balance-type equations that are coupled with the standard macroscopic balance equations (mass, linear/angular momentum and energy). For an embedding into the theory of micro-forces we refer to Gurtin [27].
Typical applications of above mentioned nonlocal theories including additional balance equations are theories of phase transformation, gradient plasticity and gradient damage. Theories of gradient plasticity are dealt with on a phenomenological level in Aifantis [1], Fleck & Hutchinson [19], Gurtin [27], Forest & Sievert [23], Gurtin & Anand [28] just to name a few. Gradient damage theories that are basically in the same spirit are considered in Peerlings et al. [68], Dimitrijevic & Hackl [17], Pham et al. [71], Frémond [25] among many others.
An important role in the modeling of dissipative processes in solids is played by incremental variational principles. They offer an elegant way to couple different physical fields, possess inherent symmetry and require only Jacobian and Hessian matrices of the underlying potential density for an implementation into typical finite element codes. In addition, if a minimization structure is at hand, structural and material stability analysis is possible, i.e., the formation of complex microstructures can be described. For contributions on the variational theory of local plasticity we refer to Hill [34], Simo & Honein [78], Hackl [29], Ortiz & Stainier [67], Ortiz & Repetto [66], Carstensen et al. [12] and Mosler & Bruhns [58]. The works of Miehe [48], Petryk [70] and Hackl & Fischer [30] deal with general inelastic behavior. Extensions towards incorporation of (at least) the first gradient of the internal variable into constitutive functions can be found in Mühlhaus & Aifantis [59], Fleck & Willis [20], Mainik & Mielke [43], Nguyen [63], Miehe [50] and Lancioni et al. [36] for gradient plasticity and in Lorentz & Andrieux [40], Mielke & Roubíček [56], Dimitrijevic & Hackl [17] and Pham et al. [71] for gradient damage. In addition, we mention the general formulations of gradient-extended dissipative solids by Svendsen [83], Francfort & Mielke [24] and Miehe [49]. A gradient plasticity theory that incorporates a fractional derivative of the plastic strain is presented in Dahlberg & Ortiz [14]. Alternatively, in damage mechanics one can account for nonlocality by considering the gradient of the total strain measure (instead of the damage variable) in the constitutive functions. Non-smooth (hemi)variational formulations of such an approach are presented in, e.g., Placidi & Barchiesi [72], Placidi et al. [74] and Timofeev et al. [85]. Studies comparing these formulations with the gradient damage approach can be found in Le et al. [37] and Placidi et al. [73]. Note that all works cited so far in this paragraph deal with dissipative processes under isothermal conditions except Hackl [29] in the last section. In the latter work, an original idea of Simo & Miehe [79] is taken up, namely to introduce a plastic configurational entropy as an additional internal variable that, as part of the total entropy, leaves the internal energy unchanged. From the viewpoint of variational principles however, the main difficulty of fully coupled thermomechanics is to account for the internal dissipation in the energy equation. The construction of a single unified potential from which all coupled thermomechanical field equations follow is outlined in the seminal work of Yang et al. [89]. They introduce a specific integrating factor that makes the linearized integral expressions, showing up in the fully coupled weak form, symmetric. This factor is based on distinguishing the equilibrium temperature from a so-called external temperature. Both temperatures coincide only at equilibrium. With this variational principle at hand, the fully coupled thermomechanical boundary value problem can be solved monolithically by a sequence of symmetric algebraic systems. Alternatively, staggered numerical algorithms were mainly used before which lead to symmetric finite element stiffness matrices for each subproblem, see Simo & Miehe [79] and Armero & Simo [3]. In the recent years, the work of Yang et al. [89] has been the basis for further model developments in thermoplasticity, see Stainier & Ortiz [81], Canadija & Mosler [10], Su et al. [82], Bartels et al. [5], Mielke [55] and Fohrmeister et al. [21]. In the latter, a specific phenomenological model of gradient plasticity together with a micromorphic extension in the sense of Forest [22] is considered. Besides incorporating the first gradient of a generic internal variable into the energy function, Mielke [55] also discusses in detail the gradient structure of thermoplasticity. In Bartels et al. [5] special focus is put on the thermodynamic (in)consistency of the Taylor-Quinney factor. This factor, usually introduced in an ad-hoc way, takes into account that only a certain amount of the plastic power is transformed into heat as observed in the experiments of Taylor & Quinney [84], see also Rosakis et al. [75] and Oliferuk & Raniecki [65].
According to the authors’ knowledge, a universal variational framework for the thermomechanics of solids with energetic as well as dissipative gradient extensions is still missing in literature. The present work outlines a generalization of the versatile framework of Miehe [49,50] for gradient-extended dissipative solids towards nonisothermal processes. Point of departure is the definition of two constitutive functions, namely (i) the internal energy function that depends on the (gradient-extended) mechanical state and the entropy and (ii) a (nonsmooth) dissipation potential function that depends on the rates of the (gradient-extended) mechanical state and the entropy. Then, at current time the rates of the macro- and micro-motion and the entropy rate are governed by a canonical saddle point principle in case of an adiabatic process and a canonical minimization principle in case of a process including heat conduction. However, since specific forms of both constitutive functions are difficult to access, (generalized) Legendre transformations of those functions are considered. Here, the concept of dual variables is rigorously pursued, i.e., the quantity conjugate to the entropy (the temperature) is distinguished from the quantity conjugate to the entropy rate (the thermal driving force). Then, the necessary condition of the (generalized) Legendre transformation of the dissipation potential function must render the structure of the energy equation in form of an entropy evolution equation. The obtained rate-type variational principle is in line with Yang et al. [89] but derived in an alternative way and extended by an additional long-range micro-motion that accounts for effects related to length scales. In addition, extended rate-type variational principles are constructed that incorporate dissipative mechanical driving forces and a temperature-dependent scalar threshold function via a Lagrange multiplier. By construction of consistent numerical time integration algorithms, variational principles valid for the time increment under consideration are obtained. Here, we especially point out a new semi-explicit numerical algorithm that, in contrast to a fully implicit scheme, evaluates the integration factor of Yang et al. [89] to the value one and, hence, gives the algorithmically consistent form of the intrinsic dissipation.
In the subsequent sections, the above aspects are carried out in detail and the novel key contributions of the presented work for the thermomechanics of dissipative multifield problems are
-
a canonical variational principle based on a dissipation potential function that depends on the entropy rate,
-
the construction of rate-type and incremental mixed variational principles via (generalized) Legendre transformations, where we propose a new semi-explicit numerical update scheme that has the structure of an operator split and is highly suitable when considering adiabatic processes,
-
a general and versatile framework for the full thermomechanical coupling in gradient-extended dissipative continua and
-
applications to gradient plasticity, gradient damage and Cahn-Hilliard diffusion, where for the latter we propose a new minimization structure with respect to the species flux vector.
The paper is organized as follows: In Sect. 2 we consider as motivating example a very simple adiabatic thermomechanical material element and derive rate-type as well as incremental variational principles based on the entropy and entropy rate as canonical variables in the energy and dissipation potential functions. Two update schemes, namely the known implicit and a new semi-explicit numerical algorithm are presented that govern the time-discrete evolution of the thermomechanical state. In Sect. 3 we set up general forms of governing equations for the thermomechanics of gradient-extended dissipative solids in a three-dimensional large-strain continuum setting. Section 4 shows that this fully coupled system is related to a variational statement. In addition, we construct extended rate-type and incremental variational principles that incorporate dissipative mechanical driving forces and threshold mechanisms that depend on the thermal state. The formulations outlined in Sect. 4 are general and can be applied to a wide spectrum of problems in thermomechanics. As examples, we specify in Sect. 5 the developed setting to Cahn-Hilliard diffusion, gradient damage and (additive) gradient plasticity with strong coupling to temperature evolution. The former is given a new variational structure in terms of the species flux vector. Finally, to demonstrate the capability of the newly proposed semi-explicit variational update scheme, we show a numerical example that is concerned with adiabatic shear band localization in softening plasticity.
2 Variational Principles for Nonisothermal Rheology
2.1 An Adiabatic Thermomechanical Material Element
2.1.1 Constitutive Functions
We consider a very simple rheological material element depicted in Fig. 1 describing a smooth linear thermo-visco-elastic behavior. The material element is understood to be embedded in a thermal environment characterized by the absolute temperature \(\theta>0\). The spring exhibits thermoelastic behavior by Hooke’s law coupled with thermal expansion. The dashpot device characterizes viscous response via Newton’s law. In addition, the material element is able to store heat. We have the fundamental constitutive relationships
Here, \(\sigma\) denotes as usual a stress, \(\varepsilon\) a strain and \(e\) an internal energy. The four involved material parameters are Young’s modulus \(E\), the thermal expansion coefficient \(\alpha_{T}\), the viscosity \(H\) and the heat capacity \(C\) at constant internal and external deformation. Without loss of generality, these material parameters are assumed to be constant, i.e., they do not depend on the temperature. Finally, \(\theta_{0}\) stands for a reference temperature. Such a simple model is able to describe classical thermomechanical coupling effects, such as the Gough-Joule effect or thermal expansion, as well as heating due to dissipation in the dashpot. The mechanical state of the rheological device is described by the total strain \(\varepsilon\) and the internal variable \(\mathfrak {q}\) characterizing the strain of the inner dashpot.
Rheological material element with internal thermoelastic and dissipative (viscous) mechanisms, loaded by an external stress \(\sigma _{\mathit{ext}}(t)\). The time-discrete evolution of the material’s state \((\varepsilon, \mathfrak {q}, \eta)\) is described by a finite sequence of incremental variational principles
We summarize these two quantities in the

Identifying the strain in the spring device by the simple kinematic relationship \(\varepsilon^{e}=\varepsilon-\mathfrak {q}\), we define the well known thermoelastic free energy function

that is not defined for nonpositive temperatures and is concave in \(\theta\). In addition, we define the dissipation potential function associated with the two dashpot devices

2.1.2 Governing System of Equations
The thermomechanical response of the material element within a time interval \({\mathcal {T}}= (0,t^{e})\subset\mathbb{R}_{+}\) is fully governed by the two constitutive functions (1) and (2) and characterized by four equations (3)–(6). First, on the mechanical side, the equilibrium equation
is a relationship between internal and external stresses. Second, the evolving internal strain state is governed by Biot’s equation
and characterizes an internal dissipative mechanism, see Biot [7]. Third, on the thermal side, the state equation
determines the current entropy \(\eta\) or in an inverse manner the current temperature \(\theta\). Finally, the evolution of the entropy is governed by a nonnegative dissipation

Equation (6)1 together with the constitutive definition of the dissipation \({\mathcal {D}}\) is a form of the first law of thermodynamics, i.e., the balance of energy for an adiabatic process under consideration. The inequality (6)2 is the second law of thermodynamics that is ensured a priori by a dissipation potential function \(\widehat{\phi}(\cdot)\) that is (i) nonnegative, (ii) zero in the origin \(\widehat{\phi}({\boldsymbol {0}}) = 0\) and (iii) convex, see, e.g., Frémond [25]. In case of a dissipation potential function that is positively homogeneous of degree \(\ell\), i.e.,  for all \(\gamma> 0\), the dissipation can be written alternatively asFootnote 1
for all \(\gamma> 0\), the dissipation can be written alternatively asFootnote 1 . Aim of the subsequent treatment is the construction of variational principles that account for the governing equations (3)–(6) of the thermomechanical device. Starting point is the definition of a (maybe unusual) dissipation potential function that depends on the entropy rate.
. Aim of the subsequent treatment is the construction of variational principles that account for the governing equations (3)–(6) of the thermomechanical device. Starting point is the definition of a (maybe unusual) dissipation potential function that depends on the entropy rate.
2.2 Canonical Variational Principle with Entropy Variable
The main difficulty in the formulation of rate-type variational principles in thermo-mechanics is to account for the full update of the thermal state via (6). For the nonisothermal case, we start by modeling the internal energy \(e\) whose corresponding function naturally depends on the entropy \(\eta\). Hence, our investigation of thermomechanics in generalized standard materials is based on assuming the constitutive functions

The internal energy function \(\widehat{e}\) determines the current internal energy stored in the material element. The newly introduced dissipation potential function \(\widehat{v}\) is assumed to be a function of the rates  and might additionally depend on the current thermomechanical state
and might additionally depend on the current thermomechanical state  . Alternatively, instead of the current entropy \(\eta\) the dissipation potential function \(\widehat{v}\) can depend on the current temperature \(\theta\) by making use of the constitutive relationship (5). Comparing \(\widehat{v}\) with the dissipation potential function \(\widehat{\phi}\) defined in (2), we observe an additional thermal slot with the dependence on \(\dot{\eta}\). This assumed dependency is the key ingredient of the subsequent construction of variational principles in dissipative thermomechanics. Based on the two constitutive functions (7), we construct the rate-type potential
. Alternatively, instead of the current entropy \(\eta\) the dissipation potential function \(\widehat{v}\) can depend on the current temperature \(\theta\) by making use of the constitutive relationship (5). Comparing \(\widehat{v}\) with the dissipation potential function \(\widehat{\phi}\) defined in (2), we observe an additional thermal slot with the dependence on \(\dot{\eta}\). This assumed dependency is the key ingredient of the subsequent construction of variational principles in dissipative thermomechanics. Based on the two constitutive functions (7), we construct the rate-type potential

at given thermomechanical state  , that accounts for energetic as well as dissipative mechanisms. Next, we define an external load function
, that accounts for energetic as well as dissipative mechanisms. Next, we define an external load function
depending on the given external stress \(\sigma_{\mathit{ext}}\), that loads the material element, see Fig. 1. Then, the rate of the thermomechanical state at current time \(t\) under adiabatic conditions is determined by the canonical saddle point principle

Note that the saddle point structure of this variational principle is governed by an assumed concavity of the dissipation potential function \(\widehat{v}\) with respect to \(\dot{\eta}\), see Sect. 2.3.2 and Footnote 2. Taking the first derivative of the potential (8) yields as necessary conditions of the variational principle (9) three Euler equations for the rate of the thermomechanical state of the material element at current time \(t\), namely
The first equation determines the rate \(\dot{\varepsilon}\) of the external strain state and is a form of the stress equilibrium (3) without inertia terms. The second equation governs the rate \(\dot{\mathfrak {q}}\) of the internal variable and is identical to (4). Finally, the third equation is a form of the balance of energy, i.e., the first law of thermodynamics (6) combined with an inverse representation of (5), which determines the rate \(\dot{\eta}\) of the entropy. However, this is a quite unusual representation. The main difficulty in this canonical setting is the formulation of the two constitutive functions \(\widehat{e}\) and \(\widehat{v}\) in terms of the entropy \(\eta\) and entropy rate \(\dot{\eta}\), respectively.Footnote 2 Hence, a formulation in terms of the temperature is more convenient.
2.3 Mixed Variational Principle with Temperature Variable
For practical applications, the above canonical variational principle is transformed into a mixed saddle point principle that incorporates the temperature as a primary variable. This transformation is achieved within two steps.
2.3.1 Variable Dual to Entropy
First, we define the internal energy function occurring in the rate-type potential (8) by a partial Legendre transformation

where \(\widehat{\psi}\) is the free energy function depending on the thermal variable \(\theta\). The necessary optimality condition of this Legendre transformation defines the entropy

in terms of the thermal variable \(\theta\). The latter is the dual quantity to the entropy \(\eta\), i.e., the temperature of the material element.
2.3.2 Variable Dual to Entropy Rate
In a second step, we define the dissipation potential function \(\widehat{v}\) occurring in the rate-type potential (8) by a partial Legendre transformation

in terms of the dissipation potential function \(\widetilde{\phi}\), that depends on the thermal variable \(T\) and, by making use of (11), is defined at current state  . The necessary condition of this Legendre transformation defines the evolution of the entropy
. The necessary condition of this Legendre transformation defines the evolution of the entropy

in terms of the thermal variable \(T\). We identify \(T\) as the quantity dual to the entropy rate \(\dot{\eta}\) and call it the thermal driving force that, up to this point, is rigorously distinguished from the temperature \(\theta\) of the material element. For the adiabatic case under consideration, (13) must have the form of the balance of energy (6) and we identify

This relationship restricts the form of the functional dependence of the dissipation potential function \(\widetilde{\phi}\) and is fulfilled if a multiplicative dependence on the thermal driving force \(T\) is assumed

To arrive at (14), we use the result that at equilibrium the thermal driving force \(T\) can be identified with the temperature \(\theta\), which is an outcome of the mixed variational principle (17) below. The scaling factor \(T/\theta\) first arised via a symmetry argument as integrating factor in the seminal work of Yang et al. [89].
2.3.3 Mixed Variational Principle
Starting from the rate-type potential (8), the two partial Legendre transformations (10) and (12) motivate the definition of a mixed rate-type potentialFootnote 3

at given thermomechanical state  in terms of the two constitutive functions \(\widehat{\psi}\) and \(\widehat{\phi}\). Inserting the necessary condition (11) on the given thermomechanical state yields the reduced mixed rate-type potential
in terms of the two constitutive functions \(\widehat{\psi}\) and \(\widehat{\phi}\). Inserting the necessary condition (11) on the given thermomechanical state yields the reduced mixed rate-type potential

at given thermomechanical state  . Based on this definition, we obtain the mixed saddle point principle
. Based on this definition, we obtain the mixed saddle point principle

that determines at current time \(t\) the rates of the external strain, internal variable and entropy as well as the thermal driving force. The Euler equations of this saddle point principle are
Again, the first equation represents the stress equilibrium and the second one Biot’s equation. The third relationship identifies the thermal driving force with the given temperature as reported in Yang et al. [89]. The last equation represents the first law of thermodynamics in the form of an evolution equation for the entropy. Clearly, within this mixed setting the entropy rate \(\dot{\eta}\) plays the role of a Lagrange multiplier. With known rates  of mechanical state and entropy, the temperature rate at current time \(t\) can be computed by taking the time derivative of (5). A constrained minimization formulation dual to the variational principle (9) is obtained by commuting the order of the infimum and the supremum in (17) (which we assume to be possible) such that
of mechanical state and entropy, the temperature rate at current time \(t\) can be computed by taking the time derivative of (5). A constrained minimization formulation dual to the variational principle (9) is obtained by commuting the order of the infimum and the supremum in (17) (which we assume to be possible) such that

For a general discussion of constructing mixed and dual variational principles we refer to the books Maugin [46], Nguyen [62] and Berdichevsky [6].
2.4 Incremental Variational Principles
We consider a finite time interval \([t_{n}, t_{n+1}] \subset\overline{{\mathcal {T}}}\) with step length \(\tau:=t_{n+1}-t_{n}>0\) and assume all thermomechanical state quantities at time \(t_{n}\) to be known. The goal is then to determine all the approximate state quantities at time \(t_{n+1}\) based on variational principles valid for the time increment under consideration. Subsequently, all variables without subscript are understood to be evaluated at time \(t_{n+1}\).
2.4.1 Mixed Variational Principle
A mixed variational principle associated with the finite time interval \([t_{n}, t_{n+1}]\) is based on the incremental potential

in terms of the continuous rate-type potential \(\widehat{\pi}\) defined in (16). Here, \(\mathit{Algo}\) stands for a numerical integration algorithm in time within the interval \([t_{n},t_{n+1}]\). The incremental potential \(\widehat{\pi}^{\tau}\) is understood to be defined at given thermomechanical state  at time \(t_{n}\). Then, the finite-step sized incremental mixed variational principle
at time \(t_{n}\). Then, the finite-step sized incremental mixed variational principle

determines the mechanical state, the entropy, the temperature and the thermal driving force at current time \(t_{n+1}\). The \(\mathit{Algo}\) operator is constructed such that the incremental variational principle (20) yields as Euler equations consistent algorithmic counterparts of the Euler equations (18) stemming from the rate-type variational principle (17). In what follows two different forms of the \(\mathit {Algo}\) operator are discussed.
2.4.2 Implicit Variational Update
As a first approach, we consider a numerical algorithm that performs an exact incrementation of the internal energy

and an incrementation of the dissipative term according to a backward Euler scheme

see Yang et al. [89]. Here,  denotes an algorithmic expression of the rate of the mechanical state. The incremental potential (19) takes the form
denotes an algorithmic expression of the rate of the mechanical state. The incremental potential (19) takes the form

Then, the incremental saddle point principle (20) gives the Euler equations
The fifth equation represents a time-discrete form of the energy equation and governs the update of the entropy \(\eta\). On the thermal side, the key equations are (23)4 and (23)5

where \(T\) has been eliminated by (23)3 and a positively homogeneous dissipation potential function \(\widehat{\phi}\) of degree \(\ell\) is assumed. By inserting (24)1 into (24)2 an update equation for the temperature \(\theta\) is obtained that includes contributions from thermoelastic heating and heating due to dissipation. The last term in (24)2 contains the algorithmic counterpart of the dissipation (6)2. However, the argument of the dissipation potential function \(\widehat{\phi}\) in (24)2 is scaled by a factor \(\theta/\theta_{n}\) which is a consequence of the implicit variational update. The same scaling factor arises in the dissipative terms of the Euler equations (23)1 and (23)2. Again, we refer to Yang et al. [89]. Finally, we observe that the incremental updates of the mechanical and thermal variables are fully coupled.
2.4.3 Semi-Explicit Variational Update
For the construction of a variational update alternative to the above implicit approach, we propose an approximate incrementation of the internal energy

based on an explicit integration of the second thermal term in the integrand. Note that \(\eta\) and \(\theta\) are given quantities in the above rate-type formulation and as such, they are frozen in the (approximate) evaluation of the integral. By (25) and the incrementation (22) of the dissipative term, the incremental potential (19) takes the form

As pointed out in Sect. 2.4.4, this potential contains an intrinsic operator split. The incremental saddle point principle (20) gives the Euler equations
Comparing this set of equations with (23), we observe essential modifications in (27)3 and (27)4. These equations identify the current thermal driving force \(T\) with the given temperature \(\theta_{n}\) at time \(t_{n}\) and define the current temperature \(\theta\) in terms of the current mechanical state  and the given entropy \(\eta_{n}\) at time \(t_{n}\). The key equations (27)4 and (27)5 on the thermal side can be recast into
and the given entropy \(\eta_{n}\) at time \(t_{n}\). The key equations (27)4 and (27)5 on the thermal side can be recast into

where \(T\) has been eliminated by (27)3 and again a positively homogeneous dissipation potential function \(\widehat{\phi}\) of degree \(\ell\) is assumed. One observes, that in sharp contrast to the governing equation (24)2 stemming from the implicit variational approach, equation (28)2 does not contain the scaling factor. Hence, by the explicit variational update the algorithmically consistent form  of the dissipation (6)2 is obtained. Furthermore, also the dissipative terms in the stress equilibrium (27)1 and Biot’s equation (27)2 do not have the scaling factor. Finally, we observe that as a consequence of the temperature update (28)1 for given entropy \(\eta_{n}\), a decoupled incremental formulation is at hand.
of the dissipation (6)2 is obtained. Furthermore, also the dissipative terms in the stress equilibrium (27)1 and Biot’s equation (27)2 do not have the scaling factor. Finally, we observe that as a consequence of the temperature update (28)1 for given entropy \(\eta_{n}\), a decoupled incremental formulation is at hand.
2.4.4 Operator Split
The two update equations (28) characterize a variational-based staggered algorithmic treatment of dissipative thermomechanics based on the potential \(\widehat{\pi}^{\tau}\) defined in (26): (i) update the mechanical state  as well as the temperature \(\theta\) at frozen entropy \(\eta_{n}\) and given (predicted) thermal driving force \(T=\theta_{n}\), and (ii) update the entropy \(\eta\) as well as the thermal driving force \(T\) which turns out to be identical to the predicted one. Hence, the semi-explicit variational update in the time interval \([t_{n}, t_{n+1}]\) can be seen as a composition of two fractional steps
as well as the temperature \(\theta\) at frozen entropy \(\eta_{n}\) and given (predicted) thermal driving force \(T=\theta_{n}\), and (ii) update the entropy \(\eta\) as well as the thermal driving force \(T\) which turns out to be identical to the predicted one. Hence, the semi-explicit variational update in the time interval \([t_{n}, t_{n+1}]\) can be seen as a composition of two fractional steps

which are both variational. This numerical algorithm falls under the category of incrementally isentropic operator splits, a specific form of which is considered in Armero & Simo [3]. Within the isentropic predictor step we first solve the variational sub-problem

that gives the mechanical state and the temperature at time \(t_{n+1}\). The resulting optimality conditions are the equations (27)1−2 and (27)4. Within a second step, the entropy corrector, the entropy as well as the thermal driving force at time \(t_{n+1}\) are obtained via the variational sub-problem

for given mechanical state  and temperature \(\theta^{*}\) stemming from the isentropic predictor (29). The resulting optimality conditions are the equations (27)3 and (27)5.
and temperature \(\theta^{*}\) stemming from the isentropic predictor (29). The resulting optimality conditions are the equations (27)3 and (27)5.
3 Thermomechanics of Gradient-Extended Dissipative Solids
In this section, we shortly summarize the basic constitutive framework for the thermomechanics of gradient-extended dissipative solids in an abstract setting and adopt the notion of Miehe [49,50]. Let \({\mathcal {B}}\subset\mathbb{R}^{d}\) with \(d \in\{2,3 \}\) be the reference placement (\(d\)-manifold) of a material body \(B\) into the Euclidean space with smooth boundary \(\partial {\mathcal {B}}\). We study the thermomechanical behavior of the body under mechanical as well as thermal loadings in a time interval \({\mathcal {T}}= (0, t_{e}) \subset\mathbb{R}_{+}\). To this end, we focus on a multiscale viewpoint in the sense that we relate dissipative effects at \(({\boldsymbol {X}},t) \in {\mathcal {B}}\times {\mathcal {T}}\) to changes in the microstructure (besides the dissipative effect stemming from heat conduction). In the phenomenological context, we account for these microstructural mechanisms by micro-motion fields that generalize the classical concept of internal variables. The evolution of the related dissipative system is considered to be nonsmooth and therefore the governing equations are written as differential inclusions. Without loss of generality, we assume within our treatment homogeneous solids only, i.e., material properties do not depend on the position \({\boldsymbol {X}}\in {\mathcal {B}}\). In what follows, we denote by \(\dot{(\cdot)} = \frac{\partial}{\partial t} (\cdot)({\boldsymbol {X}},t)\) the material time derivative and by \(\nabla(\cdot) ({\boldsymbol {X}},t)\) the gradient on the reference manifold ℬ. In addition, to keep notation short, we understand the operation \({\boldsymbol{a}}\cdot{\boldsymbol{b}}\) either as duality product between a vector and a one-form \({\boldsymbol{a}}\cdot{\boldsymbol {b}}= a^{c} \, b_{c}\) or as inner product between two vectors \({\boldsymbol{a}}\cdot{\boldsymbol {b}}= a^{c} \, b^{d} \, \delta_{\mathit{cd}}\) and two one-forms \({\boldsymbol{a}}\cdot{\boldsymbol {b}}= a_{c} \, b_{d} \, \delta^{\mathit{cd}}\), respectively. The Kronecker deltas \(\delta_{\mathit{ab}}\) and \(\delta^{\mathit {ab}}\) represent the coefficients of the metric and inverse metric tensor in a Cartesian coordinate system, respectively. Finally, we give the usual definition of a double contraction between two second-order tensors, e.g., for two mixed-variant tensors \({\boldsymbol {A}}: {\boldsymbol {B}}= A^{c}{}_{d} \, B_{c}{}^{d}\).
3.1 Basic Fields of a Solid with Microstructural Changes
3.1.1 Macro-Motion of a Body
Within the geometrically nonlinear theory, the macroscopic motion of the body is described by the macro-motion field
which maps at time \(t \in {\mathcal {T}}\) points \({\boldsymbol {X}}\in {\mathcal {B}}\) of the reference configuration ℬ to points \({\boldsymbol{x}}\in {\boldsymbol {\varphi }}_{t}({\mathcal {B}})\) of the current configuration \({\boldsymbol {\varphi }}_{t}({\mathcal {B}})\). Let \({\boldsymbol {G}}= \delta_{\mathit{AB}} {\boldsymbol {E}}^{A} \otimes {\boldsymbol {E}}^{B}\) and \({\boldsymbol{g}}= \delta_{\mathit{ab}} {\boldsymbol {e}}^{a} \otimes{\boldsymbol{e}}^{b}\) denote the Euclidean metric tensors associated with the reference and current configuration, where the Kronecker symbols refer to Cartesian coordinate systems on both manifolds. The deformation gradient \({\boldsymbol {F}}= D{\boldsymbol {\varphi }}({\boldsymbol {X}},t)\) is defined as the tangent corresponding to the macro-motion (30). Next, the convected current metric \({\boldsymbol {C}}= {\boldsymbol {F}}^{T} {\boldsymbol{g}}{\boldsymbol {F}}\) is introduced, that is often denoted as the right Cauchy-Green tensor. The macro-motion (30) is constrained by a positive Jacobian \(J=\sqrt{\det {\boldsymbol {C}}}>0\) that rules out penetration of matter. With respect to mechanical loading of the solid, the boundary of the reference configuration is decomposed into nonoverlapping parts \(\partial {\mathcal {B}}_{{\boldsymbol {\varphi }}}\) and \(\partial {\mathcal {B}}_{{\boldsymbol {t}}}\) such that \(\partial {\mathcal {B}}=\partial {\mathcal {B}}_{{\boldsymbol {\varphi }}} \cup\partial {\mathcal {B}}_{{\boldsymbol {t}}}\). We prescribe the macro-motion (Dirichlet boundary condition)
and the macro-tractions (Neumann boundary condition) on \(\partial {\mathcal {B}}_{{\boldsymbol {t}}} \times {\mathcal {T}}\) as specified in Sect. 3.3 below.
3.1.2 Micro-Motion of a Body
Microstructural dissipative changes of the body are described by additional fields related to the concept of internal variables. These variables are assembled in the micro-motion field of the solid

The array  with in total \(\delta\) scalar valued entries may contain internal variables of any tensorial rank that describe in a homogenized sense the micro-motion of the material due to structural changes on lower scales. Classical examples for members of
with in total \(\delta\) scalar valued entries may contain internal variables of any tensorial rank that describe in a homogenized sense the micro-motion of the material due to structural changes on lower scales. Classical examples for members of  are damage variables, plastic strains or phase fractions. In addition, we assume all tensorial elements of
are damage variables, plastic strains or phase fractions. In addition, we assume all tensorial elements of  to be Lagrangian objects, i.e., they are not affected by rigid body macro-motions superimposed on the current configuration \({\boldsymbol {\varphi }}_{t}({\mathcal {B}})\). Like in Miehe [49,50], we distinguish between long-range variables
to be Lagrangian objects, i.e., they are not affected by rigid body macro-motions superimposed on the current configuration \({\boldsymbol {\varphi }}_{t}({\mathcal {B}})\). Like in Miehe [49,50], we distinguish between long-range variables  (order parameters) that are governed by PDEs in form of additional balance equations and connected to given length scale parameters, and short-range variables
(order parameters) that are governed by PDEs in form of additional balance equations and connected to given length scale parameters, and short-range variables  that are determined by ODEs and represent the standard concept of local internal variables. We summarize both, long- as well as short-range variables in the array
that are determined by ODEs and represent the standard concept of local internal variables. We summarize both, long- as well as short-range variables in the array

For the treatment of each long-range micro-motion field, we decompose the boundary of the reference configuration into nonoverlapping parts  and \(\partial {\mathcal {B}}_{H}\) such that
and \(\partial {\mathcal {B}}_{H}\) such that  . We prescribe the micro-motion (Dirichlet boundary condition)
. We prescribe the micro-motion (Dirichlet boundary condition)

and the micro-tractions (Neumann boundary condition) on \(\partial {\mathcal {B}}_{H} \times {\mathcal {T}}\) as specified in Sect. 3.2.2 below. Note that the given micro-motion (32) on the Dirichlet boundary is considered to be independent of time. This is because we assume these variables to be “passive” in the sense that the deformation process cannot be driven by externally applying them.
3.1.3 Thermal Driving Force
As a third primary field in the thermomechanics of dissipative materials, we introduce the (macroscopic) thermal driving force field
As outlined in the motivating Sect. 2.3.2, the thermal driving force appears as the dual quantity to the entropy rate and is identified as the temperature. It is governed by the generalized Legendre transformation (48) introduced below. With respect to thermal loading of a heat conducting solid, we decompose the boundary of the reference configuration into nonoverlapping parts \(\partial {\mathcal {B}}_{T}\) and \(\partial {\mathcal {B}}_{q}\) such that \(\partial {\mathcal {B}}= \partial {\mathcal {B}}_{T} \cup\partial {\mathcal {B}}_{q}\). We prescribe the thermal driving force (Dirichlet boundary condition)
and the heat flux (Neumann boundary condition) on \(\partial {\mathcal {B}}_{q} \times {\mathcal {T}}\) as specified in Sect. 3.3 below. The primary fields, namely the macro-motion, the long-range micro-motion and, in case of heat conduction, the thermal driving force are depicted in Fig. 2.
Primary fields in thermomechanics of gradient-extended dissipative solids. At time \(t\), the macro-motion field \({\boldsymbol {\varphi }}({\boldsymbol {X}},t)\) is constrained by Dirichlet and Neumann boundary conditions \({\boldsymbol {\varphi }}= \bar{{\boldsymbol {\varphi }}}\) on \(\partial {\mathcal {B}}_{{\boldsymbol {\varphi }}}\) and \({\boldsymbol {P}}\, {\boldsymbol {n}}_{0} \ni \bar{{\boldsymbol {t}}}\) on \(\partial {\mathcal {B}}_{{\boldsymbol {t}}}\). The long-range micro-motion field  is at time \(t\) restricted by the conditions
is at time \(t\) restricted by the conditions  on
on  and \({\boldsymbol {H}}^{l} \, {\boldsymbol {n}}_{0} \ni {\boldsymbol {0}}\) on \(\partial {\mathcal {B}}_{H}\). Finally, for a heat conducting solid the thermal driving force field \(T({\boldsymbol {X}},t)\) is at time \(t\) constrained by the conditions \(T = \bar{T}\) on \(\partial {\mathcal {B}}_{T}\) and \({\boldsymbol {q}}\cdot {\boldsymbol {n}}_{0} = \bar{q}\) on \(\partial {\mathcal {B}}_{q}\)
and \({\boldsymbol {H}}^{l} \, {\boldsymbol {n}}_{0} \ni {\boldsymbol {0}}\) on \(\partial {\mathcal {B}}_{H}\). Finally, for a heat conducting solid the thermal driving force field \(T({\boldsymbol {X}},t)\) is at time \(t\) constrained by the conditions \(T = \bar{T}\) on \(\partial {\mathcal {B}}_{T}\) and \({\boldsymbol {q}}\cdot {\boldsymbol {n}}_{0} = \bar{q}\) on \(\partial {\mathcal {B}}_{q}\)
3.2 Constitutive Framework to Thermomechanics of Gradient-Extended Solids
3.2.1 Free Energy Function
The free energy storage in continua is governed by a free energy function. We specify it by focusing on simple materials of grade one, i.e., we include as arguments the first gradients of the micro- and macro-motionsFootnote 4

defining the mechanical constitutive state. Together with the temperature, this state is invariant under any rigid body macro-motion superimposed on the current configuration \({\boldsymbol {\varphi }}_{t}({\mathcal {B}})\), i.e., the function (34)1 is objective. We define the energetic contribution to the (contravariant) first Piola-Kirchhoff stress tensor \({\boldsymbol {P}}\) as
and the well known Clausius-Planck inequality takes the form

Here, \({\boldsymbol {P}}^{d} = {\boldsymbol {P}}- {\boldsymbol {P}}^{e}\) denotes the dissipative part of the first Piola-Kirchhoff stress tensor.
3.2.2 Dissipation Potential Functions
Dissipative mechanisms are described by dissipation potential functions. First, we take mechanical effects into account via an objective intrinsic dissipation potential function

at given thermomechanical state  . For generality, we assume in this abstract setting \(\widehat{\phi}_{\mathit{int}}\) to be nonsmooth with respect to
. For generality, we assume in this abstract setting \(\widehat{\phi}_{\mathit{int}}\) to be nonsmooth with respect to  , e.g., positively homogeneous of degree one,
, e.g., positively homogeneous of degree one,  for all \(\gamma>0\), which characterizes in the adiabatic case a rate-independent evolution, see also Footnote 7. With the intrinsic dissipation potential function at hand, we define the dissipative stress
for all \(\gamma>0\), which characterizes in the adiabatic case a rate-independent evolution, see also Footnote 7. With the intrinsic dissipation potential function at hand, we define the dissipative stress
that arises in the reduced Clausius-Planck inequality (35). As suggested in Miehe [50], we assume the evolution equationsFootnote 5 for the micro-motions together with the Neumann boundary conditions

In view of the nonsmoothness of the dissipation potential function (36), we write the micro- and macroscopic balance equations (37) and (40) as differential inclusions, i.e.,  is understood as subdifferential. Considering the global form of (35), doing integration by parts two times and taking into account the homogeneous rate-type Dirichlet boundary condition
is understood as subdifferential. Considering the global form of (35), doing integration by parts two times and taking into account the homogeneous rate-type Dirichlet boundary condition  on
on  according to (32), yields the alternative representation
according to (32), yields the alternative representation

for the intrinsic dissipation, see again Miehe [50]. Note that the micro-force balance (37)1 and the homogeneous Neumann boundary condition (37)2 are outcomes of the variational principle (59) set up below.Footnote 6
As a second contribution to entropy production, we take into account heat conduction via an objective dissipation potential

at given thermomechanical state  . With such a function at hand, we define the material heat flux vector
. With such a function at hand, we define the material heat flux vector

and the well known Fourier inequality takes the form

The inequalities (38) and (39) serve as fundamental physically-based constraints on the dissipation potential functions \(\widehat{\phi}_{\mathit {int}}\) and \(\widehat{\phi}_{\mathit{con}}\). These two conditions are satisfied a priori for dissipation potential functions that are (i) nonnegative  , (ii) zero in the origin
, (ii) zero in the origin  and (iii) convex in
and (iii) convex in  and
and  , respectively.
, respectively.
3.3 Governing Equations for Thermomechanics of Gradient-Extended Solids
We now summarize the governing equations for the thermomechanics of gradient-extended dissipative solids undergoing large deformations. First, we have the balance of linear momentum
where \(\bar{{\boldsymbol {\gamma }}}({\boldsymbol {X}},t)\) and \(\bar{{\boldsymbol {t}}}({\boldsymbol {X}},t)\) are prescribed body force and nominal surface traction fields. The balance of angular momentum \({\boldsymbol {P}}{\boldsymbol {F}}^{T} = {\boldsymbol {F}}{\boldsymbol {P}}^{T}\) is a priori satisfied by the objectivity of the free energy function (34) and the dissipation potential function (36). The evolving micro-motion is governed by the micro-force balance equation

as already given in (37). On the thermal side, the entropy is defined by the local state equation

Finally, the evolution of the entropy is governed by the energy equation

where \(\bar{r}({\boldsymbol {X}},t)\) and \(\bar{q}({\boldsymbol {X}},t)\) are prescribed heat source and material surface heat flux fields. Note that if  is positively homogeneous of degree one,Footnote 7
is positively homogeneous of degree one,Footnote 7 is a set, but the expression
is a set, but the expression  , which represents the intrinsic dissipation, evaluates to a unique value since it coincides with
, which represents the intrinsic dissipation, evaluates to a unique value since it coincides with  , see also Sect. 2.1.2. The equations (40)–(43) generalize the ODEs (3)–(6) for the rheological device to the large-strain continuum setting and include intrinsic gradient-type dissipative effects as well as heat conduction.
, see also Sect. 2.1.2. The equations (40)–(43) generalize the ODEs (3)–(6) for the rheological device to the large-strain continuum setting and include intrinsic gradient-type dissipative effects as well as heat conduction.
4 Variational Principles for Thermomechanics of Gradient-Extended Solids
We now discuss the variational structure of thermomechanics of gradient-extended dissipative solids undergoing large deformations, whose Euler equations were summarized in Sect. 3.3. Again, the starting point is the definition of canonical energy and dissipation potential functions. By means of (generalized) Legendre transformations, different rate-type and incremental mixed formulations are derived.
4.1 Canonical Energy and Dissipation Potential Functionals
We generalize the variational framework for the rheological model presented in Sect. 2 to the large-strain continuum setting of gradient-extended dissipative solids. To this end, based on the internal energy and dissipation potential functions

we introduce the energy and dissipation potential functionals

\(E\) represents the internal energy stored in the entire body ℬ due to coupled micro-macro deformations and thermal effects. The introduced functional \(V\) is related to intrinsic dissipative mechanisms and entropy production due to heat conduction. In analogy to (7), the entropy \(\eta\) as well as the entropy rate \(\dot{\eta}\) are used as canonical thermal variables. On the mechanical side, the constitutive functions (44) are assumed to depend on the constitutive state array  defined in (34)2 that makes those functions a priori objective. Note, that the dissipation potential function \(\widehat{v}\) in general depends on the current state
defined in (34)2 that makes those functions a priori objective. Note, that the dissipation potential function \(\widehat{v}\) in general depends on the current state  as well as explicitly on position and time \(({\boldsymbol {X}},t)\in {\mathcal {B}}\times {\mathcal {T}}\) stemming from a possible inhomogeneous and time-dependent thermal loading, see below.
as well as explicitly on position and time \(({\boldsymbol {X}},t)\in {\mathcal {B}}\times {\mathcal {T}}\) stemming from a possible inhomogeneous and time-dependent thermal loading, see below.
4.2 Energy and Dissipation Functionals in Terms of Temperature
For practical modeling, we transform the above energy and dissipation potential functionals into functionals that depend additionally on the temperature. This we do in analogy to Sect. 2.3.
4.2.1 Variable Dual to Entropy
First, we define the internal energy functional (45)1 by the Legendre transformation

in terms of the mixed internal energy functional

The necessary optimality condition of (46) is the statement (42) which identifies the thermal state variable \(\theta\) as the dual quantity to the entropy \(\eta\), i.e., as the temperature.
4.2.2 Variable Dual to Entropy Rate
In a second step, we define at time \(t\) the dissipation potential functional by a generalized Legendre transformationFootnote 8

in terms of the mixed dissipation potential functional

governed by a dissipation potential function \(\widetilde{\phi}\) and the thermal load functional
Note that by use of the local state equation (42), the mixed dissipation potential functional \(V^{+}\) depends on the current temperature. The maximization in (48) at time \(t\) is performed under the constraint \(T=\bar{T}\) on \(\partial {\mathcal {B}}_{T}\) and defines as necessary condition the evolution of the entropy along with a thermal boundary condition
These equations generalize the local statement (13) for the rheological device to a large-strain continuum setting including intrinsic gradient-type dissipative effects as well as heat conduction. As in Sect. 2.3.2, we call \(T\) the thermal driving force that is dual to the entropy rate \(\dot{\eta}\). The entropy evolution (51)1 must have the form (43)1 and we identify

The first of these conditions is fulfilled for \(T=\theta\) in ℬ if the dissipation potential function is specified as

which is in line with Yang et al. [89], but derived in an alternative way. The second condition (52)2 is satisfied for a volumetric thermal loading function
It remains to find an expression for the thermal surface load function \(\widehat{s}_{T}\). Note that  for \(T=\theta\) in ℬ and we identify from (43)2
for \(T=\theta\) in ℬ and we identify from (43)2
which is fulfilled for a thermal surface load function
4.2.3 Load Functionals
Besides the mixed energy and dissipation potential functionals (47) and (49), we have an external thermomechanical load functional
with decoupled mechanical and thermal contributions. On the mechanical side, we define the load functional
in terms of a given body force field \(\bar{{\boldsymbol {\gamma }}}\) and nominal surface traction field \(\bar{{\boldsymbol {t}}}\). The thermal load functional (50) attains with the identifications (54) and (55) the form
in terms of a given heat source field \(\bar{r}\) and material surface heat flux \(\bar{q}\).
4.3 Fundamental Mixed Variational Principle for Thermomechanics
4.3.1 Rate-Type Formulation
Based on the internal energy and dissipation potential functionals \(E^{+}\) and \(V^{+}\) and the thermomechanical load functional \(P_{\mathit{ext}}\), we define at current time \(t\) the rate-type potentialFootnote 9

with given state  . We write this potential with its internal and external contributions
. We write this potential with its internal and external contributions

in terms of the internal potential density

Recalling the mixed functions (47)2 and (49)2 together with (53) and inserting the necessary condition (42) on the given thermomechanical state, yields a reduced internal potential density of the form

Then, the rates of the macro- and the micro-motion as well as the rate of the entropy and the thermal driving force at current time \(t\) are governed by the variational principleFootnote 10

Here, one has to account for the rate forms of the Dirichlet boundary conditions (31) and (32) for the macro- and micro-motions, i.e.,

as well as for the Dirichlet boundary condition (33) for the thermal driving force. The variational principle (59) is as stated in Yang et al. [89], but extended by a long-range micro-motion field. By the first variation of the functional (57), we have the necessary optimality conditions

for all admissible test functions \(\delta\dot{\eta}\) and  fulfilling homogeneous forms of the Dirichlet boundary conditions. We get the Euler equations
fulfilling homogeneous forms of the Dirichlet boundary conditions. We get the Euler equations

in ℬ along with the Neumann boundary conditions

on \(\partial {\mathcal {B}}_{{\boldsymbol {t}}}\), \(\partial {\mathcal {B}}_{H}\) and \(\partial {\mathcal {B}}_{q}\), respectively. In contrast to (18), the equations are now exclusively governed by variational derivatives of the reduced potential density \(\widehat{\pi}^{+}_{\mathit{red}}\) defined in (58). The central three field equations are the quasi-static mechanical equilibrium

that governs the rate \(\dot{{\boldsymbol {\varphi }}}\) of the macro-motion, the micro-force balance

determining the rate  of the micro-motion and the energy equation
of the micro-motion and the energy equation

for the evolution \(\dot{\eta}\) of the entropy.
4.3.2 Incremental Formulation
Consider a finite time interval \([ t_{n}, t_{n+1}] \subset\overline{{\mathcal {T}}}\) with step length \(\tau= t_{n+1} - t_{n} >0\) and assume all thermomechanical field variables at time \(t_{n}\) to be known. The goal is then to determine all the approximate fields at time \(t_{n+1}\) based on variational principles valid for the time increment under consideration. Subsequently all variables without subscript are understood to be evaluated at time \(t_{n+1}\). We may formulate the incremental potential

where \(E^{+ \tau}\), \(V^{+ \tau}\) and \(P_{\mathit{ext}}^{ \tau}\) are incremental energy, dissipation and load functionals associated with the time interval \([t_{n}, t_{n+1} ]\). These functionals are defined at given state  at time \(t_{n}\). In analogy to the rate-type formulation (57), we rewrite the incremental potential
at time \(t_{n}\). In analogy to the rate-type formulation (57), we rewrite the incremental potential

in terms of an incremental internal potential density \(\widehat{\pi}^{+ \tau}\) which is defined at given state  . Such a function is obtained by a numerical integration algorithm
. Such a function is obtained by a numerical integration algorithm

that has to be constructed in such a way that the subsequent incremental variational principle gives consistent algorithmic counterparts of the Euler equations (61). In what follows, we construct an implicit as well as a semi-explicit numerical integration algorithm, compare Sect. 2.4. As a typical example we consider an integration using the approximations of the rates of state quantities

and the incremental internal potential density

with \(k=n+1\) for an implicit numerical integration algorithm according to (21) and \(k=n\) for a semi-explicit numerical integration algorithm according to (25). In (67) we dropped terms that are associated with previous time \(t_{n}\). Then, defining the incremental load functional
the incremental variational principle

determines all thermomechanical fields at time \(t_{n+1}\). Note, that the optimization has to be done considering the Dirichlet boundary conditions (31), (32) and (33) at time \(t_{n+1}\). The corresponding Euler equations read

in ℬ along with the Neumann boundary conditions

on \(\partial {\mathcal {B}}_{{\boldsymbol {t}}}\), \(\partial {\mathcal {B}}_{H}\) and \(\partial {\mathcal {B}}_{q}\), respectively. As a fundamental difference to the fully implicit numerical algorithm, a semi-explicit update identifies the thermal driving force with the given temperature at time \(t_{n}\). Hence, the scaling factor results in \(T/\theta_{n} = 1\) in ℬ such that the algorithmically consistent form of the intrinsic dissipation defined in (35) and reformulated in (38) is obtained. Especially, the incremental energy equation reads

Additionally, also the dissipative terms in the quasi-static equilibrium (69)1, micro-force balance (69)2 and the boundary conditions (70)1−2 do not contain the scaling factor. However, there are two issues that arise when using the proposed semi-explicit update for a heat conduction process: (i) on the thermal side it might be restricted to homogeneous Neumann boundary conditions (70)3 on the whole boundary, i.e., \(\bar{q} = 0\) on \(\partial {\mathcal {B}}\) and (ii) the Courant-Friedrichs-Lewy (CFL) condition gives, depending on the mesh size associated with the spatial discretization, an upper bound for the time step size \(\tau\) in order to obtain a stable numerical solution.Footnote 11 Note that the semi-explicit update can be seen as an incrementally isentropic operator split that consists of two fractional steps

First, in the isentropic predictor step we optimize the incremental potential (64) with respect to the macro- and micro-motions \({\boldsymbol {\varphi }}\) and  as well as the temperature \(\theta\), i.e.,
as well as the temperature \(\theta\), i.e.,

where the entropy is frozen. Then, the entropy \(\eta\) and the thermal driving force \(T\) are updated via the entropy corrector step

4.4 Mixed Variational Principle with Mechanical Driving Forces
We now put the focus on mixed variational principles for the thermomechanics of gradient-extended dissipative continua, where not only the microstructural variables, but also the corresponding local driving forces are taken into account and considered as additional variables. Following Miehe [49,50], we consider the equivalent representation of the intrinsic dissipation (38)

by the dual intrinsic dissipation potential function \(\widehat{\phi}_{\mathit{int}}^{*}\) depending on the mechanical driving forces

The Legendre transformation

motivates the definition of an extended mixed dissipation potential functional

in terms of the mixed dissipation potential function

which governs the subsequent extended mixed variational principle. The necessary condition of (72) readsFootnote 12

4.4.1 Rate-Type Formulation
Based on the internal energy and dissipation potential functionals \(E^{+}\) in (47) and \(V^{*}\) in (73), we are in the position to formulate a mixed rate-type variational principle that accounts for the mechanical driving forces  . We define at current time \(t\) the rate-type potentialFootnote 13
. We define at current time \(t\) the rate-type potentialFootnote 13

with given state  . We write this potential with its internal and external contributions
. We write this potential with its internal and external contributions

in terms of the extended internal potential density

Recalling the mixed functions (47)2 and (74) and inserting the necessary condition (42) on the given thermomechanical state, yields a reduced internal potential density of the form

Then, the rates of the macro- and micro-motion as well as the rate of the entropy and the thermal and mechanical driving forces at current time \(t\) are governed by the variational principle

Like in (59), one has to account for the Dirichlet boundary conditions (60) and (33). By the first variation of the functional (77), we have the necessary optimality conditions

for all admissible test functions  and
and  fulfilling homogeneous forms of the Dirichlet boundary conditions. We obtain the Euler equations
fulfilling homogeneous forms of the Dirichlet boundary conditions. We obtain the Euler equations

in ℬ along with the Neumann boundary conditions

on \(\partial {\mathcal {B}}_{{\boldsymbol {t}}}\), \(\partial {\mathcal {B}}_{H}\) and \(\partial {\mathcal {B}}_{q}\), respectively. The central three field equations are the quasi-static equilibrium

the micro-force balance

and the energy equation

They are complemented by the inverse definitions (79)5 of the mechanical driving forces which split into three evolution equations

as already given in Miehe [50], where the identity \(T=\theta\) in ℬ from (79)3 has been used. Note carefully that the driving forces  are variables and the variational derivatives in (79)1−2 with respect to \(\dot{{\boldsymbol {\varphi }}}\) and
are variables and the variational derivatives in (79)1−2 with respect to \(\dot{{\boldsymbol {\varphi }}}\) and  are understood in the ordinary sense. Hence, (79)1−2 as well as the boundary conditions (80)1−2 do not represent differential inclusions.
are understood in the ordinary sense. Hence, (79)1−2 as well as the boundary conditions (80)1−2 do not represent differential inclusions.
4.4.2 Incremental Formulation
Within a time interval \([t_{n},t_{n+1}] \subset\overline{{\mathcal {T}}}\) a variational principle can be constructed by the same avenue as outlined in Sect. 4.3.2. Using the algorithmic approximations (66) of rates of state quantities, we get the incremental internal potential density

where again \(k=n+1\) corresponds to a fully implicit and \(k=n\) to a semi-explicit update. In addition, we dropped terms that are associated with previous time \(t_{n}\). Then, with the use of the incremental load functional (68) the incremental variational principle

determines all thermomechanical fields at time \(t_{n+1}\). The corresponding Euler equations in ℬ are time-discrete forms of (79) together with (69)4 stemming from the variation with respect to the temperature \(\theta\). As before, the proposed semi-explicit integration of the rate of the internal energy yields for the scaling factor \(T/\theta_{n} = 1\) in ℬ and one obtains the algorithmically consistent form of the intrinsic dissipation, i.e., the incremental energy equation reads

In addition, the dissipative terms in the time-discrete forms of the quasi-static equilibrium (79)1, the micro-force balance (79)2 and the boundary conditions (80)1−2 as well as the dissipative terms in the time discrete forms of the evolution equations (79)5 do not contain the scaling factor. The isentropic operator split is modified by an additional optimization in the isentropic predictor step with respect to the mechanical driving forces  .
.
4.5 Mixed Variational Principle with Threshold Function
Intrinsic dissipation potential functions are often modeled by the principle of maximum dissipation. For the classical local theories of plasticity, this principle can be traced back among others to the work of Hill [34], see also Moreau [57], Simo [76] and Lubliner [42]. For a general discussion of this principle and its connection to evolution laws governed by dissipation potentials we refer to Hackl & Fischer [30] and Hackl et al. [31,32]. The intrinsic dissipation potential function for thermomechanics is defined by the constrained maximum principle

that includes at given state  a domain of admissible mechanical driving forces which we assume to be smoothFootnote 14
a domain of admissible mechanical driving forces which we assume to be smoothFootnote 14

Clearly, the function  defined in (87) is positively homogeneous of degree one. The set (88) is governed by a threshold function
defined in (87) is positively homogeneous of degree one. The set (88) is governed by a threshold function  , where
, where  is a positive threshold constant that might depend on the given thermomechanical state and \(\widehat{w}\) a level set function that is a gauge, i.e., (i) nonnegative
is a positive threshold constant that might depend on the given thermomechanical state and \(\widehat{w}\) a level set function that is a gauge, i.e., (i) nonnegative  , (ii) zero in the origin
, (ii) zero in the origin  , (iii) convex in
, (iii) convex in  and (iv) positively homogeneous of degree one in
and (iv) positively homogeneous of degree one in  . As a result of (iii), the constrained optimization problem (87) has a unique solution. By the use of the Lagrange multiplier method, we can put (87) into the form
. As a result of (iii), the constrained optimization problem (87) has a unique solution. By the use of the Lagrange multiplier method, we can put (87) into the form

whose necessary optimality condition defines the evolution of the constitutive state

where the Lagrange multiplier \(\lambda\) satisfies classical loading-unloading conditions in Kuhn-Tucker form

This is the typical structure of flow rules associated with rate-independent material behavior. Note that even though  is a subdifferential (see Footnote 7), we get for
is a subdifferential (see Footnote 7), we get for  the unique value
the unique value  . The optimization problem (89) now motivates the definition of a modified mixed dissipation potential functional
. The optimization problem (89) now motivates the definition of a modified mixed dissipation potential functional

in terms of the mixed dissipation potential function

that governs the subsequent modified mixed variational principle.
It should be mentioned that unlike for local theories, the Lagrange multiplier \(\lambda\) for \(\widehat{f} = 0\) cannot be determined at current time by a local consistency condition in terms of rates of the external quantities deformation and temperature. Hence, as, e.g., mentioned in De Borst & Mühlhaus [15] a nonlocal version has to be elaborated, see Sect. 4.5.1.
4.5.1 Rate-Type Formulation
Based on the internal energy and dissipation potential functionals \(E^{+}\) in (47) and \(V^{*}_{\lambda}\) in (92), we are in the position to formulate a mixed rate-type variational principle that accounts for dissipative threshold mechanisms. We define at current time \(t\) the rate-type potential

with given state  . We write this potential with its internal and external contributions
. We write this potential with its internal and external contributions

in terms of the extended internal potential density

Recalling the mixed functions (47)2 and (93) and inserting the necessary condition (42) on the given thermomechanical state, yields a reduced internal potential density of the form

Then, the rates of the macro- and micro-motion as well as the rate of the entropy, the thermal and mechanical driving forces and the Lagrange multiplier at current time \(t\) are governed by the variational principle

Like in (59), one has to account for the Dirichlet boundary conditions (60) and (33). By the first variation of the functional (94) we have the necessary optimality conditions

for all admissible test functions  with \(\lambda+ \delta\lambda\geq0\) in ℬ and
with \(\lambda+ \delta\lambda\geq0\) in ℬ and  fulfilling homogeneous forms of Dirichlet boundary conditions. We obtain the Euler equations
fulfilling homogeneous forms of Dirichlet boundary conditions. We obtain the Euler equations

in ℬ along with the Neumann boundary conditions (80). Note, that the condition \(\widehat{f} \leq 0\) in (98)6 follows from (97)3 if we set \(\lambda= 0\), which necessarily demands \(\delta\lambda\geq0\). On the other hand, by choosing \(\lambda>0\) the test function \(\delta\lambda\) can have any sign and we obtain from (97)3 the equality \(\widehat{f} = 0\), or in summary \(\lambda\widehat{f} = 0\) as given in (98)6. The central three field equations are identical to (81)–(83) and are complemented by the set of evolution equations (98)5 which read

as already given in Miehe [50], where the identity \(T=\theta\) in ℬ from (98)3 has been used. Note that the only formal difference to (84) is that the nonsmooth evolution is not written in form of differential inclusions but is governed by the Karush-Kuhn-Tucker conditions (98)6 containing the scalar variable \(\lambda\). We also mention that the representation (99) is possible because of the assumption of a smooth elastic domain \(\mathbb{E}\), i.e., its boundary only consists of regular points.
In addition, we have for \(\widehat{f} = 0\) the nonlocal consistency conditions

which at current time \(t\) are supplemented by rate forms of the equations (42) and (98)1−2, the evolution equations (98)5 and the rate forms of the Neumann boundary conditions (80) related to the macro- and micro-motion, respectively. To see conditions (100), consider at current time \(t\) a nonzero evolution of the mechanical constitutive state, i.e., \(\lambda_{t} > 0\). Then, the first variation of the dissipation potential functional (92) with respect to the Lagrange mulitplier vanishes
for all \(\delta\lambda\). Next, at time \(t+ \tau\), \(\tau\geq0\) we consider a state with \(\lambda_{t+\tau} \geq0\) and the first variation of the dissipation potential functional (92) with respect to the Lagrange multiplier is nonnegative
for all \(\lambda_{t+\tau} + \delta\lambda\geq0\). Subtracting (101) from (102) and dividing by \(\tau\) yields
for all \(\lambda_{t+\tau} + \delta\lambda\geq0\). For \(\tau\rightarrow0\) we have \(\lambda_{t+\tau} \rightarrow\lambda_{t} >0\), \({\mathcal {O}}(\tau^{2})/\tau\rightarrow0\) and get \(\frac{d}{\mathit{dt}}\widehat{f} = 0\) since \(\delta\lambda\) can have any sign. For \(\tau\) small enough, we assume \(\lambda_{t+\tau} = 0\) and \(\delta\lambda\) must be nonnegative yielding \(\frac{d}{\mathit{dt}}\widehat{f} \leq0\). When summarizing, we arrive at the nonlocal consistency conditions (100). From this condition the Lagrange multiplier field can be determined in terms of the rates \((\dot{{\boldsymbol {\varphi }}}, \dot{\theta})\) of the external fields deformation and temperature.
4.5.2 Incremental Formulation
Within a time interval \([t_{n}, t_{n+1}] \subset\overline{{\mathcal {T}}}\) a variational principle can be constructed by the same avenue as outlined in Sect. 4.3.2. Using the algorithmic approximations (66) of rates of state quantities, we get the incremental internal potential density

where like before \(k=n+1\) corresponds to a fully implicit and \(k=n\) to a semi-explicit update. Again, terms that are associated with previous time \(t_{n}\) are dropped. Then, with the use of the incremental load functional (68) the incremental variational principle

determines all fields at time \(t_{n+1}\). The corresponding Euler equations in ℬ are time-discrete forms of (98) together with (69)4 stemming from the variation with respect to the temperature \(\theta\). Considering the semi-explicit integration, the incrementally isentropic operator split is modified by an additional optimization in the isentropic predictor step with respect to the Lagrange multiplier \(\lambda\geq0\).
5 Representative Model Problems
We now apply the general variational setting for thermomechanics of gradient-extended dissipative solids to complex multifield problems related to evolutions of species content in elastic solids, damage and plasticity. Especially, we highlight a new minimization structure for Cahn-Hilliard diffusion with respect to the species flux. The focus is put on incremental potentials which also inherently contain the proposed operator split. The latter is applied to a numerical example which shows the formation of an adiabatic shear band.
5.1 Cahn-Hilliard Diffusion Coupled with Temperature Evolution
We consider as a first model problem the Cahn-Hilliard theory of diffusive phase separation in a rigid solid coupled with temperature evolution. In the following \(c \colon {\mathcal {B}}\times {\mathcal {T}}\rightarrow[0,1]\) denotes a dimensionless concentration field whose evolution is governed by the local form of conservation of species content

where  is the species flux vector field. To give the concentration field the character of an order parameter
is the species flux vector field. To give the concentration field the character of an order parameter  , we impose homogeneous boundary conditions \(\dot{c} = 0\) on
, we impose homogeneous boundary conditions \(\dot{c} = 0\) on  and \(\partial_{\nabla c} \widehat{\psi}\cdot {\boldsymbol {n}}_{0} = 0\) on \(\partial {\mathcal {B}}_{H}\), see Fig. 2. Hence, the dynamic process is only driven by an initial inhomogeneous distribution \(c_{0}({\boldsymbol {X}})\) of the concentration field in the domain ℬ. In the following, we neglect the phenomenon of thermal diffusion (Soret effect) that is species flow caused by a temperature gradient, see De Groot & Mazur [16] and the recent contribution Nateghi & Keip [60]. The free energy function decomposes into a local, nonlocal and purely thermal contribution
and \(\partial_{\nabla c} \widehat{\psi}\cdot {\boldsymbol {n}}_{0} = 0\) on \(\partial {\mathcal {B}}_{H}\), see Fig. 2. Hence, the dynamic process is only driven by an initial inhomogeneous distribution \(c_{0}({\boldsymbol {X}})\) of the concentration field in the domain ℬ. In the following, we neglect the phenomenon of thermal diffusion (Soret effect) that is species flow caused by a temperature gradient, see De Groot & Mazur [16] and the recent contribution Nateghi & Keip [60]. The free energy function decomposes into a local, nonlocal and purely thermal contribution

where the last term is given in (1). As considered in Cahn & Hilliard [9] we choose
in terms of the threshold and mixing energy parameters \(A\) and \(B\) as well as the diffuse interface parameter \(L\). Note the nonconvexity of \(\widehat{\psi}_{l}\) for \(B>2A\) which is related to phase separation. The evolution of the concentration is driven by the chemical potential \(\mu\) given by
It can be understood as a constitutive representation of a micro-force balance in the sense of Gurtin [26].
5.1.1 Rate-Type Minimization Principles in Isothermal Case
Point of departure is the definition of the energy and dissipation functionals

where \(\widehat{\phi}\) is the smooth dissipation potential function accounting for diffusion mechanisms. A minimization of the corresponding rate-type potential with respect to \(\dot{c}\) then yields as Euler equation the mass balance in the form
Alternative to this setting, we now propose a new minimization formulation in terms of the species flux vector. In line with Miehe et al. [54], we reformulate the rate of the energy functional (108)1 at current concentration

where we inserted the balance equation (105). The dissipation functional is defined as

in terms of the dissipation potential function \(\widehat{\chi}\) which has the simple quadratic form

Here, \(M>0\) is a so-called mobility parameter. Note that \(\widehat{\chi}(\cdot\, ; c)\) is a positively homogeneous function of degree two and its image coincides with half the dissipation in a material element, see below. With the functionals (109) and (110) at hand, we define the potential

with given concentration \(c\). Its minimization with regard to homogeneous Dirichlet-type boundary conditions  and
and  on
on  determines the current species flux field. We obtain the Euler equations
determines the current species flux field. We obtain the Euler equations

They contain necessary compatibility conditions for the given concentration field. As a post-processing step, the current rate \(\dot{c}\) of the concentration is determined via (105). Starting from (35), we now calculate the dissipation whose unique source is diffusion

where we performed integration by parts two times and inserted the balance (105) as well as the homogeneous boundary conditions. Using (112)1, we can express the dual to the species flux vector by the dissipation potential \(\widehat{\chi}\) and obtain with (111) for the dissipation associated with a volume element  .
.
5.1.2 Incremental Formulation with Temperature Evolution
In addition to (111), we consider the conductive dissipation potential function

which is convex in  with \(k>0\) being the thermal conductivity. For the incremental setting, we consider the implicit update of the species concentration
with \(k>0\) being the thermal conductivity. For the incremental setting, we consider the implicit update of the species concentration

and specify the incremental internal potential density (67) as

Here, \(\widehat{\chi}\) is the dissipation potential function (111) related to diffusion mechanisms, where an additional temperature dependence \(M=\widehat{M}(\theta)\) of the mobility parameter is taken into account. We obtain the Euler equations

in ℬ, where we recall the definition of the chemical potential (107) together with (113).
5.2 Thermomechanics of Gradient Damage
We consider as a second application the thermomechanics of a gradient damage model with an elastic stage. The scalar micro-motion field \(d \colon {\mathcal {B}}\times {\mathcal {T}}\rightarrow[0,1]\), referred to as damage variable, measures at a macroscopic point \({\boldsymbol {X}}\in {\mathcal {B}}\) the ratio between an arbitrary oriented area of microcracks and a representative reference surface in which the mentioned crack surfaces are embedded, see, e.g., Lemaitre [39]. In this sense, a value \(d=0\) characterizes an unbroken state, whereas \(d=1\) represents a fully broken state. The irreversibility of micro-cracking is usually expressed by the inequality constraint \(\dot{d}({\boldsymbol {X}},t) \geq0\) on the evolution of the damage variable. The mechanical constitutive state is specified as

and contains the right Cauchy-Green tensor \({\boldsymbol {C}}\), the damage variable as well as its first gradient. In addition, we introduce the elastic right Cauchy-Green tensor \({\boldsymbol {C}}^{e} = {\boldsymbol {F}}^{\mathit{eT}}{\boldsymbol {g}}{\boldsymbol {F}}^{e}\) that is based on the definition of an elastic, stress producing part \({\boldsymbol {F}}^{e}=J_{\theta}^{-1/3} {\boldsymbol {F}}\) of the deformation gradient in terms of a volumetric thermal expansion \(J_{\theta} = \exp[3 \alpha_{T} (\theta-\theta_{0})]\), see Lu & Pister [41]. One can then write \({\boldsymbol {C}}^{e}\) by means of \({\boldsymbol {C}}\) as \({\boldsymbol {C}}^{e} = J_{\theta}^{-2/3} {\boldsymbol {C}}\). A simple model of thermo-gradient-damage at large deformations may then be based on the objective free energy function

where \(\widehat{g}(d)=(1-d)^{2}\) is a degradation function and \(\widehat{\psi}_{\theta}\) the purely thermal contribution as given in (1). Note that the gradient of damage does not arise in this constitutive function but will exclusively enter the dissipation potential function, see below. \(\mu>0\) is the shear modulus and the second parameter \(\delta>0\) models a weak compressibility. Note that only the full elastic energy storage is degraded. From (114) we obtain the tensor functions
that represent constitutive relationships for driving forces.
5.2.1 Rate-Type Formulation Based on Indicator Function
We consider the intrinsic dissipation potential function
as the sum of a nonsmooth local and a smooth nonlocal part
Here, irreversibility of damage is ensured by the indicator function \(I_{+}(\dot{d})\) of the set of positive real numbers defined as
with \(\partial\) denoting the subdifferential. The parameter \(\widehat{c}(\theta)>0\) is a temperature-dependent force-like threshold value for the onset of damage with \(\frac{d}{d \theta} \widehat {c}<0\) and \(l\) a length scale parameter. Note that (116) is a positively homogeneous function of degree one in \((\dot{d}, \nabla\dot{d})\) and hence models for an adiabatic process a rate-independent evolution of damage. In addition, we have the conductive dissipation potential function

where the thermal conductivity is a function of the damage variable and may take the simple form \(\widehat{k}(d) = \widehat{g}(d)k_{b}\) in terms of the heat conduction coefficient \(k_{b} > 0\) of the undamaged bulk. With the constitutive functions (114), (116) and (119) at hand, we specify the internal potential density (58) as
Then, the variational principle (59) determines at current time \(t\) the rates of deformation, damage and entropy as well as the thermal driving force and gives the Euler equations
in ℬ. Observe, that the evolution of the entropy is driven by the rates of damage and gradient of damage. The nonsmooth evolution of the damage variable is governed by the differential inclusion (120)2. From there and the relation (120)3, we conclude for the determination of the rates of deformation and damage the nonlocal consistency conditionsFootnote 15
where \(\dot{\beta}^{e} = \partial^{2}_{d {\boldsymbol {C}}} \widehat{\psi}: \dot{{\boldsymbol {C}}}+ \partial_{\mathit{dd}}^{2} \widehat{\psi}\, \dot{d} + \partial_{d \theta}^{2} \widehat{\psi}\, \dot{\theta}\) and \(\dot{\theta}\) follows from taking the time derivative of the state equation (42). In addition, the rate form
of mechanical equilibrium (120)1 has to be considered together with the boundary conditions
on \(\partial {\mathcal {B}}_{{\boldsymbol {t}}}\) and \(\partial {\mathcal {B}}_{H}\), respectively. (121) are rate forms of the Neumann boundary conditions \({\boldsymbol {P}}^{e} \, {\boldsymbol {n}}_{0} = \bar{{\boldsymbol {t}}}\) on \(\partial {\mathcal {B}}_{{\boldsymbol {t}}}\) and \(\nabla d \cdot {\boldsymbol {n}}_{0} = 0\) on \(\partial {\mathcal {B}}_{H}\) which are outcomes of the variational principle.
From (38) the intrinsic dissipation is found to be
where we used integration by parts and the homogeneous boundary conditions. Hence, thermodynamic consistency is shown.
5.2.2 Incremental Formulation Based on Threshold Function
We specify the array (71) of dissipative driving forces as

where \(\beta\) is the quantity conjugate to \(d\). The Legendre transform of the local part (117)1 of the intrinsic dissipation potential function reads
and enters the incremental internal potential density (85). Note that \(\widehat{\phi}_{l}^{*}\) is the indicator function of the set (88) of admissible driving forces governed by the threshold functionFootnote 16
The latter defines the local intrinsic dissipation potential function by the constrained optimization problem
Then, with the exact time integration of the nonlocal term (117)2 of the intrinsic dissipation potential function
the incremental internal potential density (103) takes the form

As a result, the incremental variational principle (104) gives the Euler equations
in ℬ, which represent time-discrete forms of the general equations (42) and (98). We can reduce this set of equations by expressing for \(k=n\) the dissipative driving force \(\beta= - \beta^{e} + \mu l^{2} \Delta d\) via (125)2 and the Lagrange multiplier \(\tau\lambda= d - d_{n}\) via (125)6 yielding the explicit nonlocal form of the Karush-Kuhn-Tucker conditions
where we recall the definition of the driving force (115)2.
As an alternative to this setting, which is fully rate-independent in the adiabatic case, we may consider a (regularized) viscous over-force formulation based on the smooth dual local intrinsic dissipation potential function, see Footnote 12,
that approaches (122) for the vanishing viscosity limit \(\eta_{f} \rightarrow0\). Then, with (124) the incremental internal potential density (103) takes the form
and the incremental variational principle (86) yields (125)1–(125)5 together with
as Euler equations in ℬ. We can reduce this set of equations by expressing the dissipative driving force \(\beta\) from (125)2 yielding for \(k=n\) the nonlocal (regularized) update equation
for the damage variable.
5.3 Thermomechanics of Additive Gradient Plasticity
As third model problem, we consider a thermomechanically coupled formulation of additive gradient plasticity. Besides the standard metrics \({\boldsymbol {G}}\) and \({\boldsymbol{g}}\), we introduce on the reference configuration the (covariant) plastic metric tensor \({\boldsymbol {G}}^{p} \in\mathit{Sym}_{+}(3)\) that evolves in time starting from the initial state \({\boldsymbol {G}}^{p}({\boldsymbol {X}},t_{0}) = {\boldsymbol {G}}\). Following Miehe et al. [51] and as visualized in Fig. 3, a Lagrangian elastic strain variable may be based on an explicit dependence on the right Cauchy-Green tensor \({\boldsymbol {C}}\), that is the current metric pulled back to the reference configuration, and the plastic metric \({\boldsymbol {G}}^{p}\) in an additive format
where the total and plastic Hencky strain tensors
are introduced. Hence, instead of \({\boldsymbol {G}}^{p}\) we consider in what follows the logarithmic plastic strain \({\boldsymbol {\varepsilon }}^{p}\) as the local internal variable whose evolution from \({\boldsymbol {\varepsilon }}^{p}({\boldsymbol {X}},t_{0}) = {\boldsymbol {0}}\) is governed by a standard flow rule. Note that within this framework the condition of plastic incompressibility \(\det {\boldsymbol {G}}^{p} = 1\) is equivalent to a standard statement of vanishing trace \(\mathop {\mathrm {tr}}{\boldsymbol {\varepsilon }}^{p} = 0\).
Geometry of additive plasticity. a) Definition of the total Hencky strain tensor \({\boldsymbol {\varepsilon }}= \frac{1}{2} \ln {\boldsymbol {C}}\) in terms of the pull-back \({\boldsymbol {C}}\) of the standard current metric \({\boldsymbol{g}}\). b) Definition of the plastic metric tensor \({\boldsymbol {G}}^{p}\) on the reference configuration governing the plastic Hencky strain \({\boldsymbol {\varepsilon }}^{p} = \frac{1}{2} \ln {\boldsymbol {G}}^{p}\) whose evolution is given by a local flow rule. Then, \({\boldsymbol {\varepsilon }}^{e} = {\boldsymbol {\varepsilon }}- {\boldsymbol {\varepsilon }}^{p}\) is the elastic strain measure entering the free energy function
We specify the mechanical constitutive state

which contains a scalar hardening variable \(\alpha\) as well as its first gradient. In the following, we focus on metal plasticity characterized by small elastic but large plastic deformations and consider the free energy function

Here, \(\widehat{\psi}_{e}\) is the purely elastic contribution that is assumed to have the quadratic form
where \(\kappa>0\) and \(\mu>0\) are the bulk and shear modulus, respectively. \(\widehat{\psi}_{p}\) is an isotropic hardening function that also takes into account thermally induced softening. The gradient extension related to a length scale parameter \(l\) is assumed to affect the scalar hardening variable only. The coupled thermoelastic response is modeled by the constitutive function
in line with (1), where also the pure thermal contribution \(\widehat{\psi}_{\theta}\) is specified. Note, that the function (127), known as Hencky energy, is not polyconvexFootnote 17 with respect to the deformation gradient \({\boldsymbol {F}}= D {\boldsymbol {\varphi }}\) in the sense of Ball [4], but rank-one convex for a moderately high elastic deformation range, see Bruhns et al. [8]. Hence, it is applicable to the typical scenario of metal plasticity. With the free energy function (126) at hand, we can derive the tensor functions
that represent constitutive relationships for driving forces. Note the occurrence of the Laplacian term \(\mu l^{2} \Delta\alpha\) in (128)3 that is in line with the approach of Aifantis, see, e.g., Aifantis [1].
5.3.1 Incremental Formulation Based on Threshold Function
We specify the array (71) of dissipative driving forces as

where \(({\boldsymbol {s}}, \beta)\) are the quantities conjugate to \(({\boldsymbol {\varepsilon }}^{p}, \alpha)\). For von Mises-type gradient plasticity we define the yield function
that restricts the set of admissible driving forces according to (88). \(\widehat{y}(\theta)\) is a temperature dependent yield stress function with \(\frac{d}{d\theta} \widehat{y} < 0\). The corresponding intrinsic dissipation potential function is defined by the constrained optimization problem
The intrinsic dissipation follows as
where we used the evolution laws for the plastic strain and hardening variable stemming from (130) and the identities \({\boldsymbol {s}}= -{\boldsymbol {\beta }}^{e}\) and \(\beta= -\beta^{e}\) which are outcomes of the rate-type variational principle (96). Note that the last equality in (131) follows from \(\widehat{w} ({\boldsymbol {s}}, \beta) = |\, {\boldsymbol {s}}\, |+ \sqrt{2/3}\, \beta\) being a gauge, i.e., \(\widehat{w}\) is a positively homogeneous function of degree one with the resulting property \({\boldsymbol {s}}: \partial_{{\boldsymbol {s}}}\widehat{w} + \beta\, \partial_{\beta}\widehat {w} = \widehat{w}\). With (130) the incremental internal potential density (103) is specified as

where \(\widehat{\phi}_{\mathit{con}}\) is the conductive dissipation potential function defined in (119), however, with a constant heat conduction coefficient. Then, the incremental variational principle (104) gives the Euler equations
in ℬ which represent time-discrete forms of the general equations (42) and (98). We can reduce the set of equations (132) by expressing for \(k=n\) the dissipative driving forces \({\boldsymbol {s}}= - {\boldsymbol {\beta }}^{e}\) and \(\beta= - \beta^{e}\) via (132)2 and (132)3, respectively, and the Lagrange multiplier \(\tau\lambda= \sqrt{3/2} \, (\alpha- \alpha_{n})\) via (132)8 yielding the nonlocal form of the Karush-Kuhn-Tucker conditions in strain space
where we recall the definitions of the driving forces (128)2−3.
As an alternative to this setting, which is fully rate-independent in the adiabatic case, we may consider a (regularized) viscous over-force formulation based on the smooth dual intrinsic dissipation potential function
in terms of the threshold function defined in (129). Then, the incremental internal potential density (103) takes the form
and the incremental variational principle (86) yields (132)1−6 together with
as Euler equations in ℬ. This set of equations can again be reduced by expressing the dissipative driving forces \({\boldsymbol {s}}\) and \(\beta\) from (132)2 and (132)3 yielding for \(k=n\) the nonlocal (regularized) update equations
for the plastic Hencky strain as well as the hardening variable. A local finite strain thermoplasticity model that uses the same additive strain kinematics together with the plastic configurational entropy in the sense of Simo & Miehe [79] is proposed by Ulz [86]. For a comparison of rate-independent and rate-dependent formulations in isothermal gradient-plasticity of Fleck-Willis-type we refer to Nielsen & Niordson [64].
5.3.2 Numerical Example: Cross Shear Localization
For softening visco-plasticity of von Mises-type, we analyze the development of shear bands in a rectangular plate \({\mathcal {B}}= (0,L) \times(0,2L)\) with \(L=50\) mm subject to tensile loading under the condition of plane strain. The geometric setup is depicted in Fig. 4. We use the viscous over-force formulation of the mixed large deformation setting from Sect. 5.3.1 above and specify the isotropic hardening function in (126) as
Here, \(\widehat{h}\) is a temperature dependent hardening function which together with the temperature dependent yield stress function is specified as
see Simo & Miehe [79]. The used material parameters are summarized in Table 1. To trigger plasticity in the center, the initial yield stress is reduced by 3% in the element shaded in dark grey in Fig. 4. For simplicity, we neglect the effect of heat conduction which is a reasonable assumption in case of a fast formation of the shear band generated by a high loading rate. We stretch the specimen with a constant displacement rate \(\dot{\bar{u}} = 5\) mm/s within the time interval \({\mathcal {T}}= (0,1)\) s that is divided into 1000 equal increments.Footnote 18 We use the proposed semi-explicit variational update with index \(k=n\) in the incremental internal potential density (133). Since heat conduction is not taken into account, the time step size \(\tau\) is not restricted by the CFL condition. Due to the variational structure, the resulting stiffness matrix within a typical Newton-Raphson iteration step is symmetric. As (global) primary fields we take the macroscopic deformation \({\boldsymbol {\varphi }}\), the scalar hardening/softening variable \(\alpha\) and its dual driving force \(\beta\). The temperature \(\theta\) is calculated via the implicit local equation (132)5. Due to symmetry, only one quarter of the domain is discretized by \(15 \times30\), \(20 \times40\) and \(25 \times50\) quadrilateral finite elements. We use a Q1E4-Q1-Q1 element pairing which bases on a (local) enhancement of the macroscopic displacement gradient according to Simo & Armero [77]. Figure 5 shows contour plots of the equivalent plastic strain \(\alpha\) and the temperature \(\theta\) at final displacement \(\bar{u} = 5\) mm for three different plastic length scale parameters \(l \in\{0.05,0.1,0.2 \}\) mm. Clearly, the specimen experiences a rise in the temperature in the region of plastic dissipation. When increasing the plastic length scale, the equivalent plastic strain \(\alpha\) as well as the temperature \(\theta\) spread over more elements. At the same time, one observes decreasing maximum values of \(\alpha\) and \(\theta\), see also Aldakheel & Miehe [2] and the references cited therein, i.e., Voyiadjis & Faghihi [87]. As widely known, in case of a local theory (\(l=0\) mm) the plastic deformation localizes within one element width. This mesh dependency also manifests itself in the load-displacement curve of the structure as shown in Fig. 6a). In contrast, the regularization provided by the gradient theory yields mesh independent results, see Fig. 6b). There, one also observes the additional softening effect in the nonisothermal case due to locally decreasing yield stresses according to (134)2. At this point, we want to note that Wcisło & Pamin [88] incorporate a gradient-enhanced relative temperature field in their formulation in order to regularize adiabatic thermal softening behavior.
Cross Shear Localization. Geometry and mechanical loading. The process of heat conduction is neglected. Due to the symmetry of the boundary value problem, only the top right quarter of the domain is discretized by finite elements. To trigger plasticity in the center, the initial yield stress \(y_{0}\) is reduced by 3% in the dark grey element
Cross Shear Localization. Contour plots of equivalent plastic strain \(\alpha\) and temperature \(\theta\) at final displacement \(\bar {u} = 5\) mm for a discretization of one quarter of the specimen by \(20 \times40\) finite elements. The chosen plastic length scale parameters are a), d) \(l=0.05\) mm; b), e) \(l=0.1\) mm and c), f) \(l=0.2\) mm
Cross Shear Localization. Load-deflection curves. a) Mesh dependent structural response for local theory with \(l=0\) mm and b) mesh objective response for gradient theory with \(l=0.1\) mm. The dashed line in b) shows the behavior of the specimen under isothermal condition and one observes the influence of thermal softening on the yield stress according to (134)2. Note, that in b) the final displacement is \(\bar{u} = 5\) mm, whereas in a) it is \(\bar{u} = 2.5\) mm
For the used mixed setting of gradient plasticity, alternative finite element formulations are presented in Miehe et al. [53]. Note that in this context the construction of inf-sup stable finite element pairings is a difficult task which in detail has recently been investigated by Krischok & Linder [35]. Especially, our chosen element pairing results in a nonphysical oscillatory behavior of the driving force field \(\beta\). However, this instability seems to have no visible influence on the macroscopic deformation field \({\boldsymbol {\varphi }}\), the scalar plastic strain field \(\alpha\) and the temperature field \(\theta\).
6 Conclusion
We presented a unified framework for the fully coupled thermomechanics of gradient-extended dissipative solids which undergo large deformations. The key of the formulation is the consideration of the entropy and the entropy rate as canonical variables which enter besides the gradient-extended mechanical state and the rate of this state, respectively, the internal energy and dissipation functions. Here, the rate-type formulation of local thermoplasticity outlined in Yang et al. [89] is recovered by the concept of dual variables. Especially, the quantity conjugate to the entropy is rigorously distinguished from the quantity conjugate to the entropy rate. The coupled macro- and micro-balances as well as the energy equation are outcomes of the stated saddle point principle. Within this setting, the entropy is also driven by additional gradient-type dissipative effects. Emphasis was also put on extended variational formulations which incorporate dissipative mechanical driving forces and temperature dependent threshold mechanisms. In addition, we discussed variationally consistent time incrementations and suggested a semi-explicit numerical algorithm that renders the algorithmically consistent form of the intrinsic dissipation. It was shown that this algorithm has the structure of an operator split. A special focus was put on applying the framework to complex multifield problems which are of interest in the thermomechanics of solids. Three model problems, i.e., Cahn-Hilliard diffusion, gradient damage and (additive) gradient plasticity strongly coupled with temperature evolution, showed the capability of the proposed formulation. In a numerical example we studied the formation of a cross shear band under adiabatic condition.
Notes
In case of viscous dissipation we have \(\ell= 2\), see (2).
For a single linear viscous dashpot with current temperature \(\theta\) and entropy \(\eta\), respectively, and rates \((\dot{\varepsilon}, \dot{\eta})\), the internal energy function \(\widehat{e}\) and the dissipation potential function \(\widehat{v}\) take, by evaluating the partial Legendre transformations (10) and (12), the nonintuitive forms
$$ \widehat{e} (\eta) = C \theta_{0} (e^{\eta/C} - 1) \quad \text{and}\quad \widehat {v} ( \dot{\varepsilon}, \dot{\eta}; \theta) = - \frac{\theta^{2}}{2H} \left(\frac{\dot{\eta}}{\dot{\varepsilon}}\right)^{2} \, . $$To keep notation short, we subsequently do not write explicitly the dependence of functions on given states.
For the seek of a compact notation, we assume from now on the presence of long-range variables
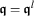 only. In case of short-range variables
only. In case of short-range variables  , the corresponding gradients vanish and no micro-mechanical boundary conditions are prescribed.
, the corresponding gradients vanish and no micro-mechanical boundary conditions are prescribed.Variational Derivative. Throughout this text, we use the notation of variational derivatives
$$ \delta_{z} \widehat{y}(z, \nabla z) = \partial_{z} \widehat{y}(z, \nabla z) - \mathrm{Div}[\, \partial_{\nabla z} \widehat{y}(z, \nabla z) \, ] \, . $$Since
 is assumed to be nonnegative and convex, positive homogeneity of degree one implies that this function is either nonsmooth at
is assumed to be nonnegative and convex, positive homogeneity of degree one implies that this function is either nonsmooth at 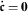 or zero everywhere.
or zero everywhere.The generalized Legendre transformation is conceptually in line with Miehe et al. [52].
To keep notation short, we subsequently do not write explicitly the dependence of functions and corresponding functionals on given quantities.
Note carefully that in case of an adiabatic process, the potential is optimized by minimizing with respect to \(T\) and maximizing with respect to \(\dot{\eta}\), see the motivating Sect. 2.3.3.
A derivation of the CFL condition for the suggested semi-explicit update scheme in case of a heat conduction process is beyond the scope of this paper. For a stability analysis of fractional step methods in thermomechanics we refer to Armero & Simo [3].
Perzyna-type dual dissipation potential function. An important example of a smooth intrinsic dual dissipation potential function is
 (75)
(75)in terms of a function
 that differs from a gauge just by an additive constant and serves as a threshold function in the (adiabatically) rate-independent setting considered in Sect. 4.5 below. \(\eta_{f} > 0\) is a material parameter and \(\langle\cdot\rangle_{+} \colon\mathbb{R} \rightarrow\mathbb{R}_{+}\), \(x \mapsto\frac{1}{2}(|x|+x)\) the ramp function. Note carefully that
that differs from a gauge just by an additive constant and serves as a threshold function in the (adiabatically) rate-independent setting considered in Sect. 4.5 below. \(\eta_{f} > 0\) is a material parameter and \(\langle\cdot\rangle_{+} \colon\mathbb{R} \rightarrow\mathbb{R}_{+}\), \(x \mapsto\frac{1}{2}(|x|+x)\) the ramp function. Note carefully that  defined in (75) is not a homogeneous function and its dual
defined in (75) is not a homogeneous function and its dual  is still nonsmooth in general, i.e.,
is still nonsmooth in general, i.e.,  (76)
(76)We can write (76)1 in the particular form
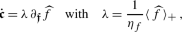
which regularizes the rate-independent structure (90)–(91) to be discussed later in Sect. 4.5. This rate-dependent setting is in line with the formulation of visco-plasticity according to Perzyna [69].
To keep notation short, we subsequently do not write explicitly the dependence of functions and corresponding functionals on given states.
For example, in case of multisurface plasticity one considers a set of \(m \geq2\) intersecting functions \(\widehat{f}_{\alpha}\), \(\alpha=1,\ldots,m\) which generate a convex but maybe nonsmooth domain \(\mathbb{E}\), see, e.g., Simo et al. [80].
These also follow from (100) by using the threshold function defined in (123) and the identifications
$$ \lambda= \dot{d} \quad \text{and}\quad \beta= - \beta^{e} + \mathrm{Div}(\partial_{\nabla \dot{d}} \widehat{\phi}_{\nabla}) $$for the Lagrange multiplier and the nonlocal driving force considered below.
An alternative intrinsic local dissipation potential function may be given by
$$ \widehat{\phi}_{l}(\dot{d}; d, \theta) = \widehat{c}(\theta) d \dot{d} + I_{+}(\dot{d}) \, , $$that in contrast to (117)1 depends explicitly on the given damage state \(d\). We obtain the threshold function
$$ \widehat{f}(\beta; d, \theta) = \beta- \widehat{c}(\theta) d \, , $$which, due to occurrence of the damage variable in the resistance term, corresponds to a model without an elastic stage, i.e., the damage starts to evolve from \(d=0\) at the instant of loading.
Neff et al. [61] introduced an exponentiated Hencky energy which is polyconvex in the two-dimensional case.
Since the process of heat conduction is neglected and the viscosity is chosen very low in order to have a formulation that is close to the nonsmooth setting, the overall thermomechanical material behavior is de facto rate-independent. Hence, the specific loading rate applied on the specimen is practically irrelevant.
References
Aifantis, E.C.: The physics of plastic deformation. Int. J. Plast. 3(3), 211–247 (1987)
Aldakheel, F., Miehe, C.: Coupled thermomechanical response of gradient plasticity. Int. J. Plast. 91, 1–24 (2017)
Armero, F., Simo, J.: A new unconditionally stable fractional step method for non-linear coupled thermomechanical problems. Int. J. Numer. Methods Eng. 35, 737–766 (1992)
Ball, J.M.: Convexity conditions and existence theorems in nonlinear elasticity. Arch. Ration. Mech. Anal. 63(4), 337–403 (1976)
Bartels, A., Bartel, T., Canadija, M., Mosler, J.: On the thermomechanical coupling in dissipative materials: a variational approach for generalized standard materials. J. Mech. Phys. Solids 82, 218–234 (2015)
Berdichevsky, V.L.: Variational Principles of Continuum Mechanics: I. Fundamentals. Springer, Berlin (2009)
Biot, M.A.: Mechanics of Incremental Deformations. Wiley, New York (1965)
Bruhns, O.T., Xiao, H., Meyers, A.: Constitutive inequalities for an isotropic elastic strain-energy function based on Hencky’s logarithmic strain tensor. Proc. R. Soc., Math. Phys. Eng. Sci. 457(2013), 2207–2226 (2001)
Cahn, J.W., Hilliard, J.E.: Free energy of a nonuniform system. I. Interfacial free energy. J. Chem. Phys. 28(2), 258–267 (1958)
Canadija, M., Mosler, J.: On the thermomechanical coupling in finite strain plasticity theory with non-linear kinematic hardening by means of incremental energy minimization. Int. J. Solids Struct. 48, 1120–1129 (2011)
Capriz, G.: Continua with Microstructure, vol. 35. Springer, Berlin (2013)
Carstensen, C., Hackl, K., Mielke, A.: Nonconvex potentials and microstructures in finite-strain plasticity. Proc. R. Soc. Lond. Ser. A 458, 299–317 (2002)
Cosserat, E., Cosserat, F.: Sur la théorie de l’élasticité. Premier mémoire. In: Annales de la Faculté des sciences de Toulouse: Mathématiques, vol. 10, pp. I1–I116 (1896)
Dahlberg, C.F.O., Ortiz, M.: Fractional strain-gradient plasticity. Eur. J. Mech. A, Solids 75, 348–354 (2019)
De Borst, R., Mühlhaus, H.-B.: Gradient-dependent plasticity: formulation and algorithmic aspects. Int. J. Numer. Methods Eng. 35(3), 521–539 (1992)
De Groot, S.R., Mazur, P.: Non-equilibrium Thermodynamics (2013). Courier Corporation
Dimitrijevic, B.J., Hackl, K.: A method for gradient enhancement of continuum damage models. Tech. Mech. 28(1), 43–52 (2008)
Eringen, A.C.: Microcontinuum Field Theories: I. Foundations and Solids. Springer, Berlin (2012)
Fleck, N.A., Hutchinson, J.W.: A reformulation of strain gradient plasticity. J. Mech. Phys. Solids 49(10), 2245–2271 (2001)
Fleck, N.A., Willis, J.R.: A mathematical basis for strain-gradient plasticity theory. Part I: scalar plastic multiplier. J. Mech. Phys. Solids 57(1), 161–177 (2009)
Fohrmeister, V., Bartels, A., Mosler, J.: Variational updates for thermomechanically coupled gradient-enhanced elastoplasticity. Implementation based on hyper-dual numbers. Comput. Methods Appl. Mech. Eng. 339, 239–261 (2018)
Forest, S.: Micromorphic approach for gradient elasticity, viscoplasticity, and damage. J. Eng. Mech. 135(3), 117–131 (2009)
Forest, S., Sievert, R.: Elastoviscoplastic constitutive frameworks for generalized continua. Acta Mech. 160(1–2), 71–111 (2003)
Francfort, G., Mielke, A.: Existence results for a class of rate-independent material models with nonconvex elastic energies. J. Reine Angew. Math. (Crelles J.) 2006(595), 55–91 (2006)
Frémond, M.: Non-smooth Thermomechanics. Springer, Berlin (2013)
Gurtin, M.E.: Generalized Ginzburg-Landau and Cahn-Hilliard equations based on a microforce balance. Physica D 92, 178–192 (1996)
Gurtin, M.E.: On a framework for small-deformation viscoplasticity: free energy, microforces, strain gradients. Int. J. Plast. 19(1), 47–90 (2003)
Gurtin, M.E., Anand, L.: A theory of strain-gradient plasticity for isotropic, plastically irrotational materials. Part I: small deformations. J. Mech. Phys. Solids 53(7), 1624–1649 (2005)
Hackl, K.: Generalized standard media and variational principles in classical finite strain elastoplasticity. J. Mech. Phys. Solids 45, 667–688 (1997)
Hackl, K., Fischer, F.D.: On the relation between the principle of maximum dissipation and inelastic evolution given by dissipation potentials. Proc. R. Soc. A, Math. Phys. Eng. Sci. 464(2089), 117–132 (2007)
Hackl, K., Fischer, F.D., Svoboda, J.: A study on the principle of maximum dissipation for coupled and non-coupled non-isothermal processes in materials. Proc. R. Soc. A, Math. Phys. Eng. Sci. 467, 1186–1196 (2011)
Hackl, K., Fischer, F.D., Svoboda, J.: Addendum. A study on the principle of maximum dissipation for coupled and non-coupled non-isothermal processes in materials. Proc. R. Soc. A, Math. Phys. Eng. Sci. 467, 2422–2426 (2011)
Halphen, B., Nguyen, Q.S.: Sur les matéraux standards généralisés. J. Méc. 40, 39–63 (1975)
Hill, R.: The Mathematical Theory of Plasticity. Oxford University Press, London (1950)
Krischok, A., Linder, C.: A generalized inf–sup test for multi-field mixed-variational methods. Comput. Methods Appl. Mech. Eng. 357, 112497 (2019)
Lancioni, G., Yalçinkaya, T., Cocks, A.: Energy-based non-local plasticity models for deformation patterning, localization and fracture. Proc. R. Soc. A, Math. Phys. Eng. Sci. 471(2180), 20150275 (2015)
Le, D.T., Marigo, J.-J., Maurini, C., Vidoli, S.: Strain-gradient vs damage-gradient regularizations of softening damage models. Comput. Methods Appl. Mech. Eng. 340, 424–450 (2018)
Leismann, T., Mahnken, R.: Comparison of hyperelastic micromorphic, micropolar and microstrain continua. Int. J. Non-Linear Mech. 77, 115–127 (2015)
Lemaitre, J.: A Course on Damage Mechanics. Springer, Berlin (1996)
Lorentz, E., Andrieux, S.: A variational formulation for nonlocal damage models. Int. J. Plast. 15(2), 119–138 (1999)
Lu, S.C.H., Pister, K.S.: Decomposition of the deformation and representation of the free energy function for isotropic thermoelastic solids. Int. J. Solids Struct. 11, 927–934 (1975)
Lubliner, J.: Plasticity Theory (2008). Courier Corporation
Mainik, A., Mielke, A.: Global existence for rate-independent gradient plasticity at finite strain. J. Nonlinear Sci. 19(3), 221–248 (2009)
Mariano, P.M.: Multifield theories in mechanics of solids. In: Advances in Applied Mechanics, vol. 38, pp. 1–93. Elsevier, Amsterdam (2002)
Maugin, G.A.: Internal variables and dissipative structures. J. Non-Equilib. Thermodyn. 15(2), 173–192 (1990)
Maugin, G.A.: The Thermomechanics of Plasticity and Fracture. Cambridge University Press, Cambridge (1992)
Maugin, G.A., Muschik, W.: Thermodynamics with internal variables. Part I. General concepts. J. Non-Equilib. Thermodyn. 19, 217–249 (1994)
Miehe, C.: Strain-driven homogenization of inelastic microstructures and composites based on an incremental variational formulation. Int. J. Numer. Methods Eng. 55, 1285–1322 (2002)
Miehe, C.: A multi-field incremental variational framework for gradient-extended standard dissipative solids. J. Mech. Phys. Solids 59, 898–923 (2011)
Miehe, C.: Variational gradient plasticity at finite strains. Part I: mixed potentials for the evolution and update problems of gradient-extended dissipative solids. Comput. Methods Appl. Mech. Eng. 268, 677–703 (2014)
Miehe, C., Apel, N., Lambrecht, M.: Anisotropic additive plasticity in the logarithmic strain space. Modular kinematic formulation and implementation based on incremental minimization principles for standard materials. Comput. Methods Appl. Mech. Eng. 191, 5383–5425 (2002)
Miehe, C., Hildebrand, F.E., Böger, L.: Mixed variational potentials and inherent symmetries of the Cahn-Hilliard theory of diffusive phase separation. Proc. R. Soc. A, Math. Phys. Eng. Sci. 470(20130641), 1–16 (2014)
Miehe, C., Welschinger, F., Aldakheel, F.: Variational gradient plasticity at finite strains. Part II: local-global updates and mixed finite elements for additive plasticity in the logarithmic strain space. Comput. Methods Appl. Mech. Eng. 268, 704–734 (2014)
Miehe, C., Mauthe, S., Teichtmeister, S.: Minimization principles for the coupled problem of Darcy-Biot-type fluid transport in porous media linked to phase field modeling of fracture. J. Mech. Phys. Solids 82, 186–217 (2015)
Mielke, A.: Free energy, free entropy, and a gradient structure for thermoplasticity. In: Innovative Numerical Approaches for Multi-Field and Multi-Scale Problems, pp. 135–160. Springer, Berlin (2016)
Mielke, A., Roubíček, T.: Rate-independent damage processes in nonlinear elasticity. Math. Models Methods Appl. Sci. 16(02), 177–209 (2006)
Moreau, J.-J.: Application of convex analysis to the treatment of elastoplastic systems. In: Applications of Methods of Functional Analysis to Problems in Mechanics, pp. 56–89. Springer, Berlin (1976)
Mosler, J., Bruhns, O.T.: On the implementation of rate-independent standard dissipative solids at finite strain–variational constitutive updates. Comput. Methods Appl. Mech. Eng. 199(9–12), 417–429 (2010)
Mühlhaus, H.-B., Aifantis, E.C.: A variational principle for gradient plasticity. Int. J. Solids Struct. 28(7), 845–857 (1991)
Nateghi, A., Keip, M.-A.: A thermo-chemo-mechanically coupled model for cathode particles in lithium–ion batteries. Acta Mech. 232, 3041–3065 (2021)
Neff, P., Ghiba, I.-D., Lankeit, J.: The exponentiated Hencky-logarithmic strain energy. Part I: constitutive issues and rank-one convexity. J. Elast. 121(2), 143–234 (2015)
Nguyen, Q.S.: Stability and Nonlinear Solid Mechanics. Wiley, New York (2000)
Nguyen, Q.S.: Variational principles in the theory of gradient plasticity. C. R., Méc. 339(12), 743–750 (2011)
Nielsen, K., Niordson, C.: A finite strain FE-implementation of the Fleck-Willis gradient theory: rate-independent versus visco-plastic formulation. Eur. J. Mech. A, Solids 75, 389–398 (2019)
Oliferuk, W., Raniecki, B.: Thermodynamic description of the plastic work partition into stored energy and heat during deformation of polycrystalline materials. Eur. J. Mech. A, Solids 71, 326–334 (2018)
Ortiz, M., Repetto, E.A.: Nonconvex energy minimization and dislocation structures in ductile single crystals. J. Mech. Phys. Solids 47(2), 397–462 (1999)
Ortiz, M., Stainier, L.: The variational formulation of viscoplastic constitutive updates. Comput. Methods Appl. Mech. Eng. 171, 419–444 (1999)
Peerlings, R.H.J., de Borst, R., Brekelmans, W.A.M., De Vree, J.H.P.: Gradient enhanced damage for quasi-brittle materials. Int. J. Numer. Methods Eng. 39(19), 3391–3403 (1996)
Perzyna, P.: Fundamental problems in viscoplasticity. Adv. Appl. Mech. 9, 243–377 (1966)
Petryk, H.: Incremental energy minimization in dissipative solids. C. R., Méc. 331(7), 469–474 (2003)
Pham, K., Amor, H., Marigo, J.-J., Maurini, C.: Gradient damage models and their use to approximate brittle fracture. Int. J. Damage Mech. 20(4), 618–652 (2011)
Placidi, L., Barchiesi, E.: Energy approach to brittle fracture in strain-gradient modelling. Proc. R. Soc. A, Math. Phys. Eng. Sci. 474(2210), 20170878 (2018)
Placidi, L., Barchiesi, E., Misra, A.: A strain gradient variational approach to damage: a comparison with damage gradient models and numerical results. Math. Mech. Complex Syst. 6(2), 77–100 (2018)
Placidi, L., Misra, A., Barchiesi, E.: Simulation results for damage with evolving microstructure and growing strain gradient moduli. Contin. Mech. Thermodyn. 31(4), 1143–1163 (2019)
Rosakis, P., Rosakis, A.J., Ravichandran, G., Hodowany, J.: A thermodynamic internal variable model for the partition of plastic work into heat and stored energy in metals. J. Mech. Phys. Solids 48, 581–607 (2000)
Simo, J.C.: A framework for finite strain elastoplasticity based on maximum plastic dissipation and the multiplicative decomposition: part I. Continuum formulation. Comput. Methods Appl. Mech. Eng. 66(2), 199–219 (1988)
Simo, J.C., Armero, F.: Geometrically nonlinear enhanced strain mixed methods and the method of incompatible modes. Int. J. Numer. Methods Eng. 33, 1413–1449 (1992)
Simo, J.C., Honein, T.: Variational formulation, discrete conservation laws, and path–domain independent integrals for elasto–viscoplasticity. J. Appl. Mech. 57, 488–497 (1990)
Simo, J.C., Miehe, C.: Associative coupled thermoplasticity at finite strains: formulation, numerical analysis and implementation. Comput. Methods Appl. Mech. Eng. 98, 41–104 (1992)
Simo, J.C., Kennedy, J.G., Govindjee, S.: Non-smooth multisurface plasticity and viscoplasticity. Loading/unloading conditions and numerical algorithms. Int. J. Numer. Methods Eng. 26(10), 2161–2185 (1988)
Stainier, L., Ortiz, M.: Study and validation of a variational theory of thermo-mechanical coupling in finite visco-plasticity. Int. J. Solids Struct. 47, 705–715 (2010)
Su, S., Stainier, L., Mercier, S.: Energy-based variational modeling of fully formed adiabatic shear bands. Eur. J. Mech. A, Solids 47, 1–13 (2014)
Svendsen, B.: On thermodynamic- and variational-based formulations of models for inelastic continua with internal lengthscales. Comput. Methods Appl. Mech. Eng. 193(48–51), 5429–5452 (2004)
Taylor, G.I., Quinney, H.: The latent energy remaining in a metal after cold working. Proc. R. Soc. A, Math. Phys. Eng. Sci. 143, 307–326 (1934)
Timofeev, D., Barchiesi, E., Misra, A., Placidi, L.: Hemivariational continuum approach for granular solids with damage-induced anisotropy evolution. Math. Mech. Solids 26(5), 738–770 (2021)
Ulz, M.H.: A Green–Naghdi approach to finite anisotropic rate-independent and rate-dependent thermo-plasticity in logarithmic Lagrangean strain–entropy space. Comput. Methods Appl. Mech. Eng. 198(41–44), 3262–3277 (2009)
Voyiadjis, G.Z., Faghihi, D.: Thermo-mechanical strain gradient plasticity with energetic and dissipative length scales. Int. J. Plast. 30, 218–247 (2012)
Wcisło, B., Pamin, J.: Local and non-local thermomechanical modeling of elastic-plastic materials undergoing large strains. Int. J. Numer. Methods Eng. 109(1), 102–124 (2017)
Yang, Q., Stainier, L., Ortiz, M.: A variational formulation of the coupled thermo-mechanical boundary-value problem for general dissipative solids. J. Mech. Phys. Solids 54(2), 401–424 (2006)
Ziegler, H.: Some extremum principles in irreversible thermodynamics with application to continuum mechanics. In: Sneddon, I.N., Hill, R. (eds.) Progress in Solid Mechanics, Vol. IV. North–Holland Publishing Company, Amsterdam (1963)
Acknowledgement
Support for this research was provided by the German Research Foundation (DFG) under Grant MI 295/20–1.
Funding
Open access funding provided by Graz University of Technology.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Teichtmeister, S., Keip, MA. A Variational Framework for the Thermomechanics of Gradient-Extended Dissipative Solids – with Applications to Diffusion, Damage and Plasticity. J Elast 148, 81–126 (2022). https://doi.org/10.1007/s10659-022-09884-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10659-022-09884-6











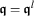 only. In case of short-range variables
only. In case of short-range variables 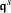 , the corresponding gradients vanish and no micro-mechanical boundary conditions are prescribed.
, the corresponding gradients vanish and no micro-mechanical boundary conditions are prescribed. is assumed to be nonnegative and convex, positive homogeneity of degree one implies that this function is either nonsmooth at
is assumed to be nonnegative and convex, positive homogeneity of degree one implies that this function is either nonsmooth at 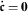 or zero everywhere.
or zero everywhere.
 that differs from a gauge just by an additive constant and serves as a threshold function in the (adiabatically) rate-independent setting considered in Sect.
that differs from a gauge just by an additive constant and serves as a threshold function in the (adiabatically) rate-independent setting considered in Sect.  defined in (
defined in ( is still nonsmooth in general, i.e.,
is still nonsmooth in general, i.e.,