Skip to main content
SpringerLink
Log in

Coordinate-free Characterization of the Symmetry Classes of Elasticity Tensors

  • Published:
Journal of Elasticity Aims and scope Submit manuscript

An Erratum to this article was published on 10 July 2007

Abstract

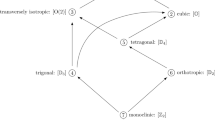
We formulate coordinate-free conditions for identifying all the symmetry classes of the elasticity tensor and prove that these conditions are both necessary and sufficient. Also, we construct a natural coordinate system of this tensor without the a priory knowledge of the symmetry axes.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Backus, G.: A geometrical picture of anisotropic elastic tensors. Rev. Geophys. Space Phys. 8(3), 633–671 (1970)

    ADS  Google Scholar 

  2. Baerheim, R.: Coordinate free representation of the hierarchically symmetric tensor of rank 4 in determination of symmetry. Ph.D. thesis. Geologica Ultraiectina, vol. 159 (1998)

  3. Boehler, J.P., Kirilov Jr., A.A., Onat, E.T.: On the polynomial invariants of elasticity tensor. J. Elast. 34, 97–110 (1994)

    MATH  Google Scholar 

  4. Bóna, A., Bucataru, I., Slawinski, M.A.: Material symmetries of elasticity tensors. Q. J. Mech. Appl. Math. 57(4), 584–598 (2004)

    Article  Google Scholar 

  5. Chadwick, P., Vianello, M., Cowin, S.C.: A new proof that the number of linear elastic symmetries is eight. J. Mech. Phys. Solids 49, 2471–2492 (2001)

    Article  MATH  MathSciNet  ADS  Google Scholar 

  6. Chapman, C.: Fundamentals of Seismic Wave Propagation. Cambridge University Press, Cambridge (2004)

    Google Scholar 

  7. Cowin, S.C., Mehrabadi, M.M.: On the identification of material symmetry for anisotropic elastic materials. Q. J. Mech. Appl. Math. 40, 451–476 (1987)

    Article  MATH  MathSciNet  Google Scholar 

  8. Cowin, S.C., Mehrabadi, M.M.: The structure of the linear anisotropic elastic symmetries. J. Mech. Phys. Solids 40(7), 1459–1471 (1992)

    Article  MATH  MathSciNet  ADS  Google Scholar 

  9. Fedorov, F.: Theory of Elastic Waves in Crystals. Plenum, New York (1968)

    Google Scholar 

  10. Forte, S., Vianello, M.: Symmetry classes for elasticity tensors. J. Elast. 43(2), 81–108 (1996)

    Article  MATH  MathSciNet  Google Scholar 

  11. Forte, S., Vianello, M.: Symmetry classes and harmonic decomposition for photoelasticity tensors. Int. J. Eng. Sci. 35(14), 1317–1326 (1997)

    Article  MATH  MathSciNet  Google Scholar 

  12. Helbig, K.: Foundations of Anisotropy for Exploration Seismics. Pergamon, New York (1994)

    Google Scholar 

  13. Herman, B.: Some theorems of the theory of anisotropic media. Comptes rendues (Doklady) de l’Académie des Sciences de l’URSS. 48(2), 89–92 (1945)

    MathSciNet  Google Scholar 

  14. Lord Kelvin (Thompson, W.): On six principal strains of an elastic solid. Phil. Trans. R. Soc. 166, 495–498 (1856)

    Google Scholar 

  15. Love, A.E.H.: Mathematical Theory of Elasticity. Cambridge University Press, Cambridge, UK (1927)

    MATH  Google Scholar 

  16. Norris, A.N.: Optimal orientation of anisotropic solids. Q. J. Mech. Appl. Math. 59, 29–53 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  17. Mehrabadi, M.M., Cowin, S.C.: Eigentensors of linear anisotropic elastic materials. Q. J. Mech. Appl. Math. 43(1), 15–41 (1990)

    Article  MATH  MathSciNet  Google Scholar 

  18. Rychlewski, J.: On Hooke’s law. Prikl. Mat. Meh. 48(3), 303–314 (1984)

    MathSciNet  Google Scholar 

  19. Rychlewski, J.: Unconventional approach to linear elasticity. Arch. Mech. 47(2), 149–171 (1995)

    MATH  MathSciNet  Google Scholar 

  20. Rychlewski, J.: A qualitative approach to Hooke’s tensors. Part I. Arch. Mech. 52(4,5), 737–759 (2000)

    MATH  MathSciNet  Google Scholar 

  21. Sutcliffe, S.: Spectral decomposition of the elasticity tensor. J. Appl. Mech. 59, 762–773 (1992)

    MATH  MathSciNet  Google Scholar 

  22. Ting, T.C.T.: Generalized Cowin–Mehrabadi theorems and a direct proof that the number of linear elastic symmetries is eight. Int. J. Solids Struct. 40, 7129–7142 (2003)

    Article  MATH  MathSciNet  Google Scholar 

  23. Voigt, W.: Lehrbuch der Kristalphysik. Teubner, Leipzig (1928)

    Google Scholar 

  24. Walpole, L.J.: Fourth-rank tensors of the thirty-two crystal classes: multiplication tables. Proc. R. Soc. Lond. A. 391, 149–179 (1984)

    MATH  ADS  MathSciNet  Google Scholar 

  25. Yang, G., Kabel, J., Van Rietbergen, B., Odgaard, A., Huiskes, R., Cowin, S.C.: The anisotropic Hooke’s law for cancellous bone and wood. J. Elast. 53, 125–146 (1999)

    Article  MATH  Google Scholar 

  26. Hou, Y.-Z., Del Piero, G.: On the completeness of the crystallographic symmetries in the description of the symmetries of the elastic tensor. J. Elast. 25, 203–246 (1991)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Earth Sciences, Memorial University, St. John’s, NL A1B 3X5, Canada

    Andrej Bóna & Michael A. Slawinski

  2. Faculty of Mathematics, “Al. I. Cuza” University, Iasi, 700506, Romania

    Ioan Bucataru

Authors
  1. Andrej Bóna
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ioan Bucataru
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Michael A. Slawinski
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ioan Bucataru.

Additional information

An erratum to this article is available at http://dx.doi.org/10.1007/s10659-007-9126-0.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Bóna, A., Bucataru, I. & Slawinski, M.A. Coordinate-free Characterization of the Symmetry Classes of Elasticity Tensors. J Elasticity 87, 109–132 (2007). https://doi.org/10.1007/s10659-007-9099-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10659-007-9099-z

Key words

Mathematics Subject Classifications (2000)

Search

Navigation