1 Introduction

Open-channel flow over a spanwise heterogeneous bed exhibits different mean flow characteristics compared to that over a flat homogeneous bed. It has been acknowledged that spanwise heterogeneity in open channel flows (OCFs) results in time-averaged streamwise helical motions, known as turbulence driven secondary currents (SCs) [8, 24, 43]. Streamwise-orientated (or longitudinal) ridges are often observed in mobile-bed (e.g. sand and/or gravel) channels and rivers [8]. Several research groups have investigated, both numerically and experimentally, flows over non-uniformly roughened surfaces in the spanwise direction in open-channel, closed-channel or boundary-layer flows e.g. Bai et al. [3], Hwang and Lee [11], Stoesser et al. [32], Wang and Chen [38, 39] or artificial ridges of various shape, e.g. trapezoidal [23], triangular [43, 44], rectangular [22, 36], or converging/diverging riblet patterns [27].

Colombini and Parker [8] distinguish three types of channel bed heterogeneities. The first type is topographical heterogeneity, referring to uniform beds with a lateral variation in the bed elevation. The second type is roughness heterogeneity, referring to topographically homogeneous beds with a lateral variation in the bed roughness. The third type relates to beds exhibiting a combination of the first and second types of spanwise heterogeneities, for example, roughened ridges overlaying a smooth bed. In the first type, upward fluid motion occurs over ridges while transverse flow in the near-bed region takes place from the trough to the crest [23]. The upward motion in the second type is found over strips of low roughness while transverse flow in the near-bed region is from the rougher strips to the less-rough strips [33]. In the third type, the two mechanisms may coexist. For example one may speculate that the roughened ridges on a smooth bed may lead to the elimination of SCs as significant roughness induces downward motion while topographical ridges induce upward motion.

Since spanwise heterogeneity has been mainly found to generate SCs with upflows/downflows and low/high-momentum pathways, various bed surfaces have been examined by researchers to investigate the appearance of SCs in flows over different types of spanwise heterogeneity. Hwang and Lee [11] investigated boundary-layer flows over a smooth surface covered with smooth longitudinal rectangular ridges (i.e., first type of spanwise heterogeneity) and suggested that the upward motions over the ridges are primarily attributed to the considerable energy production above the ridge. Stoesser et al. [32] performed a large-eddy simulation of open-channel flow over spanwise alternating rough and smooth strips (i.e., second type spanwise heterogeneity) where the width of the rough/smooth patches equals the water depth, concluding that turbulence is enhanced over rough strips and suppressed over smooth strips due to the presence of the secondary currents. In addition, the bed shear stresses over the rough strips were found to be approximately four times greater than that over the smooths strips. Yang and Anderson [42] studied closed-channel turbulent flow over surfaces with roughened ridges (comprising pyramidal roughness elements connected together in the streamwise direction) on a smooth bed, which are considered to be the third type of spanwise heterogeneity. The authors classified spanwise heterogeneous roughness into two categories which appear to be the result of the spanwise spacing s relative to the channel half height D: when \({s}/{{D}}\ge 1\), secondary currents occupy the entire depth of the outer layer (half-channel height); while for \({s}/{D}\le 0.2\), the secondary currents are smaller than the channel half height, with the turbulence statistics of the overlying flow exhibiting similar characteristics to those of a homogeneous flow.

Secondary currents in the presence of spanwise bed heterogeneities are the result of turbulent stress gradients and/or anisotropy (known as Prandtl’s second kind). They appear in time-averaged velocity fields as a pair of symmetric streamwise rotational motions along the ridge in the first type of spanwise heterogeneity. Zampiron et al. [43] inferred a new feature from pre-multiplied velocity spectra named ‘secondary current instability’ in open channel flows with smooth ridges overlying a rough bed. They further examined this feature via the distribution of the two-point correlation function in a cross-section, and the reconstruction of a low-order representation of the instantaneous velocity field from proper orthogonal decomposition, demonstrating that such instability is associated with low-amplitude meandering of the low-momentum region above ridges. In other words, the low-momentum region meandering exhibits (quasi)periodic unsteadiness. Wangsawijaya et al. [41] investigated the manifestation of secondary flows in the instantaneous flow field in boundary-layer flows using spanwise alternating rough and smooth patches and found that the streamwise wavelength of the meandering of the low-momentum pathways is a function of the spanwise wavelength of heterogeneity. Wangsawijaya and Hutchins [40] further confirmed that the most prominent meandering is found when the spanwise spacing between patches is approximately equivalent to the boundary-layer thickness and proposed an appropriate scaling (strips width or boundary-layer thickness) in different cases. Complementing the length scales, it is worth mentioning that for open channel flows Zampiron et al. [43] found that the wavelength of the secondary current instability is proportional to the vorticity thickness as well as to the spanwise spacing of the ridges.

Although the instability of secondary currents has been inferred in the previous studies from energy spectra [1, 40, 43], decomposed flow field on cross-sections [37, 43], and conditionally averaged flow field on wall-normal planes [15, 40], fewer studies attempted to quantify the periodicity of such time-dependent and spatially varying behaviour. This paper reports on large-eddy simulations of open-channel flow over streamwise ridges at two different spacings, representing the first type (i.e., topographical) of spanwise heterogeneity, together with a complementing open-channel flow over a smooth wall. The central goal of this study is to identify and quantify the meandering of the elongated high- and low-momentum streaks while considering them as instantaneous manifestation of secondary currents.

2 Numerical Framework

The open-source large eddy simulation code Hydro3D is employed to perform the simulations. The code has been validated successfully for and applied to a number of open-channel and pipe flows in which secondary currents are prominent e.g. Liu et al. [17, 18] and Nikora et al. [26]. The code solves the spatially filtered Navier–Stokes equations in an Eulerian framework reading:

$$\nabla \cdot {\mathsf{u}} = 0$$
(1)
$$\frac{\partial {\mathsf{u}}}{\partial {t}}=-\frac{1}{\rho }\nabla {{{p}}}- {{\mathsf{u}}}\cdot \nabla {{\mathsf{u}}}+\nu \nabla ^{2}{{\mathsf{u}}}-\nabla \tau +{{\textbf{f}}}+{{\textbf{g}}}$$
(2)

where u denotes the filtered resolved velocity field, p denotes the pressure, \(\nu\) is the kinematic viscosity, \({{\textbf{f}}}\) represents the volume force of the immersed boundary method exerted to the fluid and g is the gravitational acceleration. The sub-grid scale stress tensor, \(\tau\), resulting from unresolved small scale fluctuations, is approximated by the wall-adapting local eddy-viscosity (WALE) model [25] for all cases presented in this paper. Hydro3D is based on finite differences with staggered storage of three-dimensional velocity components and central storage of pressure on Cartesian grids which, together with the use of immersed boundaries, allows for fast and efficient execution of the solver despite the complexity of the flow domain [7, 16, 20, 29].

The spatially filtered governing equations Eqs. (1) and (2) are advanced in time by the fractional-step method [6]. Firstly, convection and diffusion terms are solved via an explicit three-step Runge–Kutta predictor. Fourth- and second-order central differences scheme are used to calculate convective and diffusive terms for presented cases, respectively. The non-divergence free velocity \(\widetilde{{{\textbf{u}}}}\) is predicted via the pressure gradient from the previous time step:

$$\begin{aligned} \frac{\widetilde{{{\textbf{u}}}}-{{\textbf{u}}}^{l-1}}{\Delta t}=\nu \alpha _{l}\nabla ^{2}{{\textbf{u}}}^{l-1}-\alpha _{l}\frac{1}{\rho }\nabla p^{l-1}-\alpha _{l}[\left( {{\textbf{u}}}\cdot \nabla \right) {{\textbf{u}}}] ^{l-1}-\beta _{l}[\left( {{\textbf{u}}}\cdot \nabla \right) {{\textbf{u}}}] ^{l-2} \end{aligned}$$
(3)

where l (\(=\,1,2,3\)) represents the Runge–Kutta sub-ste, and \(l=1\) refers to the values from previous time step, \(\alpha _{l}\) and \(\beta _{l}\) are the Runge–Kutta coefficients.

An additional correction to \(\widetilde{{{\textbf{u}}}}\) is necessary when external forces are exerted. For the cases presented in this study, the longtudinal ridges inside the fluid are accomplished using the immersed boundary method (IBM) described by Kara et al. [12]. This is a direct forcing IBM introduced by Fadlun et al. [10] and refined by Uhlmann [35]. The source term \({\textbf{f}}\) enforces the fluid to have the solid velocity at its location fulfilling the no-slip condition:

$$\begin{aligned} \widetilde{{{\textbf{u}}}}^{*}=\widetilde{{{\textbf{u}}}}+{\textbf{f}}\Delta t \end{aligned}$$
(4)

Secondly, a projection scalar function \({\widetilde{p}}\) is obtained from the Poisson equation via the multigrid iteration scheme [5]:

$$\begin{aligned} \nabla ^{2} {\widetilde{p}}=\frac{\nabla \cdot \widetilde{{{\textbf{u}}}}^{*}}{\Delta t} \end{aligned}$$
(5)

Equation (5) is iterated until the predicted intermediate velocity field \(\widetilde{{{\textbf{u}}}}^{*}\) satisfies the incompressiblity condition.

Then the solution velocity field at the current step is solved as:

$$\begin{aligned} {{\textbf{u}}}^{t}=\widetilde{{{\textbf{u}}}}^{*}-\Delta t \frac{1}{\rho }\nabla {\widetilde{p}} \end{aligned}$$
(6)

and pressure field is updated as:

$$\begin{aligned} p^{t}=p^{t-1}+{\widetilde{p}}-\frac{\nu \Delta t}{2}\nabla ^{2}{\widetilde{p}} \end{aligned}$$
(7)

Water surface deformations are captured by the level set method proposed by Osher and Sethian [28]. The level set method introduces a level set signed distance function \(\phi\):

$$\begin{aligned}{} & {} \phi ({{\textbf{x}}},t)<0 \quad if \quad {{\textbf{x}}}\in \Omega _{\mathrm{gas}} \end{aligned}$$
(8a)
$$\begin{aligned}{} & {} \phi ({{\textbf{x}}},t)=0 \quad if \quad {{\textbf{x}}}\in \Gamma \end{aligned}$$
(8b)
$$\begin{aligned}{} & {} \phi ({{\textbf{x}}},t)>0 \quad if \quad {{\textbf{x}}}\in \Omega _{\mathrm{liquid}} \end{aligned}$$
(8c)

where \(\Omega _{\mathrm{gas}}\) and \(\Omega _{\mathrm{liquid}}\) represent air and fluid phases, respectively and \(\Gamma\) denotes the interface. The movement of the interface is expressed in a pure advection equation of the form:

$$\frac{\partial {\phi }}{\partial {t}}+{{\mathsf{u}}}\cdot \nabla \phi =0$$
(9)

A multi-phase transition zone is accomplished via a Heaviside function to handle the numerical instabilities which could occur due the density and viscosity discontinuities across the interface. In addition, the re-initialization technique proposed by Sussman et al. [34] is employed to maintain \(|\nabla \phi = 1 |\) as time proceeds. A fifth-order weighted essentially non-oscillatory (WENO) scheme is chosen to discretise Eq. (9) to ensure stability and minimize numerical dissipation for this pure advection equation. The validity of the level set method in the current code was established previously for various complex flows such as open-channel flows over a cube or square bars [19, 21] or for flows past bridge abutments [13, 14], respectively.

The code is parallelised and the computational domain is split into a large number of subdomains. Standard message passing interface (MPI) is used to accomplish the communications between adjacent subdomains [30]. This technique manages and balances the computational load which allows the use of sufficiently fine grids near the ridges.

3 Computational Setup

The setup of the simulations is selected in analogy to the series of laboratory experiments undertaken by Patella [31]. In the experiments, streamwise ridges with square cross-sections were attached to the bed of the flume. Both the channel bed and the ridges’ surface were hydraulically smooth.

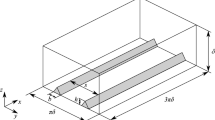
Figure 1 shows a sketch of the computational domain of one of the large-eddy simulations. The LES focuses on three cases: case s000 is a smooth-bed channel (without ridges), in case s024 ridges are half water depth apart (\(s/H=0.5\), where s is the spanwise spacing between the ridges and H is the mean water depth) and case s096 features ridges two water depths apart (\(s/H=2\)). The geometrical, hydraulic and computational details of the three cases are provided in Table 1, in which h and \(b=h/4=H/24\) are the height and width of the rectangular ridges, respectively. All cases are at the same moderate bulk Reynolds number \(Re_{b} = U_{bulk}H/\nu = 17{,}760\) (based on the average water depth and bulk velocity \(U_{bulk}\), i.e., cross-sectional mean velocity) and Froude number \(Fr = U_{bulk}/\sqrt{gH}=0.54\). The streamwise length of the computational domains for all studied cases was chosen to be \(L_{x}=42.6H\) (the potential effect of the domain length on the simulations will be discussed at the end of this section). The width \(L_{y}\) of the domain varies in accordance with the ridge spanwise spacing s, being \(L_{y}=3H\) in s024, to include 6 longitudinal ridges within the domain, and \(L_{y}=6H\) for s096 and s000, to include 3 longitudinal ridges in the s096 case. The wall-normal height of the domain \(L_{z}\) is 1.25H for all cases, including an upper adjacent air region 0.25H high. Periodic boundary conditions are applied in streamwise and spanwise directions, while the no-slip boundary condition is applied at the channel bed. The ridges are represented with the immersed boundary method. The computational domains are discretised using uniform grids in all cases. The average grid spacing in wall units \(\Delta x^{+}\), \(\Delta y^{+}\), \(\Delta z^{+}\) as well as the ridges height \(h^{+}\) (Table 1), are calculated using the LES-computed double-averaged pressure gradient \({\text{d}}{\widehat{P}}/{\text{d}}x\). The flows are driven by the streamwise pressure gradient which is adjusted at each time step to maintain a constant bulk velocity. The friction Reynolds number \(Re_{\tau }\) provided in Table 1 is calculated using the shear velocity \(u_{*}=[(1/\rho )({\text{d}}{\widehat{P}}/{\text{d}}x)H]^{0.5}\). Throughout this paper, the velocity components in the streamwise (x), spanwise (y) and wall-normal (z) directions are denoted as u, v and w, respectively.

Fig. 1
figure 1

Sketch of computational setup

Full size image
Table 1 Computational details of the three LES simulations
Full size table

The LES are run for a period of at least 50 eddy turnover times (i.e., \(H/u_{*}\)), equivalent to over 800 \(H/U_{bulk}\), to collect first and second order turbulence statistics. The power spectral density \(F_{uu}(k_{x})\) and the pre-multiplied spectrum \(k_{x} F_{uu}(k_{x})\) of the streamwise velocity fluctuations for the smooth channel case (s000) are presented in Fig. 2, where \(k_{x}=2\pi /\lambda _{x}\) denotes the streamwise wavenumber and \(\lambda _{x}\) denotes the streamwise wavelength. The power spectral density in Fig. 2a reveals that over a wide range of wavenumbers the spectral amplitudes follow a power law, within which energy is transferred from large-scales to small-scales. The energy transfer does not follow the Kolmogorov \(-5/3\) law but rather a \(-1\) slope which is probably due to one of the two reasons (or both): (1) the Reynolds numbers in this study are quite low for a clear emergence of the inertial subrange; or/and (2) part of the inertial subrange occurs within the filtered range of wave numbers, i.e., at \(k_{x}H>20\) (Fig. 2a, b). The sharp drop-off at \(k_{x}H>20\) is a result of the subgrid-scale model removing efficiently energy from the small scales. A noticeable peak at a wavelength of around 42H is observed in the pre-multiplied spectrum (Fig. 2b), which is an energy spike possibly resulting from the periodic boundary and the (insufficient) length of the domain, which artificially reduces the extent of the very-large-scale motions (VLSMs) [4, 9, 43, 45]. However, it can be seen that the pre-multiplied spectrum still captures large-scale motions (LSMs) at around 3H rather well. Moreover, it has been demonstrated by Zampiron et al. [43] that VLSMs are absent when streamwise ridges are attached to the bed and secondary current instability also features smaller wavelengths. Therefore, the presented simulations are considered to be able to resolve the length scales of interests.

Fig. 2
figure 2

Spectral analysis of case s000. a Streamwise- and spanwise averaged power spectral density of streamwise velocity fluctuations obtained at \(z=0.5H\). Dashed line is the Kolmogorov’s slope (\(-5/3\)). Dashed-dotted line represents the slope (\(-1\)); b: Streamwise- and spanwise averaged pre-multiplied spectra at \(z=0.5H\)

Full size image

4 Results and discussion

4.1 Time-averaged flow and velocity statistics

Figure 3 shows the effects of ridges on time-averaged velocity fields. Double-averaged streamwise velocity profiles and contours of streamwise velocity distributions together with vectors on y–z plane from the simulations show good agreement with the experimental data, confirming the adequacy of the grid, discretisation schemes and boundary conditions. Velocity contours in cross-sections exhibit significant spanwise variations which are most pronounced close to the wall for the cases with ridges. Low momentum pathways are observed above the ridges, while high momentum pathways appear at the mid-intervals between ridges. The secondary current cells occupy the entire flow depth for the larger spacing (\(s=2H\), s096), whereas the cells are confined within \(z/H<0.5\) for the smaller spacing (\(s=0.5H\), s024). This finding is consistent with previous studies of Yang and Anderson [42] for closed channels and Zampiron et al. [43] for OCFs. Upflows and downflows are observed over the top of the ridges and at the mid-intervals between ridges, respectively, reflecting the presence of counter-clockwise cells on the one side of each ridge, and clockwise cells on the other side.

Fig. 3
figure 3

Distributions of time-averaged velocities. a Streamwise- and spanwise-averaged streamwise velocity profile for smooth open-channel flow; d and g Streamwise-averaged streamwise velocity over a ridge. Solid lines: LES. Open circles: Experimental measurements [31]. b, e and h Contours of streamwise velocity \({\overline{u}}/U_{bulk}\) with vectors (\({\overline{v}}/U_{bulk}\),\({\overline{w}}/U_{bulk}\)) from LES; c, f and i Contours of streamwise velocity \({\overline{u}}/U_{bulk}\) with vectors (\({\overline{v}}/U_{bulk}\),\({\overline{w}}/U_{bulk}\)) from experiments [31]. Gray shade indicates the height of the ridges

Full size image

Figure 4 presents profiles and contours of the second-order statistics in terms of turbulent kinetic energy (TKE) and Reynolds stresses for all three studied flows. The peak of turbulent kinetic energy is found in the troughs of the s096 case (wide spacing), the magnitude of which is similar to that close to the smooth bed without ridges (i.e., s000) (see the solid line in Fig. 4a and the dashed line in Fig. 4i). Turbulent energy appears to be stronger in the inter-ridge region at larger spacing than at smaller spacing, probably due to stronger suppression of turbulent fluctuations by secondary currents at smaller spacing. High values of turbulent kinetic energy are found also at the top of the ridges in both s024 and s096 cases, and in the trough of s024, which are all around \(75\%\) of the peak observed in the trough of s096. In the s024 case, the two profiles (one over the ridge and one over the trough) show noticeable differences up to \(z/H=0.6\) before they collapse onto a single profile up to the water surface, whilst in s096, the turbulent kinetic energy over the ridge is always greater than that over the trough over the entire water depth above the ridge. This is consistent with the findings in flow over the third type spanwise heterogeneity (i.e., combining effects of topographic and roughness heterogeneities) from Yang and Anderson [42]. In the smaller spacing case, the outer region of the flow is not altered much by the ridges (which can also be seen in the contours plotted in Fig. 4f). On the other hand, in case s096, the presence of the ridges is ‘felt’ throughout the water depth evidenced by the fact that the profiles of the TKE do not collapse and the contours show obvious variation in the spanwise direction. The distribution of the primary Reynolds stress generally resembles that of the turbulent kinetic energy, whereas it is further strengthened in the upflow region above the ridges. It has been demonstrated by Nezu and Nakagawa [23] that the spanwise heterogeneity of the Reynolds stresses induced by spanwise bed heterogeneity (i.e., ridges) is the key to sustaining the secondary currents.

Fig. 4
figure 4

Distributions of second-order statistics: a, b, e, f, i and j streamwise-averaged turbulent kinetic energy; and c, d, g, h, k and l streamwise-averaged Reynolds stress. For the cases with ridges, solid lines show profiles over the ridges, whereas dashed lines show profiles at the troughs

Full size image

4.2 Secondary current instability and meandering of its instantaneous patterns

Figure 5 presents contours of the instantaneous streamwise velocity fluctuation (time- and spatially-averaged streamwise velocity \(\langle {\overline{u}} \rangle\) is subtracted) in wall-normal x–y planes at the height of the time-averaged centre of the secondary cells (for s024 at \(z/H=0.16\) and for s096 at \(z/H=0.5\)). The contours visualise the coherence of the flow in the streamwise direction in the form of large-scale streamwise oriented low- and high-speed streaks. Whilst the large-scale motion over the smooth bed is not confined laterally, its location is predefined above and between ridges in both s024 and s096 due to the presence of secondary motions. Elongated structures and their apparent meandering, i.e., lateral movement, of the low and high momentum regions are noticeable in all cases. However, the meandering of the low-speed structures is visibly locked within the troughs in s024 and s096, while the meandering of the structures in s000 appears to be more random.

Fig. 5
figure 5

Distributions of instantaneous streamwise velocity fluctuations at a and c \(z/H=0.5\) and b \(z/H=0.16\). Dashed horizontal lines indicate the spanwise locations of the ridges; Black solid lines depict \((u-\langle {\overline{u}} \rangle )/u_{*}=0\)

Full size image

In order to investigate the meandering of instantaneous manifestations of the secondary currents, two-point correlations in wall-parallel x–y planes at the height of the SC cell centre are computed:

$$\begin{aligned} R_{\mathrm{uu}}(x_{\mathrm{r}},y_{\mathrm{r}},\Delta x,\Delta y)=\frac{\sum \nolimits ^{t} u'(x_{\mathrm{r}},y_{\mathrm{r}},t)u'(x_{\mathrm{r}}+\Delta x,y_{\mathrm{r}}+\Delta y,t)}{\left( \sum \nolimits ^{t} [u'(x_{\mathrm{r}},y_{\mathrm{r}},t)]^{2}\right) ^{0.5}\left( \sum \nolimits ^{t} [u'(x_{\mathrm{r}}+\Delta x,y_{\mathrm{r}}+\Delta y,t)]^{2}\right) ^{0.5}} \end{aligned}$$
(10)

where \((x_{\mathrm{r}}, y_{\mathrm{r}})\) represents the coordinate of a reference point. As the two-point correlation function reflects the spatial correlations of the examined field, the reference coordinates are chosen to be the centre of one of the clockwise SC cells (s024: \(y'_{r}=0.083H\) and \(z_{r}=0.16H\); s096: \(y'_{r}=0.33H\) and \(z_{r}=0.5H\) where \(y'=0H\) denotes the spanwise location of an arbitrary ridge). Contours of the two-point correlation in space are presented in Fig. 6. In s024 and s096, an area with positive correlation is observed around the reference point, and a symmetric area in relation to the spanwise location of the ridge with negative correlation is observed, appearing on the other side of the ridge. The correlation extends to multiple pairs of secondary current cells at the large spacing (s096), while it is limited to a single ridge at the smaller spacing (s024). A streamwise repeating pattern of negative-positive correlation can be observed for s096, but it is absent for s024. This streamwise-repeating pattern suggests a strong periodicity in the streamwise direction for the velocity fluctuations \(u'\), indicating that the instantaneous manifestations of secondary currents meander in the spanwise direction which echos the behaviour observed in Fig. 5. A similar streamwise-repeating pattern in two-point correlation distributions is also observed by Kevin et al. [15] and Wangsawijaya et al. [41], in which the bed surface featured spanwise heterogeneity in boundary layer flows. The length of one negative-positive correlation in the streamwise direction observed in Fig. 6b is around 10H, which can be used as an estimate for the streamwise wavelength of such flow periodicity associated with the meandering of secondary currents. The two-point correlation distribution in cross-sections agrees well with that of Zampiron et al. [43], hence it is not shown here for brevity.

Fig. 6
figure 6

Distributions of two-point correlation function \(R_{uu}\) at a \(z/H=0.16\) b \(z/H=0.5\). Dashed horizontal lines indicate the spanwise locations of the ridges; Symbols + represent the reference coordinates

Full size image

Figure 7 presents contours of the streamwise velocity fluctuation in a horizontal plane and as a function of normalised time for the small spacing (a) and large-spacing (b) cases. The figure illustrates the quasi-periodic lateral movement of high and low momentum zones. Clearly, the lateral movement (or meandering) exhibits a time-dependent behaviour [15, 40, 41, 43], which does not appear in the time-averaged plots, such as those in Fig. 3. The lateral movement is visibly more distinct at the large spacing and occurs at a lower frequency (or longer wavelength) and at a greater amplitude compared to the small spacing case.

Fig. 7
figure 7

Distributions of instantaneous streamwise velocity at a \(z/H=0.16\) and b \(z/H=0.5\). Dashed vertical lines indicate the spanwise locations of the ridges

Full size image

Figure 8 demonstrate the signals of the streamwise velocity recorded in the centres of the time-averaged secondary cells for the s024 (a) and the s096 (b) and their respective velocity spectra (c) and (d). In order to filter out the smallest turbulent scales, a Gaussian filter is applied (red lines plot the filtered velocity signal). The width (i.e., standard deviation) of the Gaussian filter is chosen to be one flow depth H so that the filtered velocity represents large-scale structures of approximately the scale of the secondary currents as induced by the ridges. Figure 8a and b demonstrate that the LES-computed signals (black lines) are smoother after filtering, yet large-scale fluctuations are preserved. The meandering of the instantaneous secondary flow is apparent in the signal, exhibiting periodically alternating maxima and minima of the u-velocity signal, i.e., the lateral movement of high and low speed streaks lead to these positive and negative peaks in the signal. Figure 8c and d show a sharp drop-off occurring approximately one decade earlier in the red line (Gaussian-filtered signal) compared to the black line (LES-computed signal), suggesting that small-scale (i.e., higher frequency) fluctuations are effectively removed.

Fig. 8
figure 8

Example of LES-computed velocity signal and the same signal reconstructed using a Gaussian filter. a and b Streamwise velocity signals in the right SC cell centre. Open symbols: Maximum/minimum values; c and d Power spectral density of the streamwise velocity fluctuation

Full size image

In an attempt to visualise and quantify the development of the meandering of the secondary currents in space and time, phase-averaging is applied to the Gaussian-filtered velocity signals over multiple maxima–minima cycles which are marked with blue open symbols in Fig. 8a and b. The filtered velocity signal at the centre of the SC (for s024 \(y'_{r}=0.083H\) and \(z_{r}=0.16H\) and for s096 \(y'_{r}=0.33H\) and \(z_{r}=0.5H\)) is used to determine the different phases of a cycle over which the entire cross-section (y–z plane) is sampled. It is assumed that one maxima–minima–maxima cycle corresponds to one meandering period of low- and high-momentum streaks from the left-hand side of the ridge to the right-hand side, and then back to the left-hand side. In this analysis, \(n_{total}=20\) phases are chosen to represent one such cycle. Each of the 20 phases is then averaged over approximately 100 snapshots for s024 or s096, respectively. The phase-averaged Gaussian-filtered velocities are denoted as \({\dot{u}}\), \({\dot{v}}\) and \({\dot{w}}\). Figure 9 shows contours of \({\dot{u}}\) together with vectors of the secondary flow (\({\dot{v}}\), \({\dot{w}}\)) for different phases of the cycle. From top to the bottom, each row represents the 1st, 5th, 7th, 11th, 15th and 17th phase-averaged streamwise velocity contours and vectors. The red/blue dots in Fig. 9g–l, s–x indicate the centre of the right/left SC cell of the current phase. Identification of the centre of the SC cell is automated by taking the maximum/minimum value of \(\lambda _{Ci}/\sqrt{{\dot{v}}^{2}+{\dot{w}}^{2}}\) (for s024) or \(\psi /\sqrt{{\dot{v}}^{2}+{\dot{w}}^{2}}\) (for s096), where \(\lambda _{Ci}\) is the signed swirl strength and \(\psi =\int _{0}^{z}{\dot{v}}dz\) is the streamfunction. The phase-averaged streamwise velocity contours in Fig. 9a–f and m–r show that there is always a low-momentum region originating at the ridge which meanders from one side to the other, regardless of the ridge spacing. For the wide-spacing case this low momentum zone extends all the way to the water surface whereas it remains close to the bed in the small-spacing case. The vector plots in (g–l) and (s–x) show that clockwise-oriented secondary currents always appear on the right-hand side of the ridge, while counter-clockwise-oriented SCs always appear on the left-hand side. Similar to the observations in time-averaged flow, these SC cells cover the entire depth at larger spacing s096, whereas they are mostly confined close to the ridge at smaller spacing s024. What is noteworthy is that the two cells on either side of the ridge are visibly asymmetric and that one is markedly stronger than the other over one half of the cycle and then the other dominates over the second half of the cycle. This is very obvious for the small-spacing case where the ‘weak’ cell almost disappears whilst the ‘strong’ cell is prominent. The meandering of the low-momentum zone above the ridges is clearly driven by the alternation of weak and strong SC cells during the cycle whereby the strong SCs pull the low momentum zone to its side in the first half of the cycle (Fig. 9a, g, m, s). Then there is a phase where both cells are approximately equal and the low momentum zone is right above the ridge (Fig. 9b, h, n, t), before the process is reversed and the low momentum zone is pulled to the other side by the now stronger secondary cell (Fig. 9d, j, p, v) on that side of the ridge.

The observations above demonstrate that although the clockwise and the counter-clockwise SC cells are identical in size and strength in the time-averaged field, their shape and position change periodically over each cycle. One of the SC cells (either the clockwise or the counter-clockwise) is gaining strength while the other is weakening, thereby displacing the centre of rotation of each of the cells. Similar features were reported by Bai et al. [2] based on proper orthogonal decomposition of the first two modes. The emergence, development, and the collapse of the large-scale vortical motions echo the meandering of the SC currents observed in the wall-parallel plane in Fig. 5. Movie files containing reconstructed velocity fields is available as online supplementary material.

Fig. 9
figure 9

Distributions of phase-averaged quantities educed from Gaussian-filtered velocity signals. a–f, m–r Contours of the streamwise velocity \({\dot{u}}/U_{bulk}\); g–l, s–x Vectors of the secondary flow (\({\dot{v}}/U_{bulk}\), \({\dot{w}}/U_{bulk}\)). Red/blue dots are centres of instantaneous right/left SC cells

Full size image

Figure 10 plots the trajectory of the SC cell centres (red/blue dots in Fig. 9) over one meandering cycle. As stated above, the meandering cycle is divided into 20 equivalent intervals thus there are 21 snapshots captured in total (and 6 of these are shown in Fig. 9). The 21st snapshot is considered to be the end of the current SC meandering cycle (or the beginning of the next SC meandering cycle) and therefore is identical to the 1st snapshot. Interestingly, the trajectory of the cell centres (see Fig. 10a, d) shows a ‘shape of 8’ pattern for both the clockwise (coloured in red) and counter-clockwise (coloured in blue) SC cell, regardless of the ridge spacing. The two bubbles of the 8 shapes are of different sizes, i.e., smaller at the bottom and larger at the top. Figure 10e shows that the centres of the clockwise and counter-clockwise cells move almost simultaneously in spanwise direction at the large spacing s096, which is mostly true in s024 (Fig. 10b) except for the moments when the ‘weak vortex’ almost disappears. Figure 10c and f demonstrate that the wall-normal movements of the SC cell centres in s096 and s024 follow the same trend. The height of the SC cell achieves a peak between the clockwise and the counter-clockwise SC cell, corresponding to the moments at which low-momentum moves towards the left- or the right-extreme relative to the ridge, respectively.

Fig. 10
figure 10

Movement of SC cell centre within one period of SC meandering educed from phase-averaged Gaussian-reconstructed velocity field. a and d Trajectory of the SC cell centre; b and e Movement in spanwise direction in time; c and f Movement in wall-normal direction in time

Full size image

Figure 11 presents pre-multiplied streamwise velocity spectra \(k_{x}F_{uu}(k_{x})/u_{*}^{2}\) at the centre of the right (clockwise) SC cell (a,b), or at mid-depth over the ridge (c,d). The spectra are firstly computed in the frequency domain with averaging over 6000 overlapping segments with 10s duration each. The window size 10s is approximately equivalent to 5 eddy turnover times (i.e., \(5H/u_{*}\)) and 2 flow-through periods (i.e., \(2L_{x}/U_{bulk}\)). The frequency domain is then transferred into the wavenumber domain via Taylor’s frozen turbulence hypothesis \(k_{x}=2\pi f/{\overline{u}}_{local}\), where \({\overline{u}}_{local}\) refers to the time-averaged streamwise velocity at SC cell centre (a, b) or the time-averaged streamwise velocity at half of the water depth over the ridge (c, d), and is taken as the convection velocity here. The pre-multiplied spectra reflect the effect of the ridge-induced SCs. In pre-multiplied spectra at half of the water depth over the ridges(c,d), energy-containing motions with a wavelength around 3H are found, suggesting the presence of LSMs in both cases. An energy peak in the range \(4-10H\) (absent for the smooth-bed case s000) is found in the pre-multiplied spectra for s096 at the SC cell centre, which echoes the length of the of streamwise-repeating pattern in the two-point correlation distribution found in Fig. 6b, indicating the presence of the flow periodicity associated with SC meandering. This characteristic wavelength range is comparable to the wavelength characterising the meandering of the secondary currents \(\lambda _{x}=2{\overline{u}}_{local}{\overline{T}}\) (dashed line in Fig. 11b), where \({\overline{T}}\) refers to the average duration between the maximum and minimum of the streamwise velocity at the centre of the clockwise SC cell (see Fig. 8b). However for s024, a relation between the wavelength of 4.8H (dashed line in Fig. 11a) estimated using the same method based on \({\overline{T}}\) is not obvious. Although we demonstrated that the SC meandering occurs in all cases regardless of the spacing, the meandering in s024 seems to be masked by wall turbulence in the pre-multiplied spectra and two-point correlation [43], likely due to the fact that SC cells generated by the ridges are confined to the near-bed region.

Fig. 11
figure 11

Pre-multiplied spectra at multiple locations. a s024 at \(y'_{r}=0.083H\) and \(z_{r}=0.16H\); b s096 at \(y'_{r}=0.33H\) and \(z_{r}=0.5H\); c s024 at \(y'_{r}=0H\) and \(z_{r}=0.5H\); d s096 at \(y'_{r}=0H\) and \(z_{r}=0.5H\). Vertical dashed lines: Characteristic wavelengths (normalised) of meandering derived from \(\lambda _{x}=2{\overline{u}}_{local}{\overline{T}}\); Shaded area: Distinct peaks

Full size image

5 Conclusions

Large-eddy simulations (LES) of free-surface flows over streamwise-orientated ridges have been carried out for various spanwise ridge spacings. In a first step, the LES method has been validated using experimental data confirming the adequacy of the selected discretisation schemes, the mesh size, subgrid-scale model as well as boundary conditions. LES is able to reproduce the experimental data of three open-channel flow experiments to a satisfying degree regarding the time-averaged streamwise velocity profiles.

The contours of first-order statistics reveal that the size of the secondary current cells decreases with the reduction of spanwise spacing of the ridges. In terms of second-order statistics, it is shown that the ridges introduce strong spanwise heterogeneity of the flow quantities which is (together with turbulence anisotropy) the driving factor for the occurrence of the secondary currents. The meandering and instability of the SCs induced by the ridges are further examined via instantaneous plots and two-point velocity correlation contours in a wall-normal plane. The meandering of the secondary currents is manifested in zones of instantaneous high and low momentum in the cross section which is visualised and quantified via phase-averaged and Gaussian-filtered velocity signals. The meandering of the low- and high-momentum pathways is shown to be driven by the periodic or cyclic nature of secondary current cells. Over the first half of a meandering cycle one of the two SC cells adjacent to a ridge dominates thereby pulling the low momentum zone above the ridge to its side whilst the concurrent SC cell on the other side of the ridge is ‘weak’. This process is reversed over the second half of the cycle during which the ‘weak’ cell becomes dominant while the dominant one becomes weak. Moreover, the centres of the SC cells are tracked over one such cycle and it is revealed that the SC cells follow a certain pattern, resembling a shape 8 pattern for the wide-spacing case and more of an up-down pattern for the narrow-spacing case. It is noteworthy to mention here that the periodicity featuring the secondary current instability found in the present study echos the behaviours of meandering low- and high-speed streaks found in all previous studies, regardless of the flow type (boundary layers, open-channels, closed-channels, etc.) and the type of the spanwise heterogeneity. It is therefore suggested that the cyclic patterns of the secondary current cells as well as the mechanism of the secondary current instability can be extended to the majority of flows with embedded secondary currents where pairs of symmetric vortices are identified in the time-averaged field.

Pre-multiplied velocity spectra show the presence of LSMs and/or secondary current instability, respectively in flows with different spacings, and the characteristic wavelength (or frequency) observed echoes the previous findings associated with the secondary current instability induced by the presence of the streamwise ridges in the large spacing case. In the smaller spacing case, although the secondary current instability has been visualised, the corresponding spectral features, as well as the repeating pattern in the two-point correlation plot, are very weak or absent, respectively owing to the fact that the SC cells generated in the small spacing are confined near the bed, where the contribution of the wall turbulence appears dominant. This demonstrates that turbulent flows are composed of a hierarchy of scales, and similar features may occur across an entire hierarchy of scales. However, some features and/or scales might be obscured by the competing contribution from other flow mechanisms. Since recent observations have confirmed the lateral meandering behaviour of VLSMs, it is prospective to check if the mechanism of the secondary current instability can be applicable to VLSMs, which may lead to insights into the formation and evolution of VLSMs.