Undular and broken surges in dam-break flows: a review of wave breaking strategies in a Boussinesq-type framework

Abstract

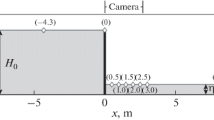
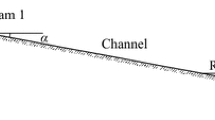
The water waves resulting from the collapse of a dam are important unsteady free surface flows in civil and environmental engineering. Considering the basic case of ideal dam break waves in a horizontal and rectangular channel the wave patterns observed experimentally depends on the initial depths downstream (h_d) and upstream (h_o) of the dam. For r = h_d/h_o above the transition domain 0.4–0.55, the surge travelling downstream is undular, a feature described by the dispersive Serre–Green–Naghdi (SGN) equations. In contrast, for r below this transition domain, the surge is broken and it is well described by the weak solution of the Saint–Venant equations, called Shallow Water Equations (SWE). Hybrid models combining SGN–SWE equations are thus used in practice, typically implementing wave breaking modules resorting to several criteria to define the onset of breaking, frequently involving case-dependent calibration of parameters. In this work, a new set of higher-order depth-averaged non-hydrostatic equations is presented. The equations consist in the SGN equations plus additional higher-order contributions originating from the variation with elevation of the velocity profile, modeled here with a Picard iteration of the potential flow equations. It is demonstrated that the higher-order terms confer wave breaking ability to the model without using any empirical parameter, such while, for r > 0.4–0.55, the model results are essentially identical to the SGN equations but, for r < 0.4–0.55, wave breaking is automatically accounted for, thereby producing broken waves as part of the solution. The transition from undular to broken surges predicted by the high-order equations is gradual and in good agreement with experimental observations. Using the solution of the new higher-order equations it was further developed a new wave breaking index based on the acceleration at the free surface to its use in hybrid SGN–SWE models.

Appendix: Solitary wave solutions

An important non-hydrostatic free surface flow is the solitary wave. Such travelling wave of permanent form is only possible when a balance between non-linearity and dispersion is achieved. In this section the existence of solitary wave solutions for the higher-order SG-B model is investigated. A wave of permanent form is steady for an observed traveling on the wave. Thus, the steady version of Eq. (14) reads

$$ M = \frac{1}{2}gh^{2} + U^{2} h\left[ {1 + \frac{1}{3}\left( {hh_{xx} - h_{x}^{2} } \right) + \frac{1}{15}\left\{ {\left( {hh_{xx} } \right)^{2} + 4h_{x}^{4} - 4h_{x}^{2} hh_{xx} } \right\}} \right] = gh_{o}^{2} \left( {\frac{1}{2} + \text{F}_{o}^{2} } \right), $$

(37)

where M is the momentum function, h_xx = d²h/dx², h_x = dh/dx and (h_o, F_o) refers to the water depth and Froude number of the undisturbed supercritical current. Manipulation of Eq. (37) permits to write it in the form a(h_xx)² + bh_xx + c = 0. Therefore, h_xx = [‒b + (b²‒4ac)^1/2]/(2a). This second-order ODE can be easily solved transforming it into a pair of first-order ODEs to determine the profiles of h and h_x. Before conducting numerical simulations it shall be noted that real solutions do not exists for b²‒4ac < 0, which settles an upper limit of F_o for existence of solitary waves. A 4^th-order Runge–Kutta scheme was used to compute the solitary wave solution for defined values (h_o, F_o) at x = 0. The value of h_x was fixed by choice to 0.001 to deviate the flow from uniform flow conditions. For a solitary wave

$$ \text{F}_{o} = \left( {1 + \frac{H}{{h_{o} }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} , $$

(38)

where H is the maximum wave elevation (solitary wave crest) above the undisturbed depth h_o. Figure 15a contains the computed free surface profile for F_o = 1.118 (H/h_o = 0.2), which is close to those conditions used for the Favre waves simulated in Fig. 8. The numerical solution of the SG-B equations is compared there with the analytical solution of the SGN equations [18, 36]. It is the solution of the reduced equation [18, 75]

$$ M = \frac{1}{2}gh^{2} + U^{2} h\left[ {1 + \frac{1}{3}\left( {hh_{xx} - h_{x}^{2} } \right)} \right] = gh_{o}^{2} \left( {\frac{1}{2} + \text{F}_{o}^{2} } \right), $$

(39)

which is obviously obtained from Eq. (37) neglecting the contribution of B. It can be verified comparing both solutions that for this case the effect of B is negligible. By numerical experimentation it was determined that solitary wave solutions ceased to exist at F_o ≈ 1.397 (H/h_o = 0.951), given that b²‒4ac < 0 for higher values. Breaking of undular surges is often activated in Boussinesq models by checking the value of H/h_o at the surge front. The accepted approximate threshold condition for breaking in the SGN equations is H/h_o = 0.8 [27], resulting F_o = 1.341, which is rather close to the value obtained using our generalized SG-B equations. For F_o > 1.397 the SG-B will introduce breaking in the solution.

Fig. 15

Solitary wave for F_o = 1.118 (H/h_o = 0.2). a steady flow computations and b unsteady flow computations

Now, let us check that the numerical solution of Eqs. (17) produces a travelling wave of permanent form. The procedure was as follows. The solitary wave analytical solution of the Serre–Green–Naghdi equations was set as an initial condition in the SG-B model, with the crest located at x = 0 for t = 0. The previous wave with H/h_o = 0.2 is considered. Obviously, this is not exactly the solitary wave solution of the SG-B model. When the numerical model is run the wave will evolve in time, producing imperceptible changes given the weak effect of B. Figure 15b shows the numerical solution of the SG-B equations at t = 20 s, and the analytical solution of the SGN equations. Note that differences are imperceptible. The numerical model produces a stable wave of permanent form, which is the solitary wave solution of the SG-B equations. Now, let us check the breaking ability of the SG-B equations. Following the same procedure, a solitary wave of H/h_o = 1.5 (F_o = 1.581) was routed and the results displayed at t = 5 s in Fig. 16. As expected, this value is above the previously detected threshold of breaking, and the numerical simulation transform the input solitary wave into a wave with a significantly reduced maximum height and steeper wave front, both features clearly resembling the wave breaking mimicking implicit in the SWE. For illustrative purposes the same simulation was conducted using the SWE, thereby transforming the solitary wave into a triangular wave with a shock front. The hybridised character of the SG-B equations between the SGN and SWE is beautifully observed in this comparison.

Fig. 16

Routing of a solitary wave of F_o = 1.581 (H/h_o = 1.5): comparison of the SWE and SG-B equations