Assessment of extreme records in environmental data through the study of stochastic orders for scale mixtures of skew normal vectors

Abstract

Scale mixtures of skew normal distributions are flexible models well-suited to handle departures from multivariate normality. This paper is concerned with the stochastic comparison of vectors that belong to the family of scale mixtures of skew normal distributions. The paper revisits some of their properties with a proposal that allows to carry out tail weight stochastic comparisons. The connections of the proposed stochastic orders with the non-normality parameters of the multivariate model are also studied for some popular distributions within the family. The role played by these parameters to tackle the non-normality of multivariate data is enhanced as a result. This work is motivated by the analysis of multivariate data in environmental studies which usually collect maximum or minimum values exhibiting departures from normality. The implications of our theoretical results in addressing the stochastic comparison of extreme environmental records is illustrated with an application to a real data study on maximum temperatures in the Iberian Peninsula throughout the last century. The resulting findings may elucidate whether extreme temperatures are evolving for such a long period.

1 Introduction

Kurtosis is a concept related to the amount of peakedness and tail weight of a distribution, a notion aimed at describing how the mass probability gets spread around its “shoulders”. The earliest measure for quantifying kurtosis dates back to Karl Pearson (Pearson 1905; Fiori and Zenga 2009) whose proposal is originally used to assess deviations from the normal distribution. Since then a plethora of measures that intuitively describe the notion of kurtosis have been proposed in the literature for scalar variables (Balanda and MacGillivray 1990; Groeneveld 1998; Seier and Bonett 2003) and multidimensional variables (Mardia 1970; Oja 1983; Song 2001; Wang and Serfling 2005), just to give a non-exhaustive record of representative works. Among them, perhaps the most popular indices are those ones based on moments, like for example the renowned Mardia’s kurtosis index (Mardia 1970; Móri et al. 1994; Kollo 2008), which is defined by the fourth moment of the scaled Mahalanobis distance of a p-dimensional vector ${\varvec{X}}$ from its mean vector $\varvec{\mu }$ as follows:

$$\begin{aligned} kurt_{M,p}=E\{[({\varvec{X}}-\varvec{\mu })^\prime \varvec{\Sigma }^{-1}({\varvec{X}}-\varvec{\mu })]^2\}, \end{aligned}$$

(1)

where $\varvec{\Sigma }$ is the variance-covariance matrix of ${\varvec{X}}$.

In order to assess asymmetry departures from multivariate normality, a popular measure is Mardia’s skewness index (Mardia 1970; Móri et al. 1994; Kollo 2008) which is defined by

$$\begin{aligned} skew_{M,p}=E\{[({\varvec{X}}_1-\varvec{\mu })^\prime \varvec{\Sigma }^{-1}({\varvec{X}}_2-\varvec{\mu })]^3\}, \end{aligned}$$

(2)

where ${\varvec{X}}_1$ and ${\varvec{X}}_2$ are independent copies of the random vector ${\varvec{X}}$.

Although appealing and intuitive, these measures and many other ones that have come up in the literature pose a serious limitation to describe complex concepts like asymmetry and tail weight behavior in a precise manner since they cannot fully capture how the mass probability spreads out from near the shoulders towards the tails of the distribution. Unlike them, stochastic orderings, like the convex transform order (Van Zwet 1964) or the likelihood ratio order (Shaked and Shanthikumar 2007), are alternative approaches that consider the whole support of the distribution so that such limitation can be overcome. Moreover, stochastic orders also provide theoretical support to decide whether existing non-normality measures are meaningful indicators of kurtosis (skewness) by studying if they preserve a well established kurtosis (skewness) stochastic ordering. From the very beginning, the convex transform order came up as a well-defined ordering to make kurtosis (skewness) stochastic comparisons (Van Zwet 1964; Oja (1981). As a result, it has acquired a paramount relevance to evaluate whether a measure is an indicator of kurtosis (skewness) or not. While works on the convex transform order and its properties, applications and implications have covered the univariate framework from the very beginning (Van Zwet 1964; Oja 1981; Balanda and MacGillivray 1990; Arnold and Groeneveld 1992; Groeneveld 1998; Seier and Bonett 2003; Kochar and Xu 2009; Barmalzan and Najafabadi 2015; Arriaza et al. 2019; Arab et al. 2021), the multivariate scenario has received less echo in the literature with only a few related works (Wang 2009; Arevalillo and Navarro 2012; Wang and Zhou 2012).

This paper addresses the multivariate scenario by means of tail weight stochastic comparisons of random vectors that belong to the family of multivariate scale mixture of skew-normal (SMSN) distributions. Some properties of the SMSN family are revisited to introduce novel approaches for the stochastic comparison of SMSN random vectors. The convex transform and the likelihood ratio orderings are examined in this parametric context along with the proposals for the stochastic comparisons. The role played by the non-normality parameters of the SMSN distribution in connection with the proposed orderings is also studied. The need for theoretical support to assess the evolution of extreme temperatures (generally speaking extremes in environmental data) and to elucidate whether climate is evolving towards seasons with episodes of more extreme temperatures motivated this theoretical study about the stochastic comparisons of SMSN vectors.

The rest of the paper is organized as follows: the next section presents some background material about multivariate SMSN distributions and the stochastic orderings that will be used in the sequel. Section 3 gives the core material of this work. It addresses the stochastic comparison of vectors that follow a multivariate SMSN distribution. The well-known Van Zwet’s convex transform (Van Zwet 1964) and likelihood ratio orders are revisited and used to introduce some proposals for the stochastic comparison of SMSN vectors. Such proposals, that rely on properties of the SMSN family, will be studied in connection with the non-normality parameters of the SMSN multivariate model for some popular SMSN distributions like the skew-t and skew-slash. The implications of our theoretical findings to assess extreme records in environmental data are illustrated in Sect. 4 by means of a real case application for the comparison of extreme temperatures in the Iberian peninsula during a period of 114 years. The paper finishes with a section containing some discussion and concluding remarks which will recap the main findings of the paper and will also hint at some ideas to address future research problems. The Appendix contains the proofs of all lemmas and propositions in the paper.

Throughout the paper, the terms “increasing” and “decreasing” are considered in a wide sense, that is, they mean the “nondecreasing” and “nonincreasing” behavior of a function, respectively. On the other hand, the acronyms for the cumulative distribution function and the probability density function are CDF and PDF, respectively.

2 Background and preliminary results

2.1 Scale mixtures of skew-normal multivariate distributions

The multivariate skew-normal (SN) distribution has become a widely used model to regulate asymmetry deviations from normality. In this paper we adopt the formulation given by Azzalini and Capitanio (1999, 2014) to introduce the multivariate SN distribution.

We say that a p-dimensional random vector ${\varvec{Z}}$ follows a normalized SN distribution if its PDF is given by

$$\begin{aligned} f({\varvec{z}}; \overline{\varvec{\Omega }},\varvec{\alpha })=2\phi _p({\varvec{z}};\overline{\varvec{\Omega }})\Phi (\varvec{\alpha }^\prime {\varvec{z}}), \end{aligned}$$

(3)

where $\overline{\varvec{\Omega }}$ is a correlation matrix, $\phi _p(\cdot ;\overline{\varvec{\Omega }})$ is the PDF of a “standardized” p-dimensional normal vector, $\Phi$ denotes the CDF of a normal N(0,1) scalar variable and $\varvec{\alpha }$ is a shape vector that accounts for the asymmetry of the multivariate model in a directional fashion.

The PDF above is actually a multivariate extension of the standard SN univariate model having PDF: $\displaystyle f(z;\alpha )=2\phi (z)\Phi (\alpha z)$, $z \in {\mathbb {R}}$, where $\alpha$ is a shape scalar parameter (see Azzalini and Capitanio (2014), p. 124).

In order to introduce location and scale parameters into the normalized SN vector ${\varvec{Z}}$, the following transformation: ${\varvec{X}}=\varvec{\xi }+\varvec{\omega }{\varvec{Z}}$ can be applied. Here $\varvec{\xi }=(\xi _1,\ldots ,\xi _p)^\prime$ is a location vector and $\varvec{\omega }$ is a diagonal matrix with positive entries. Then the PDF of the input vector ${\varvec{X}}$ is given by

$$\begin{aligned} f({\varvec{x}}; \varvec{\xi },\varvec{\Omega },\varvec{\alpha })=2\phi _p({\varvec{x}}-\varvec{\xi };\varvec{\Omega })\Phi (\varvec{\alpha }^\prime \varvec{\omega }^{-1}({\varvec{x}}-\varvec{\xi })), \hspace{0.25cm}{\varvec{x}}\in {\mathbb {R}}^p, \end{aligned}$$

(4)

where $\phi _p(\cdot ;\varvec{\Omega })$ denotes the PDF of a p-dimensional normal variate with zero mean vector and covariance matrix $\varvec{\Omega }$, $\varvec{\omega }$ is a diagonal matrix with positive entries such that $\varvec{\Omega }=\varvec{\omega }\overline{\varvec{\Omega }}\varvec{\omega }$ and $\varvec{\alpha }$ (or $\varvec{\eta }=\varvec{\omega }^{-1}\varvec{\alpha }$) is the shape vector that regulates the asymmetry of the model. We put ${\varvec{X}} \sim SN_p(\varvec{\xi },\varvec{\Omega },\varvec{\alpha })$ to denote that ${\varvec{X}}$ has PDF (4). It can be noted that when $\varvec{\alpha }= {\varvec{0}}_p$, the PDF of the SN model becomes the density of a p-dimensional normal variate.

The stochastic representation: ${\varvec{X}}=\varvec{\xi }+\varvec{\omega }{\varvec{Z}}$ of a SN vector is appealing and provides a quite natural way to extend the SN to the SMSN family which handles asymmetry and tail weight simultaneously (Branco and Dey 2001). Due to its flexibility, this family has received increasing attention in the literature (Kim 2008; Basso et al. 2010; Kim and Kim 2017; Capitanio 2020; Arevalillo and Navarro 2020, 2021). We now use the formulation from Capitanio (2020) to define the SMSN family as follows:

Definition 1

Let ${\varvec{Z}}$ be a random vector such that ${\varvec{Z}} \sim SN_p({\varvec{0}},\overline{\varvec{\Omega }},\varvec{\alpha })$, with PDF (3) and let S be a non-negative random variable, independent of ${\varvec{Z}}$. The random vector ${\varvec{X}}=\varvec{\xi }+\varvec{\omega }S{\varvec{Z}}$, where $\varvec{\omega }$ is a diagonal matrix with positive entries, is said to follow a multivariate SMSN distribution.

We put ${\varvec{X}} \sim SMSN_p(\varvec{\xi },\varvec{\Omega },\varvec{\alpha },H)$, where H is the distribution function of the mixing variable S, to indicate that ${\varvec{X}}$ follows a p-dimensiontal SMSN distribution. When $\varvec{\alpha }\varvec{=}{\varvec{0}}_p$, we obtain a vector ${\varvec{X}}_0$ which follows a scale mixture of normal (SMN) distributions so we put ${\varvec{X}}_0 \sim SMN_p(\varvec{\xi },\varvec{\Omega },H)$ for denoting this case. On the other hand, if H is degenerate at $S=1$ , then ${\varvec{X}}$ has a $SN_p(\varvec{\xi },\varvec{\Omega },\varvec{\alpha })$ distribution.

2.2 Some popular SMSN multivariate distributions

The multivariate skew-t (ST) distribution arises when the mixing variable of the SMSN vector is $S=U^{-1/2}$ with $U\sim \chi _\nu ^2/\nu$. Its PDF (Azzalini and Capitanio 2003) is given by

$$\begin{aligned} f({\varvec{x}}; \varvec{\xi },\varvec{\Omega },\varvec{\alpha },\nu )=2\,t_p({\varvec{x}};\nu )T_1\left( \varvec{\alpha }^\prime \varvec{\omega }^{-1}({\varvec{x}}-\varvec{\xi })\left( \frac{\nu +p}{q({{\varvec{x}}})+\nu }\right) ^{1/2}; \nu +p\right) \end{aligned}$$

(5)

for ${\varvec{x}}\in {\mathbb {R}}^p$, where $t_p({\varvec{x}};\nu )$ is the PDF of a p-dimensional Student-t variable with $\nu$ degrees of freedom given by

$$\begin{aligned} t_p({\varvec{x}};\nu )=\frac{\Gamma ((\nu +p)/2)}{\vert \varvec{\Omega }\vert ^{1/2}(\pi \nu )^{p/2}\Gamma (\nu /2)}\left( 1+\frac{q({{\varvec{x}}})}{\nu }\right) ^{-(\nu +p)/2}, \end{aligned}$$

(6)

$T_1(y; \nu +p)$ is the distribution function of a Student-t scalar variable with $\nu +p$ degrees of freedom and $q({{\varvec{x}}})=({\varvec{x}}-\varvec{\xi })^\prime \varvec{\Omega }^{-1}({\varvec{x}}-\varvec{\xi })$.

We write ${\varvec{X}} \sim ST_p(\varvec{\xi },\varvec{\Omega },\varvec{\alpha },\nu )$ to indicate that ${\varvec{X}}$ follows a p-dimensional ST distribution with PDF (5).

Another flexible model that simultaneously accounts for asymmetry and tail weight is the skew-slash (SSL) multivariate distribution (Wang and Genton 2006). It arises when we consider the mixing variable $S=U^{-1/2}$ with $U\sim Beta(q/2,1)$, where q is a tail weight parameter such that $q>0$. We put ${\varvec{X}} \sim SSL_p(\varvec{\xi },\varvec{\Omega },\varvec{\alpha },q)$ to indicate that the input vector ${\varvec{X}}$ follows a p-dimensional SSL distribution with location $\varvec{\xi }$, scale matrix $\varvec{\Omega }=\varvec{\omega }\overline{\varvec{\Omega }}\varvec{\omega }$, shape vector $\varvec{\alpha }$ and tail weight parameter $q>0$.

It can be noted that when $q\rightarrow \infty$, then SSL becomes a SN distribution. On the other hand, when we take $\varvec{\alpha }={\varvec{0}}_p$ the distribution of the input vector ${\varvec{X}}$ reduces to the multivariate slash distribution.

The skew-contaminated normal model arises when the mixing variable of the SMSN distribution is $S=U^{-1/2}$ with U a scalar variable having a discrete distribution such that

$$\begin{aligned} P(U=\gamma )=\epsilon \,\,\hbox { and } \, P(U=1)=1-\epsilon , \end{aligned}$$

where $0\le \epsilon \le 1$ quantifies the mixing proportion and $0<\gamma \le 1$ is an inflation factor (Lachos et al. 2010). The PDF of a skew-contaminated normal vector ${\varvec{X}}$ is given by

$$\begin{aligned} f({\varvec{x}}; \varvec{\xi },\varvec{\Omega },\varvec{\alpha },\gamma ,\epsilon )&= 2\left[ \epsilon \phi _p({\varvec{x}}-\varvec{\xi };\gamma ^{-1}\varvec{\Omega })\Phi (\gamma ^{1/2}\varvec{\alpha }^\prime \varvec{\omega }^{-1}({\varvec{x}}-\varvec{\xi }))\right. \nonumber \\&\left. +(1-\epsilon )\phi _p({\varvec{x}}-\varvec{\xi };\varvec{\Omega })\Phi (\varvec{\alpha }^\prime \varvec{\omega }^{-1}({\varvec{x}}-\varvec{\xi }))\right] . \end{aligned}$$

(7)

We put ${\varvec{X}} \sim SCoN_p(\varvec{\xi },\varvec{\Omega },\varvec{\alpha },\gamma ,\epsilon )$ to denote that the vector ${\varvec{X}}$ follows a p-dimensional skew-contaminated normal distribution. It can be observed that if we take $\epsilon =0$ or $\gamma =1$ then the model reduces to the multivariate SN distribution.

2.3 Stochastic orders

We now introduce some stochastic orders for scalar random variables that will be used in the paper. Their main properties and applications can be seen in Shaked and Shanthikumar (2007), and Van Zwet (1964). We also include here some new properties that will be used later.

Let X and Y be two random variables with respective CDFs F and G and PDFs f and g. Then we say that X is less than Y in:

• the (usual) stochastic order (denoted by $X\le _{st}Y$) if $F\ge G$;

•  the likelihood ratio order (denoted by ($X\le _{lr}Y$) if g/f is increasing in the union of their supports;

• the convex transform order (denoted by $X\le _{c} Y$) if $G^{-1}(F(x))$ is convex.

When $X\le _{st}Y$ and $Y\le _{st}X$, the variables have the same distribution and we denote it by $X{\mathop {=}\limits ^{st}}Y$. It is well know that $X\le _{lr}Y$ implies $X\le _{st}Y$, see Shaked and Shanthikumar (2007). The convex transform order was introduced in Van Zwet’s early work on convex transformations (Van Zwet 1964). Later on, it was revisited as a proposal for carrying out skewness and kurtosis stochastic comparisons (Oja 1981). For other convex orders, see the monograph work by Shaked and Shanthikumar (2007).

We will need the following ordering properties of the product of independent and non-negative random variables that also have an independent interest in the theory of stochastic orders.

Proposition 1

Let $S_1,S_2,Z$ be independent random variables with PDFs $f_1,f_2,g$ respectively. Then the following properties hold:

• (i) if $Z>0$ and $S_1\le _{st}S_2$, then $S_1Z\le _{st}S_2Z$;

• (ii) if $Z>0$ and $0<s_1\le s_2$ and

  $$\begin{aligned} \frac{xg'(x)}{g(x)} \text { is decreasing in } (0,\infty ), \end{aligned}$$

  (8)

  then $s_1Z\le _{lr}s_2Z$;

• (iii) if $Z,S_1,S_2>0$, $S_1\le _{lr}S_2$ and (8) holds, then $S_1Z\le _{lr}S_2Z$.

The function $\alpha _g(x)=xg'(x)/g(x)$ used in condition (8) is called the elasticity function associated with g. This condition is equivalent to the aging class called increasing proportional likelihood ratio (IPLR) defined in Ramos-Romero and Sordo-Díaz (2001). There are many probability models that satisfy (8). A straightforward calculation shows that such condition holds for exponential, gamma, Pareto type II and Weibull distributions. It is worthwhile noting that condition (8) cannot be dropped out from the statement of the previous lemma.

Moreover, we have the following property for the st-ordering of univariate SN distributions. This property cannot be extended to the lr order.

Proposition 2

Let us consider two univariate SN variables such that $Z_i\sim SN_1(0,1,\alpha _i)$ for $i=1,2$ with $\alpha _1<\alpha _2$. Then $Z_1\le _{st}Z_2$.

3 Stochastic comparisons of SMSN vectors

Let ${\varvec{X}}$ be a random vector such that ${\varvec{X}} \sim SMSN_p(\varvec{\xi },\varvec{\Omega },\varvec{\alpha },H)$, where H is the CDF of the mixing variable S. When $\varvec{\alpha }\varvec{=}{\varvec{0}}_p$, the non-skewed SMN random vector ${\varvec{X}}_0$ is obtained. On the other hand, taking into account that ${\varvec{X}}_0$ is elliptically distributed, then it will admit the following stochastic representation:

$$\begin{aligned} {\varvec{X}}_0 {\mathop {=}\limits ^{st}}\varvec{\xi }+{\varvec{A}}^\prime R {\varvec{U}}^{(p)}, \end{aligned}$$

(9)

where ${\varvec{A}}$ is a square matrix such that ${\varvec{A}}^\prime {\varvec{A}} =\varvec{\Omega }$, ${\varvec{U}}^{(p)}$ is a p-dimensional vector with uniform distribution on the unit hypersphere and R is the so-called squared modular scalar variable (Fang et al. 1990). This representation, in combination with the modulation invariance property of the multivariate SN model (Azzalini and Capitanio 2014), will lead to the following proposition.

Proposition 3

Let ${\varvec{X}}$ be a random vector such that ${\varvec{X}} \sim SMSN_p(\varvec{\xi },\varvec{\Omega },\varvec{\alpha },H)$ and let ${\varvec{X}}_0$ be its non-skewed version with $\varvec{\alpha }\varvec{=}{\varvec{0}}_p$ so that ${\varvec{X}}_0 \sim SMN_p(\varvec{\xi },\varvec{\Omega },H)$. Then their quadratic forms given by $Q_{X}=({\varvec{X}}- \varvec{\xi })^\prime \varvec{\Omega }^{-1}({\varvec{X}}- \varvec{\xi })$ and $Q_{X_0}=({\varvec{X}}_0- \varvec{\xi })^\prime \varvec{\Omega }^{-1}({\varvec{X}}_0- \varvec{\xi })$ have the same distribution as $R^2$, where R is the modular variable in (9).

As $Q_{X}=({\varvec{X}}- \varvec{\xi })^\prime \varvec{\Omega }^{-1}({\varvec{X}}- \varvec{\xi }){\mathop {=}\limits ^{st}}S^2 Q$, with $Q={\varvec{Z}}^\prime \overline{\varvec{\Omega }}^{-1}{\varvec{Z}}$ a scalar variable having $\chi _p^2$ distribution and ${\varvec{Z}} \sim SN_p({\varvec{0}},\overline{\varvec{\Omega }},\varvec{\alpha })$, we can assert that the quadratic form $Q_X$ (or $R^2$) follows a scale mixture of $\chi _p^2$ distributions.

It is worthwhile noting that the distribution of $Q_{X}$ does not depend on location, scale and asymmetry vector parameters. Hence, it has the same distribution for all SMSN vectors with a common CDF for the mixing variable S. This fact suggests the following stochastic relation ${\mathcal {R}}$ between SMSN vectors: for any two SMSN vectors ${\varvec{X}}_1$ and ${\varvec{X}}_2$ such that ${\varvec{X}}_i \sim SMSN_p(\varvec{\xi }_i,\varvec{\Omega }_i,\varvec{\alpha }_i,H_i)$, for $i=1,2$, we say that ${\varvec{X}}_1$ is related to ${\varvec{X}}_2$, and we denote it by ${\varvec{X}}_1 {\mathcal {R}} {\varvec{X}}_2$, if and only if the quadratic forms $Q_{X_1}$ and $Q_{X_2}$ are equally distributed. It can be seen that ${\mathcal {R}}$ is an equivalence relation. Each equivalence class is composed of all SMSN vectors with the same CDF H so we could take as a class representative element the SMSN vector with location at $\varvec{\xi }={\varvec{0}}_p$, identity scale matrix $\varvec{\Omega }={\varvec{I}}_p$ and zero shape asymmetry vector $\varvec{\alpha }={\varvec{0}}_p$.

On the other hand, as the distribution of $Q_{X}$ does not depend on $\varvec{\xi }$, $\varvec{\Omega }$ and $\varvec{\alpha }$, a natural way to carry out comparisons of SMSN random vectors, irrespective of their location, scale and asymmetry, is to do it by comparing their modular quadratic forms using different stochastic orders. As a result, these comparisons may be interpreted as tail weight comparisons between the input random vectors. This intuition is formalized in the next definition.

Definition 2

Let ${\varvec{X}}_1$ and ${\varvec{X}}_2$ be vectors such that ${\varvec{X}}_i \sim SMSN_p(\varvec{\xi }_i,\varvec{\Omega }_i,\varvec{\alpha }_i,H_i)$ and let us consider their quadratic forms: $Q_i=({\varvec{X}}_i- \varvec{\xi }_i)^\prime \varvec{\Omega }_i^{-1}({\varvec{X}}_i- \varvec{\xi }_i): i=1,2$. We say that ${\varvec{X}}_1$ is less tail weighted than ${\varvec{X}}_2$ in a given $*$-order (shortly written ${\textbf{X}}_1\le _{*-tw}{\textbf{X}}_2$) if such order holds for the associated quadratic forms, that is, $Q_1\le _{*} Q_2$.

It can be noted that $Q_{X}{\mathop {=}\limits ^{st}}S_i^2 Q$ with $Q\sim \chi _p^2$. Therefore, the $*-tw$ comparison of SMSN vectors will essentially involve the CDFs of the mixing variables $S_i$. We now investigate the stochastic comparison for specific choices of the $*$-order like the standard stochastic order, the likelihood ratio order and the convex transform order.

3.1 The stochastic and likelihood ratio orders for tail weight comparisons

We now deal with the stochastic comparisons of SNSM vectors by using the standard st and likelihood ratio lr versions for the ordering proposed by Definition 2. The next proposition formalizes the issue.

Proposition 4

Let ${\textbf{X}}_i\sim SMSN_p(\varvec{\xi }_i,\varvec{\Omega }_i,\varvec{\alpha }_i, H_i)$ where $H_i$ is the CDF of $S_i$ and let $Q_i=({\textbf{X}}_i-\varvec{\xi }_i)'\varvec{\Omega }_i^{-1}({\textbf{X}}_i-\varvec{\xi }_i)$ be the associated quadratic forms for $i=1,2$. Then the following properties hold:

• (i) if $S_1\le _{st}S_2$, then $Q_{1}\le _{st}Q_{2}$ and consequently ${\varvec{X}}_1 \le _{st-tw} {\varvec{X}}_2$;

• (ii) if $S_1\le _{lr}S_2$, then $Q_{1}\le _{lr}Q_{2}$ and consequently ${\varvec{X}}_1 \le _{lr-tw} {\varvec{X}}_2$.

Note that the orderings derived in the preceding propositions are actually meaningful as they imply comparisons in dispersion (kurtosis) of the respective random vectors ${\textbf{X}}_1$ and ${\textbf{X}}_2$.

It is worthwhile noting that the $st-tw$ order does not hold for the skew-t since if $U_i\sim \chi _{\nu _i}^2/\nu _i$ for $i=1,2$, then $E(U_1)=E(U_2)=1$. So, if $S_1\le _{st} S_2$ holds, from Theorem 1.A.3 in Shaked and Shanthikumar (2007, p. 6.), $U_1\ge _{st}U_2$ holds. Therefore, taking into account Theorem 1.A.8 in Shaked and Shanthikumar (2007, p. 8.), we get $U_1{\mathop {=}\limits ^{st}}U_2$; and thus $S_1{\mathop {=}\limits ^{st}}S_2$ holds, i.e. $\nu _1=\nu _2$.

This is not the case of the skew-slash for which the following result is obtained.

Corollary 1

Let ${\varvec{X}}_i \sim SSL_p(\varvec{\xi }_i,\varvec{\alpha }_i,\varvec{\Omega }_i,q_i)$ for $i=1,2$. Then $0<q_1\le q_2$ implies $Q_1\ge _{lr} Q_2$ and as a result ${\varvec{X}}_2 \le _{lr-tw} {\varvec{X}}_1$.

For multivariate skew-contamined normal distributions we get the following direct result.

Corollary 2

Let ${\varvec{X}}_i \sim SCoN_p(\varvec{\xi }_i,\varvec{\alpha }_i,\varvec{\Omega }_i,\gamma _i,\epsilon _i)$ for $i=1,2$. Then $\gamma _1\le \gamma _2$ and $\epsilon _1<\epsilon _2$ imply $Q_1\le _{lr} Q_2$ and as a result ${\varvec{X}}_1 \le _{lr-tw} {\varvec{X}}_2$.

3.2 The convex transform order for tail weight comparisons

The non-normality of the SMSN distribution is regulated by the asymmetry shape vector $\varvec{\alpha }$ and the CDF H of the mixing variable. We also know that the distribution of the quadratic form $Q_X$ associated with a SMSN vector accounts for its non-normal behavior irrespective of location, scale and asymmetry. Thus, the tail weight stochastic comparison of SMSN vectors could be assessed by the comparison of their quadratic forms. The following definition adapts to the SNSM family a previous proposal on the convex transform ordering (Wang 2009).

Definition 3

Let ${\varvec{X}}_1$ and ${\varvec{X}}_2$ be vectors such that ${\varvec{X}}_i \sim SMSN_p(\varvec{\xi }_i,\varvec{\Omega }_i,\varvec{\alpha }_i,H_i)$ for $i=1,2$ with modular quadratic forms denoted by $Q_1$ and $Q_2$. We say that ${\varvec{X}}_1$ is less than or equal to ${\varvec{X}}_2$ in the convex transform tw-ordering, ${\varvec{X}}_1 \le _{c-tw} {\varvec{X}}_2$, if $Q_1\le _{c} Q_2$.

The definition settles the stochastic comparison of SMSN vectors in terms of Van Zwet’s transform order (Van Zwet 1964) of their quadratic forms $Q_1$ and $Q_2$. This is in turn implied by the convexity of the function $F_{Q_1}^{-1}(F_{Q_2}(x))$ with $F_{Q_i}$ the CDFs of $Q_i$ for $i=1,2$. Since $F_{Q_i}$ is usually indexed by a tail weight parameter, we now examine the connection between the $c-tw$ order and the tail weight parameters of some popular SMSN distributions.

3.2.1 The case of the multivariate skew-t distribution

The multivariate ST distribution arises when the mixing variable of the SMSN model is $S=V^{-1/2}$ with $V\sim \chi _\nu ^2/\nu$ (Azzalini and Capitanio 2003). Its PDF is given by (5).

The next proposition states that the order from Definition 3 is a total order within the ST family. It also enhances the relevance of the degrees of freedom $\nu$ to account for the tail weight/peaked behavior of the ST model.

Proposition 5

Let ${\varvec{X}}_1$ and ${\varvec{X}}_2$ be two p-dimensional random vectors such that ${\varvec{X}}_1 \sim ST_p(\varvec{\xi }_1,\varvec{\Omega }_1,\varvec{\alpha }_1,\nu _1)$ and ${\varvec{X}}_2 \sim ST_p(\varvec{\xi }_2,\varvec{\Omega }_2,\varvec{\alpha }_2,\nu _2)$. If $\nu _1\le \nu _2$ then ${\varvec{X}}_2 \le _{c-tw} {\varvec{X}}_1$..

3.2.2 The case of the multivariate skew-slash distribution

Recall that the multivariate SSL distribution is obtained when we take as mixing variable $S=U^{-1/2}$ with $U\sim Beta(q/2,1)$, where q is a tail weight parameter such that $q>0$.

In this section we study the relationship between the tail weight parameter q and the convex transform tw order in Definition 3. Actually, such connection implies that $c-tw$ is a total order within the SSL family as Proposition 6 shows. Before proving the proposition, we need a first lemma, which gives the CDF and the PDF of the modular quadratic variable associated to the SSL multivariate distribution, and a second instrumental lemma.

Lemma 1

Let ${\varvec{X}}$ be a random vector such that ${\varvec{X}} \sim SSL_p(\varvec{\xi },\varvec{\Omega },\varvec{\alpha },q)$. Then for every $p\ge 2$ its modular quadratic form $Q_X$ has a CDF and a unimodal PDF given respectively by

$$\begin{aligned}{} & {} F_{Q_{X}}(x)=G_{p}(x)-\left( \frac{2}{x}\right) ^{q/2} \frac{\Gamma \left( \frac{p+q}{2}\right) }{\Gamma \left( \frac{p}{2}\right) }G_{p+q}(x), \\{} & {} f_{Q_{X}}(x)=\frac{q}{4}\left( \frac{2}{x}\right) ^{q/2+1} \frac{\Gamma \left( \frac{p+q}{2}\right) }{\Gamma \left( \frac{p}{2}\right) }G_{p+q}(x) \end{aligned}$$

for $x > 0$ (zero otherwise), where $G_r$ is the CDF of a $\chi _r^2$ random variable.

The next lemma is concerned with the study of the behavior of an auxiliary function (the elasticity of the CDF of a chi-square random variable) related to the first derivative of $\log (f_{Q_{X}}(x))$.

Lemma 2

Let $M_r$ be the function defined by $M_r(x) =xg_r(x)/G_r(x)$ for $x > 0$, where $g_r$ and $G_r$ are the PDF and CDF of a $\chi ^2_r$ random variable with $r>2$. Then $M_r$ is a decreasing function in $(0,\infty )$ for which it holds that

$$\begin{aligned}{} & {} \lim _{x\rightarrow \infty } M_r(x) =\lim _{x\rightarrow \infty } M'_r(x) =0,\\{} & {} \lim _{x\downarrow 0} M_r(x)=\frac{r}{2} \,\hbox { and }\lim _{x\downarrow 0} M'_r(x)=-\frac{1}{2}\ \frac{r}{r+2}. \end{aligned}$$

It is worthwhile noting that the decreasing condition for  the behavior of $\displaystyle M_r$ implies that $\displaystyle \alpha (x)=xf_Q^\prime (x)/f_Q(x)$ is decreasing. This finding brings back condition (8) and shows that the elasticity function $\alpha$ associated to the PDF $f_Q$ is decreasing.

Now, we can establish the connection between the convex transform $c-tw$ order between SSL vectors and the tail weight parameter q of the multivariate model. The connection is stated by the following proposition.

Proposition 6

Let ${\varvec{X}}_1$ and ${\varvec{X}}_2$ be two p-dimensional random vectors such that ${\varvec{X}}_1 \sim SSL_p(\varvec{\xi }_1,\varvec{\Omega }_1,\varvec{\alpha }_1,q_1)$ and ${\varvec{X}}_2 \sim SSL_p(\varvec{\xi }_2,\varvec{\Omega }_2,\varvec{\alpha }_2,q_2)$ with $p\ge 2$. If $q_1<q_2$ then ${\varvec{X}}_2 \le _{c-tw} {\varvec{X}}_1$.

3.2.3 The case of the multivariate skew-contaminated normal distribution

We now come back to the multivariate skew-contaminated (SCoN) model which is obtained when the mixing variable is $S=U^{-1/2}$ with U a scalar variable having a discrete distribution (see Sect. 2.2).

In this case the inflation factor $\gamma$ of the SCoN distribution also serves to assess tail weight stochastic comparisons of skew-contaminated normal vectors in the $c-tw$ order provided that the vectors under comparison have the same mixing proportion $\epsilon$. This assertion can be proved by showing the convexity of the theoretical Q-Q plot for two scalar modular variables $Q_1$ and $Q_2$ with inflation factors $\gamma _1$ and $\gamma _2$ such that $\gamma _1\le \gamma _2$, i.e., the convexity of the function displaying the quantile function $F^{-1}_{Q_1}$ against $F^{-1}_{Q_2}$. Many numerical trials with R code have shown such convexity. The following proposition is a formal conjecture of these findings.

Proposition 7

Let ${\varvec{X}}_1$ and ${\varvec{X}}_2$ be two p-dimensional random variables such that ${\varvec{X}}_i \sim SCoN_p(\varvec{\xi }_i,\varvec{\alpha }_i,\varvec{\Omega }_i,\gamma _i,\epsilon )$ for $i=1,2$. Then $\gamma _1\le \gamma _2$ implies that ${\varvec{X}}_2 \le _{c-tw} {\varvec{X}}_1$.

3.3 Chebyshev’s type bounds for the tails

In this section we derive Chebyshev’s type bounds for which the mean vector and the covariance matrix are replaced by the location vector $\varvec{\xi }$ and the scale matrix $\varvec{\Omega }$ of the SMSN model. The bounds are based on the results of Proposition 3. They will show how the upper bounds for tail probabilities are related to the tail weight behavior of the models enhancing their relationship with tail weight non-normality parameters and the convex transform orderings of Sect. 3.2. These bounds give us information about the weight of the extreme values in the vector ${\varvec{X}}$; so they can also be seen as kurtosis measures.

Proposition 8

Let ${\varvec{X}}$ be a random vector such that ${\varvec{X}} \sim SMSN_p(\varvec{\xi },\varvec{\Omega },\varvec{\alpha },H)$. Then

$$\begin{aligned} \Pr (({\varvec{X}}- \varvec{\xi })^\prime \varvec{\Omega }^{-1}({\varvec{X}}- \varvec{\xi })\ge \varepsilon )\le \frac{p}{\varepsilon }E(S^2) \end{aligned}$$

(10)

for all $\varepsilon >0$, where S is the mixing variable and we assume that $E(S^2)$ is finite.

Note that the mean vector and covariance matrix used in the multivariate Chebyshev’s bounds are replaced here by the location vector $\varvec{\xi }$ and the scale matrix $\varvec{\Omega }$. Moreover, the bounds just depend on the second order moment $E(S^2)$ of the mixing scalar variable. Obviously, we can also obtain lower bounds for the probabilities in the ellipsoids defined from $\varvec{\xi }$ and $\varvec{\Omega }$ as follows:

$$\begin{aligned} \Pr (({\varvec{X}}- \varvec{\xi })^\prime \varvec{\Omega }^{-1}({\varvec{X}}- \varvec{\xi })<\varepsilon )\ge 1-\frac{p}{\varepsilon }E(S^2). \end{aligned}$$

Let us see some examples:

1. Multivariate skew-t. In this case we know that $S=U^{-1/2}$ with $U\sim \chi _\nu ^2/\nu$. Moreover, from the expression in Azzalini and Capitanio (2003, p. 381), we get

$$\begin{aligned} E(S^2)=E(U^{-1})=\frac{(\nu /2)\Gamma ((\nu -2)/2))}{\Gamma ( \nu /2)}=\frac{\nu }{\nu -2}. \end{aligned}$$

Therefore, from Proposition 8, we obtain

$$\begin{aligned} \Pr (({\varvec{X}}- \varvec{\xi })^\prime \varvec{\Omega }^{-1}({\varvec{X}}- \varvec{\xi })\ge \varepsilon )\le \frac{p}{\varepsilon }\frac{\nu }{\nu -2} \end{aligned}$$

for all $\varepsilon >0$. Note that the bound coincides with the bound for the associated non-mixed vector and with the bound for the classical multivariate Chebyshev’s inequality when $\nu \rightarrow \infty$.

2. Multivariate skew-slash. In this case we know that $S=U^{-1/2}$ with $U\sim Beta (q/2,1)$. Then a straightforward calculation shows that $\displaystyle E(S^2)=\frac{q}{q-2}$ for $q>2$. Therefore, from Proposition 8, we obtain

$$\begin{aligned} \Pr (({\varvec{X}}- \varvec{\xi })^\prime \varvec{\Omega }^{-1}({\varvec{X}}- \varvec{\xi })\ge \varepsilon )\le \frac{pq}{(q-2)\varepsilon } \end{aligned}$$

for all $\varepsilon >0$ and all $q>2$. Note that this bound is decreasing in q and that the bound for the associated non-mixed vector and the bound for the classical multivariate Chebyshev’s inequality are obtained when $q\rightarrow \infty$.

3. Multivariate skew-contaminated. In this case $S=U^{-1/2}$ with

$$\begin{aligned} P(U=\gamma )=\epsilon \,\,\hbox { and } \, P(U=1)=1-\epsilon \end{aligned}$$

where $0\le \epsilon \le 1$ is a parameter quantifying the amount of contamination and $0<\gamma \le 1$ is a scale inflation factor.

Then a straightforward calculation shows that $E(S^2)=1-\epsilon +\gamma ^{-1} \epsilon$. Therefore, from Proposition 8, we obtain

$$\begin{aligned} \Pr (({\varvec{X}}- \varvec{\xi })^\prime \varvec{\Omega }^{-1}({\varvec{X}}- \varvec{\xi })\ge \varepsilon )\le \frac{p(1-\epsilon +\gamma ^{-1} \epsilon )}{\varepsilon } \end{aligned}$$

for all $\varepsilon >0$. The bounds for the non-mixed vector and for the classical multivariate Chebyshev’s inequality are obtained when $\epsilon \rightarrow 0$ or $\gamma \rightarrow 1$.

3.4 Other stochastic orders from the canonical form of SMSN vectors

Another relevant property of SN and SMSN multivariate models is concerned with the canonical form of SN and SMSN multivariate distributions (Azzalini and Capitanio 1999; Loperfido 2010; Capitanio 2020) which allows to transform the input vector into a new one that absorbs all the multivariate asymmetry into a single component. This property is stated by the following proposition borrowed from Capitanio (2020).

Proposition 9

Let us consider a vector ${\varvec{X}}$ such that ${\varvec{X}} \sim SMSN_p(\varvec{\xi },\varvec{\Omega },\varvec{\alpha },H)$ with stochastic representation: ${\varvec{X}}=\varvec{\xi }+\varvec{\omega }{\varvec{Y}}$, where ${\varvec{Y}} = S{\varvec{Z}}$ and ${\varvec{Z}} \sim SN_p({\varvec{0}},\overline{\varvec{\Omega }},\varvec{\alpha })$ with H the CDF of the mixing variable S. Then there exists a transformation ${\varvec{Y}}^*={\varvec{C}} {\varvec{Y}}$, with ${\varvec{C}}$ a matrix such that the components of ${\varvec{Y}}^*$ are uncorrelated variables with only one component (say the first one) following a skewed distribution and the others being non-skewed variables. Moreover, the first canonical variable $Y_1^*$ is a scale mixture of SN variables such that $Y_1^*=S Z_1^*$ with $Z_1^*\sim SN_1(0,1,\alpha _*)$ and $\alpha _*=(\varvec{\alpha }^\prime \overline{\varvec{\Omega }}\varvec{\alpha })^{1/2}$.

When the mixing variable is degenerate at $S=1$ , then ${\varvec{X}} \sim SN_p(\varvec{\xi },\varvec{\Omega },\varvec{\alpha })$. In this case, the canonical components are independent scalar variables such that $Z_1^*\sim SN_1(0,1,\alpha _*)$ with $\alpha _*=(\varvec{\alpha }^\prime \overline{\varvec{\Omega }}\varvec{\alpha })^{1/2}= (\varvec{\eta }^\prime \varvec{\Omega }\varvec{\eta })^{1/2}$, whereas the remaining non-skewed variables follow a standard normal distribution (Azzalini 2005; Capitanio 2020).

In order to compare SNSM vectors in asymmetry, we resort to their canonical representation in Proposition 9. Our proposal settles the problem in terms of the canonical transformation of the SMSN input vectors by comparing the skewed components of their canonical forms. The idea is inspired by previous work (Arevalillo and Navarro 2019) and can be formalized as follows.

Definition 4

Let ${\varvec{X}}_1$ and ${\varvec{X}}_2$ be two multivariate random variates such that ${\varvec{X}}_i \sim SMSN_p(\varvec{\xi }_i,\varvec{\Omega }_i,\varvec{\alpha }_i,H)$ for $i=1,2$ and let us denote by $Y_1^{*(i)}=S Z_1^{*(i)}$ for $i=1,2$ their skewed canonical components, where $Z_1^{*(i)}\sim SN_1(0,1,\alpha _{*}^{(i)})$ with $\alpha _{*}^{(i)}=(\varvec{\alpha }_i^\prime \overline{\varvec{\Omega }}_i\varvec{\alpha }_i)^{1/2}$ for $i=1,2$. Then we say that ${\varvec{X}}_1$ is less skewed than ${\varvec{X}}_2$ in a specified $*$-order (shortly written ${\textbf{X}}_1\le _{*-sk}{\textbf{X}}_2$) if such order holds for the skewed canonical variables, that is, $Y_1^{*(1)}\le _{*} Y_1^{*(2)}$.

Clearly, three reasonable choices for the $*$-order may be the usual st stochastic order, the likelihood ratio order lr and the convex transform order. Now we can state the following result for the $st-sk$ order which is an immediate consequence of Propositions 1 and 2.

Proposition 10

Let ${\varvec{X}}_1$ and ${\varvec{X}}_2$ be two multivariate random variates such that ${\varvec{X}}_i \sim SMSN_p(\varvec{\xi }_i,\varvec{\Omega }_i,\varvec{\alpha }_i,H_i)$ for $i=1,2$, with skewed canonical scalar variables $Y_1^{*(i)}=S Z_1^{*(i)}$ for $i=1,2$ such that $Z_1^{*(i)}\sim SN_1(0,1,\alpha _{*}^{(i)})$ with $\alpha _{*}^{(i)}=(\varvec{\alpha }_i^\prime \overline{\varvec{\Omega }}_i\varvec{\alpha }_i)^{1/2}$ for $i=1,2$. Then $0<\alpha _{*}^{(1)}<\alpha _{*}^{(2)}$ implies ${\textbf{X}}_1\le _{st-sk}{\textbf{X}}_2$.

The result of the proposition has an outstanding implication when the SNSM input vectors share the same scale matrix, i.e., when $\varvec{\Omega }_1=\varvec{\Omega }_2=\varvec{\Omega }$. In this case the dominating multivariate distribution with respect to the $st-sk$ ordering is attained for a shape vector proportional to the dominant eigenvector of the common scale matrix $\varvec{\Omega }$ or, equivalently, the maximal asymmetric distribution in terms of the $st-sk$ ordering is determined by a shape vector lying on the direction of the first principal component of the scale matrix $\varvec{\Omega }$.

4 Application to environmental data

Previous applied work on stochastic comparisons of environmental data focused on skewness (Mulero et al. 2016). Our application contributes by addressing kurtosis within the multivariate scenario framed by our theoretical findings. In this section we address the comparison of extreme records in environmental data related to maximum temperatures during the period from 1901 to 2014 in the Spanish Iberian Peninsula. The STEAD (Spanish TEmperature At Daily scale) dataset contains a high-resolution grid of daily maximum temperatures covering the whole Spanish peninsular territory during the aforementioned period. The records were obtained by application of data quality control and gridding procedures to temperature values recorded by climate observatory stations (Serrano-Notivoli et al. 2019).

The application of our theoretical findings to this type of data has interest on its own since the assessment of changes in extreme records of temperature data is nowadays a hot topic in environmental studies. Our goal is to elucidate whether summers evolve towards more extreme temperature episodes along time. A simple visualization analysis, which uses heat temperature maps for specific dates seems to highlight the previous hypothesis, as shown by the plots depicted in Fig. 1. More detailed visualizations are provided by the animations of the Supplementary Material, which show how summer temperatures evolve along time . Although visual inspection seemingly highlights temperature changes along time, we need a theoretically supported tool that can confirm our initial guess. Our results on stochastic orderings in connection with the role played by the tail weight parameter in the SMSN family are helpful to address this need.

To illustrate the application of our theoretical results in the assessment of temperature changes along the period of study, we consider a few locations representing three different climate scenarios in the Iberian Península: Continental, Mediterranean of the East coast of Spain and Atlantic of the North coast. For the first one we take interior cities: Ávila, Burgos, Cuenca, Guadalajara, Madrid, Palencia, Segovia, Soria, Toledo and Valladolid. For the second one, the locations Alicante, Almería, Castellón de la Plana, Murcia and Valencia at the East coast, whereas for the third scenario we focus on the North coast locations: Bilbao, Coruña, Oviedo, Pontevedra, Santander and San Sebastián.

A data filtering first step is carried out to extract daily max temperatures at the selected locations for the summer months June, July and August. Then the data are arranged in a matrix format for the comparison of extreme temperature by decades during a period that comprises eleven decades (from 1901–1910 to 2001–2010). The facilities of the raster R package (Hijmans 2022) are employed to achieve all these data management tasks so we end up with $10488 \times 10$, $10488 \times 5$ and $10488 \times 6$ matrices for the Continental, Mediterranean and Atlantic scenarios.

Fig. 1

Heat maps of maximum temperatures for the following specific dates: 1901-07-15 (top left), 1951-07-15 (top right), 2001-07-15 (bottom left) and 2013-07-15 (bottom right). For more maps see the animations of the Supplementary Material

We now carry out statistical testing to assess the multivariate normality of the data obtained after the processing step. The following statistical tests are used: Shapiro–Wilk’s test (Villasenor Alva and Estrada 2009;  Gonzalez-Estrada 2017), the skewness and kurtosis tests implemented in the ICS R package (Nordhausen et al. 2008), and also (Mardia 1974), Henze–Zirkler (Henze and Zirkler 1990), Doornik-Hansen (Doornik and Hansen 2008) tests implemented in the MVN R package (Korkmaz et al. 2014). The p-values obtained from the tests are shown in Tables 1, 2 and 3 for the Atlantic, Continental and Mediterranean climate scenarios and three representative decades. The results show that the normality hypothesis is rejected in all the cases (similar results, not reported here for the sake of space, are obtained for the other decades). Moreover, the estimations of multivariate Mardia skewness and kurtosis measures (2) and (1) are also provided for completeness at the last two rows of the tables. The resulting estimations also highlight the multivariate non-normality of the data.

Table 1 p-Values of non-normality tests and multivariate Mardia skewness and kurtosis measures (Atlantic scenario)

Table 2 p-Values of non-normality tests and multivariate Mardia skewness and kurtosis measures (Continental scenario)

Table 3 p-Values of non-normality tests and multivariate Mardia skewness and kurtosis measures (Mediterranean scenario)

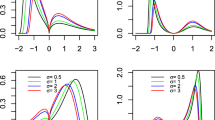
Once the multivariate normality has been rejected, we will use P–P plots to assess the goodness-of-fit of other models. The P–P plots of Fig. 2 have been depicted using the tools provided by the sn R package (Azzalini 2022) and they allow to visualize the goodness-of-fit of normal, SN and ST distributions for the decades: 1901-1910, 1951-1960 and 2001-2010. They show that the ST model gives the best fit for all decades and climate scenarios— with the most remarkable differences between the ST and the other fits being observed for the last decade—and the normal model the worst fit as expected. Hence, we advocate the use of the ST distribution for modeling multivariate data on maximum temperatures. Actually, this is a flexible model for handling tail weight and asymmetry deviations from the multivariate normal distribution, as the P–P plots reveal.

The convex transform tail weight ordering, together with the results established by Proposition 5, are helpful to interpret the stochastic comparison of multivariate maximum temperature data in terms of the evolution of extreme records so that we can assess whether summers are evolving towards scenarios having more episodes of extreme values. The evolution of extreme episodes along time can be assessed by the estimation of the tail weight parameter $\nu$ of the ST model from data for all the decades under consideration. The function selm of the sn R package (Azzalini 2022) is used to carry out the estimation. The results provide revealing findings, as shown by the left plot of Fig. 3, which displays the estimations of the tail weight parameter from the first decade ($1901-1910$) to the last one ($2001-2010$) for the locations corresponding to the Atlantic, Continental and Mediterranean climate scenarios. It can be observed a decreasing trend along the time, which means that temperatures have evolved towards more extreme summers along time. Perhaps this fact is less noticeable for the locations at the Continental scenario, as the smoother decay of the tail weight estimations is highlighted. Interestingly, the estimations of Mardia kurtosis measure (1) by decade apparently follow an increasing trend (see the right plot of Fig. 3). This is a quite natural observation since the higher tail weights correspond to the lower kurtosis values.

Fig. 2

P–P plots for Normal (blue), SN (green) and ST (red) fits of daily maximum temperature data at the climate scenarios: Atlantic (top), Continental (middle) and Mediterranean (bottom) at the selected locations for the periods $1901-1910$ (left), $1951-1960$ (middle) and $2001-2010$ (right)

Fig. 3

Plots showing the estimations of the tail weight parameter (left) and multivariate Mardia kurtosis measure (right) along time for the Atlantic (green), Continental (blue) and Mediterranean (brown) scenarios

5 Discussion and concluding remarks

This work has revisited the scale mixtures of skew-normal distributions with some proposals to carry out stochastic comparisons. Our purpose is to provide a grounded theoretical support to assess the comparisons of extreme records in environmental data. As these data usually exhibit obvious departures from multivariate normality, we advocate the use of SMSN models to handle the non-normal features of data as well as the use of stochastic orders to assess changes in extreme environmental records along time. As a result, conclusions on climate changes can be supported by solid theoretical results on stochastic orderings.

The proposals for the stochastic comparisons rely on the quadratic form of the SMSN vector whose distribution depends on a single tail weight parameter. Using this property, some novel multivariate stochastic ($st-tw$), likelihood ratio ($lr-tw$) and convex transform ($c-tw$) orders have been proposed and investigated. We have found that the convex transform order is well suited for the stochastic comparison of SMSN vectors with the tail weight parameters of their distributions being indicators compatible with the proposed ordering. Therefore, the comparisons of extreme records can be assessed in these models by a single parameter which can be estimated from data. For example, in the specific case of the ST distribution, the tail weight parameter $\nu$ is compatible with the convex transform tw-ordering, so there is theoretical support for comparing ST vectors by means of a single parameter $\nu$. As a result, the present paper provides a theoretically supported tool to carry out the assessment of extreme temperature changes by estimating the tail weight parameter along time.

The application to elucidate whether there exist changes on summer extreme temperatures during the last century in Spain illustrates the usefulness of our results when applied to environmental studies. Temperature changes for Atlantic, Continental and Mediterranean climates were assessed through the stochastic comparison of multivariate ST models. Our findings revealed an evolving trend in time towards summers having more extreme temperature episodes, with a remarkable pattern being observed at the Mediterranean climate scenario. Therefore, we can conclude the existence of temperature changes during the last century period, a conclusion supported by our theoretical results on the multivariate convex transform stochastic order.

Our findings hint at several future research problems: firstly, the study of the canonical form of SMSN vectors along with related stochastic orders, as outlined in Sect. 3.4. We think that previous work  (Arevalillo and Navarro 2019) may help to progress along this line. The second point is about the generalization of our results to wider families of distributions like skew-elliptical distributions (Genton 2004; Adcock and Azzalini 2020) and generalized skew-elliptical distributions (Genton and Loperfido 2005) or, on the contrary, focusing on specific families like for example the multivariate skew-exponential power (Arevalillo and Navarro 2023). Finally, the application to other type of environmental studies like rainfall data, drought data and so on would strength the potential of the theoretical tools on stochastic orders discussed in this paper.

Appendix A Proofs

Proof of Proposition 1

To prove (i) we write the CDF of $S_iZ$ as

$$\begin{aligned} G_i(x)=\Pr (S_iZ\le x)=\int _0^\infty F_i(x/s) g(s)ds \end{aligned}$$

for $i=1,2$, where $G,F_1,F_2$ are the CDFs of $Z,S_1,S_2$. Then we note that $S_1\le _{st}S_2$ implies $F_1\ge F_2$. Hence, for any fixed real value x, we get

$$\begin{aligned} G_1(x)=\int _0^\infty F_1(x/s) g(s)ds\ge \int _0^\infty F_2(x/s) g(s)ds=G_2(x). \end{aligned}$$

Therefore $G_1\ge G_2$, and so $S_1Z\le _{st}S_2Z$ holds.

To prove (ii) we note that the CDF of $s_iZ$ can be written for $x\ge 0$ as $H_i(x)=\Pr (s_iZ\le x)=G(x/s_i)$. Hence its PDF is $h_i(x)=(1/s_i)g(x/s_i)$. To prove that $s_1Z\le _{lr}s_2Z$ we consider the ratio of the respective PDFs

$$\begin{aligned} r(x)=\frac{h_{2}(x)}{h_{1}(x)}=\frac{s_1g(x/s_2)}{s_2g(x/s_1)}. \end{aligned}$$

Its derivative satisfies

$$\begin{aligned} \frac{s_2}{s_1}\frac{g(x/s_1)}{g(x/s_2)}xr'(x)= \frac{(x/s_2)g'(x/s_2)}{g(x/s_2)}- \frac{(x/s_1)g'(x/s_1)}{g(x/s_1)}. \end{aligned}$$

As $0<s_1<s_2$, then $x/s_1>x/s_2>0$ and, by using (8), we get $r'(x)\ge 0$ for $x>0$. Hence, r is increasing, so it holds that $s_1Z\le _{lr}s_2Z$.

Finally, item (iii) is proved by writing the PDF of $S_iZ$ for $i=1,2$ as

$$\begin{aligned} g_i(x)=\int _0^\infty \frac{1}{s} g(x/s) f_i(s)ds=E_{S_i}\left[ (1/S_i) g(x/S_i) \right] . \end{aligned}$$

Here $h_s(x)=(1/s)g(x/s)$ is the PDF of sZ for a given $s>0$. Therefore, $g_i$ is a mixture of the PDFs $h_s$ with mixing PDF $f_i$. Then, from $S_1\le _{lr}S_2$, $s_1Z\le _{lr}s_2Z$ for $s_1<s_2$, and Theorem 1.C.17 in Shaked and Shanthikumar (2007), we obtain that $S_1Z\le _{lr}S_2Z$. $\square$

Proof of Proposition 2

Let us denote by $F_1$ and $F_2$ the CDFs of $Z_1$ and $Z_2$. The CDF of a SN variable has a well-known analytical form (Azzalini 1985) so we can put

$$\begin{aligned} F_i(x)=\Phi (x)-2T(x,\alpha _i), \text { for }i=1,2, \end{aligned}$$

where $\displaystyle T(x,\lambda )=\phi (x)\int _0^\lambda \frac{\phi (xz)}{1+z^2}\,dz$ is the Owen’s T function and $\phi$ the standard normal PDF. Since $0\le T(x,\alpha _1)\le T(x,\alpha _2)$ for $\alpha _1\le \alpha _2$, we get $F_1(x)\ge F_2(x)$ for all x, as we aimed to prove. $\square$

Proof of Proposition 3

From the stochastic representation of the SMSN vector and the application of Corollary 5.9 in Azzalini and Capitanio (2014), it follows that $Q_{X}{\mathop {=}\limits ^{st}} Q_{X_0}$. On the other hand, from (9) we get $R^2=({\varvec{X}}_0- \varvec{\xi })^\prime \varvec{\Omega }^{-1}({\varvec{X}}_0- \varvec{\xi })=Q_{X_0}$ which implies that $Q_{X}{\mathop {=}\limits ^{st}} R^2$. $\square$

Proof of Proposition 4

As we have mentioned before, the quadratics forms $Q_{X_i}$ are equal in distribution to $S_i^2Q$ for $i=1,2$, where Q is an independent random variable with a $\chi ^2_p$ distribution.

From Theorem 1.A.3 in Shaked and Shanthikumar (2007, p. 6). and $S_1\le _{st}S_2$, we get $S_1^2\le _{st}S_2^2$. Hence the proof of item (i) is immediate from our result in Proposition 1 (i) and from Theorem 1.A.3 in Shaked and Shanthikumar (2007, p. 6).

In order to prove (ii), we note that the PDF of Q is

$$\begin{aligned} g(x)= c x^{p/2-1} e^{-x/2} \end{aligned}$$

for $x>0$ (zero elsewhere), where c is the normalizing constant. Hence

$$\begin{aligned} g'(x)= c (p/2-1)x^{p/2-2} e^{-x/2}- (c/2) x^{p/2-1} e^{-x/2} \end{aligned}$$

and

$$\begin{aligned} \frac{xg'(x)}{g(x)}=\frac{(p/2-1)x^{p/2-1} e^{-x/2}- (1/2) x x^{p/2-1} e^{-x/2}}{x^{p/2-1} e^{-x/2}}=\frac{p}{2}-1-\frac{1}{2} x. \end{aligned}$$

Therefore, g satisfies (8).

On the other hand, from Theorem 1.C.8 in Shaked and Shanthikumar (2007, p. 46), $S_1\le _{lr}S_2$ implies $S^2_1\le _{lr}S^2_2$ since $S_1$ and $S_2$ are non-negative random variables and $\psi (x)=x^2$ is increasing in $(0,\infty )$. Hence, from Proposition 1 (iii) we get $Q_{X_1}\le _{lr}Q_{X_2}$. $\square$

Proof of Corollary 1

As we have mentioned above, $Q_i$ is equal in law to $S_i^2 Q$ where $S_i$ and Q are independent random variables, Q has a $\chi ^2_p$ distribution and $S_i^2=U_i^{-1}$ with $U_i$ a $Beta(q_i/2,1)$ random variable having PDF

$$\begin{aligned} f_i(u)=\frac{q_i}{2} u^{q_i/2-1} \end{aligned}$$

for $u\in (0,1)$ and $i=1,2$. Hence, since $q_1<q_2$ the ratio of PDFs:

$$\begin{aligned} \displaystyle \frac{f_2(u)}{f_1(u)}= \frac{q_2}{q_1} u^{(q_2-q_1) /2} \end{aligned}$$

(A1)

is increasing for $u\in (0,1)$. So $U_1\le _{lr}U_2$ holds. Then from Theorem 1.C.8 in Shaked and Shanthikumar (2007, p. 46), $U_1\le _{lr}U_2$ implies $S_1\ge _{lr}S_2$. Finally, from Proposition 4, (ii), we get $Q_1\ge _{lr} Q_2$. $\square$

Proof of Corollary 2

As we have mentioned above, $Q_i$ is equal in law to $S_i^2 Q$ where $S_i$ and Q are independent random variables such that Q follows a $\chi ^2_p$ distribution and $S_i^2$ is a discrete variable taking the values $S_i^2=\gamma _i$ and $S_i^2=1$ with probabilities $\epsilon _i\in (0,1)$ and $1-\epsilon _i$ for $i=1,2$. Hence, $Q_i$ has a mixture distribution of $\gamma _iQ$ and Q with mixing probabilities $\epsilon _i$ and $1-\epsilon _i$ for $i=1,2$.

Note that $0<\gamma _1\le \gamma _2\le 1$, implies

$$\begin{aligned} \gamma _1Q\le _{lr} \gamma _2Q\le _{lr} Q. \end{aligned}$$

Moreover, if $Z_i$ represents the discrete random variable which takes the values 0 and 1 with probabilities $\epsilon _i$ and $1-\epsilon _i$, respectively for $i=1,2$, then $Z_1\le _{lr}Z_2$ holds. Finally, by applying Theorem 1.C.17 in Shaked and Shanthikumar (2007, p. 49-for discrete mixing distributions), we get the result of the statement. $\square$

Proof of Proposition 5

From the statement of Proposition 3 it follows that $Q_{i}{\mathop {=}\limits ^{st}} Q^0_{i}: i=1,2$, where $Q^0_{i}$ are the quadratic forms defined by

$$\begin{aligned} Q^0_{i} =({\varvec{X}}^0_{i}- \varvec{\xi }_i)^\prime \varvec{\Omega }_i^{-1}({\varvec{X}}^0_{i}- \varvec{\xi }_i), \end{aligned}$$

with ${\varvec{X}}^0_{i}$ a random vector following a multivariate t distribution with $\nu _i$ degrees of freedom for $i=1,2$. Since the quadratic forms $Q^0_{i}$ are the squared modular variables of multivariate Student-t models, the result will follow by application of Theorem 3.2 and Corollary 3.1 of Wang (2009). $\square$

Proof of Lemma 1

We know that $Q_X{\mathop {=}\limits ^{st}}U^{-1}Q$, where U and Q are independent Beta(q/2, 1) and $\chi _p^2$ variables, respectively. Then its CDF is

$$\begin{aligned} F_{Q_{X}}(x)=P(Q_{X}\le x)=\int _{0}^{\infty }B(x/s)g_p(s)ds \end{aligned}$$

with B the CDF of $U^{-1}$ (defined by $B(u)=1-u^{-q/2}$ if $u>1$ and $B(u)=0$ otherwise) and $g_p$ the PDF of a $\chi _p^2$ random variable. Consequently,

$$\begin{aligned} F_{Q_{X}}(x)=\int _{0}^{x}[1-(s/x)^{q/2}]g_p(s)ds= G_{p}(x)-\left( \frac{2}{x}\right) ^{q/2} \frac{\Gamma \left( \frac{p+q}{2}\right) }{\Gamma \left( \frac{p}{2}\right) }G_{p+q}(x). \end{aligned}$$

Its first derivative gives the PDF of the statement by considering that

$$\begin{aligned} \displaystyle \left( \frac{2}{x}\right) ^{q/2} \frac{\Gamma \left( \frac{p+q}{2}\right) }{\Gamma \left( \frac{p}{2}\right) }G_{p+q}^\prime (x)=G_{p}^\prime (x). \end{aligned}$$

The unimodality can be proved as follows: let us write $f_Q$ as

$$\begin{aligned} f_{Q_{X}}(x)=c x^{-1-q/2}G_{p+q}(x) \end{aligned}$$

for a constant $c>0$. Then

$$\begin{aligned} \displaystyle \frac{1}{c} x^{2+q/2}f'_{Q_{X}}(x)=x g_{p+q}(x)-\left( 1+\frac{q}{2}\right) G_{p+q}(x). \end{aligned}$$

So we need to study the function

$$\begin{aligned} \psi (x)=x g_{p+q}(x)-\left( 1+\frac{q}{2}\right) G_{p+q}(x) \end{aligned}$$

for $x\in [0,\infty )$. Clearly $\psi (0)=0$ and $\psi (\infty )=-1-q/2<0$. Moreover,

$$\begin{aligned} \psi '(x)=g_{p+q}(x)+x g'_{p+q}(x)-\left( 1+\frac{q}{2}\right) g_{p+q}(x)=g_{p+q}(x)\left( x(\log (g_{p+q}(x)))'-\frac{q}{2}\right) \end{aligned}$$

with

$$\begin{aligned} \log (g_{p+q}(x))=-\frac{p+q}{2} \log 2-\log \Gamma \left( \frac{p+q}{2}\right) +\left( \frac{p+q}{2}-1\right) \log x-\frac{x}{2}. \end{aligned}$$

Hence

$$\begin{aligned} (\log (g_{p+q}(x)))'= \left( \frac{p+q}{2}-1\right) \frac{1}{x}-\frac{1}{2} \end{aligned}$$

and

$$\begin{aligned} \frac{\psi '(x)}{g_{p+q}(x)}=\frac{p+q}{2}-1-\frac{x}{2}-\frac{q}{2} =\frac{p-2}{2}-\frac{x}{2}. \end{aligned}$$

Therefore, for $p>2$, $\psi$ is increasing in $[0,p-2]$ and decreasing in $[p-2,\infty )$. As it is continuous in $[0,\infty )$, $\psi (0)=0$ and $\psi (\infty )=-1-q/2<0$, there exists a unique $x_0>0$ such that $\psi (x_0)=0$, being $\psi$ positive in $[0,x_0)$ and negative in $(x_0,\infty )$. Therefore, $f_{Q_X}$ is strictly increasing in $[0,x_0]$ and strictly decreasing in $[x_0,\infty )$, having a unique maximum value at $x_0$.

For $p=2$, $\displaystyle \frac{\psi '(x)}{g_{p+q}(x)}=-\frac{x}{2}\le 0$. Hence, $\psi (x)\le 0$ and $f_{Q_X}$ has a unique maximum at $x_0=0$, being strictly decreasing in $[0,\infty )$; so it is unimodal. $\square$

Proof of Lemma 2

It is straightforward that the derivative of $\log (M_r(x))$ is

$$\begin{aligned} \frac{M_{r}^\prime (x)}{M_{r}(x)}=\frac{1}{x}+\frac{g_{r}^\prime (x)}{g_{r}(x)}-\frac{g_{r}(x)}{G_{r}(x)} =\frac{1}{x}\left[ \frac{r}{2}-\frac{x}{2}-\frac{xg_{r}(x)}{G_{r}(x)}\right] =\frac{1}{x}\left[ \frac{r}{2}-1-\frac{x}{2}-\frac{\Psi (x)}{G_{r}(x)}\right] \end{aligned},$$

where the function $\Psi$ is defined as $\Psi (x)=xg_r(x)-G_r(x)$ for $x\ge 0$. For this function, we have $\Psi (0)=0$, $\Psi (\infty )= -1$ and $\Psi ^\prime (x)= x g_r^\prime (x)$. The expression above can be rewritten as $[\log (M_{r}(x))]'=R(x)/(xG_{r}(x))$, where

$$\begin{aligned} R(x)=xG_{r}(x)\frac{M_{r}^\prime (x)}{M_{r}(x)} =\left( \frac{r}{2}-1 \right) G_{r}(x)-\frac{x}{2}G_{r}(x)-\Psi (x) \end{aligned},$$

whose first derivative is given by

$$\begin{aligned} R^\prime (x)&=\left( \frac{r}{2}-1 \right) g_{r}(x)-\frac{1}{2}G_{r}(x)-\frac{x}{2}g_{r}(x)-\left( \frac{r}{2}-1 \right) g_{r}(x)+\frac{x}{2}g_{r}(x)=-\frac{1}{2}G_{r}(x) \end{aligned},$$

Then R is a decreasing function such that $R(0)=0$ and $R(\infty )=-\infty$. Hence, $R(x)<0$ for all $x>0$ which in turn implies that $M_{r}$ is decreasing in $(0,\infty )$.

The first two limits of the statement for $x\rightarrow \infty$ are straightforward. For the third one, L’Hôpital’s rule and some simple calculations lead to

$$\begin{aligned} \lim _{x\downarrow 0} M_{r}(x)&=\lim _{x\downarrow 0} \frac{g_{r}(x)+xg_{r}^\prime (x)}{g_{r}(x)}= \lim _{x\downarrow 0}\left[ 1+\frac{r}{2}-1-\frac{x}{2}\right] =\frac{r}{2}. \end{aligned}$$

For the last limit we have

$$\begin{aligned} \lim _{x\downarrow 0} M^\prime _{r}(x)&=\lim _{x\downarrow 0} M_{r}(x) \frac{R(x)}{xG_{r}(x)}=\frac{r}{2} \lim _{x\downarrow 0} \frac{R(x)}{xG_{r}(x)} \end{aligned}$$

and by applying again L’Hôpital’s rule we get

$$\begin{aligned} \lim _{x\downarrow 0} M^\prime _{r}(x)&= \frac{r}{2} \lim _{x\downarrow 0} \frac{R(x)}{xG_{r}(x)}=\frac{r}{2} \lim _{x\downarrow 0} \frac{R'(x)}{G_{r}(x)+xg_{r}(x)}\\&=-\frac{r}{4} \lim _{x\downarrow 0} \frac{G_r(x)}{G_{r}(x)+xg_{r}(x)}=-\frac{r}{4} \lim _{x\downarrow 0} \frac{1}{1+M_{r}(x)}=-\frac{1}{2}\ \frac{r}{r+2}. \end{aligned}$$

$\square$

Proof of Proposition 6

We use $+$ and − to denote the positiveness and negativeness of a function and the symbols $\nearrow$ and $\searrow$ to denote its increasing and decreasing behavior.

Let $Q_1$ and $Q_2$ be the modular quadratic forms associated to ${\varvec{X}}_1$ and ${\varvec{X}}_2$ with $F_{Q_1}$ and $F_{Q_2}$ their CDFs. To prove the ordering $F_{Q_2}\le _c F_{Q_1}$, we must show that $C(x)=F_{Q_1}^{-1}(F_{Q_2}(x))$ is convex for $x\ge 0$; so it will suffice to show that, for any straight line $a+bx$, the function $C(x)-(a+bx)$ has at most two zeros and whenever it has two zeros it takes negative values between them.

The proof is trivial when $b\le 0$ since C is a strictly increasing function. The case $b> 0$ requires more lengthy arguments as follows: Let us define the function $D(x)=F_{Q_2}(x)-F_{Q_1}(a+bx)$ for $x\ge 0$. We can see that the number of zeros of $C(x)-(a+bx)$ is equal to the number of zeros of the function D.

The function D has limit behavior: $\lim _{x\rightarrow \infty } D(x)=0$ and $D(0)=0$ if $a\le 0$, $D(0)=-F_{Q_1}(a)<0$ if $a>0$. On the other hand, its first derivative is given by

$$\begin{aligned} D^\prime (x)=F_{Q_2}^\prime (x)-bF_{Q_1}^\prime (a+bx)=f_{Q_2}(x)-bf_{Q_1}(a+bx) \end{aligned}$$

where $f_{Q_2}(x)$ and $bf_{Q_1}(a+bx)$ are the PDFs of the scalar variables $Q_2$ and $(Q_1-a)/b$ (see Lemma 1). Its limit behavior is given by $\lim _{x\rightarrow \infty } D^\prime (x)=0$ and

$$\begin{aligned} \lim _{x\downarrow 0} D^\prime (x)= {\left\{ \begin{array}{ll} \frac{1}{2}\left( \frac{q_2}{q_2+2}-b\frac{q_1}{q_1+2}\right) , &{} \,\hbox {if } p=2 \,\hbox { with } a=0 \\ \frac{1}{2}\frac{q_2}{q_2+2}, &{} \,\hbox {if } p=2 \,\hbox { with } a<0 \\ 0, &{} \,\hbox {if } p>2 \,\hbox { with } a\le 0 \\ \frac{1}{2}\frac{q_2}{q_2+2}-bf_{Q_1}(a), &{} \,\hbox {if } p=2 \,\hbox { with } a>0 \\ -bf_{Q_1}(a), &{} \,\hbox {if } p>2 \,\hbox { with } a>0 \end{array}\right. } \end{aligned}.$$

We now consider all the possible alternatives.

For $a=0$ and $b\le 1$ we put $\displaystyle D^\prime (x)=bf_{Q_1}(bx)[f_{Q_2}(x)/bf_{Q_1}(bx)-1]$. The number of zeros of $D^\prime$ coincides with the number of crossings between $f_{Q_2}(x)/bf_{Q_1}(bx)$ and the horizontal line $y=1$. From Lemmas 1 and 2 it is obtained that

$$\begin{aligned} \displaystyle \frac{xf_Q^\prime (x)}{f_Q(x)}=M_{p+q}(x)-\left( \frac{q}{2}+1\right) \end{aligned}$$

is a decreasing function so the PDF $f_Q$ meets the condition in (8) and, as a result, we get $Q_1\le _{lr}Q_1/b$ by simple application of Proposition 1 (ii). This finding, together with Corollary 1, will lead to $Q_2\le _{lr}Q_1\le _{lr}Q_1/b$ which in turn implies that $f_{Q_2}(x)/bf_{Q_1}(bx)$ is $\searrow$. Moreover, as we know that

$$\begin{aligned} \lim _{x\rightarrow \infty }\frac{f_{Q_2}(x)}{bf_{Q_1}(bx)}=C(p,q,b)\lim _{x\rightarrow \infty }x^{\frac{q_1-q_2}{2}} \frac{G_{p+q_2}(x)}{G_{p+q_1}(bx)}=0, \end{aligned}$$

with C(p, q, b) summarizing the normalizing constants involved in the ratio of PDFs, we obtain that $f_{Q_2}(x)/bf_{Q_1}(bx)$ crosses the horizontal line $y=1$ once. Consequently, $D'$ follows the $+-$ pattern which implies that D is $\nearrow \searrow$. Taking into account the limit behavior of D, we can conclude that $D(x)\ge 0$.

The remaining cases can be addressed similarly as in the work by Van Zwet (1964, p. 60, 61), by rewriting the function $D^\prime (x)$ as

$$\begin{aligned} D^\prime (x)=bf_{Q_1}(a+bx)\left( e^{S_{a,b}(x)}-1\right) \end{aligned}$$

with $S_{a,b}$ defined by $S_{a,b}(x)=\log \left( \frac{f_{Q_2}(x)}{bf_{Q_1}(a+bx)}\right)$, with asymptotic behavior: $S_{a,b}(\infty )=-\infty$. Its first derivative is given by

$$\begin{aligned} S_{a,b}^\prime (x)&=\frac{g_{p+q_2}(x)}{G_{p+q_2}(x)}-\left( \frac{q_2}{2}+1\right) \frac{1}{x}-\frac{bg_{p+q_1}(a+bx)}{G_{p+q_1}(a+bx)} +\left( \frac{q_1}{2}+1\right) \frac{b}{a+bx}\\&=\frac{1}{x}\left[ M_{p+q_2}(x)-\left( \frac{q_2}{2}+1\right) \right] -\frac{b}{a+bx}\left[ M_{p+q_1}(a+bx)-\left( \frac{q_1}{2}+1\right) \right] \end{aligned}$$

which has an asymptote at $y=0$, i.e. $S_{a,b}^\prime (\infty )=0$ (see Lemma 2).

Now, it will suffice to study the sign of the functions $S_{a,b}$ and $S_{a,b}^\prime$, in combination with the limit behavior of D and $D^\prime$, to get the sign pattern of D.

When $a=0$ and $b>1$, it can be shown that $S_{0,b}^\prime (x)$ has at most one zero in $(0,\infty )$. On the other hand, from the limits in Lemma 2 at $x=0$, we get

$$\begin{aligned} S_{0,b}^\prime (0)&=\lim _{x\downarrow 0}\frac{1}{x}\left( M_{p+q_2}(x)-M_{p+q_1}(bx)-\frac{q_2-q_1}{2}\right) \\&=\lim _{x\downarrow 0}\left( M_{p+q_2}^\prime (x)-bM_{p+q_1}^\prime (bx)\right) =\frac{1}{2}\left( b\frac{p+q_1}{p+2+q_1}-\frac{p+q_2}{p+2+q_2}\right) . \end{aligned}$$

Therefore, we conclude that $S_{0,b}^\prime (0)\ge 0$ if $\left( b\frac{p+q_1}{p+2+q_1}-\frac{p+q_2}{p+2+q_2}\right) \ge 0$ and $S_{0,b}^\prime (0)< 0$ otherwise, whereas it always holds that $S_{0,b}^\prime (\infty )=0$.

For the case $S_{0,b}^\prime (0)\ge 0$, some numerical work shows that $S_{0,b}^\prime$ has a $+-$ sign pattern which in turn yields a $\nearrow \searrow$ $S_{0,b}$ function; so it turns out that $S_{0,b}$ may have one or two zeros depending on whether $S_{0,b}(0)\ge 0$ or $S_{0,b}(0)<0$ (recall that $S_{0,b}(\infty )=-\infty$). Hence, $D^\prime$ will follow either the $+-$ pattern or the $-+-$ sign pattern (as the alternative $D^\prime (x)<0$ for all $x>0$ is incompatible with the limit behavior of D). The first pattern would lead to a D being $\nearrow \searrow$, while the second one to a D having a $\searrow \nearrow \searrow$ behavior. Consequently, we can conclude that either $D(x)\ge 0$ or D has only one zero with sign pattern $-+$.

For the case $S_{0,b}^\prime (0)< 0$, it must hold that $S_{0,b}^\prime (x)\le 0$ (as the sign pattern $-+$ is incompatible with the asymptotic behavior of $S_{0,b}$). Hence, the functions $S_{0,b}$ and $f_{Q_2}(x)/bf_{Q_1}(bx)$ are $\searrow$ so we could argue as before once again.

When $a>0$, it can also be shown that $S_{a,b}^\prime$ has at most one zero. Specifically, from the limits in Lemma 2 we obtain that $S_{a,b}^\prime (0)=\infty$ for $p>2$ and

$$\begin{aligned} \displaystyle S_{a,b}^\prime (0)=-\frac{1}{2}\frac{2+q_2}{4+q_2}-\frac{b}{a}\left[ M_{2+q_1}(a)-\left( \frac{q_1}{2}+1\right) \right] \end{aligned}$$

for $p=2$. Thus, the function $S_{a,b}^\prime$ will be $+-$ for $p>2$, a pattern already discussed so we refer the reader to our previous findings (note that the alternative $S_{a,b}^\prime (x)\ge 0$ is not compatible with the asymptotic behavior $S_{a,b}(\infty )=-\infty$). When $p=2$ it may happen that $S_{a,b}^\prime (0)\ge 0$ or $S_{a,b}^\prime (0)< 0$ so we can argue as done before with the case $a=0, b=1$ and arrive to the same conclusions.

We now address the case $a<0$ by distinguishing once again between the cases $p>2$ and $p=2$. As we know that $D(x)>0$ for $0<x\le -a/b$ with $D(-a/b)=F_{Q_2}(-a/b)$, we can confine the study to the interval $[-a/b,\infty )$.

When $p>2$ some simple calculus gives

$$\begin{aligned} S_{a,b}^\prime (-a/b)=&-\frac{b}{a}\left[ M_{p+q_2}(-a/b)-\left( \frac{q_2}{2}+1\right) \right] \\&-b\lim _{y\downarrow 0}\frac{1}{y}\left[ M_{p+q_1}(y)-\left( \frac{q_1}{2}+1\right) \right] =-\infty \end{aligned}$$

by using Lemma 2. It also holds that $S_{a,b}^\prime (\infty )=0$ as before. Now, it can be shown that either $S_{a,b}^\prime (x)\le 0$, for all $x>0$, or $S_{a,b}^\prime$ has sign pattern $-+-$. In the first case, $S_{a,b}$ is $\searrow$ with $S_{a,b}(-a/b)=\infty$ and $S_{a,b}(\infty )=-\infty$ so $D^\prime$ is $+-$ and D is $\nearrow \searrow$. Since $D(-a/b)>0$ and $D(\infty )=0$ we get $D(x)\ge 0$. If the first derivative $S_{a,b}^\prime$ had the sign pattern $-+-$, we have a $\searrow \nearrow \searrow$ $S_{a,b}$ which, by considering that $S_{a,b}(-a/b)=\infty$ and $S_{a,b}(\infty )=-\infty$, implies that $S_{a,b}$ is $+-$ or $+-+-$. Consequently, it holds that either D is $\nearrow \searrow$ with $D(x)\ge 0$ or D is $\nearrow \searrow \nearrow \searrow$ from which, taking into account that $D(-a/b)>0$ and $D(\infty )=0$, we obtain that either $D(x)\ge 0$, for all $x>0$, or D follows the sign pattern $+-+$, i.e. D has two zeros, being negative between the zeros.

When $p=2$ we also have $S_{a,b}^\prime (\infty )=0$, but in this case it is obtained that

$$\begin{aligned} S_{a,b}^\prime (-a/b)&=-\frac{b}{a}\left[ M_{2+q_2}(-a/b)-\left( \frac{q_2}{2}+1\right) \right] -b\lim _{y\downarrow 0}\frac{1}{y}\left[ M_{2+q_1}(y)-\left( \frac{q_1}{2}+1\right) \right] \\&=-\frac{b}{a}\left[ M_{2+q_2}(-a/b)-\left( \frac{q_2}{2}+1\right) \right] +\frac{b}{2}\frac{2+q_1}{4+q_1} \end{aligned}$$

by using again the limits from Lemma 2. It is not easy to find a simple condition that determines whether $S_{a,b}^\prime (-a/b)\ge 0$ or $S_{a,b}^\prime (-a/b)<0$. Anyway, it can be shown that $S_{a,b}^\prime$ has at most two zeros implying that, whenever $S_{a,b}^\prime (-a/b)\ge 0$, then $S_{a,b}^\prime$ follows the pattern $+-$ (as the signs $+$ and $+-+$ are incompatible with $S_{a,b}(\infty )=-\infty$), which has already been studied. Meanwhile, if $S_{a,b}^\prime (-a/b)< 0$ then $S_{a,b}^\prime$ has sign patterns − or $-+-$ (note that $-+$ is incompatible with $S_{a,b}(\infty )=-\infty$), which are the same as those appearing for the case $p>2$.

All the combinations that have been analyzed show that D has at most two zeros and whenever it has two zeros it takes negative values between them. $\square$

Proof of Proposition 8

Let $Q_{X}=({\varvec{X}}- \varvec{\xi })^\prime \varvec{\Omega }^{-1}({\varvec{X}}- \varvec{\xi })$ be the associated quadratic form. From Proposition 3 (and the comments after it), we have that

$$\begin{aligned} Q_{X}{\mathop {=}\limits ^{st}}S^2 Q\ge 0, \end{aligned}$$

with S and Q independent such that $Q\sim \chi _p^2$. Now, Markov’s inequality gives

$$\begin{aligned} \Pr (Q_{X}\ge \varepsilon )\le \frac{E(Q_{X})}{\varepsilon } \end{aligned}$$

for all $\varepsilon >0$, provided that the mean $E(S^2)$ exists. Therefore, as we know that $\displaystyle E(Q_{X})=E(S^2Q)=E(S^2)E(Q)=pE(S^2),$ we get (10). $\square$