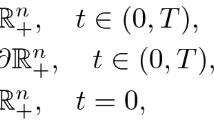Skip to main content
SpringerLink
Log in

Blowup solutions in a problem for the nonlinear heat equation on a small interval

  • Published:
Computational Mathematics and Modeling Aims and scope Submit manuscript

The article considers a one-dimensional quasi-linear heat equation with a volume heat source and a nonlinear thermal conductivity. The analysis is conducted for parameter values where selfsimilar solutions of the equations evolve in an LS-regime with blowup. Heat localization is observed in this case, and the combustion process in the developed stage is in the form of simple or complex structures of contracting half-width. We study the evolution dynamics of various initial distributions and their achievement of the self-similar regime, and also the dependence of the size of the localization region on the shape of the initial compactly supported distribution. The possibility of cyclic evolution of solutions against the background of overall growth with blowup is demonstrated. We particularly focus on the case when the size of the spatial region is much less than the characteristic size of the localization region, and heat flow is obstructed by the physical boundaries. In this case all initial perturbations achieve the self-similar regime, but the corresponding scenario has certain specific features. We present an example of formation of a complex spatial structure that evolves with blowup on a small interval.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. A. N. Tikhonov, A. A. Samarskii, L. A. Zaklyaz’minskii, et al., “Nonlinear effect of formation of self-sustaining high-temperature electrically conducting gas layer in time-dependent magnetohydrodynamic processes,” Dokl. Akad. Nauk SSSR, 173, No. 4, 808–811 (1967).

    Google Scholar 

  2. N. V. Zmitrenko, S. P. Kurdyumov, A. P. Mikhailov, and A. A. Samarskii, “Localization of thermonuclear combustion in a plasma with electron heat conduction,” Pis’ma ZhÉTF, 26, No. 9 (1978).

  3. S. P. Kurdyumov, G. G. Malinetskii, and A. B. Potapov, “Time-dependent structures, dynamical chaos, cellular automata,” in: Innovations in Synergetics. Puzzles in the World of Nonequilibrium Structures [in Russian], Nauka, Moscow (1996), pp. 95–164.

    Google Scholar 

  4. A. I. Lobanov and T. K. Starozhilova, “Time-dependent structures in a model of blood clotting,” in: Innovations in Synergetics. A Look into the Third Millennium [in Russian], Nauka, Moscow (2002), pp. 346–367.

    Google Scholar 

  5. N. A. Kirichenko, “Localized time-dependent structures in laser thermochemistry,” in: Blowup Regimes. The Evolution of an Idea [in Russian], Nauka, Moscow (1998), pp. 217–230.

    Google Scholar 

  6. S. P. Kapitsa, S. P. Kurdyumov, and G. G. Malinetskii, Synergetics and Predicting the Future [in Russian], Editorial URSS, Moscow (2001).

    Google Scholar 

  7. V. A. Belavin, S. P. Kapitsa, and S. P. Kurdyumov, “Mathematical model of demographic processes allowing for spatial distribution,” Zh. Vychisl. Matem. Mat. Fiziki, 38, No. 6, 885–902 (1998).

    Google Scholar 

  8. E. N. Knyazeva and S. P. Kurdyumov, Foundations of Synergetics, Aleteya, St. Peterburg (2002).

    Google Scholar 

  9. G. G. Malinetskii (ed.), Blowup Regimes. The Evolution of an Idea [in Russian], Fizmatlit, Moscow (2006).

    Google Scholar 

  10. A. A. Samarskii, V. A. Galaktionov, S. P. Kurdyumov, and A. P. Mikhailov, Blowup in Problems for Quasilinear Parabolic Equations [in Russian], Nauka, Moscow (1987).

    Google Scholar 

  11. V. A. Galaktionov and J. L. Vazquez, “The problem of blow-up in nonlinear parabolic equations,” J. Discr. Cont. Dynam. Syst., 8, No. 2, 399–433 (2002).

    Article  MATH  MathSciNet  Google Scholar 

  12. G. G. Elenin, S. P. Kurdyumov, and A. A. Samarskii, “Time-dependent dissipative structures in a nonlinear heat-conducting medium,” Zh. Vychisl. Matem. Mat. Fiziki, 23, No. 2, 380–390 (1983).

    MATH  MathSciNet  Google Scholar 

  13. S. P. Kurdyumov, “Combustion eigenfunctions in a nonlinear medium and constructive laws of their organization,” in: Modern Issues in Mathematical Physics and Computational Mathematics [in Russian], Nauka, Moscow (1982), pp. 217–243.

    Google Scholar 

  14. A. A. Samarskii, N. V. Zmitrenko, S. P. Kurdyumov, and A. P. Mikhailov, “Thermal structures and fundamental length in a medium with nonlinear thermal conductivity and a volume heat source,” Dokl. Akad. Nauk SSSR, 227, No. 2 (1976).

    Google Scholar 

  15. V. A. Galaktionov, “Proof of localization of unbounded solutions of the nonlinear parabolic equation u t  = (u σ u x ) x  + u β ,” Diff. Uravn., 21, No. 1, 15–23 (1985).

    MathSciNet  Google Scholar 

  16. E. S. Kurkina and S. P. Kurdyumov, “The spectrum of dissipative structures evolving with blowup,” Dokl. Akad. Nauk, 395, No. 6, 1–6 (2004).

    MathSciNet  Google Scholar 

  17. S. P. Kurdyumov and E. S. Kurkina, “The eigenfunction spectrum of the self-similar problem for nonlinear heat equation with a source,” Zh. Vychisl. Matem. Mat. Fiziki, 44, No. 9, 1619–1637 (2004).

    MATH  MathSciNet  Google Scholar 

  18. A. A. Samarskii, Theory of Finite-Difference Schemes [in Russian], Nauka, Moscow (1983).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Faculty of Computational Mathematics and Cybernetics, Moscow State University, Moscow, Russia

    E. D. Kuretova & E. S. Kurkina

Authors
  1. E. D. Kuretova
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. E. S. Kurkina
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to E. D. Kuretova.

Additional information

Translated from Prikladnaya Matematika i Informatika, No. 29, 2008, pp. 88–112.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Kuretova, E.D., Kurkina, E.S. Blowup solutions in a problem for the nonlinear heat equation on a small interval. Comput Math Model 20, 173–191 (2009). https://doi.org/10.1007/s10598-009-9027-0

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10598-009-9027-0

Keywords

Search

Navigation