Skip to main content
SpringerLink
Log in

Mixed unsplit-field perfectly matched layers for transient simulations of scalar waves in heterogeneous domains

  • Original Paper
  • Published:
Computational Geosciences Aims and scope Submit manuscript

Abstract

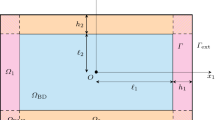
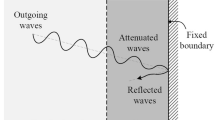
We discuss a new formulation for transient scalar wave simulations in heterogeneous semi-infinite domains. To deal with the semi-infinite extent of the physical domains, we introduce truncation boundaries and adopt perfectly matched layers (PMLs) as the boundary wave absorbers. Within this framework, we develop a new mixed displacement-stress (or stress memory) finite element formulation based on unsplit-field PMLs. We use, as typically done, complex-coordinate stretching transformations in the frequency domain, and recover the governing partial differential equations in the time-domain through the inverse Fourier transform. Upon spatial discretization, the resulting equations lead to a mixed semi-discrete form, where both displacements and stresses (or stress histories/memories) are treated as independent unknowns. We propose approximant pairs, which, numerically, are shown to be stable. The resulting mixed finite element scheme is relatively simple and straightforward to implement, when compared against split-field PML techniques. It also bypasses the need for complicated time integration schemes that arise when recent displacement-based formulations are used. We report numerical results for 1D and 2D scalar wave propagation in semi-infinite domains truncated by PMLs. We also conduct parametric studies and report on the effect the various PML parameter choices have on the simulation error.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Mindlin, R.D., Bleich, H.H.: Response of an elastic cylindrical shell to a transverse, step shock wave. ASME J. Appl. Mech. 20, 189–195 (1953)

    MATH  MathSciNet  Google Scholar 

  2. Schmidt, F.: A new approach to coupled interior-exterior Helmholtz-type problems: theory and applications. Habilitation Thesis, Konrad-Zuse-Zentrum Berlin, Fachbereich Mathematik und Informatik, FU Berlin (2001)

  3. Schmidt, F., Hohage, T., Klose, R., Schadle, A., Zschiedrich, L.: Pole condition: a numerical method for Helmholtz-type scattering problem with inhomogeneous exterior domain. J. Comput. Appl. Math. 218, 61–69 (2008)

    Article  MATH  MathSciNet  Google Scholar 

  4. Zschiedrich, L., Klose, R., Schadle, A., Schmidt, F.: A new finite element realization of the perfectly matched layer method for Helmholtz scattering problems on polygonal domains in two dimensions. J. Comput. Appl. Math. 188, 12–32 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  5. Givoli, D., Keller, J.B.: A finite element method for large domains. Comput. Methods Appl. Mech. Eng. 76, 41–66 (1989)

    Article  MATH  MathSciNet  Google Scholar 

  6. Givoli, D., Keller, J.B.: Non-reflecting boundary conditions for elastic waves. Wave Motion 12(3), 261–279 (1990)

    Article  MATH  MathSciNet  Google Scholar 

  7. Engquist, B., Majda, A.: Absorbing boundary conditions for the numerical simulation of waves. Math. Comput. 31(139), 629–651 (1977)

    MATH  MathSciNet  Google Scholar 

  8. Bayliss, A., Turkel, E.: Radiation boundary conditions for wave-like equations. Commun. Pure Appl. Math. 33, 707–725 (1980)

    Article  MATH  MathSciNet  Google Scholar 

  9. Higdon, R.L.: Absorbing boundary conditions for elastic waves. Geophysics 56(2), 231–241 (1991)

    Article  Google Scholar 

  10. Givoli, D., Neta, B.: High-order non-reflecting boundary scheme for time-dependent waves. J. Comput. Phys. 186(1), 24–46 (2003)

    Article  MATH  MathSciNet  Google Scholar 

  11. Kallivokas, L.F., Lee, S.: Local absorbing boundaries of elliptical shape for scalar waves. Comput. Methods Appl. Mech. Eng. 193, 4979–5015 (2004)

    Article  MATH  MathSciNet  Google Scholar 

  12. Bérenger, J.-P.: A perfectly matched layer for the absorption of electromagnetic waves. J. Comput. Phys. 114(2), 185–200 (1994)

    Article  MATH  MathSciNet  Google Scholar 

  13. Chew, W.C., Weedon, W.H.: A 3D perfectly matched medium from modified Maxwell’s equations with stretched coordinates. Microw. Opt. Technol. Lett. 7(13), 599–604 (1994)

    Article  Google Scholar 

  14. Hu, F.Q.: On absorbing boundary conditions for linearized Euler equations by a perfectly matched layer. J. Comput. Phys. 129, 201–219 (1996)

    Article  MATH  MathSciNet  Google Scholar 

  15. Hesthaven, J.S.: On the analysis and construction of perfectly matched layers for the linearized Euler equations. J. Comput. Phys. 142, 129–147 (1998)

    Article  MATH  MathSciNet  Google Scholar 

  16. Harari, I., Slavutin, M., Turkel, E.: Analytical and numerical studies of a finite element PML for the helmholtz equation. J. Comput. Acoust. 8(1), 121–137 (2000)

    MathSciNet  Google Scholar 

  17. Harari, I., Albocher, U.: Studies of FE/PML for exterior problems of time-harmonic elastic waves. Comput. Methods Appl. Mech. Eng. 195, 3854–3879 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  18. Turkel, E., Yefet, A.: Absorbing PML boundary layers for wave-like equations. Appl. Numer. Math. 27, 533–557 (1998)

    Article  MATH  MathSciNet  Google Scholar 

  19. Israeli, M., Orszag, S.: Approximation of radiation boundary conditions. J. Comput. Phys. 41, 115–135 (1981)

    Article  MATH  MathSciNet  Google Scholar 

  20. Qi, Q., Geers, T.L.: Evaluation of the perfectly matched layer for computational acoustics. J. Comput. Phys. 139(1), 166–183 (1998)

    Article  MATH  Google Scholar 

  21. Zeng, Y.Q., He, J.Q., Liu, Q.H.: The application of the perfectly matched layer in numerical modeling of wave propagation in poroelastic media. Geophysics 66(4), 1258–1266 (2001)

    Article  Google Scholar 

  22. Chew, W.C., Liu, Q.H.: Perfectly matched layers for elastodynamics: a new absorbing boundary condition. J. Comput. Acoust. 4(4), 341–359 (1996)

    Article  Google Scholar 

  23. Hastings, F.D., Schneider, J.B., Broschat, S.L.: Application of the perfectly matched layer (PML) absorbing boundary condition to elastic wave propagation. J. Acoust. Soc. Am. 100(5), 3061–3069 (1996)

    Article  Google Scholar 

  24. Liu, Q.H.: Perfectly matched layers for elastic waves in cylindrical and spherical coordinates. J. Acoust. Soc. Am. 105(4), 2075–2084 (1999)

    Article  Google Scholar 

  25. Collino, F., Monk, P.: The perfectly matched layer in curvilinear coordinates. SIAM J. Sci. Comput. 19(6), 2061–2090 (1998)

    Article  MATH  MathSciNet  Google Scholar 

  26. Collino, F., Tsogka, C.: Application of the perfectly matched absorbing layer model to the linear elastodynamic problem in anisotropic heterogeneous media. Geophysics 66(1), 294–307 (2001)

    Article  Google Scholar 

  27. Zheng, Y., Huang, X.: Anisotropic perfectly matched layers for elastic waves in cartesian and curvilinear coordinates. Earth Research Laboratory Report, Massachusetts Institute of Technology, Cambridge (2002)

  28. Abarbanel, S., Gottlieb, D.: A mathematical analysis of the PML method. J. Comput. Phys. 134, 357–363 (1997)

    Article  MATH  MathSciNet  Google Scholar 

  29. Becache, E., Fauqueux, S., Joly, P.: Stability of perfectly matched layers, group velocities and anisotropic waves. J. Comput. Phys. 188, 399–433 (2003)

    Article  MATH  MathSciNet  Google Scholar 

  30. Becache, E., Petropoulos, P.G., Gedney, S.D.: On the long-time behavior of unsplit perfectly matched layers. IEEE Trans. Antennas Propag. 52(5), 1335–1342 (2004)

    Article  MathSciNet  Google Scholar 

  31. Komatitsch, D., Tromp, J.: A perfectly matched layer absorbing boundary condition for the second-order seismic wave equation. Geophys. J. Int. 154, 146–153 (2003)

    Article  Google Scholar 

  32. Basu, U., Chopra, A.K.: Perfectly matched layers for transient elastodynamics of unbounded domains. Int. J. Numer. Methods Eng. 59, 1039–1074 (2004)

    Article  MATH  MathSciNet  Google Scholar 

  33. Basu, U., Chopra, A.K.: Perfectly matched layers for time-harmonic elastodynamics of unbounded domains: theory and finite-element implementation. Comput. Methods Appl. Mech. Eng. 192, 1337–1375 (2003)

    Article  MATH  Google Scholar 

  34. Oden, J.T., Reddy, J.N.: On mixed finite element approximations. SIAM J. Numer. Anal. 13(3), 393–404 (1976)

    Article  MATH  MathSciNet  Google Scholar 

  35. Sheu, M.-G.: On theories and applications of mixed finite element methods for linear boundary-value problems. Comput. Math. Appl. 4(4), 333–347 (1978)

    Article  MATH  MathSciNet  Google Scholar 

  36. Brezzi, F., Bathe, K.J.: A discourse on the stability conditions for mixed finite element formulations. Comput. Methods Appl. Mech. Eng. 82, 27–57 (1990)

    Article  MATH  MathSciNet  Google Scholar 

  37. Carey, G.F., Oden, J.T.: Finite Elements—A Second Course, vol. II. Prentice Hall, Englewood Cliffs (1983)

    Google Scholar 

  38. Brezzi, F., Fortin, M.: Mixed And Hybrid Finite Element Methods. Springer, New York (1991)

    MATH  Google Scholar 

  39. Arnold, D. N.: Mixed finite element methods for elliptic problems. Comput. Methods Appl. Mech. Eng. 82, 281–300 (1990)

    Article  MATH  Google Scholar 

  40. Brezzi, F.: A survey of mixed finite element method. In: Dwoyer, D., Hussaini, M., Voigt, R. (eds.) Finite Elements Theory and Application, pp. 34–49. Springer, New York (1988)

    Google Scholar 

  41. Raviart, P.A., Thomas, J.M.: A mixed finite element method for second order elliptic problems. In: Galligani, I., Magenes, E. (eds.) Mathematical Aspects of the Finite Element Method. Lecture Notes in Mathematics, vol. 606, pp. 292–315. Springer, New York (1977)

    Chapter  Google Scholar 

  42. Johnson, C., Mercier, B.: Some equilibrium finite element methods for two-dimensional elasticity problems. Numer. Math. 30, 103–116 (1978)

    Article  MATH  MathSciNet  Google Scholar 

  43. Brezzi, F., Douglas, J., Marini, L.D.: Two families of mixed finite element methods for second order elliptic problems. Numer. Math. 47, 217–235 (1985)

    Article  MATH  MathSciNet  Google Scholar 

  44. Arnold, D.N., Brezzi, F., Fortin, M.: A stable finite element for the Stokes equations. Calcolo 21, 337–344 (1984)

    Article  MATH  MathSciNet  Google Scholar 

  45. Arnold, D.N., Brezzi, F., Douglas, J.: PEERS: a new mixed finite element for plane elasticity. Jpn. J. Appl. Math. 1, 347–367 (1984)

    Article  MATH  Google Scholar 

  46. Nédélec, J.C.: Mixed finite elements in R 3. Numer. Math. 35, 315–341 (1980)

    Article  MATH  MathSciNet  Google Scholar 

  47. Arnold, D.N., Douglas, J., Gupta, C.P.: A family of higher order mixed finite element methods for plane elasticity. Numer. Math. 45, 1–22 (1984)

    Article  MATH  MathSciNet  Google Scholar 

  48. Marini, L.D.: An inexpensive method for the evaluation of the solution of the lowest order raviart-thomas mixed method. SIAM J. Numer. Anal. 22(3), 493–496 (1985)

    Article  MATH  MathSciNet  Google Scholar 

  49. Nédélec, J.C.: A new family of mixed finite elements in R 3. Numer. Math. 50, 57–81 (1986)

    Article  MATH  MathSciNet  Google Scholar 

  50. Arnold, D.N., Falk, R.S.: A new mixed formulation for elasticity. Numer. Math. 53, 13–30 (1988)

    Article  MATH  MathSciNet  Google Scholar 

  51. Stenberg, R.: A family of mixed finite elements for the elasticity problem. Numer. Math. 53, 513–538 (1988)

    Article  MATH  MathSciNet  Google Scholar 

  52. Frasca, L.P., Hughes, T.J.R., Loula, A.F.D., Miranda, I.: A new family of stable elements for nearly incompressible elasticity based on a mixed Petrov-Galerkin finite element formulation. Numer. Math. 53, 123–141 (1988)

    Article  MathSciNet  Google Scholar 

  53. Morley, M.E.: A family of mixed finite elements for linear elasticity. Numer. Math. 55, 633–666 (1989)

    Article  MATH  MathSciNet  Google Scholar 

  54. Brezzi, F., Marini, D.: A survey on mixed finite element approximations. IEEE Trans. Magn. 30(5), 3547–3551 (1994)

    Article  Google Scholar 

  55. Bécache, E., Joly, P., Tsogka, C.: An analysis of new mixed finite elements for the approximation of wave propagation problems. SIAM J. Numer. Anal. 37(4), 1053–1084 (2000)

    Article  MATH  MathSciNet  Google Scholar 

  56. Arnold, D.N., Winther, R.: Mixed finite elements for elasticity. Numer. Math. 92, 401–419 (2002)

    Article  MATH  MathSciNet  Google Scholar 

  57. Bécache, E., Joly, P., Tsogka, C.: A new family of mixed finite elements for the linear elastodynamic problem. SIAM J. Numer. Anal. 39(6), 2109–2132 (2002)

    Article  MATH  MathSciNet  Google Scholar 

  58. Arnold, D.N., Winther, R.: Mixed finite elements for elasticity in the stress-displacement formulation. In: Chen, Z., Glowinski, R., Li, K. (eds.) Current Trends in Scientific Computing, Contemporary Mathematics, vol. 329, pp. 33–42 (2003)

  59. Arnold, D.N., Awanou, G.: Rectangular mixed finite elements for elasticity. Math. Models Methods Appl. Sci. 15(9), 1417–1429 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  60. Chen, Z.: Finite Element Methods and Their Applications, 1st edn. Springer, New York (2005)

    MATH  Google Scholar 

  61. Arnold, D.N., Falk, R.S., Winther, R.: Mixed finite element methods for linear elasticity with weakly imposed symmetry. Math. Comput. 76(260), 1699–1723 (2005)

    MathSciNet  Google Scholar 

  62. Festa, G., Vilotte, J.-P.: The Newmark scheme as velocity-stress time-staggering: an efficient PML implementation for spectral element simulations of elastodynamics. Geophys. J. Int. 161, 789–812 (2005)

    Article  Google Scholar 

  63. Cohen, G., Fauqueux, S.: Mixed spectral finite elements for the linear elasticity system in unbounded domains. SIAM J. Sci. Comput. 26(3), 864–884 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  64. Chen, J., Chen, Z.: An adaptive perfectly matched layer technique for 3-D time-harmonic electromagnetic scattering problems. Math. Comput. 77(262), 673–698 (2008)

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Civil, Architectural and Environmental Engineering, The University of Texas at Austin, 1 University Station, C1748, Austin, TX, 78712, USA

    Jun Won Kang & Loukas F. Kallivokas

Authors
  1. Jun Won Kang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Loukas F. Kallivokas
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Loukas F. Kallivokas.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Kang, J.W., Kallivokas, L.F. Mixed unsplit-field perfectly matched layers for transient simulations of scalar waves in heterogeneous domains. Comput Geosci 14, 623–648 (2010). https://doi.org/10.1007/s10596-009-9176-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10596-009-9176-4

Keywords

Search

Navigation