Abstract
In this study, we utilize a novel approach to solve the Ekman equations for eddy-viscosity profiles in the stable boundary-layer. By doing so, a well-known expression for the stable boundary-layer height by Zilitinkevich (Boundary-Layer Meteorology, 1972, Vol. 3, 141–145) is rediscovered.
Similar content being viewed by others
1 Introduction
Sergej Zilitinkevich was one of the giants of atmospheric physics who carried the field of boundary-layer meteorology (BLM) on his shoulder for more than half a century. We, representing the BLM community at large, are indebted forever for his ingenious efforts and lifelong dedication in advancing our field. In the arena of stable boundary layers (SBLs), Zilitinkevich made numerous ground-breaking contributions. As a matter of fact, it would be difficult to find any contemporary article on SBLs which does not make at least one reference to an original publication of Zilitinkevich. The present paper is also following the same tradition.
In this study, we utilize the Ekman equations to analytically derive a stable boundary-layer height formulation which was originally proposed by Zilitinkevich (1972) based on scaling arguments. During the process, we also derive equations for the vertical profiles of eddy viscosity. To the best of our knowledge, it is the first time that estimates are given for the eddy-viscosity profiles directly from the Ekman equations.
2 Formulation of SBL Height by Zilitinkevich (1972)
Using boundary layer scaling arguments, Zilitinkevich (1972) proposed that the height (h) of stationary SBLs can be written as:
Here, the surface friction velocity and surface Obukhov length are denoted by \(u_{*0}\) and L, respectively; \(B_s\) is the surface buoyancy flux. The Coriolis parameter is represented by \(f_{cor} = \text {sgn}(f_{cor}) |f_{cor}|\). In the northern and southern hemispheres the value of \(\text {sgn}(f_{cor})\) is + 1 and − 1, respectively (Garratt 1994). The proportionality constants \(\gamma \) and \(C_h\) are related as follows:
where \(\kappa \) is the von Kármán constant assumed to be equal to 0.4.
Zilitinkevich (1972) assumed \(C_h\) to be order of one. In an analytical study, Businger and Arya (1974) estimated \(\gamma \) to be equal to 0.72. A much lower value of \(\gamma \approx 0.4\) was estimated by Brost and Wyngaard (1978) using a second-order closure model. Garratt (1982) who analyzed observational data from several field campaigns also found \(\gamma \approx 0.4\). In his local-scaling paper, Nieuwstadt (1984) found \(\gamma \approx 0.35\) to be consistent with other equations. Zilitinkevich (1989) summarized \(C_h\) from several studies and found it to vary within the range of 0.55–1.58. A unique aspect of the present study is that we analytically derive \(\gamma \) (and \(C_h\)) with limited assumptions.
We would like to point out that Eq. 1 predicts physically unrealistic boundary-layer heights for two situations: (i) close to the equator (i.e., \(f_{cor} \rightarrow 0\)); and (ii) for near-neutral conditions (i.e., \(L \rightarrow \infty \)). To circumvent the second issue, a few interpolation approaches have been proposed in the literature (e.g.,Nieuwstadt 1981; Zilitinkevich 1989).
3 Momentum and Sensible Heat Flux Profiles
In SBL flows, the profiles of friction velocity and sensible heat flux are often expressed as follows (Nieuwstadt 1984; Sorbjan 1986):
Here, the friction velocity, momentum flux components, and sensible heat flux at height z are denoted by \(u_{*L}\), \(\overline{uw}_L\), \(\overline{vw}_L\), and \(\overline{w\theta }_L\), respectively. The subscript ‘0’ is used to demarcate the corresponding surface values. These equations imply that the magnitudes of turbulent fluxes are maximum near the surface and they monotonically decrease to zero at the top of the boundary layer.
The exponents \(\alpha \) and \(\beta \) in Eqs. 3a and 3b are not universal constants. By utilizing his local-scaling hypothesis, Nieuwstadt (1984) suggested \(\alpha = 1.5\). He also proved that \(\beta \) should be equal to 1 under the assumptions of horizontal homogeneity and stationarity. In contrast, based on observational data from the well-known Minnesota field campaign (Caughey et al. 1979), Sorbjan (1986) estimated \(\alpha = 2\), and \(\beta = 3\) for evolving SBLs. In another observational study, Lenschow et al. (1988) considered the additional effects of radiational cooling and found the optimal \(\alpha \) and \(\beta \) to be equal to 1.75 and 1.5, respectively.
Using the definition of Obukhov length (Stull 1988) in conjunction with Eqs. 3a and 3b, we get:
where \(\Lambda \) is the so-called local Obukhov length at height z.
The first and second derivatives of \(f_m\) function in Eq. 3a can be written as:
We will make use of these derivatives in a later section.
4 Eddy-Viscosity Profile in the Ekman Layer
According to the K-theory, based on the celebrated hypothesis of Boussinesq (1877), turbulent fluxes can be approximated as products of the eddy exchange coefficients and the mean gradients (Lumley and Panofsky 1964):
here \(K_M\) is the so-called eddy-viscosity coefficient. The mean velocity components in x and y directions are denoted as U and V, respectively. Based on these equations, we can write:
where S is the magnitude of wind velocity shear.
For boundary layer flows over homogeneous and flat terrain, under steady-state conditions, the averaged equations of motions can be simplified as follows (Zilitinkevich et al. 1967; Brown 1974; Garratt 1994):
The geostrophic velocity components are denoted by \(U_g\) and \(V_g\). In the literature, these equations are commonly known as the Ekman-layer equations (Brown 1974; Nieuwstadt 1983).
In a landmark paper, Ekman (1905) first analytically solved Eqs. 8a and 8b with the assumption of constant eddy-viscosity (\(K_M\)) in conjunction with appropriate boundary conditions. Over the years, a few more closed-form analytical solutions of the Ekman equations have been reported in the literature (e.g.,Wippermann 1973; Brown 1974; Nieuwstadt 1983; Grisogono 1995; Parmhed et al. 2005). In all these papers, simplified profiles of \(K_M\) were always assumed. In this paper, we take a radically different approach. We only assume that Eq. 3a is valid and then deduce \(K_M\) profile from the Ekman equations as shown below.
For barotropic conditions, the Ekman equations can be re-written as:
Next, by utilizing Eqs. 6a and 6b, these equations are transformed as follows:
Dividing Eq. 10a by Eq. 10b and rearranging we arrive at:
The momentum flux components can be decomposed in terms of local friction velocity as follows (Businger and Arya 1974):
Here, \(\delta \) is the angle between the flux vector and the x-axis. By plugging Eq. 3a in Eqs. 12a and 12b, we get:
These equations can be differentiated as follows:
After differentiating one more time we arrive at:
By combining Eqs. 11, 13a, 13b, 15a, 15b, and simplifying we get:
Please note that we have used \(\left[ \text {sgn}(f_{cor})\right] ^2 = 1\).
By invoking the Pythagorean trigonometric identity, we can further simplify this equation to:
Thus,
Substituting \(f_m\) and \(f_m''\) from Eqs. 3a and 5b in 18, we find:
The second derivative of \(\delta \) is:
Please note that these derivatives have real values if \(\alpha \) is greater than one.
Now, we can directly estimate the \(K_M\) profile from Eqs. 10a, 13b, 15a, 19, and 20:
We would like to emphasize that this formulation of \(K_M\) is derived directly from the Ekman equations with very limited assumptions. To the best of our knowledge, similar formulation and derivation have not been reported in the literature.
Similar to other Ekman layer findings, Eq. 21 is only valid in the outer layer. It does not represent surface-layer conditions. In the literature, various patching and asymptotic matching approaches (e.g.,Taylor 1915; Blackadar and Tennekes 1968; Brown 1974; Zilitinkevich 1975) have been proposed to combine outer layer and inner layer (i.e., surface layer) solutions. A nice overview was given by Hess and Garratt (2002). In Sects. 6 and 7, we utilize an unorthodox strategy.
5 Conventional K-profile Approach
One of the most widely used first-order formulation for \(K_M\) is the K-profile approach (Stensrud 2007). O’Brien (1970) was one of the first researchers to propose a K-profile which portrays desirable surface layer behavior, attains a maximum value within the planetary boundary layer (PBL), and decreases to a background diffusion level above the PBL. Based on a second-order closure model, Brost and Wyngaard (1978) proposed a different K-profile formulation for stably stratified flows:
Here, \(\phi _M\) is a type of non-dimensional velocity gradient, defined later. The exponent p is a priori not known. For neutrally stratified flows in the surface layer, Eq. 22 reduces to \(K_M = \kappa z u_*\); this equation is in complete agreement with the well-established logarithmic law of the wall. Furthermore, for stably stratified surface layers, one can deduce a stability-corrected logarithmic law of the wall (e.g.,Businger et al. 1971) from Eq. 22.
The K-profile approach was modified by Troen and Mahrt (1986), Holtslag and Moeng (1991), Holtslag and Boville (1993), Hong and Pan (1996), Noh et al. (2003), Hong et al. (2006), and other researchers for its application in the unstable regime. They included a counter-gradient term to include the effects of large-scale eddies on local fluxes. They also considered entrainment fluxes at the top of the PBL. Holtslag and Moeng (1991) estimated p to be equal to 2 for unstable conditions.
In the context of numerical stability, the K-profile approach is quite robust (Beljaars 1992). Thus, it is not surprising that it is widely used in numerical weather prediction models. As a matter of fact, the default PBL scheme (called the YSU scheme) of the popular Weather Research and Forecasting (WRF) model uses the K-profile approach for both unstable and stable conditions.
In spite of its wide usage, Eq. 22 suffers from two limitations for stable conditions. First, there is uncertainty in the value of the exponent p. Brost and Wyngaard (1978) found p to be equal to 1.5 based on their simulations. On the other hand, based on field campaign data from Minnesota, Sorbjan (1989) found \(p = 1\). In the absence of reliable field observations, Troen and Mahrt (1986) used an integer value of \(p = 2\). The local scaling hypothesis by Nieuwstadt (1984) also leads to \(p = 2\). In the present study, we estimate p analytically.
The other limitation is related to the parameterization of \(\phi _M\). The K-profile formulation uses the following normalized velocity gradient:
Please note that in this equation surface friction velocity (\(u_{*0}\)) is used. However, in contrast to well-known surface-layer formulations, z is not limited to the depth of the surface layer. Instead, z ranges from the surface to the top of the boundary layer. Function \(\phi _M\) is commonly parameterized as (e.g.,Brost and Wyngaard 1978):
where c is a constant often assumed equal to 5. In the surface layer, for \(z/L < 1\), numerous studies documented the validity of this equation. However, its applicability for the outer layer (i.e., above surface layer) is questionable. Furthermore, this equation (incorrectly) implies that the logarithmic law of the wall applies to the entire boundary layer for neutral conditions (i.e., \(h/L = 0\)).
6 Alternative K-profile Approaches
In this section, we derive two competing K-profile formulations. Both the formulations are applicable for the entire SBL (i.e., including the surface layer and the outer layer).
6.1 Option 1
Multiplying both sides of Eq. 7 by \(\left( \kappa z/u_{*0}\right) \), we get:
By using Eq. 3a, we deduce:
Thus,
This equation is identical to the one proposed by Brost and Wyngaard (1978) based on the second-order turbulence modeling. Except, in case of Eq. 24c, the exponent \(\alpha \) is the same as in Eq. 3a.
6.2 Option 2
An alternate expression for \(K_M\) profile can be found by multiplying Eq. 7 by \((\kappa z/u_{*L})\):
or
By using Eq. 3a, we get:
Hence,
In these equations, \(\phi _{ML} (= \kappa z S/u_{*L})\) is a local non-dimensional velocity gradient as it utilizes local friction velocity (\(u_{*L}\)) from height z. It is straightforward to show that:
Equation 26 implies that \(\phi _M\) decreases more strongly with height than \(\phi _{ML}\). Several past simulation studies (e.g., Basu and Porté-Agel 2006; Zilitinkevich and Esau 2007; van de Wiel et al. 2008) found the following parameterization for \(\phi _{ML}\):
In those studies, \(c_L\) was found to be between 3 and 5. By regression analysis of field observations, Mahrt and Vickers (2003) found \(c_L\) = 3.7. Here, we assume \(c_L = 4\).
7 Matching of \(K_M\) Profiles in the Outer Layer
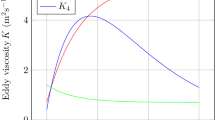
Thus far, we have derived 3 different K-profiles. Note that Eq. 21 is only valid in the outer layer. In contrast, Eqs. 24c and 25d are valid in the entire SBL. In the following sub-sections, we match these \(K_M\) profiles for the outer layer when \(z/L \gg 1\) and \(z/\Lambda \gg 1\).
7.1 Option 1
In the outer layer, for \(z/L \gg 1\), Eq. 24c simplifies to:
If we assume \(\alpha = 2\), then we get:
Similarly, by plugging in \(\alpha = 2\) in Eq. 21, we get:
By directly matching Eq. 29 with Eq. 30 we arrive at:
Further simplification leads to the SBL height parameterization of Zilitinkevich (1972):
where:
For \(c = 5\), we have: \(\gamma _1 = 0.583\).
7.2 Option 2
Similar to option 1, in the outer layer, for \(z/\Lambda \gg 1\), Eq. 25d simplifies to:
In this derivation, we used Eq. 4 in the conversion of \(\Lambda \) to L. If we assume \(\alpha = 3/2\) and \(\beta = 1\), we get:
Comparing this equation with Eq. 21, we arrive at:
where:
If \(c_L = 4\), we get \(\gamma _2 = 0.416\).
Interestingly, both the options 1 and 2 lead to the SBL height parameterization of Zilitinkevich (1972). The estimated proportionality constants, \(\gamma _1\) and \(\gamma _2\), fall within the range of previous observation-based and simulation-based empirical values. Furthermore, based on the literature, both \(\alpha = 3/2\) and \(\alpha = 2\) are plausible in SBLs. However, using \(\phi _M = 1 + 5 z/L\) for the entire SBL, as commonly done in practice, does not seem physically meaningful and is in contrast with observations (e.g, Holtslag 1984, among many others). From this perspective, option 2 seems to be a better option.
8 Conclusion
Fifty years ago, Zilitinkevich (1972) proposed a formulation for the SBL height by using boundary-layer scaling arguments. In this study, we derive the same formulation from an analytical approach involving the Ekman layer equations. In addition, we provide novel derivations for eddy-viscosity profiles in the SBL. Our approach makes use of the following assumptions: (i) the magnitude of turbulent fluxes decrease monotonically with height and go to zero at the top of the boundary layer; (ii) the K theory is applicable for stably stratified conditions; and (iii) under steady-state condition, for flows over homogeneous and flat terrain, geostrophic balance holds in the boundary layer. None of these assumptions are unorthodox. In our future work, we hope to extend our analytical approach to derive geostrophic drag laws for SBLs.
Data Availability
No datasets were generated or analyzed during the current study.
References
Basu S, Porté-Agel F (2006) Large-eddy simulation of stably stratified atmospheric boundary layer turbulence: a scale-dependent dynamic modeling approach. J Atmos Sci 63:2074–2091
Beljaars A (1992) The parametrization of the planetary boundary layer. ECMWF Meteorol Train Course Lect Ser 1–57
Blackadar AK, Tennekes H (1968) Asymptotic similarity in neutral barotropic planetary boundary layers. J Atmos Sci 25:1015–1020
Brost RA, Wyngaard JC (1978) A model study of the stably stratified planetary boundary layer. J Atmos Sci 35:1427–1440
Brown RA (1974) Analytical methods in planetary boundary-layer modelling. Wiley, New Jersey
Businger JA, Arya SPS (1974) Height of the mixed layer in the stably stratified planetary boundary layer. Adv Geophys, vol 18. Elsevier, Amsterdam, pp 73–92
Businger JA, Wyngaard JC, Izumi Y, Bradley EF (1971) Flux-profile relationships in the atmospheric surface layer. J Atmos Sci 28:181–189
Caughey SJ, Wyngaard JC, Kaimal JC (1979) Turbulence in the evolving stable boundary layer. J Atmos Sci 36:1041–1052
Ekman VW (1905) On the influence of the earth’s rotation on ocean currents. Arkiv Math Astros Fyjik 2:1–52
Garratt JR (1982) Observations in the nocturnal boundary layer. Boundary-Layer Meteorol 22:21–48
Garratt JR (1994) The atmospheric boundary layer. Cambridge University Press, Cambridge
Grisogono B (1995) A generalized Ekman layer profile with gradually varying eddy diffusivities. Q J R Meteorol Soc 121:445–453
Hess GD, Garratt JR (2002) Evaluating models of the neutral, barotropic planetary boundary layer using integral measures: Part i. overview. Boundary-Layer Meteorol 104:333–358
Holtslag AAM, Moeng CH (1991) Eddy diffusivity and countergradient transport in the convective atmospheric boundary layer. J Atmos Sci 48:1690–1698
Holtslag AAM (1984) Estimates of diabatic wind speed profiles from near-surface weather observations. Boundary-Layer Meteorol 29:225–250
Holtslag AAM, Boville BA (1993) Local versus nonlocal boundary-layer diffusion in a global climate model. J Clim 6:1825–1842
Hong SY, Pan HL (1996) Nonlocal boundary layer vertical diffusion in a medium-range forecast model. Mon Weather Rev 124:2322–2339
Hong SY, Noh Y, Dudhia J (2006) A new vertical diffusion package with an explicit treatment of entrainment processes. Mon Weather Rev 134:2318–2341
Lenschow DH, Li XS, Zhu CJ, Stankov BB (1988) The stably stratified boundary layer over the Great Plains: I. Mean and turbulence structure. Boundary-Layer Meteorol 42:95–121
Lumley JL, Panofsky HA (1964) The structure of atmospheric turbulence. Interscience Publishers, Hoboken
Mahrt L, Vickers D (2003) Formulation of turbulent fluxes in the stable boundary layer. J Atmos Sci 60:2538–2548
Nieuwstadt FTM (1981) The steady-state height and resistance laws of the nocturnal boundary layer: theory compared with Cabauw observations. Boundary-Layer Meteorol 20:3–17
Nieuwstadt FTM (1983) On the solution of the stationary, baroclinic Ekman-layer equations with a finite boundary-layer height. Boundary-Layer Meteorol 26:377–390
Nieuwstadt FTM (1984) The turbulent structure of the stable, nocturnal boundary layer. J Atmos Sci 41:2202–2216
Noh Y, Cheon WG, Hong SY, Raasch S (2003) Improvement of the K-profile model for the planetary boundary layer based on large eddy simulation data. Boundary-Layer Meteorol 107:401–427
O’Brien JJ (1970) A note on the vertical structure of the eddy exchange coefficient in the planetary boundary layer. J Atmos Sci 27:1213–1215
Parmhed O, Kos I, Grisogono B (2005) An improved Ekman layer approximation for smooth eddy diffusivity profiles. Boundary-Layer Meteorol 115:399–407
Sorbjan Z (1986) On similarity in the atmospheric boundary layer. Boundary-Layer Meteorol 34:377–397
Sorbjan Z (1989) Structure of atmospheric boundary layer. Prentice-Hall, Englewood Cliffs, NJ, p 317
Stensrud DJ (2007) Parameterization schemes: keys to understanding numerical weather prediction models. Cambridge University Press, Cambridge
Stull RB (1988) An introduction to boundary layer meteorology. Kluwer Academic, New York
Taylor GI (1915) Eddy motion in the atmosphere. philos Trans R Soc Lond Ser A 215:1–26
Troen I, Mahrt L (1986) A simple model of the atmospheric boundary layer: sensitivity to surface evaporation. Boundary-Layer Meteorol 37:129–148
van de Wiel BJH, Moene AF, De Ronde WH, Jonker HJJ (2008) Local similarity in the stable boundary layer and mixing-length approaches: consistency of concepts. Boundary-Layer Meteorol 128:103–116
Wippermann F (1973) The planetary boundary layer of the atmosphere. Deutsche Wetterdienst
Zilitinkevich SS (1972) On the determination of the height of the Ekman boundary layer. Boundary-Layer Meteorol 3:141–145
Zilitinkevich SS (1975) Resistance laws and prediction equations for the depth of the planetary boundary layer. J Atmos Sci 32:741–752
Zilitinkevich SS (1989) Velocity profiles, the resistance law and the dissipation rate of mean flow kinetic energy in a neutrally and stably stratified planetary boundary layer. Boundary-Layer Meteorol 46:367–387
Zilitinkevich SS, Esau IN (2007) Similarity theory and calculation of turbulent fluxes at the surface for the stably stratified atmospheric boundary layer. Boundary-Layer Meteorol 193–205
Zilitinkevich SS, Laikhtman DL, Monin AS (1967) Dynamics of the atmospheric boundary layer. Izv Atmos Ocean Phys 3:297–333
Acknowledgements
The first author is indebted to Pouriya Alinaghi, Branko Kosović, and Arquímedes Ruiz-Columbié for useful discussions and their assistance in cross-checking the analytical derivations. The second author acknowledges the many discussions and interactions he had with Sergej Zilitinkevich over the years.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have not disclosed any competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Basu, S., Holtslag, A.A.M. A Novel Approach for Deriving the Stable Boundary Layer Height and Eddy Viscosity Profiles from the Ekman Equations. Boundary-Layer Meteorol 187, 105–115 (2023). https://doi.org/10.1007/s10546-022-00757-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10546-022-00757-y