Grid-Resolution Requirements for Large-Eddy Simulations of the Atmospheric Boundary Layer

Abstract

Large-eddy simulations are widely used to study flows in the atmospheric boundary layer. As atmospheric boundary-layer flows of different atmospheric stratification have very different flow characteristics on different length scales, well-resolved simulations of these flows require very different meshes. The Parallelized Large-Eddy Simulation Model combined with a realizable dynamic subgrid model is used to identify the best method for evaluating the resolution requirements for boundary-layer flows simulated by large-eddy simulations. In particular, we consider three atmospheric boundary-layer set-ups with different stratifications (stable, neutral, convective) to investigate how the quality of the simulation changes with the grid resolution. By following the work of Davidson (Int J Heat Fluid Flow 30(5):1016–1025, 2009), the results are examined using criteria such as the convergence of mean profiles, the ratio of modelled and resolved turbulence kinetic energy, and the two-point correlation. We conclude that the two-point correlation is the best measure to evaluate whether the resolution demands for a specific flow are fulfilled.

1 Introduction

Large-eddy simulation (LES) is a powerful tool for the investigation of atmospheric boundary-layer (ABL) flows (Mason 1994; Porté-Agel et al. 2000; Kosović and Curry 2000), such as flow downstream of wind turbines and within wind farms in both neutral and non-neutral stability (Calaf et al. 2010; Porté-Agel et al. 2011; Witha et al. 2014; Abkar and Porté-Agel 2015; Dörenkämper et al. 2015; Vollmer et al. 2015), and the flow above urban areas of very complex topology (Letzel et al. 2008; Park et al. 2012).

The LES approach aims to explicitly resolve the large-scale motions of the turbulent flow, while modelling the sub-filter motions. As the discretization and subgrid-scale-model errors increase with decreasing resolution (Chow and Moin 2003; Meyers et al. 2007), the resolution is chosen to be fine enough to minimize these errors, with the size of the simulated domain large enough to contain the relevant boundary-layer structures. As the need for a large domain and the importance of properly resolving the physical processes may imply very high computational costs, a preferably coarse but sufficiently fine resolution is desired.

The characteristics of a typical ABL flow strongly depend on the heat flux at the lower boundary of the model domain, and thus on the stability (Garratt 1994). Surface heating results in rising plumes, large turbulent structures in the flow, and a thick boundary layer, while surface cooling inhibits vertical movement, causes smaller turbulent structures, and thin boundary layers. Hence, the necessary resolution for capturing the large-scale motion can be fundamentally different for different stratifications, even for similar boundary conditions, such as the topography or the presence of wind turbines. Many have investigated the resolution requirements for LES models in general (Celik et al. 2005; Klein 2005; Celik et al. 2006, 2009; Davidson 2009; Gant 2010; Sullivan and Patton 2011; Xiao et al. 2014), suggesting measures of resolution including the fluid viscosity, but these are not applicable to boundary layers of infinite Reynolds number (that neglect the viscosity of the air). More specific LES investigations of the boundary layer have been performed, for example, by Beare et al. (2006), who compared several models of different resolution in stable stratification, and used the convergence of the mean statistics as the main criterion for the quality of the simulations. The sensitivity of the convective boundary layer to the LES grid resolution has been addressed by Sullivan and Patton (2011), who found that the majority of low-order-moment statistics become independent of the grid resolution when $z_i/\varDelta > 60$, where $z_i$ is the height of the convective boundary layer (inversion height) and $\varDelta$ is the size of a grid cell. Furthermore, they observed that the growth of the boundary layer is a sensitive measure of the LES solution convergence, since it becomes grid independent when the entrainment region is sufficiently resolved. A general and widely-used method to estimate the quality of LES results was introduced by Pope (2004), who suggested that the resolved turbulence kinetic energy (TKE) should be more than 80% of the total TKE to enable a well-resolved simulation. Matheou and Chung (2014) recommend resolving at least 90% of the TKE for the reliable prediction of the mean statistics. Geurts and Fröhlich (2002) suggested using a subgrid-activity parameter, which Celik et al. (2005) showed was insufficiently sensitive to be used as an assessment parameter. Davidson (2009) described several methods for evaluating the resolution of an LES model coupled to an unsteady Reynolds-averaged Navier–Stokes model near the wall of a fully-developed channel flow at a Reynolds number $Re=4000$. He investigated the influence of the resolution on several measures, and concluded that the two-point correlation is the best method for estimating the required LES resolution in the case of a channel flow.

We evaluate here whether the two-point correlation is also a good measure for classifying the LES resolution of ABL flows, which are assumed to have an infinite Reynolds number (the viscosity of the air is neglected, with only the eddy viscosity taken into account). We address the question of how to decide if the resolution of an LES model of the ABL is sufficient by determining which is the coarsest resolution that still captures the relevant physical processes without leading to a poorly simulated ABL flow. Our objective is to identify a criterion for the assessment of the resolution of ABL flows, for which we expect that a refinement of the resolution leads to a convergence of the mean quantities and variances, implying the simulation results no longer depend on any further refinement of the mesh size.

2 Model

All simulations were performed using the Parallelized Large-Eddy Simulation Model (PALM, version 4, revision 2351), whose detailed description is given by Maronga et al. (2015), and is a model mostly used to simulate the ABL, but has also been used for oceanic flows (Noh et al. 2010). The model has been used with very fine grid spacing in stable situations (Beare et al. 2006), heterogeneously heated convective flows (Letzel and Raasch 2003), as well as urban canopy flows (Park et al. 2012). The model governing equations are

$$\begin{aligned}&\displaystyle \frac{\partial {\overline{u}}_i}{\partial t} = -\frac{\partial {\overline{u}}_i{\overline{u}}_j}{\partial x_j} - \epsilon _{ijk}f_j{\overline{u}}_k + \epsilon _{i3k}f_3u_{g,k} - \frac{1}{\rho _0}\frac{\partial {\overline{p}}^*}{\partial x_i} + g \frac{{\overline{\theta }}-\langle {\overline{\theta }}\rangle }{\langle \overline{\theta }\rangle }\delta _{i3} - \frac{\partial }{\partial x_j}\tau _{ij}, \end{aligned}$$

(1)

$$\begin{aligned}&\displaystyle \frac{\partial {\overline{u}}_j}{\partial x_j} = 0, \end{aligned}$$

(2)

$$\begin{aligned}&\displaystyle \frac{\partial {\overline{\theta }}}{\partial t} = -\frac{\partial {\overline{u}}_j{\overline{\theta }}}{\partial x_j} - \frac{\partial }{\partial x_j}\tau _{\theta j}, \end{aligned}$$

(3)

where the indices $i,j,k \in {1,2,3}$ and the summation convention is used, ${\overline{u}}_i$ are the velocity components at the locations $x_i$, t is the time, and the overbar indicates a filtered quantity using a filter width $\varDelta$. Implicit filtering is used, so $\varDelta$ equals the grid-cell size; $f_i$ is the Coriolis parameter, $\mathbf {f} = (0,2\varOmega \cos (\phi )$, $2\varOmega \sin (\phi ))$, with $\varOmega$ the Earth’s angular velocity, and $\phi$ the latitude; $u_{g,k}$ are the geostrophic velocity components, $\rho _0$ is the density of dry air, ${\overline{p}}^*$ is the perturbation pressure, ${\overline{\theta }}$ is the potential temperature, and $\delta _{ij}$ is the Kronecker delta. The tensor $\tau _{ij}=\overline{u_iu_j}-\overline{u_i}\overline{u_j}$ is the subgrid stress, and $\tau _{\theta i} = \overline{u_i\theta }-\overline{u_i}{\overline{\theta }}$ is the subgrid heat flux. The model equations are closed by determination of the subgrid stress $\tau _{ij}$ and the subgrid heat flux $\tau _{\theta i}$, as described by Heinz (2008). The closure model was not part of the standard PALM version. The deviatoric subgrid stress reads $\tau _{ij}^d = \tau _{ij}-\frac{1}{3}\tau _{kk}\delta _{ij}$ (the superscript d denotes the deviatoric part of a tensor), and is modelled as

$$\begin{aligned} \tau _{ij}^d = -2\nu _t{\overline{S}}_{ij}, \end{aligned}$$

(4)

where $\nu _t$ is the subgrid-scale (SGS) viscosity, and ${\overline{S}}_{ij} = \frac{1}{2}(\partial \overline{u_i}/\partial x_j + \partial \overline{u_j}/\partial x_i )$ the strain tensor. The SGS viscosity is $\nu _t=c_*\varDelta k_{SGS}^{1/2}$, with $c_*$ dynamically calculated at each timestep, and $k_{SGS}$ is the subgrid TKE. Following Germano et al. (1991), the test filter $\varDelta _T = 2\varDelta$ is introduced in our case. The subgrid stress on the test-filter scale is then $T_{ij} = \widehat{\overline{u_iu_j}} - \widehat{{\overline{u}}}_i\widehat{{\overline{u}}}_j$, where the hat denotes the filter operation on the test-filter level, where $T_{ij}$ is also unknown since it includes unresolved parts of the flow. The difference between the subgrid stress on the test-filter level and test-filtered subgrid stress is described by the Germano identity $L_{ij} = T_{ij} - {\widehat{\tau }}_{ij} = \widehat{{\overline{u}}_i{\overline{u}}_j} - \widehat{{\overline{u}}}_i\widehat{{\overline{u}}}_j$, and can be calculated directly by application of the test filter to the resolved quantities. The quantity $c_*$ is then calculated via

$$\begin{aligned} c_*=-\frac{L_{ij}^d\widehat{{\overline{S}}}^d_{ij}}{2\nu _t^T\widehat{{\overline{S}}} _{lk}^d\widehat{{\overline{S}}}_{kl}^d}. \end{aligned}$$

(5)

The closure scheme applied here uses the prognostic equation for the subgrid TKE

$$\begin{aligned} \frac{\partial k_{SGS}}{\partial t} = -{\overline{u}}_j\frac{\partial k_{SGS}}{\partial x_j} - \tau _{ij}\frac{\partial {\overline{u}}_i}{\partial x_j} + \frac{g}{{\overline{\theta }}_0}\tau _{\theta 3} + \frac{\partial }{\partial x_j}\left[ 2\nu _t\frac{\partial k_{SGS}}{\partial x_j}\right] - c_\epsilon \frac{k_{SGS}^{3/2}}{l}, \end{aligned}$$

(6)

where $c_\epsilon =0.19+0.74l/\varDelta$, and the length scale $l=\min (\varDelta ,1.8z$,$0.76\sqrt{k_{SGS}}$$(g/{\overline{\theta }} _0\partial {\overline{\theta }}/\partial z)^{-1/2})$, and z is the height above the ground. Unlike other dynamic models, this formulation of the parameter $c_*$ is not derived using model assumptions for the subgrid stress and the stress on the test-filter level, but is derived as a consequence of stochastic analysis (Heinz 2008; Heinz and Gopalan 2012). Furthermore, the stability of the simulation is ensured by using dynamic bounds to maintain $c_*$ values in the range

$$\begin{aligned} |c_*| \le \frac{23}{24\sqrt{3}}\frac{k_{SGS}^{1/2}}{\varDelta |{\overline{S}}|}, \end{aligned}$$

(7)

as derived by Mokhtarpoor and Heinz (2017). This model does not need artificial clipping for stable runs, and allows the occurrence of backscattering (negative values of $\nu _t$). For the computation of the advection, the upwind-biased fifth-order-differencing scheme of Wicker and Skamarock (2002) is used in combination with a third-order Runge–Kutta timestep scheme.

The main difference to the LES model used by Davidson (2009) is the explicit treatment of temperature, which means that buoyancy effects are taken into account. Furthermore, the Coriolis term, which leads to a deviation of the mean flow direction in the boundary layer from the geostrophic velocity above, is considered in the PALM model, but neglected by Davidson (2009).

Lower boundary conditions are described by Monin–Obukhov similarity theory, which assumes a constant-flux layer between the surface and the first grid level. The momentum fluxes and the horizontal velocity components are then calculated as described by Maronga et al. (2015). The horizontal boundary conditions are periodic.

3 Model Set-up

Since the characteristics of the boundary-layer flow strongly depend on the atmospheric stability, we consider simulations with three different stratifications (stable, neutral, convective), and perform a set of several simulations with different resolutions for each.

Table 1 Parameters for the different stratifications

3.1 General

Tables 1, 2, 3 and 4 present the simulation settings chosen based on previous work (Andren et al. 1994; Noh et al. 2003; Esau 2004; Beare et al. 2006; Basu and Porté-Agel 2006; Lu and Porté-Agel 2011; Sullivan and Patton 2011) to enable comparison with our results. As measurements of turbulent quantities over the entire boundary layer are not available for a direct comparison, we compare the results with Monin–Obukhov similarity theory and the Townsend theory to assess the quality of our idealized set-up.

All simulations start with a neutral temperature profile ($\partial \theta /\partial z =0$) within an ABL capped by a strong inversion ($\partial \theta /\partial z >0$) to prevent unlimited growth. The convective ABL with a strong positive heat flux elevates the inversion further so that the domain height for the convective case is much larger than that for the stable ABL. Close to the upper boundary, the flow is damped to prevent waves from being reflected downwards as described in Maronga et al. (2015). The roughness length for all simulations was set to $z_0=0.1$ m.

Table 2 Parameters of the stable simulations, where $\varDelta$ is the grid-cell size, which is spatially uniform, $n_x$, $n_y$ and $n_z$ are the number of grid points in the x-, y- and z-direction, respectively, $T_{\mathrm{sim}}$ is the total duration of the simulation, and $T_{\mathrm{avg}}$ is the time over which mean values are calculated

Table 3 Parameters of the neutral simulations

Table 4 Parameters of the convective simulations

The large-eddy turnover time is defined as $\tau _*=z_i/w_*$ for the convective case and $\tau _*=h/u_*$ for the neutral and stably stratified cases (Moeng and Sullivan 1994), where $z_i$ is the inversion height, h is the boundary-layer height, $u_*=(\overline{u'w'}^2_0+\overline{u'w'}_0^2)^{1/4}$ is the characteristic velocity, and $w_*=[\frac{g}{{\overline{\theta }}_0}\overline{w'\theta '}_0z_i]^{1/3}$ is the convective velocity (the index 0 denotes surface values). The simulation time $T_{\mathrm{sim}}$ and the time interval over which the variables are averaged are chosen to give a spin-up time > 20 $\tau _*$ and averaging intervals > 2 $\tau _*$ for the stable and convective cases. To remove inertial oscillations in the neutral case, we used a longer spin-up time and a longer averaging interval, as in Andren et al. (1994), who used a spin-up time of 10 $f^{-1}$ and Calaf et al. (2010), who used a spin-up time of 60 $\tau _*$.

For the estimation of the boundary-layer height in the stable and neutral cases, we follow Kosović and Curry (2000) by defining $h_{0.05}$ as the height at which the turbulent stress decreases to $5\%$ of its surface value, giving a boundary-layer height $h=h_{0.05}/0.95$. For the convective simulations, the inversion height $z_i$ is determined using the “maximum-gradient method” described by Sullivan et al. (1998), which assumes $z_i$ is the height at which the quantity $\partial \langle \theta \rangle /\partial z$ reaches its maximum value.

3.2 Stable Case

The set-up of the stable boundary layer is similar to the GEWEX (Global Energy and Water Cycle Experiment) ABL set-up, used by Beare et al. (2006), Basu and Porté-Agel (2006), Lu and Porté-Agel (2011) and others. At the lower boundary, the development of the temperature is described by a cooling rate of $-0.25$ K h$^{-1}$. The prescribed Coriolis parameter $f=1.39\times 10^{-4}$ s$^{-1}$ corresponds to a latitude of $73^\circ$, and all simulations use a geostrophic wind speed $u_g=8$ m s$^{-1}$. The initial profile of the subgrid TKE decreases linearly from 0.4 m$^2$ s$^{-2}$ to zero from the surface to a height of 250 m.

3.3 Neutral Case

For the neutral case, we prescribed a geostrophic wind speed $u_{g,1}=10$ m s$^{-1}$ as done by Andren et al. (1994), Meeder and Nieuwstadt (2000), and Chow et al. (2005), which is also comparable to the wind speed obtained at the boundary-layer top by Calaf et al. (2010), Porté-Agel et al. (2000), and Bou-Zeid et al. (2004), although they simulated a pressure-gradient-driven boundary layer without the Coriolis force. The domain size in the horizontal direction was set to 4000 m, which agrees with the domain considered by Esau (2004), but larger than the domain considered by Brasseur and Wei (2010) and Calaf et al. (2010). The boundary-layer height is around 1000 m, and the Coriolis parameter was set to $f=10^{-4}$ s$^{-1}$.

3.4 Convective Case

The convective simulations were performed on a grid extending 8000 m horizontally, which is larger than those used by Sullivan and Patton (2011) and Noh et al. (2003), but the boundary-layer height is similar, yielding comparable flow conditions. A moderate kinematic heat flux of 0.05 K m s$^{-1}$ is prescribed at the surface, which is equivalent to the setting of Noh et al. (2003) and similar to the setting used by Khanna and Brasseur (1998). The geostrophic wind speed was again $u_g=10$ m s$^{-1}$ and the Coriolis parameter $f=10^{-4}$ s$^{-1}$.

For each of the three stratifications (stable, neutral, convective), several simulations with different resolutions were run for unchanged domain size and flow parameters (see Table 2, 3, and 4). Thus, the differences in the results of runs for a specific type of stratification are exclusively a result of the change in resolution.

4 Results and Discussion

We present the effects of grid size by first illustrating how the grid affects the mean flow and turbulence variables, and then by analyzing how these grid effects are related to the flow resolution as predicted by several resolution criteria.

4.1 Mean Flow and Turbulence Variables

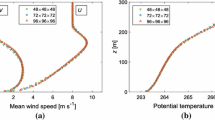
While the wind-speed profiles (Fig. 1) show only a moderate dependence on the resolution, finer resolutions tend to produce lower wind speeds in the lower part of the boundary layer in the stable and neutral cases. The convective case shows nearly no differences in the lower boundary layer, but near the top, the kink in the profile is more pronounced for finer resolutions. As the boundary-layer height is limited by a temperature inversion, the thermal stratification at this altitude is actually stable. The height shown in Fig. 1 is normalized by the boundary-layer height, so differences in the absolute height h are not visible. Usually, finer resolutions tend to result in lower boundary-layer heights. The simulation S1.25 shows a lower inversion height than the other stably stratified simulations. In the convective case, the convergence of the inversion height is evaluated in terms of the resolution criterion below.

Fig. 1

Simulated wind-speed profiles of stable a, neutral b, and convective stratification c for different resolutions (see the panel legends). $\mathrm{ln}(c)$, $h=z_{i}$

In the neutral surface layer, the relation (assuming a constant $u_*$ value)

$$\begin{aligned} \frac{\partial {{U}}}{\partial z} = \frac{u_*}{\kappa z} \end{aligned}$$

(8)

where U is the wind speed, and when integrated gives the wind-speed profile

$$\begin{aligned} {{U}}(z) = \frac{u_*}{\kappa }\ln \left( \frac{z}{z_0}\right) . \end{aligned}$$

(9)

To investigate whether this can be reproduced by the simulations, the dimensionless gradient

$$\begin{aligned} \varphi _M\left( \zeta \right) = \frac{\partial {\overline{u}}}{\partial z}\frac{\kappa z}{u_*} \end{aligned}$$

(10)

is calculated from the simulation results. Figure 2 shows logarithmic plots of the normalized wind speed as well as the dimensionless gradients of the neutral simulations, illustrating that the value of $\varphi _M$ does not deviate very strongly from unity for any of the resolutions. Above the surface, the profiles of the dimensionless gradient grow to around 1.2 and then fall to 0.8 in the layers above. This behaviour is evident in all profiles, whereas only the height of the peak depends on the resolution, as observed by Brasseur and Wei (2010). Values of $\phi \approx 1.2$ were also observed in simulations with other models using a dynamic subgrid closure (Porté-Agel et al. 2000; Brasseur and Wei 2010).

Fig. 2

Results from the neutral simulations showing (left) $U/u_*$ values with respect to the theoretical profile $U/u_*=ln(z/z_0)/\kappa$, $\kappa = 0.4$, and (right) dimensionless gradient for different resolutions

Profiles of the resolved shear stresses $\overline{u'w'}$ and $\overline{v'w'}$ (not shown) and the inferred square of the characteristic velocity $u^2_*=(\overline{u'w'}^2+\overline{v'w'}^2)^{1/2}$ vary slightly with the resolution (see Fig. 3). For stable stratification, all cases are similar, except for the 1.25-m-resolution case, which may be the result of a smaller boundary-layer height for this case. The profiles of the neutral simulations clearly show that the finer grids yield lower values of $u_*$. At resolutions of 10 m and lower, the profiles converge. The profiles of the convective case show more erratic behaviour, which may be caused by the relatively small averaging interval of 30 min, which is probably not sufficient to fully average over the large eddies in the convective case. The use of a larger averaging interval is not feasible because of the strong growth of the inversion height.

Fig. 3

Characteristic squared friction velocities $u^2_*$ of the stable a, neutral b, and convective c simulations of different resolutions

The resolved TKE of the stable case is strongly influenced by the resolution (Fig. 4). In a large part of the boundary layer, coarser grids imply a higher TKE, so it may seem counterintuitive that the resolved TKE decreases with increasing grid resolution. Ideally, the LES approach resolves a part of the total TKE, with the unresolved TKE modelled by the SGS model. With a finer resolution, the resolved TKE should increase as the modelled TKE decreases, while the total energy remains unchanged. However, in the stable case, the modelled TKE decreases with a finer resolution, which was noted by Beare et al. (2006), and an attempted explanation is given by Celik et al. (2005) in their Appendix B. According to Celik et al. (2005), in wall-bounded flows, the resolved strain ${\overline{S}}_{ij}$ becomes too small, which leads to a small resolved dissipation $\epsilon = 2\nu _{SGS}{\overline{S}}_{ij}{\overline{S}}_{ij}$ and a too high resolved TKE. However, near the surface, finer grids show a higher TKE. The normalized profiles do converge (the cases S1.25 and S2.5 behave similarly), but not regarding the absolute values of the TKE (not shown). The difference between the absolute values for the cases S1.25 and S2.5 is balanced by the surface values of $u_*$, which are lower for the S1.25 case than for the S2.5 case, as mentioned above. All three cases with different stability show that the TKE close to the ground, where vertical motion is limited due to the proximity of the ground, is dependent on the resolution of the computational grid. In all three cases, finer grids resolve more TKE in this specific region. Moreover, in the convective ABL, the top part of the boundary layer also shows a strong influence of the resolution on the TKE. Here, a capping inversion prevents vertical movement, while the convective ABL is also well mixed with regard to the TKE in the bulk of the convective ABL, which leads to a strong gradient of TKE at the top of the boundary layer. To summarize,the convective ABL is affected by the grid resolution at both the top and the bottom of the boundary layer.

Fig. 4

Resolved TKE of the stable a, neutral b, and convective c simulations of different resolutions

Fig. 5

Normalized resolved fluctuations of the u-component for the stable a, neutral b, and convective c simulations as a function of $\ln (z/h)$ for different resolutions. All points between the second grid point above the surface and the height 0.15h are shown. The dashed black line has a slope of $-1$

According to the theory of Townsend (1980) and Perry and Chong (1982), the streamwise turbulence intensity follows logarithmic functions of the distance from the wall in the inertial region of a wall-bounded flow

$$\begin{aligned} \overline{u^{\prime 2}}/u_*^2 = B_1-A_1 \ln \left( \frac{z}{h}\right) , \end{aligned}$$

(11)

which Marusic et al. (2013) show is valid for a large range of Reynolds numbers (see also Marusic and Hutchins (2008), Meneveau and Marusic (2013)). Measurements in wind tunnels as well as in the ABL show a logarithmic behaviour of $\overline{u^{\prime 2}}/u_*^2$, which suggests a universal (Townsend–Perry) constant of $A_1 = 1.25$ (Marusic and Kunkel 2003; Smits et al. 2011; Hultmark et al. 2012; Marusic et al. 2013), while the parameter $B_1$ depends on the flow conditions and geometry, which is also reproduced by LES models of wall-bounded flows (Stevens et al. 2014). The derivation of the logarithmic law in Eq. 11 by Banerjee and Katul (2013) using a spectral budget predicts that the value of $A_1$ is not constant. Another derivation by Katul et al. (2016) suggests a dependence of the value of $A_1$ on the Reynolds number, predicting $A_1 \rightarrow 1$ for $Re \rightarrow \infty$. Moreover, the direct numerical simulations of Katul et al. (2016) showed values of $A_1 < 1$ (see their supplementary material). Consistent with Marusic et al. (2013), we assume that the outer bound of the inertial region lies at 15% of the boundary-layer height.

Nearly all of our simulations show a logarithmic region with slopes $A_1 \approx 1$ from the second grid point above the surface (see Fig. 5). Below the second grid point, the turbulence is not resolved well enough, so the resolved turbulence decreases when approaching the surface. For the coarse simulations, there is either no data left (S10, C80) or only very little data between the second grid point and the upper limit of the logarithmic region at $z = 0.15h$ (N40). The best agreement can be seen for the convective simulations (Fig. 5 c), where the slope is close to unity in the whole inertial region. In the stable and neutral simulations, the slope is not constant throughout the inertial region. After the third grid point, the slope is mostly close to unity, but becomes smaller when approaching $z = 0.15 h$, especially for the well-resolved simulations.

4.2 Resolution Criteria Evaluation I: Turbulence-Resolving Measures

Before focusing in Sect. 4.3 on the use of two-point correlations as a measure of the resolution, we first consider the deficiencies of standard approaches.

The resolution ratio of the resolved to total TKE is defined as the parameter

$$\begin{aligned} \gamma = \frac{k_{res}}{k_{tot}} = \frac{k_{res}}{k_{res}+k_{SGS}}, \end{aligned}$$

(12)

whose vertical profiles for all simulations are shown in Fig. 6. In general, the profiles start at low values and approach a more or less constant value throughout the middle of the boundary layer (more constant for finer resolutions). In the upper part of the boundary layer, the profiles merge and reach $\gamma =1$, which means that, above the inversion, the value of $k_{SGS}$ tends to zero faster than the resolved TKE $k_{res}$. In the middle part of the boundary layer (approximately from $z/h=0.2$ to 0.8), the ratio is strongly dependent on the resolution, and the value of $\gamma$ is always higher for coarser grids than for finer grids. However, the value of $\gamma$ is not constant throughout the boundary layer, since it is higher near the surface and usually declines towards the top of the boundary layer. For example, in the stable simulation with 10-m resolution, the value of $\gamma$ grows almost linearly with height. Also, the other coarse simulations N40 and C80 show a $\gamma$ value growing with increasing height in the middle part of the boundary layer. Hence, a threshold value can only indicate well-resolved parts of the simulation. For all stabilities, the finer-resolution profiles are more constant in the middle part of the boundary layer. At all heights, $\gamma > 0.8$, which is the suggested criterion for a well-resolved turbulent flow according to Pope (2004). For the coarsest simulations, $\gamma \approx 0.95$ in the middle of the boundary layer, although these simulations are definitely poorly resolved. Based on the well-resolved simulations, a better threshold would be $\gamma \approx 0.97$ in the stable case, and $\gamma \approx 0.985$ in the neutral and convective cases, implying the parameter $\gamma$ definitely depends on the stability.

Fig. 6

The parameter $\gamma$ describing the ratio of the resolved TKE to total energy of the stable a, neutral b, and convective c simulations of different resolutions

Apparently, the ratio $\gamma$ depends on the SGS model. Celik et al. (2005) suggested a quality index deduced from Eq. 12, but independent of the subgrid TKE $k_{SGS}$, whereby instead of using $k_{SGS}$, which is computed by the model, only the resolved TKE of two simulations with different resolutions are used to calculate the index via Richardson extrapolation. Nevertheless, the application to our simulations reveals an inconsistency: depending on whether a simulation is compared to a coarser or a finer simulation, the index yields quite different values (not shown). Furthermore, the use of this index needs two simulations of different resolution.

Another way of evaluating the resolution is through the energy spectra, which, according to Kolmogorov’s theory of inertial turbulence, the spectral energy

$$\begin{aligned} E(k) \sim u_*^2d^{-2/3}k^{-5/3}, \end{aligned}$$

(13)

and is a function of the wavelength k, where d is a characteristic length assumed to be proportional to the height above ground z. The part of the measured spectra that follows the behaviour described by Eq. 13 is called the inertial subrange. Because of the different resolutions, the spectra of our simulations extend over different wavenumbers (see Fig. 7 where only the neutral simulation is shown, since the results are similar), and their shape depends little on the resolution. Most of the spectra show an inertial subrange, which becomes wider for the simulations of finer resolution, but there are no significant differences between the spectra that would reveal the quality of resolution. Hence, as a criterion for the evaluation of the resolution, the energy spectrum is not very informative.

Fig. 7

Energy spectra $E_{uu}(k_x)$a and $E_{vv}(k_y)$ of the neutral case b

A criterion, especially for convective boundary layers, was proposed by Sullivan and Patton (2011), who suggest the convergence of the boundary-layer growth is a sensitive measure of numerical convergence. For the estimation of the inversion height in the convective case, we used the “maximum-gradient method”. At every position i,j (horizontal indices), the vertical position of the maximum of the term $\partial \theta /\partial z$ is determined, and then averaged. As shown in Fig. 8, simulations with a resolution of 20 m or smaller show a very similar inversion height, which agrees with Sullivan and Patton (2011).

Fig. 8

Boundary-layer height of the convective simulations, where $z_i$ is computed according to the maximum-gradient method

In addition, Sullivan and Patton (2011) showed that a daytime convective boundary-layer convergence is reached if the ratio of the inversion height to the grid-cell size exceeds 60. For our own well-resolved simulation C20, the ratio $z_i/\varDelta = 62$. An exact evaluation of the recommendation $z_i/\varDelta >60$ is not possible with our data—more simulations with only slightly different grid resolutions would have been necessary. However, our observation of a converged simulation for a ratio of 62 does not contradict the findings of Sullivan and Patton (2011).

4.3 Resolution Criteria Evaluation II: Two-Point Correlations

We show here how information on the LES resolution quality is obtained from an analysis of the two-point correlations of the velocity components.

The two-point correlation of the u-component of velocity is defined as

$$\begin{aligned} B_{uu}(x^*) = \langle u'(x)u'(x-x^*)\rangle /\sigma _u^2, \end{aligned}$$

(14)

with other velocity-component combinations and directions are defined accordingly, and normalized by the variance of the particular velocity component, giving $B_{uu}(0)=1$. Two-point correlations are calculated from instantaneous values of the velocity fields (i.e., snapshots of the flow, as presented in Fig. 10), with at least five snapshots taken at the end of each simulation in intervals of 2000 s, implying at least one large-eddy turnover time T between two snapshots. To compute the two-point correlation in the streamwise and spanwise directions, the grid is rotated in a way that the new x-component is parallel to the mean flow direction at the height of the snapshot. The rotation angles were between 5$^\circ$ and 25$^\circ$. However, the rotation has little influence on the results compared with the unrotated grids. Given that the energy spectra of the velocity components are available, the two-point correlation can also be computed via a Fourier transformation

$$\begin{aligned} B_{uu}(n) = \frac{1}{\sigma _u^2}\sum _{k=0}^{N_x-1}E_{uu}(k)\cos \left( 2\pi i\frac{kn}{N_x}\right) . \end{aligned}$$

(15)

In our case, the energy spectra were calculated during the simulation and averaged over intervals of 2000 s to include much more data than with the snapshots. Hence, in the following, all two-point correlations are calculated from the spectra.

Figure 9 presents the two-point correlations of the u-component in the x-direction of all stabilities, illustrating curves starting at one and approaching zero with increasing distance $x^*/h$. The form of the two-point correlation may be used to determine the average size of the structures of the velocity field and the number of cells needed to resolve these structures. As in Davidson (2009), we assume grid points belong to the same structure for $B_{uu}(x^*) > 0.3$. The value of $x^*$ for which $B_{uu}(x^*) = 0.3$ is defined as $\sigma$, which is one half of the average size of structures in the flow, since $B_{uu}$ is an even function of $x^*$. The number of cells from $B_{uu}(0)=1$ to $B_{uu}(\sigma )=0.3$ is defined as $n_{c}$, and specifies the number of cells resolving an average structure. These quantities are connected by

$$\begin{aligned} \sigma = n_c\varDelta . \end{aligned}$$

(16)

As the scale $x^*\rightarrow \infty$, $B_{uu}(x^*)$ is expected to approach zero, since, statistically, the velocity structures should not be correlated over large distances. If the domain size is too small, the two-point correlations may not decrease to zero because of the periodic boundary conditions.

The two-point correlations of the stable case in Fig. 9 show a very systematic behaviour. When the grid resolution is refined, the quantity $B_{uu}$ decreases faster, meaning that the average size of the turbulent structures $\sigma$, i.e., the intersection with the line $B_{uu} = 0.3$, decreases with the grid-cell size. Nevertheless, the number of cells by which the mean structure is resolved $n_{c}$ increases with a smaller grid-cell size. Figure 10 a, b, and c shows snapshots of the velocity component u for stable stratification for the same timestep for three different resolutions, clearly illustrating how the size of the structures increases with increasing grid-cell size. A fundamental principle of the LES approach is that only the large eddies are resolved, and the small eddies are modelled. The length scale $\sigma$ that is deduced from the two-point correlation can be understood as an average eddy size of the flow. When the grid-cell size is reduced, then more of the smaller eddies are resolved, which should lead to a smaller value of $\sigma$. The minimum $\sigma$ value is reached when the grid-cell size reaches the Kolmogorov microscale. Since an LES model does not resolve the small eddies, this minimum is not reached by a well-resolved simulation.

The two-point correlations of the neutral case show a slightly different behaviour. Near $x^*/h=0$, coarser grids show higher correlations, as in the stable case. But while simulations N40, N20, and N10 still behave similarly to the stable simulations, two-point correlations for simulations N8 and N5 decrease to zero at a slower rate. Simulation N5 falls below 0.3 even later than in simulation N8, which means that the average size of the turbulent structures is reduced from simulation N40 to N10, and then grows again for the simulations N8 and N5. A possible reason is that the refinement of the grid resolution enables the evolution of long meandering features or streaks as were observed by, for example, Hutchins and Marusic (2007), Hutchins et al. (2011) and Dennis and Nickels (2011). The two-point correlation in the spanwise direction does not show this behaviour. The streaks can also be seen in Fig. 10 d, e, and f. In the flow of the finest resolution, more small-scale details of the flow are evident, but the streaks appear to be more pronounced and persistent compared with the coarser simulations, which may temper the decrease in the two-point correlation in the direction of the flow.

In the convective case, the curves are closer together (see Fig. 13). In the upper part, they show a similar pattern as the other cases, i.e., smaller structures with finer resolution. But at $x^*/h\approx 0.4$, the curves merge, and are very similar for larger distances. The sizes of the structures at the line $B_{uu} = 0.3$ are in the range 0.43–0.52 h.

Fig. 9

Normalized two-point correlation for an elevation of 100 m of the stable a, neutral b, and convective c cases for different resolutions

Fig. 10

Snapshot of the u-component of velocity near 100-m elevation after the end of the simulation. The panels a, b, and c show grid-cell sizes of 1.25 m, 2.5 m, and 10 m of the stable simulation, respectively. The panels d, e, and f show grid-cell sizes of 5 m, 10 m, and 40 m of the neutral simulation, respectively. The panels g, h, and i show grid-cell sizes of 5 m, 10 m, and 40 m of the convective simulation, respectively. The numbers in the panels represent the horizontal coordinates in metres

Figure 9 also contains a magnification of the upper parts (values between 0.8 and 1) of the two-point correlations of all stabilities, illustrating that the behaviour of all curves is similar, which means that coarser resolutions lead to larger correlations. It can be seen that the upper parts of the curves converge as the resolution is reduced. Only in the stable case does convergence not seem to be reached yet. The upper part of the neutral curves as well as of the convective curves do not change much for resolutions $\le$ 10 m.

As the grid in our simulations is isotropic, the resolution is the same in all three directions. However, the velocity components show quite different structure sizes for different directions: The u-component in the x-direction usually shows the biggest structures, while the size of the structures of the u-component in the y-direction, and of the v-component are a bit smaller. The smallest structures are observed in the w-component, for which the structures in the y-direction are a bit smaller than the ones in the x-direction. Since our grid is isotropic, the smallest structures of the flow define how well the flow is resolved. When the smallest structures of the flow can be considered well-resolved, then the treatment of all other velocity components is even better. Hence, the number of cells by which the structures of the w-component in the y-direction are resolved defines the quality of the simulation of the flow.

Fig. 11

Normalized two-point correlation $B_{ww}(y)$ at an elevation of 100 m a, number of cells resolving the dominant structures b, and the size of the dominant structures c, for the stable case

Fig. 12

Normalized two-point correlation $B_{ww}(y)$ at an elevation of 100 m of the neutral case a, number of cells resolving the dominant structures b, and the size of the dominant structures c

Figure 11a shows the two-point correlation of the w-component in the y-direction $B_{ww}(y)$ for the stable case. The form in general is very similar to the form of $B_{uu}(x^*)$ in Fig. 9, though decreasing faster, which means that the structures are smaller. The size of the structures for the case S10 is $\sigma \approx 0.14h$ with $n_c\approx 2.7$. In Fig. 11c, the size of the structures $\sigma /h$ is plotted against the grid-cell size $\varDelta /h$ (both normalized). As the relation between them is approximately linear, they are connected via

$$\begin{aligned} \frac{\sigma }{h} = \alpha \frac{\varDelta }{h} +\beta , \end{aligned}$$

(17)

for which linear regression yields $\alpha = 2.45$ and $\beta = 0.014$. As mentioned above, the general relationship between the number of cells and the size of the structure is $n_c = \sigma /\varDelta$, which, together with Eq. 17, leads to the relationship between the number of cells and the resolution

$$\begin{aligned} n_c = \alpha + \beta \frac{h}{\varDelta }. \end{aligned}$$

(18)

Figure 11c shows that this fit leads to an unambiguous relation between the parameters $n_c$ and $\varDelta$, which enables us to predict very well the number of cells for which the smallest structure of the flow is resolved for a specific resolution. Hence, when the number of cells $n_c$ is chosen corresponding to the w-structures in y-direction to be resolved, then Eq. 18 can be transformed to obtain the necessary resolution by

$$\begin{aligned} \varDelta = \frac{h \beta }{n_c-\alpha }. \end{aligned}$$

(19)

Since we can estimate the quality of the simulations by the investigations in Sect. 4.1, we are able to determine which resolution is sufficient for our set-up. Using the two-point correlation, we can connect the quality of the simulation to a number of cells that are needed for a well-resolved flow. However, the prerequisite to use Eq. 19 for the estimation of a necessary resolution is to know the values of $\alpha$ and $\beta$.

In the stable case, it is unclear if even the simulation with $\varDelta _x=1.25$ m can be considered well-resolved, because, although the normalized values of the TKE seem to converge, the absolute ones do not. In addition, the two-point correlations do not seem to have converged, which indeed may not be necessary for a good simulation, as justified above. It would be interesting to investigate how the two-point correlation evolves with a further refinement of the grid, but this would become computationally very expensive, as simulation S1.25 already required a considerable computational time of 23 h on 1600 nodes. Halving the grid-cell size would increase these requirements by a factor of eight. Stoll and Porté-Agel (2008) used a similar set-up, and concluded that satisfactory results can be achieved for a grid-cell size of 6 m or less. Beare et al. (2006) concluded that “a grid length of 3.125 m or less is ideal for a robust LES of this moderately stable regime”. Our results suggest that, rather, a grid length of 2.5 m or less is required, since with a coarser resolution, no inertial range is visible in the spectra. The resolution of 2.5 m corresponds to $B_{uu}(x^*)$ and $B_{ww}(y^*)$ structures that are resolved by 11 and 3.5 cells, respectively.

The two-point correlation $B_{ww}(y)$ of the neutral case appears very different from that of the u-component in the streamwise direction $B_{uu}(x^*)$ (Fig. 12), being more comparable to the stable case with a clear tendency to smaller structures with finer resolution. Hence, the relation between the parameters $\sigma$ and $\varDelta$ is again quite linear, with the linear regression yielding $\alpha = 1.76$ and $\beta = 0.0176$.

According to the convergence of the wind-speed profiles, the neutral simulation is sufficiently resolved at a grid-cell size around 10 m, which corresponds to $B_{uu}(x^*)$ and $B_{ww}(y^*)$ structures that are resolved by 18 and 3.6 cells, respectively.

Fig. 13

Normalized two-point correlation $B_{ww}(y)$ at an elevation of 100 m of the convective case a, number of cells resolving the dominant structures b, and the size of the dominant structures c

For the convective case (Fig. 13), the values of $B_{ww}(y)$ appear similar to the stable and neutral cases, but the variation of $\sigma$ with $\varDelta$ shows that the finer resolved simulations deviate from a linear relation. This effect is similar to the one we observed for the u-component in the x-direction: a refinement of the grid leads to smaller structures in the flow until a certain limit is reached, when the size of the structures remains unchanged or even starts to grow again. Excluding the simulations C8m and C5m results in a linear relation between the parameters $\sigma$ and $\varDelta$ for the other simulations, with $\alpha = 2.1$ and $\beta = 0.028$. As the subsequently derived relation between the parameters $n_c$ and $\varDelta$ underestimates the number of cells for the finer resolved simulations (see Fig. 13c), the procedure using Eq. 19 can still be used to estimate a lower limit of the grid-cell size to obtain a certain number of cells.

The convective simulations already converge at a resolution of 20 m, while in the TKE profiles, and the two-point correlations, this can also be seen in the convergence of the boundary-layer growth. The resolution of 20 m corresponds to $B_{uu}(x^*)$ and $B_{ww}(y^*)$ structures that are resolved by 40 and 3.7 cells, respectively.

Table 5 shows an overview of some parameters characterizing the flow, as well as the values for $\alpha$ and $\beta$ that describe the connection between the resolution and the size of the structures in the two-point correlation $B_{ww}(y)$. Although the flows are quite different, the values for $\alpha$ and $\beta$ are similar, with $\alpha \approx 2$, and the value of $\beta$ seeming to increase with the boundary-layer height h. However, the three different simulations presented here do not provide enough data to derive a general dependence of the coefficients $\alpha$ and $\beta$ on the parameters listed in Table 5.

In summary, the simulations that we consider well-resolved have resolutions of 2.5 m (stable), 10 m (neutral) and 20 m (convective). Their average $B_{uu}(x^*)$ structures are resolved by 11, 18, and 40 cells, respectively, while their average $B_{ww}(y^*)$ structures are all resolved by 3.5, 3.6, and 3.7 cells, respectively. It is noticeable that the largest structures of the well-resolved simulations of different stabilities are resolved by a very different number of cells, while the smallest structures are resolved by around 3.6 cells.

Table 5 Parameters of the regression of the structure size $\sigma$ with respect to the grid-cell size $\varDelta$, and other parameters characterizing the simulation

5 Conclusions

We used an LES model to investigate the influence of the grid resolution on simple inversion-topped ABL flows for three different stratifications. The simulations were performed using the model PALM, which was amended by a dynamic subgrid model with dynamic bounds. Each of the stratifications was simulated several times with at least four different resolutions. The wide range of resolutions ensured that we had both poorly-resolved and well-resolved simulations for each stratification. To determine whether a simulation with a certain resolution is well resolved, we used the profiles of the mean variables, the TKE, the turbulent stresses, and the spectra. From this overview, we identified those simulations that can be considered well resolved, and these correspond to grid-cell sizes of 2.5 m, 10 m, and 20 m for the stable, neutral and convective simulations, respectively. On this basis, we checked if commonly-used criteria for the LES resolution agree with these findings, and assessed the resolution of our simulations appropriately.

Throughout the boundary layer in all simulations, the ratio of the resolved energy to the total energy $\gamma$ is strongly related to the resolution, which makes it a possible criterion of a well-resolved flow. According to Pope (2004), an LES model is well resolved when $\gamma>$ 0.8. While all of our simulations show a ratio well above this limit, not all of the simulations can be considered well resolved. Since the subgrid TKE is a modelled quantity depending on the type of SGS model, a value of $\gamma$ as a recommendation for a well-resolved simulation depends on the model used. Ludwig et al. (2009) demonstrated how strongly the choice of the SGS model can influence the results. Therefore, the recommendation that a sufficiently fine resolution is reached when the fixed threshold $\gamma =0.8$ is exceeded, may be misleading. Furthermore, the resolved TKE with the LES approach can be higher than the total TKE from direct numerical simulations, as shown by (Celik et al. 2005; Klein 2005), which makes it a questionable indicator of grid resolution. An investigation of an adapted criterion of Celik et al. (2005), which is also based on the ratio of resolved to total energy, showed inconsistencies, which makes it also unreliable for the estimation of resolution quality.

The convergence of the boundary-layer growth is a specific criterion for the convective boundary layer, which Sullivan and Patton (2011) conclude is a strong measure for solution convergence. We also see this convergence in our results, and that it coincides with other properties that indicate a good resolution, such as the convergence of the wind speed and TKE. These findings suggest that the simulation is well resolved with a resolution of 20 m or less. However, to be able to see a convergence of the boundary-layer growth, several simulations of different resolution have to be performed, which is quite an expensive way to check whether a simulation is sufficiently resolved. Another recommendation of Sullivan and Patton (2011) was to use $z_i/\varDelta >60$, which seems to be plausible, since measures such as the two-point correlation are not available in advance, whereas the inversion height $z_i$ can be reasonably estimated. This is consistent with our 20-m simulation for which $z_i/\varDelta \approx 62$.

The two-point correlations of the velocity components allow an estimation of the size of the average flow structures, which we found can be very different for the various velocity components and directions, and that the smallest structures of the flow are in the w-component in the y-direction for all stability cases and all resolutions investigated. The interpretation of the two-point correlation surely depends on the choice of the threshold value. Consistent with Davidson (2009), we selected a value of 0.3. The definition of the threshold directly influences the size of the average structure in the flow, and by how many cells this structure is considered to be resolved. However, we do not expect that the results will change much in a qualitative way by a change of the threshold value.

Davidson recommends eight cells for a coarse simulation, and mentions that to be well resolved, “some 16 cells [...] should be sufficient”, with this number related to the structures of the streamwise and spanwise velocity components. Our results show that a recommendation of a fixed number of cells for the $B_{uu}(x^*)$ structures does not seem to be suitable for the simulation of differently stratified boundary layers, since the $B_{uu}(x^*)$ structures of the well-resolved simulations of the stable, neutral, and convective case are quite different. The recommendation of 16 cells for a well-resolved simulation only fits to the neutral case, and is too high for the stably stratified case, and too low for the convective case. However, the number of cells of the $B_{ww}(y^*)$ structures is very similar for all well-resolved simulations, which is an argument to concentrate on the smallest structures of the flow. The fact that the number of cells is only slightly lower than four for the well-resolved flows may be a feature of the vertical velocity component, which was not investigated by Davidson (2009). Using the linear relation of the size of the $B_{ww}(y^*)$ structures and the grid resolution to determine the resolution requirements for a flow with $B_{ww}(y^*)$ structures resolved by four cells, Eq. 19 gives a resolution of 1.7 m, 8 m and 18 m for the stable, neutral and convective simulations, respectively. This is consistent with the grid resolutions identified as sufficient in the examination of the flow in Sect. 4. But, as suspected, the stably-stratified simulation needs to be refined even more before being considered to be well resolved according to this four-cell criterion.

The set-ups investigated are idealized situations with horizontally-homogeneous conditions, which enable production of the necessary data for a well-averaged two-point correlation. For more complex flows, it is less convenient to obtain sufficient data (a time average instead of a spatial average), and to define the direction of the correlation. Furthermore, the two-point correlation can only be calculated after a simulation has already been carried out.

We conclude that the two-point-correlation method is a very good measure for evaluating the resolution of an LES model of the boundary layer, with most of the other measures for the evaluation of the resolution showing inconsistencies or limitations. The two-point correlation provides the number of cells required to resolve the average structures and is independent of the subgrid TKE calculated by the subgrid model. The four-cell criterion can rate a simulation without the examination of convergence, which can significantly reduce the use of computational resources, since the most expensive simulation is always the one that shows that convergence has already been reached. Theoretically, the two-point-correlation method is also applicable to flows in complex terrain. However, in this case, the correlation calculation cannot take advantage of the spatial homogeneity of the flow. Thus, two-point correlations would need to be derived most likely from an ensemble of simulations, which means a significantly increased amount of computing time. The linear connection between the number of cells by which the smallest structures of the flow are resolved and the grid-cell size can help in the selection of an adequate resolution. Further simulations of boundary-layer flows may lead to a better understanding of this connection, and even yield a more general function of the parameters of the flow, such as the Richardson number and the boundary-layer height for estimation of the resolution quality in advance.