Dependence of Turbulent Velocities on Wind Speed and Stratification

Abstract

We examine the dependence of several turbulence quantities on the wind speed and stability using nocturnal data from the Shallow Cold Pool Experiment. The turbulent quantities (velocities) are defined in terms of the standard deviation of the horizontal and vertical velocity fluctuations, two different calculations of the friction velocity, and two turbulent velocities based on the heat flux. The dependence of the turbulent velocities on the wind speed shows a transition between the weak-wind regime of small slope and the stronger wind regime of larger slope, as found in previous studies. This transition occurs for all of the turbulent velocities examined and occurs for a wide range of averaging times. Although this study concentrates primarily on data over a flat surface above the valley, the transition also occurs at the other 18 stations that have non-zero local slopes up to about 10 %. At the same time, the relationship between the turbulence and the wind speed cannot be universal because of the influence of stratification and site-dependent non-stationarity in the weak-wind regime. The wind speed of the transition increases with increasing stratification at a rate that is an order of magnitude slower than that predicted by a constant transition bulk Richardson number. For the weakest winds, the impact of stratification is unexpectedly small.

1 Introduction

Turbulence velocities, such as the square root of the turbulence kinetic energy, are observed to increase slowly with increasing wind speed for stable conditions until the speed reaches a transition value (Sun et al. 2012). The turbulence increases more rapidly with increasing wind speed when the wind speed exceeds the transition value. This rapid increase is attributed to bulk shear instability on vertical scales large enough to include the observational level such that the observed coherent structures interact directly with the ground. Sun et al. (2012) find that the transition value of the wind speed increases with height, and van de Wiel et al. (2012b) find that the transition wind speed depends on surface thermal characteristics through the surface energy budget, while Mahrt et al. (2013) find that the transition wind speed decreases with increasing surface roughness.

Variations of the wind speed can cause the flow to switch back and forth between the two flow regimes leading to intermittency of the turbulence (Sun et al. 2012). Such non-stationarity can be internally forced through interactions of the turbulence with the mean flow (van de Wiel et al. 2012a) or forced by submeso motions (Mahrt 2010b). Acevedo et al. (2014) find that the submeso motions introduce a site dependency for the relationship between the turbulence and the mean flow for stable conditions. In addition, non-turbulent large coherent structures may also be generated within a stratified boundary layer due to intrinsic development (Ansorge and Mellado 2014) without propagating modes or surface heterogeneity.

The turbulent transition is not as well-defined in terms of the gradient Richardson number where the turbulence decreases rapidly with increasing Richardson number in the weakly stable regime, and smoothly approaches very small values that may not vary detectably with further increase in the gradient Richardson number (Sorbjan and Grachev 2010). There is no critical gradient Richardson number that corresponds to complete collapse of the turbulence (Galperin et al. 2007). For weak winds in the stable boundary layer, the wind profiles are always non-stationary and often complex. Grachev et al. (2013) find that the inertial subrange is no longer definable in the very stable weak-wind regime. Conversion of perturbation potential energy back to turbulent kinetic energy becomes important (Zilitinkevich et al. 2007) and the velocity fluctuations more effectively transfer material in the horizontal than in the vertical (Sukorianski and Galperin 2013). Although the vertical diffusion in the weak-wind stably-stratified boundary layer is quite weak, it significantly influences the nocturnal minimum surface temperature, potential fog formation and concentrations of contaminants.

For wind speeds less than the transition value, the turbulence appears to be fine scale. Indirect evidence for fine-scale turbulence includes the close relationship of the turbulence and the momentum flux to local shear on vertical scales of a metre or less, in the presence of a near-surface wind maximum (Mahrt et al. 2014). A minimum of turbulence at the wind maximum suggests that the turbulence above the wind maximum is partially decoupled from the surface turbulence (Horst and Doran 1988; Conangla and Cuxart 2006; Grisogono et al. 2007). Turbulence that does not directly interact with the ground can be referred to as a form of “z-less” turbulence (e.g. Grisogono 2010).

For weak winds and sufficiently strong stratification, Sun et al. (2012) and Mahrt et al. (2013) find that the changes of stratification are not significantly correlated with triggering the transition between regimes, although the influence of stratification for the weak-wind case might be masked by large non-stationarity and the influence of complex wind profiles. The primary role of the reduction of vertical fluctuations by the stratification may be indirect through the reduction of downward transport of momentum, which in turn reduces the wind speed and shear generation of the turbulence (Shah and Bou-Zeid 2014). Downward transport of turbulence and scalars is an important feature of some very stable boundary layers (Williams et al. 2013). As an additional complication for strong stability, Stoll and Porté-Agel (2009) find that even modest surface heterogeneity modifies the structure of the stable boundary layer. The turbulence is generally observed to remain non-zero with vanishing winds. Based on data from three different field programs, Mahrt et al. (2013) inferentially argued that observed turbulence for very weak winds can be due to (1) shear generation by non-turbulent submeso motions eliminated by the averaging process used to compute the mean flow, (2) downward transport of the turbulence toward the surface, (3) decaying turbulence from recent more significant flow and (4) complex wind profiles including inflection points, locally vanishing wind with non-zero shear and wind directional shear.

An important goal of the present study is the re-examination of the transition between the weak-wind weak-turbulence regime and the stronger wind stronger turbulence regime through the use of new turbulence velocities and their dependence on wind speed and several stability parameters. The intention is to examine the unexpected weak impact of stratification for weak wind conditions. We do not evaluate similarity theory nor seek quantitative empirical relationships, since we consider formulation of similarity theory to be premature for the stratified weak wind regime because the governing physics is not yet sufficiently understood. We examine the behaviour of the weak-wind regime and the transition between the two turbulence regimes using primarily observations over a flat surface outside the valley in the Shallow Cold Pool Experiment.

2 Data and Analyses

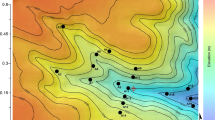
The Shallow Cold Pool (SCP) Experiment was conducted over semi-arid grasslands in north-eastern Colorado, USA at approximately 1660 m above sea level from 1 October to 1 December 2012. Details can be found at https://www.eol.ucar.edu/field_projects/scp and in Mahrt et al. (2014). Figure 1 shows the domain and station locations; the main valley is relatively small, roughly 12 m deep and 270 m across. The width of the valley bottom averages about 5 m with an average downvalley slope of 2 %, increasing to about 3 % in the upvalley tributary gullies. The side slopes of the valley are order of 10 % or less. Here, we analyze primarily Campbell CSAT sonic anemometer data at 1-m height from 19 stations and from the main tower. Most of the analysis concentrates on Station A1, which is located over relatively flat terrain outside of the valley. For weak winds and strong stratification, flux loss is expected due to pathlength averaging (Horst and Oncley 2006). Sun et al. (2013) found that the flux loss due to pathlength averaging at 0.5 m was only 0.4  % for near-neutral conditions, but expected to increase with increasing stability. We do not apply spectral corrections for this error because the spectra often become erratic for weak winds with significant stratification. The pathlength averaging error decreases with increasing wind speed and size of the main transporting eddies. Therefore this error acts to underestimate the turbulence for the weakest winds and does not contribute to the slowness of the increase of the computed turbulence with increasing weak wind.

Fig. 1

A map of the SCP Experiment study area with sonic anemometer stations (black dots, the A stations) and the 20 m main tower (red M). The map also includes a short 3-m tower (green C). In the station naming, the $p$ notation indicates pressure measurements and the $h$ notation indicates Handar anemometers at 0.5 m. Solid lines are isolines of constant elevation labelled in metres above sea level and are separated by only 1-m intervals. The terrain slopes are generally less than 10 %

We estimate the stratification from 1-Hz temperature data from NCAR ventilated hygrothermometers deployed at the 0.5-m and 2-m levels at the 19 stations. Data are analyzed only for the nocturnal period defined as 1700-0700 local standard time (LST).

2.1 Scatter and Sampling

In weak-wind conditions, the flow is strongly non-stationary and the scatter in the relationship between turbulent and mean flow variables is large. Attempting to reduce the scatter by increasing the averaging time leads to more ambiguous results by capturing more non-stationarity within the averaging window. To avoid increasing the averaging time yet reducing the scatter, some of the analyses in this study are based on averaging quantities for different intervals of the wind speed or stability, referred to as interval or bin averaging. Ratios are computed from averaged quantities rather than averaging the ratios directly. Intervals with less than 10 samples are discarded.

2.2 Momentum Flux Calculation

Computation of the momentum flux can become problematic for weak winds and weak turbulence. The computed momentum flux is more sensitive to the sonic alignment than are the scalar fluxes. Misalignment becomes problematic in very stable conditions because the eddies may be relatively flat with small attack angles. The choice of the best correction method becomes ambiguous with strong stratification where real mean vertical motions can be induced by minor terrain features and even weak surface heterogeneity (Mahrt 2010a). Here, the coordinate system has been rotated using the planar fit method (Wilczak et al. 2001) applied to the entire dataset. This rotation significantly affected the momentum flux for the weakest winds at several of the stations on sloped terrain.

The need to composite the momentum flux over intervals of wind speed or stability leads to complications because the momentum flux is a vector quantity. Directly averaging the friction velocity $u_*$ can lead to augmented values because random errors are inadvertently converted to systematic errors (Mahrt 2010a) although random errors are not formally defined in a non-stationary environment. When averaging $u_*$ values, the crosswind momentum flux contributes to each $u_*$ value and augments the composited $u_*$ value particularly for weak winds. We refer to this averaging method as the upper estimate of $u_*$.

The second method aligns the coordinate system into the wind direction for each averaging window and composites the along-wind and cross-wind momentum fluxes separately to provide an estimate of the lower limit of $u_*$. The crosswind momentum flux normally composites to near zero. This method may be biased because the rotation into the wind direction leads to smaller composited $u_*$ values but does not lead to smaller values of the wind speed. Neither method is completely satisfactory but they provide an envelope for $u_*$ by providing an upper and lower estimate.

2.3 Averaging Time

The choice of averaging time for defining the “mean” flow and fluctuations from the mean flow is complicated because the turbulence is confined to much smaller time scales for very stable conditions compared to weakly stable conditions. However, we decide against using a stability dependent averaging time because it is sometimes ambiguous and complicates the interpretation of results. As an example of scale dependence, the heat flux based on 10-s averaging windows (red solid, Fig. 2a) appears to lose 10–15 % of the downward heat flux when compared to the heat flux based on 5-min averaging windows (black dashed) for wind speeds $>$4 m s$^{-1}$. This study emphasizes wind speeds $<$ few ms$^{-1}$, in which case the loss of heat flux for the 10-s averages is much less.

Fig. 2

a The composited 1-m heat flux at station A1 for intervals of wind speed based on 5-min averages (black dashed) and 10-s averages (red). b The composited correlation between $w$ and $\theta$ (red) as a function of wind speed at station A1 for 5-min averages (black dashed) and 10-s averages (red solid)

Correlation coefficients are composited by averaging them directly and also computed by first averaging fluxes and standard deviations and then taking the ratio. The differences between the two methods are small and we proceed with direct averages of the correlation coefficient. For wind speeds $<$1 m s$^{-1}$, the correlation coefficients for the heat flux based on 5-min averages (black dashed, Fig. 2b) are significantly smaller than those computed from 10-s averages (red solid). In fact the correlation coefficients based on 5-min averaging windows essentially vanish for the weakest winds, suggesting that the deviations from 5-min averages are heavily contaminated by non-turbulent motions for the weakest winds.

Here, we focus on relatively weak winds and the transition zone where most of the flux is captured by 10-s windows (Fig. 2). We choose 10-s averaging windows to avoid contamination of the fluctuations by non-turbulent motions. The intention here is not to capture absolutely all of the flux, which would require a larger averaging window. Some calculations are made for 5-min averaging windows for comparison. Fluxes for 10-s averaging windows are particularly variable. The relationship between turbulent velocities based on fluxes and wind speed or stability is examined in subsequent sections by compositing all of the nocturnal 10-s flux values falling within different intervals of the wind speed or one of the stability parameters (Sect. 4).

3 Averaging Operators

All averaging involves simple unweighted averages; we define an averaging time, $\tau$, that attempts to partition the flow between turbulent fluctuations on time scales smaller than $\tau$ and larger scale non-turbulent motions,

$$\begin{aligned} \phi = \phi ' + \overline{\phi } \end{aligned}$$

(1)

where $\phi$ is one of the transported variables such as potential temperature or one of the velocity components, $\overline{\phi }$ is the average over time scale $\tau$, and $\phi '$ is the deviation from such an average. The vertical flux of $\phi$ is then computed as $\overline{w' \phi '}$.

In Sect. 5.3, time-averaged quantities will be subsequently averaged over the SCP network of observations, which might also be interpreted as averaging over a model grid area. The spatial averaging is represented by square brackets, $[\phi ]$. Partitioning the local time average, $\overline{\phi }$, in terms of a spatial average, $[\phi ]$, and the deviation of the local time average from the spatial average, $\phi ^*$, we write

$$\begin{aligned} \overline{\phi } \equiv \phi ^* + [\phi ]. \end{aligned}$$

(2)

The local instantaneous value can then be decomposed as

$$\begin{aligned} \phi = \phi ' + \phi ^* + [\phi ]. \end{aligned}$$

(3)

Averaging $\overline{w'\phi '}$ over the spatial domain yields the spatially-averaged turbulent flux $[ \overline{w'\phi '}]$. For efficiency, the averaging operator $\{\;\;\}$ will refer to time averaging or spatial averaging of the time average.

4 Basic Variables

The intensity of the turbulence is generally represented by the square root of the turbulent kinetic energy. Here we distinguish between horizontal and vertical fluctuations and define

$$\begin{aligned} \sigma _\mathrm{V} \equiv \sqrt{\{u'^2\} +\{v'^2\}}. \end{aligned}$$

(4)

For very stable conditions, $\sigma _\mathrm{V}$ can be dominated by non-turbulent two-dimensional modes even at relatively small scales. In this respect, $\sigma _w$ is a better indicator of the turbulence than the horizontal velocity fluctuations or the turbulence kinetic energy.

Turbulent velocities based on fluxes, such as $u_*$, more effectively filter out non-turbulent motions assuming that the vertical transport is due mainly to turbulence. However, estimation of fluxes requires a larger sample size compared to variances and standard deviations. In addition, $u_*$ is more affected by the alignment of the sonic anemometer compared to standard deviations of the velocity fluctuations.

We also evaluate a turbulent velocity based on the heat flux, which effectively filters out non-turbulent motions compared to $\sigma _w$, defined as (Mahrt et al. 2014)

$$\begin{aligned} V_{w\theta } \equiv -\frac{\{w' \theta ' \}}{\sigma _{\theta }} = R_{w\theta } \sigma _w \end{aligned}$$

(5)

where $R_{w\theta }$ is the correlation coefficient between potential temperature and vertical velocity fluctuations. Alternatively, one can represent the turbulence intensity as

$$\begin{aligned} V_{\delta \theta } \equiv - \frac{\{w' \theta ' \}}{\delta \theta } \end{aligned}$$

(6)

where $\delta \theta$ is the difference of potential temperature ${\theta }$ between two levels. This turbulent velocity is motivated by the bulk relation, $\{w' \theta ' \} = C_\mathrm{h} V \delta \theta$, in which case Eq. 6 can be written as

$$\begin{aligned} V_{\delta \theta } \equiv - \frac{\{w' \theta ' \}}{\delta \theta } = C_\mathrm{h} V. \end{aligned}$$

(7)

Although this turbulent velocity links directly to the bulk relation, it is by definition based on a mix of the turbulence and mean flow and is vulnerable to self correlation when plotted against the bulk Richardson number. It will not be incorporated into the analysis until Sect. 7.

Collectively, we symbolize the turbulence velocities $\sigma _\mathrm{V}, \sigma _w, u_*$ and $V_{w\theta }$ as $u_\mathrm{t}$. In the next section, we relate $u_\mathrm{t}$ to the wind speed

$$\begin{aligned} V \equiv \sqrt{\{u\}^2 + \{v\}^2}. \end{aligned}$$

(8)

A normalized version of the turbulent velocities, $C_{u_\mathrm{t}}$, is computed by dividing the turbulent velocities by the wind speed

$$\begin{aligned} C_{u_\mathrm{t}} \equiv \frac{u_\mathrm{t}}{V} \end{aligned}$$

(9)

and evaluated in Sect. 7. For $u_\mathrm{t}$ = $V_{\delta \theta }, C_{u_\mathrm{t}}$ becomes the transfer coefficient for heat, $C_\mathrm{h}$. For $u_\mathrm{t} = u_*, C_{u_\mathrm{t}}$ is the square root of the drag coefficient. Interpretation of the non-dimensional turbulence velocities must recognize the influence of self correlation through use of the wind speed in both the non-dimensional turbulence velocity and the mean flow parameter, which is the wind speed or the stability parameter.

For bookkeeping convenience, the stratification can be expressed in terms of

$$\begin{aligned} V_\mathrm{b} \equiv \sqrt{ \frac{ gz \delta \theta }{ \Theta } } \end{aligned}$$

(10)

where again $\delta \theta$ is the time-averaged vertical difference of the potential temperature. Then the stability can be written as a bulk Richardson number

$$\begin{aligned} R_\mathrm{b} \equiv \left( \frac{ V_\mathrm{b}}{V} \right) ^2 \end{aligned}$$

(11)

or as a version of the Froude number

$$\begin{aligned} Fr \equiv \frac{V}{V_\mathrm{b}} \end{aligned}$$

(12)

where again $V$ is the speed of the vector-averaged wind (Eq. 8). Even though $Fr$ and $R_\mathrm{b}$ contain the same information, the bulk Richardson number varies less erratically for near-neutral conditions while $Fr$ varies less erratically for very stable conditions. That is, the ratio quantities vary erratically when the denominator becomes very small leading to highly skewed distributions. For very stable conditions, $R_\mathrm{b}$ often changes by an order of magnitude over a period of a few minutes due to the non-stationarity of the (weak)wind speed, which appears quadratically in the denominator of $R_\mathrm{b}$. Here, the calculation of $R_\mathrm{b}$ and $Fr$ from the data is asymmetric in that $\delta \theta$ is computed between the 0.5-m and 2-m levels while the velocity difference is computed between 2 m and the surface where it is assumed to be zero.

The turbulent velocities can be related to the stability in a dimensionally consistent way by representing stability as

$$\begin{aligned} V_\mathrm{F} \equiv V /\sqrt{\frac{\delta \theta }{ \Theta }}. \end{aligned}$$

(13)

This generalization is somewhat cosmetic because $V_\mathrm{F}$ has a one-to-one relationship to $Fr$ at a given height although $V_\mathrm{F}$ excludes the square-root dependence on the height above the ground. Typically, $V_\mathrm{F}$ is an order of magnitude larger than the wind speed for stable conditions because $\delta \theta /\Theta$ is of order $10^{-2}$.

5 Dependence of Turbulence Velocities on Wind Speed

We now examine the dependence of the turbulent velocities on wind speed and stability using the 1-m sonic anemometer data at station A1 located on a relatively flat surface. Again, averaging is based on the short 10-s windows unless otherwise noted.

5.1 Contrasting Turbulent Velocities

Comparison between the different turbulent velocities is difficult due to their significant differences in magnitude. The turbulence velocities based on standard deviations of the velocity fluctuations are generally substantially larger than those based on fluxes. Fluxes are reduced by relatively low correlations for weak-wind stable conditions. To reduce this difference for visualization, we normalize each turbulent velocity by its value at a specified wind speed to produce $U_\mathrm{t} \equiv u_\mathrm{t}/u_\mathrm{t} (V_\mathrm{s})$, where, $V_\mathrm{s}$ is chosen to be 4 m s$^{-1}, \sigma _\mathrm{V} = 0.81$ m s$^{-1}$, $\sigma _w = 0.34$ m s$^{-1}$, $u_* = 0.31$ m s$^{-1}$ for both calculation methods and $V_{w\theta } = 0.10$ m s$^{-1}$. The dependence of the normalized turbulent velocities $U_\mathrm{t}$ on wind speed is qualitatively the same for any choice of $V_\mathrm{s}$ that is greater than the transition wind speed. The normalized values approximately collapse onto a single curve for wind speeds greater than the transition value (Fig. 3a).

For weak winds, the turbulent velocities all increase slowly with increasing wind speed until the wind speed increases to a transition value of about 1–1.25 m s $^{-1}$ (Fig. 3a) and then increase more rapidly with further increase in wind speed, as observed by Sun et al. (2012) in terms of the square root of the turbulent kinetic energy. The transition value reported here is approximated as the centre of the transition between the two regimes of roughly constant slope. The transition in Fig. 3 is smooth, partly because it is an average over a variety of situations occurring over a two-month period. The observed transition is smooth also due to the failure of the turbulence to maintain equilibrium with the non-stationary flow. We use the term “transition” with the understanding that the transition occurs over a finite range of wind speeds. For wind speeds $\gtrsim$3 m s$^{-1}$ (Fig. 3a), the slope of $u_\mathrm{t} (V)$ decreases although this second slope transition is much weaker than the main transition and is outside the scope of this study.

Differences between the different turbulent velocities develop for wind speeds less than the transition wind speed (Fig. 3). Because the correlations of the vertical velocity fluctuations with the horizontal velocity and temperature fluctuations are smaller than those expected for fully developed turbulence, the velocities based on the standard deviation of the velocity components might be contaminated by non-turbulent motions even for the small 10-s averaging window. $u_*$ is numerically reduced less compared to $V_{w\theta }$ because it is the square root of a flux.

The difference between the upper and lower estimates of $u_*$ becomes significant for the weakest winds (Fig. 3). The upper estimate of $u_*$ is about twice the lower estimate for the smallest wind-speed interval of 0–0.25 m s$^{-1}$. The upper estimate of $u_*$ is the simple average of $u_*$ and more indicative of the intensity of the turbulence while the lower estimate is based on the composites of the along-wind and cross-wind momentum fluxes and is influenced by the degree of persistence of the relationship of the stress direction to the wind direction. For this reason, the upper estimate shows better defined constant slope regions and slope transition. Below, the calculations of $u_*$ are based on the upper estimate unless otherwise noted.

Fig. 3

Interval-averaged velocities for the 1-m sonic anemometers at the upland station A1, scaled by the value at 4 m s $^{-1}$ for, a 10-s averaging window and b 5-min averaging window. Shown are the normalized $\sigma _\mathrm{V}$ (blue), $\sigma _w$ (black), $V_{w\theta }$ (red), $u_*$ based on averaged components (green dashed) and $u_*$ based on direct averages of individual $u_*$ values (green) as a function of interval-averaged wind speed

5.2 Dependence on Scale

For 5-min averaging windows, the different turbulent velocities no longer collapse onto a single line even for wind speeds $>$ transition value (Fig. 3b). The differences are greater for wind speeds $<$ transition value as compared to weak-wind conditions for 10-s averages. This is probably due to important non-turbulent contributions to $\sigma _w$ and particularly $\sigma _\mathrm{V}$ on time scales between 10 s and 5 min that are most important for weak winds. The curves are noisier due to a much smaller sample size for 5-min averages compared to 10-s averages.

5.3 Spatial Variation

The above results are based on the 1-m sonic anemometer data at station A1 that is located on an upland relatively flat surface. To briefly examine the spatial variation, the interval averaged quantities for $u_*(V)$ have been separately averaged over the upland stations, stations in the up-valley tributary gullies, valley sideslope stations and valley bottom stations (Fig. 4). Although weak winds in the valley often permit down-valley cold-air drainage with near-surface wind maxima, the transition in $u_*(V)$ is similar for all of the four sub-regions.

Fig. 4

The dependence of $u_{*}$ on $V$ based on averages over the upland stations (black, A1, A4 and A14), up-valley gully stations (red, A2, A3 and A5), the mid slope stations (blue, A10, A12, A13, A18 and A19) and the valley-floor stations (green, A7, A8, A11 and A16). Station locations are identified in Fig. 1

5.4 Vanishing Speed

Figure 3 indicates that all of the turbulent velocities retain non-zero values with vanishing wind speed even for the small 10-s averages used here. In fact the asymptotic value of $u_\mathrm{t}$ with vanishing wind speed can exceed the difference of $u_\mathrm{t}$ between $V=0$ and the transition value of $V$. A number of mechanisms for maintaining non-zero turbulence with vanishing wind speed were noted earlier, and include shear generation by non-stationary submeso motions, non-equilibrium turbulence, complex vertical wind profiles and downward transport of turbulence from higher levels.

5.5 Shear

Theoretically, $u_\mathrm{t}$ should be more closely related to the wind shear than the wind speed itself. The shear was computed using sonic anemometers at the 0.5-m and 2-m levels on the main tower. Relating $u_\mathrm{t}$ to the shear instead of wind speed (not shown) identifies two well defined regimes for $V_{w\theta }$ but the two regimes become more obscure for $\sigma _\mathrm{V}, \sigma _w$ and $u_*$ relative to the dependence on wind speed alone based on the 1-m level at the main tower. The dependence of $u_\mathrm{t}$ on the shear also depends on the depth of the shear calculation using the eight levels of sonic anemometers on the 20-m tower. The shear calculations may also be influenced by increased errors due to small differences between larger values. The failure of the shear to better predict the turbulence compared to the wind speed occurred in a number of other datasets not reported here.

6 Relation of the Turbulent Velocities to Stability

We now examine the relationship between $u_*$ and the stability parameters and then try to isolate the influence of stratification in Sect. 6.2. The term “dependence” refers to a statistical dependence and does not refers to cause and effect.

6.1 Relation to Stability Parameters

The shape of the dependence of $U_\mathrm{t}$ on $V_\mathrm{F}$ (Fig. 5b) is not affected by the choice of the normalization for computation of $U_\mathrm{t}$ as long as the chosen value of $V_\mathrm{F}$ is greater than the transition value. Here, $u_\mathrm{t}$ is scaled by the values at $V_\mathrm{F} = 40$ m s$^{-1}$. To examine the relationship of $U_\mathrm{t}$ to $R_\mathrm{b}, u_\mathrm{t}$ is scaled by the average $u_\mathrm{t}$ for the first interval with at least 10 samples corresponding to an interval mean $R_\mathrm{b} = 0.024$. Recall that this normalization does not affect the shape of $u_\mathrm{t}$ for an individual turbulent velocity but only adjusts the magnitude of each turbulent velocity so that values collapse to unity at the point of normalization. On average $V_\mathrm{F}$ is roughly 10$V$ though the relationship between $V$ and $V_\mathrm{F}$ is characterized by considerable scatter partly due to the role of stratification.

The relationship of the scaled turbulent velocities $U_\mathrm{t}$ on the stability dependent velocity $V_\mathrm{F}$ (Fig. 5b) is qualitatively similar to the relationship to the wind speed (Fig. 5a) but the transitions appear to be a little sharper. The value of $V_\mathrm{F}$ at the slope transition is a little less than 10 m s$^{-1}$, and corresponds to a bulk Richardson number, $R_\mathrm{b} = gz/{V_\mathrm{F}}^{2}$, of a little greater than unity. However, the slope transition in terms of $R_\mathrm{b}$ (Fig. 5c) is somewhat more diffuse compared to the dependence on $V_\mathrm{F}$ in spite of the use of $\hbox {log}(R_\mathrm{b})$. The transition is even more spread out in terms of $R_\mathrm{b}$ itself without the log transform, and is smoother partly because $R_\mathrm{b}$ becomes especially sensitive to the non-stationarity of weak winds, which appear quadratically in the denominator. Thus $R_\mathrm{b}$ varies erratically in time for weak-wind conditions, which in the presence of non-stationarity and non-equilibrium turbulence, leads to smoothing of $U_\mathrm{t} (R_\mathrm{b} )$. In addition, a linear dependence of $U_\mathrm{t}$ on $V_\mathrm{F}$ converts to an inverse square-root dependence on $R_\mathrm{b}$. The transition between two inverse square-root functions is more difficult to detect from observations than a transition in linear slope. Herein, we use $Fr$ instead of $R_\mathrm{b}$ for the measure of stability, recognising that $Fr$ becomes problematic for near-neutral conditions.

Fig. 5

Interval-averaged scaled turbulent velocities, $U_\mathrm{t}$ for station A1. Shown are $\sigma _w$ (black), $V_{w\theta }$ (red) and $u_*$ based on averaged components (green) as a function of a interval-averaged wind speed, b $V_\mathrm{F}$, and c the bulk Richardson number. $U_\mathrm{t}$ is computed by normalizing with the values at $V = 4$ m s$^{-1}$, $V_\mathrm{F} = 40$ m s$^{-1}$ and $R_\mathrm{b} = 0.024$

6.2 Relation to Stratification

While the relationship of $U_\mathrm{t}$ to $V_\mathrm{F}$ appears to be characterized by a sharper change of slope compared to the relationship to $V$, this evidence is subjective and of unknown significance. The influence of $\delta \theta$ on the turbulent velocities is difficult to isolate from the influence of the wind speed because $\delta \theta$ is generally inversely related to the wind speed. For the SCP experiment this inverse relation is characterized by considerable scatter (Fig. 6), which is partly due to frequent partly cloudy or cloudy conditions, leading to numerous points with small $\delta \theta$ for weak winds (lower left corner of Fig. 6). These points terminate the overall increase of $\delta \theta$ with decreasing wind speed.

Fig. 6

The relationship of $\delta \theta$ between 0.5-m and 2.0-m levels to the wind speed for individual 10-s periods and the composite of $\delta \theta$ for intervals of wind speed (red). The lower right corner corresponds to large values of $Fr$ and $V_\mathrm{F}$ while the upper left corner corresponds to small values

For the weak-wind range that includes the transition region ($V< 3$ m s$^{-1}$), both $V_{w\theta }$ and $u_*$ decrease smoothly with increasing stratification without a transition in slope (Fig. 7). The relatively well-defined transition in $u_\mathrm{t}(V)$ is thought to be due to shear instability that is closely related to the wind speed. The within-interval standard deviations and standard error of $V_{w\theta }$ and $u_*$ are significantly reduced when related to $V_\mathrm{F}$ instead of $V$, for values of $V$ near or above the transition value $\approx$1.25 m s$^{-1}$, as shown for $u_*$ in Fig. 8a. The interval width of $V$ is 0.25 m s$^{-1}$, which roughly corresponds to 2.5 m s$^{-1}$ intervals in $V_\mathrm{F}$, although only the general trend is of interest here. The within-interval standard deviation of $u_*$ based on $V_\mathrm{F}$ is a little less than 70 % of that for intervals based on $V$ for values of $V$ near and greater than the transition value. This might imply that about half of the variance of $u_*$ within intervals of wind speed is due to stratification.

Fig. 7

The relationship of the interval-averaged $V_{w\theta }$ (red) and $u_*$ (green) to the stratification $\delta \theta$ for $V< 3$ m s$^{-1}$

Fig. 8

a Ratio of the within-interval standard deviation for the dependence of $u_*$ on $V_\mathrm{F}$ ($Sd_\mathrm{VF}$) to the within-interval standard deviation for the dependence on $V$ ($Sd_{V}$), as a function of wind speed. $V_\mathrm{F}$ averages about 10$V$. b The dependence of the interval averaged $u_*$ on wind speed for $\delta \theta < 1$ K (solid black) and for $\delta \theta > 3$ K (green dashed)

In contrast, for wind speeds that are significantly smaller than the transition wind speed, inclusion of information on the stratification through $V_\mathrm{F}$ does not appreciably reduce the within-interval standard deviation as indicated by Fig. 8a. In other terms, the turbulence for $V$ significantly weaker than the transition value does not decrease significantly with increasing stratification.

The within-interval standard deviations of $u_* (V)$ are about half of the interval mean values. The standard error is generally less than 1 % of the magnitude of $u_*$ for dependencies on both $V_\mathrm{F}$ and $V$ because of the large sample size for the 10-s averages. The standard error is computed as the standard deviation of the observations within a given interval (bin) divided by the square root of the number of data points within the interval. However, the assumptions of a Gaussian distribution and independence required for estimation of the standard error are probably not adequately met for the 10-s averages. Thus, the standard error is only a casual measure of the uncertainty of the interval mean without formal mathematical support. The ratio of the “standard errors” of $u_*$ within intervals of $V_\mathrm{F}$ to that within intervals of $V$ follows a pattern similar to that for the ratio of within-interval standard deviations (not shown).

The impact of the stratification on $u_\mathrm{t}$ is now posed in terms of $u_*$ as a function of wind speed for different classes of $\delta \theta$ (Fig. 8b). Differences emerge for distinctly separated classes of stratification. Here we choose $\delta \theta < 1$ K for the weakly stratified case and $\delta \theta > 3$ K for the class of stronger stratification where, again, $\delta \theta$ is the difference of potential temperature between the 0.5-m and 2.0-m levels. The interval-averaged value of $u_*$ is significantly larger for weaker stratification (black solid line, Fig. 8b) compared to the class of stronger stratification (green dashed line) for wind speeds between 1 and 2 m s$^{-1}$. The vanishing difference for the weakest winds reflects the general unimportance of the value of stratification for weak winds. For wind speeds substantially greater than the transition value, the inclusion of stratification through $V_\mathrm{F}$ reduces the within-interval scatter (Fig. 8a) but the stratification does not affect the mean value of $u_*$ (Fig. 8b).

The class of strong stratification unexpectedly includes some cases of significant winds. These 10-s records appear to correspond to the initial stage of acceleration where turbulence development is just beginning and the reduction of the stratification by mixing has not yet been realized. In other words, these cases may result from the non-stationarity and phase lag between acceleration, subsequent increased mixing and reduction of stratification. Definitive conclusions require information moving with the flow rather than measurements from fixed sites.

For the class of weak stratification (black line, Fig. 8b), the transition between the two regimes is more diffuse and corresponds to a smaller change of slope compared to the class of stronger stratification. In fact for even weaker stratification ($\delta \theta < 0.5 K$), the two regimes and transition are difficult to identify (not shown). These results suggest that a certain degree of stratification is required before the transitions emerge. With very small stratification, the weak-wind regime with small slope of $u_\mathrm{t}(V)$ does not develop or it occurs at wind speeds too small to detect with the interval-averaging analysis. From another point of view, the slope of $u_\mathrm{t}(V)$ at a given low wind speed decreases with increasing stratification. As the stratification increases, the weak-wind regime of small slope for $u_\mathrm{t}(V)$ extends to more significant winds. The transition wind speed, assuming the ability to quantify such a transition, increases with increasing stratification. This dependence suggests the possibility of a transition bulk Richardson number. With this hypothesis, the transition wind speed would increase as the square root of the stratification $\delta \theta$ as is also predicted by a constant transition value for $Fr$. The two stratification classes in Fig. 8b correspond to averaged $\delta \theta = 0.4$ and 4.2 K, corresponding to almost a 10-fold increase, predicting the transition velocity to increase by a factor of a little more than 3. Attempting to estimate the transition wind speed for each stratification subclass in Fig. 8b in terms of maximum curvature yields transition speeds of about 1 and 1.3 m s$^{-1}$. This observed 30 % increase of the transition velocity is an order of magnitude smaller than that predicted by a constant transition Richardson number. It is possible to improve the performance of $R_\mathrm{b}$ and $Fr$ by including a power dependence on ${\delta \theta }/{\Theta }$ but this is beyond the scope of the present study and not recommended based on a single site.

The weak relationship of the transition wind speed to $\delta \theta$ might be due to different phase and time scales of the wind, turbulence and stratification. Turbulence increases rapidly through shear instability. The impact of the stratification through buoyancy destruction of turbulence becomes significant after the turbulence is generated and persists as long as the enhanced turbulence survives. In addition, for weak-wind stable conditions, the wind profile is observed to be considerably more non-stationary than the temperature profile. Evidently, the wind field responds quickly to short-term variations of the pressure gradient. The denominator of the bulk Richardson number operates on a more rapid time scale than the numerator. A similar mix of time scales would occur in the denominators and numerators of $Fr$ and $V_\mathrm{F}$

7 Normalizing with the Mean Wind Speed and the Bulk Relation

The slow decrease of the turbulent velocities, $u_\mathrm{t}$, with decreasing weak wind speed and non-zero values of $u_\mathrm{t}$ for vanishing wind speed, leads to a breakdown in the bulk relation. The difficulty results from the normalization of $u_\mathrm{t}$ by the wind speed required to construct the surface exchange coefficients. Here, $u_*$, normalized by the wind speed, is the square root of the drag coefficient, $\sqrt{C_\mathrm{d}}$, while $V_{\delta \theta }$ scaled by the wind speed is the transfer coefficient for heat, $C_\mathrm{h}$. Because $u_*$ and $V_{\delta \theta }$ do not vanish as the wind speed vanishes, $C_\mathrm{h}$ and particularly $C_\mathrm{d}$ increase as the wind speed becomes small. This increase carries over to the dimensionally consistent plot of $C_\mathrm{d}$ and $C_\mathrm{h}$ as a function of $Fr$ (Fig. 9). Normalizing $u_\mathrm{t}$ by the wind speed is a form of self correlation because the stability parameters ($Fr$ or $R_\mathrm{b}$) also contain the wind speed. In the weak-wind region where $u_\mathrm{t}$ varies only slowly with wind speed, the relationship between $u_\mathrm{t}$ and the stability is dominated by the shared variable, the wind speed. The impact on $C_\mathrm{d}$ is greater than the impact on $C_\mathrm{h}$ because the calculation of $C_\mathrm{d}$ depends inverse quadratically on the wind speed. Use of 5-min averaging instead of 10-s averaging increases the increase of $C_\mathrm{d}$ and $C_\mathrm{h}$ for small $Fr$ because unresolved submeso motions on time scales $<$5 min contribute to the generation of turbulence with vanishing wind speed.

$C_\mathrm{h}$ increases more rapidly with decreasing stability than $C_\mathrm{d}$ does (right side of Fig. 9). Such behaviour is consistent with self correlation between $C_\mathrm{h}$ and $Fr$ due to the shared variable $\delta \theta$. Application of the bulk relation specifies $C_\mathrm{d}$ and $C_\mathrm{h}$ to decrease slowly with increasing stability. Such formulations predict the fluxes to vanish with vanishing resolved wind although the models often include additional constraints on the minimum wind speed, minimum $u_*$ or maximum allowed stability. Without such constraints, the bulk relation grossly underestimates the turbulent transport for weak-wind conditions. This parametrization problem is currently under investigation.

Fig. 9

Interval-averaged $C_\mathrm{h}$ (red dashed), $C_\mathrm{d}$ based on averaged flux components (black solid) and $C_\mathrm{d}$ based on the interval-averaged $u_*$ (black dashed) as a function of $Fr$. $R_\mathrm{b}$ increases to the left. On average for this dataset, $Fr$ is about 10$\times$ the wind speed

8 Conclusions

A number of turbulent velocities, $u_\mathrm{t}$, were related to the non-turbulent mean flow represented by the wind speed, a stability dependent velocity ($V_\mathrm{F}$), the bulk Richardson number and $Fr$ (inverse square root of the bulk Richardson number). Here, $u_\mathrm{t}$ includes the standard deviations of the horizontal velocity fluctuations, vertical fluctuations, two versions of $u_*$ and two turbulent velocities based on the heat flux. In the weak wind stable regime, the turbulent velocities increase only gradually with increasing wind speed and/or decreasing stability. Once the wind speed exceeds a transition value, the turbulence velocities increase with wind speed at a rate that is an order of magnitude greater. The two regimes occur whether defining the forcing in terms of the wind speed, the stability dependent velocity $V_\mathrm{F}$, or $Fr$. For weak winds, $R_\mathrm{b}$ varies more erratically than $V, V_\mathrm{F}$, and $Fr$ because the weak non-stationary wind speed appears quadratically in the denominator. The two regimes occur at all of the 19 stations in the SCP experiment in spite of the influence of a variety of slopes.

These results are qualitatively similar using a wide range of averaging times. The current study emphasizes a short 10-s averaging window that minimizes contamination by non-turbulent motions yet includes most of the flux for weak-wind conditions. The transition wind speed increases with increasing stratification but at a rate that is much slower than the square-root dependence predicted by a constant transition bulk Richardson number. For this particular site, the average impact of the stratification becomes very small as the wind speed vanishes. The secondary role of the stratification may be partly due to the fact that shear instability is responsible for the generation of turbulence while the influence of stratification through buoyancy destruction of turbulence responds on a longer time scale (Sun et al. 2012). The influence of stratification on the turbulence for weak winds competes with the influences of non-stationarity, the downward transport of turbulence energy, wind directional shear and complex wind profiles with inflection points.

The turbulent velocities do not vanish as the wind speed vanishes ($u_\mathrm{t} (V\rightarrow 0)$) probably due, at least partly, to influences noted in the Introduction. Because the drag coefficient and the transfer coefficient for heat are versions of $u_\mathrm{t} /V$, they increase significantly with decreasing wind speed. That is, $u_\mathrm{t}$ decreases only slowly with decreasing $V$ such that $u_\mathrm{t}/V$ becomes large with decreasing weak wind.

Because the relationship between the turbulence and the weak stratified flow depends on the site-dependent submeso motions, this turbulence relationship is site dependent (Acevedo et al. 2014) and the above results cannot be interpreted as universal. The turbulence behaviour needs further examination in terms of variations within the network and should also be extended to other field sites. In particular, the generality of the minimal impact of stratification on the turbulence for the lowest wind speeds needs to be investigated using other datasets. Improved understanding requires better assessment of the impact of the downward transport of turbulence and momentum using approaches such as developed by Williams et al. (2013).