Skip to main content

Advertisement

SpringerLink
Log in

Energy behaviour of the Boris method for charged-particle dynamics

  • Published:
BIT Numerical Mathematics Aims and scope Submit manuscript

Abstract

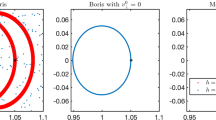
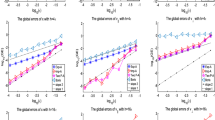
The Boris algorithm is a widely used numerical integrator for the motion of particles in a magnetic field. This article proves near-conservation of energy over very long times in the special cases where the magnetic field is constant or the electric potential is quadratic. When none of these assumptions is satisfied, it is illustrated by numerical examples that the numerical energy can have a linear drift or its error can behave like a random walk. If the system has a rotational symmetry and the magnetic field is constant, then also the momentum is approximately preserved over very long times, but in a spatially varying magnetic field this is generally not satisfied.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Fig. 1
Fig. 2

Similar content being viewed by others

References

  1. Boris, J.P.: Relativistic plasma simulation-optimization of a hybrid code. In: Proceeding of Fourth Conference on Numerical Simulations of Plasmas, pp. 3–67 (1970)

  2. Ellison, C.L., Burby, J.W., Qin, H.: Comment on “Symplectic integration of magnetic systems”: a proof that the Boris algorithm is not variational. J. Comput. Phys. 301, 489–493 (2015)

    Article  MathSciNet  Google Scholar 

  3. Hairer, E., Lubich, C.: Symmetric multistep methods for charged particle dynamics. SMAI J. Comput. Math. 3, 205–218 (2017)

    Article  MathSciNet  Google Scholar 

  4. Hairer, E., Lubich, C., Wanner, G.: Geometric numerical integration illustrated by the Störmer–Verlet method. Acta Numer. 12, 399–450 (2003)

    Article  MathSciNet  Google Scholar 

  5. Hairer, E., Lubich, C., Wanner, G.: Geometric Numerical Integration. Structure-Preserving Algorithms for Ordinary Differential Equations. Springer Series in Computational Mathematics, vol. 31, 2nd edn. Springer, Berlin (2006)

    MATH  Google Scholar 

  6. Hairer, E., McLachlan, R.I., Skeel, R.D.: On energy conservation of the simplified Takahashi–Imada method. M2AN. Math. Model. Numer. Anal. 43(4), 631–644 (2009)

    Article  MathSciNet  Google Scholar 

  7. He, Yang, Zhou, Zhaoqi, Sun, Yajuan, Liu, Jian, Qin, Hong: Explicit \(K\)-symplectic algorithms for charged particle dynamics. Phys. Lett. A 381(6), 568–573 (2017)

    Article  MathSciNet  Google Scholar 

  8. Knapp, C., Kendl, A., Koskela, A., Ostermann, A.: Splitting methods for time integration of trajectories in combined electric and magnetic fields. Phys. Rev. E 92, 063310 (2015)

    Article  MathSciNet  Google Scholar 

  9. Qin, H., Zhang, S., Xiao, J., Liu, J., Sun, Y., Tang, W.M.: Why is Boris algorithm so good? Phys. Plasmas 20(8), 084503.1–084503.4 (2013)

    Article  Google Scholar 

  10. Tao, M.: Explicit high-order symplectic integrators for charged particles in general electromagnetic fields. J. Comput. Phys. 327, 245–251 (2016)

    Article  MathSciNet  Google Scholar 

  11. Zhang, Ruili, Qin, Hong, Tang, Yifa, Liu, Jian, He, Yang, Xiao, Jianyuan: Explicit symplectic algorithms based on generating functions for charged particle dynamics. Phys. Rev. E 94(1), 013205 (2016)

    Article  Google Scholar 

Download references

Acknowledgements

We thank our colleague Martin Gander for drawing our attention to the long-time behaviour of the Boris algorithm. The research for this article has been partially supported by the Fonds National Suisse, Project No. 200020_159856.

Author information

Authors and Affiliations

  1. Département de Mathématiques, Université de Genève, 1211, Geneva 24, Switzerland

    Ernst Hairer

  2. Mathematisches Institut, University of Tübingen, 72076, Tübingen, Germany

    Christian Lubich

Authors
  1. Ernst Hairer
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Christian Lubich
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Christian Lubich.

Additional information

Communicated by Antonella Zanna Munthe-Kaas.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Hairer, E., Lubich, C. Energy behaviour of the Boris method for charged-particle dynamics. Bit Numer Math 58, 969–979 (2018). https://doi.org/10.1007/s10543-018-0713-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10543-018-0713-1

Keywords

Mathematics Subject Classification

Search

Navigation