Combined Linkage and Association Mapping of Quantitative Trait Loci with Missing Completely at Random Genotype Data

Abstract

In genetics study, the genotypes or phenotypes can be missing due to various reasons. In this paper, the impact of missing genotypes is investigated for high resolution combined linkage and association mapping of quantitative trait loci (QTL). We assume that the genotype data are missing completely at random (MCAR). Two regression models, “genotype effect model” and “additive effect model”, are proposed to model the association between the markers and the trait locus. If the marker genotype is not missing, the model is exactly the same as those of our previous study, i.e., the number of genotype or allele is used as weight to model the effect of the genotype or allele in single marker case. If the marker genotype is missing, the expected number of genotype or allele is used as weight to model the effect of the genotype or allele. By analytical formulae, we show that the “genotype effect model” can be used to model the additive and dominance effects simultaneously, and the “additive effect model” can only be used to model the additive effect. Based on the two models, F-test statistics are proposed to test association between the QTL and markers. The non-centrality parameter approximations of F-test statistics are derived to calculate power and to compare power, which show that the power of the F-tests is reduced due to the missingness. By simulation study, we show that the two models have reasonable type I error rates for a dataset of moderate sample size. However, the type I error rates can be very slightly inflated if all individuals with missing genotypes are removed from analysis. Hence, the proposed method can help to get correct type I error rates although it does not improve power. As a practical example, the method is applied to analyze the angiotensin-1 converting enzyme (ACE) data.

Appendices

Appendix A

Multiplying both sides of the “genotype effect model” (1) by $1_{(G_{Aij}=A_gA_h)}$ and taking expectation lead to

$$ \begin{aligned} \hbox{E} (y_{ij} 1_{(G_{Aij}=A_gA_h)}) &=w_{ij} \gamma \hbox{E} [1_{(G_{Aij}=A_gA_h)}]+ \hbox{E} [1_{(G_{Aij}=A_gA_h)}] \beta_{gh} \\ &= \left\{ \begin{array}{ll}(1-\varepsilon_A)[w_{ij} \gamma +\beta_{gg} ] P_{A_g}^2 &\hbox{ if }g=h \\ (1-\varepsilon_A)[w_{ij} \gamma +\beta_{gh} ] \cdot 2 P_{A_g}P_{A_h} &\hbox{ if }g \neq h\end{array}\right..\end{aligned} $$

(17)

Let G _Qij be genotype of the j-th individual of the i-th family at the trait locus Q. A true random effect model describing the trait value is y _ij  = w _ij γ + g _ij + H _ij  + e _ij , where

$$g_{ij} = \left\{ \begin{array}{ll}a & G_{Qij}=Q_1Q_1 \\ d & G_{Qij}=Q_1Q_2 \\ -a & G_{Qij}=Q_2Q_2 \end{array}\right..$$

Since the missing mechanism is missing completely at random, we have

$$ \begin{aligned} P(G_{Qij}=Q_1 Q_1, G_{Aij}=A_gA_g|G_{Aij} \neq ?) &= [P(Q_1A_g)]^2, \\ P(G_{Qij}=Q_1 Q_2, G_{Aij}=A_gA_g|G_{Aij} \neq ?) &= 2 P(Q_1A_g) P(Q_2A_g), \\ P(G_{Qij}=Q_2 Q_2, G_{Aij}=A_gA_g|G_{Aij} \neq ?) &= [P(Q_2A_g)]^2. \end{aligned} $$

Utilizing relations $P(Q_1A_g)=-D_{A_gQ}+P_{A_g}q_1$ and $P(Q_2A_g)=-D_{A_gQ}+P_{A_g}q_2,$ we have

$$ \begin{aligned} \hbox{E} (y_{ij} 1_{(G_{Aij}=A_gA_g)}) &=w_{ij} \gamma \hbox{E} [1_{(G_{Aij}=A_gA_g)}]+ \hbox{E} [ g_{ij} 1_{(G_{Aij}=A_gA_g)}] \\ &= w_{ij} \gamma P(A_g A_g | G_{Aij} \neq ?)P(G_{Aij} \neq ?) + \hbox{E} [ g_{ij} 1_{(G_{Aij}=A_gA_g)}| G_{Aij} \neq ?] P(G_{Aij} \neq ?) \\ &= (1-\varepsilon_A) \left[ w_{ij}\gamma P_{A_g}^2+ a [P(Q_1A_g)]^2 + d \cdot 2P(Q_1A_g)P(Q_2A_g)-a [P(Q_2A_g]^2 \right] \\ &=(1-\varepsilon_A) \left[ w_{ij}\gamma P_{A_g}^2+ \mu P_{A_g}^2+ 2 D_{A_gQ} \alpha_Q P_{A_g}-\delta_Q D^2_{A_gQ} \right]. \end{aligned} $$

(18)

Equating Eqs. 17 and 18, we show the Eq. 5 when g = h. Now assume that g ≠ h. Since the missing mechanism is missing completely at random, we have

$$ \begin{aligned} P(G_{Qij}=Q_1 Q_1, G_{Aij}=A_gA_h|G_{Aij} \neq ?) &= 2 P(Q_1A_g) P(Q_1A_h), \\ P(G_{Qij}=Q_1 Q_2, G_{Aij}=A_gA_h|G_{Aij} \neq ?) &= 2P(Q_1A_g) P(Q_2A_h) + 2P(Q_1A_h) P(Q_2A_g), \\ P(G_{Qij}=Q_2 Q_2, G_{Aij}=A_gA_h|G_{Aij} \neq ?) &= 2P(Q_2A_g) P(Q_2A_h). \end{aligned} $$

Utilizing relations $P(Q_1A_g)=D_{A_gQ}+P_{A_g}q_1,\,\, P(Q_2A_g)=-D_{A_gQ}+P_{A_g}q_2,\,\, P(Q_1A_h)=D_{A_hQ}+P_{A_h}q_1,\,\, P(Q_2A_h)=-D_{A_hQ}+P_{A_h}q_2,$ we have

$$ \begin{aligned} \hbox{E} (y_{ij} 1_{(G_{Aij}=A_gA_h)}) &=w_{ij} \gamma \hbox{E} [1_{(G_{Aij}=A_gA_h)}]+ \hbox{E} [ g 1_{(G_{Aij}=A_gA_h)}] \\ &= w_{ij} \gamma P(A_g A_h | G_{Aij} \neq ?)P(G_{Aij} \neq ?) + \hbox{E} [ g 1_{(G_{Aij}=A_gA_h)}| G_{Aij} \neq ?] P(G_{Aij} \neq ?) \\ &= (1-\varepsilon_A) \left[ w_{ij}\gamma\,\cdot\,2P_{A_g} P_{A_h}+ 2a \left(P(Q_1A_g)P(Q_1A_h) - P(Q_2A_g)P(Q_2A_h) \right) \right.\\ &\left. + d \left(2P(Q_1A_g)P(Q_2A_h) + 2P(Q_2A_g)P(Q_1A_h) \right) \right] \\ &= (1-\varepsilon_A) \left[ 2P_{A_g} P_{A_h} w_{ij}\gamma+ 2P_{A_g} P_{A_h} \mu + 2 \alpha_Q \left(D_{A_gQ} P_{A_h}+ D_{A_hQ} P_{A_g} \right) -2 \delta_Q D_{A_gQ} D_{A_hQ} \right]. \\ \end{aligned} $$

(19)

Equating Eqs. 17 and 18, we show the Eq. 5 when g ≠ h.

Appendix B

In relations (17), replacing β _gh by α _g  + α _h and taking summation lead to

$$ \begin{aligned} \hbox{E} (y_{ij}1_{(G_{Aij} \neq ?)}) &= \sum_{1 \le g \le h \le m} \hbox{E} (y_{ij} 1_{(G_{Aij}=A_gA_h)}) \\ &= (1-\varepsilon_A)\sum_{g=1}^m \sum_{h=1}^m \left(w_{ij} \gamma +\alpha_g+\alpha_h \right) P_{A_g}P_{A_h}\\ &= (1-\varepsilon_A) \left(w_{ij} \gamma + 2\sum_{g=1}^m \alpha_gP_{A_g} \right).\end{aligned} $$

Since the missing mechanism is missing completely at random, one has E(y _ij 1_{(G_Aij ≠ ?)}) = E(y _ij |G _Aij ≠ ?)(1 − ɛ _A ) = (1−ɛ _A )Ey _ij  = (1 − ɛ _A )(w _ij γ + μ). Thus, $\sum_{g=1}^m \alpha_gP_{A_g} = \mu/2.$

Again, replacing β _gh by α _g  + α _h in relations (17) and taking summation with respect to h lead to

$$ \begin{aligned} \hbox{E} \left[ y_{ij}1_{(G_{Aij} =A_gA_g)} + \frac{1}{2} \sum_{h \neq g} y_{ij}1_{(G_{Aij} =A_gA_h)} \right] &=(1-\varepsilon_A) \sum_{h=1}^m \left(w_{ij} \gamma +\alpha_g+\alpha_h \right) P_{A_g}P_{A_h} \\ &= (1-\varepsilon_A)P_{A_g} \left(w_{ij} \gamma + \alpha_g+ \sum_{h=1}^m \alpha_hP_{A_h} \right) \\ &= (1-\varepsilon_A)P_{A_g} \left(w_{ij} \gamma + \alpha_g+ \mu/2 \right). \end{aligned} $$

(20)

Notice $\sum_{g=1}^m D_{A_g Q} =0.$ Taking summation of relations (18) and (19) leads to

$$ \hbox{E} \left[ y_{ij}1_{(G_{Aij} =A_gA_g)} + \frac{1}{2} \sum_{h \neq g} y_{ij}1_{(G_{Aij} =A_gA_h)} \right] =(1-\varepsilon_A)P_{A_g} \left[ w_{ij} \gamma +\mu +D_{A_gQ} \alpha_Q /P_{A_g} \right]. $$

(21)

Equating the right-hand terms of relations (20) and (21) leads to (6).

Appendix C

Assume that there are no covariates, and the dataset is a population sample. Then the model matrix of “genotype effect model” (1) is $X_i=X_{Ai1}^{\tau}= (x_{Ai1}^{(11)},\ldots, x_{Ai1}^{(mm)}, x_{Ai1}^{(12)},\ldots, x_{Ai1}^{(1m)},\ldots,x_{Ai1}^{(m-1,m)}), i=1,\ldots, N.$ To show non-centrality parameter approximation (7), we first notice the following relation

$$ \hbox{E} [ X_1^{\tau} X_1] = (1- \varepsilon_A) \hbox{diag} (P_{A_1}^2, v^{\tau}) + \varepsilon_A \left(\begin{array}{c}P_{A_1}^2 \\ v \end{array}\right) (P_{A_1}^2, v^{\tau}), $$

(22)

where v is a column vector given by $v^{\tau} =\left(P_{A_2}^2,\ldots, P_{A_m}^2, 2P_{A_1}P_{A_2},\ldots, 2P_{A_1}P_{A_m},\ldots,2P_{A_{m-1}}P_{A_m} \right).$ In addition, $\hbox{diag} (P_{A_1}^2,v^{\tau})$ is a diagonal matrix, whose elements on the diagonal are given by the elements of $(P_{A_1}^2,v^{\tau}).$ We may verify (22) by $E [(x_{A11}^{(gh)})^2] = \hbox{E} 1_{(G_{{A11}=A_gA_h)}}+P(A_gA_h)^2 \hbox{E} 1_{(G_{A11}=?)}=P(A_gA_h)(1-\varepsilon_A)+P(A_gA_h)^2\varepsilon_A,$ and for $(g,h) \neq (k,l), \ E [x_{A11}^{(gh)} x_{A11}^{(kl)} ] = P(A_gA_h)P(A_kA_l) \hbox{E} 1_{(G_{A11}=?)} =P(A_gA_h)P(A_kA_l) \varepsilon_A.$

Let us denote $u=\left(P_{A_2}^{-2},\ldots, P_{A_m}^{-2}, [2P_{A_1}P_{A_2}]^{-2},\ldots, [2P_{A_1}P_{A_m}]^{-2}, \cdots, [2P_{A_{m-1}}P_{A_m}]^{-2} \right).$ Applying the large number law and a fact of inverse matrix $(M+a b^{\tau})^{-1} = M^{-1}-(M^{-1} a) (b^{\tau} M^{-1})/ (1+ b^{\tau} M^{-1} a),$ we can calculate the following approximation

$$ \begin{aligned} T (X^{\tau} X)^{-1} T^{\tau} &\approx T \left[N \hbox{E} \left(X_1^{\tau} X_1 \right) \right]^{-1} T^{\tau} \\&= N^{-1} \cdot T \left[ (1- \varepsilon_A) \hbox{diag}(P_{A_1}^2,v^{\tau}) + \varepsilon_A\begin{pmatrix} P_{A_1}^2 \\ v\end{pmatrix}(P_{A_1}^2, v^{\tau}) \right]^{-1} T^{\tau}\\ &= [(1-\varepsilon_A)N]^{-1} \cdot T \left[ \hbox{diag} (P_{A_1}^{-2},u^{\tau})- \varepsilon_A \left(\begin{array}{c} 1\\ 1 \\ \vdots\\ 1 \end{array}\right)(1,1,\ldots,1) \right] T^{\tau}\\ &= [(1-\varepsilon_A)N]^{-1} \cdot T \hbox{diag} (P_{A_1}^{-2}, u^{\tau})T^{\tau}. \end{aligned} $$

Utilizing above relation, we may show non-centrality parameter approximation (7) in the same way as Appendix III, Fan et al. (2006).

Appendix D

Assume that there are no covariates, and the dataset is a population sample. Then the model matrix of “additive effect model” (3) is $X_i=Z_{Ai1}^{\tau}= (x_{Ai1}^{(1)},\ldots, x_{Ai1}^{(m)}), i=1,\ldots, N.$ To show non-centrality parameter approximation (8), we first notice the following relation

$$ \hbox{E} [ Z_{A11} Z_{A11}^{\tau}] = 2(1- \varepsilon_A) \left[ \hbox{diag} (P_{A_1}, \cdots, P_{A_m}) + \left(\begin{array}{c} P_{A_1} \\ \vdots \\ P_{A_m}\end{array}\right)(P_{A_1}, \cdots, P_{A_m}) \right] + 4 \varepsilon_A \left(\begin{array}{c}P_{A_1} \\ \vdots \\ P_{A_m}\end{array}\right)(P_{A_1}, \cdots, P_{A_m}), $$

which can be verified by $E [(x_{A11}^{(g)})^2] = 4\hbox{E} 1_{(G_{A11}=A_gA_g)}+\sum_{h \neq g} \hbox{E} 1_{(G_{A11} =A_gA_h)} + 4P_{A_g}^2 \hbox{E} 1_{(G_{A11}=?)} =2(1-\varepsilon_A)P_{A_g} [1+ P_{A_g}] +4P_{A_g}^2\varepsilon_A,$ and for $h \neq g, \ E [x_{A11}^{(g)} x_{A11}^{(h)} ]=(1- \varepsilon_A)\,\cdot\,2P_{A_g}P_{A_h} + 4P_{A_g}P_{A_h} \varepsilon_A.$ Let $X=(Z_{A11},\ldots, Z_{AN1})^{\tau}.$ Applying the large number law and a fact of inverse matrix $(M+a b^{\tau})^{-1} = M^{-1}-(M^{-1} a) (b^{\tau} M^{-1})/ (1+ b^{\tau} M^{-1} a),$ we can calculate the following approximation

$$ \begin{aligned} K (X^{\tau} X)^{-1} K^{\tau} &\approx K \left[ N \hbox{E} \left(Z_{A11} Z_{A11}^{\tau} \right) \right]^{-1} K^{\tau} \\ &= N^{-1} \cdot K \left[ 2(1- \varepsilon_A) \hbox{diag} (P_{A_1},\ldots, P_{A_m}) +2(1+ \varepsilon_A) \left(\begin{array}{c} P_{A_1} \\ \vdots \\ P_{A_M} \end{array}\right) (P_{A_1},\ldots, P_{A_m}) \right]^{-1} K^{\tau}\\ &= [2(1- \varepsilon_A)N]^{-1} \cdot K \left[ \hbox{diag} (P_{A_1}^{-1},\ldots, P_{A_m}^{-1})- (1+\varepsilon_A) \left(\begin{array}{c} 1 \\ 1 \\ \vdots \\ 1 \end{array}\right) (1,1,\ldots,1)/2 \right] K^{\tau}\\ &= [2(1- \varepsilon_A)N]^{-1} \cdot K \hbox{diag} (P_{A_1}^{-1},\ldots, P_{A_m}^{-1}) K^{\tau}. \end{aligned} $$

Utilizing above relation, we may show non-centrality parameter approximation (8) in the same way as Appendix IV, Fan et al. (2006).

Appendix E

For g = 1,2,…,m, k = 1,…,n, let us denote $D_{A_gB_k}=P(A_gB_k)-P_{A_g}P_{B_k},$which are measures of LD between markers A and B. Here, P(A _g B _k ) is frequency of haplotype A _g B _k . It can be shown that for g ≠ h, k ≠ l, h ≠ h′, l ≠ l′, (g,h) ≠ (g′,h′), (k,l) ≠ (k′,l′)

$$ \begin{array}{l} \hbox{E}\,x_{Aij}^{(g)}=2P_{A_g}, \hbox{E} (x_{Aij}^{(g)})^2 =(1-\varepsilon_A)(2P_{A_g}^2 +2P_{A_g})+4P_{A_g}^2 \varepsilon_A, \hbox{E} [x_{Aij}^{(g)} x_{Aij}^{(h)}] = 2P_{A_g}P_{A_h}(1-\varepsilon_A)+ 4P_{A_g}P_{A_h} \varepsilon_A, \\ \hbox{E}\,x_{Bij}^{(k)}=2P_{B_k}, \hbox{E} (x_{Bij}^{(k)})^2 = (1-\varepsilon_B)(2P_{B_k}^2 +2P_{B_k})+4P_{B_k}^2 \varepsilon_B,\hbox{E} [x_{Bij}^{(k)} x_{Bij}^{(l)}] = 2P_{B_k}P_{B_l}(1-\varepsilon_B)+ 4P_{B_k}P_{B_l} \varepsilon_B, \\ \hbox{E}\,z_{Aij}^{(gh)}=0, \hbox{E} (z_{Aij}^{(gh)})^2=(1-\varepsilon_A)P_{A_g}^2 P_{A_h}^2 [ P_{A_g}+P_{A_h}]^2, \hbox{E}\,z_{Bij}^{(kl)}=0, \hbox{E} (z_{Bij}^{(kl)})^2=(1-\varepsilon_B) P_{B_k}^2 P_{B_l}^2[ P_{B_k}+P_{B_l}]^2, \\ \hbox{E} [ x_{Aij}^{(g)} z_{Aij}^{(gh)} ]= \hbox{E} [ x_{Aij}^{(g)} z_{Aij}^{(hh^{\prime})} ]=\hbox{E} [ x_{Bij}^{(k)} z_{Bij}^{(kl)} ]= \hbox{E} [ x_{Bij}^{(k)} z_{Bij}^{(ll^{\prime})} ]=\hbox{E} [ x_{Aij}^{(g)} z_{Bij}^{(kl)} ]=\hbox{E} [ x_{Bij}^{(k)} z_{Aij}^{(gh)} ]=0, \\ \hbox{E} [ x_{Aij}^{(g)} x_{Bij}^{(k)} ]=2D_{A_gB_k}(1-\varepsilon_A)(1-\varepsilon_B) +4P_{A_g}P_{B_k},\hbox{E} [ z_{Aij}^{(gh)} z_{Aij}^{(gh^{\prime})}]=(P_{A_g}P_{A_h}P_{A_h^{\prime}})^2(1-\varepsilon_A), \\ \hbox{E} [ z_{Aij}^{(gh)} z_{Aij}^{(g^{\prime}h^{\prime})} ]=0,\hbox{E} [ z_{Bij}^{(kl)} z_{Bij}^{(kl^{\prime})} ] =(P_{B_k}P_{B_l}P_{B_l^{\prime}})^2(1-\varepsilon_B), \hbox{E} [ z_{Bij}^{(kl)} z_{Bij}^{(k^{\prime}l^{\prime})} ]=0,\\ \hbox{E} [ z_{Aij}^{(gh)} z_{Bij}^{(kl)} ]= \left[ P_{A_h} \left(P_{B_l}D_{A_gB_k}-P_{B_k} D_{A_gB_l} \right) - P_{A_g} \left(P_{B_l}D_{A_hB_k}-P_{B_k} D_{A_hB_l} \right) \right]^2(1-\varepsilon_A) (1-\varepsilon_B), \\ \hbox{E} [ y_{ij} x_{Aij}^{(g)} ] = 2P_{A_g} (w_{ij} \gamma + \mu)+2 \alpha_Q D_{A_gQ}(1-\varepsilon_A), \hbox{E} [ y_{ij} x_{Bij}^{(k)} ] = 2P_{B_k} (w_{ij} \gamma + \mu)+2 \alpha_Q D_{B_kQ}(1-\varepsilon_B), \\ \hbox{E} [ y_{ij} z_{Aij}^{(gh)} ] = \delta_Q \left[ P_{A_g} D_{A_h Q} - P_{A_h} D_{A_g Q} \right]^2(1-\varepsilon_A),\hbox{E} [ y_{ij} z_{Bij}^{(kl)} ] = \delta_Q \left[ P_{B_k} D_{B_l Q} - P_{B_l} D_{B_k Q} \right]^2 (1-\varepsilon_B). \end{array} $$

(23)

The quantities in (23) imply that the elements of V _A are given by

$$ \begin{aligned} \hbox{Cov} \left(x_{Aij}^{(g)}, x_{Aij}^{(h)}\right) &= -2 P_{A_g}P_{A_h} (1-\varepsilon_A), \\ \hbox{Var} \left(x_{Aij}^{(g)}\right) = 2 P_{A_g}(1-P_{A_g})(1-\varepsilon_A), \\ \hbox{Cov} \left(x_{Aij}^{(g)}, x_{Bij}^{(k)}\right)&= 2D_{A_g B_k } (1-\varepsilon_A)(1-\varepsilon_B), \\ \hbox{Cov} \left(x_{Bij}^{(k)}, x_{Bij}^{(l)}\right)&= -2 P_{B_k}P_{B_l} (1-\varepsilon_B), \\ \hbox{Var} \left(x_{Bij}^{(k)}\right) = 2 P_{B_k}(1-P_{B_k})(1-\varepsilon_B). \end{aligned} $$

Since $\hbox{E}\,Z_{A \cup B}^{(ij)}$ is a vector of 0s by the quantities in (23), it can be shown that $V_D =\hbox{Cov}\left(Z_{A \cup B}^{(ij)}, Z_{A \cup B}^{(ij)}\right) = \hbox{E} \left(Z_{A \cup B}^{(ij)} (Z_{A \cup B}^{(ij)})^\tau\right).$ Moreover, the quantities in (23) imply that the covariance matrix $\hbox{Cov}\left(X_{A \cup B}^{(ij)}, Z_{A \cup B}^{(ij)}\right)$ is a 0 matrix. In addition, the covariances between the trait value y _ij and variables $x_{Aij}^{(g)}, x_{Bij}^{(k)}, z_{Aij}^{(gh)}$ and $z_{Bij}^{(kl)}$ are

$$ \begin{aligned} \hbox{Cov} \left(y_{ij}, x_{Aij}^{(g)}\right) &= 2 \alpha_Q (1-\varepsilon_A) D_{A_gQ}, \\ \hbox{Cov} \left(y_{ij}, x_{Bij}^{(k)}\right) = 2\alpha_Q (1-\varepsilon_B) D_{B_kQ},\\ \hbox{Cov} \left(y_{ij},z_{Aij}^{(gh)}\right)&=\hbox{E} \left[y_{ij} z_{Aij}^{(gh)}\right],\\ \hbox{Cov} (y_{ij},z_{Bij}^{(kl)})=\hbox{E} \left[y_{ij} z_{Bij}^{(kl)}\right]. \end{aligned} $$

Taking variance–covariance between y _ij and $x_{Aij}^{(g)}, x_{Bij}^{(k)}, z_{Aij}^{(gh)}, z_{Bij}^{(kl)}$ based on relation (12), we may get the regression coefficients (13) of models (10) and (12).

Appendix F

Notice $\Upsigma_i^{-1}= \frac 1 {\sigma^2} (\gamma_{hj})_{(s+2) \times (s+2)}.$ Let X _i be the model matrix of family i = 1, 2, …, I. Then

$$ X_i=\left(\begin{array}{ccccccccccccc}1 & x_{Ai1}^{(1)}& \cdots & x_{Ai1}^{(m-1)} & x_{Bi1}^{(1)}& \cdots & x_{Bi1}^{(n-1)} & z_{Ai1}^{(12)}& \cdots & z_{Ai1}^{(m-1,m)} & z_{Bi1}^{(12)}& \cdots & z_{Bi1}^{(n-1,n)}\\ 1 & x_{Ai2}^{(1)}& \cdots & x_{Ai2}^{(m-1)} & x_{Bi2}^{(1)}& \cdots & x_{Bi2}^{(n-1)} & z_{Ai2}^{(12)}& \cdots & z_{Ai2}^{(m-1,m)} & z_{Bi2}^{(12)}& \cdots & z_{Bi2}^{(n-1,n)}\\ \vdots & \vdots& \cdots & \vdots & \vdots& \cdots & \vdots & \vdots& \cdots & \vdots & \vdots& \cdots & \vdots \\ 1 & x_{Ai,s+2}^{(1)}& \cdots & x_{Ai,s+2}^{(m-1)} & x_{Bi,s+2}^{(1)}& \cdots & x_{Bi,s+2}^{(n-1)} & z_{Ai,s+2}^{(12)}& \cdots & z_{Ai,s+2}^{(m-1,m)} & z_{Bi,s+2}^{(12)}& \cdots & z_{Bi,s+2}^{(n-1,n)}\end{array}\right).$$

Denote $\gamma= \sum_{k=1}^{s+2} \sum_{l=1}^{s+2} \gamma_{kl}.$ Applying large number law leads to an approximation as

$$ \begin{array}{l} \sum_{i=1}^I X_i^{\tau} \Upsigma_i^{-1} X_i / I \approx\\ \frac 1 {\sigma^2} \left(\begin{array}{ccc} \gamma & \gamma [ \hbox{E}(X_{A \cup B}^{(11)})]^{\tau} & O_1 \\ \gamma \hbox{E} (X_{A \cup B}^{(11)}) & \sum_{k=1}^{s+2} \gamma_{kk} V_A+b V_{A2}+\gamma \hbox{E} (X_{A \cup B}^{(11)}) [\hbox{E} (X_{A \cup B}^{(11)})]^{\tau} & O_2 \\ O_3 & O_4 &\sum_{k=1}^{s+2} \gamma_{kk} V_D+ \sum_{k=3}^{s+2} \sum_{l=k+1}^{s+2} \gamma_{kl} V_{D2}/2 \end{array}\right), \end{array} $$

(24)

where O _i , i = 1,2,3,4 are zero vectors or matrices, and $\hbox{E}\left( X_{A \cup B}^{(11)}\right) = (2 P_{A_1},\ldots, 2 P_{A_{m-1}}, 2 P_{B_1},\ldots, 2 P_{B_{n-1}})^{\tau}.$

Let

$$S=\left(\begin{array}{ccccc} 0 & 1 & 0 & \cdots & 0 \\ 0 & 0 & 1 & \cdots & 0 \\ 0 & 0 & 0 & \cdots & 1 \end{array}\right)$$

be the test matrix corresponding to hypothesis H _ABad0, and ${\phi=}({\alpha,}\,\alpha_{A1},\ldots, \alpha_{A(m-1)}, \alpha_{B1},\ldots, \alpha_{B(m-1)},\delta_{A12},\ldots, \delta_{A(m-1)m},\delta_{B12},\ldots, \delta_{B(n-1)n})^{\tau}$ be the column vector of regression coefficient of “genotype effect model” (12). Utilizing regression coefficients (13), we may show (15) by plugging approximation (24) into $\lambda_{ABad} =(S \phi)^{\tau}[S(\sum_{i=1}^I X_i^{\tau}\Upsigma_i^{-1} X_i)^{-1} S^{\tau}]^{-1}(S \phi).$ One may want to notice that we may use Theorem 8.5.11, Harville (1997), to calculate the inverse of the right-hand matrix of (24).

Appendix G

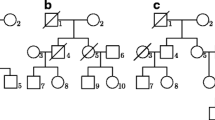
For pedigrees in graph A of Fig. 1, the constants b ₁ and b ₂ of λ _AB,ad in (16) are given by

$$ \begin{aligned} b_1 &= [ \gamma_{15} +(\gamma_{17} + \cdots + \gamma_{1,11})/2]+ [ \gamma_{25} +(\gamma_{27} + \cdots + \gamma_{2,11})/2] \\ & + [ \gamma_{36} +(\gamma_{37} + \cdots + \gamma_{3,11})/2]+ [ \gamma_{46} +(\gamma_{47} + \cdots +\gamma_{4,11})/2] \\ & +(\gamma_{57} + \cdots +\gamma_{5,11})+(\gamma_{67} + \cdots +\gamma_{6,11}) +\sum_{k=7}^{11} \sum_{l=k+1}^{11} \gamma_{kl}, \\ b_2&= \sum_{k=7}^{11} \sum_{l=k+1}^{11} \gamma_{kl}/2. \end{aligned} $$

For pedigrees in graph B of Fig. 1, constants b ₁ and b ₂ are given by

$$ \begin{aligned} b_1 &= \gamma_{1,12}+[ \gamma_{2,12} +(\gamma_{2,13} + \cdots + \gamma_{2,16})/2]+ [ \gamma_{3,12}+ \cdots+ \gamma_{3,16}]/2 \\ & +[ \gamma_{4,12} +\cdots+ \gamma_{4,16}]/2 +[ \gamma_{5,12}/2+ (\gamma_{5,13} + \cdots + \gamma_{5,16})] \\ & + [ (\gamma_{6,13}+\cdots +\gamma_{6,16})+ (\gamma_{6,17}+\gamma_{6,18})/2]+ [ \gamma_{7,13} + \cdots+ \gamma_{7,18}]/2 \\ & +[(\gamma_{8,13} + \cdots +\gamma_{8,16})/2 +(\gamma_{8,17}+\gamma_{8,18}) ] +(\gamma_{9,17}+\gamma_{9,18})+ (\gamma_{10,17}+\gamma_{10,18})/2 \\ & +(\gamma_{11,17}+\gamma_{11,18})/2 +(\gamma_{12,13} + \cdots +\gamma_{12,16})/4+(\gamma_{13,14} + \gamma_{13,15} +\gamma_{13,16}) \\ & +(\gamma_{14,15} +\gamma_{14,16}) +\gamma_{15,16}+[ \gamma_{13,17} + \cdots+ \gamma_{16,17}]/4+[ \gamma_{13,18} + \cdots+ \gamma_{16,18}]/4 +\gamma_{17,18}, \\ b_2&= [(\gamma_{13,14} +\gamma_{13,15}+ \gamma_{13,16})+(\gamma_{14,15} +\gamma_{14,16})+ \gamma_{15,16}]/2 +\gamma_{17,18}/2. \end{aligned} $$