1 Introduction

International shipping contributed approximately 2% to global energy-related CO\(_{2}\) emissions in 2021. After a brief decline in 2020 due to the impact of the Covid-19 pandemic and associated restrictions on international trade, CO\(_2\) emissions arising from international shipping have started to rebound, resuming the upward trend they have exhibited over the last decades (Connelly et al. 2023). According to the 2023 Strategy of the International Maritime Organization on reduction of greenhouse gas (GHG) emissions from ships, for GHG emissions to reach net zero by 2050, total annual GHG emissions from international shipping will need to be reduced by at least 20% by 2030, and by at least 70% by 2040 compared to 2008 levels (IMO 2023). With the forecast increase in international trade, these targets will be difficult to achieve. Currently, International Shipping is rated as ‘Not on track’ by the International Energy Agency (IEA 2023) and it is unlikely that this sector will meet its near-term targets for reduction in CO\(_2\) emissions.

Many cargo ships are still powered by low-grade fuels such as marine residual oil due to their competitive price. An increase in the use of low-carbon fuels, such as biofuels and hydrogen, is envisioned to make a large contribution towards achieving carbon emissions reduction targets. However, it will be challenging to scale up production of low carbon fuels to meet demand, since other sectors, such as road-based transportation and aviation, will also rely partially or fully on increased use of low-carbon fuels in meeting their CO\(_2\) reduction targets. Furthermore, it is not sufficient to consider operational emissions only, but upstream greenhouse emissions associated with producing and supplying low carbon fuels also need to be taken into account (Argyros et al. 2014). For example, in the case of liquid biofuels potential savings in greenhouse gas emissions vary widely depending on the feedstocks used. Emissions could be reduced by circa 80% when using biofuels made from waste fats, oils and greases, whereas biofuels made from purpose-grown crops would yield at best minimal reductions in greenhouse gas emissions (Zhou et al. 2020). Therefore, increased use of low-carbon fuels alone is unlikely to be sufficient to achieve the targets of the IEA’s roadmap for the international shipping sector. In addition, the overall energy usage of this sector will need to be reduced. Other than a reduction in international trade, which would have adverse impact on the globalized economy and human development, the only way to achieve further significant reductions in emissions in the international shipping sector is to make vessels more energy efficient, e.g., by reducing the resistance of ships and thus their energy consumption.

For a typical merchant ship, friction drag makes the dominant contribution to the total resistance. Depending on hull shape and speed of the ship, friction drag accounts for approximately 70% to 90% of the total drag of a ship (see, e.g., discussion by Chung et al. (2021) and Regitasyali et al. (2022)). The drag of a ship hull significantly increases if its hull is in a hydrodynamically rough state. One of the most common forms of roughness on a ship hull is marine biofouling which is caused by the settlement of various organisms, such as bacteria, algae, molluscs, and crustaceans, on the hull’s surface due to its long-term exposure to sea water. Of the various forms of biofouling, calcareous macrofouling, i.e., fouling by organisms such as barnacles, tubeworms, or mussels, which have a calcareous outer shell, is considered one of the most severe forms of biofouling. Schultz (2007) estimated for a typical naval surface ship of the US Navy (Oliver Hazard Perry class frigate) an increase of the total resistance by approximately 36% for medium calcareous fouling and 55% for heavy calcareous fouling. Therefore, understanding the effects of different forms of biofouling on friction drag is of importance for the accurate assessment of the frictional resistance of ship hulls and the timely and cost-effective scheduling of maintenance intervals for hull cleaning (Schultz et al. 2011; Chung et al. 2021).

In the present study, direct numerical simulations (DNS) are used to investigate the Reynolds number dependency of turbulent flow over a surface affected by a common form of calcareous macrofouling, namely fouling by acorn barnacles (order Sessilia). In Sect. 2, the DNS methodology to obtain the fluid-dynamic properties of the surface is presented. Mean flow and turbulence statistics are presented in Sect. 3 and compared to statistics for other forms of engineering roughness. Section 4 gives conclusions and suggestions for future work.

2 Methodology

Direct numerical simulations of turbulent channel flow are used to obtain the fluid dynamic behaviour of a rough surface for a range of friction Reynolds numbers \(Re_{\tau }\). In this section first the rough surface under investigation is characterised and then the approach applied in the DNS is described.

2.1 Description of Surface Roughness

Fig. 1
figure 1

Illustration of the barnacle-fouled surface with 10% fouling. Also shown is the Gaussian surface from an earlier study by Jelly and Busse (2019) that will be used for comparison

Full size image
Table 1 Overview of key surface topographical parameters: Sa: mean roughness height; Sq: rms roughness height; k: geometric roughness height; Ssk, Sku: skewness and kurtosis of height distribution; ES: effective slope, \(\lambda _p\): planform solidity (fraction of surface covered by roughness features)
Full size table

A barnacle-fouled surface was generated using the BaRGE algorithm which mimics the settlement behaviour of barnacles on a smooth surface (Sarakinos and Busse 2019). Barnacles are represented as conical frustra following Sadique (2016), which is a widely used simplified representation of the shape a barnacle (Womack et al. 2022; Sarakinos and Busse 2022; Kaminaris et al. 2023).

10% of the surface is covered by barnacle features, while the rest of the surface remains smooth. A visualisation of the surface is shown in Fig. 1. This surface can also serve as an example for heterogeneous roughness, a class of roughness that has received to date far less attention than homogeneous rough surfaces which are statistically uniformly covered by roughness features (Chung et al. 2021). The same surface was previously used as part of a series of surfaces in a study on the fluid dynamic effects of coverage by barnacles at fixed friction Reynolds number (Sarakinos and Busse 2022). Data from an earlier study by Jelly and Busse (2019) on an homogeneous irregular rough surface, which is also shown in Fig. 1, is used for comparison. This surface is fully covered by roughness features and has an approximately Gaussian height distribution. It serves as a representative example for many forms of engineering roughness which frequently exhibit moderate skewness and kurtosis values.

Key surface parameters for both surfaces are summarized in Table 1. Length scales are given in units of \(\delta\) which is the mean channel half-height. For the barnacle surface, the geometric roughness height k is defined as the maximum barnacle height. In the case of the Gaussian roughness, k is set to the mean peak-to-valley height. As can be observed, the barnacle surface has significantly lower effective slope (or frontal solidity \(\lambda _f=ES/2\)) than the Gaussian surface. Its height distribution exhibits high positive skewness and high kurtosis, since it is an example for the early stages of ‘additive’ roughness formation, i.e., roughness formation processes where roughness emerges because fouling, i.e., extra material, accumulates on top of an initially smooth surface (Busse and Jelly 2023).

2.2 Setup of Direct Numerical Simulations

Table 2 Overview of simulation parameters for the barnacle roughness simulations: k geometric roughness height; \(N_x\), \(N_y\), \(N_z\): number of grid points in streamwise, spanwise and wall-normal direction
Full size table
Table 3 Overview of simulation parameters for the smooth-wall simulations: \(N_x\), \(N_y\), \(N_z\): number of grid points in streamwise, spanwise and wall-normal direction
Full size table
Fig. 2
figure 2

Schematic illustration of the channel flow domain. The rough surface is applied to both walls of the channel. On the upper wall, the rough surface pattern is shifted to minimize local blockage effects

Full size image

Direct numerical simulations of rough-wall turbulent channel flow driven by a constant mean streamwise pressure gradient were conducted using the code iIMB (Busse et al. 2015) which is second order in space and time and employs an iterative version of the embedded boundary method of Yang and Balaras (2006) to resolve the roughness features. In the following, x denotes the streamwise, y the spanwise, and z the wall-normal direction, and u, v and w are used for the corresponding velocity components. The roughness is applied to both the lower and the upper wall of the channel (see Fig. 2). The pattern on the upper wall is shifted by half the domain size in the streamwise and spanwise direction to minimize local blockage effects. Periodic boundary conditions are applied in the streamwise and spanwise direction. A small wall-normal offset, \(z_0\), was applied to the barnacle surface, so that the roughness mean plane \(\langle h(x,y)\rangle\), where h(x, y) is the heightmap, is located at \(z=0\).

Key simulation parameters are summarised in Table 2 for the barnacle surface and in Table 3 for the smooth-wall reference case. Uniform grid spacing was used in the streamwise and spanwise direction of the flow. In the wall-normal direction, uniform spacing at \(\Delta z_{\textrm{min}}^+\) was applied across the height of the roughness. Above the highest barnacle, the wall-normal grid spacing was gradually increased, reaching its maximum value \(\Delta z_{\textrm{max}}^+\) at the channel centre. The roughness Reynolds number \(k^+=k/\ell _d\), where k is set to the maximum barnacle height and \(\ell _d\) is the viscous length scale of the flow, was varied using the method of Thakkar et al. (2018): For high \(k^+\) the friction Reynolds number \(Re_{\tau }\) of the channel flow was varied, while for low \(k^+\) the friction Reynolds number was kept fixed and the size of the roughness features in outer units \(k/\delta\), where \(\delta\) is the channel half-height, was decreased using a ‘scaling and tiling’ approach. In all cases, a domain length \(L_x=2\pi \delta\) and width \(L_y=\pi \delta\) was used. Similar conditions were employed in the previous investigation on the Gaussian rough surface where a total of four simulations were conducted at \(Re_{\tau }=180,\,240,\,360\), and 540 using a domain length of \(L_x=6 \delta\) and width \(L_y=3\delta\) (for full details see Jelly and Busse (2019)).

The intrinsic average is used for the computation of the mean flow and turbulence statistics, i.e., below the maximum roughness height averages are taken over fluid occupied areas only. A triple decomposition of the velocity field (Raupach et al. 1991) is applied to separate Reynolds from dispersive stresses:

$$\begin{aligned} u(x,y,z,t)= & {} \langle {\overline{u}}\rangle (z) + {\widetilde{u}}(x,y,z) + u^{\prime }(x,y,z,t), \end{aligned}$$
(1)
$$\begin{aligned} v(x,y,z,t)= & {} \langle {\overline{v}}\rangle (z) + {\widetilde{v}}(x,y,z) + v^{\prime }(x,y,z,t), \end{aligned}$$
(2)
$$\begin{aligned} w(x,y,z,t)= & {} \langle {\overline{w}}\rangle (z) + {\widetilde{w}}(x,y,z) + w^{\prime }(x,y,z,t). \end{aligned}$$
(3)

Here, \(\overline{\,\cdot \,}\) denotes the average in time and \(\langle \,\cdot \, \rangle\) the spatial average across wall-parallel (x-y-) planes. The velocity fluctuations in time around the local time-averaged velocity field give rise to the Reynolds stresses (\(\langle \overline{u^{\prime }u^{\prime }}\rangle\), \(\langle \overline{u^{\prime }w^{\prime }}\rangle\), etc.) and the spatial variations in the time-averaged velocity field result in the dispersive stresses (\(\langle {\widetilde{u}} {\widetilde{u}}\rangle\), \(\langle {\widetilde{u}} {\widetilde{w}}\rangle\), etc.)

3 Results

In this section, first the changes in the mean streamwise velocity profiles and the Reynolds and dispersive stress profiles for the flow over the barnacle surface with increasing Reynolds number will be discussed and compared to equivalent data for the Gaussian surface. In the second part, a ‘smooth-rough’ decomposition will be applied to investigate the emergence of distinctive features that emerge in some of the profiles for the flow over the barnacle surface at higher Reynolds number.

3.1 Mean Flow Statistics

Fig. 3
figure 3

Mean streamwise velocity profiles for barnacle (a) and Gaussian (b) surface; velocity profiles in defect form for barnacle (c) and Gaussian (d) surface. In panel a the vertical lines indicate the maximum barnacle height in inner units for the corresponding cases

Full size image

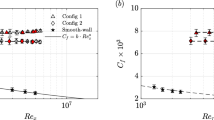
The mean streamwise velocity profiles for the barnacle surfaces are shown in Fig. 3a. As expected, an approximately logarithmic scaling is recovered closely above the maximum roughness height and the extent in inner units of the logarithmic scaling region rises with Reynolds number. A distinctive feature can be observed to emerge at the higher Reynolds numbers, namely an inflection point in the profile that appears approximately at the wall-normal location of the maximum barnacle height when the profile is plotted in semi-logarithmic axes. In comparison, no such feature can be observed for the Gaussian rough surface (see Fig. 3b). For both surfaces a good level of recovery of outer-layer similarity can be observed in the velocity defect profiles (see Fig. 3c, d).

Fig. 4
figure 4

Roughness function \(\Delta U^+\) versus equivalent sand-grain roughness \(k_s^+\) for the barnacle surface. For comparison, data for tubeworm roughness (Monty et al. 2016), Gaussian roughness (Jelly and Busse 2019), and sand-grain roughness (Nikuradse 1933) is also shown. The thick continuous black line indicates Colebrook’s empirical formula (Colebrook 1939)

Full size image

The Hama roughness function \(\Delta U^+\), i.e., the downwards shift in the mean streamwise velocity profile compared to smooth-wall conditions, is shown in Fig. 4. Fully rough behaviour is approached at the highest Reynolds number and the equivalent sand grain roughness \(k_s\) corresponds to approximately 0.5k. Compared to Nikuradse (1933)’s sand-grain roughness a more gradual increase in \(\Delta U^+\) can be observed over the transitionally rough region with the barnacle surface showing a trend that is close to Colebrook (1939)’s formula approaching the fully rough asymptote from above; in contrast, the Gaussian roughness shows a more sandgrain-roughness-like behaviour with a steeper increase in \(\Delta U^+\) in the upper transitionally rough region approaching the fully rough asymptote from below. Data by Monty et al. (2016) for another type of calcareous macrofouling found on ship hulls, namely fouling by tubeworms, shows in the upper transitionally rough region, i.e. for \(\Delta U^+ \gtrapprox 3\), a trend that is much closer to standard sand-grain roughness behaviour. This could be a result of the fact that tubeworms, based on the surface scan shown in Monty et al. (2016), do not exhibit clustering, i.e., the tubeworm features are approximately uniformly randomly distribution over the surface, and thus the tubeworm surface is more uniformly rough than the present, strongly clustered barnacle surface.

3.2 Reynolds Stress Statistics

Fig. 5
figure 5

Normal Reynolds stress profiles. a, c, e Barnacle 10% surface; b, d, f Gaussian roughness; a, b: streamwise, c, d: spanwise, e, f: wall-normal Reynolds stress

Full size image

A dependency of the flow statistics on the roughness type can also be observed when considering the Reynolds stress statistics. For the Gaussian surface, the streamwise Reynolds stress, shown in Fig. 5b, decreases with increasing \(Re_{\tau }\). For the barnacle surface, a similar decrease can be observed at low Reynolds numbers (see Fig. 5a), but \(\langle \overline{u^{\prime } u^{\prime }}\rangle\) levels do not reduce further for \(Re_{\tau }=270\) and above. For the higher Reynolds number cases, the streamwise Reynolds stress profiles display a ‘roughness’ peak which is associated with the crests of the barnacle features which is at an approximately fixed distance from the wall when measured in outer units, i.e., units of \(\delta\) (see Fig. 6a). In addition, a smooth-wall like ‘inner’ peak emerges, which falls into the buffer layer relative to the smooth surface and remains at an approximately fixed distance from the wall when measured in inner units, i.e., in units of the viscous length scale \(\ell _{d }\). No such feature can be observed for the Gaussian rough surface.

The spanwise Reynolds stresses, shown in Fig. 5c and (d), increase with Reynolds number for both surfaces, as would also be expected for the smooth-wall case. While at low \(k^+\) values the streamwise Reynolds stress fluctuations clearly dominate over the spanwise velocity fluctuations, the spanwise Reynolds stress contribute an increasing fraction to the turbulent kinetic energy as \(k^+\) increases. Compared to the location of the smooth-wall peak of \(\langle \overline{v^{\prime } v^{\prime }}\rangle\), the peak of the spanwise velocity fluctuations for the barnacle surface is shifted to higher wall-normal locations. However, for the barnacle surface, the peak of \(\langle \overline{v^{\prime } v^{\prime }}\rangle\) is at the same time located deeper within the rough surface compared to the outer peak in the \(\langle \overline{u^{\prime } u^{\prime }}\rangle\) profiles, indicating that high roughness-induced spanwise velocity fluctuations are associated with in-plane circumnavigation of clusters of barnacles, whereas the highest roughness-induced streamwise velocity fluctuations are caused by the interaction of the outer flow with the barnacle crests.

As for the spanwise Reynolds stresses, a clear increasing trend can be observed with \(k^+\) for the wall-normal Reynolds stresses (see Fig. 5e and f); an increase in the wall-normal velocity fluctuations as a function of the Reynolds number would also be expected for the smooth-wall case (Hu et al. 2006). A distinctive difference that emerges for the barnacle case is that the peak of \(\langle \overline{w^{\prime } w^{\prime }}\rangle\) clearly exceeds the smooth-wall peak at the corresponding Reynolds number for the high \(k^+\) cases, showing that the barnacle clusters are much more effective in generating high wall-normal velocity fluctuations than the Gaussian surface. At the same time, the Gaussian surface has a stronger effect on the mean flow field since it induces higher \(\Delta U^+\) values. Enhanced wall-normal velocity fluctuations therefore do not always go hand in hand with a stronger roughness effect.

Fig. 6
figure 6

Streamwise normal Reynolds stress profiles in linear axes (a, b) and Reynolds shear stress (c, d) profiles. a, c Barnacle 10 % surface; b, d Gaussian roughness; line styles as in Fig. 5

Full size image

The Reynolds shear stress profiles, shown in Fig. 6, also exhibit a distinctive feature for the barnacle surface: for the higher \(Re_{\tau }\) cases, a near-wall peak develops around the location of the maximum barnacle height which exceeds smooth-wall Reynolds shear stress levels. In contrast, the Gaussian roughness shows for all cases Reynolds shear stress levels that are less or equal to the corresponding smooth-wall Reynolds shear stress.

3.3 Dispersive Stress Statistics

The dispersive stresses allow to quantify the roughness-induced inhomogeneity of the time-averaged velocity field in a given wall-parallel (x-y-) plane.

Fig. 7
figure 7

Dispersive normal stress profiles. a, c, e Barnacle 10% surface; b, d, f Gaussian roughness; a, b: streamwise, c, d spanwise, e, f: wall-normal dispersive stress

Full size image
Fig. 8
figure 8

Visualisation of time-averaged streamwise velocity field in a horizontal plane at a distance of \((z-z_0)^+=15\) from the smooth-wall plane for case \(Re_{\tau }=720\)

Full size image

In the streamwise dispersive shear stress profiles, shown in Fig. 7a, b, for both surfaces the peaks fall within the roughness layer. An increasing trend with Reynolds number can be observed for the Gaussian surface. For the barnacle surface, for low Reynolds number also an increase with Reynolds number can be seen. However, for the three highest Reynolds numbers, the profiles of \(\langle {\tilde{u}} {\tilde{u}}\rangle\) are almost identical: little difference in the peak value can be observed and the main observable change is a slight shift in the peak value closer to the wall as the Reynolds number increases. For the barnacle surface, the streamwise dispersive shear stress attains significantly higher values than for the Gaussian surface. This can be attributed to the fact that the Gaussian surface is a statistically homogeneous surface where the local deviations in the time-averaged streamwise velocity field from the spatially averaged value do not attain as high values as for the barnacle surface, which is strongly heterogeneous due to the strong difference in surface texture between the barnacle clusters and the surrounding large connected smooth-wall sections (see Fig. 8).

In the spanwise dispersive stress profiles, shown in Fig. 7c, d, significant Reynolds number dependence of the profiles can be observed for both surfaces. However, the Reynolds number dependency is again significantly stronger for the Gaussian surface compared to the barnacle surface. In both cases, the peak value moves deeper within the roughness, i.e., to lower z values, as Reynolds number increases. For the Gaussian surface, the shape of the profile does not change significantly, other than the significant increase in peak value. For the barnacle surface, the profile shape becomes increasingly positively skewed as Reynolds number increases and the peak approaches the smooth-wall location.

For both surfaces, a clear increasing trend with Reynolds number can be observed in the wall-normal dispersive stresses (see Fig. 7e, f). For the Gaussian surface significant recirculating flows are induced within the many pits of this surface resulting in a ‘double-peak’ structure in the wall-normal dispersive stress profile. In contrast, for the barnacle surface, no such feature is evident. This is because the amount of recirculating flow for this surface is in comparison negligible due to the low coverage. For barnacle surfaces with high coverage, a double-peak structure would emerge (Sarakinos and Busse 2022).

Fig. 9
figure 9

Dispersive shear stress profiles. a Barnacle 10% surface; b Gaussian roughness; line styles as in Fig. 7

Full size image

The dispersive shear stress profiles, shown in Fig. 9, give some insight into the distinct feature that was observed for the Reynolds shear stress profile at the higher Reynolds numbers. While for the Gaussian surface, \(-\langle {\tilde{u}}{\tilde{w}}\rangle\) remains greater or approximately zero across the whole height of the channel, for the barnacle surface, a distinct minimum for \(-\langle {\tilde{u}}{\tilde{w}}\rangle\) develops for the shear stress profile around the location of the maximum barnacle height, which compensates for the higher Reynolds shear stress values that were observed at the same wall-normal location. For both surfaces, a positive \(-\langle {\tilde{u}}{\tilde{w}}\rangle\) peak develops within the rough surface. This peak is significantly higher and more Reynolds number dependent for the Gaussian compared to the barnacle surface.

3.4 Smooth-Rough Decomposition

Fig. 10
figure 10

Illustration of the mask used for the decomposition of the streamwise Reynolds stress profiles. The blue areas indicate ‘smooth’ patches; areas coloured in yellow correspond to ‘rough’ patches, i.e., the planform area of the barnacles

Full size image

For the barnacle surface, several distinctive features were observed in the Reynolds stress statistics, such as the existence of an ‘inner’ peak in the streamwise normal Reynolds stress profiles. To look into the causes for the emergence of these features, a simple geometric decomposition is applied to compute the contribution to the streamwise Reynolds stress profiles that arise above the barnacle features (‘rough patches’) and above the surrounding smooth surface sections (‘smooth patches’) by defining a corresponding mask \(\psi (x,y)\) (see Fig. 10) to extract the corresponding data from the fields of time averaged velocity and local variance / co-variance of the velocity fluctuations. The resulting profiles are shown in Figs. 11, 12, 13, 14 and 15. For all profiles, the friction velocity \(u_{\tau }\) and the viscous length scale \(\ell _{d }\) used for the normalization are based on the global flow properties. The addition of the smooth-patch and the rough-patch profiles recovers the corresponding global profiles discussed in Sects. 3.1 and 3.2.

Fig. 11
figure 11

Decomposed streamwise velocity profiles: a contribution above smooth patches; b contributions above rough patches. The coloured dotted vertical lines indicate the maximum barnacle height

Full size image

The decomposed streamwise velocity profile (see Fig. 11) shows for the profile contribution from the ‘smooth’ sections hints of the emergence of two logarithmic scaling regions at the highest \(Re_{\tau }\): between \((z-z_0)^+\approx 30 \dots 60\) an approximately logarithmic scaling can be observed in addition to the clearly developed logarithmic region in the part of the profile above the rough surface. It is conceivable that at higher Reynolds number a wider logarithmic scaling range could develop over the smooth sections of the barnacle surfaces beneath the roughness height, similar to the internal boundary layers that form over surfaces with a rough to smooth transition (Elliott 1958; Antonia and Luxton 1972; Garratt 1990).

Fig. 12
figure 12

Decomposed normal Reynolds stress profiles: a, c, e contribution above smooth patches; b, d, f contributions above rough patches. a, b Streamwise, c, d spanwise, and e, f wall-normal Reynolds tresses. The coloured dotted vertical lines indicate the maximum barnacle height. The vertical black dash-dotted lines indicate the approximate peak location of the corresponding smooth-wall Reynolds stress profiles at \(Re_{\tau }=720\)

Full size image
Fig. 13
figure 13

Visualisation of time-averaged root-mean square streamwise velocity fluctuations in a horizontal plane at a distance of \((z-z_0)^+=15\) from the smooth-wall plane for case \(Re_{\tau }=720\)

Full size image
Fig. 14
figure 14

Visualisation of instantaneous streamwise velocity field in a horizontal plane at a distance of \((z-z_0)^+=5\) from the smooth-wall plane for case \(Re_{\tau }=720\)

Full size image

Results for the decomposed normal Reynolds stress profiles are shown in Fig. 12. It is evident that the inner peak in the streamwise Reynolds stresses arises from the smooth-wall patches, indicating a partial recovery of smooth-wall behaviour over the large connected smooth sections of this surface where \(\overline{u^{\prime }u^{\prime }}\) attains approximately constant values (see Fig. 13) and streak-like structures can be observed in the vicinity of the wall (see Fig. 14). A similar mixed scaling was observed by Hanson and Ganapathisubramani (2016) for turbulent boundary layers over a surface with a rough to smooth transition in texture. The inner peak in the streamwise Reynolds stress profile appears to become Reynolds-number independent at the highest three \(Re_{\tau }\) values investigated. Above the rough patches, only the outer peak can be observed, which consistently is located around the maximum barnacle height and slowly grows with Reynolds number over the three highest \(Re_{\tau }\) cases investigated. A test of the decomposition performed on the streamwise Reynolds stresses based on data for barnacle surfaces with increasing coverage (Sarakinos and Busse 2022), showed that partial recovery of smooth-wall behaviour can only be observed for low coverage states (not shown).

The decomposed spanwise normal Reynolds stresses show that the shift in the peak observed in the spanwise Reynolds stress profiles (Fig. 5c) is caused by the ‘roughness’ part of the decomposed profiles which is consistent with the view that enhancement of spanwise velocity fluctuations is a result of in-plane circumnavigation of the tapering roughness shapes. The peak in the ‘roughness’ part of the profile occurs around the maximum barnacle height, although it shifts (in outer units) closer to the smooth-wall surface as Reynolds number is increased. The peak magnitude shows a strong growth with Reynolds number.

The decomposed wall-normal Reynolds stresses show in their rough-wall part a similar strong growth in the peak value with Reynolds number. In all cases, this peak is located above the maximum barnacle height, however, it moves closer to the roughness crests as Reynolds number increases. For the smooth-wall part of the profiles the peak location falls at the higher Reynolds numbers below the location of the corresponding smooth-wall peak at all \(Re_{\tau }\).

Fig. 15
figure 15

Decomposed Reynolds stress stress profiles: a contribution above smooth patches; b contributions above rough patches. Line styles as in Fig. 12. The vertical black dash-dotted line indicates the maximum barnacle height for the full-scale cases

Full size image
Fig. 16
figure 16

Visualisation of time-averaged local Reynolds shear stress fluctuations in a horizontal plane at a distance of \((z-z_0)\approx 0.12\delta\) from the smooth-wall plane for case \(Re_{\tau }=720\); the smooth wall-value at the corresponding wall-normal location was subtracted to highlight areas of excess local Reynolds shear stress fluctuations

Full size image

The rough-smooth decomposition of the Reynolds shear stress profiles is shown in Fig. 15). The distinctive feature causing the increase of the Reynolds shear stress profile above smooth-wall reference values that was observed in Fig. 6 is evident in the part of the profile associated with the smooth surface sections. This may appear surprising at first, since one would assume this to be associated with the rough surface sections. However, high \(-\overline{u^{\prime } w^{\prime }}\) values occur in the wakes of the barnacles which extend behind the barnacle clusters over part of the smooth-wall sections and thus make contribution to the ‘smooth’ part of the profile (see Fig. 16).

4 Conclusions

A surface partially fouled by barnacles clusters was investigated using direct numerical simulations. A comparison to data for a generic Gaussian roughness shows clear differences in the Reynolds number dependency, with the barnacle surface exhibiting a Colebrook-like behaviour whereas the Gaussian rough-surface approaches the fully rough asymptote from below. There are also clear qualitative differences in the shapes and Reynolds number dependency of the profiles of mean velocity, and Reynolds and dispersive stresses when comparing the barnacle surface and the Gaussian surface. The differences are mainly caused by the large connected smooth sections that are present on the barnacle surface. This allows a partial recovery of smooth-wall behaviour over these sections, leading to characteristic features such as an inner peak in the \(\langle \overline{u^{\prime } u^{\prime }}\rangle\) profiles, which are reminiscent of the behaviour of boundary layers with rough to smooth transitions (Hanson and Ganapathisubramani 2016). While no clear inner-peak features were observed for the other Reynolds stress components, it is likely that these would emerge at much higher \(Re_{\tau }\) where there is a clearer scale separation between the distance of the corresponding smooth-wall peak from the wall and the maximum barnacle height, where the ‘outer’ peaks of the Reynolds stress profiles are expected to be approximately located irrespective of the Reynolds number.