Bayesian Optimization of Wall-Normal Blowing and Suction-Based Flow Control of a NACA 4412 Wing Profile

Abstract

Active flow-control techniques have shown promise for achieving high levels of drag reduction. However, these techniques are often complex and involve multiple tunable parameters, making it challenging to optimize their efficiency. Here, we present a Bayesian optimization (BO) approach based on Gaussian process regression to optimize a wall-normal blowing and suction control scheme for a NACA 4412 wing profile at two angles of attack: 5 and 11 $^\circ$, corresponding to cruise and high-lift scenarios, respectively. An automated framework is developed by linking the BO code to the CFD solver OpenFOAM. RANS simulations (validated against high-fidelity LES and experimental data) are used in order to evaluate the different flow cases. BO is shown to provide rapid convergence towards a global maximum, even when the complexity of the response function is increased by introducing a model for the cost of the flow control actuation. The importance of considering the actuation cost is highlighted: while some cases yield a net drag reduction (NDR), they may result in an overall power increase. Furthermore, optimizing for NDR or net power reduction (NPR) can lead to significantly different actuation strategies. Finally, by considering losses and efficiencies representative of real-world applications, still a significant NPR is achieved in the 11$^\circ$ case, while net power reduction is only marginally positive in the 5$^\circ$ case.

1 Introduction

Over the last few decades, concerns about global warming and environmental degradation have been a major focus of social discourse and, as a consequence, of policy-makers’ agendas. As a result, a number of national and international policies, such as the Paris agreement (UNFCCC 2015) or the UN’s 2030 agenda for Sustainable Development (Transforming our World 2015), have been implemented with the aim of reducing global emissions. One area that has received significant attention in this regard is transportation sector, particularly aviation, which is estimated to account for approximately 4$\%$ of human-induced global warming (Klöwer et al. 2021) and is projected to grow rapidly in the coming years (Brazzola et al. 2022). Enhancing the efficiency of aircraft and other transportation systems is therefore critical for reducing their environmental impact.

To this end, the development, analysis and deployment of drag-reduction and flow-control technologies is an important pathway towards achieving a more efficient and sustainable transportation. Flow-control methods can be broadly classified into two categories: passive and active. Passive techniques, which do not require any additional power to operate, are generally simpler to implement than active methods. One example of a well-studied passive control method is the use of riblets, which were found to improve the overall efficiency of an aircraft in an in-flight test by 4$\%$ (Walsh 1986). However, the complexity of manufacturing surfaces covered by riblets, along with their limited efficiency gain, has so far hindered their widespread adoption by industry.

Active flow-control techniques, on the other hand, promise higher efficiency gains than their passive counterparts, albeit at a higher complexity and cost. For instance, boundary-layer suction can be used to delay transition from a laminar to a turbulent boundary layer (TBL), thereby avoiding the associated increase in friction drag (Beck et al. 2018; Schrauf et al. 2020). This technique has been extensively researched and has even been implemented in the aviation industry, with suction being used in the tail-plane of a Boeing 787 for transition-delay (Krishnan et al. 2017). Although high efficiency gains can be achieved by delaying transition, the BL will eventually become turbulent, making the development of flow-control techniques for this regime highly relevant. In fact, some drag-reduction techniques even focus on enhancing turbulence by exciting specific frequencies in order to avoid flow separation (Feero et al. 2017). For already developed TBLs, wall-normal blowing is a common technique used to reduce viscous contributions to drag (also known as friction drag), with some of the first studies dating back to the 1950s (Mickley 1954). More recent studies (Kametani and Fukagata 2011; Stroh et al. 2016) using high-fidelity simulations have confirmed the skin friction reduction capabilities of blowing. Atzori et al. (2020, 2021) investigated a combination of uniform wall-normal blowing and suction flow-control schemes applied to a NACA 4412 wing profile using well-resolved LES, finding the highest aerodynamic efficiency gain when suction was performed on the suction side (SS) and blowing on the pressure side (PS) of the airfoil. Fahland et al. (2021) extended these results for different NACA-family profiles, angles of attack and Reynolds numbers through RANS simulations, confirming the trends reported by Atzori et al. (2020, 2021). However, when the cost of the actuation was accounted for, the efficiency of performing suction on the SS degraded considerably, specially at moderate angles of attack corresponding to cruise conditions.

Active flow control applications are often complex, both in terms of implementation and the number of tunable parameters required for their efficiency. For example, uniform suction or blowing used in previous studies on control strategies for airfoils, such as those reported by Fahland et al. (2021) and Atzori et al. (2020, 2021), may not be optimal due to the non-equilibrium nature of the turbulent boundary layer (TBL) developing around an airfoil. Therefore, active flow control strategies are ideal for optimization methods. Recently, new developments in machine learning have been successfully transferred to the field of flow-control, with both evolutionary algorithms (Castellanos et al. 2023) and deep reinforcement learning (Guastoni et al. 2023) successfully tested on zero-pressure gradient TBLs and channel flow, respectively. However, their application to real-world problems, such as the flow around wings, remains difficult due to the large number of flow realizations required by the optimization techniques. The high cost associated with the evaluation of the response, which could be performed experimentally or through computational fluid dynamics (CFD), is a bottleneck in CFD optimizations (Slotnick et al. 2014) that also affects traditional gradient-based optimization methods. Bayesian optimization (Shahriari et al. 2015) appears as a suitable strategy, as it allows to converge to a global optimum with a few response evaluations. BO was successfully applied to a multiple fluid-mechanics problems (see for example the work by Morita et al. (2022)), as well as to a variety of flow-control cases, including drag reduction in zero-pressure gradient TBLs (Mahfoze et al. 2019; O’Connor et al. 2023), fluidic pinball drag reduction (Blanchard et al. 2021), and the optimization of travelling wave parameters for drag reduction in turbulent channel flow (Nabae and Fukagata 2021).

The present study increases the complexity of the flow case with respect to previous studies, optimizing the wall-normal blowing and suction actuation around a NACA 4412 airfoil to improve its aerodynamic or power efficiency. This is an extension of the previous works by Atzori et al. (2020, 2021) and Fahland et al. (2021), which studied uniform blowing and suction actuations for the same wing profile. Here, special care is taken to model the control actuation cost, and the optimization is run for two different scenarios: a cruise and a high-lift configuration. The manuscript is divided into four main sections. In Sect. 2, the flow case, numerical methods, flow-control strategy, and cost are described. A primer on Bayesian optimization based on Gaussian process regression (GPR) is also provided. Section 3 presents the results obtained from the Bayesian optimization, commenting on both the optimization itself and the implications of the obtained control strategies. Finally, Sect. 4 summarizes the main results of the manuscript.

2 Methodology

2.1 Flow Case and Simulation Technique

The present study focuses on the incompressible turbulent flow around a NACA 4412 wing profile, with the aim of improving its aerodynamic performance by finding optimal blowing and suction control strategies. Two different angles of attack (AoA) of 5 and 11 $^\circ$ are considered. The former represents a typical efficient cruise configuration in which the flow remains attached over the entire chord (c), whereas the latter represents a take-off or landing configuration for which a higher lift coefficient is required. In this configuration, the flow separates towards the trailing edge (TE) of the airfoil, resulting in an increase in drag. For both cases, the chord-based Reynolds number ($Re=c U_\infty /\nu$, where $\nu$ is the kinematic viscosity and $U_\infty$ the free-stream velocity) is set to $1\cdot 10^6$.

Reynolds-averaged Navier-Stokes (RANS) simulations are carried out with the finite-volume open-source CFD code OpenFOAM (Weller et al. 1998), using the semi-implicit method for pressure-linked equations (SIMPLE) solver (Jasak 1996). Second-order Gaussian integration was used for the gradient terms, and second-order accurate interpolation schemes for the divergence terms. The $k-\omega$ SST turbulence model (Menter et al. 2003) was selected, as it blends both the $k-\omega$ and $k-\varepsilon$ models, achieving good results both in the turbulent boundary layer (TBL) and in the free-shear region, the latter appearing in the wake and separated regions near the TE.

Fig. 1

Sketch of the computational domain (top left) and close-up views of the mesh around the wing (left) and its leading edge (bottom right)

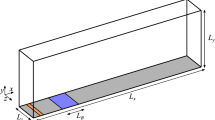
The computational domain , shown in Fig. 1, is a two-dimensional square of sides L equal to 100c. The airfoil is located in the center of the domain, at the specified AoA, with a structured region formed by rectangular elements present both around it (covering the whole boundary layer) and in the near-wake region. A very fine resolution is used around the airfoil, with he wall-normal distance of the first point below one viscous unit ($l^+$), with $l^+=\nu /u_\tau$ where $u_\tau$ is the friction velocity. The rest of the domain (far-field) is unstructured and is comprised of triangular elements. In total, each of the two-dimensional meshes is comprised of a bit above 250,000 cells, with approximately half of them located in the boundary layer and near-wake regions. A parallel flow with velocity $U_\infty$ in the streamwise direction is imposed using a Dirichlet boundary condition (BC) and a homogeneous Neumann BC for the pressure at the inflow. Neumann and Dirichlet BCs are imposed on the velocity and pressure a the outflow, respectively. A no-slip Dirichlet BC is used in the baseline cases around the wing. For the other cases, the control actuation (blowing or suction) is imposed as a wall-normal velocity Dirichlet BC (positive for blowing and negative for suction) in the control region. For all cases, a Neumann BC is used for the pressure at the wall.

Fig. 2

Validation of the pressure (bottom) and friction (top) coefficient distributions of the baseline (no-control) RANS simulations. The 5 and 11$^\circ$ AoAs are represented by blue and red colors, respectively. The results are presented using solid lines for RANS simulations, dashed lines for LES, and circular markers for experimental data

The RANS simulations are validated against high-fidelity reference data coming from both well-resolved LES performed with the spectral-element method code Nek5000 (Vinuesa et al. 2018; Tanarro et al. 2020; Atzori et al. 2023), and experimental data obtained at the Minimum Turbulence Level (MTL) wind tunnel located at KTH (Stockholm) (Mallor 2019; Tabatabaei et al. 2022). In order to better match the high-fidelity data, the free-stream turbulent kinetic energy (k) is set to 0 and a numerical tripping consisting of a k source region at 0.1 x/c is applied on both sides of the airfoil. This approach, similar to that described by Fahland et al. (2021) or Tabatabaei et al. (2022), leads to an excellent agreement between RANS, high-fidelity LES (as those by Atzori et al. (2021) and Vinuesa et al. (2018)) and experimental results (Tabatabaei et al. 2022), as shown in Fig. 2. For the RANS pressure coefficient distribution (bottom plot of Fig. 2) a small over-prediction of the suction peak appears in comparison to the reference data, nevertheless, the bulk of the distribution is on top of the reference data. As for the friction coefficient (top plot in Fig. 2), only LES data was used as a baseline, as no experimental data is available. Moreover, the high-fidelity LES data shown for the 11$^\circ$ corresponds to an ongoing set of simulations at high angles of attack and is therefore not fully converged yet as not enough time could be ran in order to obtain fully converged statistics at the present time, as opposed to the fully converged result at a lower $Re_c$ described in the recent work by Atzori et al. (2023). However, for the purpose of the present comparison, the LES data appears sufficient, as an excellent agreement is found between RANS and the LES $c_f$ distributions, with the flow separation point in the 11$^\circ$ case located at the same chord location in both the RANS and LES.

Considering the validation of the actuated cases, the Reynolds number ($1\cdot 10^6$) is larger than that studied for previous control applications by Atzori et al. (2020, 2021) using LES. Therefore we could only compare the baseline (no control) cases directly against reference data. Nonetheless, both Fahland et al. (2021) and Semprini Cesari (2023) validated RANS cases with blowing and suction at a lower $Re_c$ against well-resolved LES, using the same type of actuation (blowing and suction). These comparisons were showing the ability of RANS to capture the correct physics and trends introduced by the flow-control actuation albeit with a small systematic error. Since we could not perform a resolved actuated simulation at the present Reynolds numbers, we are still confident that the RANS-LES comparisons at lower $Re_c$ provide sufficient evidence for the accuracy of the RANS prediction.

2.2 Control Strategy and Cost Estimation

The flow around the wing is controlled by means of wall-normal blowing and suction of air through the (permeable) wing’s surface. The control actuation is limited to the region between $x/c=0.25$ and $x/c=0.86$, as in the work by Atzori et al. (2020, 2021) and Fahland et al. (2021). In order to avoid flow separation caused by an excessive blowing intensity (which could lead to un-physical results in the RANS simulations), the blowing or suction magnitude ($v_{blw}$ and $v_{suc}$) is limited to $0.25\%$ of the inflow velocity ($U_\infty$).

The control is implemented by a parameterized blowing/suction profile on the wing’s surfaces. For that purpose, five equidistant (in arch length) knot points are defined on each side on the wing surface, with their wall-normal velocity magnitude ($v_i$) being the design parameters (${\textbf{q}}$) of the Bayesian optimization. A quadratic spline interpolation using the aforementioned knot points is then used to define the actual blowing velocity profile for the control , as shown in Figs. 3 and 4. Naturally, more knot points will allow for a finer resolution of the blowing/suction profiles, but potentially also complicate the optimization process. This discussion is provided in Appendix B.

In the present work, the objective of the control actuation is that of increasing the aerodynamic efficiency of the profile ($E {=c_L/c_D}$), defined as the ratio between the lift and drag coefficients ($c_L$ and $c_D$, respectively). Both can be further divided into their friction and pressure contributions:

$$\begin{aligned}{} & {} c_D = c_{D_f} + c_{D_p} = \frac{1}{\frac{1}{2}\rho U_\infty ^2 S} \left( \iint _{S} \tau _w ({\hat{t}}\cdot {\hat{i}}) \,\mathrm ds + \iint _{S} (p-p_0) ({\hat{n}}\cdot {\hat{i}}) \,\mathrm ds \right) \,, \end{aligned}$$

(1)

$$\begin{aligned}{} & {} \quad c_L = c_{L_f} + c_{L_p} = \frac{1}{\frac{1}{2}\rho U_\infty ^2 S} \left( \iint _{S} \tau _w ({\hat{t}}\cdot {\hat{j}}) \,\mathrm ds + \iint _{S} (p-p_0) ({\hat{n}}\cdot {\hat{j}}) \,\mathrm ds \right) \,, \end{aligned}$$

(2)

where ${\hat{i}}$, ${\hat{j}}$, ${\hat{t}}$ and ${\hat{n}}$ are the unit vectors with directions parallel and perpendicular to the streamwise inflow $U_\infty$, and (locally) tangent and normal to the airfoil surface; p and $p_0$ are the surface and reference static pressures, $\tau _w$ is the (wall-parallel) wall shear stress, and $p_{dyn_\infty }=\frac{1}{2}\rho U_\infty ^2$ is the dynamic pressure in the freestream.

Fig. 3

Schematic of the flow control system considered in the present study. Arrows indicate the direction of air flow (blue, red and black arrows represent suction, blowing and internal massflows respectively), and gray circles turbines or pumps driving the system

Although done as part of this study and in many previous studies in flow control, aiming at maximizing E could lead to unrealizable control strategies which result in a net loss in overall power needed. Moreover, as recently discussed by Fahland et al. (2023), looking at the airfoil in isolation, i.e. without taking into account the systems needed for the control actuation and computing $c_L$ and $c_D$ based only on the pressure and friction distributions around the airfoil, leads to an exaggeration of the gains obtained by blowing: as the mass injected into the system is not accounted for in the body-force balance, the body drag ($c_{D_{body}}$) and the wake-survey (momentum-deficit in the wake of the airfoil) drag ($c_{D_{wake}}$, obtained through a control-volume momentum-balance) diverge. In extreme cases, the momentum injection can even result in a negative body drag (i.e. thrust). Therefore, the total mass injected into the system should be taken into account when computing the net drag reduction. Moreover, as discussed by both Beck et al. (2018) and Fahland et al. (2021), suction requires a reservoir of air at a pressure lower than the lowest pressure in the suction region of the wing ($p_{suc}<\min \{p_{wing\Vert suc}\}$). The opposite is true for blowing: it requires a reservoir of air at a pressure higher than the highest pressure of the blowing region ($p_{blw}>\max \{p_{wing\Vert blw}\}$). Furthermore, the tubing necessary to connect the reservoirs with the permeable surfaces through which the air is sucked/blown adds losses into the system. Such losses may be accounted for by introducing a penalty of $\Delta c_p = \pm 0.1$ to the reservoirs’ pressure coefficient (i.e. increasing and reducing the required pressure for the blowing and suction chambers, respectively). This loss, in line with Beck et al. (2018) and Fahland et al. (2021), implies that the total pressure losses scale with the square of the free-stream velocity.

Another important consideration is the source (or sink, in the case of suction) of the control massflow. Two main options are available: the continuous ingestion or exhaustion of excess control fluid to the surrounding atmosphere, or its onboard storage. The latter can become problematic for a control actuation that is maintained over a long period of time: assuming an actuation covering $25\%$ of the 125 m$^2$ wing span area of a Boeing 737 cruising at an altitude of 10 km (where $\rho _\infty =0.4135$ kg/m$^3$) at 225 m/s, more than 7 kilograms of air would be ingested per second. In the case of blowing, that figure represents the quantity of air needed to be stored before take-off in order to operate the control. The cost of carrying that mass would surely outweigh any possible aerodynamic gain achieved through the actuation itself. Therefore, any ingested air should be exhausted, and vice versa. This requirement can be alleviated by connecting suction and blowing reservoirs (as shown in Fig. 3), in this way, sucked air can be used to cover some (or all) of the blowing requirements. If the actuation has a larger massflow ($\dot{m}=\int _{S_c}\rho v_c dS$) requirement for blowing than for suction, the extra massflow ($\dot{m}_{blw}-\dot{m}_{suc}$) is supplied from the free-stream. In a real application, the extra air could be tapped from one of the compressor stages of the aircraft engines (bleed air). However, in the present study, we consider the wing as an isolated system, as shown in Fig. 3. This leads us to assume a worst-case scenario, in which the excess blowing air is acquired at the stagnation point of the airfoil (where $c_p=1$). For cases in which $\dot{m}_{suc}>\dot{m}_{blw}$, the excess suction massflow is exhausted from the suction reservoir into the free-stream (at $p=p_\infty$).

In order to drive the air for the blowing actuation, the airflow coming into the blowing reservoir (either from the free-stream or the suction chamber) should be pressurized. This can be achieved with a pump. Moreover, turbines can be also utilized where the pressure differential is favourable, allowing to recover some energy to be used to help drive the pumps. Both pumps and turbines are represented by a gray circle in Fig. 3.

From the previous considerations, two sources of power consumption from the flow-control actuation arise: the control fluid air-supply and the turbomachinery-related power. The effect of the required control air-supply massflow ($c_{P, as}$) can be included as an additional thrust term (positive or negative, for net suction or blowing respectively) produced by the deceleration (net blowing) or acceleration (net suction) of the excess control fluid. It is proportional to the total massflow exhausted or ingested (${\dot{m}}_{wing \rightarrow \infty }$) times its velocity ($U_{jet}$).

$$\begin{aligned} c_{P, as} = \frac{{\dot{m}}_{wing \rightarrow \infty } U_{jet}}{\frac{1}{2}\rho _\infty U_\infty ^2 S} \end{aligned}$$

(3)

where $U_{jet}$ is equal to $U_\infty$ for the net blowing case (the worst-case scenario assumed in the present work in which fluid is decelerated from the free-stream), and equal to $\eta _{pump} \cdot U_\infty$ for control schemes with net suction (with $\eta _{pump}$ referring to the isentropic efficiency of the pump used to pressurize the air from $p_{suc}$ to $p_\infty$). The latter results from minimizing the total power incurred when considering both the pump power and the thrust gained from jettisoning the excess sucked air, as discussed by Beck et al. (2018).

The turbomachinery (pump or turbine) power can be computed from the change in total enthalpy of the fluid between two different states (e.g. between the conditions in the free-stream and those in the blowing reservoir), which for an incompressible fluid is computed as the product of the massflow (${\dot{m}}_{1 \rightarrow 2}$) and the total pressure differential between the two states (where the total pressure is given by $p_t = p + \tfrac{1}{2}\rho U^2$):

$$\begin{aligned} c_{P, p \mid t} = \frac{{\dot{m}}_{1 \rightarrow 2} (p_{t,2} -p_{t,1})}{\rho _\infty \frac{1}{2}\rho _\infty U_\infty ^3 S} \end{aligned}$$

(4)

Nonetheless, the previous formula assumes that no losses are incurred due to the use of turbomachinery. In order to model such losses (which would be present in a real-world application), an isentropic efficiency for both pump and turbine is introduced:

$$\begin{aligned}{} & {} c_{P, p}^* = \frac{c_{P, p}}{\eta _{p}} \end{aligned}$$

(5)

$$\begin{aligned}{} & {} \quad c_{P, t}^* = \eta _{t}c_{P, t} \end{aligned}$$

(6)

Once the power consumption of the flow-control actuation has been determined, a better assessment of the efficacy of the control scheme can be achieved through a modified aerodynamic efficiency ($\mathrm {E_{power}}$). Instead of having just the drag in the denominator, the non-dimensional power consumption is added to the former. This sum is a measure of the total drag ($c_{D_T}$), which the thrust provided by the aircraft engines needs to overcome.

$$\begin{aligned} \mathrm {E_{power}} = \frac{c_L}{c_{D_T}}=\frac{c_L}{c_D+c_P}= \frac{c_L}{c_D+{c_{P, as}}+\sum c_{P, p \mid t} } \end{aligned}$$

(7)

In the present study, three different scenarios will be considered for each of the angles of attack (5 and 11$^\circ$), progressively increasing the complexity and realism of the objective function:

• Ideal scenario ( $\mathbf {\textrm{E}}$) The aerodynamic efficiency is maximized, without taking into account the cost of the actuation.

• Realistic scenario with no efficiencies nor losses ( $\mathbf {\mathrm {E_{power}}}$) The ratio between $c_L$ and $c_{D_T}$ is maximized, with $\eta _{p}=\eta _{t}=1$ and $\Delta c_p =0$.

• Realistic scenario with efficiencies and losses ( $\mathbf {\mathrm {E_{power, \eta }}}$) The ratio between $c_L$ and $c_{D_T}$ is maximized, with $\eta _{p}=0.8$, $\eta _{t}=0.9$ (isentropic efficiencies corresponding to a (good) polytropic efficiency of around 0.85 (Razak 2013)) and $\Delta c_p =0.1$.

Fig. 4

Flowchart of the optimization process used. Green boxes represent quantities and processes related to the Bayesian optimization (and Gaussian process regression), whereas blue boxes represent quantities and processes related to the numerical simulation

2.3 Bayesian Optimization

Data-driven optimization techniques are outer-loop problems, as they require several realizations of the flow when exploring the space of the design parameters. In standard blackbox optimization methods, first a surrogate for the response function is constructed using a given set of samples, and then the optimization is performed on the surrogate. In contrast, in the Bayesian optimization (BO) technique (Shahriari et al. 2015) a sequence of samples is drawn from the space of the design parameters that converges to the global optimum of the objective function after a finite number of iterations. As shown in Ref. Morita et al. (2022), BO based on the GPR can be efficient even for a relatively large number of design parameters, hence it can be superior (in a relative-cost sense) to more traditional gradient-based approaches or evolutionary algorithms for multidimensional problems. This is an important advantage, noting that performing CFD simulations and experiments can be both expensive when aiming for optimizing the shape of the actuation (blowing/suction magnitude distribution over the suction and pressure sides).

Any Bayesian optimization consists of two main components: the method used to construct a (inexpensive) surrogate of the model response, and an acquisition function used to determine the sequence of parameters samples. In the present study, a single-variate response r (the aerodynamic efficiency) is considered that is a function of the design parameters ${\textbf{q}}$. In particular, ${\textbf{q}}$ is taken to be 10-dimensional corresponding to the values of the wall-normal velocity (blowing/suction) at each of the 5 points per airfoil side as mentioned before. The reasoning behind choosing a limited number of parameters to define the control actuation is related with the curse of dimensionality: by increasing the number of points, the dimension of the optimization space increases accordingly, leading to a slower (and unsure) convergence of the problem. Therefore, a balance between the dimension of the problem, and the flexibility (in terms of shape) of the control actuation must be struck. A further investigation of the effect of reducing or increasing the number of points used in the parametrization of the control actuation is presented in Appendix B. The admissible space of ${\textbf{q}}$ is the hypercube ${\mathbb {Q}}=[-0.0025 U_\infty ,0.0025U_\infty ]$, in order to avoid triggering flow separation. The objective is that of finding the optimal set of input parameters (${\textbf{q}}_{opt}$) which maximize the response r. In order to evaluate the response given a sample in the parameter space, a full CFD simulation is carried out. In general, such observations might be contaminated by observational uncertainties ($\varepsilon$). Although such uncertainties could be observation-dependent (e.g. larger modelling errors for the samples in the parameter space which lead to separation in the RANS simulation), we assume that they are independent and identically distributed as Gaussian: $\varepsilon \sim {\mathcal {N}}(0,\sigma ^2)$. Moreover, as no analytic relationship is known between the parameters and response spaces, a surrogate model ($\tilde{f}({\textbf{q}})$) is used to represent such relationship,

$$\begin{aligned} r({\textbf{q}}) = f({\textbf{q}}) + \varepsilon \approx \tilde{f}({\textbf{q}}) +{\mathcal {N}}(0,\sigma ^2) \ . \end{aligned}$$

(8)

In the present work, Gaussian process (GP) regression (Rasmussen and Williams 2006) is used as the surrogate model. A GP is a multivariate Gaussian distribution fully defined by its mean, m, and covariance, c, functions.

$$\begin{aligned} \tilde{f}({\textbf{q}}) \sim \textrm{GP}(m({\textbf{q}}),c({\textbf{q}},{\textbf{q}}^\prime )) \ . \end{aligned}$$

(9)

In practice, kernel functions which rely on a set of hyperparameters ${\varvec{\beta }}$ are used to model the mean and covariance functions. In the present work, the mean function and covariance kernel are chosen to be a constant function and a Matern52 kernel (Rasmussen and Williams 2006), respectively. Given a set of training data ${\mathcal {D}}=\{{\textbf{q}}^{(i)},r^{(i)}\}_{i=1}^n$, the hyperparameters ${\varvec{\beta }}$ are optimized, and thus the posterior and posterior predictive of the surrogate model can be inferred. The posterior predictive has also a multivariate Gaussian distribution with the following mean and variance at a set of test samples ${\textbf{Q}}^*$:

$$\begin{aligned}{} & {} m({\textbf{R}}^* \mid {\mathcal {D}}, \mathbf {Q^*} ) = {\textbf{C}}(\mathbf {Q^*},{\textbf{Q}}) ( {\textbf{C}}({\textbf{Q}},{\textbf{Q}}) + {\textbf{C}}_N)^{-1} {\textbf{R}}^T \,, \end{aligned}$$

(10)

$$\begin{aligned}{} & {} \quad v({\textbf{R}}^* \mid {\mathcal {D}}, \mathbf {Q^*} ) = {\textbf{C}}(\mathbf {Q^*},\mathbf {Q^*}) - {\textbf{C}}(\mathbf {Q^*},{\textbf{Q}}) ( {\textbf{C}}({\textbf{Q}},{\textbf{Q}}) + {\textbf{C}}_N)^{-1} {\textbf{C}}({\textbf{Q}},\mathbf {Q^*}) \,, \end{aligned}$$

(11)

where, ${\textbf{R}}_i=r^{(i)}$, ${\textbf{R}}^*_i=r^{*{(i)}}$, ${\textbf{C}}_{ij}({\textbf{Q}},{\textbf{Q}}') = c({\textbf{q}}^{(i)},{\textbf{q}}'^{(j)})$, and ${\textbf{C}}_N$ specifies the covariance matrix of the noise in the training data ${\mathcal {D}}$. BO-GPR is a sequential algorithm, which starts from a set of initial samples for ${\textbf{q}}$, based on which a GP surrogate is constructed. At each iteration, the training dataset ${\mathcal {D}}$ is updated by adding new samples. The decision about the new samples of ${\textbf{q}}$ is made using the so-called acquisition function for which various options have been proposed in the literature including the Probability of Improvement (PI) (Jones et al. 1998), the Expected Improvement (EI) (Jones et al. 1998), and the Lower Confidence Bound (LCB) (Srinivas et al. 2009). Here, we use the EI acquisition function as it offers a good balance between exploration of the admissible space of ${\textbf{q}}$ (to reduce the uncertainty of the surrogate), and exploitation of the regions close to a suspected optimum (efficient use of the best sample available in the set, ${\textbf{q}}^ \dagger$). By maximizing the EI function defined as,

$$\begin{aligned} \textrm{EI}({\textbf{q}}) = {\mathbb {E}}[ \max (r({\textbf{q}}^ \dagger ) -r({\textbf{q}}), 0) ] \,, \end{aligned}$$

(12)

the next sample of ${\textbf{q}}$ is obtained. For a standard GP with constant noise standard deviation $\sigma$, a closed form for the $\textrm{EI}$ was introduced by Jones et al. (1998):

$$\begin{aligned} \textrm{EI}({\textbf{q}}) = {\left\{ \begin{array}{ll} (r({\textbf{q}}^ \dagger )- m({\textbf{q}}) + \xi )\Phi (\zeta )+s({\textbf{q}})\varphi (\zeta ), &{} s({\textbf{q}})>0\\ 0, &{} s({\textbf{q}})=0 \end{array}\right. } \,, \end{aligned}$$

(13)

where $s({\textbf{q}})$ is the standard deviation of the GP, and $\Phi (\zeta )$ and $\varphi (\zeta )$ are the cumulative distribution and probability distribution functions of the standard Gaussian distribution of $\zeta$, respectively, where

$$\begin{aligned} \zeta = {\left\{ \begin{array}{ll} (r({\textbf{q}}^ \dagger )- m({\textbf{q}}) + \xi )/s({\textbf{q}}), &{} s({\textbf{q}})>0 \\ 0, &{} s({\textbf{q}})=0 \end{array}\right. } \ . \end{aligned}$$

(14)

In the equations above, $\xi$ is a hyperparameter that balances exploration and exploitation. Note that both mechanisms are critical to achieve a global optimum: Too much emphasis on exploitation can cause the optimizer to get stuck in a local optimum. On the other hand, excessive focus on exploration can slow down convergence to the optimum, which would hinder one of the main advantages of using BO over other optimization methods.

In this work, the BO is implemented in Python, making use of the open-source libraries GPyOpt GPy: GPy (2012) and GPy GPyOpt: GPyOpt (2016). The optimization code is coupled seamlessly to the CFD software OpenFOAM (Weller et al. 1998), which acts as a black box to the optimizer. At each iteration of the BO-GPR, the new sample of ${\textbf{q}}$ (10 dimensional) is transformed into a smooth boundary condition covering the whole actuation region by means of a quadratic spline interpolant. The wall boundary condition is updated in OpenFOAM, and the flow case is simulated using a RANS method. Once the CFD solver has converged, the relevant aerodynamic quantities of interest are extracted, and the cost of the actuation is computed. The iterations continue until convergence. In the present case, a total of 50 iterations (i.e. simulations) are done, although as discussed later, even less would be sufficient for convergence. The whole automated workflow is described graphically in Fig. 4. Note that there is no accepted and generally valid stopping criterion for this iteration, even though monitoring both the evolution of r and EI during the iterations gives useful hints on the state of convergence. For further discussion in this regard, see Ref. Morita et al. (2022).

The computational cost of an iteration of the optimizer is essentially driven by the evaluation of the objective function, i.e. the cost of running OpenFOAM for a specific input configuration. The cost due to optimization of the underlying Gaussian process regression and the evaluation of the EI can be neglected in comparison.

3 Results

In this section, the results of the Bayesian optimization applied to the flow-control strategy (with different objectives) for the two angles of attack (5 and 11$^\circ$) are presented. All results reported as line plots share a unique color coding: Black solid line, blue solid line, green solid line, and purple solid line colors are used for the no-control (baseline), ideal ($\textrm{E}$), realistic with no losses ($\mathrm {E_{power}}$), and realistic with losses ($\mathrm {E_{power, \eta }}$) scenarios, respectively.

3.1 Optimization Convergence and Results

Fig. 5

Evolution of the expected improvement EI acquisition function (left), and the cumulative maximum response value sampled for different objective functions (right) at an 5$^\circ$ (a) and $11^\circ$ (b) AoA. In the plots in (right), solid lines and shaded areas indicate the predicted maxima and their $95\%$ confidence interval extracted from the GP-surrogate; and the dots represent the best sampled value (through a RANS simulation)

Determining convergence in Bayesian optimizations is not straight-forward, as with other black-box optimization methods. The convergence rate depends on the chosen acquisition function and its hyperparameter (in this case $\xi$), and the initial random samples for design parameters ${\textbf{q}}$ may also have an impact. Unlike gradient-descent based methods, the path towards finding a global optima can be far from smooth. Thus, conventional convergence measures such as the distance between two consecutively tested samples, in input or response spaces, should not be used as a stopping criterion, especially when dealing with high-dimensional problems like the one at hand. Nevertheless, as shown in Fig. 5, Bayesian optimizations do converge, and their convergence can be tracked using alternative metrics. The evolution of the maximum of the expected improvement function (which determines the next sampling point), is a suitable choice, as it would be logical for the EI to decrease as the optimization progresses. Although this is supported by our findings (shown in the left plots of Fig. 5), the path and rate of decrease are far from smooth or trivial. Moreover, establishing a well-defined EI threshold at which to stop the optimization progress is not general or robust which, combined with the aforementioned issue, makes tracking the EI evolution far from an ideal metric (at least in isolation). A second, and more promising, convergence metric consists of tracking the maximum of the response, and stopping the optimization once its value is seen to be stable or even unchanged over a large number of iterations that is determined in practice by the available computational budget. This can be done in two ways, by tracking either the best evaluated value, or the GP-surrogate predicted optima (for which a prediction of its uncertainty can also be tracked as a bonus). Nonetheless, both values should converge given a high-enough number of iterations and a well-selected EI hyperparameter $\xi$ (which does not over-emphasize exploration). The main downside of this method is the fact that the number of iterations with a stabilized best value needed before confidently stopping the optimization process is not known a priori, and an early-stoppage could lead to a suboptimal result. An example of this would be choosing an $n=6$ ( which could be thought of as a high enough value (specially if the problem evaluation is expensive) in the $\mathrm {E_{power}}$ case at 11$^\circ$: the simulation would be stopped at iteration 10, just before an increase in the optimal response from $14.7$ to $18.3\%$ was achieved. Nevertheless, falling into this kind of early stoppage could be avoided by both looking at the value (and trend) of the EI, as well as to the predicted uncertainty at the optimum: if both are high, and not decreasing appropriately, the optimization process should be continued (even though the maximum value may have been stagnant for a while). Therefore, tracking the convergence of a BO is a tricky, but doable, problem, for which a single metric cannot be trusted in isolation. Despite this, one may approach this problem by combining the evolution of the value of the acquisition function, as well as predicted optimum and its uncertainty.

Fig. 6

Best control strategies tested after 50 iterations of the Bayesian optimization for the different cases considered (columns by AoA, and rows by objective function). The length and color intensity of the arrows represent the magnitude of the wall-normal blowing (outward facing, red) or suction (inward facing, blue) applied at the wing’s surface

Fig. 7

Contour plots of the mean (m, left column) and standard deviation (s, right column) of the posterior prediction of the GP surrogate for the optimal set of parameters (${\textbf{q}}_{opt}$) at a 5$^\circ$ AoA. The labels $q_0$ and $q_1$ refer to the first and second nodal points on the suction side of the wing. Black circular markers indicate samples taken during the BO, and the green star is the reported optimum ${\textbf{q}}_{opt}$

Although in the present work all optimization cases are run with the same number of iterations (50), it is clear from Fig. 5 that convergence was achieved much earlier for all cases. Another conclusion that can be drawn together from both the convergence (Fig. 5) and the optimal control actuations found (Fig. 6) is that the number of iterations needed to converge to an optimal solution is directly related to the complexity of the optimization problem. The simplest case considered is the 5$^\circ$ AoA with objective function $r=\textrm{E}$, both from the flow perspective, as it is fully attached, and the objective function perspective, as the aim is just maximizing $\textrm{E}$, without considering the cost of the actuation (which depends non-linearly on the input parameters). In this case, convergence is reached after just a total of 13 iterations, that is in stark contrast with the most complex case for the same AoA where $r=\mathrm {E_{power,\eta }}$, for which a double number of iterations (>20) is needed in order to find the optimum.Apart from having a simpler response function (leading to a smoother response space), the faster convergence is also related to the position in the parameter space of the optimal control strategy $\mathrm {{\textbf{q}}_{opt}}$: The optimum for the $r=\textrm{E}$ case consists of the maximum suction and blowing allowable on the suction and pressure sides of the airfoil, respectively. This positions ${\textbf{q}}_{opt}$ on the boundaries of the admissible space ${\mathbb {Q}}$ as shown in Fig. 7, which simplifies the maxima search process in the BO. In contrast, the optimal control policy when the cost is accounted for ($r=\mathrm {E_{power,\eta }}$) results in a balance between the wall-normal massflows and their associated cost. Moreover, their magnitude is no longer uniform across all parameters, due to the different effect that blowing/suction at different chord-wise locations has on the final cost-adjusted efficiency achieved, introducing an extra degree of complexity into the function, as seen in Figs. 6 and 7. This complexity is reflected as well in the increased predicted uncertainty. Although we do not show the prediction contours for the 11$^\circ$ AoA cases, the same trends and conclusions also hold for them.

Table 1 Aerodynamic properties and power consumption of the baseline and optimal control strategies

The aerodynamic performance of the baseline and controlled cases (best actuations found by the BO for each considered case) are summarized in Table 1, with the responses subject to the optimization ($r({\textbf{q}})$) in bold. In all scenarios, the response function is increased compared to the associated baseline (no-control) cases. The specifics of how and why each of the aerodynamic quantities change are provided in the next section. Regarding the optimization itself, it is interesting to note the importance of the correct choice of the objective function (i.e. the response $r({\textbf{q}})$ in the BO algorithm): By focusing only on the aerodynamic efficiency, significant gains are achieved (28 and 42$\%$), however the cost of such actuations (even though it is computed without taking any losses or efficiencies into account) is the highest among all the optimized cases. In the 5$^\circ$ case, this leads to a reduction in the power efficiency when compared to the baseline, which would render the proposed actuation worthless in a real application. By taking into account the costs already into the response, more interesting and useful optimal actuations in terms of net power savings are achieved. Moreover, if the design efficiencies of the control scheme are known a priori, they can be incorporated into the BO, leading to optimal control policies tailored to the specific system at hand (as demonstrated by the clear differences in the optimal control policies shown in the last two rows of Fig. 6).

3.2 Control Effects on the Flow

Table 2 Breakdown of the drag and power contributions for the baseline and optimal control strategies

As mentioned before, performing a BO on the aerodynamic efficiency yields notable gains. Such gains are due to an increase in lift (around 8$\%$ for both AoAs) and a decrease in drag ($-$16 and $-$23$\%$ for 5 and 11$^\circ$ AoAs, respectively). Focusing on the drag component, its reduction can be fully attributed to a decrease in its pressure component ($c_{D_p}$), as shown in Table 2. In fact, the friction drag ($c_{D_v}$) increases marginally for all optimized cases. This result can be understood by looking at the trends present in all optimized control strategies (shown in Fig. 6): a strong suction is performed on the suction side of the wing for all cases, whereas an equal or lower-magnitude blowing prevails on the pressure side.

Fig. 8

Pressure (left) and friction (right) coefficients for the no-control (baseline) and optimal control strategies.

The effects of such trends on both the pressure and friction coefficients’ distributions is reported in Fig. 8. Similar to what was reported by Atzori et al. (2020, 2021), blowing leads to a decrease in friction, while suction enhances it. Apart from having a larger magnitude, suction applied to the SS has a larger influence on the friction coefficient than the blowing on the PS (per unit magnitude). This, as explained in Atzori et al. (2021), is due to the higher receptivity of adverse-pressure gradient TBLs to the actuation. Moreover, as shown in Figs. 9, 11 and 12, suction on the SS leads to a shift and reduction in the core of the wake, both in terms of the defect velocity and turbulent kinetic energy. As the APG is reduced, the growth of the TBL (i.e. increasing its thickness) is reduced, leading to a more attached flow in the trailing edge region when compared to the baseline cases. In turn, a thinner and less pronounced wake develops which results in a reduced form (pressure) drag. Moreover, as clearly seen in Fig. 9, the wake is shifted down, which is directly associated with an increased circulation ($\Gamma$) around the airfoil, producing a higher lift force. The latter effect is felt as well in the leading edge of the airfoil, and its imprint on the pressure coefficient: a more pronounced suction peak appears (Fig. 8). Hence, the effect of the wall-normal suction on the SS is analogous to increasing the AoA, but without the associated increase in the form drag produced by the increased APG. This also explains the higher gain in efficiency reported for the high-AoA case (11$^\circ$): in the baseline case, the flow detaches at around $x/c=0.85$ but the maintained suction over the SS pushes the point of separation back to $x/c\approx 0.95$, see Fig. 8. For this case, the shift and reduction of the wake is more pronounced (Fig. 9). Furthermore, the level of reduction in the turbulent kinetic energy (TKE) is much higher than in cruise condition, which is also beneficial from a noise-reduction standpoint.

Fig. 9

Streamwise velocity deficit (left) and kinetic energy (right) at half a chord downstream of the airfoil’s trailing edge

3.3 Effect of Control Cost and Efficiencies

Although the same trends are seen for all optimized cases, despite the differences in the objective function used, the introduction of power (and losses) into the evaluated response has a clear effect both on the optimal control strategies (Fig. 6) and the efficiency gains (Tables 1 and 3). As mentioned before, most of the efficiency gain comes from the increase in lift and decrease in drag produced by reducing the APG effects by introducing suction in the SS. It is therefore not surprising that even in those cases in which the cost of the actuation is accounted for in the final efficiency calculation, suction on the SS remains the most relevant feature of the actuation. On the other hand, as blowing on the PS has only a minor drag-reduction benefit (per unit cost of the actuation) and virtually no effect on the lift, the introduction of cost into the efficiency leads to actuations in which blowing is substantially reduced. This results in net-suction policies the cost of which is associated to the consumption of the pump power needed to create the pressure difference. Part of that air can then be further pressurized and blown through the PS in order to reduce friction, and the excess air is dumped out into the free-stream as a jet (i.e. thrust is generated, hence the negative $c_{P_{as}}$ indicating a power gain in Table 2), recovering some of the power consumed at the compression stage.

Apart from the different effect that considering power has on the control applied to each sides of the airfoil, it is interesting to note the differences between the cruise and high-lift configurations: in the former, the suction magnitude on the SS is reduced, especially at the beginning and end of the control region, as seen in Fig. 6. Moreover, when efficiencies and losses in the system are accounted for (bottom row of Fig. 6), the suction magnitude is reduced drastically. This is in stark contrast to what occurs for the high-lift configuration: the magnitude of suction over the SS remains high, even when losses and efficiencies are included in the cost calculation, especially close to the trailing edge. This is directly related to the different physics appearing in each of the cases: while in the cruise configuration the flow remains attached along the entirety of the airfoil, the flow separates in the high-lift configuration. Therefore, the flow-separation delay becomes the main source of aerodynamics improvement in the 11$^\circ$ case, while in the 5$^\circ$ case the main gain comes from just reducing the overall form drag created by the attached flow, which directly translates into reducing the thickness of the TBL (which can be seen as mitigating the overall effect of the APG), something that is far less productive in a cost-adjusted basis when compared to flow-separation control.

Fig. 10

Contours of the percentage gain in power efficiency (with respect to the baseline case) for the 5$^\circ$ (left) and 11$^\circ$ AoAs. The black circle indicates the position of the optimized cases ($r=\mathrm {E_{power,\eta }}$) used to evaluate the power efficiency gain dependence on the efficiency and losses

The effects of losses and turbomachinery efficiencies on power-efficiency gain is illustrated in Fig. 10. Losses are translated into higher pressure requirements at the blowing/suction reservoirs. In this case, only the pump efficiency is considered for turbomachinery efficiencies, since only pressurization occurs in the optimized cases. Fixing the blowing and suction distributions to the optimal $r=\mathrm {E_{power,\eta }}$ control policies shown in the last row of Fig. 6, the gain or loss in power efficiency is computed by varying both $\Delta c_p$. Therefore, it should be noted that the reported contours represent the performance in an off-design condition, where a control policy optimized for a certain $\Delta c_p$ and $\eta _p$ is used in a system with different values. This constitutes a worst-case scenario, as better performances could be achieved by optimizing the control policy for the system’s actual $\Delta c_p$ and $\eta _p$ values.

Valuable conclusions can be drawn from this efficiency map. Applying a successful control strategy to an airfoil in a cruise configuration is highly challenging, as a combination of high efficiencies and low losses is required to achieve a meaningful gain that justifies the design, mounting and operation of control actuators. However, high-lift configurations are an ideal use-case for such control strategies. Even in off-design conditions with low pump efficiencies or high losses, the optimized strategy can produce substantial increases in power efficiency, justifying the expense and added weight of mounting the flow control system. We can therefore conclude that for distributed steady blowing/suction on airplane wings, the main application is during the initial and final phases of a flight, and not during the cruising phase. This realisation is important insofar that technical implementations need to account for the possibility of switching on and off the control actuation, and to ensure that the modified surfaces do not negatively impact the cruise conditions.

For now we have only studied angles of attack that ensure that the bulk of the flow is attached at all times, and studied the effect of control on those conditions. Of course, higher angles of attack would potentially lead to (incipient) separation, and adequate control methods could be designed, potentially based on blowing and suction, to delay the onset of separation. Typically, time-dependent actuation is required in those situations, and would thus not fall within the type of actuations studied in this article.

Finally, it should be noted that the for the present estimation of the gains, the additional weight has not been taken into account, simply as such an estimate is difficult given the unclear engineering implementation.

4 Conclusions

In the present work, we used Bayesian optimization (BO) based on Gaussian process regression (GPR) to optimize a flow-control strategy consisting of wall-normal blowing and suction of air on a NACA 4412 wing profile. We performed 6 different optimizations, considering 3 different response functions (aerodynamic efficiency, and power efficiency with and without considering losses and turbomachinery efficiencies) at two different angles of attack, 5$^\circ$ and 11$^\circ$ corresponding to cruise and high-lift configurations. BO is shown to be a powerful tool for flow-control optimizations, in which the evaluation of the effect of the control actuation on the flow is expensive, as the number of iterations needed to converge towards a global optimum is comparably low, even for complex response functions. Determining a stopping criterion for BO can be challenging, but tracking the acquisition function along with the best values tested and predicted by the GP surrogate (together with their uncertainty) was found to be a suitable convergence metric.

Similar to the results reported by Atzori et al. (2020, 2021) and Fahland et al. (2021), a clear trend towards doing suction on the suction side and blowing on the pressure side of the airfoil is found. The former decreases the form drag either by reducing the thickness of the TBL (and wake) or by delaying the flow-separation point in the SS, which also increases lift; and the latter leads to a reduction in friction. Nevertheless, constant blowing and suction as those tested in the aforementioned works is only optimal when considering the optimization of the aerodynamic efficiency alone. The introduction of an actuation cost penalization into the optimizer yields substantially different optimal control policy profiles (shown in Fig. 6) with a clear impact on the performances, as summarized in Table 3.

Table 3 Summary with the most relevant changes in aerodynamic performance relative to the baseline cases, as well as the contribution of actuation cost to the total drag for the different optimized flow-control actuations

Results from optimizing cases that take into account pressure losses and turbomachinery efficiencies indicate that wall-normal suction or blowing actuations may be only cost-effective when used in high-lift configurations. In order to achieve meaningful improvements in power efficiency at cruise conditions, the actuation system must be very well-designed, with low pressure losses and high efficiencies. In contrast, actuations at high AoAs that delay separation result in robust improvements in power efficiency even when tested at off-design conditions with poor efficiencies and high pressure losses.

Further practical implementations of such blowing/suction mechanisms are suggested to be designed mainly for high-lift configurations, where the predicted gains are much more robust and thus sustainable. For such configurations, future considerations may include changes in wing geometry due to flaps or slats. Another important aspect for future investigation is the transonic flow regime, particularly relevant to potential gains for cruise conditions. Blowing and suction may affect shock waves and their position, leading to more significant gains even at low angle of attacks.

Even though the optimization algorithm shown in this work was working efficiently and reached the global optimum in a low number of iterations, a more in-depth analysis of the potential curse of dimensionality may be interesting. In particular, a comparison with traditional adjoint-based gradient-descent methods, such as those successfully employed in shape optimization, is certainly relevant.

Appendices

Appendix A

In this Appendix, we supplement contours of the streamwise velocity (U) and turbulence kinetic energy (TKE), that are shown for the baseline and BO results for both the 5$^\circ$ (Fig. 11) and 11$^\circ$ (Fig. 12) AoAs. As discussed in the main part of the paper, the main effects of the control for the lower angle of attack are the reduction of the form drag created by the boundary layers, and a marginal reduction of the turbulence intensity in the wake. For the high-lift configuration, Fig. 12, the reduction of separation, and thus the width the wake, becomes the dominant aspect of the control activity. For a more in-depth discussion of the physical effects, please refer to the main part of the article.

Fig. 11

Contours of the streamwise velocity (left) and turbulent kinetic energy, TKE, (right) for optimization cases with different objective functions at a 5$^\circ$ AoA

Fig. 12

Contours of the streamwise velocity (left) and turbulent kinetic energy, TKE, (right) for optimization cases with different objective functions for the high-lift configuration

Appendix B

In this appendix, the effect of the number of control points per surface ($n_{par}$) used to parameterize the control actuation on the results is analyzed. In order to do so, two additional simulations with $n_{par}$ equal to 3 and 7 ran for the 5$^\circ$ AoA case in which the power actuation and system efficiencies were included into the optimization objective ($E_{power,\eta }$).

Table 4 Aerodynamic properties and power consumption of the optimal control strategies with different parametrization of the control surface

As seen in Fig. 14, the optimal control actuation does change depending on the number of points used in the optimization. Nevertheless, the main features reported in the original manuscript are common throughout the different cases: The total blowing on the pressure side is reduced (although in the 7 degree case it is concentrated in 2 regions, instead of being more smoothly distributed), and suction on the suction side is maintained, being more prominent in the region towards the center of the airfoil, and tapering off both at the beginning and end of the control regions. In fact, the pressure and friction distributions of the optimal cases exhibit the same behaviour, as shown in Fig. 13: the suction peak is enhanced (lower minimum $c_p$), leading to an increased lift, while the increase in friction associated to sucking air in the suction side is partially offset by the blowing introduced in the pressure side. Lastly, as shown in Table 4, the aerodynamic performance of the three different cases (i.e. the objective function) is similar for all the cases. In terms of convergence, an increase in the number of parameters used in the optimization leads to a slower rate of convergence (Fig. 15). This result further demonstrates the need of a careful choice of the parametrization, which should allow for some flexibility in the optimization space, while keeping the number of optimized parameters as small as possible. It should be noted that it is a common observation that in optimization in higher dimensions several very similar optima exist, and it can be viewed as a quantification of sensitivity of the optima.

See Fig.

Fig. 13

Pressure (left) and friction (right) coefficients for the no-control (base- line) and optimal control strategies using different $n_{par}$

13

Fig. 14

Optimal control strategies found when 3 (top), 5 (middle) and 7 (bottom) points per side were used to parameterize the control actuation shape. The length and color intensity of the arrows represent the magnitude of the wall-normal blowing (outward facing, red) or suction (inward facing, blue) applied at the wing’s surface

, 14

Fig. 15

Evolution of the expected improvement EI acquisition function (left), and the cumulative maximum response value sampled for different $n_{par}$

and 15.