1 Introduction and literature review

Advancements across manufacturing, transportation, and information technology have pushed modern supply chains to become increasingly intricate. The benefits of these expanded capabilities have resultingly led to the implementation of previously infeasible inventory management policies now demonstrating improved efficiency. Although this undeniably represents growth, there also have been recent instances of inflated supply chain vulnerabilities (Altay & Pal, 2023; Ergun et al., 2023). Major events such as hurricanes, earthquakes, and global pandemics have contributed to the exposure of various forms of risk associated with modern supply chains. From the perspective of inventory policies specifically, we focus on risks directly related to retailers facing disproportionate demand and supply.

In the context of retail inventory management, stockout costs arise when the on-hand inventory cannot satisfy demand. There exist a variety of unforeseen reasons for potential stockout scenarios to occur, and it is crucial to acknowledge the relevant forms of stockout costs when choosing an inventory policy to employ (Anderson et al., 2006; Corsten & Gruen, 2004; Gruen & Corsten, 2002). One obvious example of realizable stockout costs are lost opportunities to generate revenue and losing future customers. Another example could be expedited shipping or offering discounts to fulfill backorders and effectively reducing profit. Although these examples represent sources that can contribute to a retailer’s stockout costs, it should be noted that other forms can also be considered (Çetinkaya & Parlar, 1998a, b, 2002). While the concept of stockout costs can be generalized in terms of penalization for coping with insufficient inventory, the composition of these costs actually depends on the stockout policy (SOP) in place (Nahmias & Olsen, 2015). In this paper, the SOP dictates how excess demand is handled when a stockout scenario is realized. We look to analyze and compare two practical SOPs that represent contrasting approaches.

Specifically, we look to evaluate two opposing SOPs that conflict in terms of how excess demand is handled and resultingly face distinctive stockout cost components. The first policy is referred to as “while supplies last” (WSL). The WSL policy is set to fulfill demand only while inventory is available. This means that if/when the retailer runs out of inventory, they quit accepting orders and begin realizing lost sales and the opportunity cost from not obtaining the excess demand profit. The second policy we consider is called “accepting backorders” (ABO). The ABO policy is capable of satisfying all levels of demand even if a stockout scenario arises. Further, the retailer will continue to accept orders even if the current inventory levels are depleted and utilize an extra production cycle subject to additional costs. Although WSL and ABO face different forms of stockout costs, characterizations of such policies are commonly employed in practice. This motivates the exploration of circumstances that give rise to choosing one of these SOPs over the other.

1.1 The newsvendor setting

We focus on implementation of the WSL and ABO policies and choose to utilize a representative optimization framework found throughout inventory management literature, the newsvendor (NV) setting (Arrow et al., 1951). In the classical NV setting, the retailer (newsvendor) is responsible for determining the quantity of supply to order in preparation for the upcoming period of sales. After ordering and preparing a specifically chosen level of inventory, a stochastic demand for this single product will be realized. Depending on the magnitude of the realized demand, the retailer may or may not be entirely out of inventory. In the case of having insufficient inventory (stockout), the retailer will realize opportunity cost and shortage penalization through lost sales. Conversely, if the retailer has inventory remaining after realizing demand, the excess inventory can be salvaged but typically for a fraction of the initial production cost. Overall, the goal is to determine the optimal single-period order policy that accounts for the costs associated with overage (too much inventory) and underage (too little inventory) outcomes. The classical NV setting described above corresponds to the case where the WSL policy is implemented.

As an extension to the classical NV setting, the recourse NV setting grants the retailer an opportunity to utilize an additional production option. In the case of a stockout, this capability allows the retailer to obtain additional units after realizing demand for the purpose of satisfying order levels that exceed the initial supply. Although this recourse option allows all demand to be satisfied, the recourse supply units may correspond to an increased ordering cost in comparison to the initial ordering cost. Similar to the setting considered in this paper, existing literature provides examples of NV settings incorporating recourse options (Agrawal & Seshadri, 2000; Eeckhoudt et al., 1995; Gallego & Moon, 1993; Khouja, 1996; Vipin & Amit, 2017). Clearly, the ability to fulfill excess demand and obtain additional profit via recourse has the potential to be advantageous over realizing otherwise lost sales. In the context of this paper, the NV settings offering recourse capabilities are directly related to ABO policies. That is, within the category of models with recourse option, we also include the inventory models allowing backorders for a variety of NV settings (Pando et al., 2013; Xu et al., 2017; Zhang et al., 2020).

Given the vast applicability of the NV setting, supplemental models have been thoroughly studied for decades. This has led to books and review articles dedicated to the variety of extensions and proposed future research directions (Choi, 2012; Khouja, 1999; Petruzzi & Dada, 1999; Qin et al., 2011). The standard modeling approach relates to the maximization of expected profit which correspondingly represents a risk-neutral (RN) attitude by the retailer. However, there can be a deviation between this modeling approach and reality in terms of the risk attitude of the retailer (MacCrimmon et al., 1988; Kahn, 1992; Fisher & Raman, 1996; Schweitzer & Cachon, 2000). Existence of such evidence (empirical/experimental) revealing this deviation, a.k.a., newsvendor decision bias, resultingly may necessitate consideration of objectives beyond the traditional expected profit maximization. Hence, the development of more representative modeling approaches beyond RN attitude, such as those capturing risk-averse (RA) preferences, is important.

A particularly popular approach incorporating the RA attitude in the context of optimization models relies on the criterion known as conditional value-at-risk (CVaR) and represents the approach adopted in the current paper (Chen et al., 2009; Chen, 2023; Gotoh & Takano, 2007; Jammernegg & Kischka, 2012; Rockafellar & Uryasev, 2002; Sawik, 2020; Xu & Li, 2010). Other examples of modeling approaches can include expected utility (EU) theory (Eeckhoudt et al., 1995; Horowitz, 1970), loss-aversion (Schweitzer & Cachon, 2000; Wang & Webster, 2009), and mean-variance analysis (MVA) (Choi et al., 2008; Wu et al., 2009). However, these approaches are beyond the scope of the current paper.

As the breadth of risk-based modeling approaches applied to the NV problem has expanded, a comparison among the resulting RN versus RA decisions has also been explored. Moreover, such comparisons lend the ability to assess newsvendor decision bias through analyzing deviations between expected profit maximizing order quantities and order quantities that satisfy optimality for objectives related to RA attitudes (Schweitzer & Cachon, 2000; Wang & Webster, 2009; Katariya et al., 2014; Xinsheng et al., 2015). Nonetheless, the previous work on the topic does not take into account the impact of alternative SOPs on resulting expected profits, CVaR criteria, stockout probabilities, and expected excess inventory encountered by the retailer as potential performance metrics. To the best of our knowledge, the current paper is the first to compare and contrast explicit impacts of WSL and ABO policies on these performance metrics vis-a-vis the retailer’s risk attitude (i.e., RN or RA–as modeled using the CVaR criterion). Additionally, we supplement these analytical findings with a numerical study revealing mean order quantity deviations between risk attitudes (decision bias) as well as the modeling approaches and counterpart optimal solutions that either maintain outperformance (resiliency) or lead to underperformance (sensitivity) when evaluated across all objective function criteria. Our goal is to deliver a complete set of comparative results revealing the advantages and disadvantages of WSL and ABO policies and possibly the optimal SOP while also developing solutions of corresponding NV problems (based on the CVaR criterion) that have not been studied previously.

1.2 Contributions

In terms of the NV problems based-on CVaR criterion, we consider two specific loss functions directly relating to objective functions of the resulting optimization formulations. Namely, we consider total cost (TC) as represented by the sum of overage and underage cost components as well as net loss (NL) as represented by a negated profit function. Hence, TC and NL symbolize risks directly associated with costs increasing and profit decreasing, respectively.

In order to deliver the comparative results of interest, we build on the existing literature and consider the following six problems:

  • RN retailer problems with an expected profit objective under WSL and ABO, denoted by RN\(_W\) and RN\(_A\), respectively; and

  • RA retailer problems (as modeled using the CVaR criterion) with the TC loss function under WSL and ABO, denoted by RA-TC\(_W\) and RA-TC\(_A\), respectively; and

  • RA retailer problems (as modeled using the CVaR criterion) with the NL loss function under WSL and ABO, denoted by RA-NL\(_W\) and RA-NL\(_A\), respectively.

Table 1 An evaluation of modeling approaches and relevant problem comparisons for related papers that incorporate the CVaR criterion within NV settings
Full size table

Table 1 provides an overview of the most relevant previous work considering risk attitudes within NV settings as they relate to the comparative analysis presented in this paper. Among the six problems of interest noted in the table, the current paper is the first to develop the optimal solutions of RA-TC\(_A\) and RA-NL\(_W\). Meanwhile, revisiting the earlier work that considered RN\(_W\), RA-TC\(_W\), RA-NL\(_W\), and RN\(_A\) and adopting a consistent notation for a comparative analysis, the current paper is also the first to compare and contrast the complete set of six problems highlighting the advantages and disadvantages of WSL and ABO policies. Hence, the main contribution of the paper is centered on an insightful comparison of these two SOPs with an eye on the impact of RN and RA attitudes.

We note that among the papers listed in Table 1, our work is most closely related to Gotoh and Takano (2007) and Katariya et al. (2014) which consider the WSL policy only. A modified SOP is considered in Zhang et al. (2020) to model risk aversion via explicit consideration of the NL loss function only. The modified SOP is such that the retailer may choose to satisfy a portion of the backlogged demand at a discounted price; and, hence, it captures both WSL and ABO. However, the parametric setting considered in Zhang et al. (2020) is favorable to ABO policies in the sense that the results assume cost of underage associated with ABO is less than cost of underage associated with WSL. In this paper, we analyze a general parametric setting that reveals overall optimality between WSL or ABO depending on the overall problem dynamics without any restrictions on the relative values of underage and overage costs of the SOPs.

We continue in Sect. 2 by introducing the basic notation and key modeling fundamentals of the NV setting while incorporating both the WSL and ABO policies. In Sect. 3, we consider the case of a RN retailer and solve the associated profit maximization problems (RN\(_W\) and RN\(_A\)). We follow up with a comparative analysis to determine the particular instances such that one policy outperforms the other. Next, in Sect. 4, we present the mathematical formulations of Problems RA-TC\(_W\), RA-TC\(_A\), RA-NL\(_W\), and RA-NL\(_A\) to consider the CVaR criterion for two relevant loss functions (TC and NL). In doing so, we eventually provide closed-form optimal solutions of the underlying problems and explore potential analytical comparisons. Finally, in Sect. 5, we demonstrate numerical implementation for all derivations with goals of (i) highlighting particular modeling approaches (RN, RA-TC, or RA-NL) that either maintain outperformance (resiliency) or yield underperformance (sensitivity) when the optimal SOP is evaluated across all three objective functions, (ii) evaluate existing decision bias generalizations between the two modeling approaches involving CVaR criterion and (iii) validate analytical results presented in the previous sections for a variety of representative demand probability distributions and parameter values.

2 Newsvendor with SOPs

We now look to establish the basic notationFootnote 1 used in the remainder of the paper.

We let c denote the initial ordering cost per unit and p denote the selling price per unit. Also, we define v, s, and r as the salvage value per unit, shortage penalty per unit, and recourse production cost per unit, respectively. The ordering cost per unit c is faced by the retailer at the beginning of the period before the upcoming demand is known whereas the recourse production cost r is associated with having to obtain additional units through the recourse option (if pursued) after demand is realized. We assume \(0< v< c < \min \{p,r\},~s > 0\) so that cost/profit parameters make practical sense and trivial cases are avoided.

At the initialization of the planning period, the retailer orders q units of inventory for the purpose of satisfying the upcoming unrealized random demand of X units (with distribution and density functions \(F_X(\cdot )\) and \(f_X(\cdot )\), respectively, and an inverse distribution function \(F_X^{-1}(\cdot )\)) and adopts either the WSL or ABO policy. We note that the WSL and ABO policies differ only in the instances relating to underages and that overages lead to identical salvage opportunities. Altogether, the temporal structure of the setting under consideration can be enumerated:

  1. 1.

    The retailer places an order for q units at a cost of \(c\cdot q\) in preparation for the upcoming single-period of demand.

  2. 2.

    With a chosen stockout policy in place and q units of available inventory, the random demand, X, is realized. In return, the retailer will face costs relating to either an overage or underage.

  3. 3.

    If the initial order quantity results in an overage \((q>X)\), then the retailer can then salvage all excess units to obtain \(v\cdot (q-X)\) regardless of the SOP in place.

  4. 4.

    If the initial order quantity leads to an underage \((q<X)\), the resulting course of action depends on the SOP in place.

    1. (i)

      For WSL, the retailer realizes shortage penalty proportional to the excess demand, \(s\cdot (X-q)\).

    2. (ii)

      For ABO, the retailer utilizes the recourse option and has additional units produced at cost \(r\cdot (X-q)\).

Going forward, we use subscripts \(i=W\) and \(i=A\) to correspond to the WSL and ABO policies, respectively. Now, letting \(\Pi _i\) denote the profit function under policy \(i\in \{W,A\}\) gives

$$\begin{aligned} \Pi _W(q,X)= {\left\{ \begin{array}{ll} pX - cq + v(q-X) &{}, \text { if } X \le q, \quad \quad \quad \quad \quad (\text {Overage-WSL}) \\ pq - cq - s(X-q) &{}, \text { if } X > q,\quad \quad \quad \quad \quad (\text {Underage-WSL}) \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} \Pi _A(q,X) = {\left\{ \begin{array}{ll} pX - cq + v(q-X) &{}, \text { if } X \le q, \quad \quad \quad \quad \quad {(\text {Overage-ABO})}\\ pX - cq - r(X-q) &{}, \text { if } X > q. \quad \quad \quad \quad \quad {\text {(Underage-ABO)}} \end{array}\right. } \end{aligned}$$

As mentioned previously, the policies lead to equivalent profit when an overage is realized. However, the deviation between \(\Pi _W(q,X)\) and \(\Pi _A(q,X)\) is noticeable when comparing the underage instances. Further, in the case of underages, the retailer employing WSL only realizes revenue pq while also facing the shortage penalization s. Conversely, a retailer employing ABO will realize revenue for the entire magnitude of demand (pX) but faces the recourse production cost r for the remaining \((X-q)\) units once inventory levels are depleted.

We look to conceptually simplify the components of the profit functions. Moreover, we can succinctly write each of the profit function expressions (\(\Pi _W(q,X)\) and \(\Pi _A(q,X)\)) in terms of two components: the profit \((\mathcal {P})\) and total costs \((\mathcal {C}_i)\) for policy \(i\in \{W,A\}\). For the profit component, we designate \(\mathcal {P} = p-c\). Let \(\mathcal {C}_i(q,X)\) denote the total cost of ordering q units of inventory subject to random demand X for SOP \(i\in \{W,A\}\). Due to WSL and ABO presenting equivalent overage expressions, we let \(c^o = c-v\) represent the overage cost component applicable to both policies. Conversely, we denote \(c_W^u = p+s-c\) and \(c_A^u = r-c\) as the underage cost components for WSL and ABO, respectively. It then follows that

$$\begin{aligned} \mathcal {C}_i(q,X) = c^o\cdot \max \{q-X,0\} + c^u_i\cdot \max \{X-q,0\}, \quad i\in \{W,A\}, \end{aligned}$$
(3)

and

$$\begin{aligned} \Pi _i(q,X) = \mathcal {P}\cdot X - \mathcal {C}_i(q,X), \quad i\in \{W,A\}. \end{aligned}$$
(4)

Going forward, we present all of the remaining expressions and results in terms of the overage and underage cost components. As intuition and our parametric assumptions suggest, the profit and cost components for both policies are all positive, i.e., \(\mathcal {P}, c^o, c^u_W, c^u_A >0\). With the differing SOPs and their respective cost components in place, we can now turn to establish the RN and RA retailer problems of interest.

3 The RN retailer

Using Eqs. (3) and (4), the expected profit maximization approach representative of RN attitude lead to

figure a

for \(i\in \{W,A\}\).

3.1 Problems RN\(_W\) & RN\(_A\)

Letting \(q_i^{RN}\), \(i\in \{W,A\}\) denote the optimal order quantity associated with Problems (RN\(_W\)) and (RN\(_A\)), it is now straightforward to verify that

$$\begin{aligned} q_{i}^{RN} = F_X^{-1}\Bigg (\frac{c_i^u}{c^o+c_i^u}\Bigg ),\quad i\in \{W,A\}. \end{aligned}$$
(5)

Given the above closed-form expressions \(q_i^{RN}\), next we compare and contrast these quantities and the counterpart expected profit functions \(\mathbb {E}[\Pi _i(q,X)]\), with the goal of analyzing the performances of WSL and ABO policies for a retailer with a RN attitude. Specifically, we evaluate three metrics under the optimal order quantity for policy \(i\in \{W,A\}\) to include the resulting:

  1. (1)

    expected profit (i.e., \(\mathbb {E}[\Pi _i(q_{i}^{RN},X)] \equiv \Pi ^{RN}_i\)),

  2. (2)

    stockout probability (i.e., \(P(X \ge q_{i}^{RN}) \equiv \bar{F}^{RN}_i\)), and

  3. (3)

    expected excess inventory (i.e., \(\max \left\{ 0, E[q_{i}^{RN}-X] \right\} \equiv E^{RN}_i\)).

3.2 Comparison of WSL & ABO for the RN retailer

Our intention here is to evaluate both the WSL and ABO policies in terms of resulting (1) expected profit and inventory-related risk as captured by (2) stockout probability and (3) expected excess inventory. As we have indicated earlier, these are three metrics of interest throughout the paper. Note that all proofs to formal results are located in “Appendix A.2”.

Proposition 1

(Problems (RN\(_W\)) and (RN\(_A\)) Expected Profit Comparison, Fixed q) For any positive fixed order quantity q, the comparison of expected profits under WSL and ABO policies \((\mathbb {E}[\Pi _W(q,X)]\) and \(\mathbb {E}[\Pi _A(q,X)])\) leads to the following result:

  1. (i)

    If \(c_W^u\ge c_A^u\), then \(\mathbb {E}[\Pi _W(q,X)] \le \mathbb {E}[\Pi _A(q,X)]\), \(\forall q\in \mathbb {R}^+\). That is, if the underage cost of the WSL policy exceeds that of ABO, then the latter policy outperforms in terms of the expected profit for any positive order quantity.

  2. (ii)

    If \(c_W^u \le c_A^u\), then \(\mathbb {E}[\Pi _W(q,X)] \ge \mathbb {E}[\Pi _A(q,X)]\), \(\forall q\in \mathbb {R}^+\). That is, if the underage cost of the ABO policy exceeds that of WSL, then the latter policy outperforms in terms of the expected profit for any positive order quantity.

Considering Parts (i) and (ii) of Proposition 1, we have the following observation.

Insight 1

We conclude that the relative values of underage costs of the two policies are the only indicators of the outperforming SOP in terms of the expected profit, regardless of the order quantity q. This is an insightful result because it indicates that the retailer’s decision making power (choice of q) is irrelevant for the preferred SOP.

From Proposition 1 and Insight 1, the expected profit comparison between WSL and ABO for fixed order quantities depend exclusively on the relation of the corresponding underage cost components, \(c^u_W\) and \(c^u_A\). It turns out, the same two cases carry over to the comparison of the optimal quantity magnitudes as well.

Proposition 2

(Problems (RN\(_W\)) and (RN\(_A\)): Optimal Quantity Comparison) For Problems (RN\(_W\)) and (RN\(_A\)), comparison of the optimal order quantities \((q_W^{RN} \text { and }q_A^{RN})\) reveal the following observations:

  1. (i)

    If \(c_W^u\ge c_A^u\), then \(q_W^{RN} \ge q_A^{RN}\), \(\bar{F}^{RN}_W \le \bar{F}^{RN}_A\), and \(E^{RN}_W \ge E^{RN}_A\). That is, if the underage cost of the WSL policy exceeds that of ABO, then the optimal order quantity of the former policy is larger so that the WSL policy leads to a lower stockout risk and a higher expected excess inventory level.

  2. (ii)

    If \(c_W^u\le c_A^u\), then \(q_W^{RN} \le q_A^{RN}\), \(\bar{F}^{RN}_W \ge \bar{F}^{RN}_A\), and \(E^{RN}_W \le E^{RN}_A\). That is, if the underage cost of the ABO policy exceeds that of WSL, then the optimal order quantity of the former policy is larger so that the ABO policy leads to a lower stockout risk and a higher expected excess inventory level.

Proposition 2 evaluates the relative magnitudes of the optimal order quantities \(q_W^{RN}\) and \(q_A^{RN}\). Similar to Proposition 1, the insight entirely depends on the respective underage cost components of WSL versus ABO policies.

Insight 2

Following Proposition 2, the relative values of the underage cost components between WSL and ABO directly indicate which policy \(i\in \{W,A\}\) leads to smaller optimal order quantities, \(q_i^{RN}\), resulting in less expected excess inventory, \(E_i\). However, inventory elimination is at the expense of increased stockout-risk, \(\bar{F}_i\), under the RN attitude.

That is, the relationship between underage costs is the only indicator of the resulting stockout probabilities and expected excess inventory under the counterpart optimal solutions. The next result comes directly as a consequence of both Propositions 1 and 2.

Corollary 1

(Problems (RN\(_W\)) and (RN\(_A\)): Optimal Policy) For Problems (RN\(_W\)) and (RN\(_A\)), trade-offs between the WSL and ABO policies are determined through two cases:

  1. (i)

    If \(c_W^u\ge c_A^u\), then the ABO policy with optimal order quantity \(q_A^{RN}\) outperforms the corresponding WSL policy with optimal order quantity \(q_W^{RN}\) in terms of expected profit, i.e., \(\Pi _W^{RN}\le \Pi _A^{RN}\). Hence, ABO is the overall optimal SOP and leads to smaller optimal order quantities \((q_W^{RN} \ge q_A^{RN})\).

  2. (ii)

    If \(c_W^u\le c_A^u\), then the WSL policy with optimal order quantity \(q_W^{RN}\) outperforms the corresponding ABO policy with optimal order quantity \(q_A^{RN}\) in terms of expected profit, i.e., \(\Pi _W^{RN}\ge \Pi _A^{RN}\). Hence, WSL is the overall optimal SOP and leads to smaller optimal order quantities \((q_W^{RN} \le q_A^{RN})\).

As Corollary 1 states, the underage cost components definitively indicate outperformance among objective function values (expected profit) in the context of Problems (RN\(_W\)) and (RN\(_A\)). Moreover, these comparisons between WSL and ABO will always manifest one policy exhibiting such outperformance over the other.

Table 2 A summary of the analytical implications from the underage cost component relations and resulting performance comparisons between WSL and ABO for the RN Retailer
Full size table

For Propositions 1, 2, and Corollary 1, the results all depend on \(\text {sgn}(c_W^u-c_A^u)\). In Table 2, we are able to summarize these analytical findings as they pertain to Problems (RN\(_W\)) and (RN\(_A\)) through expected profit, stockout probability, and expected excess inventory. Through Table 2, we emphasize the fact that all of the comparative findings and outperformance declarations thus far are simply obtained through evaluating the WSL and ABO underage cost components.

Fig. 1
figure 1

A Demonstrative Comparison of Expected Profit between WSL and ABO Policies across Uniform, Exponential, and Normally Distributed Demand

Full size image

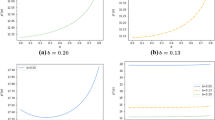
To further support the analytical results summarized in Table 2, Fig. 1 compares the WSL and ABO expected profits as functions of order quantity. In Fig. 1(a), WSL faces higher underage costs in comparison to ABO (6 versus 4) whereas in Fig. 1(b), WSL has lower underage costs relative to ABO (8 versus 10). For the uniform (left), exponential (middle), and normal (right) demand distributions all having a mean of 50, it is indicative that Propositions 1, 2, and Corollary 1 hold true. Additionally, Fig. 1 demonstrates the demand distribution clearly having an effect on the profit levels as well as the gap between the respective optimal order quantities. We now look to further evaluate an example contained in Fig. 1 and quantify the differences between the policies.

Example 1

Assume that demand follows a uniform distribution over the interval [0, 100], i.e. \(X\sim Unif(0,100)\). Further, we reconsider the parameter set and demand distribution used to generate the left plot of Fig. 1(a) with \(p=13\), \(c=8\), \(v=2\), \(s=1\), and \(r=12\). This leads to \(q_W^{RN}=50\) and \(q_A^{RN} = 40\) following Eq. (5) for \(i\in \{W,A\}\). Evaluating the expected profits, we calculate \(\mathbb {E}[\Pi _W(q_W^{RN},X)] = 100\) and \(\mathbb {E}[\Pi _A(q_A^{RN},X)] = 130\) from the objective function of Problems (RN\(_W\)) and (RN\(_A\)). In this simple example, the benefit of choosing the optimal policy (in this case ABO) can lead to a \(30\%\) increase in expected profit while requiring an an initial order quantity that is \(20\%\) less than WSL. This margin of improvement derived from choosing ABO in terms of both expected profit and expected excess inventory portray the potential value in evaluating plausible SOPs.

Although Example 1 motivates and quantifies the value in considering opposing SOPs, it must be mentioned again that the typical profit maximization approach (representative of a RN attitude) does not necessarily represent a retailer’s risk attitude in practice. With that said, there is a need to explore the same comparisons but for RA attitudes that better align with reality.

4 The RA retailer

The RA retailer looks to hedge against outcomes involving significant losses. Rather than the approach involving straight-forward computation of expected profit, risk aversion brings forth a variety of criteria that incorporate objectives beyond expected profit. For a review of NV settings that capture RA attitudes and associated modeling approaches, we refer to Choi (2012), Eeckhoudt et al. (1995), Jammernegg and Kischka (2012), Qin et al. (2011). As mentioned previously, we look to compare WSL and ABO policies through modeling approaches involving the CVaR criterion. In Sect. 4.1 we provide a mathematical introduction to the CVaR criterion as it pertains to the NV setting. In Sect. 4.2 we define the TC and NL loss functions before introducing the four resulting RA retailer problems of interest; RA-TC\(_W\), RA-TC\(_A\), RA-NL\(_W\), and RA-NL\(_A\). In Sects. 4.3 and 4.4, we provide the closed-form solutions to our four RA retailer problems before conducting analytical comparison of the optimal solutions and relative performances in Sect. 4.5.

4.1 The CVaR criterion in a NV setting

For a NV setting incorporating the CVaR criterion, a retailer considers a particular loss function characterized by a random variable and is tasked with minimizing conditional expectation for the corresponding upper tail of the loss distribution. Following (Gotoh & Takano, 2007; Katariya et al., 2014; Rockafellar & Uryasev, 2002), we consider a loss function, \(\mathcal {L}(q,X)\), which is a random variable for fixed ordering quantity q and random demand X. Then, the corresponding loss distribution function is given as

$$\begin{aligned} \phi (\eta | q):= \mathbb {P}(\mathcal {L}(q,X) \le \eta ). \end{aligned}$$

From Rockafellar and Uryasev (2002), the \(\beta \)-value-at-risk (\(\beta \)-VaR) for \(\beta \in [0,1)\) is defined as

$$\begin{aligned}\alpha _\beta (q):= \inf \{\alpha ~ | ~ \phi (\alpha |q)\ge \beta \} \end{aligned}$$

and specifies that for a given order quantity q, a loss of \(\alpha _\beta (q)\) or more occurs with probability \(1-\beta \). For our RN retailer, \(\beta = 0\) and for the RA retailer, \(\beta \in (0,1)\). Once again following (Rockafellar & Uryasev, 2002), we introduce the upper tail of the loss distribution, referred to as the \(\beta \)-tail distribution, defined as

figure b

Letting \(\mathbb {E}_\beta [\cdot ]\) denote the expectation under the \(\beta \)-tail distribution, \(\Phi _{\beta }\), the CVaR minimization problem of interest is in regards to \(\mathbb {E}_\beta [\mathcal {L}(q,X)]\) and is sometimes referred to as \(\beta \)-conditional value-at-risk \((\beta \text {-CVaR})\) of the loss function \(\mathcal {L}(q,X)\). Additionally, in Rockafellar and Uryasev (2002), it is shown that \(\beta \)-CVaR of the loss \(\mathcal {L}(q,X)\) is approximately equivalent to the conditional expectation of the loss distribution exceeding \(\alpha _\beta (q)\) with fixed q and validates the minimization of \(\beta \)-CVaR through a simpler corresponding auxiliary function given as

$$\begin{aligned} Z(q,\alpha ):= \alpha + \frac{1}{1-\beta }\int _0^\infty [\mathcal {L}(q,X) - \alpha ]^+ f_X(x)dx, \quad \text { where } ~[t]^+ = \max \{0,t\}. \end{aligned}$$
(7)

Resultingly, minimizing \(Z(q,\alpha )\) in terms of \(q\in \mathbb {R}^+\) and \(\alpha \in \mathbb {R}\) simultaneously is representative of our RA retailer problems of interest. Therefore, we look to incorporate the CVaR criterion for our NV setting and turn to the direct implementation of WSL and ABO policies within the auxiliary function from Eq. (7). Figure 2 provides an illustration supporting our introduction of the CVaR criterion as it applies to the NV setting.

Fig. 2
figure 2

A Visual Demonstration of the CVaR Criterion as it pertains to the \(\beta \)-tail Distribution for a Loss Function \(\mathcal {L}(q,X)\)

Full size image

4.2 Loss functions and the RA retailer problems

We turn to utilize the CVaR criterion across two practical loss functions: TC and NL (Gotoh & Takano, 2007; Katariya et al., 2014). The basic distinction between these are that NL simply represents the negated profit function whereas TC is solely related to the underage and overage cost components without inclusion of a profit component. Referring to the profit function Expression (4), the NL and TC loss functions denoted \(\mathcal {L}_i^{NL}(q,X)\) and \(\mathcal {L}_i^{TC}(q,X)\) for SOP \(i\in \{W,A\}\), respectively are

$$\begin{aligned} \mathcal {L}_i^{NL}(q,X):= -\mathcal {P}\cdot X + \mathcal {C}_i(q,X), \quad i\in \{W,A\}, \end{aligned}$$
(8)

and

$$\begin{aligned} \mathcal {L}_i^{TC}(q,X):= \mathcal {C}_i(q,X), \quad i\in \{W,A\}. \end{aligned}$$
(9)

Notice that Eq. (9) represents a special case of Eq. (8) \((\mathcal {P}=0)\). From Rockafellar and Uryasev (2002) and the parametric assumptions in our NV setting, we ensure convexity of \(Z(q,\alpha )\) in Equation (7) for both loss functions \(\mathcal {L}_i^{NL}(q,X)\) and \(\mathcal {L}_i^{TC}(q,X)\), \(i\in \{W,A\}\), and we can turn to utilizing the CVaR criterion for representing RA retailers across WSL and ABO. More specifically, we look to address all four problems

figure c
figure d

Our aim is to provide closed-form optimal solutions denoted \((q_i^{TC},\alpha _i^{TC})\) and \((q_i^{NL},\alpha _i^{NL})\) for each policy \(i\in \{W,A\}\). This will then allow a transition into directly comparing WSL and ABO as was done for the RN retailer in Sect. 3.2. Although our main focus is not in terms of directly comparing optimal solutions across the TC and NL loss functions, we refer to Gotoh and Takano (2007), Katariya et al. (2014) for results pertaining to this.

4.3 Problems RA-TC\(_W\) & RA-TC\(_A\)

We now turn our focus to Problems (RA-TC\(_W\)) and (RA-TC\(_A\)). As was the case for Problems (RN\(_W\)) and (RN\(_A\)), we are able to solve these problems in a general sense that encompasses both WSL and ABO policies simultaneously.

Proposition 3

(Problems (RA-TC\(_W\)) and (RA-TC\(_A\)): Optimal Solutions) For \(\beta \in [0,1)\) and \(i\in \{W,A\}\), the optimal solutions \((q_i^{TC},\alpha _i^{TC})\) to Problems (RA-TC\(_W\)) and (RA-TC\(_A\)) are

$$\begin{aligned} q_i^{TC}&= \Bigg (\frac{c^o}{c^o+c^u_i}\Bigg )\cdot F^{-1}_X\Bigg (\frac{c^u_i(1-\beta )}{c^o+c^u_i}\Bigg )+\Bigg (\frac{c^u_i}{c^o+c^u_i}\Bigg )\cdot F^{-1}_X\Bigg (\frac{\beta \cdot c^o+c^u_i}{c^o+c^u_i}\Bigg ),\end{aligned}$$
(10)
$$\begin{aligned} \alpha _i^{TC}&= \Bigg (\frac{c^o\cdot c^u_i}{c^o+c^u_i}\Bigg )\cdot \Bigg (F^{-1}_X\Bigg (\frac{\beta \cdot c^o+c^u_i}{c^o+c^u_i}\Bigg ) - F^{-1}_X\Bigg (\frac{c^u_i(1-\beta )}{c^o+c^u_i}\Bigg )\Bigg ). \end{aligned}$$
(11)

In particular, when \(\beta =0\), \(q_i^{TC}\) reduces to the corresponding Problem (RN\(_W\)) or (RN\(_A\)) optimal order quantity solution (Eq. (5)).

There exists a particularly unique simplification of the optimal order quantity in Eq. (10) when demand follows a specific distribution family.

Corollary 2

When demand is uniformly distributed (i.e., \(X\sim Unif(a,b)\) for \(a,b\in \mathbb {R}\) and \(a\le b\)), the optimal order quantity for the RA retailer under the CVaR criterion with the TC loss function coincides with the corresponding RN retailer optimal order quantity. In other words, Eq. (10) simplifies to Eq. (5), regardless of the value of \(\beta \) implying \(q_i^{TC} = q_i^{RN}\) for \(i\in \{W,A\}\).

We must note that the closed-form optimal solutions obtained for Problem (RA-TC\(_W\)) (Eqs. (10), (11) with \(i=W\)) are consistent with what is provided in Gotoh and Takano (2007). Next, we look to derive optimal solutions corresponding to Problems (RA-NL\(_W\)) and (RA-NL\(_A\)).

4.4 Problems RA-NL\(_W\) & RA-NL\(_A\)

Turning to Problems (RA-NL\(_W\)) and (RA-NL\(_A\)), we reiterate that the optimal solutions in regards to Problem (RA-NL\(_W\)) continue to be consistent with what is provided in Gotoh and Takano (2007). For the sake of completeness, we still choose to derive the expressions with our chosen notation.

4.4.1 Problem RA-NL\(_W\)

Now, we revisit the optimal pair corresponding to the NL loss function \((q_W^{NL}, \alpha _W^{NL})\) from Gotoh and Takano (2007). This optimal solution is verified by solving Problem (RA-NL\(_W\)) as summarized in the following Proposition.

Proposition 4

(Problem (RA-NL\(_W\)): Optimal Solution) For \(\beta \in [0,1)\), the optimal solution \((q_W^{NL},\alpha _W^{NL})\) to Problem (RA-NL\(_W\)) is

$$\begin{aligned} q_W^{NL}&= \Bigg (\frac{c^o+\mathcal {P}}{c^o+c^u_W}\Bigg )\cdot F^{-1}_X\Bigg (\frac{c^u_W(1-\beta )}{c^o+c^u_W}\Bigg )+\Bigg (\frac{c^u_W-\mathcal {P}}{c^o+c^u_W}\Bigg )\cdot F^{-1}_X\Bigg (\frac{\beta \cdot c^o+c^u_W}{c^o+c^u_W}\Bigg ),\end{aligned}$$
(12)
$$\begin{aligned} \alpha _W^{NL}&= \Bigg (\frac{c^o(c^u_W-\mathcal {P})}{c^o+c^u_W}\Bigg )\cdot F^{-1}_X\Bigg (\frac{\beta \cdot c^o+c^u_W}{c^o+c^u_W}\Bigg ) - \Bigg (\frac{c^u_W(c^o+\mathcal {P})}{c^o+c^u_W}\Bigg )\cdot F^{-1}_X\Bigg (\frac{c^u_W(1-\beta )}{c^o+c^u_W}\Bigg ). \end{aligned}$$
(13)

In particular, when \(\beta =0\), \(q_W^{NL}\) reduces to the corresponding Problem (RN\(_W\)) optimal order quantity solution (Eq. (5) with \(i=W\)).

In the context of WSL, comparing the optimal solution in Eqs. (12), (13) to the optimal solution to Problem (RA-TC\(_W\)) given in Eqs. (10), (11) for \(i=W\), there are recognizable similarities. However, notice that \((q_W^{TC},\alpha _W^{TC})\) is a particular instance of \((q_W^{NL},\alpha _W^{NL})\), as previously mentioned (when \(\mathcal {P}=0\)). Going forward, we must now solve Problem (RA-NL\(_A\)).

4.4.2 Problem RA-NL\(_A\)

In solving Problem (RA-NL\(_A\)), there are distinct parametric cases to consider. Due to potentially varying relationships between the selling price, p, and the recourse production cost, r, the objective function will differ depending on \(\text {sgn}(p-r)\). Resultingly, this yields unique optimal solutions for both parametric cases \(p>r\) and \(p<r\).

Proposition 5

(Problem (RA-NL\(_A\)): Optimal Solution, \(p>r\)) For \(\beta \in [0,1)\), the optimal solution \((q_A^{NL},\alpha _A^{NL})\) to Problem (RA-NL\(_A\)) is given through the following two cases

\(\underline{\textrm{Case 1}: p>r}\)

$$\begin{aligned} q_A^{NL}&= F^{-1}_X\Bigg (\frac{c^u_A(1-\beta )}{c^o+c^u_A}\Bigg ),\end{aligned}$$
(14)
$$\begin{aligned} \alpha _A^{NL}&= (c^u_A-\mathcal {P})\cdot F^{-1}_X\Big (1-\beta \Big ) - c^u_A\cdot F^{-1}_X\Bigg (\frac{c^u_A(1-\beta )}{c^o+c^u_A}\Bigg ). \end{aligned}$$
(15)

In particular, when \(\beta =0\) and for any \(\alpha _A^{NL}\) satisfying \(\alpha _A^{NL}\le -q_A^{NL}\cdot \mathcal {P}\), the solution satisfies optimality and \(q_A^{NL}\) reduces to the corresponding Problem (RN\(_A\)) optimal order quantity solution (Eq. (5) with \(i=A\)).

\(\underline{\textrm{Case 2}: p<r}\)

$$\begin{aligned} q_A^{NL}&= \Bigg (\frac{c^o+\mathcal {P}}{c^o+c^u_A}\Bigg )\cdot F^{-1}_X\Bigg (\frac{c^u_A(1-\beta )}{c^o+c^u_A}\Bigg )+\Bigg (\frac{c^u_A-\mathcal {P}}{c^o+c^u_A}\Bigg )\cdot F^{-1}_X\Bigg (\frac{\beta \cdot c^o+c^u_A}{c^o+c^u_A}\Bigg ), \end{aligned}$$
(16)
$$\begin{aligned} \alpha _A^{NL}&= \Bigg (\frac{c^o(c^u_A-\mathcal {P})}{c^o+c^u_A}\Bigg )\cdot F^{-1}_X\Bigg (\frac{\beta \cdot c^o+c^u_A}{c^o+c^u_A}\Bigg ) - \Bigg (\frac{c^u_A(c^o+\mathcal {P})}{c^o+c^u_A}\Bigg )\cdot F^{-1}_X\Bigg (\frac{c^u_A(1-\beta )}{c^o+c^u_A}\Bigg ). \end{aligned}$$
(17)

In particular, when \(\beta =0\), \(q_A^{NL}\) reduces to the corresponding Problem (RN\(_A\)) optimal order quantity solution (Eq. (5) with \(i=A\)).

For the case of \(p>r\), we easily determine that the optimal quantity given in Eq. (14) will be less than the corresponding optimal solution to Problem (RN\(_A\)), i.e., \(q_A^{NL}\le q_A^{RN}\) when \(p>r\). For the case with \(p<r\), it appears that \((q_A^{NL}, \alpha _A^{NL})\) fits the same general form as \((q_W^{NL}, \alpha _W^{NL})\) from Eqs. (12) and (13). At this point, we have derived all desired optimal solutions and focus on comparison across the policies. Further, for policy \(i\in \{W,A\}\), we evaluate the optimal solutions across the resulting:

  1. (1)

    CVaR under TC (i.e., \(\mathcal {T}_i(q_{i}^{TC},\alpha _i^{TC}) \equiv \mathcal {T}^{TC}_i\)),

  2. (2)

    CVaR under NL (i.e., \(\mathcal {N}_i(q_{i}^{NL},\alpha _i^{NL}) \equiv \mathcal {N}^{NL}_i\)),

  3. (3)

    stockout probabilities (i.e., \(P(X \ge q_{i}^{TC}) \equiv \bar{F}^{TC}_i\) and \(P(X \ge q_{i}^{NL}) \equiv \bar{F}^{NL}_i\)), and

  4. (4)

    expected excess inventory (i.e., \(\max \left\{ 0, E[q_{i}^{TC}-X] \right\} \equiv E^{TC}_i\) and \(\max \left\{ 0, E[q_{i}^{NL}-X] \right\} \equiv E^{NL}_i\)).

4.5 Comparison of WSL & ABO for the RA retailer

Similar to the comparisons in Sect. 3.2, we continue with our analysis between WSL and ABO but in the context of a RA retailer. Our collection of closed-form optimal solutions to Problems (RA-TC\(_W\)), (RA-TC\(_A\)), (RA-NL\(_W\)), and (RA-NL\(_A\)) do lend reasonable analytical evaluations among the corresponding objective function values \((\mathcal {T}\) and \(\mathcal {N})\). Additionally, between WSL and ABO, we are able to assess and compare magnitudes of the optimal order quantities \((q_W^{TC}\) vs. \(q_A^{TC}\) and \(q_W^{NL}\) vs. \(q_A^{NL})\). Consequently, this also leads to insight regarding stockout probabilities \((\bar{F}_W^{TC}\) vs. \(\bar{F}_A^{TC}\) and \(\bar{F}_W^{NL}\) vs. \(\bar{F}_A^{NL})\) as well as expected excess inventory \((E_W^{TC}\) vs. \(E_A^{TC}\) and \(E_W^{NL}\) vs. \(E_A^{NL})\).

Proposition 6

(Problems (RA-TC\(_W\)), (RA-TC\(_A\)), (RA-NL\(_W\)), and (RA-NL\(_A\)) CVaR Comparison, Fixed \((q,\alpha )\)) Let \(\beta \in [0,1)\) and \((q,\alpha )\) be a fixed solution to either Problems (RA-TC\(_W\)) and (RA-TC\(_A\)) or (RA-NL\(_W\)) and (RA-NL\(_A\)). Then, the CVaR comparison between WSL and ABO policies under either TC or NL loss functions \((\mathcal {T}_W(q,\alpha ) \text { vs. } \mathcal {T}_A(q,\alpha ))\) or \((\mathcal {N}_W(q,\alpha ) \text { vs. } \mathcal {N}_A(q,\alpha ))\) leads to the following results:

  1. (i)

    If \(c_W^u\ge c_A^u\), then \(\mathcal {T}_W(q,\alpha ) \ge \mathcal {T}_A(q,\alpha )\) and \(\mathcal {N}_W(q,\alpha ) \ge \mathcal {N}_A(q,\alpha )\), \(\forall q\in \mathbb {R}^+\), \(\alpha \in \mathbb {R}\). That is, if the underage cost of the WSL policy exceeds that of ABO, then the latter policy outperforms in terms of CVaR regardless of the loss function (TC or NL).

  2. (ii)

    If \(c_W^u\le c_A^u\), then \(\mathcal {T}_W(q,\alpha ) \le \mathcal {T}_A(q,\alpha )\) and \(\mathcal {N}_W(q,\alpha ) \le \mathcal {N}_A(q,\alpha )\), \(\forall q\in \mathbb {R}^+\), \(\alpha \in \mathbb {R}\). That is, if the underage cost of the ABO policy exceeds that of WSL, then the latter policy outperforms in terms of CVaR regardless of the loss function (TC or NL).

Notice the analytical results provided in Proposition 6 hold for all parametric cases and determine which policy yields the lower objective function value between Problems (RA-TC\(_W\)) and (RA-TC\(_A\)) or (RA-NL\(_W\)) and (RA-NL\(_A\)) when the solutions are fixed.

Following Parts (i) and (ii) of Propositions 6, we have the following observation.

Insight 3

Analogous to Insight 1, we conclude that the relative values of underage costs of the two policies are the only indicators of the outperforming SOP in terms of CVaR under TC or NL, regardless of the values of the order quantity \(q\in \mathbb {R}^+\) and quantile \(\alpha \in \mathbb {R}\). Therefore, no matter the risk attitude and corresponding modeling approach, the underage costs indicate the retailer’s decision making power is irrelevant for the preferred SOP.

From Proposition 6 and Insight 3, given a solution, the CVaR objective function (under either TC or NL) comparison between WSL and ABO depend exclusively on the relation of the corresponding underage cost components, \(c^u_W\) and \(c^u_A\). Similar to Proposition 2, we find that the relative underage costs carry over to the comparison of optimal order quantity magnitudes as well.

Proposition 7

(Problems (RA-TC\(_W\)), (RA-TC\(_A\)), (RA-NL\(_W\)), and (RA-NL\(_A\)): Optimal Quantity Comparison) For Problems (RA-TC\(_W\)) and (RA-TC\(_A\)) or (RA-NL\(_W\)) and (RA-NL\(_A\)), comparison between the optimal order quantities \((q_W^{TC} \text { and }q_A^{TC})\) or \((q_W^{NL} \text { and }q_A^{NL})\) reveal the following observations:

  1. (i)

    If \(c_W^u\ge c_A^u\), then \(q_W^{j} \ge q_A^{j}\), \(\bar{F}^{j}_W \le \bar{F}^{j}_A\), and \(E^{j}_W \ge E^{j}_A\) for \(j\in \{TC,NL\}\). That is, if the underage cost of the WSL policy exceeds that of ABO, then the optimal order quantity of the WSL policy is larger than the optimal order quantity of the ABO policy. This also leads to lower stockout risk and a higher expected excess inventory level for the WSL policy.

  2. (ii)

    If \(c_W^u\le c_A^u\), then \(q_W^{j} \le q_A^{j}\), \(\bar{F}^{j}_W \ge \bar{F}^{j}_A\), and \(E^{j}_W \le E^{j}_A\) for \(j\in \{TC,NL\}\). That is, if the underage cost of the ABO policy exceeds that of WSL, then the optimal order quantity of the ABO policy is larger than the optimal order quantity of the WSL policy. This also leads to lower stockout risk and a higher expected excess inventory level for the ABO policy.

Proposition 7 addresses relative comparison of optimal quantities, stockout probabilities, and expected excess inventory with takeaways identical to those from Proposition 2, but in the context of Problems (RA-TC\(_W\)) and (RA-TC\(_A\)) or (RA-NL\(_W\)) and (RA-NL\(_A\)) for the RA retailer. Considering Parts i) and ii) of Propositions 2 and 7, we have the following takeaway.

Insight 4

Following Propositions 2 and 7, across all risk attitudes and corresponding modeling approaches that we’ve examined, the underage cost component relations between WSL and ABO solely indicate the policy comparisons among optimal quantities, stockout probabilities, and expected excess inventory.

That is, the relationship between underage costs is the only indicator of the resulting stockout probabilities and expected excess inventory under the counterpart optimal solutions. As was the case for Corollary 1, the next result comes directly as a consequence of both Propositions 6 and 7.

Corollary 3

(Problems (RA-TC\(_W\)), (RA-TC\(_A\)), (RA-NL\(_W\)), and (RA-NL\(_A\)): Optimal Policy) For Problems (RA-TC\(_W\)) and (RA-TC\(_A\)) or (RA-NL\(_W\)) and (RA-NL\(_A\)), trade-offs between the WSL and ABO policies are determined through two cases:

  1. (i)

    If \(c_W^u\ge c_A^u\), then the ABO policy with optimal solution \((q_A^{TC},\alpha _A^{TC})\) or \((q_A^{NL},\alpha _A^{NL})\) outperforms the corresponding WSL policy with optimal solution \((q_W^{TC},\alpha _W^{TC})\) or \((q_W^{NL},\alpha _W^{NL})\), i.e., \(\mathcal {T}^{TC}_W\ge \mathcal {T}^{TC}_A\) or \(\mathcal {N}^{NL}_W\ge \mathcal {N}^{NL}_A\). Hence, ABO is the overall optimal SOP and leads to smaller optimal order quantities \(((q_W^{TC} \ge q_A^{TC})\) or \((q_W^{NL} \ge q_A^{NL}))\).

  2. (ii)

    If \(c_W^u\le c_A^u\), then the WSL policy with optimal solution \((q_W^{TC},\alpha _W^{TC})\) or \((q_W^{NL},\alpha _W^{NL})\) outperforms the corresponding ABO policy with optimal solution \((q_A^{TC},\alpha _A^{TC})\) or \((q_A^{NL},\alpha _A^{NL})\), i.e., \(\mathcal {T}^{TC}_W\le \mathcal {T}^{TC}_A\) or \(\mathcal {N}^{NL}_W\le \mathcal {N}^{NL}_A\). Hence, WSL is the overall optimal SOP and leads to smaller optimal order quantities \(((q_W^{TC} \le q_A^{TC})\) or \((q_W^{NL} \le q_A^{NL}))\).

As Corollary 3 states, the underage cost components definitively indicate outperformance among objective function values (CVaR) in the context of Problems (RA-TC\(_W\)) and (RA-TC\(_A\)) or (RA-NL\(_W\)) and (RA-NL\(_A\)). Similar to the RN retailer, these comparisons between WSL and ABO will always result in one policy exhibiting such outperformance over the other.

Table 3 A Summary of the Analytical Implications from the Underage Cost Component Relations and Resulting Performance Comparisons between WSL and ABO for the RA Retailer
Full size table

For Propositions 6, 7, and Corollary 3, the results all depend on \(\text {sgn}(c_W^u-c_A^u)\). In Table 3, we are able to summarize these analytical findings as they pertain to Problems (RA-TC\(_W\)), (RA-TC\(_A\)), (RA-NL\(_W\)), and (RA-NL\(_A\)) through CVaR, stockout probability, and expected excess inventory.

Insight 5

Following both Corollaries 1 and 3, the relative values of the WSL and ABO underage cost components completely determine the optimal SOP. That is, across all risk attitudes and corresponding modeling approaches explored in this paper, the values of \(c^u_W\) and \(c^u_A\) are sufficient in determining the outperforming SOP as well as the relative stockout and excess inventory risks.

Through Tables 2 and 3 and Insight 5, we again highlight that all of the comparative findings and outperformance declarations are simply obtained through evaluating the WSL and ABO underage cost components. We now turn to numerical implementation of all optimal solutions obtained.

5 Numerical experimentation

We have presented three modeling approaches for choosing the optimal order quantity under the WSL and ABO policies. Namely, we’ve considered Problems (RN\(_W\)), (RA-TC\(_W\)), and (RA-NL\(_W\)) for WSL and Problems (RN\(_A\)), (RA-TC\(_A\)), and (RA-NL\(_A\)) for ABO. From analyzing each problem we’ve discovered that, regardless of the approach, the outperforming policy is revealed by the relative values of the underage cost components (\(c_W^u\) and \(c_A^u\)). That is, as summarized by Insight 5, WSL is the optimal SOP when \(c_W^u\le c_A^u\) whereas ABO is the optimal SOP when \(c_W^u\ge c_A^u\).

For all practical purposes, given a problem instance with fixed parameter values and a known demand distribution, we can determine the optimal SOP by evaluating \(c_W^u\) and \(c_A^u\). Once the optimal SOP has been identified, the next set of fundamental questions are in regards to the tradeoffs between using the RN, TC, or NL modeling approaches to pick the order quantity as described below:

  • Suppose the problem instance is such that ABO is the optimal policy \((c_W^u\ge c_A^u)\). Then, let’s also suppose that we choose to implement the corresponding optimal solution to Problem (RA-TC\(_A\)) \((q_A^{TC}, \alpha _A^{TC})\), i.e., we adopt the RA modeling approach with a TC loss function. This choice introduces unavoidable tradeoffs in terms of the expected profit \((\mathbb {E}[\Pi (q^{TC}_A,X)]:=\Pi _A^{TC})\) and net loss \((\mathcal {N}(q^{TC}_A,\alpha _A^{TC}):=\mathcal {N}_A^{TC})\). In other words, by choosing to implement the optimal solution to Problem (RA-TC\(_A\)), \((q_A^{TC}, \alpha _A^{TC})\), we are inherently deviating from the optimal expected profit maximizer \((q^{RN}_A)\) and the optimal CVaR minimizer under NL \((q^{NL}_A,\alpha _A^{NL})\) for the problem instance at hand. That is, for the above example, while \(\mathcal {T}_A^{TC}\le \mathcal {T}_W^{TC}\) can we additionally verify \(\Pi _A^{TC}\ge \Pi _W^{TC}\) and \(\mathcal {N}_A(q_A^{TC},\alpha _A^{TC})\le \mathcal {N}_W(q_W^{TC},\alpha _W^{TC})\)? Hence, at the core of the numerical results presented in the remainder of the paper are the answers to the following two questions referred as Q1 and and Q2:

    1. Q1

      For a given problem instance with the three alternative order quantity solutions under the optimal SOP, does a particular alternative maintain outperformance across all three objective function criteria? If there exists such an alternative, then we refer to this alternative as resilient.

    2. Q2

      For a given problem instance with the three alternative order quantity solutions under the optimal SOP, does a particular alternative lead to underperformance in terms of the other two alternative objective functions? If there exists such an alternative, then we refer to this alternative as sensitive.

  • Moreover, what can we expect in terms of the order quantity magnitude deviations between the expected profit maximizer \((q^{RN}_A)\) and the optimal CVaR minimizer under TC \((q^{TC}_A)\)? That is, what effect does the RA attitude have on optimal inventory levels in comparison to the RN attitude? Given our results, we synthesize these kind of deviations using a carefully designed numerical study and look to answer the following additional question:

    1. Q3

      For a given SOP and the three alternative order quantity solutions, we define decision bias as the percentage difference between the optimal CVaR minimizing order quantity (under TC or NL) and the expected profit maximizing order quantity. Hence, the last question of interest, referred as Q3, is: What are the generalized decision bias characteristics for CVaR under TC and CVaR under NL?

In addition to validating our analytical findings, we keep Questions 1, 2, and 3 at the heart of our numerical study and look to first produce a resilient/sensitive evaluation of WSL and ABO across each of the three objective function criteria (\(\Pi \), \(\mathcal {T}\), and \(\mathcal {N}\)). Provided that we consider four models ((RA-TC\(_W\)), (RA-TC\(_A\)), (RA-NL\(_W\)), and (RA-NL\(_A\))) with objectives not inline with the RN retailer expected profit maximization, our second aim is to assess decision bias across each of the four RA retailer problems. To compute our notion of decision bias as the percentage deviation between expected profit maximizing order quantities and order quantities that satisfy optimality for objectives related to RA retailer, we utilize

$$\begin{aligned} \mathcal {D}_i^{TC}:= 100\cdot \bigg (\frac{q_i^{TC}-q_i^{RN}}{q_i^{RN}}\bigg )\qquad \text { and }\qquad \mathcal {D}_i^{NL}:= 100\cdot \bigg (\frac{q_i^{NL}-q_i^{RN}}{q_i^{RN}}\bigg ),\quad i\in \{W,A\}.\nonumber \\ \end{aligned}$$
(18)

The experiment setup and results are reported below. Throughout the numerical experimentation, we will consider a total of three demand distributions. We employ uniform \((X\sim Unif(0,200))\), exponential \((X\sim Exp(1/100))\), and normal \((X\sim N(100, 25))\) distributions all with the same mean value of 100. As is noted in Gotoh and Takano (2007), even though product demand intuitively has a non-negative support, we utilize the normal distribution to contribute to the comparison of WSL and ABO performances across demand distributions with contrasting shapes.

In terms of the experiment parameters, we first establish values for those found in the two profit functions (c, p, v, s, and r) from Sect. 2. For these five parameters, we consider a total of eight values each. From there, we impose the same parametric relationships assumed throughout. As an additional restriction, we avoid any instances satisfying \(c_W^u = c_A^u\) as they do not make practical sense.

Table 4 Numerical experiment parameter values and feasible instances
Full size table

Table 4 provides all of the values for each of the parameters considered. We determine that this particular collection of \(8^5\) parameter combinations subject to our parameter relationship assumptions produces 8838 feasible instances. These instances are then separated into three parameter classes denoted P1, P2, and P3. We note that these three parameter classes are mutually exclusive and collectively exhaustive in regards to our NV setting. Additionally, notice that our three classes are sufficient given that a parameter class characterized with assumptions of \(p>r\) and \(c_W^u< c_A^u\) leads to an empty set.

Table 5 The assumptions, total instances, and optimal policy for parameter classes P1, P2, and P3
Full size table

We summarize the parameter classes in Table 5 as well as how many of the 8838 feasible instances are compartmentalized into each of the three classes. We also provide the optimal policy as they correspond to each parameter class. Finally, for the evaluation of optimal solutions corresponding to Problems (RA-TC\(_W\)), (RA-TC\(_A\)), (RA-NL\(_W\)), and (RA-NL\(_A\)), we choose to fix \(\beta \) so that the optimization is in regards to the upper \(10\%\) of the loss distribution \((\beta = 0.9)\).

In order to answer Questions 1 and 2, we provide results that summarize the percentage of instances associated with parameter classes P1, P2, and P3 under each of the three demand distributions such that the following relationships hold: \(\Pi ^j_W > \Pi ^j_A\), \(\Pi ^j_W < \Pi ^j_A\), \(\mathcal {T}^j_W > \mathcal {T}^j_A\), \(\mathcal {T}^j_W < \mathcal {T}^j_A\), \(\mathcal {N}^j_W > \mathcal {N}^j_A\), and \(\mathcal {N}^j_W < \mathcal {N}^j_A\). Recall the usage of superscripts \(j\in \{RN, TC, NL\}\) and subscripts \(i\in \{W,A\}\) indicate which of the six optimal solutions to Problems (RN\(_W\)), (RN\(_A\)), (RA-TC\(_W\)), (RA-TC\(_A\)), (RA-NL\(_W\)), or (RA-NL\(_A\)) is being evaluated at a particular objective function \((\Pi , \mathcal {T}, \text { or }\mathcal {N})\).

For example, we know that under uniform demand and parameter class P1, ABO is the declared optimal SOP (Table 5). However, in Table 6, we find the optimal order quantity solution to Problem (RN\(_A\)) \((q_A^{RN})\) actually leads to net loss that is worse than the optimal order quantity solution corresponding to Problem (RN\(_W\)) \((q_W^{RN})\), i.e., \(\mathcal {N}_A^{RN} > \mathcal {N}_W^{RN}\), for a majority of instances (69.23%). We embolden the cells corresponding to such drastic cases of sensitivity and characterize the alternative as such in the final column. Notice that there do exist particular parameter class and demand distribution combinations where the outperforming policy may not exhibit outperformance over all instances, but does so a majority of the time. We do not embolden these cells as they still suggest favor to the outperforming policy, but we are not able to report the alternative as resilient in the final column as outperformance is not achieved across all objective function criteria for 100% of the instances. The results lead to several takeaways worthy of mentioning.

Table 6 An examination of resiliency and sensitivity of the optimal policy (WSL vs. ABO) in terms of expected profit and CVaR criteria
Full size table

Insight 6

In answering 1, optimal solutions to Problems (RA-TC\(_W\)) and (RA-TC\(_A\)) represent the only alternative that universally maintain resiliency across all three objective function criteria. Moreover, we found that choosing this RA modeling approach with a TC loss function is resilient for 100% of problem instances (WSL in P2, ABO in P1 and P3), regardless of the parameter class or demand distribution.

As mentioned in Insight 6, the RA modeling approach under the TC loss function is resilient in terms of the optimal SOP and is the only alternative to achieve 100% resiliency for every possible parameter class and demand distribution combination (see final column of Table 6). Therefore, based on our results with this modeling approach, the WSL (ABO) policy will maintain outperformance in parameter class P2 (P1 and P3) across all three objective function criteria. It should be noted that the RN modeling approach leads to the same conclusion but only in parameter classes P2 and P3. In parameter class P1, the optimal solutions to Problems (RN\(_W\)) and (RN\(_A\)) led to the optimal policy (ABO) achieving worse net loss than WSL, i.e., \(\mathcal {N}_A^{RN} > \mathcal {N}_W^{RN}\) a majority of instances and for every demand distribution. With that said, it appears that the most significant performance sensitivity is attained from the solutions to Problems (RA-NL\(_W\)) and (RA-NL\(_A\)).

Insight 7

In answering 2, we found mixed results in terms of modeling approaches that impose sensitivity on the optimal SOP. Specifically, optimal solutions to Problems (RA-NL\(_W\)) and (RA-NL\(_A\)) perform moderately well in parameter class P1 and support the optimal SOP for a majority of instances, regardless of the demand distribution. However, in P2 and P3, the RA modeling approach with a NL loss function yields several examples of the optimal SOP producing sensitive results across the other two objective function criteria \((\Pi \text { and }\mathcal {T})\). Additionally, optimal solutions to Problems (RA-NL\(_W\)) and (RA-NL\(_A\)) were the only to not achieve resiliency for any parameter class and demand distribution combination.

Although NL represents a generalization of the corresponding TC loss function (when \(\mathcal {P}=0\)), Insights 6 and 7 indicate that these modeling approaches actually produced sufficiently different resilient/sensitive evaluation results. For example, between \(q_i^{TC}\) and \(q_i^{NL}\) for \(i\in \{W,A\}\), we had four of the nine parameter class and demand distribution combinations yield expected profit output favoring opposing policies. Therefore, just within the RA modeling approaches, whether the RA retailer chooses to incorporate the TC or NL loss function can significantly affect the resulting resiliency/sensitivity.

In order to answer Question 3, we look to report the mean values of \(\mathcal {D}_W^{TC}\), \(\mathcal {D}_A^{TC}\), \(\mathcal {D}_W^{NL}\), and \(\mathcal {D}_A^{NL}\) across parameter classes P1, P2, and P3 under each of the three demand distributions. Following Eq. (18), these evaluations and percentage calculations are in relation to the corresponding SOP expected profit maximizing order quantity given in Eq. (5). The average decision bias output for WSL and ABO is reported for all nine combinations of parameter classes and demand distributions.

Table 7 The mean decision bias (%) evaluation for optimal order quantity solutions to RA retailer problems (RA-TC\(_W\)), (RA-TC\(_A\)), (RA-NL\(_W\)), and (RA-NL\(_A\))
Full size table

From Table 7, we immediately verify Corollary 2 as the order quantity solutions to Problems (RA-TC\(_W\)) and (RA-TC\(_A\)) both coincide with their corresponding RN retailer optimal order quantity (decision bias is zero) when demand is uniformly distributed. Beyond this observation, there do appear to be general relationships in terms of decision bias among the alternative modeling approaches involving the CVaR criterion. Based on the results in Table 7, CVaR under TC reveals non-negative mean decision bias percentages whereas CVaR under NL mostly shows negative mean decision bias. Notice that although there are two positive percentages reported under exponential demand for CVaR under NL (17.66% and 22.03%), these increases represent smaller deviations than the corresponding output for the TC loss function.

Insight 8

In answering 3, optimal order quantity solutions to Problems (RA-TC\(_W\)) and (RA-TC\(_A\)) led to decision bias in the form of relatively larger inventory levels compared to the RN retailer. Conversely, for optimal order quantity solutions to Problems (RA-NL\(_W\)) and (RA-NL\(_A\)), the mean decision bias output reveals a general decrease in inventory levels. Throughout all mean decision bias calculations for CVaR under TC and NL, the extent of these increases and decreases were noticeably dependent on the assumed demand distribution and parameter class.

As impactful as the choice between WSL and ABO can be, the risk attitude and corresponding modeling approach for deriving optimal solutions also prove to sometimes have a significant effect on additional performance evaluations in terms of the resulting resiliency/sensitivity. Regarding decision bias and comparison with the RN retailer order quantities, across both SOPs the RA retailer can generally expect significant increases (decreases) in optimal inventory levels with the TC (NL) loss function. Given these general takeaways of our numerical findings, for all practical purposes, we emphasize the need to evaluate sensitivity, resiliency, and decision bias for carefully estimated parameters and demand information of interest.

6 Conclusion

We expand on the large body of optimization literature that incorporates both risk-neutrality and risk-aversion within the NV setting. We also make a general distinction between the NV settings which do and do not allow recourse production. In turn, this distinction aligns precisely with two common practices for handling stockout scenarios. Utilizing the well-recognized and accommodating NV setting, we implement a setup amenable to the direct comparison between two practically relevant SOPs referred to as the WSL and ABO policies throughout this work. We develop methodology to compute the optimal order quantities and discover the optimal SOP for both RN and RA risk attitudes and counterpart modeling approaches represented by Problems (RN\(_i\)), (RA-TC\(_i\)), and (RA-NL\(_i\)). As the first paper to do so, we provide direct comparison between two opposing stockout policies and evaluate performances for both RN and RA attitudes. In doing so, we employ the CVaR criterion across two loss functions found in existing literature (Gotoh & Takano, 2007; Katariya et al., 2014), but for both WSL and ABO policies. We provide methodological contributions through solving two new CVaR minimization problems as they correspond to the ABO policy and provide a comparative framework amenable to analytical and numerical comparisons.

The findings in this paper lend us the ability to analytically prove that, regardless of the modeling approach or the retailer’s risk attitude, the optimal SOP is dictated by the relative values of the underage cost components between WSL and ABO policies. Further, the relationships between the WSL and ABO order quantities, stockout probabilities, and expected excess inventory are conclusively deduced based on the underage cost components for any risk attitude as well. This qualitative result intrinsically highlights the value in accurately measuring and quantifying underage costs. Needless to say, this finding should not and does not undervalue the fact that each problem considered here ((RN\(_W\)), (RN\(_A\)), (RA-TC\(_W\)), (RA-TC\(_A\)), (RA-NL\(_W\)), and (RA-NL\(_A\))) is representative of a different risk-attitude and/or modeling approach leading to its own unique analytical representation and solution (see Eq. (5) for Problems (RN\(_i\)), Eqs. (10) and (11) for Problems (RA-TC\(_i\)), Eqs. (12) and (13) for Problem (RA-NL\(_W\)), and Eqs. (14)–(17) for (RA-NL\(_A\))). Hence, the quantitative result of each modeling approach is distinct.

While the qualitative result of the overall analysis reveals that the preferred SOP is deduced by a comparison of the relative values of the underage costs, the actual operational policy parameters as dictated by the order quantities (quantitative results) indeed depend on the risk-attitude and modeling approach as revealed by Eqs. (5), (10), (12), (14), and (16). With these findings at hand, we also resort to numerical experimentation to evaluate the three alternative modeling approaches (leading to six unique models) across varying combinations of parameter classes and demand distributions. In doing so, we determine which alternative approaches perform with resiliency or sensitivity when evaluated across expected profit and CVaR objective function criteria. Additionally, we are able to assess the general decision bias characteristics between CVaR under TC and CVaR under NL as they correspond to the RA retailer.

In general, we found that products yielding sufficient profit margins (e.g., high-end durable goods) yield advantageous opportunities for the ABO policy. Conversely, products with relatively lower profit (e.g., single-use non-durable goods) tend to produce favorable performance with the WSL policy. Interestingly, in our numerical experimentation, we found that the RA modeling approaches produced both the most resilient (RA-TC\(_i\)) and sensitive (RA-NL\(_i\)) performances across expected profit and CVaR objective function criteria.

Given the full spectrum of analytical results, the analysis presented here can be replicated for any applicable products, demand information, or parameter data. However, throughout this work, it was assumed that all parameters and demand distributions were known and that all consumers were willing to purchase the backordered item. In reality, measuring or quantifying the relative costs, demand, and consumer preferences can be difficult. As our intention was to provide a general comparison between the two contrasting SOPs, exploration among specific industries and products with appropriate modeling approaches and assumptions should be considered. Further, expanding SOP comparisons and newsvendor decision bias across additional risk-based methodology (e.g., expected utility, loss-aversion, and mean-variance analysis) also represent important directions for related future work.