On the mixed connectivity conjecture of Beineke and Harary

Abstract

The conjecture of Beineke and Harary states that for any two vertices which can be separated by k vertices and l edges for $l\ge 1$ but neither by k vertices and $l-1$ edges nor $k-1$ vertices and l edges there are $k+l$ edge-disjoint paths connecting these two vertices of which $k+1$ are internally disjoint.In this paper we prove this conjecture for $l=2$ and every $k\in \mathbb {N}$.We utilize this result to prove that the conjecture holds for all graphs of treewidth at most 3 and all k and l.

1 Introduction

Connectivity is an extensively studied property of graphs. A well-known Theorem of Menger establishes equality between the vertex connectivity for a given pair of non-adjacent vertices and the maximum number of internally disjoint paths between this pair as well as the edge connectivity for a given pair of vertices and the maximum number of edge-disjoint paths between this pair. There are many variation and extensions of Menger’s Theorem. For example Aharoni and Berger (2008) proved a version of Menger’s Theorem for infinite graphs and Borndörfer and Karbstein (2012) interpreted and proved Menger’s Theorem in hypergraphs. In this paper we focus on a form of connectivity in which vertices and edges may be removed at the same time. One variant of mixed connectivity was considered by Egawa et al. (1991). They prove the following mixed version of Menger’s Theorem: Between two vertices v, w of a graph there are $\lambda$ edge-disjoint unions of k internally disjoint paths if and only if for each set S of $0\le r\le \min \{k-1, |V(G)|-2\}$ vertices the graph $G-S$ contains $\lambda (k-r)$ edge-disjoint v-w paths.

Beineke and Harary (1967) proposed an alternative form of mixed connectivity between pairs of vertices. They call a pair of non-negative integers (k, l) connectivity pair for distinct vertices s and t if they can be separated by removing k vertices and l edges, but neither by k vertices and $l-1$ edges nor $k-1$ vertices and l edges. In the same publication Beineke and Harary claim to have proved a mixed version of Menger’s Theorem: If (k, l) is a connectivity pair for s and t, then there exist $k+l$ edge-disjoint s-t paths k of which are internally disjoint. Mader (1979) pointed out that the proof is erroneous.

More recently, mixed connectivity has been revisited by Erves and Zerovnik (2016), who regard transferrance of mixed connectivity along cartesian graph products and bundles, and Bonnet and Cabello (2021) who regard the parametrized complexity of mixed connectivity.

The main focus of this paper, however, is the conjecture by Beineke and Harary. The most meaningful result on the conjecture to date is due to Enomoto and Kaneko (1994). They first extended the conjecture claiming that it is possible to find $k+1$ internally disjoint paths instead of just k under the additional assumption that $l\ge 1$ and then proved their statement for certain k and l. The exact result is restated as Theorem 5 in Sect. 2.

From our studies the following conjecture originally formulated by Beineke and Harary and extended by Enomoto and Kaneko may hold. In the remainder of this article we refer to the conjecture by the name Beineke-Harary-Conjecture.

Conjecture

(Beineke-Harary-Conjecture) Let G be a graph, $s,t\in V(G)$ distinct vertices and k, l non-negative integers with $l\ge 1$. If (k, l) is a connectivity pair for s and t in G, then there exist $k+l$ edge-disjoint paths, of which $k+1$ are internally disjoint.

Our main contribution is to prove the conjecture for $l=2$ and any $k\in \mathbb {N}$. It is worth noting that for $l=2$ the conjecture has not been proved for any $k>1$. In particular, the result of Enomoto and Kaneko does not apply to these cases and their proof does not appear to have an easy adaption for these cases. The techniques used to prove the conjecture for $l=2$ are novel. The main idea is to start with k internally disjoint paths and then find the missing path by inductively moving through the graph and adjusting the k internally disjoint paths whenever necessary. We observe that our result, together with the result due to Enomoto and Kaneko, cf. Theorem 5, implies that the Beineke-Harary-Conjecture holds for $k=2$ and all $l\in \mathbb {N}$. We then utilize this fact to prove the Beineke-Harary-Conjecture for all graphs that have treewidth at most 3.

Outline. After we state some basic definitions in Sect. 2, we establish some preliminary results on connectivity pairs and the Beineke-Harary-Conjecture in Sect. 3. We present the proof of our main result in the subsequent Sect. 4. Section 5 focuses on proving the conjecture on graphs of small treewidth.

The results of this article are also published in the PhD theses of Johann (2021) and Streicher (2021).

2 Preliminaries

Most of our notation is standard graph terminology as can be found in West (2001). We recall some basic notations in the following. The graphs under consideration may contain parallels but no loops. For a graph G, we refer to the vertex set of the graph G by V(G) and to the edge set by E(G). We denote an edge joining vertices ${u,v\in V(G)}$ by uv. Note that the exact choice of the edge, if parallel edges are present, is not of relevance to any of our proofs. For $U,V\subseteq V(G)$ and $u\in U$ and $v\in V$ we call uv a U-V edge. The set of all U-V edges in E(G) is denoted by E(U, V); instead of $E(\{u\},V)$ and $E(U,\{v\})$ we write E(u, V) and E(U, v). If H is another graph we denote by ${G\cup H}$ the graph with vertex set $V(G)\cup V(H)$ and edge set $E(G)\cup E(H)$, where we assume that equal edges join the same set of endvertices. For a subset of vertices $S\subseteq V(G)$ we denote by G[S] the graph induced by S, that has vertex set S and all edges joining vertices of S. Further, we denote by $G-S$ the graph $G[V(G)\setminus S]$. For a subset ${E^\prime \subseteq E}$ we write $G-E^\prime$ for the graph with vertex set V(G) and edge set ${E\setminus E^\prime }$. To simplify notation we write $G-v$ and $G-e$ instead of $G-\{v\}$ and ${G-\{e\}}$ for ${v\in V(G)}$ and $e\in E(G)$.

A path $P=v_0\ldots v_k$ is a graph with vertex set $\{v_0,\ldots ,v_k\}$ and associated edge set $\{v_iv_{i+1}:i=0,\dots ,k-1\}$, where all vertices are distinct except possibly $v_0$ and $v_k$. If $v_0\ne v_k$ we refer to P as a $v_0$-$v_k$ path. We denote by $v_iPv_j$ with $i \le j$ the subpath $v_iv_{i+1}\ldots v_j$. If $v_i=v_0$ ($v_j=v_k$) for simplicity of notation we also write $Pv_j$ ($v_iP$). Two or more paths are edge-disjoint if no two paths use the same edge. Two or more s-t paths are internally disjoint if they only share the vertices s and t. If $P_1,\dots , P_k$ are internally disjoint s-t paths, we call the graph $\bigcup _{i=1}^k P_i$ an s-t k-skein.

For distinct vertices s and t we say that a set $W\subseteq V(G){\setminus }\{s,t\}$ ($F\subseteq E(G)$) separates s and t in G if s and t are not connected in $G-W$ ($G-F$). In this case we call W (F) an s-t vertex-(edge-)separator. If s and t are non-adjacent, we denote by $\kappa _G(s,t)$ the size of a smallest vertex-separator for s and t, where we omit the subscript G if the graph is clear from context. For a graph G a set W is a vertex-separator if $G-W$ is not connected.

3 Connectivity pairs and foundations of the Beineke–Harary-conjecture

In this section we provide the formal definition for connectivity pairs, recall some basic results on the Beineke–Harary-Conjecture, and establish further basic results on mixed separators and the conjecture.

Definition 1

(Disconnecting pair) Let G be a graph and $S,T\subseteq V(G)$. We call a pair (W, F) with $W\subseteq V(G)\setminus \left( S\cup T\right)$ and $F\subseteq E(G)$ an S-T disconnecting pair if in $G-W - F$ there is no path from a vertex in S to a vertex in T.

We call the number of edges in a disconnecting pair its size, the number of vertices in a disconnecting pair its order and the number of elements $|W|+|F|$ to be its cardinality.

If $S=\{s\}$ or $T=\{t\}$ consists of only one element we omit the set brackets in the notation and also write s-t disconnecting pair.

Beineke and Harary (1967) introduced connectivity pairs. We recall their definition in the following.

Definition 2

(Connectivity Pairs) Let G be a graph and $s,t\in V(G)$ distinct vertices. We call an ordered pair of non-negative integers (k, l) a connectivity pair for s and t in G if

• (i) there exists an s-t disconnecting pair of order k and size l and

• (ii) there is no s-t disconnecting pair of cardinality less than $k+l$ having order at most k and size at most l.

As Property (ii) implies, that there exist k vertices other than s and t and at least l edges, we may replace Property (ii) by

• (ii) there is no s-t disconnecting pair of order k and size $l-1$ or order $k-1$ and size l.

Further, if there are fewer than l edges between s and t, then we can replace Property (ii) by

• (ii) there is no s-t disconnecting pair of order k and size $l-1$

This is true since we may replace any edge in an s-t disconnecting pair by a vertex incident to it unless the edge joins s and t.

The Beineke-Harary-Conjecture is, in some sense, a mixed version of Menger’s Theorem. As we make use of it, we recall three versions of Menger’s Theorem here.

Theorem 1

(Menger’s Theorem) Let s and t be two distinct vertices of a graph G.

• (i) If $st\notin E(G)$, then the minimum number of vertices separating s and t in G is equal to the maximum number of internally disjoint s-t paths.

• (ii) The minimum number of edges separating s and t in G is equal to the maximum number of edge-disjoint s-t paths in G.

• (iii) The minimum cardinality of an s-t disconnecting pair is equal to the maximum number of internally disjoint s-t paths.

Proof

Proofs for the statements (i) and (ii) can be found, for example, in West (2001). The statement (iii) is a direct consequence of (i): Any edge joining s and t induces an s-t path that is internally disjoint to all other s-t paths. Also every edge joining s and t is contained in every s-t disconnecting pair. The statement now follows considering that any edge in an s-t disconnecting pair that does not join s and t can be replaced by one of its endvertices. $\square$

Menger’s Theorem implies the Beineke-Harary-Conjecture for a couple of base cases regarding the integers k and l.

Observation 2

Let $k\ge 0$ and $l\ge 1$ be integers and let s and t be two distinct vertices of a graph G.

• (i) If (k, 0) is a connectivity pair for s and t, then s and t are not adjacent. Further, the minimum number of vertices separating s and t is k and, by Menger’s Theorem, there exist k internally disjoint s-t paths.

• (ii) If (k, 1) is a connectivity pair for s and t, then s and t are $k+1$ vertex-connected in G and hence, by Menger’s Theorem, there are $k+1$ internally disjoint paths between s and t.

• (iii) If (0, l) is a connectivity pair for s and t, then s and t are l edge-connected in G and hence, by Menger’s Theorem, there are l edge-disjoint paths between s and t.

Another rather basic result implies that it suffices to prove the Beineke-Harary-Conjecture for non-adjacent vertices as we see in the following two lemmas.

Lemma 3

Let G be a graph, $s,t\in V(G)$ be two distinct vertices and let k, l be non-negative integers. The pair (k, l) is a connectivity pair for s and t in G if and only if $(k,l-|E(s,t)|)$ is a connectivity pair for s and t in $G-E(s,t)$.

Proof

Any s-t disconnecting pair in G has to contain all edges in E(s, t). Thus, we get a one-to-one correspondence between the s-t disconnecting pairs in G and the ones in $G-E(s,t)$ by mapping a pair (W, F) to the pair $(W,F\setminus E(s,t))$. The desired result follows immediately. $\square$

Lemma 4

Let $\mathcal {G}$ be a class of graphs which is closed under deletion of edges. If the Beineke-Harary-Conjecture holds for all graphs $G\in \mathcal {G}$ and all vertices $s,t\in V(G)$ such that s and t are not adjacent, then the conjecture holds for all graphs $G\in \mathcal {G}$ and all vertices $s,t\in V(G)$.

Proof

Assume the Beineke-Harary-Conjecture holds for all graphs $G^\prime \in \mathcal {G}$ and all vertices $s,t\in V(G^\prime )$ with $|E(s,t)|=0$. Let $G\in \mathcal {G}$ be a graph, $s,t\in V(G)$ distinct vertices with $|E(s,t)|\ge 1$, and let (k, l) be a connectivity pair for s and t in G. By Lemma 3, $(k,l-|E(s,t)|)$ is a connectivity pair for s and t in $G-E(s,t)$. Thus, by assumption there exist $k+l-|E(s,t)|$ edge-disjoint s-t paths of which at least k are internally disjoint in $G-E(s,t)$. Note that we cannot assume that $k+1$ paths are internally disjoint, as $l-|E(s,t)|=0$ is a possibility. Nevertheless, the $k+l-|E(s,t)|$ paths together with the edges in E(s, t) yield $k+l$ edge-disjoint s-t paths of which at least $k+1$ are internally disjoint, as the edges in E(s, t) are internally disjoint to all s-t paths and by assumption $|E(s,t)|\ge 1$. $\square$

Other than these simple observation the only meaningful result on the Beineke-Harary-Conjecture to date is due to Enomoto and Kaneko (1994). Their result implies the correctness for further base cases regarding the integers k and l. We mention one explicit choice as a corollary, as we make use of the statement later on.

Theorem 5

(Enomoto and Kaneko (1994)) Let q, r, k and l be integers with $k\ge 0$ and $l\ge 1$ such that $k+l=q(k+1)+r$, $1\le r\le k+1$, and let s and t be distinct vertices of a graph G. If $q+r>k$ and if (k, l) is a connectivity pair for s and t, then G contains $k+l$ edge-disjoint s-t paths of which $k+1$ are internally disjoint. $\square$

Corollary 6

Let (1, l) be a connectivity pair for two distinct vertices s and t of a graph G, then there are $l+1$ edge-disjoint s-t paths of which two are internally disjoint.

Proof

For $l=1$ the statement holds due to Observation 2. For $l\ge 2$ and $q,r\in \mathbb {N}$ with $1+l = q\cdot 2 + r$ and $1\le r\le 2$ we have $q+r>1$ and by Theorem 5 we get the desired paths. $\square$

Before we turn to the proof of the Beineke-Harary-Conjecture for $l=2$, we discuss an erroneous claim made by Sadeghi and Fan (2019). This serves to illustrate the difficulties when trying to prove Beineke-Harary-Conjecture and further shows why the conjecture does not claim equivalence of the existence of connectivity pairs and paths. The statement by Sadeghi and Fan is the following:

When $V(G)\ge k+l+1$, $k\ge 0$ and $l\ge 1$, a graph G has $k+l$ edge-disjoint paths of which $k+1$ are internally disjoint between any two vertices, if and only if the graph cannot be disconnected by removing k vertices and $l-1$ edges.

In Sadeghi and Fan (2019) for integers $k,l\ge 1$ a graph G with at least $k+l+1$ vertices is called (k, l)-connected if it cannot be disconnected by removing k vertices and $l-1$  edges. The following claim is then made.

$$\begin{aligned}&\text {Let}\; k,l\ge 1 \text {and }\;G \;\text {be a graph with at least} k+l+1~\text {vertices. Then}~G\nonumber \\&\text { is }(k,l)-\text {connected if and only if }G \; \text {is}\; k + 1~\text {vertex-connected and}\\&k+l~\text {edge-connected}.\nonumber \end{aligned}$$

(1)

If G is in fact (k, l)-connected it can readily be observed that it is also $k+1$ vertex-connected and $k+l$ edge-connected. On the other hand G being $k+1$ vertex-connected and $k+l$ edge-connected does not imply (k, l)-connectivity. To see this, consider the two complete graphs $G_1$ and $G_2$ on the vertex sets $\{x_1,x_2,x_3,x_4\}$ and $\{x_1, x_5, x_6, x_7\}$. We construct a graph G by regarding the union of $G_1$ and $G_2$ and additionally adding an edge between vertices $x_5$ and $x_2$. Figure 1 displays the constructed graph. The graph G is 2-vertex-connected and 3-edge-connected, but it is not (1, 2)-connected as the removal of the vertex $x_1$ and the edge $x_2x_5$ disconnects the graph. Thus, the Claim (1) cannot hold. As a corollary of Claim (1), Sadeghi and Fan state the following.

$$\begin{aligned}&\text {Let}\; k\ge 0, l\ge 1, \;\text {and }\;G \;\text {be a graph with} \text {at least }k+l+1~\text {vertices.} \nonumber \\&\text {Then }G \;\text {is}\; (k,l)-\text {connected if and only if it has} k+l \text {edge-disjoint}\\&\text {paths between every pair of vertices of which }k+1 ~\text {paths are }\nonumber \\&\text {internally disjoint}.\nonumber \end{aligned}$$

(2)

As a corollary to Claim (1), Claim (2) cannot be considered proven. We give a counterexample to the claim in Proposition 7.

In the original conjecture by Beineke and Harary (1967) and in the extension due to Enomoto and Kaneko (1994) it is never claimed that the existence of the desired paths is sufficient for (k, l)-connectivity and, in fact, it is not. For the sake of completeness we argue why the existence of the paths in Claim (2) is not sufficient.

Proposition 7

The graph G constructed above contains a separator of one vertex and one edge and between any pair of vertices there exist three edge-disjoint paths of which two are internally disjoint.

Fig. 1

A graph containing a vertex-edge separator, such that between any pair of vertices there exist three edge-disjoint paths of which two are internally disjoint

Proof

Consider the graph G above, that also provided a counterexample to Claim (1), see Fig. 1. The vertex $x_1$ together with the edge $x_5x_2$ disconnects the graph. Now let $v_1,v_2\in V(G)$. If $v_1,v_2\in V(G_i)$ for some $i\in \{1,2\}$, then there are three internally disjoint $v_1$-$v_2$ paths. Otherwise, without loss of generality $v_1\in \{x_2,x_3,x_4\}$ and ${v_2\in \{x_5,x_6,x_7\}}$. Denote by $P_1$ a shortest path from $v_1$ to $x_2$ (This is either a single edge or the path without edges) and by $P_2$ a shortest path from $x_5$ to $v_2$. We define the $v_1$-$v_2$ path $P:=(P_1\cup P_2)+x_2x_5$. Further, let $Q=v_1x_1v_2$. Finally, let $w_1\in \{x_3,x_4\}{\setminus }\{v_1\}$ and $w_2\in \{x_6,x_7\}{\setminus }\{v_2\}$ and define the path $R=v_1w_1x_1w_2v_2$. It is easily verified that P, Q, R are three edge-disjoint $v_1$-$v_2$ paths and P and Q are also internally disjoint. $\square$

The graph in Fig. 1 illustrates two things. On the one hand it shows that we may not hope to prove an equivalence in the fashion of Claim (2). On the other hand it shows that it is not possible to replace the mixed form of connectivity by two separate statements on pure connectivity in the fashion of Claim (1). This is one of the reasons why the Beineke-Harary-Conjecture is not a consequence of Menger’s Theorem and its proof has not been established as of yet. It also suggests that the usual techniques used for proofs of Menger’s Theorem might not transfer to the mixed statement. In the following we use a novel technique for proving the Beineke-Harary-Conjecture for the case that $l=2$. The idea is to keep the desired $k+1$ internally disjoint paths and move from s to t along the remaining path. The statement is then proved by induction.

4 The Beineke–Harary-Conjecture for disconnecting pairs of size 2

Now that we have established some foundations for connectivity pairs and the Beineke-Harary-Conjecture, we turn to the main result of this contribution. We prove that the Beineke–Harary-Conjecture holds for all non-negative integers k if $l=2$.

Theorem 8

Let G be a graph and $s,t\in V(G)$. Further, let (k, 2) be a connectivity pair for s and t. Then, there exist $k+2$ edge-disjoint s-t paths of which $k+1$ are internally disjoint.

Before we begin with the proof, note that the result of Theorem 8 has only been proved for $k=1$. In particular, the result of Enomoto and Kaneko, cf. Theorem 5, basically tackles the conjecture from a different angle: In their statement for $k\ge 2$ and $l=2$, the sum $q+r$ always equals 2, which leads to a large gap between k and $q+r$ for large k.

The idea of the proof of Theorem 8 for vertices $s_1$ and t is to always keep an $s_{1}$-$t$ $(k+1)$-skein and inductively move along some other $s_1$-t path P which is edge-disjoint to the currently regarded $s$-$t$ $(k+1)$-skein. In order to use induction we generalize the claim of Theorem 8.

Theorem 9

Let G be a graph, $s_1,s_2,t\in V(G)$ with $s_1\ne t$. Further, assume that

• (i) there exists an $s_2$-t path in G,

• (ii) there exists an $s_1$-$t$ $(k+1)$-skein in G, and

• (iii) there is no $\{s_1,s_2\}$-t disconnecting pair of cardinality $k+1$ and order at most k in G.

Then, there exist $k+2$ edge-disjoint paths, of which $k+1$ are internally disjoint $s_1$-t paths and one is an $s_2$-t path.

Proof

Let G be a graph, $s_1,s_2,t\in V(G)$ with $s_1\ne t$ satisfying Properties (i) to (iii). We prove the claim by induction on the number of edges $|E(G)|$. If $|E(G)|\le k$, then there cannot be $k+1$ internally disjoint $s_1$-t paths, as $s_1\ne t$. The base case of the induction is thereby represented by all graphs with at most k edges. Thus, from now on we may assume the following.

$$\begin{aligned} \begin{aligned}&Let G^\prime be a\,graph\,with\,|E(G^\prime )|<|E(G)|\,and\,vertices\,s_1^\prime ,\,s_2^\prime ,\,t^\prime \!{\in } V(G^\prime )\,with\\&s_1^\prime \ne \,t^\prime .\, If\,Properties\,(i)\, to\,(iii)\,are\,satisfied\,in\,\,G^\prime ,\,then\,there\, exist\,\,k+2\\&edge-disjoint\,\,paths\,of\,which\,k+1\,are\,internally\,disjoint\, s_1^\prime -t^\prime \,\,paths\,\\&and\,of \,which\,one\,is\,an\,s_2^\prime -t^\prime \, path. \end{aligned} \end{aligned}$$

(3)

We begin by proving the induction step for the case that $s_2$ is contained in an $s_1$-$t$ $(k+1)$-skein and afterwards use this result to prove the induction step for the case that $s_2$ is not contained in such a skein.

Case 1: The vertex $s_2$ is contained in an $s_1$-$t$ $(k+1)$-skein.

If $s_2=t$, then the $k+1$ internally disjoint paths from Property (ii) together with the $s_2$-t path $s_2=t$ form the desired paths. Thus, we may assume that ${s_2\ne t}$. Denote by $P_1,\dots , P_{k+1}$ the $s_1$-t paths of an $s_1$-$t$ $(k+1)$-skein containing $s_2$. Without loss of generality we may assume $s_2\in V(P_{k+1})$. Denote by $s_2^\prime$ the vertex succeeding $s_2$ on $P_{k+1}$, i. e. $P_{k+1}=s_1\dots s_2s_2^\prime \dots t$, cf. Fig. 4. Note that $s_1=s_2$ is not forbidden at this point. We now want to use the induction hypothesis for $G-s_2s_2^\prime$ and the vertices $s_1$, $s_2^\prime$ and t, cf. Fig. 2 a).

Fig. 2

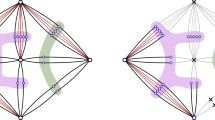
Case 1 in the proof of Theorem 9: Supposed separation of $s_1$ and t. The colored diamonds correspond to elements in (W, F). The dotted lines are mutually internally disjoint. The solid line is a single edge. The colored lines that are not solid indicate a connection of vertices that does not touch colored vertices or edges

Fig. 3

Case 1 in the proof of Theorem 9: Supposed separation of $\{s_1,s_2^\prime \}$ and t. The colored diamonds correspond to elements in (W, F). The dotted lines are mutually internally disjoint. The solid line is a single edge. The colored lines indicate a connection of vertices that does not touch (W, F)

Property (i) is satisfied as $s_2^\prime P_{k+1}$ is an $s_2^\prime$-t path in $G-s_2s_2^\prime$. Suppose that there do not exist $k+1$ internally disjoint $s_1$-t paths in $G-s_2s_2^\prime$. By Menger’s Theorem there is an $s_1$-t disconnecting pair (W, F) of cardinality k. Since in $G-s_2s_2^\prime$ the internally disjoint paths $P_1,\dots , P_k$ still exist, all elements of (W, F) are contained in the paths $P_1,\dots , P_k$, cf. Fig. 2 a). Thus, the path $P_{k+1}s_2$ still exists in $G-s_2s_2^\prime -W-F$ and (W, F) is an $\{s_1,s_2\}$-t disconnecting pair in $G-s_2s_2^\prime$, cf. Fig. 2 b). By assumption $(W, F\cup \{s_2s_2^\prime \})$ is not an $\{s_1,s_2\}$-t disconnecting pair in G and there exists some $\{s_1,s_2\}$-t path in $G-W-F-s_2s_2^\prime$, cf. Fig. 2 c), which yields a contradiction. Hence, Property  (ii) is satisfied in $G-s_2s_2^\prime$ and $s_1,s_2^\prime , t$.

Now suppose there exists an $\{s_1,s_2^\prime \}$-t disconnecting pair (W, F) of cardinality $k+1$ and order at most k in $G-s_2s_2^\prime$. As the paths $P_1,\dots ,P_k,s_2^\prime P_{k+1}$ are internally disjoint, each element of (W, F) is contained in one of these paths, cf. Fig. 3 a). Thus, $P_{k+1}s_2$ still exists in $G-s_2s_2^\prime -W- F$ and neither $s_2$ nor $s_2^\prime$ are contained in the same component as t in $G-s_2s_2^\prime -W -F$. This implies that (W, F) is an $\{s_1,s_2\}$-t disconnecting pair in G, cf. Fig. 3 b). Again this is a contradiction to Property (iii) in G, cf. Fig. 3 c) and hence Property (iii) is satisfied for $G-s_2s_2^\prime$ and $s_1,s_2^\prime , t$.

As $G-s_2s_2^\prime$ contains $|E(G)|-1$ edges, statement (3) is applicable and there exist $k+2$ edge-disjoint paths of which $k+1$ are internally disjoint $s_1$-t paths, say $P_1^\prime ,\dots , P_{k+1}^\prime$, and of which one is an $s_2^\prime$-t path, say $P_{k+2}^\prime$, cf. Fig. 4 b).

If $s_2\in V(P_{k+2}^\prime )$ the paths $P_1^\prime ,\dots , P_{k+1}^\prime , s_2P_{k+2}^\prime$ are the desired paths in G. Otherwise the paths $P_1^\prime ,\dots , P_{k+1}^\prime ,s_2s_2^\prime \cup P_{k+2}^\prime$ form the desired paths, cf. Fig. 4 c).

Thus from now on, in addition to (3), we may assume:

$$\begin{aligned} \begin{aligned}&{Let }\, G^\prime \, be\, a\, graph\, with\, |E(G^\prime )|=|E(G)|\, and\, vertices\, s_1^\prime ,\, s_2^\prime ,\, t^\prime \in V(G^\prime )\, such \\&that\, s_1^\prime \ne t\, and\, s_2^\prime \, is\, contained\, in\, an \,s_1-t (k+1)-skein.If Properties~(i)\\&through~(iii) are satisfied, then there exist k+2 edge-disjoint paths of \\&which k+1 are internally disjoint s_1^\prime -t^\prime paths and of which one is an s_2^\prime -t^\prime path. \end{aligned} \end{aligned}$$

(4)

Case 2: The vertex $s_2$ is not contained in any $s_1$-$t$ $(k+1)$-skein.

Denote by $s_2^\prime$ a vertex on an $s_1$-$t$ $(k+1)$-skein that is closest (with respect to the number of edges) to $s_2$ among all vertices on $s_1$-$t$ $(k+1)$-skeins, cf. Fig. 6. Now we show that the assumptions still hold if we replace $s_2$ by $s_2^\prime$.

Fig. 4

Paths in Case 1 of the proof of Theorem 9. The dotted lines are mutually internally disjoint. The dashed line is edge-disjoint to the dotted lines. The solid line is a single edge not contained in any of the displayed paths. The colored lines form $k+2$ edge-disjoint paths of which $k+1$ are internally disjoint

Fig. 5

Case 2 in the proof of Theorem 9: Supposed separation of $\{s_1,s_2^\prime \}$ and t. The colored diamonds correspond to (W, F). The dotted lines are mutually internally disjoint. The colored lines indicate a connection of vertices that does not touch (W, F)

Observe that Properties (i) and (ii) are satisfied when replacing $s_2$ by $s_2^\prime$. To see that Property (iii) still holds, suppose that there exists an $\{s_1,s_2^\prime \}$-t disconnecting pair (W, F) of cardinality $k+1$ and order at most k. As there cannot be any $s_1$-t path left in $G-W-F$, all elements of the disconnecting pair are contained in some $s_1$-$t$ $(k+1)$-skein, cf. Fig. 5 a). The vertex set W may also not contain $s_2^\prime$ by definition. Thus, the vertices $s_1$, $s_2$ and $s_2^\prime$ are contained in the same component of $G-W-F$, cf. Fig. 5 b). In G, the pair (W, F) cannot be $\{s_1,s_2\}$-t disconnecting by assumption, cf. Fig. 5 c). This contradicts (W, F) being $\{s_1,s_2^\prime \}$-t disconnecting in G and Property (iii) is satisfied.

Fig. 6

Paths in Case 2 of the proof of Theorem 9. The dotted lines are internally disjoint. The dashed lines are edge-disjoint to the dotted lines. The colored lines form $k+2$ edge-disjoint paths of which $k+1$ are internally disjoint

Thus, by (4) there exist $k+2$ edge-disjoint paths, say $P_1,\dots ,P_{k+2}$, such that the paths $P_1,\dots P_{k+1}$ are internally disjoint $s_1$-t paths and $P_{k+2}$ is an $s_2^\prime$-t path, cf. Fig. 6 b). Denote by $P^\prime$ a shortest $s_2$-$s_2^\prime$ path. Note that no element of $P^\prime$, except possibly $s_2^\prime$, is contained in $P_1,\dots ,P_{k+1}$ as no vertex or edge on an $s_1$-$t$ $(k+1)$-skein is closer to $s_2$ than $s_2^\prime$. Further denote by $s^\prime$ the vertex on $P^\prime$ closest to $s_2$ that is also contained in $P_{k+2}$, cf. Fig. 6 c). Then $P^\prime s^\prime \cup s^\prime P_{k+2}$ is an $s_2$-t path that is edge-disjoint to all $P_1,\dots , P_{k+1}$ and we obtain the desired paths. $\square$

Proof of Theorem 8

If s and t are adjacent, then (k, 1) is a connectivity pair in $G-st$ and there exist $k+1$ internally disjoint s-t paths in G by Observation 2 (ii). Together with the deleted edge we get the desired paths in G. So assume that s and t are not adjacent. We show that Properties (i) through (ii) of Theorem 9 hold for G, $s_1=s_2=s$, and t.

By the definition of a connectivity pair, there is no s-t disconnecting pair of cardinality less than $k+2$, order at most k and size at most 2. Thus, by Menger’s Theorem there exist $k+1$ internally disjoint s-t paths and Properties (i) and (ii) are satisfied. Now suppose Property iii is not satisfied and let (W, F) be an s-t disconnecting pair of cardinality $k+1$ and order at most k. As s and t are not adjacent, any edge in F has an endvertex not contained in $\{s,t\}$. Thus, replacing all but one edge in (W, F) with one of its endvertices that is not contained in $\{s,t\}$ we get an s-t disconnecting pair of cardinality at most $k+1$, order at most k, and size 1. Such a pair does not exist, as (k, 2) is a connectivity pair for s and t yielding a contradiction. Thus, the assumptions of Theorem 9 are satisfied and there exist $k+2$ edge-disjoint s-t paths in G of which $k+1$ are internally disjoint. $\square$

Theorem 8 is not only a stand-alone result, but can also be of help when proving the Beineke-Harary-Conjecture for some restricted graph classes. We illustrate this fact by proving the conjecture for graphs with treewidth at most 3 in the next section.

5 The Beineke–Harary-conjecture for graphs with small treewidth

In this section we prove the Beineke-Harary-Conjecture for graphs of treewidth at most 3. To this end we recall the definition of treewidth and some basic results on tree decompositions. For more details, see (Bodlaender, 1998).

For a graph G a tree decomposition $(\mathcal {B},\mathcal {T})$ of G consists of a tree $\mathcal {T}$ and a set $\mathcal {B} = \{B_i :i \in V(\mathcal {T}) \}$ of bags $B_i \subseteq V(G)$ such that $V(G) = \bigcup _{i \in V(\mathcal {T})} B_i$. Further, for each edge ${vw \in E(G)}$ there exists a node $i \in V(\mathcal {T})$ such that $v,w \in B_i$, and if $v \in B_{j_1} \cap B_{j_2}$, then ${v \in B_i}$ for each node i on the simple path connecting $j_1$ and $j_2$ in $\mathcal {T}$. A tree decomposition $(\mathcal {B},\mathcal {T})$ has width k if each bag is of cardinality at most $k+1$ and there exists some bag of size $k+1$. The treewidth of G is the smallest integer k for which there is a width k tree decomposition of G. We write ${\text {tw}}(G) = k$. We call a tree decomposition small if no bag is completely contained in any other bag. Every graph G has a small tree decomposition of width ${\text {tw}}(G)$.

The following result is well known and can, for example, be found in Diestel (2000). We formulate it here as an observation:

Observation 10

Let G be a graph and $(\mathcal {B},\mathcal {T})$ a tree decomposition of G. Further, let $ij\in E(\mathcal {T})$ and denote by $T_i$ and $T_j$ the two subtrees of $\mathcal {T}-ij$ with $i\in V(T_i)$ and $j\in V(T_j)$. If $u\in B_{i^\prime }{\setminus } (B_i\cap B_j)$ for some $i^\prime \in V(T_i)$ and $v\in B_{j^\prime }{\setminus }(B_i\cap B_j)$ for some $j^\prime \in V(T_j)$, then $B_i\cap B_j$ is a separator for u and v in G.

We are now ready to prove the Beineke-Harary-Conjecture for a subclass of graphs of treewidth at most 3.

Lemma 11

Let G be a graph of treewidth at most 3, let $s,t\in V(G)$ be distinct and non-adjacent, and let $k\ge 0$ and $l\ge 1$ be integers. Further, let $(\mathcal {B},\mathcal {T})$ be a tree decomposition of width at most 3 such that for no bag $B\in \mathcal {B}$ we have $s,t\in B$. If (k, l) is a connectivity pair for s and t in G, then there exist $k+l$ edge-disjoint s-t paths of which $k+1$ are internally disjoint.

Proof

Denote by $T_s$ ($T_t$) the subtree of $\mathcal {T}$ induced by all nodes corresponding to bags containing s (t). As $V(T_s)\cap V(T_t)=\emptyset$, there exists an edge $ij\in E(\mathcal {T})$ that separates $V(T_s)$ from $V(T_t)$. Thus, by Observation 10, the set $B_i\cap B_j$ is an s-t vertex-separator in G. We may assume without loss of generality that $B_i\ne B_j$ and therefore get ${|B_i\cap B_j|\le 3}$. The pair (k, l) is a connectivity pair and $l\ge 1$, which implies $k\le 2$. If $l=1$ the result follows from Observation 2 (ii). If $l=2$ the result follows from Theorem 8. Further, if $k=1$ the result follows form Corollary 6. Finally if $l > 2$, $k=2$, and q, r integers such that $2+l=q\cdot 3 +r$ with $1\le r\le 3$, we get that $q+r>2=k$ and the desired result follows from Theorem 5. $\square$

Note that in the proof of Lemma 11, we used our main result, Theorem 8, from the previous section. It is worth noting, that no other result in this paper or another easy argument seems to be able to replace Theorem 8 in the proof of the lemma. In fact, the proof of the theorem was the only piece missing for proving the Beineke-Harary-Conjecture for graphs of treewidth at most 3 for some time.

We observe that the Beineke-Harary-Conjecture holds for graphs of treewidth 1: If for a graph G the underlying simple graph is a tree, either s and t are adjacent or there exists a vertex $a\in V(G)\setminus \{s,t\}$ separating s and t. In both cases the only possible connectivity pairs for s and t are of the form (0, l) for $l\ge 1$ or (1, 0). The conjecture follows from Observation 2.

Observation 12

Let G be a graph of treewidth 1 and vertices $s,t\in V(G)$. Further, let (k, l) be a connectivity pair for s and t in G, with $k\ge 0$ and $l\ge 1$. Then there exist $k+l$ edge-disjoint s-t paths, $k+1$ of which are internally disjoint.

In the next step we prove the conjecture for graphs of treewidth at most 2. Although Theorem 14 is implied by Theorem 15 and the proof could be included into the one of Theorem 15, for better readability, we prove the theorems separately. The structure of the two proofs is similar and therefore the proof of Theorem 14 can be regarded as a warm-up for the one of Theorem 15. The following lemma comes in handy to establish a case distinction in the proofs of the Beineke-Harary-Conjecture for graphs with small treewidth. It allows us to use Lemma 11 in the main proof.

Lemma 13

Let G be a graph of treewidth at most k for some integer $k\ge 1$ and let $s,t\in V(G)$ be distinct and non-adjacent. Assume that every tree decomposition of width at most k has a bag containing s and t. Then, there exists a tree decomposition $D=(\mathcal {B},\mathcal {T})$ of width k, such that there is some $ij\in E(\mathcal {T})$ with $s,t\in B_i\cap B_j$, $|B_i\cap B_j|\le k$ and $G-(B_i\cap B_j)$ not connected. In particular, s and t are contained in a vertex-separator in G containing at most k vertices.

Proof

Let G be a graph of treewidth k and $s,t\in V(G)$ distinct and non-adjacent. Moreover, assume that every tree decomposition of width k has a bag that contains s and t. We claim that in this case every tree decomposition of width k has at least two bags containing s and t.

Suppose that $(\mathcal {B}, \mathcal {T})$ is a tree decomposition of G of treewidth k, such that s and t share exactly one bag $B_i$. Let $j_1,\dots , j_r$ be the neighbors of i in $\mathcal {T}$ whose bags contain s. We construct a new tree decomposition by replacing the node i with two adjacent nodes $i_1$ and $i_2$ with corresponding bags $B_{i_1}=B_i\setminus \{t\}$ and $B_{i_2}=B_i\setminus \{s\}$, making $j_1,\dots , j_r$ adjacent to $i_1$ and making the remaining neighbors of i adjacent to $i_2$. As s and t are not adjacent, the result is in fact a tree decomposition of width at most k, in which no bag contains both s and t. This is a contradiction. Thus, we may assume that every tree decomposition of width at most k has at least two bags containing s and t.

Consider a small tree decomposition $(\mathcal {B},\mathcal {T})$ of width k. By the arguments above we may assume that there is an edge $ij\in E(\mathcal {T})$ such that $s,t\in B_i\cap B_j$. Since $(\mathcal {B},\mathcal {T})$ is a small tree decomposition we have $B_i\nsubseteq B_j$ and $B_j\nsubseteq B_i$. Thus, there is a $u\in B_i\setminus B_j$ and a $v\in B_j{\setminus } B_i$ and by Observation 10 the set $W=B_i\cap B_j$ separates u and v. Since W has at most k vertices, $s,t\in W$ and $G-W$ is disconnected, the lemma follows. $\square$

Theorem 14

Let G be a graph of treewidth at most 2 with distinct vertices $s,t\in V(G)$ and $k\ge 0$ and $l\ge 1$ integers. If (k, l) is a connectivity pair for s and t, then G contains $k+l$ edge-disjoint s-t paths of which $k+1$ are internally disjoint.

Proof

Let G be a graph, $s,t\in V(G)$ be distinct vertices and let (k, l) be a connectivity pair for s and t with $l\ge 1$. If ${\text {tw}}(G)=1$ the result follows from Observation 12. By Lemma 4 we may assume that s and t are not adjacent in G.

We prove the theorem by induction on the number of vertices in V(G). If we have $|V(G)|\le 3$, as s and t are not adjacent, there always exists a tree decomposition of G in which no bag contains both, s and t. The claim follows from Lemma 11. So assume the claim holds for all graphs with less than $|V(G)|$ vertices.

If there exists a tree decomposition of G in which no bag contains both s and t, the claim is again implied by Lemma 11. Otherwise, by Lemma 13, the set $\{s,t\}$ is a vertex-separator in G. Let C be a component of $G-\{s,t\}$ and denote the graph induced by $C\cup \{s,t\}$ by $G_1$. Let $G_2=G - C$. Note that $|V(G_i)|<|V(G)|$ for $i\in \{1,2\}$ and $E(G_1)\cap E(G_2)=\emptyset$. Consider some s-t disconnecting pair (W, F) of order k and size l in G. For $i\in \{1,2\}$, the pair induces an s-t disconnecting pair $(W_i,F_i)$ in $G_i$, with $W_i=W\cap V(G_i)$ and $F_i=F\cap E(G_i)$. Let $k_i=|W_i|$ and $l_i=|F_i|$. Then, $(k_i,l_i)$ is a connectivity pair for s and t in $G_i$. Further, $k_1+k_2=k$, $l_1+l_2=l$ and without loss of generality we may assume $l_2\ge 1$ since $E_G(s,t)\subseteq E(G_2)$. Thus, in $G_1$ there exist $k_1+l_1$ edge-disjoint paths of which $k_1$ are internally disjoint. Note that we cannot assume that there exist $k_1+1$ internally disjoint paths as $l_1$ may equal 0. In $G_2$, by induction, we get $k_2+l_2$ edge-disjoint paths of which $k_2+1$ are internally disjoint. For any two paths $P_1$ in $G_1$ and $P_2$ in $G_2$ it holds that $P_1$ and $P_2$ are internally disjoint in G. Thus, there exist $k_1+k_2+l_1+l_2=k+l$ edge-disjoint s-t paths in G of which $k_1+k_2+1=k+1$ are internally disjoint. $\square$

Finally, we turn to the proof of the Beineke-Harary-Conjecture for graphs of treewidth at most 3. The structure of the proof is very similar to the one in Theorem 14. It is quite possible that this structure also generalizes to graphs with larger treewidth. The main reason why we do not prove the conjecture for graphs of treewidth at most 4 (or even larger) is, that in order for Lemma 11 to hold for this class of graphs, we would have to prove the conjecture for $l=3$ or find another way of proving this. The idea of the proof is to divide the graph at some separator containing s and t and use paths found in the resulting graphs by induction. In contrast to Theorem 14, a separator containing s and t may now also contain a third vertex a. Thus, it is possible that some of the searched path actually cross at this vertex. To address this issue we introduce artificial edges that simulate part of the paths in the other component.

Theorem 15

Let G be a graph of treewidth at most 3. Let $s,t\in V(G)$ be two distinct vertices and $k\ge 0$, $l\ge 1$ integers. If (k, l) is a connectivity pair for s and t, then G contains $k+l$ edge-disjoint s-t paths of which $k+1$ are internally disjoint.

Proof

Let G be a graph, $s,t\in V(G)$ distinct vertices and let (k, l) be a connectivity pair for s and t with $l\ge 1$. If ${\text {tw}}(G)\le 2$ the result follows from Theorem 14. By Lemma 4 we may assume that s and t are not adjacent in G.

As in the proof of Theorem 14, we do the proof by induction on the number of vertices. If $|V(G)|\le 4$, there exists a tree decomposition of G of width 3 in which no bag contains both, s and t, and the claim is implied by Lemma 11. So assume the claim holds for all graphs of treewidth at most 3 and $|V(G)|\le 4$.

If there exists a tree decomposition of G of width 3 in which no bag contains both, s and t, the claim is again implied by Lemma 11. Otherwise, by Lemma 13, there exists a tree decomposition $D=(\mathcal {B},\mathcal {T})$ containing an edge $xy\in \mathcal {T}$ such that for  $B:=B_x\cap B_y$ it holds that $s,t\in B$, $|B|\le 3$, and $G-B$ is not connected. If $B=\{{s,t}\}$ is a vertex-separator, we may simply repeat the arguments in the proof of Theorem 14. So assume there is a vertex $a\in V(G)\setminus \{{s,t}\}$, such that $B=\{{s,t,a}\}$. Let C be a component of $G-B$, denote by $G_1$ the graph induced by $V(C)\cup B$ and let $G_2$ be the graph $G-V(C)-E_G(s,a)-E_G(a,t)$, cf. Fig. 7.

Fig. 7

Case 1 of the proof of Theorem 15: Partitioning the Graph G into $G_1$ and $G_2$ on the left. Defining the graphs $H_1$ and $H_2$ on the right. Colored elements form s-t disconnecting pair. Dotted lines indicate a connection between vertices

Note that $|V(G_i)| < |V(G)|$ for $i\in \{{1,2}\}$. Further, as $B_x\cap B_y=\{{s,t,a}\}$, the two components of $\mathcal {T}-xy$ induce tree decompositions of $G_1$ and $G_2$ and we get ${\text {tw}}(G_1)\le 3$ and ${\text {tw}}(G_2)\le 3$. As the vertices s, t and a are contained in both $B_x$ and $B_y$, adding edges between these vertices in $G_1$ or $G_2$ does not increase the treewidth of the graphs. We distinguish two cases.

Case 1: The vertex a is contained in an s-t disconnecting pair of order k and size l in G.

In $G-a$ the pair $(k-1,l)$ is a connectivity pair for s and t. Let (W, F) be an s-t disconnecting pair of order k and size l with $a\in W$. For $i=1,2$, the pair (W, F) induces an s-t disconnecting pair $(W_i,F_i)$ in $G_i-a$ of order $k_i$ and size $l_i$ such that $k_1+k_2=k-1$ and $l_1+l_2=l$. Without loss of generality we may assume $l_1\ge 1$.

Claim 1

$(k_i,l_i)$ is a connectivity pair for s and t in $G_i-a$.

Proof

Suppose $(k_i,l_i)$ is not a connectivity pair. As $(W_i,F_i)$ is a disconnecting pair of order $k_i$ and size $l_i$ such a pair exists. Thus, there is a disconnecting pair $(W^\prime , F^\prime )$ of order $k^\prime \le k_i$, size $l^\prime \le l_i$ and cardinality $k^\prime +l^\prime <k_i+l_i$, but then $(W^\prime \cup W_j\cup \{a\},F^\prime \cup F_j)$ with $j\in \{1,2\}{\setminus } \{i\}$ is an s-t disconnecting pair in G of order at most k, size at most l and cardinality less than $k+l$ which yields a contradiction. $\square$

Next we show that if $(k_2,l_2)$ is not a connectivity pair for s and t in $G_2$, the desired paths exist. If $(k_2,l_2)$ is in fact not a connectivity pair, then $(k_2, l_2 + p)$ is a connectivity pair for some integer ${p\ge 1}$. By induction we get $k_2+l_2+p$ edge-disjoint s-t paths in $G_2$, $k_2+1$ of which are internally disjoint. As $(k_1, l_1)$ is a connectivity pair in $G_1-a$ again by induction we get $k_1+l_1$ edge-disjoint s-t paths in $G_1-a$ of which $k_1+1$ are internally disjoint (recall that $l_1\ge 1$). Together we get $k_2 + l_2 + p + k_1 + l_1\ge k+l$ edge-disjoint s-t paths in G of which $k_1+1+k_2+1=k+1$ are internally disjoint. Thus, we may assume that $(k_2,l_2)$ is a connectivity pair for s and t in $G_2$.

Now a cannot be contained in any s-t disconnecting pair in $G_2$ of order $k_2$ and size $l_2$, as otherwise $(k_2,l_2)$ would not be a connectivity pair for s and t in $G_2-a$. We fix some s-t disconnecting pair $(W_2^\prime , F_2^\prime )$ in $G_2$ that has order $k_2$ and size $l_2$. As in $G_2-W^\prime _2- F^\prime _2$, the vertex a cannot be connected to both, s and t, without loss of generality we may assume that a is not connected to t. Thus, for the remainder of Case 1 we assume

$$\begin{aligned} \begin{aligned}&(k_2,l_2)\,\, is\,\, a\,\, connectivity\,\, pair \,\,for\,\, s\,\, and\,\, t\,\, in\,\, G_2,\,\, (W_2^\prime , F_2^\prime )\,\, is \,\,an\,\, s-t\,\, discon-\\&necting\,\, pair\,\, \,\,of\,\, order\,\,~k_2\,\, and\,\, size~l_2 \,\,that \,\,does\,\, not\,\, contain\,\, a,\,\, and\,\, the \,\,\\&vertices\,\,a\,\, and\,\, t \,\,are\,\, not \,\,connected \,\,in G_2-W^\prime _2-F^\prime _2. \end{aligned} \end{aligned}$$

(5)

We define $0\le q\le l_1$ to be the unique integer such that ${(k_1+1, l_1-q)}$ is a connectivity pair for s and t in $G_1$. Note that this is well-defined as $(W_1\cup \{a\},F_1)$ is an s-t disconnecting pair of order $k_1+1$ and size $l_1$.

Denote by $H_1$ the graph arising from $G_1$ by adding q parallel edges $e_1,\dots ,e_q$ between a and s, cf. Fig. 7. Then the following holds:

Claim 2

$(k_1+1,l_1)$ is a connectivity pair for s and t in $H_1$.

Proof

As argued before, we have that $(W_1\cup \{a\}, F_1)$ is an s-t disconnecting pair of order $k_1+1$ and size $l_1$ in $G_1$ and thereby also disconnecting in $H_1$. Suppose that there exists an s-t disconnecting pair of order $k_1+1$ and size at most $l_1-1$. Let $(W^{\prime }, F^{\prime })$ be one such pair of minimal size. Suppose that $e_i\in F^{\prime }$ for some $i\in \{1,\dots ,q\}$. As the size of the disconnecting pair is minimal, this implies $e_i\in F^{\prime }$ for all $i\in \{1,\dots ,q\}$. If this is the case $(W^\prime , F^\prime {\setminus }\{e_1,\dots ,e_q\})$ is an s-t disconnecting pair in $G_1$ of order at most $k_1+1$ and size at most $l_1-1-q$ in contradiction to $(k_1+1, l_1-q)$ being a connectivity pair in $G_1$. Thus, either $a\in W^\prime$ or a and s are contained in the same component of $H_1-W^\prime -F^\prime$. In particular, there is no a-t path in $G_1-W^\prime -F^\prime$. But then $(W^\prime \cup W_2^\prime , F^\prime \cup F_2^\prime )$ is an s-t disconnecting pair in G of order at most k and size at most $l-1$ by (5). This contradicts (k, l) being a connectivity pair for s and t in G. $\square$

Next, denote by $H_2$ the graph arising from $G_2$ by adding q parallel edges $f_1,\dots , f_q$ between a and t, cf. Fig. 7. We prove the following:

Claim 3

$(k_2,l_2+q)$ is a connectivity pair for s and t in $H_2$.

Proof

If $q=0$ the statement holds by (5), so assume that $q\ge 1$. The pair $(W_2^\prime ,F_2^\prime \cup \{f_1,\dots ,f_q\})$ is an s-t disconnecting pair in $H_2$ and a and t are not in the same component in $H_2-W_2'-F_2'\cup \{f_1,\ldots ,f_q\}$. So suppose there exists an s-t disconnecting pair of order $k_2$ and size $l_2+q-1$. Let $(W^\prime , F^\prime )$ be one such pair of minimal size. With the same arguments as in the previous claim we get that $f_i\notin F^\prime$ for all $i\in \{1,\dots ,q\}$. Thus, $a\in W^\prime$ or a and t are in the same component in $H_2-W^\prime -F^\prime$. In particular, there is no s-a path in $G_2-W^\prime -F^\prime$. As $(k_1+1,l_1-q)$ is a connectivity pair for $G_1$, there exists an s-t disconnecting pair $(W_1^\prime , F_1^\prime )$ in $G_1$ of order $k_1+1$ and size $l_1-q$. Suppose there exists an s-a path in $G_1-W_1^\prime -F_1^\prime$. Then, there is no a-t path and $(W_1^\prime \cup W_2^\prime , F_1^\prime \cup F_2^\prime )$ is an s-t disconnecting pair in G of order k and size $l_2 + l_1 - q < l$ by (5) — a contradiction. On the other hand if there does not exist an s-a path in $G_1-W_1^\prime - F_1^\prime$, then the pair $(W_1^\prime \cup W^\prime , F_1^\prime \cup F^\prime )$ is s-t disconnecting in G and of order k and size $l-1$, which again yields a contradiction. $\square$

Fig. 8

Case 1 of the proof of Theorem 15: s-t paths in $H_1$ and $H_2$ given by induction on the left. Creation of desired s-t paths in G on the right. Colored dotted lines indicate internally disjoint s-t paths. Dashed line indicates an s-t path that is edge-disjoint to all other indicated paths. Solid lines are single edges

Note that for $i\in \{{1,2}\}$ it is $V(H_i)=V(G_i)< V(G)$ and ${\text {tw}}(H_i)\le 3$ as ${\text {tw}}(G_i)\le 3$ and we only added edges between s and a, respectively a and t to get to $H_i$ from $G_i$. By Claim 2 and the induction hypothesis there are $k_1+1+l_1$ edge-disjoint s-t paths in $H_1$, say $P_1,\dots , P_{k_1+l_1+1}$, of which $k_1+2$ are internally disjoint, cf. Fig. 8. Without loss of generality let $P_1,\dots ,P_{r_1}$ be the paths using edges from $\{e_1,\dots , e_q\}$, where from these we denote by $P_1$ the path that is among the $k_1+2$ internally disjoint paths, if one such path exists. If $q=l_2=0$, then $(k_2,0)$ is a connectivity pair for s and t in $G_2-a$ by Claim 1, and by Observation 2 there are $k_2$ internally disjoint s-t paths in $G_2-a$. Together with $P_1,\dots ,P_{k_1+l_1+1}$ we get the desired paths for G. So assume that $q+l_2>0$. By Claim 3 and the induction hypothesis there are $k_2+l_2+q$ edge-disjoint s-t paths in $H_2$, say $Q_1,\dots ,Q_{k_2+l_2+q}$ of which $k_2+1$ are internally disjoint, cf. Fig. 8. Without loss of generality let $Q_1,\dots ,Q_{r_2}$ for $r_2\le q$ be the paths using edges from $\{f_1,\dots ,f_q\}$, where again from these we denote by $Q_1$ the path that is among the $k_2+1$ internally disjoint paths, if one such path exists. We now claim that for $r:=\min \{r_1,r_2\}$ the paths

$$\begin{aligned} Q_1a\cup aP_1,\dots , Q_ra\cup aP_r, P_{r_1+1},\dots , P_{k_1+l_1+1}, Q_{r_2+1},\dots ,Q_{k_2+l_2+q} \end{aligned}$$

are at least $k+l$ edge-disjoint s-t paths of which at least $k+1$ are internally disjoint, cf. Fig. 8. First note, that the number of paths is exactly

$$\begin{aligned} r+\left( k_1+l_1+1\right) -r_1 +\left( k_2+l_2+q\right) -r_2 = k+l+q+r -r_1 - r_2. \end{aligned}$$

As r is equal to $r_i$ for some i and q is greater than or equal to $r_1$ and $r_2$ we get that the number of paths is at least $k+l$. To see that among the paths above there are at least $k+1$ internally disjoint paths, note that we started off with a set of $k_1+2+k_2+1= k+2$ internally disjoint paths $\mathcal {P}\subseteq \{P_1,\dots ,P_{k_1+l_1+1},Q_1,\dots ,Q_{k_2+l_2+q}\}$.

The only vertex besides s and t that may be contained in more than one path of $\mathcal {P}$ is a. If $Q_1, P_1\in \mathcal {P}$ they are glued together and $k+1$ internally disjoint paths still remain. If only one of $P_1$ and $Q_1$, say $P_1$, is among the internally disjoint paths, then $\mathcal {P}\setminus \{P_1\}$ is a set of $k+1$ internally disjoint paths, as only one other path than $P_1$ may contain a. Finally if neither $P_1$ nor $Q_1$ are among the internally disjoint paths, then $\mathcal {P}$ contains a subset of internally disjoint paths of size $k+1$ as at most two paths in $\mathcal {P}$ may contain a. This concludes Case 1.

Case 2: The vertex a is not contained in any s-t disconnecting pair of order k and size l.

Denote by (W, F) an s-t disconnecting pair of order k and size l and for $i\in \{1,2\}$ let $W_i =V(G_i)\cap W$, $k_i=|W_i|$, $F_i=E(G_i)\cap E_i$, and $l_i=|F_i|$. Then $k_1+k_2=k$ and $l_1+l_2=l$. Without loss of generality we may assume that there is no s-a path in $G-W-F$ and thereby also no s-a path in $G_i-W_i-F_i$ for $i\in \{1,2\}$.

For $i\in \{1,2\}$ denote by $0\le q_i\le l_i$ the unique integer such that $(k_i,l_i-q_i)$ is a connectivity pair for s and t in $G_i$. Note that this is well-defined as $(W_i, F_i)$ is an s-t disconnecting pair in $G_i$. We define $q=\max \{q_1,q_2\}$ and assume that $q=q_1$ (the case $q=q_2$ follows analogously). Let $(W_1^\prime , F_1^\prime )$ be an s-t disconnecting pair in $G_1$ of order $k_1$ and size $l_1-q$ and denote by $H_1$ the graph arising from $G_1$ by adding q edges $e_1,\dots ,e_{q}$ between a and t.

Claim 4

$(k_1,l_1)$ is a connectivity pair for s and t in $H_1$.

Proof

If $q=0$, then the claim holds by definition of q. So assume that $q\ge 1$. Clearly $(W_1^\prime , F_1^\prime \cup \{e_1,\dots , e_{q}\})$ is an s-t disconnecting pair in $H_1$ of order $k_1$ and size $l_1$. So suppose there exits an s-t disconnecting pair of order $k_1$ and size at most $l_1 -1$. Let $(W^\prime , F^\prime )$ be such a pair of minimal size. If $e_1,\dots , e_q\in F^\prime$ the pair $(W^\prime , F^\prime {\setminus }\{e_1,\dots , e_q\})$ is s-t disconnecting in $G_1$ and of order $k_1$ and size at most $l_1-q-1$, contradicting the fact that $(k_1,l_1-q)$ is a connectivity pair for s and t in $G_1$. Thus, either $a\in W^\prime$ or a and t are contained in the same component in $H_1-W^\prime - F^\prime$. In particular, there is no s-a path in $G_1 - W^\prime - F^\prime$ and thereby the pair $(W^\prime \cup W_2, F^\prime \cup F_2)$ is s-t disconnecting in G and of order k and size at most $l-1$. A contradiction to (k, l) being a connectivity pair for s and t in G. $\square$

Let now $H_2$ be the graph arising from $G_2$ by adding q edges $f_1,\dots , f_{q}$ between a and s. For $H_2$ we can also find a connectivity pair.

Claim 5

$(k_2, l_2 + q)$ is a connectivity pair for $H_2$.

Proof

Again, if $q=0$ the claim is immediate by definition of q. So let $q\ge 1$.In this case we have that $(W_2, F_2\cup \{f_1,\dots , f_{q}\})$ is an s-t disconnecting pair of order $k_2$ and size $l_2+q$ in $H_2$. So suppose there exists an s-t disconnecting pair of order $k_2$ and size at most $l_2+q-1$. Let $(W^\prime , F^\prime )$ be such a pair of minimal size. If $f_1,\dots , f_{q}\in F^\prime$, then there is no s-a path in $H_2-W^\prime -F^\prime$. This implies that $(W^\prime \cup W_1, F^\prime \setminus \{f_1,\dots ,f_{q^\prime }\}\cup F_1)$ is a disconnecting pair in G of order at most k and size at most $l-1$ yielding a contradiction. Thus, either $a\in W^\prime$ or a and s are contained in the same component in $H_2-W^\prime -F^\prime$. In particular, there is no a-t path in $G_2-W^\prime - F^\prime$. If there is also no a-t path in $G_1-W_1^\prime -F_1^\prime$, the pair $(W^\prime \cup W_1^\prime , F^\prime \cup F_1^\prime )$ is disconnecting in G and of order at most k and size at most $l-1$. This yields a contradiction to (k, l) being a connectivity pair for s and t in G. So suppose that there is an a-t path in $G_1-W_1^\prime -F_1^\prime$. Then there is no s-a path in $G_1-W_1^\prime -F_1^\prime$ and $(W_1^\prime \cup W_2, F_1^\prime \cup F_2)$ is an s-t disconnecting pair in G, that has order at most k and size at most $l_1-q+l_2<l$ as $q\ge 1$. Again this contradicts the fact that (k, l) is a connectivity pair for s and t in G. $\square$

As in the proof of Case 1 we use the induction hypothesis on $H_1$ and $H_2$ to get the desired paths. If neither $l_1=0$ nor $l_2+q=0$ we get the paths in G in the same manner as in Case 1 and therefore do not repeat the arguments here.

For the other case, let $l_1^\prime =l_1$ and $l_2^\prime =l_2+q$. If we can show for $i\in \{1,2\}$, that if $l_i^\prime =0$, then in $G_i-a$ the pair $(k_i,0)$ is a connectivity pair, we can again proceed as in Case 1 and get the desired paths. To see this we simply observe that a is not contained in any $k_i$-vertex separator in $G_i$ as this would imply that a is contained in an s-t disconnecting pair of order k and size l in G. $\square$

6 Conclusion and open problems

In this article we considered a form of mixed connectivity in graphs introduced by Beineke and Harary, namely connectivity pairs. We prove the Beineke Harary Conjecture for the case that $l=2$. This result substantially differs from previous results in the literature and can be used to prove the conjecture on restricted graph classes. We illustrate the latter fact by proving the conjecture for graphs of treewidth at most 3. From our studies the Beineke-Harary-Conjecture may hold:

Conjecture

(Beineke-Harary-Conjecture) Let G be a graph, $s,t\in V(G)$ distinct vertices and k, l non-negative integers with $l\ge 1$. If (k, l) is a connectivity pair for s and t in G, then there exist $k+l$ edge-disjoint paths, of which $k+1$ are internally disjoint.