Design of a class-based order picking system with stochastic demands and priority consideration

Abstract

An MIAPP-NALT system is an order picking system in which cases are picked at multiple in-the-aisle pick positions (MIAPP) and storage and retrieval operations are performed by a narrow aisle lift truck (NALT). In this paper, the operation of such a system involving three classes of stock keeping units with random demands for storage and retrieval operations is modeled as an M/G/1 queue, where “customers” are storage and retrieval requests, the “server” is the NALT, and retrieval requests have non-preemptive priority over storage requests. Our goal is to explore a methodology and solution method to obtain the optimal layout design of a class-based MIAPP-NALT system with stochastic demands and priority service. To this end, an operation time model of the system is developed and the first two moments for the operation time are derived. To overcome the challenge in finding the desired optimal layout, a near-optimal layout obtained via a heuristic approach is obtained at first and is improved afterwards. Based on the optimal layout, some valuable queueing results demonstrate the benefit of using a priority-based discipline. Moreover, some useful insights regarding the selection of dedicated versus random storage policies are obtained.

Appendices

Appendix

Key derivations of interested travel times

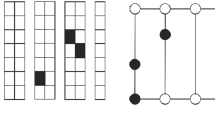
See Figs. 10 and 11

Fig. 10

Layout with three classes of SKUs

Fig. 11

Possible travel paths for retrieval operations

.

Appendix A First two moments for vertical travel time

(a) First two moments for vertical travel time for a floor-level storage location to perform a storage operation or retrieval operation

For subclass A₁, B₁, or C₁ SKUs at floor-level storage locations in Fig. 10, regardless of storage or retrieval operation, the fork of the NALT will be lifted from a floor-level location to a random reserve-storage location of subclass A₁, B₁, or C₁, pick up or deposit a pallet there, and lower the forks to a floor-level location. The expression for NALT vertical travel time T is $T\left( Y \right) = 2Y$, where $Y\sim {\text{unif}}\left[ {0,b/2} \right]$ with pdf $f\left( y \right) = \frac{2}{b}$. Then, the first two moments of T can be expressed as:

$$ E\left[ T \right] = \mathop \int \limits_{0}^{{{\text{b}}/2}} t\left( y \right)f\left( y \right)dy = \mathop \int \limits_{0}^{{{\text{b}}/2}} \frac{4y}{b}dy = \frac{b}{2} $$

(A1)

$$ E\left[ {T^{2} } \right] = \mathop \int \limits_{0}^{{{\text{b}}/2}} \left[ {t\left( y \right)} \right]^{2} f\left( y \right)dy = \mathop \int \limits_{0}^{{{\text{b}}/2}} \frac{{8y^{2} }}{b}dy = \frac{{b^{2} }}{3} $$

(A2)

(b) First two moments for vertical travel time for a mezzanine-level storage location to perform a retrieval operation with dedicated storage or to perform a storage operation

For subclass A₂, B₂, or C₂ SKUs at mezzanine-level storage locations, to perform a retrieval operation with dedicated storage or to perform a storage operation with either dedicated storage or random storage, as shown in Fig. 10, the forks of the NALT will be lifted from a floor-level location to a random reserve-storage location of subclass A₂, B₂, or C₂, pick up or deposit a pallet, and, be lowered to the floor-level location. The expression for NALT vertical travel time T is $T\left( Y \right) = 2Y$, where $Y\sim {\text{unif}}\left[ {b/2,b} \right]$ with pdf $f\left( y \right) = \frac{2}{b}$. The first two moments of T are:

$$ E\left[ T \right] = \mathop \int \limits_{b/2}^{b} t\left( y \right)f\left( y \right)dy = \mathop \int \limits_{b/2}^{b} \frac{4y}{b}dy = \frac{3b}{2} $$

(A3)

$$ E\left[ {T^{2} } \right] = \mathop \int \limits_{b/2}^{b} \left[ {t\left( y \right)} \right]^{2} f\left( y \right)dy = \mathop \int \limits_{b/2}^{b} \frac{{8y^{2} }}{b}dy = \frac{{7b^{2} }}{3} $$

(A4)

(c) First two moments for vertical travel time for a mezzanine-level storage location to perform a retrieval operation with random storage

For subclass A₂, B₂, or C₂ SKUs at mezzanine-level storage locations for retrieval operation with random storage in Fig. 10, as depicted by the red line in Fig. 1, to perform a retrieval operation with a random-storage policy, the NALT forks will be raised from a floor-level location to a random reserve-storage location of subclass A₂, B₂, or C₂, pick up a pallet, and be lowered to the floor-level location (before moving horizontally to the appropriate position to access the desired mezzanine location), the forks will be raised to the mezzanine level for placement of the pallet at the deposit point for the pick position, and then the forks will be lowered to the floor-level location. The expression for NALT vertical travel time T is $T\left( Y \right) = 2Y + b$, where $Y\sim {\text{unif}}\left[ {b/2,b} \right]$ with pdf $f\left( y \right) = \frac{2}{b}$. The first two moments of T are:

$$ E\left[ T \right] = \mathop \int \limits_{b/2}^{b} t\left( y \right)f\left( y \right)dy = \mathop \int \limits_{b/2}^{b} \frac{4y + 2b}{b}dy = \frac{5b}{2} $$

(A5)

$$ E\left[ {T^{2} } \right] = \mathop \int \limits_{b/2}^{b} \left[ {t\left( y \right)} \right]^{2} f\left( y \right)dy = \mathop \int \limits_{b/2}^{b} \frac{{2\left( {2y + b} \right)^{2} }}{b}dy = \frac{{19b^{2} }}{3} $$

(A6)

Appendix B: First two moments for horizontal travel time to perform a storage operation

In Fig. 10, for any possible travel path, the NALT travels from a random floor-level location $X_{i} \sim {\text{unif}}\left[ {Z_{1} ,Z_{2} } \right]$ within six subclasses A₁, A₂, B₁, B₂, C₁ and C₂ to the input station; then, the NALT travels to another random floor-level location $X_{j} \sim {\text{unif}}\left[ {Z_{3} ,Z_{4} } \right]$ within six subclasses A₁, A₂, B₁, B₂, C₁ and C₂. The expression for the NALT horizontal travel time T is $T\left( {X_{i} , X_{j} } \right) = X_{i} + X_{j}$, where $X_{i} \sim {\text{unif}}\left[ {Z_{1} ,Z_{2} } \right]$ and $X_{j} \sim {\text{unif}}\left[ {Z_{3} ,Z_{4} } \right]$ with a joint pdf $f\left( {x_{i} , x_{j} } \right) = f\left( {x_{i} } \right)f\left( {x_{j} } \right) = \frac{1}{{\left( {Z_{2} - Z_{1} } \right)\left( {Z_{4} - Z_{3} } \right)}}$. Then, the first two moments of T can be expressed as:

$$ E\left[ T \right] = \mathop \int \limits_{{Z_{1} }}^{{Z_{2} }} \mathop \int \limits_{{Z_{3} }}^{{Z_{4} }} t\left( {x_{i} , x_{j} } \right)f\left( {x_{i} , x_{j} } \right)dx_{j} dx_{i} = \mathop \int \limits_{{Z_{1} }}^{{Z_{2} }} \mathop \int \limits_{{Z_{3} }}^{{Z_{4} }} \frac{{x_{i} + x_{j} }}{{\left( {Z_{2} - Z_{1} } \right)\left( {Z_{4} - Z_{3} } \right)}}dx_{j} dx_{i} = \frac{1}{2}\left( {Z_{1} + Z_{2} + Z_{3} + Z_{4} } \right) $$

(A7)

$$ \begin{aligned} E\left[ {T^{2} } \right] =&\mathop \int \limits_{{Z_{1} }}^{{Z_{2} }} \mathop \int \limits_{{Z_{3} }}^{{Z_{4} }} \left[ {t\left( {x_{i} , x_{j} }\right)} \right]^{2} f\left( {x_{i} , x_{j} } \right)dx_{j} dx_{i} =\mathop \int \limits_{{Z_{1} }}^{{Z_{2} }} \mathop \int \limits_{{Z_{3} }}^{{Z_{4} }} \frac{{\left( {x_{i} + x_{j} }\right)^{2} }}{{\left( {Z_{2} - Z_{1} } \right)\left( {Z_{4} - Z_{3}} \right)}}dx_{j} dx_{i} \hfill \\ =&\frac{1}{6}\left( 2Z_{1}^{2} + 2Z_{2}^{2} + 2Z_{3}^{2} + 2Z_{4}^{2}+ 2Z_{1} Z_{2} + 3Z_{1} Z_{3} \right.\\&\left.+ 3Z_{1} Z_{4} + 3Z_{2} Z_{3} + 3Z_{2}Z_{4} + 2Z_{3} Z_{4} \right) \hfill \\ \end{aligned}$$

(A8)

Appendix C: First two moments for horizontal travel time to perform a retrieval operation with a dedicated-storage policy

The three travel patterns in Fig. 11 represent possible travel paths in Fig. 10. For horizontal travel with dedicated storage, NALT travel time for travel path from E to F and travel path from F to E are the same, therefore, only one set of first two moments must be derived for each travel pattern in Fig. 11.

Travel pattern (a) with $Z_{2} \le Z_{3}$

Because, if travel is from E to F or from F to E, the expression for horizontal travel time T is $T\left( {X_{i} , X_{j} } \right) = \left| {X_{i} - X_{j} } \right| = X_{j} - X_{i}$, where $X_{i} \sim {\text{unif}}\left[ {Z_{1} ,Z_{2} } \right]$ and $X_{j} \sim {\text{unif}}\left[ {Z_{3} ,Z_{4} } \right]$ with a joint pdf $f\left( {x_{i} , x_{j} } \right) = f\left( {x_{i} } \right)f\left( {x_{j} } \right) = \frac{1}{{\left( {Z_{2} - Z_{1} } \right)\left( {Z_{4} - Z_{3} } \right)}}$. The first two moments of T are:

$$ \begin{gathered} E\left[ T \right] = E\left[ T \right] = \mathop \int \limits_{{Z_{1} }}^{{Z_{2} }} \mathop \int \limits_{{Z_{3} }}^{{Z_{4} }} t\left( {x_{i} , x_{j} } \right)f\left( {x_{i} , x_{j} } \right)dx_{j} dx_{i} \hfill \\ \quad \quad \quad = \mathop \int \limits_{{Z_{1} }}^{{Z_{2} }} \mathop \int \limits_{{Z_{3} }}^{{Z_{4} }} \frac{{x_{j} - x_{i} }}{{\left( {Z_{2} - Z_{1} } \right)\left( {Z_{4} - Z_{3} } \right)}}dx_{j} dx_{i} = \frac{1}{2}\left( {Z_{3} + Z_{4} - Z_{1} - Z_{2} } \right) \hfill \\ \end{gathered} $$

(A9)

$$ \begin{gathered} E\left[ {T^{2} } \right] = \mathop \int \limits_{{Z_{1} }}^{{Z_{2} }} \mathop \int \limits_{{Z_{3} }}^{{Z_{4} }} \left[ {t\left( {x_{i} , x_{j} } \right)} \right]^{2} f\left( {x_{i} , x_{j} } \right)dx_{j} dx_{i} = \mathop \int \limits_{{Z_{1} }}^{{Z_{2} }} \mathop \int \limits_{{Z_{3} }}^{{Z_{4} }} \frac{{\left( {x_{j} - x_{i} } \right)^{2} }}{{\left( {Z_{2} - Z_{1} } \right)\left( {Z_{4} - Z_{3} } \right)}}dx_{j} dx_{i} \hfill \\ \quad \quad \quad \quad = \frac{1}{6}\left( {2Z_{1}^{2} + 2Z_{2}^{2} + 2Z_{3}^{2} + 2Z_{4}^{2} + 2Z_{1} Z_{2} - 3Z_{1} Z_{3} - 3Z_{1} Z_{4} - 3Z_{2} Z_{3} - 3Z_{2} Z_{4} + 2Z_{3} Z_{4} } \right) \hfill \\ \end{gathered} $$

(A10)

Travel pattern (b) with $Z_{1} \le Z_{3} \le Z_{2} \le Z_{4}$,

If travel is from E to F or from F to E, the expression for travel time T is

$$ T\left( {X_{i} , X_{j} } \right) = \left| {X_{i} - X_{j} } \right| = \left\{ {\begin{array}{*{20}c} {X_{j} - X_{i} X_{j} \ge X_{i} {\text{Case }}1} \\ {X_{i} - X_{j} X_{j} < X_{i} {\text{Case }}2} \\ \end{array} } \right. $$

where $X_{i} \sim {\text{unif}}\left[ {Z_{1} ,Z_{2} } \right]$ and $X_{j} \sim {\text{unif}}\left[ {Z_{3} ,Z_{4} } \right]$ with a joint pdf $f\left( {x_{i} , x_{j} } \right) = f\left( {x_{i} } \right)f\left( {x_{j} } \right) = \frac{1}{{\left( {Z_{2} - Z_{1} } \right)\left( {Z_{4} - Z_{3} } \right)}}$. The expected value of T is:

$$ \begin{aligned} E\left[ T \right] =&\mathop \int \limits_{{Z_{1} }}^{{Z_{2} }} \mathop \int \limits_{{{\text{max}}(Z_{3} , x_{i} )}}^{{Z_{4} }} t\left( {x_{i} ,x_{j} } \right)f\left( {x_{i} , x_{j} } \right)dx_{j} dx_{i} +\mathop \int \limits_{{Z_{3} }}^{{Z_{2} }} \mathop \int \limits_{{Z_{3} }}^{{x_{i} }} t\left( {x_{i} , x_{j} }\right)f\left( {x_{i} , x_{j} } \right)dx_{j} dx_{i} \hfill \\=& \mathop \int \limits_{{Z_{1} }}^{{Z_{3} }} \mathop \int \limits_{{Z_{3} }}^{{Z_{4} }} \frac{{x_{j} - x_{i} }}{{\left( {Z_{2}- Z_{1} } \right)\left( {Z_{4} - Z_{3} } \right)}}dx_{j} dx_{i} +\mathop \int \limits_{{Z_{3} }}^{{Z_{2} }} \mathop \int \limits_{{x_{i} }}^{{Z_{4} }} \frac{{x_{j} - x_{i} }}{{\left( {Z_{2}- Z_{1} } \right)\left( {Z_{4} - Z_{3} } \right)}}dx_{j} dx_{i} \\&+\mathop \int \limits_{{Z_{3} }}^{{Z_{2} }} \mathop \int \limits_{{Z_{3} }}^{{x_{i} }} \frac{{x_{i} - x_{j} }}{{\left( {Z_{2}- Z_{1} } \right)\left( {Z_{4} - Z_{3} } \right)}}dx_{j} dx_{i}\hfill \\ =& \frac{1}{{6\left( {Z_{2} - Z_{1} }\right)\left( {Z_{4} - Z_{3} } \right)}}\left( 2Z_{2}^{3} -2Z_{3}^{3} + 3Z_{1} Z_{3}^{2} - 3Z_{1} Z_{4}^{2} - 3Z_{1}^{2} Z_{3}+ 3Z_{1}^{2} Z_{4} \right.\\&\left.+ 3Z_{2} Z_{3}^{2} + 3Z_{2} Z_{4}^{2} -3Z_{2}^{2} Z_{3} - 3Z_{2}^{2} Z_{4} \right) \hfill \\\end{aligned} $$

(A11)

For the second moment of T, the formula is the same as the $E\left[{T}^{2}\right]$ for travel pattern (a) because E[|X_i-X_j|²] = E[(X_i-X_j)²] = E[Xi 2] + E[Xj2]-2E[Xi]E[Xj], so the $E\left[{T}^{2}\right]$ is:

$$ E\left[ {T^{2} } \right] = \frac{1}{6}\left( {2Z_{1}^{2} + 2Z_{2}^{2} + 2Z_{3}^{2} + 2Z_{4}^{2} + 2Z_{1} Z_{2} - 3Z_{1} Z_{3} - 3Z_{1} Z_{4} - 3Z_{2} Z_{3} - 3Z_{2} Z_{4} + 2Z_{3} Z_{4} } \right) $$

(A12)

Travel pattern (c) with ${\varvec{Z}}_{3} \le {\varvec{Z}}_{1} \le {\varvec{Z}}_{2} \le {\varvec{Z}}_{4}$.

If travel is from E to F or from F to E, the expression for travel time T is

$$ T\left( {X_{i} , X_{j} } \right) = \left| {X_{i} - X_{j} } \right| = \left\{ {\begin{array}{*{20}c} {X_{j} - X_{i} X_{j} \ge X_{i} \quad {\text{Case }}1} \\ {X_{i} - X_{j} X < X_{i} \quad {\text{Case }}2} \\ \end{array} } \right. $$

where $X_{i} \sim {\text{unif}}\left[ {Z_{1} ,Z_{2} } \right]$ and $X_{j} \sim {\text{unif}}\left[ {Z_{3} ,Z_{4} } \right]$ with a joint pdf $f\left( {x_{i} , x_{j} } \right) = f\left( {x_{i} } \right)f\left( {x_{j} } \right) = \frac{1}{{\left( {Z_{2} - Z_{1} } \right)\left( {Z_{4} - Z_{3} } \right)}}$. The expected value of T is:

$$ \begin{gathered} E\left[ T \right] = \mathop \int \limits_{{Z_{1} }}^{{Z_{2} }} \mathop \int \limits_{{x_{i} }}^{{Z_{4} }} t\left( {x_{i} , x_{j} } \right)f\left( {x_{i} , x_{j} } \right)dx_{j} dx_{i} + \mathop \int \limits_{{Z_{1} }}^{{Z_{2} }} \mathop \int \limits_{{Z_{3} }}^{{x_{i} }} t\left( {x_{i} , x_{j} } \right)f\left( {x_{i} , x_{j} } \right)dx_{j} dx_{i} \hfill \\ \quad \quad = \mathop \int \limits_{{Z_{1} }}^{{Z_{2} }} \mathop \int \limits_{{x_{i} }}^{{Z_{4} }} \frac{{x_{j} - x_{i} }}{{\left( {Z_{2} - Z_{1} } \right)\left( {Z_{4} - Z_{3} } \right)}}dx_{j} dx_{i} + \mathop \int \limits_{{Z_{1} }}^{{Z_{2} }} \mathop \int \limits_{{Z_{3} }}^{{x_{i} }} \frac{{x_{i} - x_{j} }}{{\left( {Z_{2} - Z_{1} } \right)\left( {Z_{4} - Z_{3} } \right)}}dx_{j} dx_{i} \hfill \\ \quad \quad = \frac{1}{{6\left( {Z_{4} - Z_{3} } \right)}}\left( {2Z_{1}^{2} + 2Z_{2}^{2} + 3Z_{3}^{2} + 3Z_{4}^{2} + 2Z_{1} Z_{2} - 3Z_{1} Z_{3} - 3Z_{1} Z_{4} - 3Z_{2} Z_{3} - 3Z_{2} Z_{4} } \right) \hfill \\ \end{gathered} $$

For the second moment of T, the formula is the same as the $E\left[ {T^{2} } \right]$ for travel pattern (a) because E[|X_i-X_j|²] = E[(X_i-X_j)²] = E[Xi 2] + E[Xj2]-2E[Xi]E[Xj], so the $E\left[ {T^{2} } \right]$ is:

$$ E\left[ {T^{2} } \right] = \frac{1}{6}\left( {2Z_{1}^{2} + 2Z_{2}^{2} + 2Z_{3}^{2} + 2Z_{4}^{2} + 2Z_{1} Z_{2} - 3Z_{1} Z_{3} - 3Z_{1} Z_{4} - 3Z_{2} Z_{3} - 3Z_{2} Z_{4} + 2Z_{3} Z_{4} } \right) $$

(A14)

Appendix D: First two moments for horizontal travel time to perform a retrieval operation with a random-storage policy

Three travel patterns in Fig. 11 are considered. For horizontal travel with random storage, NALT travel time for travel from E to F differs from travel from F to E; therefore, two sets of first two moments are derived for each travel pattern in Fig. 11.

Travel pattern (a) with $Z_{2} \le Z_{3}$.

For travel from E to F, the expression for travel time T is

$$ T\left( {X, X_{i} , X_{j} } \right) = X - X_{i} + \left| {X_{j} - X} \right| = \left\{ {\begin{array}{*{20}c} {X_{j} - X_{i} X_{j} \ge X {\text{Case }}1} \\ {2X - X_{i} - X_{j} X_{j} < X {\text{Case }}2} \\ \end{array} } \right. $$

where $X_{i} \sim {\text{unif}}\left[ {Z_{1} ,Z_{2} } \right]$ and $X, X_{j} \sim {\text{unif}}\left[ {Z_{3} ,Z_{4} } \right]$ with a joint pdf $f\left( {x, x_{i} , x_{j} } \right) = f\left( x \right)f\left( {x_{i} } \right)f\left( {x_{j} } \right) = \frac{1}{{\left( {Z_{2} - Z_{1} } \right)\left( {Z_{4} - Z_{3} } \right)^{2} }}$. The first two moments of T are:

$$ \begin{aligned} E\left[ T \right] =&\mathop \int \limits_{{Z_{3} }}^{{Z_{4} }} \mathop \int \limits_{x}^{{Z_{4} }} \mathop \int \limits_{{Z_{1} }}^{{Z_{2} }}t\left( {x, x_{i} , x_{j} } \right)f\left( {x, x_{i} , x_{j} }\right)dx_{i} dx_{j} dx\\& + \mathop \int \limits_{{Z_{3} }}^{{Z_{4} }}\mathop \int \limits_{{Z_{3} }}^{x} \mathop \int \limits_{{Z_{1}}}^{{Z_{2} }} t\left( {x, x_{i} , x_{j} } \right)f\left( {x, x_{i} ,x_{j} } \right)dx_{i} dx_{j} dx \hfill \\ =&\mathop \int \limits_{{Z_{3} }}^{{Z_{4} }} \mathop \int \limits_{x}^{{Z_{4} }} \mathop \int \limits_{{Z_{1} }}^{{Z_{2} }}\frac{{x_{j} - x_{i} }}{{\left( {Z_{2} - Z_{1} } \right)\left({Z_{4} - Z_{3} } \right)^{2} }}dx_{i} dx_{j} dx\\& + \mathop \int \limits_{{Z_{3} }}^{{Z_{4} }} \mathop \int \limits_{{Z_{3} }}^{x}\mathop \int \limits_{{Z_{1} }}^{{Z_{2} }} \frac{{2x - x_{i} - x_{j}}}{{\left( {Z_{2} - Z_{1} } \right)\left( {Z_{4} - Z_{3} }\right)^{2} }}dx_{i} dx_{j} dx = \frac{1}{6}\left( { - 3Z_{1} -3Z_{2} + Z_{3} + 5Z_{4} } \right) \hfill \\ \end{aligned}$$

(A15)

$$ \begin{aligned} E\left[ {T^{2} } \right] =&\mathop \int \limits_{{Z_{3} }}^{{Z_{4} }} \mathop \int \limits_{{\text{x}}}^{{Z_{4} }} \mathop \int \limits_{{Z_{1}}}^{{Z_{2} }} \left[ {t\left( {x, x_{i} , x_{j} } \right)}\right]^{2} f\left( {x, x_{i} , x_{j} } \right)dx_{i} dx_{j} dx\\& +\mathop \int \limits_{{Z_{3} }}^{{Z_{4} }} \mathop \int \limits_{{Z_{3} }}^{{\text{x}}} \mathop \int \limits_{{Z_{1}}}^{{Z_{2} }} \left[ {t\left( {x, x_{i} , x_{j} } \right)}\right]^{2} f\left( {x, x_{i} , x_{j} } \right)dx_{i} dx_{j} dx \hfill \\=& \mathop \int \limits_{{Z_{3}}}^{{Z_{4} }} \mathop \int \limits_{{\text{x}}}^{{Z_{4} }} \mathop \int \limits_{{Z_{1} }}^{{Z_{2} }} \frac{{\left( {x_{j} - x_{i} }\right)^{2} }}{{\left( {Z_{2} - Z_{1} } \right)\left( {Z_{4} - Z_{3}} \right)^{2} }}dx_{i} dx_{j} dx \\&+ \mathop \int \limits_{{Z_{3}}}^{{Z_{4} }} \mathop \int \limits_{{Z_{3} }}^{{\text{x}}} \mathop \int \limits_{{Z_{1} }}^{{Z_{2} }} \frac{{\left( {2x - x_{i} - x_{j}} \right)^{2} }}{{\left( {Z_{2} - Z_{1} } \right)\left( {Z_{4} -Z_{3} } \right)^{2} }}dx_{i} dx_{j} dx \hfill \\ =& \frac{1}{6}\left( {2Z_{1}^{2} + 2Z_{2}^{2} + Z_{3}^{2} + 5Z_{4}^{2}+ 2Z_{1} Z_{2} - Z_{1} Z_{3} - 5Z_{1} Z_{4} - Z_{2} Z_{3} - 5Z_{2}Z_{4} } \right) \hfill \\ \end{aligned}$$

(A16)

For travel from F to E, the expression for travel time T is

$$ T = X_{i} - X + \left| {X - X_{j} } \right| = \left\{ \begin{gathered} X_{i} - X_{j} X \ge X_{j} \quad \quad \quad {\text{Case}}\;1 \hfill \\ X_{i} + X_{j} - 2XX < X_{j} \quad {\text{Case}}\;2 \hfill \\ \end{gathered} \right.$$

where $X, X_{j} \sim {\text{unif}}\left[ {Z_{1} ,Z_{2} }\right]$ and $X_{i} \sim {\text{unif}}\left[ {Z_{3} ,Z_{4} }\right]$ with a joint pdf $f\left( {x, x_{i} , x_{j} } \right) =f\left( x \right)f\left( {x_{i} } \right)f\left( {x_{j} } \right) =\frac{1}{{\left( {Z_{2} - Z_{1} } \right)^{2} \left( {Z_{4} - Z_{3}} \right)}}$. The first two moments of T are:

$$ \begin{aligned} E\left[ T \right] =&\mathop \int \limits_{{Z_{1} }}^{{Z_{2} }} \mathop \int \limits_{{x_{j} }}^{{Z_{2} }} \mathop \int \limits_{{Z_{3}}}^{{Z_{4} }} t\left( {x, x_{i} , x_{j} } \right)f\left( {x, x_{i} ,x_{j} } \right)dx_{i} dxdx_{j} \\&+ \mathop \int \limits_{{Z_{1}}}^{{Z_{2} }} \mathop \int \limits_{{Z_{1} }}^{{x_{j} }} \mathop \int \limits_{{Z_{3} }}^{{Z_{4} }} t\left( {x, x_{i} , x_{j} }\right)f\left( {x, x_{i} , x_{j} } \right)dx_{i} dxdx_{j} \hfill \\=& \mathop \int \limits_{{Z_{1} }}^{{Z_{2} }} \mathop \int \limits_{{x_{j} }}^{{Z_{2} }} \mathop \int \limits_{{Z_{3}}}^{{Z_{4} }} \frac{{x_{i} - x_{j} }}{{\left( {Z_{2} - Z_{1} }\right)\left( {Z_{4} - Z_{3} } \right)^{2} }}dx_{i} dxdx_{j}\\& +\mathop \int \limits_{{Z_{1} }}^{{Z_{2} }} \mathop \int \limits_{{Z_{1} }}^{{x_{j} }} \mathop \int \limits_{{Z_{3}}}^{{Z_{4} }} \frac{{x_{i} + x_{j} - 2x}}{{\left( {Z_{2} - Z_{1} }\right)\left( {Z_{4} - Z_{3} } \right)^{2} }}dx_{i} dxdx_{j} \hfill \\ =& \frac{1}{6}\left( { - 5Z_{1} - Z_{2} + 3Z_{3} + 3Z_{4} }\right) \hfill \\ \end{aligned}$$

(A17)

$$ \begin{aligned} E\left[ {T^{2} } \right] =&\mathop \int \limits_{{Z_{1} }}^{{Z_{2} }} \mathop \int \limits_{{x_{j} }}^{{Z_{2} }} \mathop \int \limits_{{Z_{3}}}^{{Z_{4} }} \left[ {t\left( {x, x_{i} , x_{j} } \right)}\right]^{2} f\left( {x, x_{i} , x_{j} } \right)dx_{i} dxdx_{j}\\& +\mathop \int \limits_{{Z_{1} }}^{{Z_{2} }} \mathop \int \limits_{{Z_{1} }}^{{x_{j} }} \mathop \int \limits_{{Z_{3}}}^{{Z_{4} }} \left[ {t\left( {x, x_{i} , x_{j} } \right)}\right]^{2} f\left( {x, x_{i} , x_{j} } \right)dx_{i} dxdx_{j}\hfill \\ =& \mathop \int \limits_{{Z_{1}}}^{{Z_{2} }} \mathop \int \limits_{{x_{j} }}^{{Z_{2} }} \mathop \int \limits_{{Z_{3} }}^{{Z_{4} }} \frac{{\left( {x_{i} - x_{j} }\right)^{2} }}{{\left( {Z_{2} - Z_{1} } \right)\left( {Z_{4} - Z_{3}} \right)^{2} }}dx_{i} dxdx_{j} \\&+ \mathop \int \limits_{{Z_{1}}}^{{Z_{2} }} \mathop \int \limits_{{Z_{1} }}^{{x_{j} }} \mathop \int \limits_{{Z_{3} }}^{{Z_{4} }} \frac{{\left( {x_{i} + x_{j} -2x} \right)^{2} }}{{\left( {Z_{2} - Z_{1} } \right)\left( {Z_{4} -Z_{3} } \right)^{2} }}dx_{i} dxdx_{j} \hfill \\ =&\frac{1}{6}\left( {5Z_{1}^{2} + Z_{2}^{2} + 2Z_{3}^{2} + 2Z_{4}^{2}- 5Z_{1} Z_{3} - 5Z_{1} Z_{4} - Z_{2} Z_{3} - Z_{2} Z_{4} + 2Z_{3}Z_{4} } \right) \hfill \\ \end{aligned}$$

(A18)

Travel pattern (b) with $Z_{1} \le Z_{3}\le Z_{2} \le Z_{4}$.

For travel from E to F, the expression for travel time T is

$$ T\left( {X,~X_{i} ,~X_{j} } \right) = \left| {X - X_{i} \left| + \right|X - X_{j} } \right| = \left\{ \begin{gathered} 2X - X_{i} - X_{j} \quad X \ge X_{i} ,~X \ge X_{j} \quad {\text{Case}}\;1 \hfill \\ X_{j} - X_{i} \quad \quad \quad \quad X \ge X_{i} ,~X < X_{j} \quad {\text{Case~}}\;2 \hfill \\ X_{i} - X_{j} \quad \quad \quad \quad X < X_{i} ,~X \ge X_{j} \quad {\text{Case}}\;3 \hfill \\ X_{i} + X_{j} - 2X\quad X < X_{i} ,~X < X_{j} \quad {\text{Case~}}\;4 \hfill \\ \end{gathered} \right. $$

where $X_{i} \sim {\text{unif}}\left[ {Z_{1} ,Z_{2}} \right]$ and $X, X_{j} \sim {\text{unif}}\left[ {Z_{3} ,Z_{4} }\right]$ with a joint pdf $f\left( {x, x_{i} , x_{j} } \right) =f\left( x \right)f\left( {x_{i} } \right)f\left( {x_{j} } \right) =\frac{1}{{\left( {Z_{2} - Z_{1} } \right)\left( {Z_{4} - Z_{3} }\right)^{2} }}$. The first two moments of T are:

$$ \begin{aligned} E\left[ T \right] =&\mathop \int \limits_{{Z_{3} }}^{{Z_{4} }} \mathop \int \limits_{{Z_{3} }}^{x} \mathop \int \limits_{{Z_{1} }}^{{\min \left({x, Z_{2} } \right)}} t\left( {x, x_{i} , x_{j} } \right)f\left( {x,x_{i} , x_{j} } \right)dx_{i} dx_{j} dx\\& + \mathop \int \limits_{{Z_{3} }}^{{Z_{4} }} \mathop \int \limits_{x}^{{Z_{4} }}\mathop \int \limits_{{Z_{1} }}^{{\min \left( {x, Z_{2} } \right)}}t\left( {x, x_{i} , x_{j} } \right)f\left( {x, x_{i} , x_{j} }\right)dx_{i} dx_{j} dx \hfill \\& + \mathop \int \limits_{{Z_{3} }}^{{Z_{2} }} \mathop \int \limits_{{Z_{3} }}^{x}\mathop \int \limits_{x}^{{Z_{2} }} t\left( {x, x_{i} , x_{j} }\right)f\left( {x, x_{i} , x_{j} } \right)dx_{i} dx_{j} dx\\& + \mathop \int \limits_{{Z_{3} }}^{{Z_{2} }} \mathop \int \limits_{x}^{{Z_{4}}} \mathop \int \limits_{x}^{{Z_{2} }} t\left( {x, x_{i} , x_{j} }\right)f\left( {x, x_{i} , x_{j} } \right)dx_{i} dx_{j} dx \hfill \\=& \mathop \int \limits_{{Z_{3} }}^{{Z_{2} }}\mathop \int \limits_{{Z_{3} }}^{x} \mathop \int \limits_{{Z_{1}}}^{x} \frac{{2x - x_{i} - x_{j} }}{{\left( {Z_{2} - Z_{1} }\right)\left( {Z_{4} - Z_{3} } \right)^{2} }}dx_{i} dx_{j} dx \\&+ \mathop \int \limits_{{Z_{2} }}^{{Z_{4} }} \mathop \int \limits_{{Z_{3} }}^{x} \mathop \int \limits_{{Z_{1} }}^{{Z_{2} }}\frac{{2x - x_{i} - x_{j} }}{{\left( {Z_{2} - Z_{1} } \right)\left({Z_{4} - Z_{3} } \right)^{2} }}dx_{i} dx_{j} dx \hfill \\&+ \mathop \int \limits_{{Z_{3} }}^{{Z_{2} }} \mathop \int \limits_{x}^{{Z_{4} }} \mathop \int \limits_{{Z_{1} }}^{x}\frac{{x_{j} - x_{i} }}{{\left( {Z_{2} - Z_{1} } \right)\left({Z_{4} - Z_{3} } \right)^{2} }}dx_{i} dx_{j} dx\\& + \mathop \int \limits_{{Z_{2} }}^{{Z_{4} }} \mathop \int \limits_{x}^{{Z_{4} }}\mathop \int \limits_{{Z_{1} }}^{{Z_{2} }} \frac{{x_{j} - x_{i}}}{{\left( {Z_{2} - Z_{1} } \right)\left( {Z_{4} - Z_{3} }\right)^{2} }}dx_{i} dx_{j} dx \hfill \\ &+ \mathop \int \limits_{{Z_{3} }}^{{Z_{2} }} \mathop \int \limits_{{Z_{3}}}^{x} \mathop \int \limits_{x}^{{Z_{2} }} \frac{{x_{i} - x_{j}}}{{\left( {Z_{2} - Z_{1} } \right)\left( {Z_{4} - Z_{3} }\right)^{2} }}dx_{i} dx_{j} dx \\&+ \mathop \int \limits_{{Z_{3}}}^{{Z_{2} }} \mathop \int \limits_{x}^{{Z_{4} }} \mathop \int \limits_{x}^{{Z_{2} }} \frac{{x_{i} + x_{j} - 2x}}{{\left( {Z_{2} -Z_{1} } \right)\left( {Z_{4} - Z_{3} } \right)^{2} }}dx_{i} dx_{j}dx \hfill \\ =& \frac{1}{{6\left( {Z_{2} - Z_{1} }\right)\left( {Z_{4} - Z_{3} } \right)}}\left( 2Z_{2}^{3} -2Z_{3}^{3} + Z_{1} Z_{3}^{2} - 5Z_{1} Z_{4}^{2} - 3Z_{1}^{2} Z_{3} +3Z_{1}^{2} Z_{4} \right.\\&\left.+ 5Z_{2} Z_{3}^{2} + 5Z_{2} Z_{4}^{2}- 3Z_{2}^{2}Z_{3} - 3Z_{2}^{2} Z_{4} + 4Z_{1} Z_{3} Z_{4} - 4Z_{2} Z_{3} Z_{4}\right) \hfill \\ \end{aligned}$$

(A19)

$$ \begin{aligned} E\left[ {T^{2} } \right] =&\mathop \int \limits_{{Z_{3} }}^{{Z_{4} }} \mathop \int \limits_{{Z_{3} }}^{x} \mathop \int \limits_{{Z_{1} }}^{{\min \left({x, Z_{2} } \right)}} \left[ {t\left( {x, x_{i} , x_{j} } \right)}\right]^{2} f\left( {x, x_{i} , x_{j} } \right)dx_{i} dx_{j} dx \\&+\mathop \int \limits_{{Z_{3} }}^{{Z_{4} }} \mathop \int \limits_{x}^{{Z_{4} }} \mathop \int \limits_{{Z_{1} }}^{{\min \left({x, Z_{2} } \right)}} \left[ {t\left( {x, x_{i} , x_{j} } \right)}\right]^{2} f\left( {x, x_{i} , x_{j} } \right)dx_{i} dx_{j} dx \hfill \\ &+ \mathop \int \limits_{{Z_{3}}}^{{Z_{2} }} \mathop \int \limits_{{Z_{3} }}^{x} \mathop \int \limits_{x}^{{Z_{2} }} \left[ {t\left( {x, x_{i} , x_{j} } \right)}\right]^{2} f\left( {x, x_{i} , x_{j} } \right)dx_{i} dx_{j} dx \\&+\mathop \int \limits_{{Z_{3} }}^{{Z_{2} }} \mathop \int \limits_{x}^{{Z_{4} }} \mathop \int \limits_{x}^{{Z_{2} }} \left[{t\left( {x, x_{i} , x_{j} } \right)} \right]^{2} f\left( {x, x_{i}, x_{j} } \right)dx_{i} dx_{j} dx \hfill \\=& \mathop \int \limits_{{Z_{3} }}^{{Z_{2} }} \mathop \int \limits_{{Z_{3} }}^{x} \mathop \int \limits_{{Z_{1} }}^{x}\frac{{\left( {2x - x_{i} - x_{j} } \right)^{2} }}{{\left( {Z_{2} -Z_{1} } \right)\left( {Z_{4} - Z_{3} } \right)^{2} }}dx_{i} dx_{j}dx \\&+ \mathop \int \limits_{{Z_{2} }}^{{Z_{4} }} \mathop \int \limits_{{Z_{3} }}^{x} \mathop \int \limits_{{Z_{1} }}^{{Z_{2} }}\frac{{\left( {2x - x_{i} - x_{j} } \right)^{2} }}{{\left( {Z_{2} -Z_{1} } \right)\left( {Z_{4} - Z_{3} } \right)^{2} }}dx_{i} dx_{j}dx \hfill \\&+ \mathop \int \limits_{{Z_{3}}}^{{Z_{2} }} \mathop \int \limits_{x}^{{Z_{4} }} \mathop \int \limits_{{Z_{1} }}^{x} \frac{{\left( {x_{j} - x_{i} } \right)^{2}}}{{\left( {Z_{2} - Z_{1} } \right)\left( {Z_{4} - Z_{3} }\right)^{2} }}dx_{i} dx_{j} dx \\&+ \mathop \int \limits_{{Z_{2}}}^{{Z_{4} }} \mathop \int \limits_{x}^{{Z_{4} }} \mathop \int \limits_{{Z_{1} }}^{{Z_{2} }} \frac{{\left( {x_{j} - x_{i} }\right)^{2} }}{{\left( {Z_{2} - Z_{1} } \right)\left( {Z_{4} - Z_{3}} \right)^{2} }}dx_{i} dx_{j} dx \hfill \\& +\mathop \int \limits_{{Z_{3} }}^{{Z_{2} }} \mathop \int \limits_{{Z_{3} }}^{x} \mathop \int \limits_{x}^{{Z_{2} }}\frac{{\left( {x_{i} - x_{j} } \right)^{2} }}{{\left( {Z_{2} - Z_{1}} \right)\left( {Z_{4} - Z_{3} } \right)^{2} }}dx_{i} dx_{j} dx \\&+ \mathop \int \limits_{{Z_{3} }}^{{Z_{2} }} \mathop \int \limits_{x}^{{Z_{4} }} \mathop \int \limits_{x}^{{Z_{2} }}\frac{{\left( {x_{i} + x_{j} - 2x} \right)^{2} }}{{\left( {Z_{2} -Z_{1} } \right)\left( {Z_{4} - Z_{3} } \right)^{2} }}dx_{i} dx_{j}dx \hfill \\=& \frac{1}{{30\left( {Z_{2} - Z_{1} }\right)\left( {Z_{4} - Z_{3} } \right)^{2} }} \ge \left( 2Z_{2}^{5}- 7 Z_{3}^{5} - 5 Z_{1} Z_{3}^{4} - 25Z_{1} Z_{4}^{4} + 5 Z_{1}^{2}Z_{3}^{3} \right. \hfill \\&+ 25Z_{1}^{2} Z_{4}^{3} - 10Z_{1}^{3} Z_{3}^{2} - 10 Z_{1}^{3} Z_{4}^{2} + 25Z_{2} Z_{3}^{4} + 25Z_{2} Z_{4}^{4}- 25Z_{2}^{2} Z_{3}^{3} \\&-25Z_{2}^{2} Z_{4}^{3} + 20 Z_{2}^{3} Z_{3}^{2} + 20Z_{2}^{3}Z_{4}^{2}\\& - 5Z_{2}^{4} Z_{3} - 5Z_{2}^{4} Z_{4} - 10Z_{3}^{3}Z_{4}^{2} + 15Z_{3}^{4} Z_{4} + 50 Z_{1} Z_{3} Z_{4}^{3} - 30 Z_{1}Z_{3}^{2} Z_{4}^{2} \\&+ 10 Z_{1} Z_{3}^{3} Z_{4} - 45Z_{1}^{2} Z_{3}Z_{4}^{2} + 15Z_{1}^{2} Z_{3}^{2} Z_{4} + 20 Z_{1}^{3} Z_{3} Z_{4} - 50 Z_{2} Z_{3} Z_{4}^{3} \hfill \\&\left. {+60Z_{2} Z_{3}^{2} Z_{4}^{2} - 50 Z_{2} Z_{3}^{3} Z_{4} + 15Z_{2}^{2}Z_{3} Z_{4}^{2} + 15Z_{2}^{2} Z_{3}^{2} Z_{4} - 20Z_{2}^{3} Z_{3}Z_{4} } \right) \hfill \\ \end{aligned}$$

(A20)

For travel from F to E, the expression for travel time T is

$$ T\left( {X,~X_{i} ,~X_{j} } \right) = \left| {X - X_{i} \left| + \right|X - X_{j} } \right| = \left\{ \begin{gathered} 2X - X_{i} - X_{j} \quad \quad X \ge X_{i} ,~X \ge X_{j} \quad \quad {\text{Case~}}\;1 \hfill \\ X_{j} - X_{i} \quad \quad \quad \quad X \ge X_{i} ,~X < X_{j} \quad \quad {\text{Case~}}\;2 \hfill \\ X_{i} - X_{j} \quad \quad \quad \quad X < X_{i} ,~X \ge X_{j} \quad \quad {\text{Case~}}\;3 \hfill \\ X_{i} + X_{j} - 2X\quad \quad X < X_{i} ,~X < X_{j} \quad \quad {\text{Case~}}\;4 \hfill \\ \end{gathered} \right. $$

where $x, x_{j} \sim {\text{unif}}\left[ {Z_{1} ,Z_{2} } \right]$ and $x_{i} \sim {\text{unif}}\left[ {Z_{3} ,Z_{4} } \right]$ with a joint pdf $f\left( {x, x_{i} , x_{j} } \right) = f\left( x \right)f\left( {x_{i} } \right)f\left( {x_{j} } \right) = \frac{1}{{\left( {Z_{4} - Z_{3} } \right)\left( {Z_{2} - Z_{1} } \right)^{2} }}$. The first two moments of T are:

$$\begin{aligned}E\left[T\right]=&{\int }_{{Z}_{3}}^{{Z}_{2}}{\int }_{{Z}_{1}}^{x}{\int }_{{Z}_{3}}^{x}t({x,x}_{i}, {x}_{j})f(x, {x}_{i}, {x}_{j})d{x}_{i}d{x}_{j}dx\\&+{\int }_{{Z}_{3}}^{{Z}_{2}}{\int }_{x}^{{Z}_{2}}{\int }_{{Z}_{3}}^{x}t({x,x}_{i}, {x}_{j})f(x, {x}_{i}, {x}_{j})d{x}_{i}d{x}_{j}dx\\&+{\int }_{{Z}_{1}}^{{Z}_{2}}{\int }_{{Z}_{1}}^{x}{\int }_{{\mathrm{max}(x,Z}_{3})}^{{Z}_{4}}t({x, x}_{i}, {x}_{j})f(x, {x}_{i},{x}_{j})d{x}_{i}d{x}_{j}dx\\&+{\int }_{{Z}_{1}}^{{Z}_{2}}{\int }_{x}^{{Z}_{2}}{\int }_{{\mathrm{max}(x, Z}_{3})}^{{Z}_{2}}t({x,x}_{i}, {x}_{j})f(x, {x}_{i}, {x}_{j})d{x}_{i}d{x}_{j}dx\\=&{\int }_{{Z}_{3}}^{{Z}_{2}}{\int }_{{Z}_{1}}^{x}{\int }_{{Z}_{3}}^{x}\frac{{2x-x}_{i}-{x}_{j}}{\left({Z}_{4}-{Z}_{3}\right){\left({Z}_{2}-{Z}_{1}\right)}^{2}}d{x}_{i}d{x}_{j}dx\\&+{\int }_{{Z}_{3}}^{{Z}_{2}}{\int }_{x}^{{Z}_{2}}{\int }_{{Z}_{3}}^{x}\frac{{{x}_{j}-x}_{i}}{\left({Z}_{4}-{Z}_{3}\right){\left({Z}_{2}-{Z}_{1}\right)}^{2}}d{x}_{i}d{x}_{j}dx\\&+{\int }_{{Z}_{1}}^{{Z}_{3}}{\int }_{{Z}_{1}}^{x}{\int }_{{Z}_{3}}^{{Z}_{4}}\frac{{x}_{i}-{x}_{j}}{\left({Z}_{4}-{Z}_{3}\right){\left({Z}_{2}-{Z}_{1}\right)}^{2}}d{x}_{i}d{x}_{j}dx\\&+{\int }_{{Z}_{3}}^{{Z}_{2}}{\int }_{{Z}_{1}}^{x}{\int }_{x}^{{Z}_{4}}\frac{{x}_{i}-{x}_{j}}{\left({Z}_{4}-{Z}_{3}\right){\left({Z}_{2}-{Z}_{1}\right)}^{2}}d{x}_{i}d{x}_{j}dx\\&+{\int }_{{Z}_{1}}^{{Z}_{3}}{\int }_{x}^{{Z}_{2}}{\int }_{{Z}_{3}}^{{Z}_{2}}\frac{{x}_{i}+{x}_{j}-2x}{\left({Z}_{4}-{Z}_{3}\right){\left({Z}_{2}-{Z}_{1}\right)}^{2}}d{x}_{i}d{x}_{j}dx\\&+{\int }_{{Z}_{3}}^{{Z}_{2}}{\int }_{x}^{{Z}_{2}}{\int }_{x}^{{Z}_{4}}\frac{{x}_{i}+{x}_{j}-2x}{\left({Z}_{4}-{Z}_{3}\right){\left({Z}_{2}-{Z}_{1}\right)}^{2}}d{x}_{i}d{x}_{j}dx\\=&\frac{1}{6({Z}_{2}-{Z}_{1})({Z}_{4}-{Z}_{3})}\left(2 {{Z}_{2}}^{3}-2{{Z}_{3}}^{3}+3{Z}_{1}{{Z}_{3}}^{2}-3{Z}_{1}{{Z}_{4}}^{2}-5 {{Z}_{1}}^{2}{Z}_{3}+5{{Z}_{1}}^{2}{Z}_{4}\right.\\&\left.+3{Z}_{2}{{Z}_{3}}^{2}+3 {Z}_{2}{{Z}_{4}}^{2}-5{{Z}_{2}}^{2}{Z}_{3}-{{Z}_{2}}^{2}{Z}_{4}+4{Z}_{1}{Z}_{2}{Z}_{3}-4{Z}_{1}{Z}_{2}{Z}_{4}\right)\end{aligned}$$

(A21)

$$\begin{aligned}E\left[{T}^{2}\right]=&{\int }_{{Z}_{3}}^{{Z}_{2}}{\int }_{{Z}_{1}}^{x}{\int }_{{Z}_{3}}^{x}{\left[t(x, {x}_{i}, {x}_{j})\right]}^{2}f(x,{x}_{i}, {x}_{j})d{x}_{i}d{x}_{j}dx\\&+{\int }_{{Z}_{3}}^{{Z}_{2}}{\int }_{x}^{{Z}_{2}}{\int }_{{Z}_{3}}^{x}{\left[t(x, {x}_{i},{x}_{j})\right]}^{2}f(x, {x}_{i}, {x}_{j})d{x}_{i}d{x}_{j}dx\\&+{\int }_{{Z}_{1}}^{{Z}_{2}}{\int }_{{Z}_{1}}^{x}{\int }_{{\mathrm{max}(x,Z}_{3})}^{{Z}_{4}}{\left[t(x, {x}_{i}, {x}_{j})\right]}^{2}f(x,{x}_{i}, {x}_{j})d{x}_{i}d{x}_{j}dx\\&+{\int }_{{Z}_{1}}^{{Z}_{2}}{\int }_{x}^{{Z}_{2}}{\int }_{{\mathrm{max}(x,Z}_{3})}^{{Z}_{2}}{\left[t(x, {x}_{i}, {x}_{j})\right]}^{2}f(x,{x}_{i}, {x}_{j})d{x}_{i}d{x}_{j}dx\\=&{\int }_{{Z}_{3}}^{{Z}_{2}}{\int }_{{Z}_{1}}^{x}{\int }_{{Z}_{3}}^{x}\frac{{({2x-x}_{i}-{x}_{j})}^{2}}{\left({Z}_{4}-{Z}_{3}\right){\left({Z}_{2}-{Z}_{1}\right)}^{2}}d{x}_{i}d{x}_{j}dx\\&+{\int }_{{Z}_{3}}^{{Z}_{2}}{\int }_{x}^{{Z}_{2}}{\int }_{{Z}_{3}}^{x}\frac{{({{x}_{j}-x}_{i})}^{2}}{\left({Z}_{4}-{Z}_{3}\right){\left({Z}_{2}-{Z}_{1}\right)}^{2}}d{x}_{i}d{x}_{j}dx\\&+{\int }_{{Z}_{1}}^{{Z}_{3}}{\int }_{{Z}_{1}}^{x}{\int }_{{Z}_{3}}^{{Z}_{4}}\frac{{({x}_{i}-{x}_{j})}^{2}}{\left({Z}_{4}-{Z}_{3}\right){\left({Z}_{2}-{Z}_{1}\right)}^{2}}d{x}_{i}d{x}_{j}dx\\&+{\int }_{{Z}_{3}}^{{Z}_{2}}{\int }_{{Z}_{1}}^{x}{\int }_{x}^{{Z}_{4}}\frac{{({x}_{i}-{x}_{j})}^{2}}{\left({Z}_{4}-{Z}_{3}\right){\left({Z}_{2}-{Z}_{1}\right)}^{2}}d{x}_{i}d{x}_{j}dx\\&+{\int }_{{Z}_{1}}^{{Z}_{3}}{\int }_{x}^{{Z}_{2}}{\int }_{{Z}_{3}}^{{Z}_{2}}\frac{{({x}_{i}+{x}_{j}-2x)}^{2}}{\left({Z}_{4}-{Z}_{3}\right){\left({Z}_{2}-{Z}_{1}\right)}^{2}}d{x}_{i}d{x}_{j}dx\\&+{\int }_{{Z}_{3}}^{{Z}_{2}}{\int }_{x}^{{Z}_{2}}{\int }_{x}^{{Z}_{4}}\frac{{({x}_{i}+{x}_{j}-2x)}^{2}}{\left({Z}_{4}-{Z}_{3}\right){\left({Z}_{2}-{Z}_{1}\right)}^{2}}d{x}_{i}d{x}_{j}dx\\=& \frac{1}{{30(Z_{2} - Z_{1} )^{2} (Z_{4} - Z_{3} )}}(7Z_{2} ^{5} - 2Z_{3} ^{5} - 15Z_{1} Z_{2} ^{4} + 5Z_{1} Z_{3} ^{4} + 10Z_{1} ^{2} Z_{2} ^{3} \hfill \\&- 20Z_{1} ^{2} Z_{3} ^{3} + 10Z_{1} ^{2} Z_{4} ^{3} + 25Z_{1} ^{3} Z_{3} ^{2}- 25Z_{1} ^{3} Z_{4} ^{2} - 25Z_{1} ^{4} Z_{3} + 25Z_{1} ^{4}Z_{4} \hfill \\ & + 5Z_{2} Z_{3} ^{4} - 20Z_{2} ^{2} Z_{3} ^{3}+ 10Z_{2} ^{2} Z_{4} ^{3} + 25Z_{2} ^{3} Z_{3} ^{2} - 5Z_{2} ^{3}Z_{4} ^{2} - 25Z_{2} ^{4} Z_{3} \hfill \\ & + 5Z_{2} ^{4} Z_{4}+ 20Z_{1} Z_{2} Z_{3} ^{3} - 20Z_{1} Z_{2} Z_{4} ^{3} - 15Z_{1}Z_{2} ^{2} Z_{3} ^{2} - 15Z_{1} Z_{2} ^{2} Z_{4} ^{2} \hfill \\&+ 50Z_{1} Z_{2} ^{3} Z_{3} - 10Z_{1} Z_{2} ^{3} Z_{4} - 15Z_{1}^{2} Z_{2} Z_{3} ^{2} + 45Z_{1} ^{2} Z_{2} Z_{4} ^{2} - 60Z_{1}^{2} Z_{2} ^{2} Z_{3} \hfill \\ & + 30Z_{1} ^{2} Z_{2} ^{2} Z_{4}+ 50Z_{1} ^{3} Z_{2} Z_{3} - 50Z_{1} ^{3} Z_{2} Z_{4})\end{aligned}$$

(A22)

Travel pattern (c) with $Z_{3} \le Z_{1}\le Z_{2} \le Z_{4}$

For travel from E to F, the expression for travel time T is

$$T(X, {X}_{i},{X}_{j})=|X-{X}_{i}|+|X-{X}_{j}|=\left\{\begin{array}{l@{\quad}l}{2X-X}_{i}-{X}_{j}& X\ge {X}_{i}, X\ge {X}_{j}\,\,\, \mathrm{Case }\,1\\{{X}_{j}-X}_{i} &X\ge {X}_{i}, X<{X}_{j} \,\,\,\mathrm{Case }\,2\\{X}_{i}-{X}_{j} &X<{X}_{i}, X\ge {X}_{j} \,\,\,\mathrm{Case }\,3\\{X}_{i}+{X}_{j}-2X &X<{X}_{i}, X<{X}_{j} \,\,\,\mathrm{Case }\,4 \end{array}\right.$$

where $x_{i} \sim {\text{unif}}\left[ {Z_{1} ,Z_{2}} \right]$ and $x,{ }x_{j} \sim {\text{unif}}\left[ {Z_{3} ,Z_{4} }\right]$ with a joint pdf $f\left( {x,{ }x_{i} ,{ }x_{j} } \right) =f\left( x \right)f\left( {x_{i} } \right)f\left( {x_{j} } \right) =\frac{1}{{\left( {Z_{2} - Z_{1} } \right)\left( {Z_{4} - Z_{3} }\right)^{2} }}$. The first two moments of T are:

$$ \begin{aligned} E\left[ T \right] =&\mathop \int \limits_{{Z_{1} }}^{{Z_{4} }} \mathop \int \limits_{{Z_{3} }}^{x} \mathop \int \limits_{{Z_{1} }}^{{min\left({x, Z_{2} } \right)}} t\left( {x, x_{i} , x_{j} } \right)f\left( {x,x_{i} , x_{j} } \right)dx_{i} dx_{j} dx\\& + \mathop \int \limits_{{Z_{1} }}^{{Z_{4} }} \mathop \int \limits_{x}^{{Z_{4} }}\mathop \int \limits_{{Z_{1} }}^{{min\left( {x, Z_{2} } \right)}}t\left( {x, x_{i} , x_{j} } \right)f\left( {x, x_{i} , x_{j} }\right)dx_{i} dx_{j} dx \hfill \\ & + \mathop \int \limits_{{Z_{3} }}^{{Z_{2} }} \mathop \int \limits_{{Z_{3} }}^{x}\mathop \int \limits_{{max\left( {x, Z_{1} } \right)}}^{{Z_{2} }}t\left( {x, x_{i} , x_{j} } \right)f\left( {x, x_{i} , x_{j} }\right)dx_{i} dx_{j} dx\\& + \mathop \int \limits_{{Z_{3} }}^{{Z_{2} }}\mathop \int \limits_{x}^{{Z_{4} }} \mathop \int \limits_{{max\left({x, Z_{1} } \right)}}^{{Z_{2} }} t\left( {x, x_{i} , x_{j} }\right)f\left( {x, x_{i} , x_{j} } \right)dx_{i} dx_{j} dx \hfill \\&= \mathop \int \limits_{{Z_{1} }}^{{Z_{2} }} \mathop \int \limits_{{Z_{3} }}^{x} \mathop \int \limits_{{Z_{1} }}^{x}\frac{{2x - x_{i} - x_{j} }}{{\left( {Z_{2} - Z_{1} } \right)\left({Z_{4} - Z_{3} } \right)^{2} }}dx_{i} dx_{j} dx \\&+ \mathop \int \limits_{{Z_{2} }}^{{Z_{4} }} \mathop \int \limits_{{Z_{3} }}^{x}\mathop \int \limits_{{Z_{1} }}^{{Z_{2} }} \frac{{2x - x_{i} - x_{j}}}{{\left( {Z_{2} - Z_{1} } \right)\left( {Z_{4} - Z_{3} }\right)^{2} }}dx_{i} dx_{j} dx \hfill \\& + \mathop \int \limits_{{Z_{1} }}^{{Z_{2} }} \mathop \int \limits_{x}^{{Z_{4} }}\mathop \int \limits_{{Z_{1} }}^{x} \frac{{x_{j} - x_{i} }}{{\left({Z_{2} - Z_{1} } \right)\left( {Z_{4} - Z_{3} } \right)^{2} }}dx_{i}dx_{j} dx\\& + \mathop \int \limits_{{Z_{2} }}^{{Z_{4} }} \mathop \int \limits_{x}^{{Z_{4} }} \mathop \int \limits_{{Z_{1} }}^{{Z_{2} }}\frac{{x_{j} - x_{i} }}{{\left( {Z_{2} - Z_{1} } \right)\left({Z_{4} - Z_{3} } \right)^{2} }}dx_{i} dx_{j} dx \hfill \\&+ \mathop \int \limits_{{Z_{3} }}^{{Z_{1} }} \mathop \int \limits_{{Z_{3} }}^{x} \mathop \int \limits_{{Z_{1} }}^{{Z_{2} }}\frac{{x_{i} - x_{j} }}{{\left( {Z_{2} - Z_{1} } \right)\left({Z_{4} - Z_{3} } \right)^{2} }}dx_{i} dx_{j} dx\\& + \mathop \int \limits_{{Z_{1} }}^{{Z_{2} }} \mathop \int \limits_{{Z_{3} }}^{x}\mathop \int \limits_{x}^{{Z_{2} }} \frac{{x_{i} - x_{j} }}{{\left({Z_{2} - Z_{1} } \right)\left( {Z_{4} - Z_{3} } \right)^{2} }}dx_{i}dx_{j} dx \hfill \\&+ \mathop \int \limits_{{Z_{3}}}^{{Z_{1} }} \mathop \int \limits_{x}^{{Z_{4} }} \mathop \int \limits_{{Z_{1} }}^{{Z_{2} }} \frac{{x_{i} + x_{j} - 2x}}{{\left({Z_{2} - Z_{1} } \right)\left( {Z_{4} - Z_{3} } \right)^{2} }}dx_{i}dx_{j} dx \\&+ \mathop \int \limits_{{Z_{1} }}^{{Z_{2} }} \mathop \int \limits_{x}^{{Z_{4} }} \mathop \int \limits_{x}^{{Z_{2} }}\frac{{x_{i} + x_{j} - 2x}}{{\left( {Z_{2} - Z_{1} } \right)\left({Z_{4} - Z_{3} } \right)^{2} }}dx_{i} dx_{j} dx \hfill \\=& \frac{1}{{6\left( {Z_{4} - Z_{3} } \right)}}\left({2Z_{1}^{2} + 2Z_{2}^{2} + 5Z_{3}^{2} + 5Z_{4}^{2} + 2Z_{1} Z_{2} -3Z_{1} Z_{3} - 3Z_{1} Z_{4} } \right. \hfill \\&\left. { - 3Z_{2} Z_{3} - 3Z_{2} Z_{4} - 4Z_{3} Z_{4} } \right)\hfill \\ \end{aligned} $$

(A23)

$$ \begin{aligned} \left[ {T^{2} } \right] =&\mathop \int \limits_{{Z_{1} }}^{{Z_{4} }} \mathop \int \limits_{{Z_{3} }}^{x} \mathop \int \limits_{{Z_{1} }}^{{min\left({x, Z_{2} } \right)}} \left[ {t\left( {x, x_{i} , x_{j} } \right)}\right]^{2} f\left( {x, x_{i} , x_{j} } \right)dx_{i} dx_{j} dx\\& + \mathop \int \limits_{{Z_{1} }}^{{Z_{4} }} \mathop \int \limits_{x}^{{Z_{4} }} \mathop \int \limits_{{Z_{1} }}^{{min\left({x, Z_{2} } \right)}} \left[ {t\left( {x, x_{i} , x_{j} } \right)}\right]^{2} f\left( {x, x_{i} , x_{j} } \right)dx_{i} dx_{j} dx \hfill \\ &+ \mathop \int \limits_{{Z_{3}}}^{{Z_{2} }} \mathop \int \limits_{{Z_{3} }}^{x} \mathop \int \limits_{{max\left( {x, Z_{1} } \right)}}^{{Z_{2} }} \left[ {t\left({x, x_{i} , x_{j} } \right)} \right]^{2} f\left( {x, x_{i} , x_{j} }\right)dx_{i} dx_{j} dx \\&+ \mathop \int \limits_{{Z_{3} }}^{{Z_{2} }}\mathop \int \limits_{x}^{{Z_{4} }} \mathop \int \limits_{{max\left({x, Z_{1} } \right)}}^{{Z_{2} }} \left[ {t\left( {x, x_{i} , x_{j} }\right)} \right]^{2} f\left( {x, x_{i} , x_{j} } \right)dx_{i}dx_{j} dx \hfill \\ =& \mathop \int \limits_{{Z_{1}}}^{{Z_{2} }} \mathop \int \limits_{{Z_{3} }}^{x} \mathop \int \limits_{{Z_{1} }}^{x} \frac{{\left( {2x - x_{i} - x_{j} }\right)^{2} }}{{\left( {Z_{2} - Z_{1} } \right)\left( {Z_{4} - Z_{3}} \right)^{2} }}dx_{i} dx_{j} dx\\& + \mathop \int \limits_{{Z_{2}}}^{{Z_{4} }} \mathop \int \limits_{{Z_{3} }}^{x} \mathop \int \limits_{{Z_{1} }}^{{Z_{2} }} \frac{{\left( {2x - x_{i} - x_{j} }\right)^{2} }}{{\left( {Z_{2} - Z_{1} } \right)\left( {Z_{4} - Z_{3}} \right)^{2} }}dx_{i} dx_{j} dx \hfill \\&+ \mathop \int \limits_{{Z_{1} }}^{{Z_{2} }} \mathop \int \limits_{x}^{{Z_{4} }} \mathop \int \limits_{{Z_{1} }}^{x}\frac{{\left( {x_{j} - x_{i} } \right)^{2} }}{{\left( {Z_{2} - Z_{1}} \right)\left( {Z_{4} - Z_{3} } \right)^{2} }}dx_{i} dx_{j} dx \\&+ \mathop \int \limits_{{Z_{2} }}^{{Z_{4} }} \mathop \int \limits_{x}^{{Z_{4} }} \mathop \int \limits_{{Z_{1} }}^{{Z_{2} }}\frac{{\left( {x_{j} - x_{i} } \right)^{2} }}{{\left( {Z_{2} - Z_{1}} \right)\left( {Z_{4} - Z_{3} } \right)^{2} }}dx_{i} dx_{j} dx \hfill \\&+ \mathop \int \limits_{{Z_{3}}}^{{Z_{1} }} \mathop \int \limits_{{Z_{3} }}^{x} \mathop \int \limits_{{Z_{1} }}^{{Z_{2} }} \frac{{\left( {x_{i} - x_{j} }\right)^{2} }}{{\left( {Z_{2} - Z_{1} } \right)\left( {Z_{4} - Z_{3}} \right)^{2} }}dx_{i} dx_{j} dx \\&+ \mathop \int \limits_{{Z_{1}}}^{{Z_{2} }} \mathop \int \limits_{{Z_{3} }}^{x} \mathop \int \limits_{x}^{{Z_{2} }} \frac{{\left( {x_{i} - x_{j} } \right)^{2}}}{{\left( {Z_{2} - Z_{1} } \right)\left( {Z_{4} - Z_{3} }\right)^{2} }}dx_{i} dx_{j} dx \hfill \\&+ \mathop \int \limits_{{Z_{3} }}^{{Z_{1} }} \mathop \int \limits_{x}^{{Z_{4}}} \mathop \int \limits_{{Z_{1} }}^{{Z_{2} }} \frac{{\left( {x_{i} +x_{j} - 2x} \right)^{2} }}{{\left( {Z_{2} - Z_{1} } \right)\left({Z_{4} - Z_{3} } \right)^{2} }}dx_{i} dx_{j} dx\\&+ \mathop \int \limits_{{Z_{1} }}^{{Z_{2} }} \mathop \int \limits_{x}^{{Z_{4} }}\mathop \int \limits_{x}^{{Z_{2} }} \frac{{\left( {x_{i} + x_{j} -2x} \right)^{2} }}{{\left( {Z_{2} - Z_{1} } \right)\left( {Z_{4} -Z_{3} } \right)^{2} }}dx_{i} dx_{j} dx \hfill \\=& \frac{1}{{30\left( {Z_{4} - Z_{3} } \right)^{2} }}\left( {2Z_{1}^{4}+ 2{ }Z_{2}^{4} + 25{ }Z_{3}^{4} + 25Z_{4}^{4} + 2Z_{1} Z_{2}^{3} -25{ }Z_{1} Z_{3}^{3} } \right. \hfill \\&- 25{ }Z_{1} Z_{4}^{3} + 2{ }Z_{1}^{2}Z_{2}^{2} + 20{ }Z_{1}^{2} Z_{3}^{2} \\&+ 20{ }Z_{1}^{2} Z_{4}^{2} + 2Z_{1}^{3} Z_{2} - 5{ }Z_{1}^{3}Z_{3} - 5{ }Z_{1}^{3} Z_{4} - 25Z_{2} Z_{3}^{3} { } - 25{ }Z_{2}Z_{4}^{3} \\&+ 20Z_{2}^{2} Z_{3}^{2} + 20Z_{2}^{2} Z_{4}^{2} -5Z_{2}^{3} Z_{3} - 5{ }Z_{2}^{3} Z_{4} \hfill \\&- 50{ }Z_{3} Z_{4}^{3} + 60Z_{3}^{2} Z_{4}^{2} { } - 50{ }Z_{3}^{3}Z_{4} { } + 20{ }Z_{1} Z_{2} Z_{3}^{2} + 20{ }Z_{1} Z_{2} Z_{4}^{2}\\&+ 15{ }Z_{1} Z_{3} Z_{4}^{2} - 5Z_{1} Z_{2}^{2} Z_{3} - 5{ }Z_{1}Z_{2}^{2} Z_{4} \hfill \\&+ 15{ }Z_{1}Z_{3}^{2} Z_{4} - 5Z_{1}^{2} Z_{2} Z_{3} - 5Z_{1}^{2} Z_{2} Z_{4} -20Z_{1}^{2} Z_{3} Z_{4}\\&\left. { + 15Z_{2} Z_{3} Z_{4}^{2} { } + 15{ }Z_{2}Z_{3}^{2} Z_{4} - 20{ }Z_{2}^{2} Z_{3} Z_{4} - 20Z_{1} Z_{2} Z_{3}Z_{4} } \right) \hfill \\ \end{aligned}$$

(A24)

For travel from F to E, the expression for travel time T is

$$ T\left( {X,~X_{i} ,~X_{j} } \right) = \left| {X - X_{i} \left| + \right|X - X_{j} } \right| = \left\{ \begin{gathered} 2X - X_{i} - X_{j} \quad \quad X \ge X_{i} ,~X \ge X_{j} \quad \quad {\text{Case~}}\;1 \hfill \\ X_{j} - X_{i} \quad \quad \quad \quad X \ge X_{i} ,~X < X_{j} \quad \quad {\text{Case~}}\;2 \hfill \\ X_{i} - X_{j} ~\quad \quad \quad \quad X < X_{i} ,~X \ge X_{j} \quad \quad {\text{Case~}}\;3 \hfill \\ X_{i} + X_{j} - 2X~\quad \quad X < X_{i} ,~X < X_{j} \quad \quad {\text{Case~}}\;4 \hfill \\ \end{gathered} \right. $$

where $X,{ }X_{j} \sim {\text{unif}}\left[ {Z_{1},Z_{2} } \right]$ and $X_{i} \sim {\text{unif}}\left[ {Z_{3} ,Z_{4}} \right]$ with a joint pdf $f\left( {x,{ }x_{i} ,{ }x_{j} } \right) =f\left( x \right)f\left( {x_{i} } \right)f\left( {x_{j} } \right) =\frac{1}{{\left( {Z_{2} - Z_{1} } \right)^{2} \left( {Z_{4} - Z_{3}} \right)}}$. The first two moments of T are:

$$ \begin{gathered} E\left[ T \right] =\mathop \int \limits_{{Z_{1} }}^{{Z_{2} }} \mathop \int \limits_{{Z_{1} }}^{x} \mathop \int \limits_{{Z_{3} }}^{x} t\left({x, x_{i} , x_{j} } \right)f\left( {x, x_{i} , x_{j} } \right)dx_{i}dx_{j} dx + \mathop \int \limits_{{Z_{1} }}^{{Z_{2} }} \mathop \int \limits_{x}^{{Z_{2} }} \mathop \int \limits_{{Z_{3} }}^{x} t\left({x, x_{i} , x_{j} } \right)f\left( {x, x_{i} , x_{j} } \right)dx_{i}dx_{j} dx \hfill \\ \quad \quad \quad + \mathop \int \limits_{{Z_{1}}}^{{Z_{2} }} \mathop \int \limits_{{Z_{1} }}^{x} \mathop \int \limits_{x}^{{Z_{4} }} t\left( {x, x_{i} , x_{j} } \right)f\left({x, x_{i} , x_{j} } \right)dx_{i} dx_{j} dx + \mathop \int \limits_{{Z_{1} }}^{{Z_{2} }} \mathop \int \limits_{x}^{{Z_{2} }}\mathop \int \limits_{x}^{{Z_{4} }} t\left( {x, x_{i} , x_{j} }\right)f\left( {x, x_{i} , x_{j} } \right)dx_{i} dx_{j} dx \hfill \\\quad \quad \quad = \mathop \int \limits_{{Z_{1} }}^{{Z_{2} }}\mathop \int \limits_{{Z_{1} }}^{x} \mathop \int \limits_{{Z_{3}}}^{x} \frac{{2x - x_{i} - x_{j} }}{{\left( {Z_{4} - Z_{3} }\right)\left( {Z_{2} - Z_{1} } \right)^{2} }}dx_{i} dx_{j} dx +\mathop \int \limits_{{Z_{1} }}^{{Z_{2} }} \mathop \int \limits_{x}^{{Z_{2} }} \mathop \int \limits_{{Z_{3} }}^{x}\frac{{x_{j} - x_{i} }}{{\left( {Z_{4} - Z_{3} } \right)\left({Z_{2} - Z_{1} } \right)^{2} }}dx_{i} dx_{j} dx \hfill \\ \quad \quad \quad + \mathop \int \limits_{{Z_{1} }}^{{Z_{2} }} \mathop \int \limits_{{Z_{1} }}^{x} \mathop \int \limits_{x}^{{Z_{4} }}\frac{{x_{i} - x_{j} }}{{\left( {Z_{4} - Z_{3} } \right)\left({Z_{2} - Z_{1} } \right)^{2} }}dx_{i} dx_{j} dx + \mathop \int \limits_{{Z_{1} }}^{{Z_{2} }} \mathop \int \limits_{x}^{{Z_{2} }}\mathop \int \limits_{x}^{{Z_{4} }} \frac{{x_{i} + x_{j} -2x}}{{\left( {Z_{4} - Z_{3} } \right)\left( {Z_{2} - Z_{1} }\right)^{2} }}dx_{i} dx_{j} dx \hfill \\ \quad \quad \quad =\frac{1}{{6\left( {Z_{4} - Z_{3} } \right)}}\left( {2Z_{1}^{2} +2Z_{2}^{2} + 3Z_{3}^{2} + 3Z_{4}^{2} + 2Z_{1} Z_{2} - Z_{1} Z_{3} -5Z_{1} Z_{4} - 5Z_{2} Z_{3} - Z_{2} Z_{4} } \right) \hfill \\\end{gathered} $$

(A25)

$$ \begin{gathered} E\left[ {T^{2} } \right] =\mathop \int \limits_{{Z_{1} }}^{{Z_{2} }} \mathop \int \limits_{{Z_{1} }}^{x} \mathop \int \limits_{{Z_{3} }}^{x} \left[{t\left( {x, x_{i} , x_{j} } \right)} \right]^{2} f\left( {x, x_{i}, x_{j} } \right)dx_{i} dx_{j} dx \hfill \\ \quad \quad \quad +\mathop \int \limits_{{Z_{1} }}^{{Z_{2} }} \mathop \int \limits_{x}^{{Z_{2} }} \mathop \int \limits_{{Z_{3} }}^{x} \left[{t\left( {x, x_{i} , x_{j} } \right)} \right]^{2} f\left( {x, x_{i}, x_{j} } \right)dx_{i} dx_{j} dx \hfill \\ \quad \quad \quad +\mathop \int \limits_{{Z_{1} }}^{{Z_{2} }} \mathop \int \limits_{{Z_{1} }}^{x} \mathop \int \limits_{x}^{{Z_{4} }} \left[{t\left( {x, x_{i} , x_{j} } \right)} \right]^{2} f\left( {x, x_{i}, x_{j} } \right)dx_{i} dx_{j} dx \hfill \\ \quad \quad \quad =\mathop \int \limits_{{Z_{1} }}^{{Z_{2} }} \mathop \int \limits_{x}^{{Z_{2} }} \mathop \int \limits_{x}^{{Z_{4} }} \left[{t\left( {x, x_{i} , x_{j} } \right)} \right]^{2} f\left( {x, x_{i}, x_{j} } \right)dx_{i} dx_{j} dx \hfill \\ \quad \quad \quad =\mathop \int \limits_{{Z_{1} }}^{{Z_{2} }} \mathop \int \limits_{{Z_{1} }}^{x} \mathop \int \limits_{{Z_{3} }}^{x}\frac{{\left( {2x - x_{i} - x_{j} } \right)^{2} }}{{\left( {Z_{4} -Z_{3} } \right)\left( {Z_{2} - Z_{1} } \right)^{2} }}dx_{i} dx_{j}dx + \mathop \int \limits_{{Z_{1} }}^{{Z_{2} }} \mathop \int \limits_{x}^{{Z_{2} }} \mathop \int \limits_{{Z_{3} }}^{x}\frac{{\left( {x_{j} - x_{i} } \right)^{2} }}{{\left( {Z_{4} - Z_{3}} \right)\left( {Z_{2} - Z_{1} } \right)^{2} }}dx_{i} dx_{j} dx \hfill \\ \quad \quad \quad + \mathop \int \limits_{{Z_{1}}}^{{Z_{2} }} \mathop \int \limits_{{Z_{1} }}^{x} \mathop \int \limits_{x}^{{Z_{4} }} \frac{{\left( {x_{i} - x_{j} } \right)^{2}}}{{\left( {Z_{4} - Z_{3} } \right)\left( {Z_{2} - Z_{1} }\right)^{2} }}dx_{i} dx_{j} dx + \mathop \int \limits_{{Z_{1}}}^{{Z_{2} }} \mathop \int \limits_{x}^{{Z_{2} }} \mathop \int \limits_{x}^{{Z_{4} }} \frac{{\left( {x_{i} + x_{j} - 2x}\right)^{2} }}{{\left( {Z_{4} - Z_{3} } \right)\left( {Z_{2} - Z_{1}} \right)^{2} }}dx_{i} dx_{j} dx \hfill \\ \quad \quad \quad =\frac{1}{{30\left( {Z_{4} - Z_{3} } \right)}}\left( { - 7Z_{1}^{3} +7{ }Z_{2}^{3} - 10{ }Z_{3}^{3} + 10Z_{4}^{3} - Z_{1} Z_{2}^{2} +5Z_{1} Z_{3}^{2} - 25Z_{1} Z_{4}^{2} } \right. \hfill \\ \left.{\quad \quad \quad + Z_{1}^{2} Z_{2} - 5Z_{1}^{2} Z_{3} +25Z_{1}^{2} Z_{4} + 25Z_{2} Z_{3}^{2} - 5Z_{2} Z_{4}^{2} -25Z_{2}^{2} Z_{3} + 5Z_{2}^{2} Z_{4} } \right) \hfill \\\end{gathered} $$

(A26)