Optimal channel structure for a green supply chain with consumer green-awareness demand

Abstract

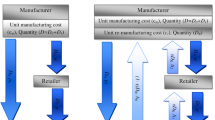
This paper examines the optimal channel structure of a green supply chain consisting of one manufacturer and one retailer. The manufacturer, who is the Stackelberg leader, is responsible for green technology costs. Consumers prefer green products and therefore are green aware. We study four channel structures: a manufacturer’s dual-channel supply chain, a retailer’s dual-channel supply chain, a manufacturer-online and retailer-offline (hybrid I) structure, and a manufacturer-offline and retailer-online (hybrid II) structure. For each structure, we analytically investigate the impact of consumers’ green awareness and proportion of online and offline consumers on the level of green technology, profits, and retail prices. We also examine the effect on the optimal solutions of the manufacturer and retailer when they share the green cost. The results show that the manufacturer’s dual-channel supply chain performs the best in improving the greenness of products and its own profits. Concerning hybrid dual-channel supply chains, the manufacturer will always choose the channel with the majority of consumers to directly sell products through. The retailer, in most cases, also prefers to operate two channels simultaneously. In addition, regardless of the type of channel structure involved, consumers’ green awareness encourages the manufacturer to improve the greenness of its products; however, the proportion of online consumers has a positive effect on the greenness of products in the retailer-offline and manufacturer-online cases but a negative effect in the retailer-online and manufacturer-offline cases.

Appendices

Appendix

1.1 To save space, this section can be provided in a separate file if the paper is accepted.

For the simplicity of calculation, we define some useful expressions as follows:

${\text{T = }}\gamma^{2} \left( {2\rho - 1 + s\left( {1 + \beta } \right)} \right)$, ${\text{L}} = 1 - \beta^{2}$, $K = \rho + \beta - \rho \beta$,

$G = \gamma^{2} \left( {1 - 2\rho + 3s\left( {1 + \beta } \right)} \right)$, $F = \rho b - \rho + 1$.

Part 1: Proof of Proposition and Lemma

2.1 Proof of Proposition1

This paper uses the Stackelberg model. The manufacturer is the leader. In the manufacturer’s dual-channel model, there is no retailer, and the manufacturer’s profit is the profit of the entire supply chain.

The manufacturer’s profit function is:

$$ \prod_{MM} = p_{d} D_{d} + \left( {p_{n} - s} \right)D_{n} - \frac{{t^{2} }}{2} $$

The first order conditions are as follows:

$$ \frac{{\partial \prod_{MM} }}{{\partial p_{d} }} = - 2p_{d} + 2\beta p_{n} + \rho + \gamma t - \beta s $$

$$ \frac{{\partial \prod_{MM} }}{{\partial p_{n} }} = - 2p_{n} + 2\beta p_{d} - \rho + \gamma t + 1 + s $$

$$ \frac{{\partial \prod_{MM} }}{\partial t} = - t + p_{d} \gamma + \left( {p_{n} - s} \right)\gamma $$

Thus, equating the first order conditions to 0 and solving the equations simultaneously, we get:

$$ p_{d}^{M} = \frac{2K - T}{{4\left( {{\upbeta } + 1} \right)\left( {{1} - {\upgamma }^{2} - {\upbeta }} \right)}} $$

$$ p_{n}^{M} = \frac{2F + 2sL - G}{{4\left( {\beta + 1} \right)\left( {{1} - {\upgamma }^{2} - {\upbeta }} \right)}} $$

$$ t^{M} = \frac{{{\upgamma }\left( {1 - s\left( {1 - \beta } \right)} \right)}}{{2\left( {{1} - {\upgamma }^{2} - {\upbeta }} \right)}} $$

Substituting the values in the expressions for the demand of each channel and supply chain profit function gives us the other results.

For $t^{M} > 0$, $1 - s\left( {1 - \beta } \right) > 0$ to make sure the solution is meaningful, there is an implicit condition that ${1} - {\upgamma }^{2} - {\upbeta } > 0$.

Additionally, we have.

$\frac{{\partial^{2} \prod_{MM} }}{{\partial p_{d}^{2} }} = - 2 < 0$, $\left[ {\begin{array}{*{20}c} {\frac{{\partial^{2} \prod_{MM} }}{{\partial p_{d}^{2} }}} & {\frac{{\partial^{2} \prod_{MM} }}{{\partial p_{d} \partial p_{n} }}} \\ {\frac{{\partial^{2} \prod_{MM} }}{{\partial p_{n} \partial p_{d} }}} & {\frac{{\partial^{2} \prod_{MM} }}{{\partial p_{n}^{2} }}} \\ \end{array} } \right] = 4 - 4\beta^{2} > 0$ and.

$\left[ {\begin{array}{*{20}c} {\frac{{\partial^{2} \prod_{MM} }}{{\left( {\partial p_{d}^{M} } \right)^{2} }}} & {\frac{{\partial^{2} \prod_{MM} }}{{\partial p_{d} \partial p_{n} }}} & {\frac{{\partial^{2} \prod_{MM} }}{{\partial p_{d} \partial t}}} \\ {\frac{{\partial^{2} \prod_{MM} }}{{\partial p_{n} \partial p_{d} }}} & {\frac{{\partial^{2} \prod_{MM} }}{{\partial p_{n}^{2} }}} & {\frac{{\partial^{2} \prod_{MM} }}{{\partial p_{n} \partial t}}} \\ {\frac{{\partial^{2} \prod_{MM} }}{{\partial t\partial p_{d} }}} & {\frac{{\partial^{2} \prod_{MM} }}{{\partial t\partial p_{n} }}} & {\frac{{\partial^{2} \prod_{MM} }}{{\partial t^{2} }}} \\ \end{array} } \right] = 4\left( {\beta^{2} + \gamma^{2} + \beta \gamma^{2} - 1} \right)$.

Since ${1} - {\upgamma }^{2} - {\upbeta } > 0$, we know $\beta^{2} + \gamma^{2} + \beta \gamma^{2} - 1 < \beta^{2} + 1 - \beta + \beta \left( {1 - \beta } \right) - 1 = 0$.

Thus, the third-order principal formula is less than zero, and the Hessian matrix is a negative definite matrix.

Proof of Lemma 1

First consider the impact of $\rho$ on prices, green technology levels and profit. We take the derivative of the decision variable with respect to the parameter $\rho$, and get the following formula:

• (1) $\frac{{\partial p_{d}^{M} }}{\partial \rho } = \frac{1}{{2\left( {\beta + 1} \right)}}$, we know $\beta + 1 > 0$, therefore $\frac{{\partial p_{d}^{M} }}{\partial \rho } > 0$.

• (2) $\frac{{\partial p_{n}^{M} }}{\partial \rho } = - \frac{1}{{2\left( {\beta + 1} \right)}}$, we know $\beta + 1 > 0$, therefore $\frac{{\partial p_{n}^{M} }}{\partial \rho } < 0$.

• (3) $\frac{{\partial t^{M} }}{\partial \rho } = 0$

• (4) $\frac{{\partial \Pi_{{{\text{MM}}}}^{ * } }}{\partial \rho } = \frac{{\left( {2\rho - 1} \right)}}{{2\left( {\beta + 1} \right)}} + \frac{s}{2}$, when $\rho > \frac{{1 - s\left( {1 + \beta } \right)}}{2}$, then $\frac{{\partial \Pi_{{{\text{MM}}}}^{ * } }}{\partial \rho } > 0$; otherwise $\frac{{\partial \Pi_{{{\text{MM}}}}^{ * } }}{\partial \rho } < 0$.

Then consider the impact of $\gamma$ on prices, green technology levels and profit. We take the derivative of the decision variable with respect to the parameter $\gamma$, and get the following formula:

• (1) The results of the derivation of prices online and offline are the same ${ }\frac{{\partial p_{d}^{M} }}{\partial \gamma } = \frac{{\partial p_{n}^{M} }}{\partial \gamma } = \frac{{\gamma \left( {1 - s\left( {1 - \beta } \right)} \right)}}{{2\left( {{1} - {\upgamma }^{2} - {\upbeta }} \right)^{2} }}$. Since $1 - s\left( {1 - \beta } \right) > 0$, then $\frac{{\partial p_{d}^{M} }}{\partial \gamma } = \frac{{\partial p_{n}^{M} }}{\partial \gamma } > 0$.

• (2) $\frac{{\partial t^{M} }}{\partial \gamma } = \frac{{\left( {\gamma^{2} - \beta + 1} \right)\left( {1 - s\left( {1 - \beta } \right)} \right)}}{{2\left( {{1} - {\upgamma }^{2} - {\upbeta }} \right)^{2} }}$, since $\gamma^{2} - \beta + 1 > 0$,$1 - s\left( {1 - \beta } \right) > 0$, then $\frac{{\partial t^{M} }}{\partial \gamma } > 0$.

• (3) $\frac{{\partial \Pi_{MM}^{ * } }}{\partial \gamma } = \frac{{\gamma \left( {1 + s\left( {\beta - 1} \right)} \right)^{2} }}{{4\left( {\beta + \gamma^{2} - 1} \right)^{2} }}$ Because the numerator and denominator are quadratic, $\frac{{\partial \Pi_{MM}^{ * } }}{\partial \gamma } > 0$.

Proof of Proposition2

In the retailer’s dual-channel supply chain, the profit functions of manufacturers and retailers are:

$$ \prod_{MR} = w\left( {D_{d} + D_{n} } \right) - \frac{{t^{2} }}{2} $$

$$ \prod_{RR} = \left( {p_{d} - w} \right)D_{d} + \left( {p_{n} - w - s} \right)D_{n} $$

Because it is a Stackelberg game led by the manufacturer, the retailer makes the decision first. The first order conditions of retailer are:

$$ \frac{{\partial \prod_{RR} }}{{\partial p_{d} }} = \left( {1 - \beta } \right)w - 2p_{d} + 2\beta p_{n} - \beta s + \rho + \gamma t $$

$$ \frac{{\partial \prod_{RR} }}{{\partial p_{n} }} = \left( {1 - \beta } \right)w - 2p_{n} + 2\beta p_{d} + \gamma t + s + 1 - \rho $$

Hessian matrix is:$H = \left[ {\begin{array}{*{20}c} { - 2} & {2\beta } \\ {2\beta } & { - 2} \\ \end{array} } \right] = 4 - 4\beta > 0$.

Equating the first order condition to 0 we get

$$ p_{d} \left( {w,t} \right) = \frac{{Lw + K + \gamma t\left( {1 + \beta } \right)}}{2L} $$

$$ p_{n} \left( {w,t} \right) = \frac{{L\left( {s + w} \right) + F + \gamma t\left( {1 + \beta } \right)}}{2L} $$

We substitute the value of $p_{d}$,$p_{n}$ into the above equation and derive $\prod_{MR}$.

The first order condition of $\prod_{MR}$

$$ \frac{{\partial \Pi_{MR} }}{\partial w} = \frac{{\left( {1 - \beta } \right)\left( {s - 4w} \right) + 1 + 2\gamma t}}{2} $$

$$ \frac{{\partial \Pi_{MR} }}{\partial t} = \gamma w - t $$

Equating the first order conditions to 0 and solving the equations simultaneously, we get $w^{R} = \frac{{1 - \left( {1 - \beta } \right)s}}{{2\left( {2 - \gamma^{2} - 2\beta } \right)}}$

$$ t^{R} = \frac{{{\upgamma }\left( {1 - s\left( {1 - {\upbeta }} \right)} \right)}}{{2\left( {2 - \gamma^{2} - 2\beta } \right)}} $$

Substituting the above value into the values of $p_{d}$ and $p_{n}$ we get

$$ p_{d}^{R} = \frac{1 + \beta - T - sL + 4K}{{4\left( {\beta + 1} \right)\left( {2 - \gamma^{2} - 2\beta } \right)}} $$

$$ p_{n}^{R} = \frac{1 + \beta + 3sL + 4F - G}{{4\left( {\beta + 1} \right)\left( {2 - \gamma^{2} - 2\beta } \right)}} $$

Substituting the values in the expressions for the demand of each channel and supply chain profit function gives us the other results.

For $t^{R} > 0$$,$ $1 - s\left( {1 - \beta } \right) > 0$, to make sure the solution is meaningful, there is an implicit condition that $2 - \gamma^{2} - 2\beta > 0$.

Hessian matrix is:$H = \left[ {\begin{array}{*{20}c} { - 2\left( {1 - \beta } \right)} & \gamma \\ \gamma & { - 1} \\ \end{array} } \right] = 2 - \gamma^{2} - 2\beta > 0$.

Proof of Lemma 2

First consider the impact of ρ on prices, green technology levels and profit.

• (1) $\frac{{\partial p_{d}^{R} }}{\partial \rho } = \frac{1}{{2\left( {\beta + 1} \right)}}$ We know $\beta + 1 > 0$, therefore $\frac{{\partial p_{d}^{R} }}{\partial \rho } > 0$.

• (2) $\frac{{\partial p_{n}^{R} }}{\partial \rho } = - \frac{1}{{2\left( {\beta + 1} \right)}}$ We know $\beta + 1 > 0$, therefore $\frac{{\partial p_{n}^{R} }}{\partial \rho } < 0$.

• (3) $\frac{{\partial t^{R} }}{\partial \rho } = 0$

• (4) $\frac{{\partial w^{R} }}{\partial \rho } = 0$

• (5) $\frac{{\partial \Pi_{{{\text{MR}}}}^{ * } }}{\partial \rho } = 0$

• (6) $\frac{{\partial \Pi_{{{\text{RR}}}}^{ * } }}{\partial \rho } = \frac{{\left( {s\left( {1 + \beta } \right) + \left( {2\rho - 1} \right)} \right)}}{{2\left( {\beta + 1} \right)}}$. $\rho > \frac{{1 - s\left( {1 + \beta } \right)}}{2}$, $\frac{{\partial \Pi_{{{\text{RR}}}}^{ * } }}{\partial \rho } > 0$; otherwise, $\frac{{\partial \Pi_{{{\text{RR}}}}^{ * } }}{\partial \rho } < 0$.

Then consider the impact of $\gamma$ on prices, green technology levels and profit.

We know ${ }1 - s\left( {1 + \beta } \right) > 0$, and then we can get the following results:

• (1) $\frac{{\partial p_{d}^{R} }}{\partial \gamma } = \frac{{3\gamma \left( {1 - s\left( {1 + \beta } \right)} \right)}}{{2\left( {2 - \gamma^{2} - 2\beta } \right)^{2} }} > 0$

• (2) $\frac{{\partial p_{n}^{R} }}{\partial \gamma } = \frac{{3\gamma \left( {1 - s\left( {1 + \beta } \right)} \right)}}{{2\left( {2 - \gamma^{2} - 2\beta } \right)^{2} }} > 0$

• (3) $\frac{{\partial t^{R} }}{\partial \gamma } = \frac{{\left( {\gamma^{2} - 2\beta + 2} \right)\left( {1 - s\left( {1 + \beta } \right)} \right)}}{{2\left( {2 - \gamma^{2} - 2\beta } \right)^{2} }} > 0$

• (4) $\frac{{\partial w^{R} }}{\partial \gamma } = \frac{{\gamma \left( {1 - s\left( {1 + \beta } \right)} \right)}}{{\left( {2 - \gamma^{2} - 2\beta } \right)^{2} }} > 0$

• (5) $\frac{{\partial \Pi_{{{\text{MR}}}}^{ * } }}{\partial \gamma } = \frac{{\gamma \left( {1 - s\left( {1 + \beta } \right)} \right)^{2} }}{{2\left( {2 - \gamma^{2} - 2\beta } \right)^{2} }} > 0$

• (6) $\frac{{\partial \Pi_{{{\text{RR}}}}^{ * } }}{\partial \gamma } = \frac{{\gamma \left( {1 - \beta } \right)\left( {1 - s\left( {1 + \beta } \right)} \right)^{2} }}{{2\left( {2 - \gamma^{2} - 2\beta } \right)^{3} }}$ For $1 - \beta > 0$,$2 - \gamma^{2} - 2\beta > 0$ then $\frac{{\partial \Pi_{{{\text{RR}}}}^{ * } }}{\partial \gamma } > 0$.

Proof of Proposition 3

The profit functions for the retailer and manufacturer are:

$$ \prod_{MH} = p_{d} D_{d} + wD_{n} - \frac{{t^{2} }}{2} $$

$$ \prod_{RH} = \left( {p_{n} - w - s} \right)D_{n} $$

First take the derivative of the retailer’s expression, the first order condition is

$$ \frac{{\partial \Pi_{RH} }}{{\partial p_{n} }} = \beta p_{d} - 2p_{n} + w + 1 + s - \rho + \gamma t $$

$$ \frac{{\partial^{2} \Pi_{RH} }}{{\partial p_{n} }} = - 2 < 0 $$

Thus the retailer's profit function is strictly concave in $p_{n}$.Equating the first order condition to 0 we get:

$$ p_{n} \left( {w,t,p_{d} } \right) = \frac{{1 + s + w - \rho + \beta p_{n} + \gamma t}}{2} $$

We substitute the value of ${ }p_{n}$ into the above equation and derive $\prod_{MH}$.

The first order conditions of $\prod_{MH}$ are:

$$\begin{aligned} \frac{{\partial \prod_{MH} }}{{\partial p_{d} }}& = \frac{{2\beta w + 2p_{d} \left( {\beta^{2} - 2} \right) + \gamma t\left( {\beta + 2} \right) + 2\rho + \beta + \beta s - \rho \beta }}{2} \\ \frac{{\partial \prod_{MH} }}{\partial w} &= \frac{{ - 2w + 2\beta p_{d} + \gamma t + 1 - s - \rho }}{2}\end{aligned} $$

$$ \frac{{\partial \prod_{MH} }}{\partial t} = \frac{{\gamma w + \gamma p_{d} \left( {\beta + 2} \right) - 2t}}{2} $$

$H = \left[ {\begin{array}{*{20}c} {2\left( {\beta^{2} - 2} \right)} & \beta & {\frac{1}{2}\gamma \left( {\beta + 2} \right)} \\ \beta & { - 1} & {\frac{1}{2}\gamma } \\ {\frac{1}{2}\gamma \left( {\beta + 2} \right)} & {\frac{1}{2}\gamma } & { - 1} \\ \end{array} } \right]$, Hessian matrix negative definite.

Equating the first order conditions to 0 and solving the equations simultaneously, we get

$$ p_{d}^{H} = \frac{4K - T}{{2\left( {\beta + 1} \right)\left( {4 - 3\gamma^{2} - \beta \gamma^{2} - 4\beta } \right)}} $$

$$ p_{n}^{H} = \frac{{4F + 4sL - \gamma^{2} \left( {\left( {1 - 2\rho } \right) + 5s + 2\beta^{2} \left( {1 + s} \right) + 7\beta s} \right)}}{{4\left( {\beta + 1} \right)\left( {4 - 3\gamma^{2} - \beta \gamma^{2} - 4\beta } \right)}} $$

$$ t^{H} = \frac{{\gamma \left( {1 + K - s\left( {1 - \beta } \right)} \right)}}{{4 - 3\gamma^{2} - \beta \gamma^{2} - 4\beta }} $$

$$ w^{H} = \frac{{2\gamma^{2} \left( {2\rho + s - 1} \right) + \beta \gamma^{2} \left( {3s + \beta s + 2\rho - 1} \right) - 4sL - 4F}}{{2\left( {\beta + 1} \right)\left( {4 - 3\gamma^{2} - \beta \gamma^{2} - 4\beta } \right)}} $$

Substituting the values in the expressions for the demand of each channel and supply chain profit function gives us the other results.

For $t^{H} > 0$, to make sure the solution is meaningful, there is an implicit condition that $4 - 3\gamma^{2} - \beta \gamma^{2} - 4\beta > 0$.

Proof of Lemma 3

First consider the impact of ρ on prices, green technology levels and profit.

We know $4 - 3\gamma^{2} - \beta \gamma^{2} - 4\beta > 0$ (see proof of proposition 3), and then we can get.

• (1) $\frac{{\partial p_{d}^{H} }}{\partial \rho } = \frac{{\left( {2 - \gamma^{2} - 2\beta } \right)}}{{\left( {\beta + 1} \right)\left( {4 - 3\gamma^{2} - \beta \gamma^{2} - 4\beta } \right)}} > 0$

• (2) $\frac{{\partial p_{n}^{H} }}{\partial \rho } = \frac{{a\left( {\beta^{2} + 2\beta \gamma^{2} + 2\beta + 3\gamma^{2} - 3} \right)}}{{\left( {\beta + 1} \right)\left( {4 - 3\gamma^{2} - \beta \gamma^{2} - 4\beta } \right)}}$ Since ${\upgamma }^{2} + {\upbeta } - 1 < 0$, then ${\upgamma }^{2} < 1 - {\upbeta }$. Bring ${\upgamma }^{2} < 1 - {\upbeta }$ into $\beta^{2} + 2\beta \gamma^{2} + 2\beta + 3\gamma^{2} - 3$ to get $\beta^{2} + 2\beta \gamma^{2} + 2\beta + 3\gamma^{2} - 3 < - \beta^{2} + \beta < 0$ and so $\beta^{2} + 2\beta \gamma^{2} + 2\beta + 3\gamma^{2} - 3 < 0$ Therefore $\frac{{\partial p_{n}^{H} }}{\partial \rho } < 0$.

• (3) $\frac{{\partial t^{H} }}{\partial \rho } = \frac{{\gamma \left( {1 - \beta } \right)}}{{4 - 3\gamma^{2} - \beta \gamma^{2} - 4\beta }} > 0$

• (4) $\frac{{\partial {\text{w}}^{H} }}{\partial \rho } = - \frac{{2 - \gamma^{2} - 2\beta }}{{\left( {\beta + 1} \right)\left( {4 - 3\gamma^{2} - \beta \gamma^{2} - 4\beta } \right)}} < 0$

Then consider the impact of $\gamma$ on prices, green technology levels and profit.

$\frac{{\partial p_{d}^{H} }}{\partial \gamma } = \frac{{4\gamma \left( {\left( {1 + \rho + \beta - \beta \rho } \right) - s\left( {1 - \beta } \right)} \right)}}{{\left( {4 - 3\gamma^{2} - \beta \gamma^{2} - 4\beta } \right)^{2} }}$

$1 + \rho + \beta - \beta \rho > 1$ and $s\left( {1 - \beta } \right) < 1$, so the conclusion will always be $\frac{{\partial p_{d}^{H} }}{\partial \gamma } > 0$.

$\frac{{\partial p_{n}^{H} }}{\partial \gamma } = \frac{{2\gamma \left( {3 - \beta } \right)\left( {\left( {1 + \rho + \beta - \beta \rho } \right) - s\left( {1 - \beta } \right)} \right)}}{{\left( {4 - 3\gamma^{2} - \beta \gamma^{2} - 4\beta } \right)^{2} }} > 0$

$$ \frac{{\partial t^{H} }}{\partial \gamma } = \frac{{\left( {\gamma^{2} \left( {\beta + 3} \right) + 4\left( {1 - \beta } \right)} \right)\left( {\left( {1 + \rho + \beta - \beta \rho } \right) - s\left( {1 - \beta } \right)} \right)}}{{\left( {4 - 3\gamma^{2} - \beta \gamma^{2} - 4\beta } \right)^{2} }} > 0 $$

$$ \frac{{\partial w^{H} }}{\partial \gamma } = \frac{{4\gamma \left( {\left( {1 + \rho + \beta - \beta \rho } \right) - s\left( {1 - \beta } \right)} \right)}}{{\left( {4 - 3\gamma^{2} - \beta \gamma^{2} - 4\beta } \right)^{2} }} > 0 $$

$$ \frac{{\partial \Pi_{{{\text{MH}}}}^{ * } }}{\partial \gamma } = \frac{{\gamma \left( {\left( {1 + \rho + \beta - \beta \rho } \right) - s\left( {1 - \beta } \right)} \right)}}{{\left( {4 - 3\gamma^{2} - \beta \gamma^{2} - 4\beta } \right)^{2} }}^{2} > 0 $$

Proof of Proposition 4

The profit expressions for manufacturers and retailers are:

$$ \prod_{MHH} = wD_{d} + p_{n} D_{n} - \frac{{t^{2} }}{2} $$

$$ \prod_{RHH} = \left( {p_{d} - w} \right)D_{d} $$

First, take the derivative of the retailer’s profit, the first order condition is

$$ \frac{{\partial \prod_{RHH} }}{{\partial p_{d} }} = - 2p_{d} + \beta p_{n} + w + \rho + \gamma t $$

$$ \frac{{\partial^{2} \prod_{RHH} }}{{\partial p_{d}^{2} }} = - 2 < 0 $$

Thus, the retailer's profit function is strictly concave in $p_{d}$. Equating the first order condition to 0 we get

$$ p_{d} \left( {w,t,p_{n} } \right) = \frac{{w + \rho + \beta p_{n} + \gamma t}}{2} $$

We substitute the value of $p_{n}$ into the above equation and derive $\prod_{MHH}$.

The first order condition of $\prod_{MHH}$

$$ \frac{{\partial \Pi_{MHH} }}{{\partial p_{n} }} = \frac{{\left( {2 - 2\rho + \rho \beta } \right) - 4p_{n} + 2s + \beta \left( {2w + \gamma t + \beta^{2} p_{n} } \right) + 2\gamma t}}{2} $$

$$ \frac{{\partial \Pi_{MHH} }}{\partial w} = \frac{{ - 2w + 2\beta p_{n} + \gamma t + \rho - \beta s}}{2} $$

$$ \frac{{\partial \Pi_{MHH} }}{\partial t} = \frac{{\gamma w + \gamma p_{n} \left( {\beta + 2} \right) - 2t - \gamma s\left( {2 + \beta } \right)}}{2} $$

$H = \left[ {\begin{array}{*{20}c} { - 4 + \beta^{3} } & \beta & {\frac{1}{2}\gamma \left( {\beta + 2} \right)} \\ \beta & { - 1} & {\frac{1}{2}\gamma } \\ {\frac{1}{2}\gamma \left( {\beta + 2} \right)} & {\frac{1}{2}\gamma } & { - 1} \\ \end{array} } \right]$, Hessian matrix negative definite.

Equating the first order conditions to 0 and solving the equations simultaneously, we get

$$ p_{d}^{HH} = \frac{{4sL + 4F - \gamma^{2} \left( {\left( {3 + 2\beta } \right)\left( {s + 1 + s\beta } \right) + 6\rho + 4\beta \rho } \right)}}{{2\left( {\beta + 1} \right)\left( {4 - 3\gamma^{2} - \beta \gamma^{2} - 4\beta } \right)}} $$

$$ p_{n}^{HH} = \frac{{4sL + 4F - \gamma^{2} \left( {\left( {1 - 2\rho } \right) + \left( {1 + \beta } \right)\left( {5 + 2\beta } \right)s} \right)}}{{2\left( {\beta + 1} \right)\left( {4 - 3\gamma^{2} - \beta \gamma^{2} - 4\beta } \right)}} $$

$$ t^{HH} = \frac{{\gamma \left( {\left( {2 - \rho + \rho \beta } \right) + \left( {1 - \beta } \right)\left( {2 + \beta } \right)s} \right)}}{{\left( {4 - 3\gamma^{2} - \beta \gamma^{2} - 4\beta } \right)}} $$

$$ w^{HH} = \frac{{\left( {4\rho + 4\left( {1 - \rho } \right)\beta + \left( {1 - 2\rho } \right)\left( {2 + \beta } \right)\gamma^{2} } \right) - \left( {1 + \beta } \right)\left( {2 + \beta } \right)\gamma^{2} s}}{{2\left( {\beta + 1} \right)\left( {4 - 3\gamma^{2} - \beta \gamma^{2} - 4\beta } \right)}} $$

Substituting the values in the expressions for the demand of each channel and supply chain profit function gives us the other results.

For $t^{HH} > 0$, to make sure the solution is meaningful, there is an implicit condition that $4 - 3\gamma^{2} - \beta \gamma^{2} - 4\beta > 0$.

Proof of Lemma 4

First consider the impact of ρ on prices, green technology levels and profit.

We know $4 - 3\gamma^{2} - \beta \gamma^{2} - 4\beta > 0$,$1 - \beta > 0$, $2 - \gamma^{2} - 2\beta > 0$, then we can get.

• (1) $\frac{{\partial p_{d}^{HH} }}{\partial \rho } = \frac{{ - \left( {\beta^{2} + 2\beta \gamma^{2} + 2\beta + 3\gamma^{2} - 3} \right)}}{{\left( {\beta + 1} \right)\left( {4 - 3\gamma^{2} - \beta \gamma^{2} - 4\beta } \right)}} > 0$, From Proposition 1 we can get $\gamma^{2} + \beta - 1 < 0$, then $\gamma^{2} < 1 - \beta$, Bring this formula into $\beta^{2} + 2\beta \gamma^{2} + 2\beta + 3\gamma^{2} - 3$, then we can get $\beta^{2} + 2\beta \gamma^{2} + 2\beta + 3\gamma^{2} - 3 < - \beta^{2} - \beta$. Since $- \beta^{2} - \beta < 0$, then $\beta^{2} + 2\beta \gamma^{2} + 2\beta + 3\gamma^{2} - 3 < 0$.

• (2) Apparently $\frac{{\partial p_{n}^{HH} }}{\partial \rho } = \frac{{ - \left( {2 - \gamma^{2} - 2\beta } \right)}}{{\left( {\beta + 1} \right)\left( {4 - 3\gamma^{2} - \beta \gamma^{2} - 4\beta } \right)}} < 0$.

• (3) Apparently $\frac{{\partial t^{HH} }}{\partial \rho } = - \frac{{\gamma \left( {1 - \beta } \right)}}{{4 - 3\gamma^{2} - \beta \gamma^{2} - 4\beta }} < 0$

• (4) $\frac{{\partial w^{HH} }}{\partial \rho } = \frac{{\left( {2 - \gamma^{2} - 2\beta } \right)}}{{\left( {\beta + 1} \right)\left( {4 - 3\gamma^{2} - \beta \gamma^{2} - 4\beta } \right)}} > 0$

Then consider the impact of $\gamma$ on prices, green technology levels and profit.

Since $\left( {2 - \rho + \rho^{2} } \right) - s\left( {2 - \rho + \rho^{2} } \right) > 0$,

then $\left( {2 - \rho + \rho^{2} } \right) - s\left( {2 - \rho - \rho \beta } \right) > \left( {2 - \rho + \rho^{2} } \right) - s\left( {2 - \rho + \rho^{2} } \right) > 0$.

• (1) $\frac{{\partial p_{d}^{HH} }}{\partial \gamma } = \frac{{2\gamma \left( {3 - \beta } \right)\left( {\left( {2 - \rho + \rho^{2} } \right) - s\left( {2 - \rho - \rho \beta } \right)} \right)}}{{\left( {4 - 3\gamma^{2} - \beta \gamma^{2} - 4\beta } \right)^{2} }} > 0$

• (2) $\frac{{\partial p_{d}^{HH} }}{\partial \gamma } = \frac{{4\gamma \left( {\left( {2 - \rho + \rho^{2} } \right) - s\left( {2 - \rho - \rho \beta } \right)} \right)}}{{\left( {4 - 3\gamma^{2} - \beta \gamma^{2} - 4\beta } \right)^{2} }} > 0$

• (3) $\frac{{\partial t^{HH} }}{\partial \gamma } = \frac{{\left( {\left( {\beta + 3} \right)\gamma^{2} + 4\left( {1 - \beta } \right)} \right)\left( {\left( {2 - \rho + \rho^{2} } \right) - s\left( {2 - \rho - \rho \beta } \right)} \right)}}{{\left( {4 - 3\gamma^{2} - \beta \gamma^{2} - 4\beta } \right)^{2} }}$,

  Since $\left( {\beta + 3} \right)\gamma^{2} + 4\left( {1 - \beta } \right) > 0$, then $\frac{{\partial t^{H} }}{\partial \gamma } > 0$.

• (4) $\frac{{\partial w^{HH} }}{\partial \gamma } = \frac{{4\gamma \left( {\left( {2 - \rho + \rho^{2} } \right) - s\left( {2 - \rho - \rho \beta } \right)} \right)}}{{\left( {4 - 3\gamma^{2} - \beta \gamma^{2} - 4\beta } \right)^{2} }} > 0$.

Part 2: Proof of Corollary

10.1 Proof of Corollary 1

10.1.1 Product green technology level

• (1) $t^{M} - t^{R} = \frac{{\gamma \left( {1 - \beta } \right)\left( {1 - s\left( {1 - \beta } \right)} \right)}}{{2\left( {2 - \gamma^{2} - 2\beta } \right)\left( {1 - \gamma^{2} - \beta } \right)}}$, since $1 - s\left( {1 - \beta } \right) > 0$,$1 - \beta > 0$, then $t^{M} > t^{R}$.

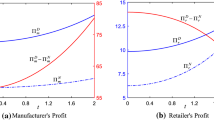
• (2) $t^{H} - t^{HH} = \frac{{\gamma \left( {1 - \beta } \right)\left( {2\rho - 1 + s\left( {1 + \beta } \right)} \right)}}{{\left( {4 - 4\beta - \beta \gamma^{2} - 3\gamma^{2} } \right)}}$. When $\rho > \frac{{1 - s\left( {1 + \beta } \right)}}{2}$, then $t^{H} > t^{HH}$; otherwise, $t^{H} < t^{HH}$, $\overline{{\rho_{0} }} = \frac{{1 - s\left( {1 + \beta } \right)}}{2}$.

• (3) $t^{H} - t^{R} = \frac{{2\rho \left( {2 - \gamma^{2} - 2\beta } \right) + \beta \left( {4 - \gamma^{2} s} \right) + \gamma^{2} \left( {1 - s} \right)}}{{\left( {4 - 4\beta - \beta \gamma^{2} - 3\gamma^{2} } \right)\left( {2 - \gamma^{2} - 2\beta } \right)}} > 0$, $t^{H} > t^{R}$.

  $t^{M} - t^{HH} = \frac{{2\rho \left( {1 - \beta - \gamma^{2} } \right) + 2\left( {1 - \beta } \right)\beta s + \gamma^{2} \left( {1 - \left( {1 + \beta } \right)s} \right)}}{{\left( {1 - \beta - \gamma^{2} } \right)}} > 0$, $t^{HH} > t^{M}$.

  $t^{H} - t^{M} = \frac{{2\rho \left( {1 - \beta - \gamma^{2} } \right) + \left( { - 2 + 2\beta + \gamma^{2} } \right) - \left( {2 - \gamma^{2} - \beta \left( {2 + \gamma^{2} } \right)} \right)s}}{{\left( {1 - \beta - \gamma^{2} } \right)\left( {4 - 3\gamma^{2} - \beta \gamma^{2} - 4\beta } \right)}}$,

  $\overline{{\rho_{1} }} = \frac{{\left( {2 - 2\beta - \gamma^{2} } \right) - \left( {2 - \gamma^{2} - \beta \left( {2 + \gamma^{2} } \right)} \right)s}}{{2a\left( {1 - \beta - \gamma^{2} } \right)}}$ if $\rho \ge \overline{{\rho_{1} }}$, then $t^{H} \ge t^{M}$;otherwise $t^{H} < t^{M}$.

  $$ t^{R} - t^{HH} = \frac{{2\left( {2 - 2\beta - \gamma^{2} } \right) + \left( {4 - \gamma^{2} } \right) + \left( {1 + \beta } \right)\gamma^{2} s - 4s\left( {1 - \beta^{2} } \right)}}{{\left( {2 - 2\beta - \gamma^{2} } \right)\left( {4 - 3\gamma^{2} - \beta \gamma^{2} - 4\beta } \right)}} $$

  $\overline{{\rho_{2} }} = \frac{{\left( {4 - \gamma^{2} } \right) + \left( {1 + \beta } \right)\gamma^{2} s - 4s\left( {1 - \beta^{2} } \right)}}{{2a\left( {2 - 2\beta - \gamma^{2} } \right)}}$ if $\rho \ge \overline{{\rho_{2} }}$, then $t^{R} \ge t^{HH}$; otherwise $t^{R} < t^{HH}$.

Proof of Corollary 2

Comparison of different channel selection on manufacturer's profit.

We know $1 - \gamma^{2} - \beta > 0$, $4 - 3\gamma^{2} - \beta \gamma^{2} - 4\beta > 0$.In the next three formulas, we will use these two inequalities.

$$ \prod_{{{\text{MM}}}}^{ * } - \prod_{{{\text{MH}}}}^{ * } = \frac{{\left( {2 - 2s - 2\beta + 2\beta s - \gamma^{2} + \gamma^{2} s + 2\rho \beta + 2\rho \gamma^{2} + \beta \gamma^{2} s} \right)^{2} }}{{8\left( {1 - \gamma^{2} - \beta } \right)\left( {4 - 3\gamma^{2} - \beta \gamma^{2} - 4\beta } \right)}} > 0 $$

$$ \prod_{{{\text{MM}}}}^{ * } - \prod_{{{\text{MHH}}}}^{ * } = \frac{{\left( { - 2\rho + 2\beta s - \gamma^{2} + 2\beta^{2} s + \gamma^{2} s + 2\rho \beta + 2\rho \gamma^{2} + \beta \gamma^{2} s} \right)^{2} }}{{8\left( {1 - \gamma^{2} - \beta } \right)\left( {4 - 3\gamma^{2} - \beta \gamma^{2} - 4\beta } \right)}} > 0 $$

$$ \prod_{{{\text{MH}}}}^{ * } - \prod_{{{\text{MHH}}}}^{ * } = \frac{{\left( {1 - \beta } \right)\left( {\left( {2\rho - 1} \right) + s\left( {1 + \beta } \right)} \right)\left( {1 + s\left( {1 - \beta } \right)} \right)}}{{2\left( {4 - 3\gamma^{2} - \beta \gamma^{2} - 4\beta } \right)}} $$

Since $1 + s\left( {1 - \beta } \right) > 0$, if $\rho > \frac{{1 - s\left( {1 + \beta } \right)}}{2}$,$\prod_{{{\text{MH}}}}^{ * } > \prod_{{{\text{MHH}}}}^{ * }$; if $\rho < \frac{{1 - s\left( {1 + \beta } \right)}}{2}$,$\prod_{{{\text{MH}}}}^{ * } < \prod_{{{\text{MHH}}}}^{ * }$.$\overline{{\rho_{0} }} = \frac{{1 - s\left( {1 + \beta } \right)}}{2}$.

Retailer

• (1) $\prod_{{{\text{RH}}}}^{ * } - \prod_{{{\text{RHH}}}}^{ * } = - \frac{{\left( {1 - \beta } \right)\left( {1 - \gamma^{2} - \beta } \right)\left( {\left( {2\rho - 1} \right) + s\left( {1 + \beta } \right)} \right)\left( {1 + s\left( {1 - \beta } \right)} \right)}}{{2\left( {4 - 3\gamma^{2} - \beta \gamma^{2} - 4\beta } \right)^{2} }}$

  when $\rho < \overline{{\rho_{0} }}$, then $\prod_{{{\text{RH}}}}^{ * } > \prod_{{{\text{RHH}}}}^{ * }$; when $\rho > \overline{{\rho_{0} }}$, then $\prod_{{{\text{RHH}}}}^{ * } > \prod_{{{\text{RH}}}}^{ * }$

• (2) $\prod_{{{\text{RR}}}}^{ * } - \prod_{{{\text{RH}}}}^{ * } = \frac{{A\rho^{2} + B\rho + C}}{{8\left( {\beta + 1} \right)\left( {\gamma^{2} + 2\beta - 2} \right)^{2} \left( {4\beta + \beta \gamma^{2} + 3\gamma^{2} - 4} \right)^{2} }}$

• (a) If A > 0 and $\Delta < 0$, then $\prod_{{{\text{RR}}}}^{ * } > \prod_{{{\text{RH}}}}^{ * }$;

• (b) If A > 0 and $\Delta > 0$, then when $0 < \rho < \rho_{1}^{*}$, $\prod_{{{\text{RR}}}}^{ * } > \prod_{{{\text{RH}}}}^{ * }$; when $\rho_{1}^{*} < \rho < \rho_{2}^{*}$, $\prod_{{{\text{RR}}}}^{ * } < \prod_{{{\text{RH}}}}^{ * }$; when $\rho_{2}^{*} < \rho < 1$, $\prod_{{{\text{RR}}}}^{ * } > \prod_{{{\text{RH}}}}^{ * }$.

• (c) If A < 0 and $\Delta < 0$, then $\prod_{{{\text{RR}}}}^{ * } < \prod_{{{\text{RH}}}}^{ * }$;

• (d) If A < 0 and $\Delta > 0$,then when $0 < \rho < \rho_{1}^{*}$, $\prod_{{{\text{RR}}}}^{ * } < \prod_{{{\text{RH}}}}^{ * }$; when $\rho_{1}^{*} < \rho < \rho_{2}^{*}$, $\prod_{{{\text{RR}}}}^{ * } > \prod_{{{\text{RH}}}}^{ * }$; when $\rho_{1}^{*} < \rho < 1$, $\prod_{{{\text{RR}}}}^{ * } < \prod_{{{\text{RH}}}}^{ * }$.

  Note: $\Delta = B^{2} - 4AC$, $\rho_{0}^{*} = \frac{{1 - s\left( {1 + \beta } \right)}}{2}$, $\rho_{1}^{*} = \frac{{ - B - \sqrt {B^{2} - 4AC} }}{2A}$,$\rho_{2}^{*} = \frac{{ - B + \sqrt {B^{2} - 4AC} }}{2A}$

  $$ A = 4\left( { - 2 + 2\beta + \gamma^{2} } \right)^{2} \left( {2\left( { - 7 + \beta } \right)\left( {1 - \beta } \right)^{2} + 4\left( {1 - \beta } \right)\left( {5 + \beta } \right)\gamma^{2} - \left( {7 + \beta \left( {4 + \beta } \right)} \right)\gamma^{4} } \right) $$
  $$ B = - 4\left( { - 2 + 2\beta + \gamma^{2} } \right)^{2} \left( \begin{gathered} \left( {12 - 18\gamma^{2} + 7\gamma^{4} } \right)\left( { - 1 + s} \right) + \beta^{3} \left( {4 + \left( {12 + 6\gamma^{2} + \gamma^{4} } \right)s} \right) \hfill \\ + \beta^{2} \left( { - 4\left( {5 + 3s} \right) + \gamma^{4} \left( { - 1 + 5s} \right) + 2\gamma^{2} \left( { - 1 + 9s} \right)} \right) \hfill \\ + \beta \left( {28 - 12s - 2\gamma^{2} \left( {8 + 3s} \right) + \gamma^{4} \left( { - 4 + 11s} \right)} \right) \hfill \\ \end{gathered} \right) $$
  $$ \begin{gathered} C = 16\beta \left( {12 + \beta \left( { - 5 + 2\beta } \right)\left( {4 + \left( { - 2 + \beta } \right)\beta } \right)} \right) + 8\beta \left( { - 42 + \beta \left( {44 + \beta \left( { - 22 + 5\beta } \right)} \right)} \right)\gamma^{2} \\ - \left( { - 1 + \beta } \right)\left( { - 109 + \beta \left( {77 + 3\left( { - 1 + \beta } \right)\beta } \right)} \right)\gamma^{4} + 4\left( { - 1 + \beta } \right)\left( {11 + \beta \left( {4 + \beta } \right)} \right)\gamma^{6} + \left( {7 + \beta \left( {4 + \beta } \right)} \right)\gamma^{8} \\ - 2\left( \begin{gathered} 48\beta \left( { - 3 + \beta \left( {2 + \left( { - 2 + \beta } \right)\left( { - 1 + \beta } \right)\beta } \right)} \right) + 24\left( { - 1 + \beta } \right)^{3} \left( {1 + \beta } \right)\left( {5 + \beta } \right)\gamma^{2} \\ + \left( {1 - \beta } \right)^{2} \left( {1 + \beta } \right)\left( {109 + \beta \left( {38 + 5\beta } \right)} \right)\gamma^{4} + 4\left( {\beta - 1} \right)\left( {1 + \beta } \right)\left( {11 + \beta \left( {5 + \beta } \right)} \right)\gamma^{6} \\ + \left( {1 + \beta } \right)\left( {7 + \beta \left( {4 + \beta } \right)} \right)\gamma^{8} )s \\ \end{gathered} \right) \\ - \left( \begin{gathered} 48\left( {1 - \beta } \right)^{4} \left( {1 + \beta } \right)^{2} + 24\left( { - 1 + \beta } \right)^{3} \left( {1 + \beta } \right)^{2} \left( {5 + \beta } \right)\gamma^{2} + \left( { - 1 + \beta^{2} } \right)^{2} \left( {109 + \beta \left( {44 + 3\beta } \right)} \right)\gamma^{4} \hfill \\ + 4\left( { - 1 + \beta } \right)\left( {1 + \beta } \right)^{2} \left( {11 + \beta \left( {6 + \beta } \right)} \right)\gamma^{6} + \left( {7 + 2\beta \left( {9 + \beta \left( {8 + 3\beta \left( {1 + 8\beta } \right)} \right)} \right)} \right)\gamma^{8} )s^{2} \hfill \\ \end{gathered} \right) \\ + 24\left( {5\gamma^{2} + 4s} \right) \\ \end{gathered} $$

• (3) $\prod_{{{\text{RR}}}}^{ * } - \prod_{{{\text{RHH}}}}^{ * } = \frac{{A_{1} \rho^{2} + B_{1} \rho + C_{1} }}{{8\left( {\beta + 1} \right)\left( {\gamma^{2} + 2\beta - 2} \right)^{2} \left( {4\beta + \beta \gamma^{2} + 3\gamma^{2} - 4} \right)^{2} }}$

  • (a) If A₁ > 0 and $\Delta_{1} < 0$, then $\prod_{{{\text{RR}}}}^{ * } > \prod_{{{\text{RHH}}}}^{ * }$;

  • (b) If A₁ > 0 and $\Delta_{1} > 0$, then when $0 < \rho < \rho_{3}^{*}$, $\prod_{{{\text{RR}}}}^{ * } > \prod_{{{\text{RHH}}}}^{ * }$; when $\rho_{3}^{*} < \rho < \rho_{4}^{*}$, $\prod_{{{\text{RR}}}}^{ * } < \prod_{{{\text{RHH}}}}^{ * }$; when $\rho_{4}^{*} < \rho < 1$, $\prod_{{{\text{RR}}}}^{ * } > \prod_{{{\text{RHH}}}}^{ * }$.

  • (c) If A₁ < 0 and $\Delta < 0$, then $\prod_{{{\text{RR}}}}^{ * } < \prod_{{{\text{RHH}}}}^{ * }$;

  • (d) If A₁ < 0 and $\Delta > 0$,then when $0 < \rho < \rho_{3}^{*}$, $\prod_{{{\text{RR}}}}^{ * } < \prod_{{{\text{RHH}}}}^{ * }$; when $\rho_{3}^{*} < \rho < \rho_{4}^{*}$, $\prod_{{{\text{RR}}}}^{ * } > \prod_{{{\text{RHH}}}}^{ * }$; when $\rho_{4}^{*} < \rho < 1$, $\prod_{{{\text{RR}}}}^{ * } < \prod_{{{\text{RHH}}}}^{ * }$.

  Note: $\Delta_{1} = B_{1}^{2} - 4A_{1} C_{1}$, $\rho_{3}^{*} = \frac{{ - B_{1} - \sqrt {B_{1}^{2} - 4A_{1} C_{1} } }}{{2A_{1} }}$,$\rho_{4}^{*} = \frac{{ - B_{1} + \sqrt {B_{1}^{2} - 4A_{1} C_{1} } }}{{2A_{1} }}$.

  $A_{1} = - 4\left( \begin{gathered} 6 - 8\beta \left( {29 + \beta \left( { - 46 + \beta \left( {34 + \left( { - 11 + \beta } \right)\beta } \right)} \right)} \right) + 8\left( { - 1 + \beta } \right)^{3} \left( {17 + \beta } \right)\gamma^{2} \hfill \\ + 2\left( { - 1 + \beta } \right)^{2} \left( {61 + \beta \left( {15 + 2\beta } \right)} \right)\gamma^{4} + 4\left( { - 1 + \beta } \right)\left( {12 + \beta \left( {5 + \beta } \right)} \right)\gamma^{6} \hfill\\ + \left( {7 + \beta \left( {4 + \beta } \right)} \right)\gamma^{8} \hfill \\ \end{gathered} \right)$ $B_{1} = 4\left( { - 2 + 2\beta + \gamma^{2} } \right)^{2} \left( \begin{gathered} - \left( { - 2 + \gamma^{2} } \right)\left( { - 8 + 7\gamma^{2} } \right)\left( { - 1 + s} \right) + 4\beta^{4} s\hfill\\ - \beta^{3} \left( {20 + 2\gamma^{2} + \gamma^{4} } \right)s \hfill \\ + \beta^{2} \left( {\gamma^{2} \left( {6 - 22s} \right) + \gamma^{4} \left( {1 - 5s} \right) + 4\left( {4 + 3s} \right)} \right) \hfill\\ + \beta \left( \begin{gathered} \gamma^{4} \left( {4 - 11s} \right) \hfill \\ + 2\gamma^{2} \left( {8 + s} \right) + 4\left( { - 8 + 5s} \right) \hfill \\ \end{gathered} \right) \hfill \\ \end{gathered} \right)$ $\begin{gathered} C_{1} = - 16\beta \left( { - 18 + \beta \left( {24 + \beta \left( { - 14 + 3\beta } \right)} \right)} \right) - 8\beta \left( {58 + \beta \left( { - 44 + 3\beta \left( {2 + \beta } \right)} \right)} \right)\gamma^{2} \hfill \\ + \left( {1 - \beta } \right)\left( { - 149 + \beta \left( {77 + \beta \left( {37 + 3\beta } \right)} \right)} \right)\gamma^{4} + 4\left( {1 - \beta } \right)\left( {13 + \beta \left( {6 + \beta } \right)} \right)\gamma^{6}\hfill \\ + \left( {7 + \beta \left( {4 + \beta } \right)} \right)\gamma^{8} - \left( {1 + \beta } \right)\left( {7 + \beta \left( {4 + \beta } \right)} \right)\gamma^{8} s\left( {2 + s + \beta s} \right) \hfill \\ + 16s\left( \begin{gathered} 10 - 10\beta \left( { - 3 + \beta \left( {2 + \left( { - 2 + \beta } \right)\left( { - 1 + \beta } \right)\beta } \right)} \right) \hfill \\ \left( { - 1 + \beta } \right)^{4} \left( {1 + \beta } \right)^{2} \left( { - 5 + 2\beta } \right)s \hfill \\ \end{gathered} \right) \hfill \\ + 4\left( {1 - \beta^{2} } \right)\gamma^{6} s\left( {26 + 2\beta \left( {5 + \beta } \right) + \left( {1 + \beta } \right)\left( {13 + \beta \left( {4 + \beta } \right)} \right)s} \right) \hfill \\ - 8\gamma^{2} \left( { - 23 + \left( { - 1 + \beta } \right)^{3} \left( {1 + \beta } \right)s\left( {23\left( {2 + s} \right) + \beta \left( {6 + \left( {18 - 5\beta } \right)s} \right)} \right)} \right) \hfill \\ - \left( { - 1 + \beta } \right)^{2} \left( {1 + \beta } \right)\gamma^{4} s\left( {149\left( {2 + s} \right) + \beta \left( {76 + 153s + \beta \left( {10 + \left( {7 + 3\beta } \right)s} \right)} \right)} \right) \hfill \\ \end{gathered}$

Proof of Corollary 3

• (1) (1) $t_{e}^{M} - t_{e}^{R} = \frac{{\gamma \left( {2\varphi - 1} \right)\left( {1 - \beta } \right)\left( {1 + \left( {1 - \beta } \right)} \right)}}{{2\left( {2\varphi - \gamma^{2} - 2\beta \varphi } \right)\left( {{1} - {\upgamma }^{2} - {\upbeta }} \right)}}$ If $\varphi < \frac{1}{2}$, $t_{e}^{M} < t_{e}^{R}$; If $\varphi > \frac{1}{2}$,$t_{e}^{M} > t_{e}^{R}$.

• (2) (2) $t_{e}^{H} - t_{e}^{HH} = - \frac{{\gamma \left( {1 - \beta } \right)\left( {\left( {1 - 2\rho } \right) - s\left( {1 + \beta } \right)} \right)}}{{4 - 3\gamma^{2} - \beta \gamma^{2} - 4\beta }}$, if $\rho < \overline{{\rho_{0} }}$, $t_{e}^{HH} > t_{e}^{H}$; if $\rho > \overline{{\rho_{0} }}$, $t_{e}^{H} < t_{e}^{HH}$.