1 Introduction

Regardless of the context, corporate or otherwise, the decision-making process is fundamental. For this reason, it is important, if not essential, to consider all available information during the analysis and evaluation activities to better support the decision making process. The modern world of sport has been required to embrace analytical tools to improve performance, to anticipate trends and to eliminate uncertainty. To the traditional qualitative methods, advanced statistical methods have been added to improve and make the evaluation of the players more reliable. Before this, only the experience of scouts and coaches was utilized. The evidence-based approach saw its early beginnings within Major League Baseball (MLB), in which it was pioneered by statesman Bill James (1985). The so-called “Sabermetric” approach (empirical analysis of baseball) analyzes and studies baseball using statistical data, to determine the conditions that lead a team to win or lose a match.Footnote 1

The algorithm developed by the former student of the University of Kansas consisted of evaluating the players in three distinct aspects of the game: batting, pitching, and fielding. These measures allowed the translation of the actions of the players and the team into analytical terms.

The theories of Bill James and Sabermetric have been, for fans of baseball and sports in general, a way to see and understand sport in a novel way.Footnote 2 Subsequently other sports have also embraced the world of statistical analysis, with an attempt to fill the gap between experience in the field and observable and verifiable data. Above all basketball, and in particular the teams of the National Basketball Association (NBA), have used statistical analysis to achieve their short and long-term goals.

If Bill James is recognized as the pioneer of statistics in baseball, in the world of basketball it is Daryl Morey and Dean Oliver, former General Manager (GM) of the Houston Rockets and Denver Nuggets, respectively, who wear this crown.

Commonly referred to as the NBA’s Billy Beane, Morey, from 2006 onwards, studied the behavior of athletes across the league, achieving important results. One of the theories implemented by Morey is based on the development of a strategy for the selection of team shots. As demonstrated by the empirical evidence, the Rockets almost never shot from medium distance (jumper), but the shooting choices coincided with the strategy, that is mainly close shots (lay-up) or 3pt shots, which have an higher value. From the statistics of the league, it emerges in fact that the Rockets almost always have the lowest percentage of shots in the so-called “no man’s land” between 16 and 23 feet from the basket (Fig. 1).

Fig. 1
figure 1

Comparison between the shooting ranges of all NBA teams and those of the Houston Rockets in 2014/2015

Full size image

This strategy is the perfect benchmark for almost all the NBA teams today, leading to a real revolution in the game of basketball in America. As can be seen in Fig. 2, the 3pt shot introduced in the league in 1980 has undergone a considerable increase in use over the years, from 2.77 (1980) to 21.25 attempts per game. This figure reflects how important and revolutionary the theory developed by Morey was. The results achieved by the GM were considered as the basis on which to build successful teams. This is the case for teams like the Golden State Warriors, winners of three championships in 4 years (2015–2018) and regarded as one of the best teams of all times, having improved the regular season winning record which previously belonged to Michael Jordan’s Chicago Bulls (72-10). The Golden State Warriors, and in particular players like Stephen Curry, played following Morey’s suggestion “three better than two”.

Fig. 2
figure 2

Evolution of the average points per game (PTS) and 3-point attempts (3PA) in the NBA since 1980

Full size image

Looking at Fig. 2, one can notice that, despite the number of 3-point attempts (3PA) increased during the time period 1980–2007, overall the average points per game decreased instead. This has mainly depended on the playstyle; indeed, although since 1995 the number of 3-point shots increased, exceeding the 10 attempts per game, on average, the League in that period still was in a primordial phase of the game, characterized by schemes that favoured High post (elbow) and Short Corner plays (Fig. 3), typical of the Lakers’ years with Magic Johnson/Kareem Abdul Jabar and before them with Wilt Chamberlain. Michael Jordan, for instance, the most important player of all times, certainly did not go down in history for his 3pt shooting percentage (just over 30% in his career). In such a scenario, Jordan was the one who changed the way of playing but using mid-range shots with his trademark fadeway. Only after, in the following years, players like Stephen Curry have increased both the attempts and the shooting outside the 3-point arc. A second factor to be considered relates to the development of the defensive capability and, hence, to the ability of individual teams to concede as few points as possible to their opponents. Differently from the previous years, after 1995 (the year in which the average points per game tended to decrease), the attention has focused on the defensive phase, such as the famous Jordan Rules.

Fig. 3
figure 3

Dimensions of an NBA court

Full size image

Kirk Goldsberry, years after Morey, wrote in his book “Sprawlball - A Visual Tour of the New Era of the NBA” (Goldsberry 2019), the following words: “Points remain the ultimate currency of basketball and teams that invest so much in two-point jump shots. They don’t get a good return on that investment. It makes much more sense to invest in shots of over seven meters rather than in those of less than three”. It has been noted that it is more effective to shoot out of the bow (an average shot produces 1.1 points), rather than with the feet inside it, but still far from the basket (an average shot, between 2.5 m and the arc, yields 0.8 points). This is not to say that the mid-range shot earning two points should not be taken, but that there are valid reasons to support the continued rise of the three-point shot, so criticized in the early days of the game. It is important to point out that the 3pt shot represents only one of the key statistics in the game. It is necessary to consider other variables relevant to the game, both internal and external, to better understand the phenomenon.

Dean Oliver, like Daryl Morey, was and still is a GM of an NBA team. His analysis, which began in the period between 1995 and 2003 when he still held the role of engineering consultant, focused on the concept of “possession”. This concept is fundamental for the analysis of basketball, since as the number of possessions increases, the chances of making shots increase and therefore implicitly the chances of scoring a shot increase.

The statesman’s analysis begins with the definition of what “possession” is, stating that possession begins when a team gains control of the ball and ends when that team loses control. There are several ways a team can lose possession, including:

  1. 1.

    successful baskets or free throws;

  2. 2.

    defensive rebounds;

  3. 3.

    turnovers.

The choice of the “possession” variable is considered valid since it is generally approximately the same for the two teams in a match, and therefore provides a useful basis for evaluating teams and individual efficiency. As in all sports, even in basketball the team that scores more points wins, and this is the reason of the importance of possession with respect to the opponents. Possessions per team or player (POSS) can be estimated using data obtained from play-by-play logs (Oliver 2004; Kubatko et al. 2007, section 2) or by using a general formula:

$$\begin{aligned} POSS= & {} (FGM+\lambda FTM) +\alpha [(FGA-FGM) +\lambda (FTA-FTM)-OREB]\nonumber \\{} & {} +(1-\alpha ) DREB_o +TO \end{aligned}$$
(1)

where

  • FGA: field goal attempts

  • FTM: free throw made

  • FGM: field goal made

  • FTA: free throw attempts

  • OREB: offensive rebounds

  • \(DREB_o\): defensive rebounds for opponent

  • TO: turnovers

  • \(\lambda \): fraction of free throws that end the possession

  • \(\alpha \): a value between zero and one.

According to Eq. (1), a FGM, which is a successful attempted basket from the field, a FTM, a free throw scored and a TO, a lost ball, constitute the beginning of a new “possession”, i.e., have a possession value of 1. Oliver’s analysis does not stray much from that carried out by the aforementioned Bill James in baseball. Possessions are in fact analogous to baseball “outs”, where teams usually have 27 outs to outrun their opponents (James 1985).

The evolution of performance analysis in sport has seen significant advances. Technological progress has had an important role in this process, which is reflected in the availability of more data and with better accuracy and higher precision. The data processing phase has also evolved from a mostly descriptive and qualitative approach to a methodological approach (Zuccolotto et al. 2020; Morgulev et al. 2017).

In the literature, there are several quantitative empirical studies for basketball based on statistical methods and data science. Kubatko et al. (2007) define and analyse the basketball statistics and the related sources of data, thereby providing a common starting point for future research in basketball. Among these the concept of possession, central to basketball analysis. The following listed studies can be grouped according to the objective into studies concerned with the statistical modeling of the success of the team and studies concerned with the statistical modeling of the success of the players, based on basketball statistics of teams or players.

In the first group Koh et al. (2011) analyse discriminating factors between successful and unsuccessful teams considering a case study in elite youth Olympic basketball games. Gabel and Redner (2011) use random walk for basketball scoring. Schwarz (2012) suggests a prediction of the maximum lead from final scores in basketball modeling the evolution of the home team lead as a Wiener diffusion process. Shortridge et al. (2014) quantify spatial relative field goal efficiency in basketball. Yang et al. (2014) evaluate the efficiency of National Basketball Association (NBA) teams under a two-stage DEA (Data Envelopment Analysis) framework. Andrew (2015) propose an approach to bracket prediction in the NCAA men’s basketball tournament based on a dual-proportion likelihood. Lopez and Matthews (2014) propose an NCAA men’s basketball predictive model based on logistic regression. Nikolaidis (2015) builds a basketball game strategy through a statistical approach. Ruiz and Perez-Cruz (2015) suggest a generative model for predicting outcomes in college basketball. Yuan et al. (2015) suggest a forecasting of the NCAA tournament outcomes. Hans (2016) suggests a modeling and forecasting study of the outcomes of NBA basketball games. Vracar et al. (2016) present a methodology for generating a plausible simulation of a basketball match between two distinct teams as a sequence of team-level play-by-play in-game events using an expert system. Steven and Luke (2018) model the offensive player movement in professional basketball. Metulini et al. (2018) analyse the dynamic pattern of surface area in basketball and its effects on team performance.

In the second group Fearnhead and Taylor (2010) study statistically the ability of NBA players using linear models controlling for the changing abilities of the other players, and using multiple seasons’ data Deshpande and Jensen (2016) estimate the NBA player’s impact on his team’s chances of winning using a Bayesian linear regression model. Engelmann (2016) analyse the possession-based player performance in basketball. Zuccolotto et al. (2018) consider big data analytics for modeling players scoring probability in basketball for studying the effect of shooting under high-pressure conditions developing a multivariate model based on the Classification And Regression Tree algorithm i. Zuccolotto et al. (2019) propose a spatial statistical method based on classification trees, aimed to define a partition of the court in rectangles with maximally different scoring probabilities of players/teams. Sandri et al. (2020) model the player’s shooting performance variability by using Markov switching models, assuming the existence of two alternating performance regimes related to the positive or negative synergies that specific combinations of players may create on the court.

Around 2010, the emergence of tracking data, which consists of spatial and temporally referenced player and game data, began to transform basketball analytics. The advent of tracking data in the NBA has provided new opportunities of statistical analysis. Cervone et al. (2014) propose a multiresolution stochastic process model for predicting basketball possession outcomes using optical player tracking data. Bornn et al. (2016) suggest a statistical analyse of basketball through the lens of player tracking data. Metulini et al. (2017) propose a space-time analysis of movements in basketball using sensor data.

Different data science applications to basketball are shown in Zuccolotto et al. (2020), where the empirical studies are performed by means of the R package BasketballAnalyzeR (Zuccolotto et al. 2019; Sandri et al. 2020; Zuccolotto et al. 2020).

Recently complex networks have been applied in sport (Ramos et al. 2017; Vaz de Melo et al. 2008; Onody and de Castro 2004 and related references).

According to the postulates of Complex Network Analysis (CNA), large systems can be modelled and studied as ensembles of punctual elements (nodes) and connections (edges). Applications of CNA have appeared in literature to study both artificial and natural systems. Beyond applications in computer simulation, CNA has provided understanding of a number of subjects such as: the World Wide Web, human interactions, food webs, the spread of diseases, genomes and protein’ structures. Those interacting organizations are made up of non-identical elements (nodes) connected through different levels of interplay (edges). For a review of these applications, see Newman (2003), Albert and Barabási (2002).

A fast growing research branch in CNA attains the detection of communities (for a review, see Newman 2018). A community in a network stands for a subset of nodes with a higher number of internal edges compared to the outward edges towards communities. So, in the World Wide Web communities correspond to websites pertaining to related subjects; in metabolic networks communities behave as functional modules, while in social networks clusters of individuals are connected by similar activities.

In a more general perspective, (Fortunato 2010) groups the definitions of network communities in three main categories: local, global and based on vertex similarities. In local definitions, the local connectivity of vertices is inspected, disregarding the rest of the graph. In global definitions the graph is analyzed as a whole and the communities are considered as structural units of the graph. Definitions based on vertex similarity select communities’ membership when nodes are similar with each other according to a quantitative criterion.

Community detection over a network is affected by the characteristics of the system at hand. In fact we observe both local and global homogeneous distributions of edges within some clusters and low concentrations between these clusters. Traditionally, network community detection aims to identify communities through an analysis of the topology of a graph. New advances also propose the detection of communities in weighted networks where not only the topology influences the shaping of clusters but also the weight of each edge in terms of resilience or strength of interaction between nodes.

Detection of communities in systems represented as graphs (networks) is of great importance in many disciplines. Communities, or clusters, are usually groups of vertices with many edges joining vertices of the same cluster and comparatively few edges joining vertices of different clusters. Such clusters, or communities, represent a partition of a graph. Detecting communities in networks is a problem not yet solved. The open questions are the definition of community and partition; the quality function measuring the community structure, the partition similarity measure used to evaluate the match between partitions (subsequent partitions or the partition detected by the method and the known benchmark partition). A comparative analysis of methods of community detection against benchmark graphs, with heterogeneous distributions of degree and community size, can be found in Danon et al. (2005), Lancichinetti and Fortunato (2009, 2014), Yang et al. (2016), Orman et al. (2011). Classical techniques for data clustering, like hierarchical clustering (agglomerative and divisive) and partitional clustering (k-means, k-medoid) solve the same problem. The main difference is that, while communities in graphs are related, explicitly or implicitly, to the concept of edge density (inside versus outside the community), in data clustering communities are sets of points which are “close” to each other, with respect to a measure of distance or similarity, defined for each pair of points. Hierarchical clustering has the advantage that it does not require a preliminary knowledge on the number and size of the clusters. However, it does not provide a way to discriminate between the many partitions obtained by the procedure, and to choose that or those that better represent the community structure of the graph. The results of the method depend on the specific similarity measure adopted. The limitation of partitional clustering is that the number of clusters must be specified at the beginning as the method is not able to derive it. A thorough exposition of the topic, the definition of the main elements of the problem, the presentation of most methods developed, the discussion of crucial issues can be found in Fortunato (2010), Fortunato and Hric (2016). Both hierarchical and partitional clustering are not robust to the presence of outliers (k-medoid shows a timid robustness to outliers).

In this paper a method based on modularity as a quality function to be maximized and on Normalized Mutual Information as a similarity measure between partitions is used. The number of communities is determined by the method, that is also robust in the sense of being able to remove weak edges (and related vertices). The performance data of the players are taken from the NBA website (nba.com/stats) for the regular season 2020–2021. The NBA was formed and started recording the data of players in each game in 1947, which assists coaches, scouts, and researchers significantly in studying team efficiency, player’s behavior, etc.. Among the performance measures, the Four Factors, according to Oliver (2004), Kubatko et al. (2007) and following studies, determine the style of playing of players and teams and represent four strategies related to success in basketball. The four factors, detailed in Sect. 3, are to score efficiently (Effective Field Goal Percentage), to grab as many rebounds as possible (Offensive Rebounding percentage), to get to the foul line as often as possible (Free Throw Attempt rate) and to protect the basketball on offense (Turnovers per possession). To score efficiently is the simplest of all, being to score the aim of a team. Oliver proposed to measure it by the field goal percentage for a team, corrected to account for three point field goals. To grab every miss and give the team a second opportunity is another winning strategy if a team cannot score on every possession. An offensive rebound extends a possession and allows for a second attempt at a field goal. The proposed measure was the percentage of offensive rebounds. The next way to score points other than scoring a field goal or giving the team a second opportunity is to get to the foul line. The proposed measure was the number of free throws made per field goal attempt. The last of the four factors is to ensure that, other than a defensive rebound, a field goal attempt or free throw attempt terminates the possession. That is, don’t turn the ball over. The proposed measure was the percentage of possessions ended in a turnover. The Four Factors, averaged over the detected communities, are predictive of wins and losses.

The paper is organized as follows. In Sect. 2 a synthetic description of complex networks is introduced. In Sect. 3 an application of complex networks to the detection of communities of basketball players is presented. Conclusions and future outlooks are proposed in Sect. 4.

2 Complex networks

The complex networks theory offers many tools for analyzing a network (Newman 2003, 2018; Caldarelli 2007). One of the most interesting lines of research is the study of whether the network accommodates a community structure characterized by having many more intragroup edges than intergroup ones (Newman and Girvan 2004; Newman 2006). A network is mathematically defined by its topological graph constituents: nodes and edges. A “node” can represent any element that has any kind of relationship with another element in the network, and this relationship is namely the “edge”. For example, in a social network, a node could be an individual and an edge the friendship/acquaintance between a couple of individuals, or in air-traffic networks, a node could be an airport and an edge a flight route between two airports. In the present case, the node is a basketball player and the edge a similarity relationship between players. Further characterization of this similarity leads to the quantification level of similarity between players as a weight attached to each edge.

On a network level a community structure is any partition of the nodes into a set of communities which enables defining, for each community, internal and external edges, that is edges connecting two nodes of the given community and edges connecting a node of the given community with a node of some other community. Of course this could lead to a lot of arbitrariness in deciding which partition is the best under some given requirements. Many algorithms have been proposed in the literature to perform such a task (Fortunato 2010). Most of them are based on a function, named Modularity (Girvan and Newman 2002; Newman 2006) (in our case weighted Modularity), that is defined as follow:

$$\begin{aligned} Q^w=\frac{1}{2W}\sum _{ij}\left( w_{ij}-\frac{s_is_j}{2W}\right) \delta (c_i,c_j), \end{aligned}$$
(2)

where

  • \(w_{ij}\) is the weight associated to the edge connecting the node i and the node j (similarity weight in our following case),

  • \(s_i=\sum _jw_{ij}\) (node strength) is the sum of the weights of the edges attached to the node i,

  • \(W=\frac{1}{2}\sum _{ij}w_{ij}\) is the sum of all the edge weights in the network,

  • \(c_i\) shows that the node i belongs to the community \(c_i\) nd \(c_j\) that the node j belongs to the community \(c_j\),

  • \(\delta (c_i,c_j)\) is different from 0 only if the nodes i and j are in the same community (Barrat et al. 2004; Newman 2004; De Montis et al. 2006).

The Modularity function tries to quantify how good is a community subdivision, among all possible ones, by computing, for a particular subdivision, how many edges there are inside the communities compared to the number of edges expected connecting randomly nodes and keeping the actual degree distribution of the nodes in that community. In this respect the modularity function quantifies how good a partition is, among all possible partitions, by computing, for a particular subdivision, how many edges are enclosed in a subdivision with respect to the random case. Modularity values range from \(-1/2\) to \(+1\) (Brandes et al. 2008). It takes positive values if in the community structure of the network there are more edges inside each community than outside; negative values if there are fewer such edges, signaling the fact that it is not worth splitting the network into communities. The value 0 corresponds to a single partition that will coincide with the whole graph.

In order to find the best community structure, the Modularity function has to be maximized. In our proposal the final number of communities is not explicitly fixed. In this way, by maximizing the Modularity, not only the best distribution of nodes across communities, but also the ideal number of communities as well is found.

The problem of maximizing the Modularity function could be a computational demanding task for networks with thousands or more nodes. In the field of community detection algorithms, the Louvain procedure is quite efficient, because it allows one to successfully approach two critical issues of optimisation methods: detecting communities in large networks in a short time and taking into account hierarchical community structure (Blondel et al. 2008). Furthermore, the Louvain algorithm may be used for both weighted and unweighted networks (Barrat et al. 2004; Newman 2004; De Montis et al. 2006). Other possible community detection methods based on Modularity are based on Spinglasses (Reichardt and Bornholdt 2006), Walktrap (Pons and Latapy 2006), Eigenvector (Newman 2006), Fastgreedy (Clauset et al. 2004).

In pure topological networks, where unweighted edges among nodes arise for a direct connection mechanism between the involved entities, the possibility to resolve the system in communities is more straightforward. When the network is built up according to a similarity criterion or a correlation measure, the density of weighted edges is high, very close to a fully connected graph, and even in the case of a heterogeneous distribution of weights, it is very hard to disentangle the module structure of the system. For this reason, sparsification procedures are often applied to remove the weakest edges, which are the most affected by experimental noise, and to reduce the density of the graph, thus making it theoretically and computationally more tractable. However, weak edges (with small weights) may also contain significant structural information, and procedures to identify the optimal tradeoff are the subject of active research (Gallos et al. 2012; Bordier et al. 2017; Newman 2018).

In the sparsification process, the network starts loosing edges and at a certain point also nodes, generating disconnected components. As it is well known from the theory of random graphs, there is a percolation transition where a giant component suddenly appears in the process of generating the topological structure from scratch, adding edges at random (Bollobás 1985). Conversely, one could expect a similar phenomenon when pruning edges from the network, and this is the case for a certain category of networks (Bordier et al. 2017). In the region where the giant component is stable we need a measure able to compare the sequence of community structures. In this work we adopted the Normalized Mutual Information (NMI) (Danon et al. 2005; Meila 2007; Vinh et al. 2010), a measure of similarity between partitions. It is defined as:

$$\begin{aligned} NMI(A,B)=\frac{-2\sum _{i=1}^{C_A} \sum _{j=1}^{C_B} N_{ij}log\big (\frac{N_{ij}N}{N_{i.}N{.j}}\big )}{\sum _{i=1}^{C_A} N_{i.}log\big (\frac{N_{i.}}{N}\big )+\sum _{j=1}^{C_B}N_{.j}log\big (\frac{N_{.j}}{N}\big ) } \end{aligned}$$
(3)

where A and B are the community structures of two networks, \(C_A\) and \(C_B\) are the number of communities in partition A and B respectively, N the total number of nodes in the networks (which is the same in A and B) and \(N_{ij}\) is the overlap between A’s community i and B’s community j; i.e., the number of common nodes. Finally, \(N_{i.}\) and \(N_{.j}\) are the total number of nodes in community i of A and j of B respectively. The NMI ranges from 0 to 1, where \(NMI = 0\) corresponds to no similarity between A’s and B’s communities, and \(NMI = 1\) to complete identity, the two partitions correspond perfectly. At the removal of each edge, starting with the weakest ones, the Modularity is computed for all candidate pruned networks, and the partition with highest Modularity is selected. At the next removal of edge the partition with highest Modularity is selected. Then the comparison between the two consecutive partitions is computed based on NMI. The procedure is repeated for all consecutive edge removals, generating a curve of the overall stability of the whole process. As explained the removal of edges may cut the network in disconnected components and typically in the first stages just single nodes detach from the giant component. NMI is computed on an overall partitioning of the networks, comprising both the communities of the giant components and the residual connected components.

3 Community structure of basket players

Oliver’s studies have moved towards a detailed analysis of every aspect that could explain the individual player in detail, reaching the definition of one of the most important statistics of the American basketball scenario, namely the “Four Factors” (https://www.espn.com/nba/stats). The “Four Factors” are the following:

  • Effective Field Goal percentage (eFG%)

  • Turnovers per possession (To Ratio%)

  • Offensive Rebounding percentage (OREB%)

  • Free Throw Attempt rate (FTA%)

Since the Field Goal percentage (FG%), defined as \(100 \times \frac{FGM}{FGA}\), does not consider in the analysis and evaluation the three points shots and the free throws, Dean Oliver has developed a new statistical measure capable of enclosing these phenomena in the statistical analysis. This measure is the effective Field Goal percentage (eFG%), which can respectively be calculated in terms of a single player or team. The variable eFG% measures the percentage of field goals that adjusts for the field goals scored by 3 points (3PM). The latter are 1.5 times more valuable than 2-point field goals :

$$\begin{aligned} eFG\%=100 \times (FGM+0.5\times 3PM)/FGA. \end{aligned}$$

The second variable, which makes up the “Four Factors”, is identified in the To Ratio, a measure that represents the percentage of turnovers of a player or an entire team, summarizing in its measure the values of FGA, FTA and Assists:

$$\begin{aligned} To \ Ratio\%=100 \times \frac{TO}{FGA+(FTA \times 0.44)+Assists + TO}. \end{aligned}$$

The third variable taken into consideration is the percentage of offensive rebounds (OREB%), a measure that indirectly significantly affects the game. Players, as well as teams, by obtaining an offensive rebound, implicitly have the possibility of having one more attempt to make a basket, which therefore contributes to increasing the chances of obtaining a win:

$$\begin{aligned} OREB\%=100 \times \frac{OREB}{OREB+DREBo}. \end{aligned}$$

The fourth variable that makes up the “Four Factors” is represented by the Free Throw Rate, a measure that expresses the number of attempts at free throws that a team makes compared to the number of shots per basket. This apparently insignificant variable embodies a very important value, as it expresses the skill that a player or team has in getting a foul every time he attempts a shot for a field goal (“ability to make foul shot”):

$$\begin{aligned} FTA\%=100 \times \frac{FTM}{FGA}. \end{aligned}$$

To these factors, Oliver has assigned a specific weight, in relation to the importance that each of them has in influencing an outcome as a winner or not: eFG = 40%, To Ratio = 25%; OREB = 20%; FTA = 15%.

Fig. 4
figure 4

Average values of the Four Factors league from 1979–1980 to 2005–2006 (Shooting = eFG%, Turnovers = To Ratio%, Rebounding = OREB%, Free Throw= FTA%) - Kubatko et al. (2007)

Full size image

The composition of these metrics thus identifies a team’s strategic strength and weakness, both in offensive and defensive terms, making reliable predictions of NBA team wins and losses (Fig. 4). Statistics in this sense offers the right tools to support the decisions of the staff in the most varied situations, whether it is necessary to decide which player is to enter the field at that moment of the game, or to take that shot in that game situation to maximize the team’s efficiency and achieve a victory.

Other variables are listed. Points (PTS) can be produced through field goals, free throws, assists, and offensive rebounds. Individual possessions are the sum of a player’s scoring possessions (field goals, free throws, plus partial credit for assists), missed field goals and free throws that the defense rebounds, and turnovers.

  • True Shooting percentage (TS%): while measuring the percentage of shot taking into account the value of the 3-point baskets, also adds to the evaluation free throws, which are now an essential variable for an accurate analysis \(TS=100 \times \frac{Points}{2 \times (FGA+0.44 \times FTA)}\);

  • Offensive Rating (OFFRtg): is a statistic used in basketball to measure a team’s points scored per 100 possessions; on a player level this statistic is team points scored per 100 possessions while they are on court \(OFFRtg=100 \times \frac{Points}{POSS}\);

  • Defensive Rating (DEFRtg): or defensive efficiency is a statistic used in basketball to measure the number of points allowed per 100 possessions by a team; for a player, it is the number of points per 100 possessions that the team allows while that individual player is on the court \( DEFRtg=100 \times \frac{Opp \ Points}{Opp \ POSS}\) where \(Opp \ Points\) is the number of points scored by an opposing player (or team) and \(Opp \ POSS\) is the number of opponent possessions;

  • Net rating (NETRtg): measures a team’s point differential per 100 possessions. On player level this statistic is the team’s point differential per 100 possessions while he is on court \( NETRtg= OFFRtg-DEFRtg \);

  • Assist percentage (AST%): percentage of teammate field goals a player assisted on while he was on the floor \( AST=100 \times \frac{AST}{TmFGM-FGM} \) where TmFGM is the number of teammate FGM;

  • Assist to Turnover Ratio (AST/TO): the number of assists for a player or team compared to the number of turnovers they have committed;

  • Assist Ratio (AST_RATIO): number of assists a player averages per 100 possessions used \( AST\_RATIO=100 \times \frac{AST}{POSS} \);

  • Defensive Rebound percentage (DREB%): the percentage of available defensive rebounds a player or team obtains while on the floor;

  • Rebound percentage (REB%): percentage of available rebounds a player or team grabbed while on the floor;

  • Usage percentage (USG%): percentage of team plays used by a player when he is on the floor; \(USG\%=100 \times \frac{(FGA + Possession \ Ending \ FTA + TO) }{POSS}\);

  • PACE: number of possessions per 48 min for a team or player;

  • Player Impact (PIE): measures a player’s overall statistical contribution against the total statistics in games they play in. PIE yields result which are comparable to other advanced statistics using a simple formula that includes PTS, FGM, FTM, FTA, DREB, OREB, AST;

  • Game played (WP): the number of games played by a player;

  • Wins (W): the number of games won by a player;

  • Losses (L): the number of games lost by a player.

The positions of the players are presented in Fig. 5.

Fig. 5
figure 5

Positions

Full size image

The variables and their summary statistics are reported in Table 1. The histograms of the Four Factors for all the players are presented in Fig. 6

Table 1 Basketball variables
Full size table
Fig. 6
figure 6

Histograms of the four factors

Full size image

A weighted complex network is used for community detection of basketball players. The nodes represent players. An adjacency matrix, A, is a square matrix, with rows and columns representing players. The entries of the adjacency matrix, called weights, reflect the intensity or strength of the edges between nodes. Undirected networks are represented in symmetric adjacency matrices, the fact that the edge between nodes i and j has no orientation is expressed in the equality \(w_{ij}=w_{ji}\). The weight of an edge represents the similarity between players. Similarity is computed as:

$$\begin{aligned} w_{ij}=1-\frac{d_{ij}-min(d_{ij})}{max(d_{ij})-min(d_{ij})} \end{aligned}$$
(4)

where \(d_{ij}\) is the euclidean distance between players i and player j over the Four Factors.

In the present case the players were 536. The players with less than 6.3 min played per game were eliminated and 479 players were obtained (1.3–6.3 is the 5 min time played interval from the minimum time played). So our starting network comprises 479 nodes and 114480 edges, with associated weights ranging from 0.02 to 1.0.

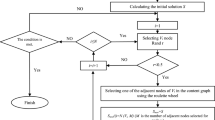
To gradually perform the sparsification on the network the edges are ordered according to their weights in increasing sizes and then removed one by one starting from the smallest. For each step the best modularity of the giant component is calculated with the Louvain algorithm repeating the procedure 5 times and retaining the maximum value (the maximization process is not deterministic).

The first interesting outcome is that the modularity increases monotonically with edge removals (Fig. 7), and this happens while the giant component, for a wide range of weights, stays very close to the original network size.

Fig. 7
figure 7

Modularity score (blue) and giant component size (red) with increasing weight edge removal

Full size image

If we had calculated the Modularity without pruning the network at all, it would have been close to zero. In some sense the weak edges, especially in very topologically dense networks, hide the genuine ground partition structure at all possible levels and the pruning process just clears out what is hidden behind some kind of information noise. Now the point is when exactly to stop in this procedure and which are the right thresholds to be considered as reliable candidates for community detection.

For a certain type of dense weighted networks, like the ones that arises from the correlation between pair of voxels in fMRI brain signals, it is known in the literature (Bordier et al. 2017), there is a sharp percolation transition for which the giant component abruptly breaks apart. This transition also produces the fragmentation of the ground truth partition, known in advance in that case, and finally signals the threshold to be considered as the maximum attainable to preserve the genuine information related to the underlying partition. This “sparsification transition” is confirmed by a maximum of the NMI behavior and other sensitivity parameters (Bordier et al. 2017). In our case (see Fig. 7) the percolation transition for the giant component is not sharp, and we need to further explore the NMI across all the threshold weight values as a “stability” parameter. In Fig. 8 the NMI measures are presented against the giant component size across sparsification thresholds with weights between 0.7 and 1 (running averages on a 150 window size of the NMI sampled every 100 thresholds). We found two stability peaks around 0.79 and 0.90.

Fig. 8
figure 8

NMI value (blue) and giant component size (red) with increasing weight sizes edge removal

Full size image

In Fig. 9 the details of the first peak are shown. In both cases, in order to have a clear landmark to be reminiscent of the percolation transition, we choose the step border correspondent to the NMI maximum (in this case size of the giant component is equal to 478). We then computed the maximum Modularity value for all the networks before the step border in the vicinity of the peak. In this way we avoid the problem to assess the peak position that can be slightly shifted due to the running averages procedure.

Fig. 9
figure 9

Detail of the peak around weight 0.79 of averaged NMI (blue) and giant component size (red) with increasing weight sizes edge removal

Full size image

In this first case, after losing the first node of the network in the very early pruning stage, we have a sequence of “node topplings” that start exactly at our first critical threshold around weight 0.79. The best network community structure that arises in the first peak is shown in Fig. 10.

Fig. 10
figure 10

Community structure obtained with the maximization of the Modularity of the pruned network in correspondence of the peak at weight 0.79. Each color represents the membership for the 3 communities

Full size image
Fig. 11
figure 11

Detail of the peak around weight 0.90 of NMI (blue) and giant component size (red) with increasing weight sizes edge removal

Full size image
Fig. 12
figure 12

Community structure obtained with the maximization of the Modularity of the pruned network in correspondence of the peak at weight 0.90. Purple community 1, orange community 2, blue community 3 and green community 4

Full size image

It contains 3 communities; one of them comprises only 3 nodes. The value of the Modularity is 0.06 (see also Fig. 7).

In this paper we analyze in more details the second peak at around 0.9025 as appears in Fig. 11. The value of the Modularity is 0.24 (see also Fig. 7). The corresponding pruned network has a better community resolution, as measured by the greater value of the modularity.

Table 2 Average values of the Four Factors in the communities and general
Full size table
Fig. 13
figure 13

Boxplots of the Four Factors in the 4 communities

Full size image
Fig. 14
figure 14

Boxplots of the profiling variables in the 4 communities

Full size image
Fig. 15
figure 15

Boxplots of the profiling variables in the 4 communities

Full size image
Fig. 16
figure 16

Boxplots of the profiling variables in the 4 communities

Full size image

In the second peak the sparsification procedure removed 9 players with IDs 386, 14, 48, 17, 349, 24, 25, 285, 30. The removal of the players is based on the removal of the weak edges, from the starting weighted complex networks. The fraction of nodes and edges of the giant component are 0.98 and 0.30, respectively (34455 edges). The value of NMI is around 0.86. The threshold of the weight for edge removal is around 0.9025 in correspondence of the step and the optimal community structure comprises 4 communities as represented in Fig. 12.

The sizes of the communities are: community 1: 183 players, community 2: 121 players, community 3: 159 players, community 4: 7 players. The average values of the clustering variables are presented in Table 2.

The boxplots of the four factors and of the profiling variables are presented in Figs. 13 and 14, 15, 16, respectively.

Then the positions of the players have been considered. As mentioned in the Introduction, a greater propensity is observed to shoot outside the semicircle; it is therefore necessary to understand how much importance, in terms of possessions, to give to players based on their position (role). The breakdown of the average of the Four Factors by position in each community is presented.

Community 1. The first community under analysis has 183 players (39.0%), including all 7 positions on the court (PG, SG, G, SF, PF, F, C). Among these, the most prevalent in both statistical and numerical terms is C, i.e., Centers (players of great height, who statistically take great shots inside the 3’ seconds area and are particularly important in terms of rebounds, both offensive and defensive) representing 28.9% of the entire community. In Table 3 it can be seen that this category presents the highest values in 3 of the 4 variables, among which a value above 60% stands out for the eFG variable. This data perfectly explains the style of play of these players, who most often end a game action with a layup rather or a dunk, therefore with shot attempts that have a higher expected value of being made. The only exception is represented by the FTA, whose highest average value is held by category F (4.4%), i.e., the Forwards (players who, unlike Centers, have more shooting range and almost a double dimension, being able to play both in front of and behind the basket) with 29.0%. The other positions in the community are SF (16.9%), PF (16.4%), SG (15.3%), PG (14.8%) and finally G (3.3%).

Community 2. The second community is slightly smaller than the first, with 121 players, or 26.0% of the entire sample under analysis (Table 4). Unlike the one previously analyzed, in this community the position with the highest frequency of players is PG (26.4%). Point guards, in summary, are players with strong shooting and passing/assist skills, which is why they can respectively present high values of the To Ratio variable. Players with similar performance can be found in the position of SG, which represents 24.0% of the community. Players in position SG show the highest values of eFG (47.1%) and FTA (16.8%), an expression of the fact that these players represent an important part of the team’s offensive system. The other positions in the community are SF (17.4%), PF (15.6%), G (6.6%) and C and F (5.0%).

Community 3. The third community is the second in terms of size (34.0%), containing 159 players (Table 5.) The largest percentage of players is in position SG (28.9%), followed by SF (20.8%), PF (18.2%), PG (17.0%), C (9.4%), G (4.4%) and finally F (1.3%). Unlike the two communities analyzed so far, the maximum values of the 4 variables are attained by players who occupy different positions. For eFG, the highest value is held by the Forward position (57.9%). FTA reaches the highest value for players in position SF, i.e. players who have a strong anatomical structure in terms of physicality, but maintain a certain elasticity, being able to make penetration as their most important characteristic. Just the penetration allows the small wings to be able to get more fouls during their shooting actions, which is why they have a value of 11.4%. As far as To Ratio is concerned, the highest value is that of players in position PF (Power Forward), while in terms of OREB, as usual, the players in position C show the best performance.

Table 3 Community 1. Average values of the Four Factors in community 1 by position played
Full size table
Table 4 Community 2. Average values of the Four Factors in community 2 by position played
Full size table
Table 5 Community 3. Average values of the Four Factors in community 3 by position played
Full size table
Table 6 Community 4. Average values of the Four Factors in community 4 by position played
Full size table

Community 4. Unlike the groups analyzed so far, the fourth community would play a marginal role if we looked only at the size (1.0%) (Table 6). In reality, this group has very good values for all the Four Factors, even if 3 out of the 7 players have played less than 10 games each. In addition in the community there are only 3 out of the 7 mentioned positions, that is C (42.9%), F (42.9%) and finally SF (14.2%). Considering the other variables, eFG (62.8%) and To Ratio (12.6%) present higher values for players in position C, while FTA (54.8%) and OREB (10.2%), reach their maximum for players in position F.

After analyzing the communities individually, the comparison between averages in the communities and general averages is considered. It emerges that the best communities are community 1 and community 4. Both communities have the highest concentration of players in position C, even if, as previously observed, community 4 has very few observations compared to community 1. If, on the one hand, the style of play of the NBA is moving further and further away from the basket, on the other hand, players operating near the basket are considered very important. It is no coincidence that the current year has seen the award of MVP (Most Valuable Player) to Nikola Jokic, starting Center of the Denver Nuggets, giving validity to the analysis carried out so far.

In Table 7 the distributions of the players by team in each community is presented. They show high heterogeneity.

Table 7 Players by team in the 4 communities
Full size table

4 Conclusions

In this paper a weighted complex network analysis is used to detect communities of basketball players on the basis of performance measurements of the players. A sparsification procedure to remove weak edges is also applied. In our proposal, to gradually perform the sparsification on the network, the edges are ordered according to their weights in increasing sizes and then removed one by one starting from the smallest. For each step the best community structure of the giant component is calculated with the Louvain algorithm, maximizing the modularity as a measure of compactness of the communities. The sparsification transition is confirmed by the Normalized Mutual Information (NMI) criterium as a “’stability” parameter between consecutive best community structures.

The analysis shows the validity of complex networks for community detection of NBA basketball players. We cross-checked the relevance of the results in terms of characteristics of each community; they are statistically homogeneous according to the current recorded performance variables of the players and the dynamics of the game. Beside th analysis of the communities individually, the comparison between averages in the communities and general averages has allowed the identification and the characteristics of the best communities, community 1 and community 4, either in terms of the Four Factors or of the profiling variables, providing insights on the style of play of players and teams. Both communities have the highest concentration of players in position CA, even if, as previously observed, community 4 has very few observations compared to community 1. If, on the one hand, the style of play of the NBA is moving further and further away from the basket, on the other hand, players operating near the basket are considered very important.

As for future developments, more has to be understood about the percolation transition in systems where it is not as well defined as in our study. The weighted random graph theory will also be considered. Furthermore the hierarchical nature of the community structure has to be uncovered, to refine the player communities into sub-communities. In particular, methods based on Statistical Inference (Stochastic Block Models and related recent developments) will be considered.