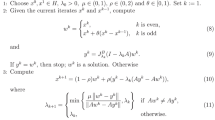Skip to main content
SpringerLink
Log in

Strongly convergent inertial forward-backward-forward algorithm without on-line rule for variational inequalities

  • Published:
Acta Mathematica Scientia Aims and scope Submit manuscript

Abstract

This paper studies a strongly convergent inertial forward-backward-forward algorithm for the variational inequality problem in Hilbert spaces. In our convergence analysis, we do not assume the on-line rule of the inertial parameters and the iterates, which have been assumed by several authors whenever a strongly convergent algorithm with an inertial extrapolation step is proposed for a variational inequality problem. Consequently, our proof arguments are different from what is obtainable in the relevant literature. Finally, we give numerical tests to confirm the theoretical analysis and show that our proposed algorithm is superior to related ones in the literature.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Aubin J P, Ekeland I. Applied Nonlinear Analysis. New York: Wiley, 1984

    Google Scholar 

  2. Baiocchi C, Capelo A. Variational and Quasivariational Inequalities: Applications to Free Boundary Problems. New York: Wiley, 1984

    Google Scholar 

  3. Boţ R I, Csetnek E R, Vuong P T. The forward-backward-forward method from continuous and discrete perspective for pseudo-monotone variational inequalities in Hilbert spaces. Eur J Oper Res, 2020, 287: 49–60

    Article  MathSciNet  Google Scholar 

  4. Censor Y, Gibali A, Reich S. The subgradient extragradient method for solving variational inequalities in Hilbert space. J Optim Theory Appl, 2011, 148: 318–335

    Article  MathSciNet  CAS  PubMed  PubMed Central  Google Scholar 

  5. Censor Y, Gibali A, Reich S. Strong convergence of subgradient extragradient methods for the variational inequality problem in Hilbert space. Optim Meth Softw, 2011, 26: 827–845

    Article  MathSciNet  Google Scholar 

  6. Cholamjiak W, Cholamjiak P, Suantai S. An inertial forward-backward splitting method for solving inclusion problems in Hilbert spaces. J Fixed Point Theory Appl, 2018, 20: Art 42

  7. Cholamjiak W, Dutta H. Viscosity modification with parallel inertial two steps forward-backward splitting methods for inclusion problems applied to signal recovery. Chaos Solitons Fractals, 2022, 157: Art 111858

  8. Dey S. A hybrid inertial and contraction proximal point algorithm for monotone variational inclusions. Numer Algor, 2023, 93: 1–25

    Article  MathSciNet  Google Scholar 

  9. Glowinski R, Lions J L, Trémolières R. Numerical Analysis of Variational Inequalities. Amsterdam: North-Holland, 1981

    Google Scholar 

  10. He B S. A class of projection and contraction methods for monotone variational inequalities. Appl Math Optim, 1997, 35: 69–76

    Article  MathSciNet  Google Scholar 

  11. Khobotov E N. Modification of the extragradient method for solving variational inequalities and certain optimization problems. USSR Comput Math Math Phys, 1989, 27: 120–127

    Article  Google Scholar 

  12. Kinderlehrer D, Stampacchia G. An Introduction to Variational Inequalities and Their Applications. New York: Academic Press, 1980

    Google Scholar 

  13. Korpelevich G M. An extragradient method for finding sadlle points and for other problems. Ekon Mat Metody, 1976, 12: 747–756

    MathSciNet  Google Scholar 

  14. Linh N X, Thong D V, Cholamjiak P, et al. Strong convergence of an inertial extragradient method with an adaptive nondecreasing step size for solving variational inequalities. Acta Math Sci, 2022, 42B(2): 795–812

    Article  MathSciNet  Google Scholar 

  15. Maingé P E. Approximation methods for common fixed points of nonexpansive mappings in Hilbert spaces. J Math Anal Appl, 2007, 325: 469–479

    Article  MathSciNet  Google Scholar 

  16. Malitsky Y, Tam M K. A forward-backward splitting method for monotone inclusions without cocoercivity. SIAM J Optim, 2020, 30(2): 1451–1472

    Article  MathSciNet  Google Scholar 

  17. Malitsky Y. Golden ratio algorithms for variational inequalities. Math Program, 2020, 184: 383–410

    Article  MathSciNet  Google Scholar 

  18. Malitsky Y. Projected reflected gradient methods for monotone variational inequalities. SIAM J Optim, 2015, 25: 502–520

    Article  MathSciNet  Google Scholar 

  19. Marcotte P. Applications of Khobotov’s algorithm to variational and network equilibrium problems. Inf Syst Oper Res, 1991, 29: 258–270

    Google Scholar 

  20. Nesterov Y. A method of solving a convex programming problem with convergence rate O(1/k2). Soviet Math Doklady, 1983, 27: 372–376

    Google Scholar 

  21. Popov L D. A modification of the Arrow-Hurwicz method for finding saddle points. Math Notes, 1980, 28: 845–848

    Article  ADS  Google Scholar 

  22. Saejung S, Yotkaew P. Approximation of zeros of inverse strongly monotone operators in Banach spaces. Nonlinear Anal, 2012, 75: 742–750

    Article  MathSciNet  Google Scholar 

  23. Tan B, Qin X, Yao J C. Strong convergence of inertial projection and contraction methods for pseudomonotone variational inequalities with applications to optimal control problems. J Global Optim, 2022, 82: 523–557

    Article  MathSciNet  Google Scholar 

  24. Tan B, Qin X. Modified inertial projection and contraction algorithms for solving variational inequality problems with non-Lipschitz continuous operators. Anal Math Phys, 2022, 12: Art 26

  25. Tan B, Cho S Y. Strong convergence of inertial forward-backward methods for solving monotone inclusions. Appl Anal, 2022, 101: 5386–5414

    Article  MathSciNet  Google Scholar 

  26. Thong D V, Vinh N T, Cho Y J. New strong convergence theorem of the inertial projection and contraction method for variational inequality problems. Numer Algor, 2020, 84: 285–305

    Article  MathSciNet  Google Scholar 

  27. Thong D V, Liu L L, Dong Q L, Long L V. Fast relaxed inertial Tseng’s method-based algorithm for solving variational inequality and fixed point problems in Hilbert spaces. J Comput Appl Math, 2023, 418: 114739

    Article  MathSciNet  Google Scholar 

  28. Thong D V, Vinh N T, Cho Y J. New strong convergence theorem of the inertial projection and contraction method for variational inequality problems. Numer Algorithms, 2020, 84: 285–305

    Article  MathSciNet  Google Scholar 

  29. Thong D V, Li X, Dong Q L, et al. Strong and linear convergence of projection-type method with an inertial term for finding minimum-norm solutions of pseudomonotone variational inequalities in Hilbert spaces. Numer Algorithms, 2023, 92: 2243–2274

    Article  MathSciNet  Google Scholar 

  30. Tseng P. A modified forward-backward splitting method for maximal monotone mappings. SIAM J Control Optim, 2000, 38: 431–446

    Article  MathSciNet  Google Scholar 

  31. Zhang C, Dong Q L, Chen J. Multi-step inertial proximal contraction algorithms for monotone variational inclusion problems. Carpathian J Math, 2000, 36: 159–177

    MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mathematical Sciences, Tiangong University, Tianjin, 300387, China

    Yonghong Yao

  2. Center for Advanced Information Technology, Kyung Hee University, Seoul, 02447, South Korea

    Yonghong Yao

  3. Operational Research Center in Healthcare, Near East University, TRNC Mersion 10, Nicosia, 99138, Turkey

    Abubakar Adamu

  4. Charles Chidume Mathematics Institute, African University of Science and Technology, Abuja, 900107, Nigeria

    Abubakar Adamu

  5. School of Mathematical Sciences, Zhejiang Normal University, Jinhua, 321004, China

    Yekini Shehu

Authors
  1. Yonghong Yao
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Abubakar Adamu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yekini Shehu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yekini Shehu.

Ethics declarations

Conflict of Interest The authors declare no conflict of interest.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yao, Y., Adamu, A. & Shehu, Y. Strongly convergent inertial forward-backward-forward algorithm without on-line rule for variational inequalities. Acta Math Sci 44, 551–566 (2024). https://doi.org/10.1007/s10473-024-0210-3

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10473-024-0210-3

Key words

2020 MR Subject Classification

Search

Navigation