Skip to main content
SpringerLink
Log in

Ultra-low power inductorless differential LNA for WSN application

  • Published:
Analog Integrated Circuits and Signal Processing Aims and scope Submit manuscript

Abstract

In this paper, a wide band inductorless differential low noise amplifier (LNA) is designed and analyzed. To attain ultra-low power consumption, several gm-enhancement techniques have been used. gm-enhancement achieved by active negative feedback and cross coupling techniques. By several gm-enhancement, in spite of the low intrinsic transconductance of the MOS transistor, low noise, high gain, and good linearity can be achieved. The LNA is designed in 180 nm CMOS technology and occupies a total area of 0.04 mm2. It has power gain of 15.64 dB, a minimum noise figure of 4.5 dB, third-order intermodulation intercept point of − 5 dBm while provides good input matching (S11 <  − 10 dB) in 0.03–3 GHz. The power consumption is 0.6 mW.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig.1
Fig. 2
Fig. 3
Fig. 4
Fig.5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig.10
Fig.11
Fig.12
Fig.13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19

Similar content being viewed by others

References

  1. Kargaran, E., Manstretta, D., & Castello, R. (2018). Design and analysis of 2.4 GHz 30μW CMOS LNAs for wearable WSN applications. IEEE Transactions on Circuits Systems, 65(3), 891–903.

    Article  Google Scholar 

  2. Parvizi, M., Allidina, K., Nabki, F., and El-Gamal, M (2013). A 04V ultra low-power UWB CMOS LNA employing noise cancellation. In Proceedings of ISCAS, pp. 2369–2372.

  3. Liu, H.-J., & Zhang, Z.-F. (2017). An ultra-low power CMOS LNA for WPAN applications. IEEE Microwave Wireless Components Letters, 27(2), 174–176.

    Article  Google Scholar 

  4. Chang, J.-F., & Lin, Y.-S. (2011). 0.99 mW 3–10 GHz common-gate CMOS UWB LNA using T-match input network and self-body-bias technique. Electronic Letters, 47(11), 658–659.

    Article  Google Scholar 

  5. Parvizi, M., Allidina, K., & El-Gamal, M. (2016). Short channel output conductance enhancement through forward body biasing to realize a 0.5 V 250 µW 0.6–42 GHz current-reuse CMOS LNA. IEEE Journal of Solid-State Circuits, 51(3), 574–586.

    Article  Google Scholar 

  6. Wang, S. B. T., Niknejad, A. M., & Brodersen, R. W. (2006). Design of a Sub-mW 960-MHz UWB CMOS LNA. IEEE Journal of Solid-State Circuits, 41(11), 2449–2456.

    Article  Google Scholar 

  7. Belmas, F., Hameau, F., & Fournier, J.-M. (2012). A low power inductorless LNA with double Gm enhancement in 130 nm CMOS. IEEE Journal of Solid-State Circuits, 47(5), 1094–1103.

    Article  Google Scholar 

  8. Parvizi, M., Allidina, K., & El-Gamal, M. (2016). An ultra-low-power wideband inductorless CMOS LNA with tunable active shunt-feedback. IEEE Transactions on Microwave Theory and Techniques, 64(6), 1843–1853.

    Article  Google Scholar 

  9. Tarighat, A. P., & Yargholi, M. (2020). Wideband input matching CMOS low noise amplifier with noise and distortion cancellation. Journal of Circuits, Systems and Computers (JCSC), 29(4), 1–11.

    Google Scholar 

  10. Yargholi, M., & Tarighat, A. P. (2012). UWB resistive feedback LNA employing noise and distortion cancellation. IEICE Electronics Express, 9(17), 1370–1377.

    Article  Google Scholar 

  11. Tarighat, A. P., & Yargholi, M. (2016). A CMOS low noise amplifier with employing noise cancellation and modified derivative superposition technique. Microelectronics Journal, 54, 116–125.

    Article  Google Scholar 

  12. Liscidini, A., Martini, G., Mastantuono, D., & Castello, R. (2008). Analysis and design of configurable LNAs in feedback common-gate topologies. IEEE Transactions on Circuits and System II, Express Briefs, 55(8), 733–737.

    Article  Google Scholar 

  13. Parvizi, M., Allidina, K., Nabki, F., and El-Gamal, M. N(2013). A 0.4 V ultra low-power UWB CMOS LNA employing noise cancellation. In: IEEE International Symposium on Circuits and Systems, pp. 2369–2372.

  14. Zhuo, W., Li, X., Shekhar, S., Embabi, S. H. K., Pineda de Gyvez, J., Allstot, D. J., & Sanchez-Sinencio, E. (2005). A capacitor cross-coupled common-gate low-noise amplifier. IEEE Transactions on Circuits and Systems II, Express Briefs, 52(12), 875–879.

    Article  Google Scholar 

  15. Sobhy, E. A., Helmy, A. A., Hoyos, S., Entesari, K., & Sánchez-Sinencio, E. (2011). A 2.8-mW Sub-2-dB noise-figure inductorless wideband CMOS LNA employing multiple feedback. IEEE Journal of Solid-State Circuits, 59(12), 3154–3161.

    Google Scholar 

  16. Tarighat, A. P., & Yargholi, M. (2019). Low power active shunt feedback CMOS low noise amplifier for wideband wireless systems. Integration, the VLSI Journal, 69(8), 189–197.

    Article  Google Scholar 

  17. Parvizi1, M., Allidina1, K., Nabki, F., and El-Gamal, M(2013). Low power active shunt feedback CMOS low noise amplifier for wideband wireless systems. In: Proceedings of IEEE International Symposium on Circuits Syst. (ISCAS), pp. 2369–2372.

  18. Tarighat, A.P., and Yargholi, M (2019). “Linearized low noise amplifier by post distortion technique. 27th Iranian Conference on Electrical Engineering (ICEE).

  19. Kargaran, E., Zoka, N., Kouzani, A. Z., Mafinezhad, K., & Nabovati, M. (2013). Highly linear low voltage low power CMOS LNA. IEICE Electronics Express, 10(21), 1–6.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Asieh Parhizkar, Payame Noor University, Rasht, Iran

    Asieh Parhizkar Tarighat

Authors
  1. Asieh Parhizkar Tarighat
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Asieh Parhizkar Tarighat.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

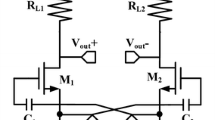
The linearity of the proposed LNA is analyzed by Volterra series, Vx, Vz, and Vo as the intermediate variable are determined in Fig. 3. The relation between Vs and Vx, Vz, and Vo are expressed up to 3rd-order as:

$$\begin{gathered} \mathop V\nolimits_{O} = \mathop A\nolimits_{1} \left( {\mathop s\nolimits_{1} } \right)o{\kern 1pt} \mathop V\nolimits_{S} + \mathop A\nolimits_{2} \left( {\mathop s\nolimits_{1} ,\mathop s\nolimits_{2} } \right)o{\kern 1pt} \mathop V\nolimits_{S}^{2} + \mathop A\nolimits_{3} \left( {\mathop s\nolimits_{1} ,\mathop s\nolimits_{2} ,\mathop s\nolimits_{3} } \right)o{\kern 1pt} \mathop V\nolimits_{S}^{3} \hfill \\ \mathop V\nolimits_{X} = \mathop B\nolimits_{1} \left( {\mathop s\nolimits_{1} } \right)o{\kern 1pt} \mathop V\nolimits_{S} + \mathop B\nolimits_{2} \left( {\mathop s\nolimits_{1} ,\mathop s\nolimits_{2} } \right)o{\kern 1pt} \mathop V\nolimits_{S}^{2} + \mathop B\nolimits_{3} \left( {\mathop s\nolimits_{1} ,\mathop s\nolimits_{2} ,\mathop s\nolimits_{3} } \right)o{\kern 1pt} \mathop V\nolimits_{S}^{3} \hfill \\ \mathop V\nolimits_{Z} = \mathop C\nolimits_{1} \left( {\mathop s\nolimits_{1} } \right)o\mathop {{\kern 1pt} V}\nolimits_{S} + \mathop C\nolimits_{2} \left( {\mathop s\nolimits_{1} ,\mathop s\nolimits_{2} } \right)o\mathop {{\kern 1pt} V}\nolimits_{S}^{2} + \mathop C\nolimits_{3} \left( {\mathop s\nolimits_{1} ,\mathop s\nolimits_{2} ,\mathop s\nolimits_{3} } \right)o{\kern 1pt} \mathop V\nolimits_{S}^{3} \hfill \\ \end{gathered}$$
(A.1)

im1, im2 and im4 are considered as follows:

$$\begin{gathered} \mathop i\nolimits_{m1} = \mathop g\nolimits_{m1} \mathop {{\kern 1pt} V}\nolimits_{S} + \frac{{\mathop g\nolimits_{m1,2} }}{2}\mathop {\,{\kern 1pt} V}\nolimits_{S}^{2} + \frac{{\mathop g\nolimits_{m1,3} }}{3!}{\kern 1pt} \,\mathop V\nolimits_{S}^{3} \hfill \\ \mathop i\nolimits_{m2} = \mathop g\nolimits_{m2} \left( {\mathop {{\kern 1pt} V}\nolimits_{X} \mathop { - {\kern 1pt} {\kern 1pt} V}\nolimits_{Z} } \right) + \frac{{\mathop g\nolimits_{m2,2} }}{2}\mathop {\left( {\mathop {{\kern 1pt} V}\nolimits_{x} - \mathop {{\kern 1pt} V}\nolimits_{z} } \right)}\nolimits^{2} + \frac{{\mathop g\nolimits_{m2,3} }}{3!}\mathop {\left( {\mathop {{\kern 1pt} V}\nolimits_{x} - {\kern 1pt} {\kern 1pt} \mathop V\nolimits_{z} } \right)}\nolimits^{3} \hfill \\ \mathop i\nolimits_{m4} = \mathop g\nolimits_{m4} \left( {\mathop {{\kern 1pt} V}\nolimits_{X} \mathop { + V}\nolimits_{O} } \right) - \frac{{\mathop g\nolimits_{m4,2} }}{2}\mathop {\left( {\mathop {{\kern 1pt} V}\nolimits_{x} + \mathop V\nolimits_{o} } \right)}\nolimits^{2} + \frac{{\mathop g\nolimits_{m4,3} }}{3!}\mathop {\left( {\mathop {{\kern 1pt} V}\nolimits_{x} + \mathop V\nolimits_{o} } \right)}\nolimits^{3} \hfill \\ \end{gathered}$$
(A.2)

(gmi,1 (i = 1,2,4) is the transconductance of transistor Mi. gmi,2 (i = 1,2,4) is the second-order non-linear coefficient of transistors Mi, gmi,3 (i = 1,2,4) is the third- order non-linear coefficient of transistors Mi.

The KCL equation for this circuit can be written as:

$$\begin{gathered} \frac{{\mathop {{\kern 1pt} V}\nolimits_{O} }}{{\mathop R\nolimits_{L} }} = \mathop i\nolimits_{m4} \hfill \\ \mathop i\nolimits_{m4} + \mathop i\nolimits_{m1} + \mathop c\nolimits_{gs2} S\left( {\mathop {\,V}\nolimits_{X} - \mathop V\nolimits_{Z} } \right) = 0 \hfill \\ \mathop i\nolimits_{m2} + \mathop c\nolimits_{gs2} S\left( {\mathop {\,V}\nolimits_{X} - \mathop V\nolimits_{Z} } \right) = \frac{{\mathop {{\kern 1pt} V}\nolimits_{z} + \mathop V\nolimits_{S} }}{{\mathop R\nolimits_{S} }} \hfill \\ \end{gathered}$$
(A.3)

To find the first, second, and third order Volterra kernels, im1, im2, and im4 in (A.2) are substituted by the first, second, and third order components of gm polynomials in (A.3). The first order Volterra kernels can then be expressed as follows:

$$\begin{gathered} \mathop A\nolimits_{1} \left( {\mathop S\nolimits_{1} } \right) = \frac{{ - \mathop g\nolimits_{m4,1} \mathop R\nolimits_{L} \mathop g\nolimits_{m1,1} \left( {1 + \mathop g\nolimits_{m2,1} \mathop R\nolimits_{S} } \right)}}{{ - \mathop g\nolimits_{m4,1} \left( {1 + \mathop g\nolimits_{m2,1} \mathop R\nolimits_{S} } \right) + \mathop c\nolimits_{gs2} \mathop R\nolimits_{S} \mathop g\nolimits_{m2,1} \mathop S\nolimits^{{}} }} \hfill \\ \mathop{\longrightarrow}\limits^{{\mathop g\nolimits_{m2} \approx 0}}\mathop A\nolimits_{1} \left( {\mathop S\nolimits_{1} } \right) = \mathop R\nolimits_{L} \mathop g\nolimits_{m1,1} \hfill \\ \mathop B\nolimits_{1} \left( {\mathop S\nolimits_{1} } \right) = \frac{{ - \mathop g\nolimits_{m1,1} \left( {1 - \mathop g\nolimits_{m4,1} \mathop R\nolimits_{L} } \right)\left( {1 + \mathop g\nolimits_{m2,1} \mathop R\nolimits_{S} } \right)}}{{\mathop g\nolimits_{m2,1} \mathop R\nolimits_{S} \mathop c\nolimits_{gs2} S - \mathop g\nolimits_{m4,1} \left( {1 + \mathop g\nolimits_{m2,1} \mathop R\nolimits_{S} } \right)}} \hfill \\ \mathop{\longrightarrow}\limits^{{\mathop g\nolimits_{m2} \approx 0}}\mathop B\nolimits_{1} \left( {\mathop S\nolimits_{1} } \right) = \frac{{\mathop g\nolimits_{m1,1} \left( {1 - \mathop g\nolimits_{m4,1} \mathop R\nolimits_{L} } \right)}}{{\mathop g\nolimits_{m4,1} }} \hfill \\ \mathop C\nolimits_{1} \left( {\mathop S\nolimits_{1} } \right) = \frac{{\mathop { - g}\nolimits_{m4,1} \left( {1 + \mathop R\nolimits_{L} \mathop R\nolimits_{S} \mathop g\nolimits_{m1,1} \mathop g\nolimits_{m2,1} } \right) + \mathop R\nolimits_{S} \mathop g\nolimits_{m1,1} \mathop g\nolimits_{m2,1} }}{{\mathop g\nolimits_{m4,1} \left( {1 + \mathop g\nolimits_{m2,1} \mathop R\nolimits_{S} } \right)}} \hfill \\ \mathop{\longrightarrow}\limits^{{\mathop g\nolimits_{m2} \approx 0}}\mathop C\nolimits_{1} \left( {\mathop S\nolimits_{1} } \right) = - 1 \hfill \\ \end{gathered}$$
(A.4)

The second order Volterra kernels can then be given as:

$$\begin{gathered} \hfill \\ \mathop B\nolimits_{2} \left( {\mathop S\nolimits_{1} ,\mathop S\nolimits_{2} } \right) = \frac{1}{{\frac{{\mathop g\nolimits_{m2} \mathop R\nolimits_{S} }}{{\mathop g\nolimits_{m2} \mathop R\nolimits_{S} + 1}} + \frac{{\mathop g\nolimits_{m4} }}{{\left( {\mathop g\nolimits_{m4} \mathop R\nolimits_{L} - 1} \right)\mathop c\nolimits_{gs2} S}}}}\left[ \begin{gathered} \frac{1}{{\mathop c\nolimits_{gs2} S}}\left( {\frac{{\mathop g\nolimits_{m4,2} }}{{2\left( {\mathop g\nolimits_{m4} \mathop R\nolimits_{L} - 1} \right)}}\mathop A\nolimits_{1} \left( {\mathop S\nolimits_{1} } \right)\mathop A\nolimits_{1} \left( {\mathop S\nolimits_{2} } \right)\mathop B\nolimits_{1} \left( {\mathop S\nolimits_{1} } \right)\mathop B\nolimits_{1} \left( {\mathop S\nolimits_{2} } \right) + \frac{{\mathop g\nolimits_{m1,2} }}{2}} \right) \hfill \\ \frac{{ - \mathop R\nolimits_{S} }}{{\mathop g\nolimits_{m2} \mathop R\nolimits_{S} + 1}}\left( {\frac{{\mathop g\nolimits_{m2,2} }}{2}\mathop B\nolimits_{1} \left( {\mathop S\nolimits_{1} } \right)\mathop B\nolimits_{1} \left( {\mathop S\nolimits_{2} } \right)\mathop C\nolimits_{1} \left( {\mathop S\nolimits_{1} } \right)\mathop C\nolimits_{1} \left( {\mathop S\nolimits_{2} } \right) - \frac{1}{{\mathop R\nolimits_{S} }}} \right) \hfill \\ \end{gathered} \right] \hfill \\ \mathop{\longrightarrow}\limits^{{\mathop g\nolimits_{m2} \approx 0}}\frac{{\mathop g\nolimits_{m4,2} }}{{2\mathop g\nolimits_{m4} }}\mathop A\nolimits_{1} \left( {\mathop S\nolimits_{1} } \right)\mathop A\nolimits_{1} \left( {\mathop S\nolimits_{2} } \right)\mathop B\nolimits_{1} \left( {\mathop S\nolimits_{1} } \right)\mathop B\nolimits_{1} \left( {\mathop S\nolimits_{2} } \right) + \frac{{\mathop g\nolimits_{m1,2} }}{2} \times \frac{{\mathop g\nolimits_{m4} \mathop R\nolimits_{L} - 1}}{{\mathop g\nolimits_{m4} }} + \frac{{\left( {\mathop g\nolimits_{m4} \mathop R\nolimits_{L} - 1} \right)\mathop c\nolimits_{gs2} S}}{{\mathop g\nolimits_{m4} }} \hfill \\ \mathop A\nolimits_{2} \left( {\mathop S\nolimits_{1} ,\mathop S\nolimits_{2} } \right) = \frac{{\mathop R\nolimits_{L} }}{{\mathop {1 - g}\nolimits_{m4} \mathop R\nolimits_{L} }}\left[ {\mathop g\nolimits_{m4} \mathop B\nolimits_{2} \left( {\mathop S\nolimits_{1} ,\mathop S\nolimits_{2} } \right) - \frac{{\mathop g\nolimits_{m4,2} }}{2}\mathop A\nolimits_{1} \left( {\mathop S\nolimits_{1} } \right)\mathop A\nolimits_{1} \left( {\mathop S\nolimits_{2} } \right)\mathop B\nolimits_{1} \left( {\mathop S\nolimits_{1} } \right)\mathop B\nolimits_{1} \left( {\mathop S\nolimits_{2} } \right)} \right] \hfill \\ \mathop C\nolimits_{2} \left( {\mathop S\nolimits_{1} ,\mathop S\nolimits_{2} } \right) = \frac{{\mathop R\nolimits_{S} }}{{\mathop g\nolimits_{m2} \mathop R\nolimits_{S} + 1}}\left[ {\mathop g\nolimits_{m2} \mathop B\nolimits_{2} \left( {\mathop S\nolimits_{1} ,\mathop S\nolimits_{2} } \right) + \frac{{\mathop g\nolimits_{m2,2} }}{2}\mathop B\nolimits_{1} \left( {\mathop S\nolimits_{1} } \right)\mathop B\nolimits_{1} \left( {\mathop S\nolimits_{2} } \right)\mathop C\nolimits_{1} \left( {\mathop S\nolimits_{1} } \right)\mathop C\nolimits_{1} \left( {\mathop S\nolimits_{2} } \right) - \frac{1}{{\mathop R\nolimits_{S} }}} \right] \hfill \\ \end{gathered}$$
(A.5)

The third order Volterra kernels can then be given as:

$$\begin{gathered} \mathop B\nolimits_{3} \left( {\mathop S\nolimits_{1} ,\mathop S\nolimits_{2} ,\mathop S\nolimits_{3} } \right) = \frac{1}{{\frac{{\mathop g\nolimits_{{m2,1}} \mathop R\nolimits_{S} }}{{1 + \mathop g\nolimits_{{m2,1}} \mathop R\nolimits_{S} }} + \frac{1}{{\mathop C\nolimits_{{g\,s2}} {\kern 1pt} \,\mathop S\nolimits_{{}} \left( {\mathop {1 - g}\nolimits_{{m4}} \mathop R\nolimits_{L} } \right)}}}}\left[ \begin{gathered} \frac{1}{{\mathop C\nolimits_{{g{\kern 1pt} s2}} \mathop {\,S}\nolimits_{{}} }}\left( \begin{gathered} \frac{{y\mathop g\nolimits_{{m4,3}} }}{{6\left( {\mathop {1 - g}\nolimits_{{m4,1}} \mathop R\nolimits_{L} } \right)\left( {\mathop g\nolimits_{{m4,1}} + \mathop C\nolimits_{{g{\kern 1pt} s2}} \mathop S\nolimits_{{}} } \right)}} + \hfill \\ \frac{1}{{\mathop g\nolimits_{{m4,1}} + \mathop C\nolimits_{{g\,s2}} {\kern 1pt} \mathop S\nolimits_{{}} }} \times \frac{{\mathop g\nolimits_{{m1,3}} }}{6} \hfill \\ \end{gathered} \right) \hfill \\ - \frac{{\mathop R\nolimits_{S} }}{{1 + \mathop g\nolimits_{{m2,1}} \mathop R\nolimits_{S} }}\left( \begin{gathered} - \frac{1}{{\mathop R\nolimits_{S} }} + \hfill \\ \frac{{\mathop g\nolimits_{{m2,3}} }}{6}\mathop C\nolimits_{1} \left( {\mathop S\nolimits_{1} } \right)\mathop C\nolimits_{1} \left( {\mathop S\nolimits_{2} } \right)\mathop C\nolimits_{1} \left( {\mathop S\nolimits_{3} } \right)\mathop B\nolimits_{1} \left( {\mathop S\nolimits_{1} } \right)\mathop B\nolimits_{1} \left( {\mathop S\nolimits_{2} } \right)\mathop B\nolimits_{1} \left( {\mathop S\nolimits_{3} } \right) + \hfill \\ \overline{{\mathop g\nolimits_{{m2,2}} \mathop C\nolimits_{1} \left( {\mathop S\nolimits_{1} } \right)\mathop C\nolimits_{2} \left( {\mathop S\nolimits_{2} ,\mathop S\nolimits_{3} } \right)\mathop B\nolimits_{1} \left( {\mathop S\nolimits_{1} } \right)\mathop B\nolimits_{2} \left( {\mathop S\nolimits_{2} ,\mathop S\nolimits_{3} } \right)}} \hfill \\ \end{gathered} \right) \hfill \\ \end{gathered} \right] \hfill \\ \xrightarrow{{\mathop g\nolimits_{{m2}} = \,0}}\mathop C\nolimits_{{g\,s2}} {\kern 1pt} \,\mathop S\nolimits_{{}} \left( {\mathop {1 - g}\nolimits_{{m4}} \mathop R\nolimits_{L} } \right)\left[ \begin{gathered} \frac{1}{{\mathop C\nolimits_{{g{\kern 1pt} s2}} \mathop S\nolimits_{{}} }}\left( \begin{gathered} \frac{{y\mathop g\nolimits_{{m4,3}} }}{{6\left( {\mathop {1 - g}\nolimits_{{m4,1}} \mathop R\nolimits_{L} } \right)\left( {\mathop g\nolimits_{{m4,1}} + \mathop C\nolimits_{{g\,s2}} \mathop S\nolimits_{{}} } \right)}} + \hfill \\ \frac{1}{{\mathop g\nolimits_{{m4,1}} + \mathop C\nolimits_{{g\,s2}} {\kern 1pt} \mathop S\nolimits_{{}} }} \times \frac{{\mathop g\nolimits_{{m1,3}} }}{6} \hfill \\ \end{gathered} \right) \hfill \\ + 1 \hfill \\ \end{gathered} \right] \hfill \\ y = \mathop A\nolimits_{1} \left( {\mathop S\nolimits_{1} } \right)\mathop A\nolimits_{1} \left( {\mathop S\nolimits_{2} } \right)\mathop A\nolimits_{1} \left( {\mathop S\nolimits_{3} } \right)\mathop B\nolimits_{1} \left( {\mathop S\nolimits_{1} } \right)\mathop B\nolimits_{1} \left( {\mathop S\nolimits_{2} } \right)\mathop B\nolimits_{1} \left( {\mathop S\nolimits_{3} } \right) - \overline{{\mathop g\nolimits_{{m4,2}} \mathop A\nolimits_{1} \left( {\mathop S\nolimits_{1} } \right)\mathop A\nolimits_{2} \left( {\mathop S\nolimits_{2} ,\mathop S\nolimits_{3} } \right)\mathop B\nolimits_{1} \left( {\mathop S\nolimits_{1} } \right)\mathop B\nolimits_{2} \left( {\mathop S\nolimits_{2} ,\mathop S\nolimits_{3} } \right)}} \hfill \\ \mathop C\nolimits_{3} \left( {\mathop S\nolimits_{1} ,\mathop S\nolimits_{2} ,\mathop S\nolimits_{3} } \right) = \frac{{\mathop R\nolimits_{S} }}{{1 + \mathop g\nolimits_{{m2,1}} \mathop R\nolimits_{S} }}\left[ \begin{gathered} - \frac{1}{{\mathop R\nolimits_{S} }} + \hfill \\ \frac{{\mathop g\nolimits_{{m2,3}} }}{6}\mathop C\nolimits_{1} \left( {\mathop S\nolimits_{1} } \right)\mathop C\nolimits_{1} \left( {\mathop S\nolimits_{2} } \right)\mathop C\nolimits_{1} \left( {\mathop S\nolimits_{3} } \right)\mathop B\nolimits_{1} \left( {\mathop S\nolimits_{1} } \right)\mathop B\nolimits_{1} \left( {\mathop S\nolimits_{2} } \right)\mathop B\nolimits_{1} \left( {\mathop S\nolimits_{3} } \right) + \hfill \\ \overline{{\mathop g\nolimits_{{m2,2}} \mathop C\nolimits_{1} \left( {\mathop S\nolimits_{1} } \right)\mathop C\nolimits_{2} \left( {\mathop S\nolimits_{2} ,\mathop S\nolimits_{3} } \right)\mathop B\nolimits_{1} \left( {\mathop S\nolimits_{1} } \right)\mathop B\nolimits_{2} \left( {\mathop S\nolimits_{2} ,\mathop S\nolimits_{3} } \right)}} + \mathop g\nolimits_{{m2,1}} \mathop B\nolimits_{3} \left( {\mathop S\nolimits_{1} ,\mathop S\nolimits_{2} ,\mathop S\nolimits_{3} } \right) \hfill \\ \end{gathered} \right] \hfill \\ \mathop A\nolimits_{3} \left( {\mathop S\nolimits_{1} ,\mathop S\nolimits_{2} ,\mathop S\nolimits_{3} } \right) = \frac{{\mathop R\nolimits_{L} }}{{\mathop {1 - g}\nolimits_{{m4,1}} \mathop R\nolimits_{L} }}\left[ \begin{gathered} \mathop g\nolimits_{{m4,1}} \mathop {{\kern 1pt} B}\nolimits_{3} \left( {\mathop S\nolimits_{1} ,\mathop S\nolimits_{2} ,\mathop S\nolimits_{3} } \right) + \hfill \\ \frac{{\mathop g\nolimits_{{m4,3}} }}{6}\mathop A\nolimits_{1} \left( {\mathop S\nolimits_{1} } \right)\mathop A\nolimits_{1} \left( {\mathop S\nolimits_{2} } \right)\mathop A\nolimits_{1} \left( {\mathop S\nolimits_{3} } \right)\mathop B\nolimits_{1} \left( {\mathop S\nolimits_{1} } \right)\mathop B\nolimits_{1} \left( {\mathop S\nolimits_{2} } \right)\mathop B\nolimits_{1} \left( {\mathop S\nolimits_{3} } \right) - \hfill \\ \overline{{\mathop g\nolimits_{{m4,2}} \mathop {{\kern 1pt} A}\nolimits_{1} \left( {\mathop S\nolimits_{1} } \right)\mathop A\nolimits_{2} \left( {\mathop S\nolimits_{2} ,\mathop S\nolimits_{3} } \right)\mathop B\nolimits_{1} \left( {\mathop S\nolimits_{1} } \right)\mathop B\nolimits_{2} \left( {\mathop S\nolimits_{2} ,\mathop S\nolimits_{3} } \right)}} \hfill \\ \end{gathered} \right] \hfill \\ \hfill \\ \end{gathered}$$
(A.6)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Tarighat, A.P. Ultra-low power inductorless differential LNA for WSN application. Analog Integr Circ Sig Process 108, 409–419 (2021). https://doi.org/10.1007/s10470-021-01892-1

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10470-021-01892-1

Keyword

Search

Navigation