Skip to main content
SpringerLink
Log in

On estimation of surrogate models for multivariate computer experiments

  • Published:
Annals of the Institute of Statistical Mathematics Aims and scope Submit manuscript

Abstract

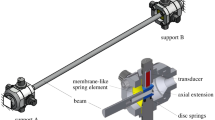
Estimation of surrogate models for computer experiments leads to nonparametric regression estimation problems without noise in the dependent variable. In this paper, we propose an empirical maximal deviation minimization principle to construct estimates in this context and analyze the rate of convergence of corresponding quantile estimates. As an application, we consider estimation of computer experiments with moderately high dimension by neural networks and show that here we can circumvent the so-called curse of dimensionality by imposing rather general assumptions on the structure of the regression function. The estimates are illustrated by applying them to simulated data and to a simulation model in mechanical engineering.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

References

  • Anthony, M., Bartlett, P. L. (1999). Neural networks and learning: Theoretical foundations. Cambridge: Cambridge University Press.

  • Barron, A. R. (1991). Complexity regularization with application to artificial neural networks. In G. Roussas (Ed.), Nonparametric functional estimation and related topics (pp. 561–576)., NATO ASI series Dordrecht: Kluwer Academic Publishers.

    Chapter  Google Scholar 

  • Barron, A. R. (1993). Universal approximation bounds for superpositions of a sigmoidal function. IEEE Transactions on Information Theory, 39, 930–944.

    Article  MathSciNet  MATH  Google Scholar 

  • Beirlant, J., Györfi, L. (1998). On the asymptotic \({L}_2\)-error in partitioning regression estimation. Journal of Statistical Planning and Inference, 71, 93–107.

  • Bichon, B. J., Eldred, M. S., Swiler, L. P., Mahadevan, S., McFarland, J. M. (2008). Efficient global reliability analysis for nonlinear implicit performance functions. AIAA Journal, 46, 2459–2468.

  • Bourinet, J.-M., Deheeger, F., Lemaire, M. (2011). Assessing small failure probabilities by combined subset simulation and support vector machines. Structural Safety, 33, 343–353.

  • Bucher, C., Bourgund, U. (1990). A fast and efficient response surface approach for structural reliability problems. Structural Safety, 7, 57–66.

  • Das, P.-K., Zheng, Y. (2000). Cumulative formation of response surface and its use in reliability analysis. Probabilistic Engineering Mechanics, 15, 309–315.

  • Deheeger, F., Lemaire, M. (2010). Support vector machines for efficient subset simulations: \(^2\)SMART method. In: Proceedings of the 10th international conference on applications of statistics and probability in civil engineering (ICASP10), Tokyo, Japan.

  • Devroye, L. (1982). Necessary and sufficient conditions for the almost everywhere convergence of nearest neighbor regression function estimates. Zeitschrift für Wahrscheinlichkeitstheorie und verwandte Gebiete, 61, 467–481.

    Article  MathSciNet  MATH  Google Scholar 

  • Devroye, L., Krzyżak, A. (1989). An equivalence theorem for \({L}_1\) convergence of the kernel regression estimate. Journal of Statistical Planning and Inference, 23, 71–82.

  • Devroye, L., Wagner, T. J. (1980). Distribution-free consistency results in nonparametric discrimination and regression function estimation. Annals of Statistics, 8, 231–239.

  • Devroye, L., Györfi, L., Krzyżak, A., Lugosi, G. (1994). On the strong universal consistency of nearest neighbor regression function estimates. Annals of Statistics, 22, 1371–1385.

  • Devroye, L., Györfi, L., Lugosi, G. (1996). A probabilistic theory of pattern recognition. New York: Springer.

  • Enss, G., Kohler, M., Krzyżak, A., Platz, R. (2016). Nonparametric quantile estimation based on surrogate models. IEEE Transactions on Information Theory, 62, 5727–5739.

  • Friedman, J. H., Stuetzle, W. (1981). Projection pursuit regression. Journal of the American Statistical Association, 76, 817–823.

  • Greblicki, W., Pawlak, M. (1985). Fourier and Hermite series estimates of regression functions. Annals of the Institute of Statistical Mathematics, 37, 443–454.

  • Györfi, L. (1981). Recent results on nonparametric regression estimate and multiple classification. Problems of Control and Information Theory, 10, 43–52.

    MathSciNet  Google Scholar 

  • Györfi, L., Kohler, M., Krzyżak, A., Walk, H. (2002). A distribution-free theory of nonparametric regression. Springer series in statistics. New York: Springer.

  • Hansmann, M., Kohler, M. (2017). Estimation of quantiles from data with additional measurement errors. Statistica Sinica, 27, 1661–1673.

  • Hastie, T., Tibshirani, R., Friedman, J. (2011). The elements of statistical learning: Data mining, inference, and prediction (2nd ed.). New York: Springer.

  • Haykin, S. O. (2008). Neural networks and learning machines (3rd ed.). New York: Prentice-Hall.

    Google Scholar 

  • Hertz, J., Krogh, A., Palmer, R. G. (1991). Introduction to the theory of neural computation. Redwood City, CA: Addison-Wesley.

  • Hurtado, J. (2004). Structural reliability—Statistical learning perspectives. Vol. 17 of lecture notes in applied and computational mechanics. Berlin: Springer.

  • Kaymaz, I. (2005). Application of Kriging method to structural reliability problems. Structural Safety, 27, 133–151.

    Article  Google Scholar 

  • Kim, S.-H., Na, S.-W. (1997). Response surface method using vector projected sampling points. Structural Safety, 19, 3–19.

  • Kohler, M. (2000). Inequalities for uniform deviations of averages from expectations with applications to nonparametric regression. Journal of Statistical Planning and Inference, 89, 1–23.

    Article  MathSciNet  MATH  Google Scholar 

  • Kohler, M. (2014). Optimal global rates of convergence for noiseless regression estimation problems with adaptively chosen design. Journal of Multivariate Analysis, 132, 197–208.

    Article  MathSciNet  MATH  Google Scholar 

  • Kohler, M., Krzyżak, A. (2001). Nonparametric regression estimation using penalized least squares. IEEE Transactions on Information Theory, 47, 3054–3058.

  • Kohler, M., & Krzyżak, A. (2005). Adaptive regression estimation with multilayer feedforward neural networks. Journal of Nonparametric Statistics, 17, 891–913.

    Article  MathSciNet  MATH  Google Scholar 

  • Kohler, M., Krzyżak, A. (2013). Optimal global rates of convergence for interpolation problems with random design. Statistics and Probability Letters, 83, 1871–1879.

  • Kohler, M., Krzyżak, A. (2017). Nonparametric regression based on hierarchical interaction models. IEEE Transaction on Information Theory, 63, 1620–1630.

  • Lazzaro, D., Montefusco, L. (2002). Radial basis functions for the multivariate interpolation of large scattered data sets. Journal of Computational and Applied Mathematics, 140, 521–536.

  • Lugosi, G., Zeger, K. (1995). Nonparametric estimation via empirical risk minimization. IEEE Transactions on Information Theory, 41, 677–687.

  • Massart, P. (1990). The tight constant in the Dvoretzky–Kiefer–Wolfowitz inequality. Annals of Probability, 18, 1269–1283.

    Article  MathSciNet  MATH  Google Scholar 

  • McCaffrey, D. F., Gallant, A. R. (1994). Convergence rates for single hidden layer feedforward networks. Neural Networks, 7, 147–158.

  • Mhaskar, H. N. (1993). Approximation properties of multilayer feedforward artificial neural network. Advances in Computational Mathematics, 1, 61–80.

    Article  MathSciNet  MATH  Google Scholar 

  • Mielniczuk, J., Tyrcha, J. (1993). Consistency of multilayer perceptron regression estimators. Neural Networks, 6, 1019–1022.

  • Nadaraya, E. A. (1964). On estimating regression. Theory of Probability and Its Applications, 9, 141–142.

    Article  MATH  Google Scholar 

  • Nadaraya, E. A. (1970). Remarks on nonparametric estimates for density functions and regression curves. Theory of Probability and Its Applications, 15, 134–137.

    Article  MATH  Google Scholar 

  • Papadrakakis, M., Lagaros, N. (2002). Reliability-based structural optimization using neural networks and Monte Carlo simulation. Computer Methods in Applied Mechanics and Engineering, 191, 3491–3507.

  • Rafajłowicz, E. (1987). Nonparametric orthogonal series estimators of regression: A class attaining the optimal convergence rate in L2. Statistics and Probability Letters, 5, 219–224.

    Article  MathSciNet  MATH  Google Scholar 

  • Ripley, B. D. (2008). Pattern recognition and neural networks. Cambridge: Cambridge University Press.

    MATH  Google Scholar 

  • Stone, C. J. (1977). Consistent nonparametric regression. Annals of Statististics, 5, 595–645.

    Article  MathSciNet  MATH  Google Scholar 

  • Stone, C. J. (1982). Optimal global rates of convergence for nonparametric regression. Annals of Statistics, 10, 1040–1053.

    Article  MathSciNet  MATH  Google Scholar 

  • Stone, C. J. (1985). Additive regression and other nonparametric models. Annals of Statistics, 13, 689–705.

    Article  MathSciNet  MATH  Google Scholar 

  • Stone, C. J. (1994). The use of polynomial splines and their tensor products in multivariate function estimation. Annals of Statistics, 22, 118–184.

    Article  MathSciNet  MATH  Google Scholar 

  • Wahba, G. (1990). Spline models for observational data. Philadelphia, PA: SIAM.

    Book  MATH  Google Scholar 

  • Watson, G. S. (1964). Smooth regression analysis. Sankhya Series A, 26, 359–372.

    MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The first three authors would like to thank the German Research Foundation (DFG) for funding this project within the Collaborative Research Centre 805. The last author would like to thank the Natural Sciences and Engineering Research Council of Canada for additional support under Grant RGPIN-2015-06412.

Author information

Authors and Affiliations

  1. Fachbereich Mathematik, Technische Universität Darmstadt, Schlossgartenstr. 7, 64289, Darmstadt, Germany

    Benedikt Bauer & Michael Kohler

  2. Fachbereich Maschinenbau, Technische Universität Darmstadt, Otto-Bernd-Str. 2, 64287, Darmstadt, Germany

    Felix Heimrich

  3. Department of Computer Science and Software Engineering, Concordia University, 1455 De Maisonneuve Blvd. West, Montreal, Quebec, H3G 1M8, Canada

    Adam Krzyżak

Authors
  1. Benedikt Bauer
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Felix Heimrich
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Michael Kohler
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Adam Krzyżak
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Adam Krzyżak.

Electronic supplementary material

Below is the link to the electronic supplementary material.

Supplementary material 1 (pdf 188 KB)

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Bauer, B., Heimrich, F., Kohler, M. et al. On estimation of surrogate models for multivariate computer experiments. Ann Inst Stat Math 71, 107–136 (2019). https://doi.org/10.1007/s10463-017-0627-8

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10463-017-0627-8

Keywords

Search

Navigation