1 Introduction

Due to its attributes encompassing supply stability, flexibility, and energy efficiency, electricity has consistently occupied a central place in the industrial sector. In recent years, with the proactive promotion of renewable energy technologies, the role of electricity in the industry has further strengthened (Lu et al. 2017; Lei et al. 2017). According to the National Bureau of Statistics of China, the industrial power consumption has witnessed consecutive yearly growth from 2013 to 2022 (Chinese National Bureau of statistics 2022), thereby maintaining its dominance in the country’s overall power consumption for over a decade (See Fig. 1), while other sectors have failed to match industrial power consumption on the same scale. As a crucial part of the industrial sector, the industrial robot industry has shown remarkable growth and holds immense market potential. In 2021, a total of 517,385 industrial robots were installed worldwide, representing an increase of 31% compared to the previous year, according to the “World Robotics 2022—Industrial Robots” report published by the International Federation of Robotics in September 2023. Thus, the industrial robot industry bears considerable responsibility for electricity energy wastage.

Fig. 1
figure 1

Electricity Consumption in China from 2013 to 2022.

Full size image

In addition, with the rapid development of sectors such as new energy vehicle manufacturing and intelligent logistics, as well as the urgent demand for the transformation and upgrading of traditional manufacturing industries, the market of China’s industrial robotics industry has continued to expand. In recent years, the production of industrial robots has seen rapid growth. In 2017, the annual production was 131,079 units, and by 2022, it increased to 366,044 units, marking a 179.26% increase over a span of five years. This sharp shift in production demand presents significant challenges to the production efficiency of industrial robot manufacturing enterprises. Therefore, industrial robot manufacturing companies in China face dual pressure to enhance production and energy utilization efficiency.

To improve energy efficiency and productivity in the industrial sector, a new energy management paradigm has emerged, incorporating energy consumption objectives into the production planning and scheduling process. This paradigm, known as energy-efficient scheduling or green scheduling (Gahm et al. 2016; Gao et al. 2020), not only enhances production efficiency but also prioritizes energy utilization efficiency. Moreover, the energy-efficient scheduling paradigm focuses on optimizing the prioritization of production orders without needing process or equipment enhancements, thus offering a cost-effective solution (Lu et al. 2022; Kong et al. 2021).

The energy-efficient scheduling paradigm has been successfully implemented across diverse industrial applications, demonstrating its practical feasibility and effectiveness. For example, in real-life welding shop scheduling problems, researchers have proposed various energy-efficient scheduling models, such as the bi-objective welding shop scheduling model and the distributed welding flow shop scheduling model. To address these models, researchers have developed meta-heuristic algorithms, including the multi-objective artificial bee colony algorithm (MOABC), the discrete artificial bee colony algorithm (DABC), the multi-objective whale swarm algorithm (MOWSA), and the non-dominated sorting Genetic Algorithm III with a restarted strategy (RNSGAIII) (Li et al. 2018a, b, 2019a; Wang et al. 2021; Rao et al. 2020). Furthermore, the energy-efficient scheduling paradigm has found application in other scenarios, such as distributed assembly workshops (Zhang et al. 2020a, b; Zhao et al. 2023a, b) and steel-making workshops (Li et al. 2018a, b; Zhang et al. 2017).

To improve the assembly efficiency of industrial robots and reduce energy consumption in assembly workshops, this study focuses on the collaborative optimization problem of multiple assembly processes, namely the body, electrical cabinet, and pipeline pack, within the industrial robot assembly process. Specifically, the body and electrical cabinet processes are representative of a typical flow shop operation environment. At the same time, the pipeline pack constitutes a distinct process responsible for connecting the assembled body and electrical cabinet to form a fully functional industrial robot product. This study is closely related to the field of energy-efficient flow shop scheduling.

The flow shop is a common production organizational pattern in which jobs are subjected to a series of operations in a predefined sequence. Adopting a flow shop enables improved productivity while effectively utilizing resources, making it an appealing choice in industrial manufacturing (Neufeld et al. 2022). Considering the imperative requirement for energy conservation in energy-intensive sectors like steel-making and glass production, the energy-efficient scheduling problems in the flow shop environment have attracted significant attention (Utama et al. 2023). The study of the energy-efficient hybrid flow shop scheduling has become a major academic focus. In a hybrid flow shop environment, the execution of jobs occurs across multiple stages, with at least one stage comprising two or more parallel machines (Ruiz and Rodríguez 2010; Pan et al. 2013; Zhang et al. 2020a, b). Considering the adjustable machine speeds, Öztop et al. (2020a, b), Wang et al. (2022), Li et al. (2019a, b), Zhang et al. (2019), and Lei et al. (2023) investigated the energy-efficient scheduling problem in the hybrid flow shop environment based on the Speed Scaling framework. To effectively tackle this problem, these researchers proposed various multi-objective meta-heuristic algorithms. The Speed Scaling framework is widely utilized in energy-efficient scheduling problems. It operates under the fundamental assumption that executing a job on a machine at a higher speed decreases processing time and increases energy consumption (Ding et al. 2016). Time-of-use (TOU) electricity prices and the ability to turn on/off machines are two other common settings (Mokhtari‑Moghadam. 2023; Wang et al. 2019; Zhang and Chiong 2016; Mouzon et al. 2007; Ding et al. 2021).

Given that the frequent starting and stopping of machines may not be viable in specific operational scenarios, researchers have begun to consider two distinct workloads, loaded and unloaded, to depict various energy consumption states of the machines (Hasani and Hosseini 2020). Blocking and No-Idle Flow Shop is similar to the above-mentioned idea, as they also involve work and standby power (Zhao et al. 2023a, b; Zhang et al. 2020a, b; Chen et al. 2019). In the context of Speed Scaling and varying machine energy consumption states (Idle Power), Lu et al. (2022) investigated the energy-efficient scheduling problem of distributed permutation flow-shop. Note that the permutation flow shop is a distinct variant of the flow shop, characterized by jobs consistently traversing the stages in the same sequence and maintaining a uniform machine processing order throughout the stages (Tiwari et al. 2015). Several other relevant studies can be referenced, such as the works of Öztop et al. (2020a, b), Tao et al. (2020), and Yüksel et al. (2020).

A study closely related to our research is the work by Niu et al. (2023). They incorporated an assembly operation into the manufacturing process of a flow shop and proposed a class of energy-efficient scheduling problems designed explicitly for distributed assembly blocking flow-shops. Another related research by Goli et al. (2023) delves into the non-permutation flow-shop scheduling problem with the objective of minimizing idle time.

Previous literature primarily focuses on green and energy-efficient scheduling problems in various sectors, including textiles, motor vehicles, and fabricated metal products (Gahm et al. 2016). However, limited research specifically targeting green and energy-efficient scheduling models in the industrial robot manufacturing industry is available. To address this research gap, this paper proposes a green scheduling model and algorithm specifically designed for the flexible manufacturing process of industrial robots. The objective is to enhance production efficiency and minimize energy consumption.

In our study, the components of orders in both the body and the electrical cabinet assembly workshops adhere to the processing order of orders, thereby establishing a conventional permutation flow-shop manufacturing process. The pipeline pack includes a singular assembly operation. Our research also considers the manufacturing system’s energy consumption during idle and working periods. Consequently, the problem investigated in our study can be precisely defined as energy-efficient scheduling for assembly-blocking permutation flow-shop (EES-ABPFS).

The main contribution of this work is summarized as follows:

  1. (1)

    Developing a new energy consumption model called EES-ABPFS.

  2. (2)

    Designing two new heuristic algorithms (i.e., H1 and H2) to solve EES-ABPFS.

  3. (3)

    Proving the designed algorithm has a better behavior than other algorithms by experiment.

  4. (4)

    Providing a new paradigm of energy management for the intelligent robotics industry.

The remaining parts of this paper are organized as follows. Section 2 proposed the primary problem model of this paper. Section 3 introduced the designed heuristic algorithm for EES-ABPFS. In Sect. 4, we compared the designed algorithm with heuristic algorithms and meta-heuristic algorithms. We gave this paper’s management insights and conclusion in Sect. 5 and Sect. 6, respectively Table 1.

Table 1 Summery of Reviewed Papers
Full size table

2 Problem description

The industrial robot assembly process is primarily managed by three groups: the body assembly group, the electric cabinet assembly group, and the pipeline pack assembly group. The body assembly is mainly composed of three processes of “base”, “big arm”, and “wrist”. The electric cabinet assembly is composed of “main computer control”, “axis computer board”, “axis servo drive”, “SMB measurement board”, and “I/O board”. The pipeline pack assembly process involves connecting the completed products from the body assembly and the electric cabinet assembly by wiring harnesses to obtain a complete industrial robot product. Based on the sequence of operations, we categorize the independent processes of the body assembly and the electric cabinet assembly as the first stage. In contrast, the pipeline pack assembly is classified as the second stage. The assembly of a order in the second stage must wait until all the components of the order processed on the two production lines in the first stage are completed. The specific process is shown in Fig. 2.

Fig. 2
figure 2

Production Flow Chart.

Full size image

Without losing the generality, assume there are \(n\) operations in the body assembly and \(m\) operations in the electric cabinet assembly. The pipeline pack assembly is a separate and complete operation. Based on real-world situations, we have made certain assumptions for our model, with the main assumptions outlined below:

  1. (i)

    There is no transportation time between every two machines.

  2. (ii)

    Each order has a fixed combination of components.

  3. (iii)

    Different components have varying processing times on the same machine.

  4. (iv)

    A machine can only process one order or component at a time.

  5. (v)

    Once processing begins, the assembly system operates and continuously uses energy

  6. (vi)

    The machine continues to consume energy while in standby state.

  7. (vii)

    The energy consumed when the machine is in operation state is higher than that consumed when it is in standby state.

Before presenting the specific model, we provide Table 2, which contains the notations used in this model.

Table 2 Notations
Full size table

Our MLP model aims to minimize total energy consumption, and the mixed integer programming model is given as follows.

$$min TEC$$
(1)

The total energy consumption \(TEC\) is expressed as below.

$$TEC=\sum_{i=1}^{{\text{n}}}\sum_{j=1}^{{\text{a}}}{w}_{i}^{(1)}*{P}_{i,j}^{(1)}+\sum_{i=1}^{{\text{m}}}\sum_{j=1}^{{\text{a}}}{w}_{i}^{(2)}*{P}_{l,j}^{(2)}+{w}^{(3)}*\sum_{j=1}^{{\text{a}}}{P}_{j}^{(3)}+\sum_{i=1}^{{\text{n}}}wk*({C}_{i,a}^{(1)}-\sum_{j=1}^{a}{P}_{i,j}^{(1)})+\sum_{i=1}^{{\text{m}}}wk*({C}_{i,a}^{(2)}-\sum_{j=1}^{a}{P}_{i,j}^{(2)})+wk*({C}_{a}^{(3)}-\sum_{j=1}^{a}{P}_{j}^{(3)})$$
(2)

The body assembly and the electric cabinet assembly occur in a typical permutation flow shop environment, highlighting the importance of establishing the assembly sequence for each order.

In the case of body assembly, the start time for each operation can be constrained as follows:

$${S}_{i,k}^{(1)}\ge {C}_{i,k-1}^{\left(1\right)}\,\, i=1,\cdots ,n;\,k=2,\cdots ,a$$
(3)
$${S}_{i,k}^{(1)}\ge {C}_{i-1,k}^{\left(1\right)}\,\, i=2,\cdots ,n;\,k=1,\cdots ,a$$
(4)

Constraints (3) indicate that the processing time for the same product in different operations of body assembly does not overlap, while Constraints (4) specify that the processing time for two consecutive tasks in the same operation of body assembly does not overlap.

Then, the completion time of each order must exceed the sum of its start time and assembly processing time, which can be expressed through the following constraints:

$${C}_{i,k}^{(1)}\ge {S}_{i,k}^{\left(1\right)}+\sum_{j=1}^{a}{X}_{j,k}{P}_{i,j}^{\left(1\right)}\,\,\, i=1,\cdots ,n;\,\,k=1,\cdots ,a$$
(5)

Similarly, for the electric cabinet assembly group, the production constraints may include the following:

$${S}_{l,k}^{(2)}\ge {C}_{l,k-1}^{\left(2\right)}\,\, l=1,\cdots ,m;\,k=2,\cdots ,a$$
(6)
$${S}_{l,k}^{(2)}\ge {C}_{l-1,k}^{\left(2\right)}\,\, l=2,\cdots ,m;\,k=1,\cdots ,a$$
(7)
$${C}_{l,k}^{(2)}\ge {S}_{l,k}^{\left(2\right)}+\sum_{j=1}^{a}{Y}_{j,k}{P}_{l,j}^{\left(2\right)}\,\, l=1,\cdots ,m;\,k=1,\cdots ,a$$
(8)

Once the two order components have undergone processing in the body assembly and electric cabinet assembly groups, they will proceed to the pipeline pack assembly group for further processing. As a result, the starting time of the pipeline pack assembly exceeds the completion time of the last operation in the body and electric cabinet assembly groups. Consequently, the starting time of the pipeline pack assembly for each order can be constrained as follows:

$${S}_{k}^{(3)}\ge {C}_{n,g}^{\left(1\right)}+M\left({X}_{j,g}-1\right)+M\left({Z}_{j,k}-1\right)\, g,\,j,\,k=1,\cdots ,a$$
(9)
$${S}_{k}^{(3)}\ge {C}_{m,g}^{\left(2\right)}+M\left({Y}_{j,g}-1\right)+M\left({Z}_{j,k}-1\right)\, g,\,j,\,k=1,\cdots ,a$$
(10)
$${S}_{k}^{(3)}\ge {C}_{k-1}^{\left(3\right)}+M\left({Z}_{j,k}-1\right)\, \,j=1,\cdots ,a;\,k=2,\cdots ,a$$
(11)

Assuming that the processing order in the pipeline pack process is order \(j\), constraints (9) impose a restriction where the starting time of the order \(j\) must be greater than or equal to the completion time of the last operation in the body assembly. Specifically, this condition holds only when and \({Y}_{j,k}=1\), they are indicating that the order is processed as the sequence in the last operation of the body assembly and as the sequence in the pipeline pack assembly. Similarly, constraints (10) guarantee that the starting time of the order \(j\) in the pipeline pack assembly exceeds the completion time of its last operation in the electric cabinet assembly. Constraints (11) indicate that the processing on the pipeline assembly is to be carried out strictly in sequence, and only one order can be processed at a time.

The completion time for each order in the pipeline pack assembly can be constrained as follows:

$${C}_{k}^{(3)}\ge {S}_{k}^{\left(3\right)}+\sum_{j=1}^{a}{Z}_{j,k}{P}_{j}^{\left(3\right)}\,\, j=1,\cdots ,a;\,k=1,\cdots ,a$$
(12)

Constraints (12) ensure that every order on the pipeline pack assembly will be processed. For the 0–1 integer decision variable, the value of Xj,k, \({Z}_{j,k}\) and \({Y}_{j,k}\) can be constrained as follows:

$$\sum_{j=1}^{a}{X}_{j,k}=1\,\, k=1,\cdots ,a$$
(13)
$$\sum_{k=1}^{a}{X}_{j,k}=1\,\,j=1,\cdots ,a$$
(14)
$$\sum_{j=1}^{a}{Y}_{j,k}=1\,\, k=1,\cdots ,a$$
(15)
$$\sum_{k=1}^{a}{Y}_{j,k}=1\,\,j=1,\cdots ,a$$
(16)
$$\sum_{j=1}^{a}{Z}_{j,k}=1\,\, k=1,\cdots ,a$$
(17)
$$\sum_{k=1}^{a}{Z}_{j,k}=1\,\, j=1,\cdots ,a$$
(18)
$${X}_{j,k},{Y}_{j,k},{Z}_{j,k}\in \left(\mathrm{0,1}\right)\,\, j=1,\cdots ,a;\,k=1,\cdots ,a,$$
(19)
$${S}_{i,k}^{(1)},{C}_{i,k}^{(1)},{S}_{l,k}^{(2)},{C}_{l,k}^{(2)},{S}_{k}^{(3)},{C}_{k}^{(3)}\ge 0\,\, i=1,\cdots ,n;\,l=1,\cdots ,m;\,k=1,\cdots ,a$$
(20)

3 Designed heuristic algorithms for the EES-ABPFS model

In the preliminary experiments, an optimal solution can be obtained by utilizing Gurobi when the number of orders is less than 10. However, Gurobi can not produce satisfactory results when orders exceed 10. It should be noted that in the actual production process, the number of orders typically exceeds 50. Hence, employing Gurobi directly to solve the model presented in this paper is not feasible. Based on this, we introduce two alternative algorithms in this section: the one-stage heuristic (H1 algorithm) and the two-stage algorithm (H2 algorithm).

3.1 H1 algorithm

In the proposed problem, we need to make three decisions for the order sequence in the body assembly, electrical cabinet assembly, and pipeline pack assembly. Figure 3 shows an example of the order decision-making sequence in three assembly groups. The order sequence in the body assembly group is {\({J}_{11},{J}_{21},{J}_{31}\)}, the order sequence in the electrical cabinet assembly group is \(\{{J}_{32},{J}_{12},{J}_{22}\)}, and the order sequence in the pipeline pack assembly group is \(\{{J}_{3},{J}_{2},{J}_{1}\)}. Where \({J}_{1}\) represents order 1, \({J}_{2}\) represents order 2, and \({J}_{3}\) represents order 3. \({J}_{11}\) represents the components of order 1 on the body assembly and \({J}_{12}\) represents the components of order 1 on the electric cabinet assembly. Similarly, \({J}_{21}\) represents the components of order 2 on the body assembly and \({J}_{22}\) represents the components of order 2 on the electric cabinet assembly.

Fig. 3
figure 3

Gantt Chart of Order Sequence Decision with \({X}_{j,k}\), \({Y}_{j,k}\) and \({Z}_{j,k}\)

Full size image

In our mathematical programming model, we use decision variables with \({X}_{j,k}\), \({Y}_{j,k}\), and \({Z}_{j,k}\) to indicate the above three order sequences. The excessive number of decision variables makes the model extremely complex and difficult to solve by commercial solvers such as Gurobi. The idea behind designing the H1 algorithm is to integrate the original three type of decision variables into one, so that the entire production line follows a single order sequence. This significantly reduces the constraints involved, thereby enhancing the algorithm’s performance. Figure 4 illustrates the operational process of the H1 algorithm. Upon establishing an order sequence, the body and electric cabinet assembly groups processes the components of each order following the designated sequence. Subsequently, the finalized components are connected in the pipeline pack assembly group adhering to the specified order sequence. Based on this innovative concept, we have refined the decision variables in the original MLP model, transitioning from variables \({X}_{j,k}\), \({Y}_{j,k}\), and \({Z}_{j,k}\) to variables \({X}_{j,k}\).

Fig. 4
figure 4

Gantt Chart of Order Sequence Decision with H1 Algorithm.

Full size image

There is only a type of decision variables in the H1 algorithm, so the original MLP model cannot be used for the H1 algorithm. Thus, we redesigned a modified model for the H1 algorithm based on the original MLP model. The modified MLP model is given below.

$$min TEC$$
(21)

s.t.

$${\text{Constraints }}\left( {3} \right) - \left( {7} \right){\text{ in original MLP model}}$$
(22)
$${C}_{l,k}^{(2)}\ge {S}_{l,k}^{(2)}+\sum_{j=1}^{a}{X}_{j,k}{P}_{l,j}^{(2)}\,\, l=1,\cdots ,m;\,k=1,\cdots ,a$$
(23)
$${S}_{k}^{(3)}\ge {C}_{n,k}^{(1)}\,\,j,k=1,\cdots ,a$$
(24)
$${S}_{k}^{(3)}\ge {C}_{m,k}^{(2)}\,\,j,k=1,\cdots ,a$$
(25)
$${S}_{k}^{(3)}\ge {C}_{k-1}^{\left(3\right)} \,\,k=2,\cdots ,a$$
(26)
$${C}_{k}^{(3)}\ge {S}_{k}^{\left(3\right)}+\sum_{j=1}^{a}{X}_{j,k}{P}_{j}^{\left(3\right)}\,\, j,k=1,\cdots ,a$$
(27)
$${X}_{j,k}\in \left(\mathrm{0,1}\right)\, \,j=1,\cdots ,a;\,\,k=1,\cdots ,a,$$
(28)
$${\text{Constraints }}\left( {{13}} \right) - \left( {{14}} \right){\text{ and Constraint}}\left( {{2}0} \right){\text{ in original MLP model}}$$
(29)

Equation (21) give the objective of a modified MLP model. Constraints (22) are the Constraints (3)-(7) in the original MLP model. Constraints (23) and (27) indicate that the sequence of the orders in the electric cabinet assembly and the pipeline pack assembly is the sequence of the orders in the body assembly, i.e., the entire production line uses only one order sequence. It also noted that the completion time of the order is greater than the start processing time. Constraints (24) and (25) indicate that an order must be processed in the body assembly and the electric cabinet assembly before it can be processed in the pipeline pack assembly. Constraint (26) indicate that an order must be assembled sequentially in the pipeline pack assembly and must wait for the previous order to be assembled before the next order can be assembled. Constraints (28) define the value of the class decision variable \({X}_{j,k}\). Constraints (29) are the Constraints (13)-(14) and Constraints (20) in the original MLP model. This modified MLP model leads to a significant reduction in the number of constraints due to the elimination of two decision variables. However, the reduction in constraints is not fixed, but varies with the scale of the orders. The larger the order size, the more constraints are reduced.

3.2 H2 algorithm

We also have developed a two-stage heuristic algorithm (H2 algorithm). The design idea behind the H2 algorithm is to separate the calculations of the first and second stages. While working on the first stage, the energy consumption of this stage is obtained, which then forms the basis for calculating the energy consumption of the second stage. Therefore, the goal of both the first and second stages is to ensure the minimum energy consumption in each stage. The first stage primarily focuses on solving decision-making problems related to the body and electrical cabinet assemblies. Based on the results of the first stage, the purpose of the second stage is to determine an efficient order sequence for pipeline pack assembly that can achieve the desired objective. In the first stage, we should give an optimal order sequence for the assembly processes of the body assembly and the electrical cabinet assembly to minimize the total energy consumption. The mathematical programming model for the first stage is given below.

$$min \sum_{i=1}^{{\text{n}}}\sum_{j=1}^{{\text{a}}}{w}_{i}^{(1)}{P}_{i,j}^{(1)}+\sum_{i=1}^{{\text{m}}}\sum_{j=1}^{{\text{a}}}{w}_{i}^{(2)}{P}_{l,j}^{(2)}+\sum_{i=1}^{{\text{n}}}wk*({C}_{n,a}^{(1)}-\sum_{j=1}^{a}{P}_{i,j}^{(1)})+\sum_{i=1}^{{\text{m}}}wk*({C}_{m,a}^{(2)}-\sum_{j=1}^{a}{P}_{i,j}^{(2)})$$
(30)

s.t.

$${\text{Constraints }}\left( {3} \right) - \left( {8} \right){\text{ in MLP model}}$$
(31)
$${\text{Constraints }}\left( {{13}} \right) - \left( {{16}} \right){\text{ in MLP model}}$$
(32)
$${X}_{j,k},{Z}_{j,k}\in (\mathrm{0,1})\,\,j=1,\cdots ,a;k=1,\cdots ,a,$$
(33)
$${S}_{i,k}^{\left(1\right)},{C}_{i,k}^{\left(1\right)},{S}_{l,k}^{\left(2\right)},{C}_{l,k}^{\left(2\right)}\ge 0\,\,i=1,\cdots ,n;k=1,\cdots ,a i=1,\cdots ,n;l=1,\cdots ,m$$
(34)

This stage is formulated with the same constraints as those specified in the original MLP model, including constraints (3)–(8) and constraints (13)–(16). These constraints ensure the correct sequence and time arrangement in the manufacturing process.

Simultaneously, it is possible to calculate the completion time for each order at the final step of the body assembly and the electric cabinet assembly. This information will serve as the basis for constructing the mathematical programming model in the second stage. The mathematical programming model for the second stage can be described as follows:

$$min {w}^{(3)}\sum_{j=1}^{{\text{a}}}{P}_{j}^{(3)}+wk*({C}_{a}^{(3)}-\sum_{j=1}^{a}{P}_{j}^{(3)})$$
(35)

s.t.

$${\text{Constraints }}\left( {9} \right) - \left( {{12}} \right){\text{ in MLP model}}$$
(36)
$${\text{Constraints }}\left( {{17}} \right) - \left( {{18}} \right){\text{ in MLP model}}$$
(37)
$${Y}_{j,k}\in (\mathrm{0,1})\,\,j=1,\cdots ,a;\,k=1,\cdots ,a,$$
(38)
$${S}_{k}^{(3)},{C}_{k}^{(3)}\ge 0\,k=1,\cdots ,a$$
(39)

In the second stage of the algorithm, our objective is to minimize the total energy consumption in second-stage. Constraints (36) are Constraints (9)–(12) in the original MLP model, and Constraints (37) are the Constraints (17)–(18) in the original MLP model. Constraints (38) indicate the values of the decision variable \({Y}_{j,k}\), Constraints (39) means the values of \({S}_{k}^{(3)}\) and must be greater than 0.

Upon careful observation, we discovered that the objective function in the second stage is \(min {w}^{(3)}\sum_{j=1}^{{\text{a}}}{P}_{j}^{(3)}+wk*({C}_{a}^{(3)}-\sum_{j=1}^{a}{P}_{j}^{(3)})\). And we can know that the values of \({w}^{(3)}\),\(wk\) and \({P}_{j}^{(3)}\) are determined. The only indeterminate variable is \({C}_{a}^{(3)}\), which represents \({C}_{max}\). Therefore, this objective function can be regarded as an objective function concerning \({C}_{max}\). Thus we can deduce that the essence of this stage’s model can be characterized as a single-machine scheduling problem with arrival time to minimize maximum order completion time, denoted as \(1|{r}_{j},{p}_{j}|{C}_{max}\). Due to the complexity of this problem, it is not suitable to directly utilize “Gurobi” to solve it again. Instead, we leverage the ERD (Earliest Release Date) rule, proposed by E. L. Lawler (E. L. Lawler. 2011), to address this problem. The ERD rule provides a solution methodology for determining the optimal schedule considering above constraints. Based on the results obtained from the first stage, we can directly apply the ERD rules to make a new sequence for all orders and solve the problem based on this approach. The framework of the H2 algorithm is given below.

H2 algorithm

Input:

Given the parameters of the proposed problem

Output:

Total Energy Consumption (TEC)

Step1

Solve the mathematical programming model for the first stage by Gurobi to obtain the completion time of each order denoted as \({r}_{1}\),\({r}_{2}\)

Step2

Obtain the arrival time for each order in the pipeline pack assembly \({r}_{3}=max({r}_{1}, {r}_{2})\)

Step3

Sort all the orders by the non-descending sequence of and execute pipeline pack assembly

Step4

Output TEC

4 Computational experiments

To demonstrate the algorithm’s effectiveness in solving the realistic EES-ABPFS problem, we conducted comparative experiments on a computer with the same configuration as Intel Core i9, 2.50 GHz, 16 GB memory, and Windows 11 operating system. Meanwhile, all algorithms were implemented in Python.

4.1 Experimental design

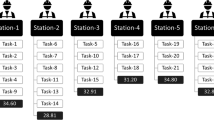
The realistic EES-ABPFS problem originates from intelligent robot manufacturing factories in China. These smart robot manufacturing factories’ main products include desktop, medium-duty, and big-duty robots. Specific production items can be found in Fig. 5.

Fig. 5
figure 5

Product Example.

Full size image

The details of the production lines for these products is shown in Fig. 6. In the factory production line, there are three operations in the body assembly group and five operations in the electric cabinet assembly group. The processing time for each order in the first and second stages is between 0 ~ 100. The energy consumption of each operation is different, and the energy consumption of assembly system during idle times remains relatively stable and can be considered a fixed value.

Fig. 6
figure 6

Production Line Layout.

Full size image

To evaluate the performance of the H1 and H2 algorithms in terms of their results and computational efficiency, we compare them with traditional heuristic algorithms and meta-heuristic algorithms. We keep the algorithm structure unchanged and conduct numerous experiments by adjusting various parameters. Extensive experimental data was collected and analyzed to compare the results and execution times of different algorithms. Table 3 lists the specific parameters used in the experiment, along with the range of actual variations for each parameter.

Table 3 Setting of problem parameters
Full size table

4.2 Heuristic algorithms

Heuristic algorithms are widely used in optimization problems because they can effectively find solutions close to optimal. Among the heuristic algorithms being compared, we have determined the processing sequence of orders in the body assembly and electric cabinet assembly based on heuristic rules. The sequence of orders for the pipeline pack assembly is determined based on the ERD rule. Table 3 provides sequencing rules for each heuristic algorithm. Inspired by Zhang et al. (2021) and Hajiaghaei-Keshteli et al. (2019), we establish a series of heuristic algorithms by combining the processing times of the body assembly and electrical cabinet assembly differently. Taking SSPT-SSPT as an example, seq1 represents the processing sequence of orders in the body assembly, which is to sort the orders based on the sum of their processing times in each operation of the body assembly, which is arranged in ascending sequence. The resulting sequence represents the processing sequence of orders in the body assembly. Similarly, seq2 represents the processing sequence of orders in the electric cabinet assembly, following the same sequencing rule as seq1. Table 4 comprehensively outlines the sequencing rules for each heuristic algorithm.

Table 4 Heuristic algorithm introduction
Full size table

we give the running procedure of the heuristic algorithm:

Heuristic algorithms (SSPT-SSPT, LSPT-LSPT,SSPT-LSPT, LSPT-SSPT, SSPPT-SSPPT.etc)

Input

Given the parameters of the proposed problem displayed in Table 1

Output

Total Energy Consumption (TEC)

Step1:

Define seq1 as the sorting method for the body assembly and seq2 as the sorting method for the electric cabinet assembly

Step2:

Calculate the energy consumption during the working time and the idle time in the body assembly and electric cabinet assembly, and calculate the starting time for the pipeline pack assembly of each order

Setp3:

Sort the orders in ascending sequence based on the starting time of the pipeline pack assembly to obtain the processing sequence of orders. Calculate the energy consumption during the working time and the idle time of each order

Setp4:

Output TEC

4.2.1 Comparison of the running results with Heuristic Algorithms

We conducted 49 runs for each heuristic algorithm across across different order sizes (a = {50, 100, 200, 300}) and obtained the mean, maximum, minimum, and standard deviation of the total energy consumption (TEC) data. The results of the comparative experiments with the heuristic algorithms are presented in Table 5, which utilizes color scale plots to visualize their performance. Darker colors indicate poorer performance, while lighter colors indicate better performance. We can determine which algorithm performs better by comparing the color differences among the algorithms. The color scale represented by the H1 algorithm is consistently light across different order sizes (a = {50, 100, 200, 300}), while the color scale under the H2 algorithm exhibits a similar lightness. In contrast, the heuristic algorithms exhibit darker colors in all cases, indicating inferior performance compared to H1 and H2 algorithms.

Table 5 Comparison of Results with the Heuristic Algorithms
Full size table

Furthermore, comparing the TEC values of each algorithm under different instances in Table 5 allows us to assess their relative performance. Lower TEC values indicate better performance, and it is evident from the results in Table 5 that the H1 algorithm consistently achieves lower values than other algorithms, regardless of the order size. This demonstrates the superior performance of the H1 algorithm over the heuristic algorithms. The H2 algorithm also shows lower values than heuristic algorithms, indicating its better performance than the heuristic algorithms.

Figure 7 provides a comprehensive visualization of the 49 run results for each algorithm. The horizontal axis represents different algorithms, while the vertical axis represents the difference between the TEC value of each algorithm and the minimum TEC value among all algorithms. Points located higher on the vertical axis indicate more significant differences from the optimal algorithm, while lower values indicate more minor differences.

Fig. 7
figure 7

TEC for Instances with 50, 100, 200, and 300 Products. (a) TEC for Instances with 50 Products, (b) TEC for Instances with100 Products, (c) TEC for Instances with 200 Products, (d) TEC for Instances with 300 Products.

Full size image

Notably, in Fig. 7, throughout all 49 runs conducted, the points representing the H1 algorithm consistently align with the horizontal axis. On the other hand, the points representing the heuristic algorithm continually position themselves away from the horizontal axis, and are always found above the points representing the H1 algorithm. This graphical representation vividly illustrates the superior performance of the H1 algorithm over the heuristic algorithm. In the same Fig. 7, the performance of the H2 algorithm is also commendable. The points representing the results of the H2 algorithm runs have aligned with the horizontal axis on multiple occasions and are consistently found below the points representing the heuristic algorithm, thereby signifying the better performance of the H2 algorithm in comparison to the heuristic algorithm. However, there is a caveat: the positions of the points representing the H2 algorithm are found to be above those representing the H1 algorithm in a significant majority of cases. This reveals that while the H2 algorithm is a step ahead of the heuristic algorithm, it lags behind when compared to the H1 algorithm’s performance.

Moreover, a notable observation from Fig. 7 is the relative position stability of the points representing the H1 algorithm across all experiments. They almost remain in a fixed position, showcasing a level of consistency and stability. In contrast, the positions of the points representing other algorithms, including the heuristic and H2 algorithms, exhibit considerable differences across different experiments. This differences highlights the stronger stability inherent in the H1 algorithm across all instances.

In general, a comprehensive analysis based on the results presented in Fig. 7 makes it abundantly clear that the H1 algorithm emerges superior among all compared algorithms. Its consistent performance and stability across a wide range of scenarios underscore its position as the most optimal choice among the algorithms compared.

In addition to comparing the TEC results, we conducted a detailed analysis of the runtime performance of the algorithms to gain further insights into their differences. Figure 8 presents line graphs depicting the runtime comparison of each algorithm. The horizontal axis represents the difference between the runtime value of each algorithm and the minimum runtime value among all algorithms. Similar to Fig. 7, the further a point is from the horizontal axis, the longer the runtime required by that algorithm, indicating poorer performance.

Fig. 8
figure 8

Comparison of Running Time with Heuristic Algorithms. (a) Running time for Instances with 50 Products, (b) Running time for Instances with 100 Products, (c) Running time for Instances with 200 Products (d) Running time for Instances with 300.

Full size image

Considering a = 100 as an example, we observe that in the 49 experiments, the points representing the H1 algorithm consistently cluster close to the horizontal axis, while the points representing the H2 algorithm align with the horizontal axis. In contrast, the points representing the heuristic algorithm deviate from the horizontal axis. This demonstrates that both the H1 and H2 algorithms have shorter running times compared to the heuristic algorithm, further confirming the superiority of our designed H1 and H2 algorithms over the heuristic algorithm.

It is worth noting that the H2 algorithm exhibits a shorter runtime than the H1 algorithm for a = 50 and a = 100. However, this does not necessarily indicate that the H2 algorithm is superior to the H1 algorithm. As the order size increases, new variations in the results emerge. When a = 200 and a = 300, we observe that in some experiments, the runtime of the H1 algorithm is comparable to that of the H2 algorithm. In most cases, the H1 algorithm demonstrates a lower runtime than the H2 algorithm. This suggests the H1 algorithm exhibits a shorter runtime and performs better as the order size increases. The H1 algorithm holds an advantage in handling large-scale problems.

4.3 Meta-heuristic algorithm

Meta-heuristic are optimization algorithms widely used to solve complex problems that may be difficult for traditional algorithms (Arabahmadi et al. 2023, Kolahi-Randji et al. 2023, Fathollahi-Fard et al. 2020, Fathollahi-Fard et al. 2019 and N. Sahebjamnia et al. 2018). Natural and biological processes inspire these algorithms, such as evolution, swarm intelligence, and physical phenomena. They provide a flexible and efficient method for finding near-optimal solutions in various fields. In comparison with meta-heuristic algorithms, we mainly applied genetic algorithm (GA), particle swarm optimization (PSO), simulated annealing (SA), artificial fish swarm algorithm (AFSA), differential evolution (DE), and immune algorithm (IA) (Dai et al. 2013, Shirazi et al. 2011, Li et al. 2015 and Villoria et al. 2014). After reviewing the existing literature, we found that an important step in using meta-heuristic algorithms is adjusting the parameters, without needing to make many changes to the algorithm itself. Since meta-heuristic algorithms are already well-known, we will not provide detailed information about them here. To adapt the meta-heuristic algorithm to the original MLP model, we made some adjustments to certain parameters in the meta-heuristic algorithm. Detailed parameter adjustments are provided in Table 6.

Table 6 Parameters of Meta-heuristic Algorithms
Full size table

Unlike heuristic algorithms, the sequence of orders in meta-heuristic algorithms is random. Here, the details of the encoding and decoding process are shown in Fig. 9. During the encoding process, we randomly assign corresponding random keys to the orders for the body assembly and the electric cabinet assembly. Each random key falls within the range of 0 to 1. During decoding, we sort all orders for the body assembly and the electric cabinet assembly in the ascending sequence of their random keys, resulting in a new sequence. For example, in Fig. 9, the random keys for the body assembly is \(\{0.25, 0.57, 0.33, 0.83, 0.72\}\), and the decoding order sequence becomes \(\{{J}_{11},{J}_{31},{J}_{21},{{J}_{51},J}_{41}\}\). The order sequence after decoding is the desired assembly sequence for the body assembly. Similarly, the electric cabinet assembly generates a new order sequence after decoding, which is the assembly sequence on the electric cabinet assembly Note that the total number of encoding and decoding elements is \(2a,\) which is twice the number of orders.

Fig. 9
figure 9

Encoding and Decoding Processes.

Full size image

4.3.1 Comparison of the running results with meta-heuristic algorithm

Table 7 presents the results for each algorithm, following a similar setup as Table 5. We conducted 49 runs for each algorithm and obtained the corresponding mean, maximum, minimum, and standard deviation values. Examining the color scale in Table 7 shows that the color related to the H1 algorithm is predominantly white, while the colors for other algorithms are significantly darker. This observation conclusively establishes the superior performance of the H1 algorithm. Although the H1 algorithm exhibits a slightly higher standard deviation than others at \(a=100\), the deviation can be considered negligible.

Table 7 Comparison of Results with Meta-heuristic Algorithms
Full size table

Moreover, compared to the meta-heuristic algorithms, the performance of the H2 algorithm is relatively poor. The results of the H2 algorithm not only fall short of the H1 algorithm but also underperform in comparison to other meta-heuristic algorithms. However, we find that the H2 algorithm outperforms the common heuristic algorithms.

Among the meta-heuristic algorithms, the SA algorithm performs remarkably in solving the proposed problem. The color scale indicates that the SA algorithm outperforms other meta-heuristic algorithms. Specifically, for \(a=50\) and \(a=100\), the standard deviation of the SA algorithm’s solutions is comparable to that of the H1 algorithm. Overall, the H1 algorithm consistently outperforms the meta-heuristic algorithms. Although the SA algorithm closely approaches the performance of the H1 algorithm at \(a=50\) and \(a=100\), its performance noticeably deteriorates compared to the H1 algorithm at \(a=200\) and \(a=300\), with the difference between them growing as the order size increases.

Figure 10 provides an line graph of the 49 experimental results for each algorithm, utilizing the same horizontal and vertical axes as Fig. 7. The line graph visually represents the differences in the running results among all the algorithms. Taking \(a=50\) as an example, the points representing the H1 algorithm consistently align with the horizontal axis, while the points representing other algorithms consistently deviate from the horizontal axis. When \(a=200\) and \(a=300\), it becomes evident that the points representing other algorithms consistently deviate from the horizontal axis, while the points representing the H1 algorithm remain on the horizontal axis. This unequivocally establishes the H1 algorithm as the optimal choice among the compared algorithms, with its advantages becoming more obvious when dealing with large-scale orders.

Fig. 10
figure 10

TEC for Instances with 50, 100, 200, and 300 Products. (a) TEC for Instances with 50 Products, (b) TEC for Instances with 100 Products, (c) TEC for Instances with 200 Products, (d) TEC for Instances with 300 Products

Full size image

Additionally, we conducted a comparison of the running time for each algorithm, as depicted in Fig. 11. The horizontal and vertical axes in Fig. 11 follow the same settings as in Fig. 8. From the results presented in Fig. 11, we observe that the running time of the H1 algorithm is longer than that of the H2 algorithm when \(a=50\) and \(a=100\). However, the running time of the H1 algorithm remains shorter than that of the meta-heuristic algorithms in most cases. When \(a=200\) and \(a=300\), the advantage of the H1 algorithm becomes highly apparent. The running time of the H1 algorithm is comparable to that of the H2 algorithm at \(a=200\), while at \(a=300,\) the running time of the H1 algorithm is shorter than that of the H2 algorithm and meta-heuristic algorithms. Furthermore, at \(a=300\), the running time of the H1 algorithm significantly outperforms other algorithms. These findings further underscore the pronounced advantage of the H1 algorithm in handling large-scale problems.

Fig. 11
figure 11

Comparison of Running Time with Meta-heuristic Algorithms. (a)Running time for Instances with 50 Products, (b)Running time for Instances with 100 Products, (c)Running time for Instances with 200 Products, (d) Running time for Instances with 300 Products.

Full size image

4.3.2 Comparison of different performances for each algorithm

To make a comprehensive comparison of the algorithms in different scenarios, we generated convergence plots, as shown in Fig. 12. These convergence plots show the iterations of each algorithm. By comparing the iteration behavior of each algorithm, we can determine which algorithm exhibits the most stable performance and yields the best results. In addition, the information represented in each plot is the average of 49 run results.

Fig.12
figure 12

Comparison of Convergence Plots with Meta-heuristic Algorithms. (a) Convergence Curve for Instance 50 Products, (b) Convergence Curve for Instance 100 Products, (c) Convergence Curve for Instance 200 Products, (d) Convergence Curve for Instance 300 Products.

Full size image

In the convergence plot, the vertical axis represents the TEC, while the horizontal axis represents the number of iterations. In this plot, if a point representing an algorithm is positioned lower on the vertical axis, it indicates a smaller TEC value and better algorithm performance. It is clear from the convergence plot that the straight line represented by the H1 algorithm is always at a lower position on the vertical axis. In comparison, the curve represented by the meta-heuristic algorithm is always at a higher position on the vertical axis, which indicates that the H1 algorithm is superior to the meta-heuristic algorithms. Taking the convergence plot for \(a=50\) as an example, the H1 algorithm results in a straight line at the bottom end, while the curve represented by the SA and other meta-heuristics is always above the line.

Moreover, we can observe that the difference between the H1 and meta-heuristic algorithms is noticeable when \(a=50\). Moreover, the gap between H1 algorithm and meta-heuristics increases as the order scale increases. This further highlights the dominance of the H1 algorithm in solving large-scale problems too.

By observing the changes in the slope of each curve, we can determine the variation speed during the execution of each meta-heuristic algorithm. Among these meta-heuristic algorithms, the PSO algorithm demonstrates the fastest variation speed, consistently reaching the convergence value ahead of others. Conversely, the SA and DE algorithms exhibit slower variation speeds, struggling to reach the convergence value in each iteration. Thus, the solutions obtained by the SA algorithm and DE algorithm are better than those obtained by PSO algorithm.

In addition, we can also observe Fig. 13, which represents the detailed results of 49 experimental runs for all algorithms in different scenarios. We can clearly see that the straight line represented by the H1 algorithm is always at a lower position on the vertical axis. In contrast, the curves represented by the other algorithms are always higher on the vertical axis than the H1 algorithm, making it evident that the H1 algorithm is superior to meta-heuristic algorithm.

Fig. 13
figure 13figure 13

Comparison of Convergence Plots with Meta-heuristic Algorithms. (a) Convergence Curve for Instances with 50 Products, (b) Convergence Curve for Instances with 100 Products, (c) Convergence Curve for Instances with 200 Products, (d) Convergence Curve for Instances with 300 Products

Full size image

4.3.3 Friedman test

The Friedman test is a non-parametric statistical test utilized to compare the performance of multiple algorithms across various experimental conditions. This test is precious when the data fails to meet the assumptions of parametric tests such as T-test. It involves ranking the results for each algorithm and calculating the average rank for each condition. The Friedman test determines whether there are significant differences in the ranks among the conditions.

To enhance the accuracy of the Friedman test, we collected extensive data for our analysis. Each algorithm was executed 49 times in different scales, and the results were applied to the Friedman test. The performance of each algorithm was compared for all instances, and the results of the Friedman test under each algorithm are presented in Table 8.

Table 8 Friedman Test with Meta-heuristics
Full size table

In our the Table 8, the Friedman test yielded a p-value of 0 for all instances, indicating statistically significant differences among the algorithms. Lower values in the table indicate better algorithm performance. Table 8 shows relatively high values for the meta-heuristic algorithms AFSA, PSO, GA, IA, and DE, indicating their inadequacy in solving this problem.

Conversely, the SA algorithm performs relatively well, indicating SA is better than other meta-heuristic algorithms in all instances. However, in all instances, the H1 algorithm consistently outperforms the SA algorithm, and the performance gap between them widens as the order scale increases. This observation is further supported by Fig. 14, where the results of the H1, SA, DE, and other inferior algorithms are visually compared.

Fig.14
figure 14

Comparison of Friedman Test with Meta-heuristic Algorithms. (a) CD Diagram with 50 Products, (b) CD Diagram with 100 Products, (c) CD Diagram with 200 Products, (d) CD Diagram with 300 Products

Full size image

For instance with \(a=50\), the test result of the H1 algorithm falls between the interval (0, 2), while the SA algorithm falls between (1.5, 3), and the DE algorithm falls within (2, 4). Because the H1 algorithm, SA algorithm, and DE algorithm overlap at \(a=50\), it does not conclusively establish the absolute superiority of the H1 algorithm over the SA and DE algorithms. However, we can observe that the AFSA, PSO, GA, and IA algorithms are notably inferior to the H1 algorithm.

When \(a=100\), we observe a different trend. The result of the H1 algorithm lies between (0.2, 1.9), with the SA algorithm still overlapping, but the DE algorithm falls within the interval (2, 4), no longer overlapping with the H1 algorithm. This indicates that as the order scale increases, the DE algorithm gradually becomes inferior to the H1 algorithm. The gap between the results of the H1 algorithm and the SA algorithm widens significantly as the scale increases to 200 and 300. Furthermore, in large-scale operations, the H1 algorithm performs superior over other meta-heuristic algorithms like DE.

Comparing the reported results, it is evident that the H1 algorithm consistently achieves lower values in terms of TEC across all instances. This indicates that the H1 algorithm outperforms the other evaluated algorithms in this study. Additionally, the p-value of 0 further strengthens the significance of these performance differences.

5 Management insights

The management insights of this research are as follows:

  1. (1)

    Importance of Green Scheduling: The research highlights the significance of implementing green scheduling models and algorithms in industrial workshop assembly processes. By incorporating environmental considerations into the scheduling decisions, management can achieve more precise and efficient assembly outcomes, reducing overall energy consumption.

  2. (2)

    Enhanced Accuracy: The study emphasizes that the proposed green scheduling model and algorithm outperform traditional workshop experience in accuracy. Management can leverage these tools to make better-informed decisions regarding the assembly process, resulting in more optimal energy consumption outcomes.

  3. (3)

    Cost Savings: The research findings demonstrate that adopting the designed model and algorithm can lead to a reduction of around 3% in total energy consumption compared to conventional workshop experience-based approaches. This translates into cost savings for the organization, as reduced energy consumption can result in lower operating expenses.

  4. (4)

    Decision Support: The research offers decision support for management by providing a framework for optimizing energy efficiency in workshop assembly processes. By considering the findings, managers can effectively plan and execute assembly activities, ensuring minimal energy waste and aligning with sustainability goals.

  5. (5)

    Potential for Scale-up: The proposed model and algorithm have the potential to address large-scale problems. This insight is valuable for management as it indicates that the tools can be applied beyond smaller-scale scenarios, allowing for improved energy efficiency in complex assembly operations.

Overall, the research demonstrates the importance of incorporating green scheduling models and algorithms into industrial workshop assembly processes. It highlights the potential to save costs, enhance accuracy, and make more informed management decisions about energy consumption. In practical production processes, enterprises can make slight adjustments according to the characteristics of production, utilizing the methods provided in this paper to formulate a reasonable order sequencing scheme, thereby reducing the energy consumption costs generated in the assembly process.

6 Conclusion and future suggestions

This paper proposed an energy-efficient scheduling problem for assembly-blocking permutation flow-shop that arise in industrial robot workshop. To solve this problem, we design two heuristic algorithms, namely H1 algorithm and H2 algorithm. We compared these two algorithms with traditional heuristics and meta-heuristics. A large number of experiments prove that the H2 algorithm is better than common heuristic algorithms, while the H1 algorithm is better than the common heuristic and meta-heuristic algorithms. Regardless of whether the order size is large or small, the H1 algorithm is superior to other algorithms in term of the best solution found and running time. Extensive experimental results demonstrate that adopting the designed model and H1 algorithm can lead to a reduction of around 3% in total energy consumption compared to conventional workshop experience-based approaches. All of these findings demonstrate the effectiveness of the proposed green models and algorithms for reducing energy consumption in practical industrial robot production.

While the proposed algorithm has a strong performance in addressing single-objective energy consumption problem, it may struggles when dealing with multi-objective models. Hence, it may not be applicable when facing upstream–downstream collaborative supply chain problems with multiple objectives, such as delay penalty and makespan.

In the following, we plan on employing a bi-level programming technology to model the above complex multi-objective supply chain scheduling problems. Deep reinforcement learning or other artificial intelligence algorithms will be considered to solve the bi-level model.