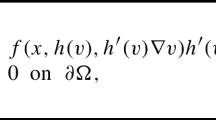Skip to main content
SpringerLink
Log in

Variational methods for solving numerically magnetostatic systems

  • Published:
Advances in Computational Mathematics Aims and scope Submit manuscript

Abstract

In this paper, we study some techniques for solving numerically magnetostatic systems. We consider fairly general assumptions on the magnetic permeability tensor. It is elliptic, but can be nonhermitian. In particular, we revisit existing classical variational methods and propose new numerical methods. The numerical approximation is either based on the classical edge finite elements or on continuous Lagrange finite elements. For the first type of discretization, we rely on the design of a new, mixed variational formulation that is obtained with the help of T-coercivity. The numerical method can be related to a perturbed approach for solving mixed problems in electromagnetism. For the second type of discretization, we rely on an augmented variational formulation obtained with the help of the weighted regularization method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Data availability

Data are available on request from authors.

References

  1. Alonso Rodriguez, A., Bertolazzi, E., Valli, A.: The curl–div system: theory and finite element approximation. Maxwell’s equations-analysis and numerics. Radon Ser. Comput. Appl. Math., vol. 24, pp. 1–43. De Gruyter, Berlin, Germany (2019)

  2. Ciarlet Jr., P.: T-coercivity: application to the discretization of Helmholtz-like problems. Comput. Math. Applic. 64, 22–34 (2012)

  3. Chesnel, L., Ciarlet Jr., P.: T-coercivity and continuous Galerkin methods: application to transmission problems with sign changing coefficients. Numer. Math. 124, 1–29 (2013)

  4. Nédélec, J.-C.: Mixed finite elements in \(\mathbb{R} ^3\). Numer Math. 35, 315–341 (1980)

    Article  MathSciNet  Google Scholar 

  5. Monk, P.: Finite element methods for Maxwell’s equations. Oxford University Press, Oxford, Great Britain (2003)

  6. Costabel, M., Dauge, M.: Weighted regularization of Maxwell’s equations in polyhedral domains. SIAM J. Numer. Anal. 93, 239–277 (2002)

    Google Scholar 

  7. Kirsch, A., Hettlich, F.: Mathematical theory of time-harmonic Maxwell’s equations. Springer, Cham, Switzerland (2016)

  8. Assous, F., Ciarlet Jr., P., Labrunie, S.: Mathematical foundations of computational electromagnetism. Springer, Cham, Switzerland (2018)

  9. Gross, P.W., Kotiuga, P.R.: Electromagnetic theory and computation: a topological approach. MSRI Publications Series, 48. Cambridge University Press, Cambridge (2004)

  10. Bossavit, A.: Computational electromagnetism. Academic Press, New York, USA (1998)

  11. Bermúdez, A., Gómez, D., Salgado, P.: Mathematical models and numerical simulation in electromagnetism. Springer, Cham, Switzerland (2014)

  12. Bermúdez, A., Rodriguez, R., Salgado, P.: A finite element method for the magnetostatic problem in terms of scalar potentials. SIAM J. Numer. Anal. 46, 1338–1363 (2008)

    Article  MathSciNet  Google Scholar 

  13. Bermúdez, A., López-Rodriguez, B., Rodriguez, R., Salgado, P.: Equivalence between two finite element methods for the eddy current problem. C. R. Acad. Sci. Paris, Ser. I. 348, 769–774 (2010)

  14. Tang, Z., Le Menach, Y., Creusé, E., Nicaise, S., Piriou, F., Nemitz, N.: Residual and equilibrated error estimators for magnetostatic problems solved by finite element method. IEEE Trans. Magn. 49, 5715–5723 (2013)

    Article  ADS  Google Scholar 

  15. Bermúdez, A., Piñiero, M., Rodriguez, R., Salgado, P.: Analysis of an ungauged \(T,{\phi }-{\phi }\) formulation of the eddy current problem with currents and voltage excitations. Math. Mod. Num. Anal. 51, 2487–2509 (2017)

    Article  MathSciNet  Google Scholar 

  16. Bermúdez, A., Piñiero, M., Salgado, P.: Mathematical and numerical analysis of a transient magnetic model with voltage drop excitations. Computers Math. Applic. 76, 2710–2722 (2018)

    Article  MathSciNet  Google Scholar 

  17. Creusé, E., Dular, P., Nicaise, S.: About the gauge conditions arising in finite element magnetostatic problems. 77, 1563–1582 (2019)

    Google Scholar 

  18. Chicaud, D., Ciarlet Jr., P., Modave, A.: Analysis of variational formulations and low-regularity solutions for time-harmonic electromagnetic problems in complex anisotropic media. SIAM J. Math. Anal. 53, 2691–2717 (2021)

  19. Chicaud, D., Ciarlet Jr., P.: Analysis of time-harmonic Maxwell impedance problems in anisotropic media. SIAM J. Math. Anal. 55, 1969–2000 (2023)

  20. Feistauer, M., Ženišek, A.: Finite element solution of nonlinear elliptic problems. Numer. Math. 50, 451–475 (1987)

    Article  MathSciNet  Google Scholar 

  21. Dello Russo, A., Alonso, A.: Finite element approximation of Maxwell eigenproblems on curved Lipschitz polyhedral domains. Appl. Numer. Math. 59, 1796–1822 (2009)

    Article  MathSciNet  Google Scholar 

  22. Bramble, J.H., Pasciak, J.E.: A new approximation technique for div-curl systems. Math. Comp. 73, 1739–1762 (2003)

    Article  ADS  MathSciNet  Google Scholar 

  23. Duan, H., Jia, F., Lin, P., Tan, R.C.E.: The local \(L^2\) projected \(C^0\) finite element method for Maxwell problem. SIAM J. Numer. Anal. 47, 1274–1303 (2009)

    Article  MathSciNet  Google Scholar 

  24. Bonito, A., Guermond, J.-L.: Approximation of the eigenvalue problem for the time harmonic Maxwell system by continuous Lagrange finite elements. Math. Comp. 80, 1887–1910 (2011)

    Article  MathSciNet  Google Scholar 

  25. Badia, S., Codina, R.: A nodal-based finite element approximation of the Maxwell problem suitable for singular solutions. SIAM J. Numer. Anal. 50, 398–417 (2012)

    Article  MathSciNet  Google Scholar 

  26. Duan, H., Du, Z., Liu, W., Zhang, S.: New mixed element for Maxwell equations. SIAM J. Numer. Anal. 57, 320–354 (2019)

    Article  MathSciNet  Google Scholar 

  27. Ern, A., Guermond, J.-L.: Finite elements II. Springer, Cham, Switzerland (2021)

  28. Jamelot, E., Ciarlet Jr., P.: Fast non-overlapping Schwarz domain decomposition methods for solving the neutron diffusion equation. J. Comput. Phys. 241, 445–463 (2013)

  29. Ciarlet Jr., P., Jamelot, E., Kpadonou, F.D.: Domain decomposition methods for the diffusion equation with low-regularity solution. Comput. Math. Applic. 74, 2369–2384 (2017)

  30. Giret, L.: Non-conforming domain decomposition for the multigroup neutron SPN equation. PhD thesis, Université Paris-Saclay (2018)

  31. Barré, M., Ciarlet Jr., P.: The T-coercivity approach for mixed problems to appear in C. R. Acad. Sci. Paris, Ser. I

  32. Jamelot, E.: Improved stability estimates for solving Stokes problem with Fortin-Soulie finite elements. Technical Report HAL (2023)

  33. Ciarlet Jr., P.: Lecture notes on Maxwell’s equations and their approximation (in French). Master’s degree analysis, modelling and simulation from paris-saclay university and institut polytechnique de paris (2022). https://hal.inria.fr/hal-03153780v3

  34. Weber, C.: A local compactness theorem for Maxwell’s equations. Math. Meth. Appl. Sci. 2, 12–25 (1980)

    Article  MathSciNet  Google Scholar 

  35. Reitzinger, S., Schöberl, J.: An algebraic multigrid method for finite element discretizations with edge elements. Numer. Linear Algebra Appl. 9, 223–238 (2002)

    Article  MathSciNet  Google Scholar 

  36. Duan, H., Li, S., Tan, R.C.E., Zheng, W.: A delta-regularization finite element method for a double curl problem with divergence-free constraint. SIAM J. Numer. Anal. 50, 3208–3230 (2012)

    Article  MathSciNet  Google Scholar 

  37. Ciarlet Jr., P., Wu, H., Zou, J.: Edge element methods for Maxwell’s equations with strong convergence for Gauss’ laws. SIAM J. Numer. Anal. 52, 779–807 (2014)

  38. Bermúdez, A., Rodriguez, R., Salgado, P.: Numerical treatment of realistic boundary conditions for the eddy current problem in an electrode via Lagrange multipliers. Math. Comp. 74, 123–151 (2005)

    Article  ADS  MathSciNet  Google Scholar 

  39. Raviart, P.-A., Thomas, J.-M.: A mixed finite element method for second order elliptic problems. In: Mathematical aspects of finite element methods. Lecture notes in mathematics, vol. 606, pp. 292–315. Springer, Berlin, Germany (1977)

  40. Bermudez, A., Gamallo, P., Nogueiras, M.R., Rodriguez, R.: Approximation of a structural acoustic vibration problem by hexahedral finite elements. IMA J. Numer. Anal. 26, 391–421 (2006)

    Article  MathSciNet  Google Scholar 

  41. Jerison, D.S., Kenig, C.E.: The Neumann problem on Lipschitz domains. Bull. Amer. Math. Soc. 4, 203–207 (1981)

    Article  MathSciNet  Google Scholar 

  42. Grisvard, P.: Elliptic problems in nonsmooth domains. Pitman, Boston, London, Melbourne (1985)

    Google Scholar 

  43. Dauge, M.: Elliptic boundary value problems on corner domains. Springer, Berlin, Germany (1988)

    Book  Google Scholar 

  44. Birman, M.S., Solomyak, M.Z.: Maxwell operator in regions with nonsmooth boundaries. Sib. Math. J. 28, 12–24 (1987)

    Article  Google Scholar 

  45. Hiptmair, R.: Finite elements in computational electromagnetics. Acta Numerica. 50, 237–339 (2002)

    Article  Google Scholar 

  46. Costabel, M., Dauge, M., Nicaise, S.: Singularities of Maxwell interface problems. Modél. Math. Anal. Numér. 33, 627–649 (1999)

    Article  MathSciNet  Google Scholar 

  47. Ciarlet Jr., P.: On the approximation of electromagnetic fields by edge finite elements. Part 1: sharp interpolation results for low-regularity fields. Computers Math. Applic. 71, 85–104 (2016)

  48. Costabel, M., Dauge, M., Nicaise, S.: Corner singularities and analytic regularity for linear elliptic systems. Part I: Smooth domains (2010). https://hal.archives-ouvertes.fr/hal-00453934v2

  49. Bonito, A., Guermond, J.-L., Luddens, F.: Regularity of the Maxwell equations in heterogeneous media and Lipschitz domains. J. Math. Anal. Appl. 408, 498–512 (2013)

    Article  MathSciNet  Google Scholar 

  50. Ciarlet Jr., P.: Augmented formulations for solving Maxwell equations. Comp. Meth. Appl. Mech. and Eng. 194, 559–586 (2005)

  51. Jamelot, E.: Continuous Galerkin methods for solving Maxwell equations (in French). PhD thesis, Ecole Polytechnique (2005)

  52. Ciarlet Jr., P., Jamelot, E.: Continuous Galerkin methods for solving the time-dependent Maxwell equations in 3D geometries. J. Comput. Phys. 226, 1122–1135 (2007)

  53. Buffa, A., Ciarlet Jr., P., Jamelot, E.: Solving electromagnetic eigenvalue problems in polyhedral domains. Numer. Math. 113, 497–518 (2009)

  54. Ciarlet Jr., P., Labrunie, S.: Numerical analysis of the generalized Maxwell equations (with an elliptic correction) for charged particle simulations. Math. Models Meth. App. Sci. 19, 1959–1994 (2009)

  55. Ciarlet Jr., P., Scheid, C.: Electrowetting of a 3D drop: numerical modelling with electrostatic vector fields. Math. Mod. Num. Anal. 44, 647–670 (2010)

  56. Otin, R.: Regularized Maxwell equations and nodal finite elements for electromagnetic field computations. Electromagnetics. 30, 190–204 (2010)

    Article  Google Scholar 

  57. Costabel, M.: A coercive bilinear form for Maxwell’s equations. J. Math. Anal. and Appl. 157, 527–541 (1991)

    Article  MathSciNet  Google Scholar 

  58. Costabel, M., Dauge, M.: Singularities of electromagnetic fields in polyhedral domains. Arch. Rational Mech. Anal. 151, 221–276 (2000)

    Article  ADS  MathSciNet  Google Scholar 

  59. Clough, R.W., Tocher, J.L.: Finite element stiffness matrices for analysis of plates in bending. In: Conference on matrix methods in structural mechanics, Wright Patterson A.F.B, Dayton, USA, pp. 515–545 (1965)

  60. Ciarlet, P.G.: Basic error estimates for elliptic problems. Handbook of numerical analysis, vol. II, pp. 17–351. North Holland, Amsterdam, The Netherlands (1991)

  61. Percell, P.: On cubic and quartic Clough-Tocher finite elements. SIAM J. Numer. Anal. 13, 100–103 (1976)

    Article  ADS  MathSciNet  Google Scholar 

  62. Alfeld, P.: A trivariate Clough-Tocher scheme for tetrahedral data. Comput. Aided Geom. Design. 1, 169–181 (1984)

    Article  Google Scholar 

  63. Sorokina, T., Worsey, A.J.: A multivariate Powell-Sabin interpolant. Adv Comput Math. 29, 71–89 (2008)

    Article  MathSciNet  Google Scholar 

  64. Badia, S., Codina, R.: A combined nodal continuous-discontinuous finite element formulation for the Maxwell problem. Appl. Math. Comput. 218, 4276–4294 (2011)

    MathSciNet  Google Scholar 

  65. Eddargani, S.: Approximation by splines functions on Powell-Sabin triangulations. PhD thesis, Universidad de Granada and Université Hassan 1er (2021)

  66. Otin, R.: Regularized Maxwell equations and nodal finite elements for electromagnetic field computations in frequency domain. PhD thesis, Polytechnic University of Catalonia (2011)

  67. Otin, R.: ERMES:a nodal-based finite element code for electromagnetic simulations in frequency domain. Comput. Phys. Commun. 184, 2588–2595 (2013)

    Article  ADS  CAS  Google Scholar 

Download references

Author information

Author notes

  1. Patrick Ciarlet Jr. and Erell Jamelot contributed equally to this work

Authors and Affiliations

  1. POEMS, CNRS, INRIA, ENSTA Paris, Institut Polytechnique de Paris, 828 Bd des Maréchaux, 91762, Palaiseau Cedex, France

    Patrick Ciarlet Jr.

  2. Université Paris-Saclay, CEA, Service de Thermo-hydraulique et de Mécanique des Fluides, 91191 , Gif-sur-Yvette, France

    Erell Jamelot

Authors
  1. Patrick Ciarlet Jr.
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Erell Jamelot
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Patrick Ciarlet Jr..

Ethics declarations

Conflict of interest

The authors declare no competing interests.

Additional information

Communicated by: Francesca Rapetti

This article is dedicated to Professor Alain Bossavit on the occasion of his 80th birthday.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ciarlet Jr., P., Jamelot, E. Variational methods for solving numerically magnetostatic systems. Adv Comput Math 50, 5 (2024). https://doi.org/10.1007/s10444-023-10089-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10444-023-10089-1

Keywords

Search

Navigation