Skip to main content
SpringerLink
Log in

Volatility spillover effects in interbank money markets

  • Original Paper
  • Published:
Review of World Economics Aims and scope Submit manuscript

Abstract

Using daily data from 2006 to 2015, this paper applies alternative multivariate GARCH models and a modified version of the spillover index methodology proposed by Diebold and Yilmaz (Int J Forecast 28(1):57–66, 2012) to test the existence of shock and volatility contagion effects across interbank money markets. Overall, we find evidence that money markets are highly interrelated, exhibiting dynamic cross market effects. Moreover, we emphasize the pertinence of conditional covariances and we show that volatility spillovers are time-varying and very responsive to the major economic events, increasing in periods of higher turbulence, which reinforces the importance of closely monitoring the evolution of money markets.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

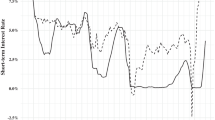
Source: Bloomberg

Fig. 2
Fig. 3

Similar content being viewed by others

Notes

  1. In this context the acronym VARMA-GARCH stands for a GARCH with the VARMA recursion for the variances. However, this expression is frequently used to mention a standard GARCH model with a VARMA specification for the conditional mean, which can originate a doubt of interpretation or a misunderstanding.

  2. As an example among different alternatives, it is possible to mention the differential between unsecured money market rates and general collateral repurchase agreement (GC Repos) for the same term or the gap between unsecured interbank money market rates with different maturity buckets.

  3. As previously discussed, in general, LIBOR rates trade above OIS rates. However, it has not been observed in the CHF money market because different fixing conventions. In truth, this effect is explained due to the monetary policy implemented by the SNB that, in December 2014, lowered its deposit rate and its target for the 3-month CHF LIBOR into negative territory. Yet, negative deposit rates were only applied to reserves above a specific threshold. So, the LIBOR fixing is established as the interest rate at which banks are willing to borrow, while the OIS fixing is defined as the interest rate at which banks are willing to lend. Given that the rate at which a bank is willing to lend hinges on its level of reserves, its comparison with a benchmark borrowing rate should be read with caution.

  4. Throughout the paper the notation used to describe the different models follows the nomenclature adopted by the respective authors in the original articles.

  5. For further details on this setting, we recommend the reading of Diebold and Yilmaz (2009, 2012, 2014).

  6. All models are estimated with p = q = r = s = 1. In spite of presenting the estimates for the conditional mean, we will focus the analysis on the estimates for the conditional volatility. Additionally, since \(\eta_{t}\) does not follow a joint multivariate normal distribution, we use the Quasi-MLE (QMLE) estimators.

  7. In fact, as the assumption of constant conditional correlations is maintained in all the estimated models, the respective matrices can be compared. Overall, the correlations between the conditional shocks for all specifications do not seem to differ substantially from one another.

  8. As argued by Cappiello et al. (2006), despite being ideal to test each series for a break at all points in time, this procedure is infeasible, whereby it is usual to choose a specific date for this purpose. In order to avoid this process, and in spirit of Blanchard and Perotti (2002), we discard the possible existence of structural breaks occurring in a stationary GARCH process by verifying that the squared residuals from the AG-DCC GARCH model do not lie outside the interval given by their corresponding mean plus/minus 2 standard deviations.

  9. The appropriate number of lags for the VAR model is determined by minimizing the SBC and, similarly to Diebold and Yilmaz (2012), we use a 10 step-ahead forecast error variance.

References

  • Abbassi, P., & Schnabel, I. (2009). Contagion among interbank money markets during the subprime crisis (Working Paper). University of Mainz.

  • Antonakakis, N. (2012). Exchange return co-movements and volatility spillovers before and after the introduction of euro. Journal of International Financial Markets, Institutions and Money, 22(5), 1091–1109.

    Article  Google Scholar 

  • Blanchard, O., & Perotti, R. (2002). An empirical characterization of the dynamic effects of changes in government spending and taxes on output. Quarterly Journal of Economics, 107(4), 1329–1368.

    Article  Google Scholar 

  • Bollerslev, T. (1986). Generalised autoregressive conditional heteroskedasticity. Journal of Econometrics, 31(3), 307–327.

    Article  Google Scholar 

  • Bollerslev, T. (1990). Modelling the coherence in short-run nominal exchange rate: A multivariate generalized ARCH approach. Review of Economics and Statistics, 72(3), 498–505.

    Article  Google Scholar 

  • Bollerslev, T., Chou, R. Y., & Kroner, K. F. (1992). ARCH modelling in finance: A review of the theory and empirical evidence. Journal of Econometrics, 52(1–2), 5–59.

    Article  Google Scholar 

  • Brunnermeier, M. (2009). Deciphering the liquidity and credit crunch 2007–2008. Journal of Economic Perspectives, 23(1), 77–100.

    Article  Google Scholar 

  • Cappiello, L., Engle, R. F., & Sheppard, K. (2006). Asymmetric dynamics in the correlations of global equity and bond returns. Journal of Financial Econometrics, 4(4), 537–572.

    Article  Google Scholar 

  • Dickey, D., & Fuller, W. (1981). Likelihood ratio statistic for autoregressive times series with a unit root. Econometrica, 49(4), 1057–1072.

    Article  Google Scholar 

  • Diebold, F. X., & Yilmaz, K. (2009). Measuring financial asset return and volatility spillovers, with application to global equity markets. Economic Journal, 119(534), 158–171.

    Article  Google Scholar 

  • Diebold, F. X., & Yilmaz, K. (2012). Better to give than to receive: Predictive directional measurement of volatility spillovers. International Journal of Forecasting, 28(1), 57–66.

    Article  Google Scholar 

  • Diebold, F. X., & Yilmaz, K. (2014). On the network topology of variance decompositions: Measuring the connectedness of financial firms. Journal of Econometrics, 182(1), 119–134.

    Article  Google Scholar 

  • Ebrahim, S. K. (2000). Volatility transmission between foreign exchange and money markets (Working Paper No. 200-16). Bank of Canada.

  • Engle, R. F. (1982). Autoregressive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation. Econometrica, 50(4), 987–1007.

    Article  Google Scholar 

  • Engle, R. F. (2002). Dynamic conditional correlation: A new simple class of multivariate GARCH models. Journal of Business and Economic Statistics, 20(3), 339–350.

    Article  Google Scholar 

  • Fengler, M., & Gisler, K. (2015). A variance spillover analysis without covariances: What do we miss. Journal of International Money and Finance, 51(1), 174–195.

    Article  Google Scholar 

  • Gefang, D., Koop, G., & Potter, S. (2011). Understanding liquidity and credit risks in the financial crisis (Working Papers No. 1114). University of Strathclyde Business School.

  • Glosten, L., Jagannathan, R., & Runkle, D. (1993). On the relation between the expected value and volatility of nominal excess return on stocks. The Journal of Finance, 48(5), 1779–1801.

    Article  Google Scholar 

  • Haß, L. H., Koziol, C., & Schweizer, D. (2014). What drives contagion in financial markets? Liquidity effects versus information spill-over. European Financial Management, 20(3), 548–573.

    Article  Google Scholar 

  • Hosking, J. M. R. (1981). Equivalent forms of the multivariate portmanteau statistic. Journal of the Royal Statistical Society B, 43(2), 261–262.

    Google Scholar 

  • Hui, C., Chang, T., & Lo, C. (2013). Using interest rate derivative prices to estimate LIBOR-OIS spread dynamics and systemic funding liquidity shock probabilities. Asian-Pacific Financial Markets, 20(2), 131–146.

    Article  Google Scholar 

  • Ji, P. I. (2012). Time-varying financial stress linkages: Evidence from the LIBOR-OIS spreads. Journal of International Financial Markets, Institutions and Money, 22(4), 647–657.

    Article  Google Scholar 

  • Kliesen, K. L., Owyang, M. T., & Vermann, E. K. (2012). Disentangling diverse measures: A survey of financial stress indexes. Federal Reserve Bank of St. Louis Review, 94(5), 369–397.

    Google Scholar 

  • Koop, G., Pesaran, M. H., & Potter, S. M. (1996). Impulse response analysis in non-linear multivariate models. Journal of Econometrics, 74(1), 119–147.

    Article  Google Scholar 

  • Kwiatkowski, D., Philips, P., Schmidt, P., & Shin, W. (1992). Testing the null hypothesis stationarity against the alternative of a unit root: How sure are we that economic time series have a unit root? Journal of Econometrics, 54(1–3), 159–178.

    Article  Google Scholar 

  • Ling, S., & McAleer, M. (2003). Asymptotic theory for a vector ARMA-GARCH model. Econometric Theory, 19, 278–308.

    Google Scholar 

  • Longstaff, F. A. (2010). The subprime credit crisis and contagion in financial markets. Journal of Financial Economics, 97(3), 436–450.

    Article  Google Scholar 

  • McAleer, M., Chan, F., & Marinova, D. (2007). An econometric analysis of asymmetric volatility: Theory and application to patents. Journal of Econometrics, 139(2), 259–284.

    Article  Google Scholar 

  • McAleer, M., Hoti, S., & Chan, F. (2009). Structure and asymptotic theory for multivariate asymmetric conditional volatility. Econometric Reviews, 28(5), 422–440.

    Article  Google Scholar 

  • McAndrews, J., Sarkar, A., & Wang, Z. (2008). The effect of the term auction facility on the London inter-bank offered rate. Staff Report No. 335, Federal Reserve Bank of New York.

  • Memmel, C., & Sachs, A. (2013). Contagion in the interbank market and its determinants. Journal of Financial Stability, 9(1), 46–54.

    Article  Google Scholar 

  • Michaud, F., & Upper, C. (2008). What drives interest rates? Evidence from the Libor panel. BIS Quarterly Review, March, 47–58.

  • Pesaran, M. H., & Shin, Y. (1998). Generalized impulse response analysis in linear multivariate models. Economics Letters, 58(1), 17–29.

    Article  Google Scholar 

  • Sack, B., & Meyer, L. (2008). TAF and liquidity policies: Keeping Libor down. Macroeconomic Advisors.

  • Sengupta, R., & Tam, Y. (2008). The LIBOR-OIS spread as a summary indicator. Monetary Trends Nov. 25, Federal Reserve Bank of St. Louis.

  • Tamakoshi, G., & Hamori, S. (2013). On the time-varying linkages among the london interbank offer rates for major European currencies. International Journal of Financial Research, 4(1), 46–53.

    Google Scholar 

  • Tamakoshi, G., & Hamori, S. (2014). On cross-currency transmissions between US dollar and euro LIBOR-OIS spreads. Research in International Business and Finance, 30(C), 83–90.

    Article  Google Scholar 

  • Taylor, J. B., & Williams, J. C. (2009). A black swan in the money market. American Economic Journal: Macroeconomics, 1(1), 58–83.

    Google Scholar 

  • Tse, Y. K. (2000). A test for constant correlations in a multivariate GARCH model. Journal of Econometrics, 98(1), 107–127.

    Article  Google Scholar 

  • van Horen, N., Jager, H., & Klaassen, F. (2006). Foreign exchange market contagion in the Asian crisis: A regression-based approach. Review of World Economics, 142(2), 374–401.

    Article  Google Scholar 

Download references

Acknowledgements

We thank Editor Cédric Tille and two anonymous reviewers for their comments and suggestions. All remaining errors are our own.

Disclaimer

The views expressed are those of the authors and do not necessarily represent those of the Banco de Portugal or the Eurosystem.

Author information

Authors and Affiliations

  1. Economics and Research Department, Banco de Portugal, Av. Almirante Reis, 71, 6th floor, 1150-012, Lisbon, Portugal

    Pedro Pires Ribeiro

  2. Instituto Universitário de Lisboa, ISCTE–IUL, UNIDE, Complexo INDEG/ISCTE, Av. Prof. Aníbal Bettencourt, 1600-189, Lisbon, Portugal

    Pedro Pires Ribeiro & José Dias Curto

Authors
  1. Pedro Pires Ribeiro
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. José Dias Curto
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to José Dias Curto.

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ribeiro, P.P., Curto, J.D. Volatility spillover effects in interbank money markets. Rev World Econ 153, 105–136 (2017). https://doi.org/10.1007/s10290-016-0268-7

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10290-016-0268-7

Keywords

JEL Classification

Search

Navigation