A tail-revisited Markowitz mean-variance approach and a portfolio network centrality

Abstract

A measure for portfolio risk management is proposed by extending the Markowitz mean-variance approach to include the left-hand tail effects of asset returns. Two risk dimensions are captured: asset covariance risk along risk in left-hand tail similarity and volatility. The key ingredient is an informative set on the left-hand tail distributions of asset returns obtained by an adaptive clustering procedure. This set allows a left tail similarity and left tail volatility to be defined, thereby providing a definition for the left-tail-covariance-like matrix. The convex combination of the two covariance matrices generates a “two-dimensional” risk that, when applied to portfolio selection, provides a measure of its systemic vulnerability due to the asset centrality. This is done by simply associating a suitable node-weighted network with the portfolio. Higher values of this risk indicate an asset allocation suffering from too much exposure to volatile assets whose return dynamics behave too similarly in left-hand tail distributions and/or co-movements, as well as being too connected to each other. Minimizing these combined risks reduces losses and increases profits, with a low variability in the profit and loss distribution. The portfolio selection compares favorably with some competing approaches. An empirical analysis is made using exchange traded fund prices over the period January 2006–February 2018.

1 Introduction

The mean variance approach proposed by Markowitz (1952) to measure portfolio risk does not account for asymmetry in the risk. This is due to the fact that covariance is a measure of portfolio risk based on moments and, as consequence, does not distinguish downside from upside risk. The quantile-based tail measures—value-at-risk (Var), expected shortfall (ES), extreme downside correlations (EDC) and p-tail risk (see, for example (Liu and Wang 2021; Harris et al. 2019))—overcome the limitation of covariance in that they are able to capture the downside risk. However, their main drawback is that they are rather insensitive to the shape of the tail distribution since they strongly depend on the a priori choice of the confidence level and/or quantiles, thereby accounting mainly for the frequency of the realizations (not their values) (Kuan et al. 2009).

In contrast to quantile-based approaches, the extreme downside hedge (EDH) (Harris et al. 2019) is estimated by regressing asset returns on some measure of market tail risk. The latter, however, suffers from the above-mentioned drawback. Nevertheless, this approach is an attempt to use the values of asset returns to measure the tail risk.

In this paper, we propose a further attempt in this direction. We introduce a new variability measure for left-hand tail risk that overcomes the mentioned drawback; it is based on the stratification procedure by Mariani et al. (2020).

This measure has the advantage that it is defined endogenously, without any a priori choice, and it captures risk from the asset volatility and co-movements as well as from the left-hand tail distribution of the asset returns, while preserving an elementary expression. According to the interpretation proposed in Diebold and Yılmaz (2014), this measure of tail risk can be read as a measure of vulnerability of the portfolio to volatility shocks that hit their assets.

In detail, we adapt the procedure in Mariani et al. (2020) to the gross returns to identify a new informative set of parameters for each asset time series. This is done by implementing an adaptive algorithm that identifies sub-groups of gross returns at each iteration by approximating their distribution with a sequence of two-component log-normal mixtures. These sub-groups are formed when a “significant” change in the mixture distribution below the median of the asset returns occurs; their boundary is called the “change point” of the mixture. The procedure ends when no further change points are observed. The result is a new informative data set which includes, among others, the parameters of the leftmost mixture distributions and the change points of all the asset time series analyzed. The assumptions about the sample size and gross returns are the same as those required by the expectation maximization method for convergence when applied to log-normal mixtures (see Yang and Chen 1998).

The informative set is then applied to asset classification via a standard clustering procedure mainly to test its ability to identify asset classes. Next, it is used to define the left-tail-covariance-like matrix via the cosine similarity and the new variability measure of portfolio risk. The off-diagonal entries of the left-tail-correlation-like matrix are computed as the scalar product of the normalized vectors defining the two assets in the informative set. This left-tail-correlation-like matrix is a positive semidefinite matrix by construction.

The left tail volatility is defined as the product of two numbers: the volatility of the leftmost component of the log-normal mixture obtained in the first iteration of the adaptive clustering procedure; and the odds ratio of the a priori probability of belonging to the leftmost component of the log-normal mixture. The left-tail-covariance-like matrix is therefore computed by pre-multiplying and post-multiplying the left-tail-correlation-like matrix by the diagonal matrix containing the left tail volatilities of the asset returns.

According to the definition by Furman et al. (2017), Gardes and Girard (2021), we prove that the proposed left tail volatility is a variability measure in the left tail of the asset log-return distribution, while the portfolio risk defined via the left-tail covariance-like matrix is a variability measure in the left tail of the portfolio distribution.

The convex combination of the covariance and left-tail-covariance-like matrices allows for a revisited Markowitz portfolio selection that is able to control two dimensions of risk: similarity and variability in time, as measured by the covariance matrix, and similarity and variability in shape, as measured by the left-tail-covariance-like matrix.

Recent literature on financial time series has investigated techniques to exploit clustering information for developing a new approach to portfolio selection [see, among others, Puerto et al. 2020; Mantegna 1999; Onnela et al. 2003a, b; Bonanno et al. 2004; Wang et al. 2018]. The idea underlying this approach is to substitute the original correlation matrix of the classical Markowitz model with an ultrametric correlation-based clustering matrix with the twofold objective of filtering the correlation matrix and improve the portfolio robustness to measurement noise. Among others, (Giudici and Polinesi 2019) exploited information included in the correlation matrices of crypto price exchanges to detect the hierarchical organization of stocks in the financial market, while (Billio et al. 2006; Billio and Caporin 2009) had previously proposed a flexible dynamic conditional correlation model based on the dynamic conditional correlation model by Engle and Sheppard (2001), Engle (2002). Nonlinear correlations were used by Baitinger and Papenbrock (2017), Miccichè et al. (2003), Hartman and Hlinka (2018), Durante et al. (2014), Abedifar et al. (2017) employed a graphical network model based on conditional independence relationships described by partial correlations. Clustering procedures that capture lower tail dependence between assets were considered in Durante et al. (2015), De Luca and Zuccolotto (2011). Specifically, Durante et al. (2015) computed the dissimilarity matrix using the coefficients obtained via a non-parametric estimator of tail dependence between assets, and De Luca and Zuccolotto (2011) introduced a similarity measure based on tail dependence coefficients calculated via a parametric approach. Moreover, Liu et al. (2018) proposed a clustering based on the coefficients of maximum tail dependence introduced by Furman et al. (2015). The recent study by Paraschiv et al. (2020) reveals that for a realistic stress test, special attention should be given to tail risk in individual returns and also tail correlations.

Another contribution of this paper is the interpretation of the proposed portfolio risk as the weighted average of the centralities of a suitably defined node-weighted network. Specifically, we relate the portfolio to a recently introduced network called node-weighted network, which has non-uniform weights on both edges and nodes (see Abbasi and Hossain 2013; Wiedermann et al. 2013). The nodes of the network are weighted assets and the edges linking two nodes are weighted with the entry of the convex combination of the covariance and left-tail-covariance-like matrices corresponding to the two assets (i.e., nodes). This allows asset risk centrality to be defined according to the node-weighted closeness/harmonic centrality proposed in Singh et al. (2020). Hence, minimizing the portfolio risk centrality makes the portfolio resilient to volatility shocks in the financial market while limiting the variability in the profit and loss distribution.

To the best of our knowledge, this interpretation is an additional contribution of the paper. In fact, only recently have researchers modeled the financial market as a weighted network with assets as nodes and edges representing relationships between assets. Far from being exhaustive, we cite the correlation-based networks of Mantegna (1999), Isogai (2016) and Puerto et al. (2020), weighted networks based on interaction measures such as the Granger causality network by Billio et al. (2006), the network incorporating tail risk by Chen and Tao (2020), Ahelegbey et al. (2021), Bayesian graph-based approach of Ahelegbey et al. (2016), and the variance decomposition network of Diebold and Yılmaz (2014), Giudici and Pagnottoni (2020).

Following the idea of a unified approach to network analysis and portfolio selection, Diebold and Yılmaz (2014), Peralta and Zareei (2016) investigated the relationship between portfolios and the associated network. Specifically, (Diebold and Yılmaz 2014) used the node centrality to measure the systemic vulnerability of a network. Peralta and Zareei (2016) studied how optimal weights in the Markowitz portfolio affect node centralities in a financial market network, while concluding that portfolio diversification avoids the allocation of wealth towards assets with high eigenvalue centrality. An initial attempt to interpret the Markowitz portfolio through a node-weighted network can be found in Cerqueti and Lupi (2017), where the weights of the nodes and edges are, respectively, the expected values of the asset returns and the covariance weighted for the related shares in the portfolio.

It is worth noting that the portfolio network also offers new insight into the Markowitz portfolio risk as a measure of the vulnerability of the portfolio to volatility shocks. The idea of correcting traditional models to define more general models is a powerful tool which is increasingly used in many contexts. For example, in Mariani et al. (2019), the Merton portfolio model was generalized to account for market friction, which is done simply by reformulating the frictionless Merton problem for corrected price dynamics. The conditional value-of-return (CVoR) portfolio of Bodnar et al. (2021), solely constructed from quantile-based measures, is also connected to the Merton model. Another generalization is the data-driven portfolio framework by Torri et al. (2019) based on two regularization methods, glasso and tlasso, that provide sparse estimates of the precision matrix, i.e. the inverse of the covariance matrix.

The remainder of this paper is organized as follows. Section 2 introduces the formulation of the adaptive mixture-based clustering method and the left-tail-covariance-like matrix. Section 3 presents the new portfolio risk as a variability measure and its interpretation as a weighted average of node centralities. Section 4 is devoted to presenting the data set used in this study and a discussion of the results. Specifically, the proposed strategy is validated on the observed prices of a set of exchange-traded funds (ETFs) representative of the assets traded via robot advisors from January 2006 to February 2018. Section 5 draws some conclusions. The Appendix collects the proofs of the main results. An online appendix illustrates a further empirical analysis using 64 equity ETFs.

2 Left tail informative set and the left-tail-covariance-like matrix

2.1 Method to determine the main features of the left-hand tail distribution

In this section, we illustrate how the recent stratification procedure applied to household incomes by Mariani et al. (2020) can be adapted to analyze the left-hand tail distribution of assets.

Bearing in mind that the procedure from Mariani et al. (2020) works on cross-sectional data, the first point to address is the factor corresponding to household income in our procedure. In our setting, incomes correspond to gross returns, that is, the exponential of the asset log-returns (or returns for short) of the price time series considered. Let $N_A>0$ be the number of assets. For $i=1,2,\ldots ,N_A$, the gross return associated with the i-th asset at time t is denoted by $y_{t,i}$ and reads

$$\begin{aligned} y_{t,i}= \exp {\left\{ \log {\left( \frac{p_{t,i}}{p_{t-\varDelta t,i}}\right) }\right\} }=\frac{p_{t,i}}{p_{t-\varDelta t,i}}, \, i=1,2,\ldots ,N_A\,, \end{aligned}$$

(1)

where $p_{t,i}$ represents the daily price of the i-th asset at time t, and $\varDelta t$ is the time step at which the prices are observed. The gross returns (1) represent the scaling factor of an investment in the asset at time t. Their use is advantageous in several ways. First, they are positive but broadly related to asset returns; second, they are concentrated around 1; and third, the gross returns of assets belonging to a very different asset class show constant behavior over time, making them attractive candidates for stationary autoregressive (AR) processes (see Feng et al. 2016). Since the stratification procedure works the same way for each financial asset i, we drop the subscript i and, in the remainder of this section, we denote the gross return at time $t=t_j=j\varDelta t$, with the simplified notation $y_j$, $j=1,2,\ldots ,n$.

We assume that gross returns of the observed prices belong to a price population composed of a collection of groups, each with a homogeneous distribution, bearing in mind that the term “price group” identifies the set of prices with homogeneous distribution. In the rest of paper, we simply refer to the gross return using the term “return".

Starting with the observed returns, the adaptive clustering procedure proceeds iteratively, splitting a suitably selected subset of the observed returns into two disjoint groups at each iteration. The density function of the selected group is drawn from a mixture of two log-normal distributions and the split looks for a return where a “significant” change in the mixture distribution is observed. This value is called “change point".

Specifically, in its first iteration, the procedure starts with the set of all returns ${\mathcal {S}}_n=\{y_1,y_2,\dots ,y_n\}$ ranked in ascending order, and a threshold value $a^1$ (i.e., the first change point) is identified to split ${\mathcal {S}}_n$ into two disjoint groups: the left group ${\mathcal {K}}_1=\{y\in {\mathcal {S}}_n\ \wedge \ y\in (0,a^1]\}$, composed of returns smaller than or equal to the threshold value, and a right group $\mathcal R_1={\mathcal {S}}_n\backslash {\mathcal {K}}_1,$ composed of returns larger than the threshold value. In the second iteration, the procedure considers the subset of ${\mathcal {S}}_n$, ${\mathcal {R}}_1$, obtained in the first iteration. It identifies a new threshold value $a^2>a^1$, and splits ${\mathcal {R}}_1$ into two disjoint groups: the left group ${\mathcal {K}}_2=\{y\in {\mathcal {S}}_n\ \wedge \, y\in (a^1,a^2]\}$ and the right group ${{\mathcal {R}}}_2=\{y\in {\mathcal {S}}_n\ \wedge \ y\in (a^{2},+\infty )\}$. In the k-th iteration, the algorithm proceeds in a similar way by identifying the threshold $a^k$ and dividing the set ${\mathcal {R}}_{k-1}$ into two groups: $\mathcal K_{k}=\{y\in {\mathcal {S}}_n\ \wedge \ y\in (a^{k-1},a^k]\}$ and ${\mathcal {R}}_{k}=\{y\in {\mathcal {S}}_n\ \wedge \ y\in (a^{k},+\infty )\}$.

Going into the details of the threshold computation, we use $g_0(x),$ $x\in {\mathbb {R}}_+,$ to denote the probability density function describing the distribution of the returns in set ${{\mathcal {S}}}_n,$ and $g_k(x)$, $x\in {\mathbb {R}}_+,$ to denote the conditional probability function defined by

$$\begin{aligned} g_k(x)=\frac{g_0\left( x+a^{k-1}\right) }{\displaystyle \int _{a^{k-1}}^{+\infty }g(s)ds}, \quad x\in {\mathbb {R}}_+,\,\,k=1,2,\ldots \,. \end{aligned}$$

(2)

The function $g_k$ is the probability density function associated with the translated return sample $\widetilde{{\mathcal {R}}}_{k-1}=\{x=y-a^{k-1}\, \wedge \, y\in {\mathcal {R}}_{k-1}\}$. We assume that $g_k$ is given by a mixture of two log-normal probability density functions

$$\begin{aligned} g_k(x)=\pi _k f_{1,k}(x)+(1-\pi _k)f_{2,k}(x),\quad x\in {\mathbb {R}}_+, \end{aligned}$$

(3)

where $f_{1,k}(x)$ and $f_{2,k}(x),$ $x\in {\mathbb {R}}_+,$ are the log-normal densities of parameters $\mu _{1,k},$ $\mu _{2,k},$ $\sigma _{1,k},$ $\sigma _{2,k}\in {\mathbb {R}}$ associated with the two mixture components and ${\underline{\varTheta }}_k = (\pi _k , \mu _{1,k} , \mu _{2,k} , \sigma _{1,k} , \sigma _{2,k})^\prime$ is the vector of unknown parameters. Here and in the rest of the paper, we use the superscript $^\prime$ to denote transpose. We assume that $\mu _{1,k}<\mu _{2,k}$, so we refer to $f_{1,k}$ as the first (or left-hand) component of the mixture and $f_{2,k}$ as the second (or right-hand) component since the median of the first component, i.e., $e^{\mu _{1,k}}$, is smaller than the median of the second one, i.e., $e^{\mu _{2,k}}$.

The vector of unknown parameters for the density functions associated with the two mixture components ${\underline{\varTheta }}_k = (\pi _k , \mu _{1,k} , \mu _{2,k} , \sigma _{1,k} , \sigma _{2,k})^\prime$ is estimated using the return in the set ${\mathcal {R}}_{k-1}$ through the expectation maximization (EM) algorithm (see Dempster et al. 1977). Note that $\pi _k\in [0,1]$ is the mixing weight representing the a priori probability that the point $x=y-a^{k-1}$, $y\in {\mathcal {K}}_{k-1},$ belongs to the first component.

At each step, k, the parameter vector ${{\underline{\varTheta }}}_k$ is estimated using the EM algorithm, and the change point of the mixture at the k-th iteration is then determined using the following rule:

$$\begin{aligned} { a^k=\min \{y\in {{\mathcal {R}}}_{k-1}\ \wedge \ \pi _k f_{1,k}(y-a^{k-1})=(1-\pi _k)f_{2,k}(y-a^{k-1})\}}. \end{aligned}$$

(4)

An explicit formula for the change points is

$$\begin{aligned} a^k=\exp \left\{ \min \{\log (a^k_+),\,\log (a^k_-)\}\right\} , \end{aligned}$$

(5)

where $\log (a^k_+),\,\log (a^k_-)$ are given by

$$\begin{aligned} \log (a^k_\pm )=\frac{{\sigma _{1,k}^2\sigma _{2,k}^2}}{\sigma _{2,k}^2-\sigma _{1,k}^2}\left[ \, \left( \frac{\mu _{1,k}}{\sigma _{1,k}^2}-\frac{\mu _{2,k}}{\sigma _{2,k}^2}\right) \pm \sqrt{\varDelta _k}\right] , \end{aligned}$$

with $\varDelta _k$ defined as

$$\begin{aligned} \varDelta _k=&\left( \frac{\mu _{1,k}}{\sigma _{1,k}^2}-\frac{\mu _{2,k}}{\sigma _{2,k}^2}\right) ^2+\left( 2\log \left( \frac{\sigma _{2,k}\pi _k}{\sigma _{1,k}(1-\pi _k)}\right) {-}\left( \frac{\mu _{1,k}}{\sigma _{1,k}}\right) ^2\right. \\ {}&\left. {+}\left( \frac{\mu _{2,k}}{\sigma _{2,k}}\right) ^2\right) \frac{(\sigma _{2,k}^2-\sigma _{1,k}^2)}{{\sigma _{1,k}^2\sigma _{2,k}^2}}. \end{aligned}$$

The change point ${a^k}$ is the frontier of the two groups $\mathcal K_k$ and ${\mathcal {R}}_k$ at the k-th iteration and, broadly speaking, $a^k$ divides the sample into two subsamples with non-homogeneous distributions. The procedure stops when a new $a^k$ cannot be determined (i.e., Eq. (4) does not admit any solution).

Further information computed by the procedure at each iteration is the misidentification error, i.e., the probability of wrongly classifying the returns below the threshold as members of the left group. This misidentification error is associated with the group as a significance level according to the definition in Pittau and Zelli (2014). It is computed as

$$\begin{aligned} F^k_{2}(a^k-a^{k-1}), \end{aligned}$$

(6)

where $F^k_{2}(x)=\int _0^x f_{2,k}(s)ds,$ $x\in {\mathbb {R}}_+,$ is the cumulative distribution function associated with the second component of the mixture. We also compute the probability of wrongly classifying the returns above the threshold as members of the right group, that is,

$$\begin{aligned} 1-F^k_{1}(a^k-a^{k-1}), \end{aligned}$$

(7)

where $F^k_{1}(x)=\int _0^x f_{1,k}(s)ds,$ $x\in {\mathbb {R}}_+,$ is the cumulative distribution function associated with the first component of the mixture. Appendices A and B in Mariani et al. (2020) provide details about the computation of threshold values $\alpha$ and the EM algorithm.

At the end of the adaptive clustering procedure, we compose a new informative data set that includes the vector of parameters ${\underline{\varTheta }}_k,$ $k=1,2,\dots$, the misidentification errors, and change points for each financial asset. For simplicity, we consider the information coming from the first two iterations (i.e., $k=1,2$). This informative set is the crucial element in defining the new portfolio risk; it is detailed in Sect. 2.2.

It is worth noting that the informative set can be computed when two main assumptions are satisfied: a) the gross return distribution can be approximated with a non-trivial two-component log-normal mixture with a change point; and b) the expectation maximization algorithm converges. The first assumption can be tested using, for example, the results in Chen and Li (2009), Chauveau et al. (2019). The assumptions for the EM approach to converge are no time interval with constant prices, no extreme outliers, and a sufficiently large sample size, as detailed in Yang and Chen (1998).

2.2 From the left-tail informative set to the left-tail-covariance-like matrix

In this section, we focus on the meaning of the parameters determined by the above-mentioned procedure.

In the simulation study and empirical analysis, we use a time window of consecutive daily observations covering $N_y$ years for each asset time series $p_{t,i}$, $i=1,2,\ldots ,N_A$, that is, we use the i-th asset prices $p_{t,i},p_{t-1,i},\dots p_{t-N_y+1,i}$ to apply the method described in Sect. 2.1. Specifically, we stop the splitting at the second iteration (i.e., $k=2$) since we are interested in determining the parameters characterizing the leftmost distribution of each asset. Thus, at time t, each asset is identified by the following twelve parameters:

• 1. The change points of the asset return distribution determined in the first two iterations of the procedure described in Sect. 2.1:

  $a^1_{t,i},$ $a^2_{t,i}$: the asset return values that identify the leftmost change point in the distribution of asset returns at time t in the first and in the second iterations of the clustering procedure;

• 2. the parameters (drift and volatility) of the left-hand component of the log-normal mixture in the first two iterations of the procedure described in Sect. 2.1: $\sigma ^1_{1,t,i}$, $\mu ^1_{1,t,i},$ $\sigma ^2_{1,t,i}$, $\mu ^2_{1,t,i}$: parameters of the leftmost component of the log-normal mixture in the first and second iterations of the clustering procedure;

• 3. the complement of the cumulative distribution functions, $1-F^1_{1,t,i}$, $1-F^2_{1,t,i}$, associated with the leftmost component of the mixture in the first and second iterations of the clustering procedure (first kind of error; for more details see (Mariani et al. 2020));

• 4. the cumulative distribution functions associated with the rightmost component of the mixture, $F^1_{2,t,i}$, $F^2_{2,t,j}$, in the first and second iterations of the clustering procedure (second kind error (for more details see Mariani et al. 2020));

• 5. $\pi ^1_{t,i}$, $\pi ^2_{t,i}$: the a priori probabilities associated with the mixture in the first and second iterations of the clustering procedure.

For any time t, the twelve parameters of each asset i,  for $i=1,2,\ldots , N_A,$ are collected in the matrix $X_t\in R^{N_A\times 10}$, that is, the left tail informative set at time t. Specifically, the i-th row of $X_t$ is the vector ${\underline{x}}^\prime _{t,i}=(X_{t,i,1}, X_{t,i,2},\ldots ,X_{t,i,10})$ of the parameters defining the left-hand tail distribution corresponding to the i-th asset, $i=1,2,\ldots , N_A$, that is,

$$\begin{aligned} {\underline{x}}^\prime _{t,i}=&({\tilde{a}}^1_{t,i}, \tilde{a}^2_{t,i},\pi ^1_{t,i},\pi ^2_{t,i}, F^1_{2,t,i}, F^2_{2,t,i}, 1-F^1_{1,t,i}, \ 1-F^2_{1,t,i}, \sigma ^1_{1,t,i}, \sigma ^2_{1,t,i}), \end{aligned}$$

where the quantities ${\tilde{a}}^1_{t,i}$ and ${\tilde{a}}^2_{t,i}$ are given by

$$\begin{aligned} {\tilde{a}}^1_{t,i}=\log a^1_{t,i}-\mu ^1_{1,t,i},\quad \tilde{a}^2_{t,i}=\log a^2_{t,i}-\mu ^2_{1,t,i}. \end{aligned}$$

The matrix $X_t$ can be interpreted as the classical tabular format representation of cases and variables, where the rows are the cases (individuals) and the columns are the variables. As shown in the empirical analysis (see Sect. 4), all variables contained in the matrix $X_t$ are relevant for describing the cases, since by applying the principal component analysis to $X_t,$ we observe that there are 10 factors needed to represent 80% of the total variance. The relevance of the informative set $X_t$ relies on the fact that it allows a covariance-like matrix for the left tail distribution to be introduced.

We detail this point by introducing some notation. For any time t and $i,j=1,2,\ldots ,N_A,$ we denote the return of the asset i at time t with $r_{t,i}=log(y_{t,i}),$ its volatility with $\sigma _{t,i}$ while the correlation coefficient between assets i and j at time t with $\rho _{t,i,j}.$ Additionally we use $C_t=(C_{t,i,j})_{i,j=1,2,\ldots ,N_A}\in {\mathbb {R}}^{N_A\times N_A}$ to denote the covariance matrix at time t and $\varGamma _t=(\varGamma _{t,i,j})_{i,j=1,2,\ldots ,N_A}=(\rho _{t,i,j})_{i,j=1,2,\ldots ,N_A}\in {\mathbb {R}}^{N_A\times N_A}$ the correlation matrix at time t.

We underline that the standard deviation of asset i at time t $\sigma _{t,i}$ in a finite sample can be estimated as the sample standard deviation, i.e., the Euclidean norm of the vector containing deviations from the mean divided by the square root of the sample size. Likewise, the covariance between the i-th and j-th returns, i.e., $C_{t,i,j}=\sigma _{t,i}\rho _{t,i,j}\sigma _{t,j}$, $i\ne j$, is the scalar product between the vectors of the scaled deviations from the mean.

Along these lines (see the Appendix for further details), we define the left-tail-correlation-like matrix ${\overline{\varGamma }}_{t}=({\overline{\varGamma }}_{t,i,j})_{i,j=1,2,\ldots ,N_A}\in {\mathbb {R}}^{N_A\times N_A}$ as follows.

Definition 1

Let assets i and j at time t be identified by their left tail informative set ${\underline{x}}_{t,i}$ and ${\underline{x}}_{t,j}$, respectively. The left tail correlation coefficient between the assets i and j is given by:

$$\begin{aligned} {\overline{\varGamma }}_{t,i,j}={\overline{\rho }}_{t,i,j}= \frac{{\underline{x}}_{t,i}^\prime \,{\underline{x}}_{t,j}}{\Vert {\underline{x}}_{t,i}\Vert \,\Vert {\underline{x}}_{t,j}\Vert }\,, \, i,j=1,2,\ldots ,N_A\,. \end{aligned}$$

(8)

Here and in the rest of the paper, $\Vert {\underline{z}}\Vert$ denotes the Euclidean norm of the vector ${\underline{z}}.$

The left tail correlation coefficient ${\overline{\rho }}_{t,i,j}$ measures the similarity in the left-hand tail distributions of the i-th and j-th assets at time t since it is the cosine of the angle determined by the i-th and j-th row vectors of the informative matrix $X_t$. The left-tail-correlation-like matrix is a similarity matrix in clustering analysis and the distance defined from (8) is very close to the Eisen cosine correlation distance (Eisen et al. 1998) defined as

$$\begin{aligned} d_{i,j}=1-\frac{\left| {\underline{x}}_{t,i}^\prime \,{\underline{x}}_{t,j}\right| }{\Vert {\underline{x}}_{t,i}\Vert \,\Vert {\underline{x}}_{t,j}\Vert }\,, \, i,j=1,2,\ldots ,N_A\,. \end{aligned}$$

(9)

Finally, we define the volatilities of the left-hand tails.

Definition 2

Let asset i be identified by its left tail informative set ${\underline{x}}_{t,i}$. The left tail volatility is defined as

$$\begin{aligned} {\overline{\sigma }}_{t,i}=\sqrt{\frac{\pi ^1_{t,i}}{1-\pi ^1_{t,i}}}\,\,{\sigma }^1_{1,t,i}, \, i=1,2,\ldots ,N_A\,, \end{aligned}$$

(10)

where ${\sigma }^1_{1,t,i}$ is the volatility of the leftmost component of the log-normal mixture that approximates the return distribution. The quantity $\frac{\pi ^1_{t,i}}{1-\pi ^1_{t,i}}$ is an odds ratio that tells us the weight of this mixture component with respect to the other. The larger the value of $\pi ^1_{t,i}$, the higher the role of the leftmost component.

Roughly speaking, the correlation coefficient defined in Definition 1 measures the similarity of the left tail informative sets of the assets considered. Thus, the higher the value of the coefficient, the higher the risk of similar behavior on the left tails of the asset. Allocating assets in portfolios with similarity in their left tails may imply similar reactions to exogenous shocks, thereby increasing exposure to systemic risk (see Balla et al. 2014).

The left tail volatility introduced in Definition 2 is a conditional volatility, ${\sigma }^1_{1,t,i},$ that is, the volatility of the asset log-return, given that the asset return is drawn from the leftmost component of the mixture scaled by the odds ratio. The scaling factor weighs the relevance of the leftmost component of the mixture with respect the rightmost.

Proposition 1

The left tail volatility, ${\overline{\sigma }}_{t,i}$, defined in (10), is a variability measure in the distribution left tail of the i-th asset log return at time t.

See the Appendix for the proof of Proposition 1.

These two ingredients allow us to define the left-tail-covariance-like matrix $\overline{C}_t=(\overline{C}_{t,i,j})_{i,j=1,2,\ldots ,N_A}\in R^{N_A\times N_A}$ as follows.

Definition 3

Given the $N_A$ assets at time t identified by their left tail informative sets ${\underline{x}}_{t,i}$, $i=1,2,\ldots ,N_A$, the left-tail-covariance-like matrix is defined by

$$\begin{aligned} \overline{C}_{t,i,j}={\overline{\sigma }}_{t,i}{\overline{\rho }}_{t,i,j}{\overline{\sigma }}_{t,j}, \, i,j=1,2,\ldots ,N_A\,. \end{aligned}$$

(11)

The matrix $\overline{C}_t$ is a positive semidefinite matrix since it can be rewritten as

$$\begin{aligned} \overline{C}_t={\overline{\varPsi }}_t'{\overline{\varPsi }}_t, \end{aligned}$$

(12)

where ${\overline{\varPsi }}_t$ is the matrix defined by

$$\begin{aligned} {\overline{\varPsi }}_{t,i,j}=\frac{{\overline{\sigma }}_{t,i}}{\Vert {\underline{x}}_{t,j}\Vert }X_{t,i,j},\, i=1,2,\ldots ,N_A\,, j=1,2,\ldots ,10. \end{aligned}$$

(13)

Although the role of the left-tail-correlation-like matrix (8) is intuitive in that it expresses similarity in the information on left tails of the assets, the role of the left-tail-covariance-like matrix (11) in asset allocation processes is not clear. We detail this point in the next section.

3 Two-dimensional risk: covariance and left tail covariance risks

In this section, we define a variability measure (see the Appendix for its definition) that combines the covariance risk and the risk due to the similarity and volatility of the left tails.

As already mentioned, both risks are defined endogenously, that is, they are computed choosing only the number of price observations to use and are expressed with positive semidefinite matrices. We therefore define a two-dimensional risk by means of the convex combination of the two matrices. This definition provides a class of variability measures depending on the coefficient of the convex combination expressing the investor’s propensity for diversification or dissimilarity in tails. A remarkable advantage is that the portfolio selection is carried out solving a linear quadratic optimization problem, in line with the mean-variance approach of Markowitz (1952).

We detail this point by explaining the role of the tail-covariance-like matrix in asset allocation problems. As usual, we view a portfolio as a linear combination of assets whose coefficients (i.e., asset weights) express the percentage of wealth invested in each asset.

Mathematically, we consider the asset returns at a fixed time t as realizations of random variables denoted by $Y_{i}$. We omit the time to keep the presentation simple. The return of the portfolio itself is a random variable given by

$$\begin{aligned} \varPi _{{\underline{w}}}=\sum _{i=1}^{N_A} w_i {\log Y_{i}}, \end{aligned}$$

(14)

where ${\underline{w}}=(w_1,w_2,\ldots ,w_{N_A})^\prime$ denotes the vector of asset weights which are non-negative $w_i\ge 0,$ for $i=1,2,\ldots ,N_A$ (short-selling is not allowed) and sum to one (i.e., $\sum _{i=1}^{N_A} w_i=1$). A very common asset allocation problem is formulated as

$$\begin{aligned}&\min _{{\underline{w}}}R(\varPi _{{\underline{w}}})\,\,\nonumber \\&\sum _{i=1}^{N_A}w_i{\log Y_i}=\overline{y},\,\quad \sum _{i=1}^{N_A}w_i=1,\,\quad w_i\ge 0, \end{aligned}$$

(15)

where $R(\varPi _{{\underline{w}}})$ is a portfolio risk, while $\overline{y}$ is a target constraint for the portfolio return. In the case of Markowitz’s portfolio, the objective function of problem (15) is the portfolio variance, which is expressed as a quadratic form in the weights, allowing for an efficient solution to (15).

We aim to preserve this simplicity while providing a portfolio risk that captures risk in several respects, including too much concentration in one asset-allocation strategy.

3.1 Portfolio selection and node-weighted network

We relate the portfolio to a node-weighted network, i.e., a network with non-uniform weights on the edges and nodes, as recently applied in Abbasi and Hossain (2013).

Specifically, given a weight vector ${\underline{w}}$ and the corresponding portfolio $\varPi _{{\underline{w}}}$, we associate the portfolio with the network $G_{{\underline{w}}}=(V, E,{\underline{w}}),$ where $V=\{1,2,\ldots ,N_A\}$ is the set of labels identifying the assets (i.e., the network nodes), $E=\{(i,j) \ : \ i,j=1,2,\ldots ,N_A\}$ is the set of network edges, and $\underline{w}$ is the vector of asset weights. Note that node self-connections and zero-weights are permitted.

Let $A=(A_{i,j})_{i,j=1,2,\ldots ,N_A}\in {\mathbb {R}}^{N_A\times N_A}$ be the extended adjacency matrix of the network $G_{{\underline{w}}}$ as defined in Wiedermann et al. (2013). We choose the extended adjacency matrix equal to the tail-covariance-like matrix $\overline{C}_t$ in (11). Dropping the subscript t to keep the notation simple, we choose the extended adjacency matrix as

$$\begin{aligned} A_{i,j}=\overline{C}_{i,j}={\overline{\sigma }}_{i}{{\overline{\sigma }}}_{j}{\overline{\rho }}_{i,j}, \ i,j=1,2,\ldots , N_A, \end{aligned}$$

(16)

where ${\overline{\sigma }}_i$ ${\overline{\sigma }}_j$ are the left tail volatilities of the i-th and j-th assets. We remember that the coefficient ${{\overline{\rho }}}_{i,j}$ in (16) is a cosine similarity between the left tail informative sets of the i-th and j-th assets and that the tail-covariance-like matrix, $\overline{C}$, is a positive semidefinite matrix.

We now generalize a suitable centrality measure to a node-weighted network following the approach proposed in Singh et al. (2020), Wiedermann et al. (2013). Specifically, according to the definition of node-weighted closeness/harmonic centrality proposed in Singh et al. (2020), we define the risk centrality of the i-th asset in the network $G_{{\underline{w}}}$ with extended adjacency matrix in (16) as

$$\begin{aligned} RC_{{\underline{w}}\,,{\overline{C}}}(i)=\sum _{j=1}^{N_A} w_j\overline{C}_{i,j},\ i=1,2,\ldots ,N_A. \end{aligned}$$

(17)

The quantity in (17) assigns a high risk centrality to assets with a large weight in the portfolio and a highly volatile left-hand tail while also being similar to assets with large portfolio weights and highly volatile left-hand tails. Here, two assets are similar if the cosine similarity between their left tail informative vectors is large. The use of weighted centrality for an asset in a portfolio is very natural since the centrality must include only assets that actually belong to the portfolio (i.e., nodes with non-zero weights), while weighing the influence of each asset via its own weight in the portfolio.

Starting with the tail risk centrality of their components, we define the left tail risk centrality associated with the portfolio $\varPi _{{\underline{w}}}$ as

$$\begin{aligned} r(\varPi _{{\underline{w}}}\,,{\overline{C}})=\sum _{i=1}^{N_A} w_i RC_{{\underline{w}}\,,{\overline{C}}}(i)={\underline{w}}^\prime \overline{C}{\underline{w}}. \end{aligned}$$

(18)

The adjective “left tail” is related to the choice of $\overline{C}$ as an adjacency matrix. It is worth noting that in choosing the covariance matrix $C=(C_{i,j})_{i,j=1,2,\ldots , N_A}$ as the extended adjacency matrix of the node-weighted centrality, the risk centrality of the i-th asset in the Markowitz portfolio is

$$\begin{aligned} RC_{{\underline{w}}\,,C}(i)=\sum _{j=1}^{N_A} w_j C_{i,j},\ i=1,2,\ldots , N_A, \end{aligned}$$

(19)

and the risk centrality associated with the portfolio is

$$\begin{aligned} r(\varPi _{{\underline{w}}}\,,C)=\sum _{i=1}^m w_i RC_{\underline{w}\,,C}(i)={\underline{w}}^\prime C{\underline{w}}=Var(\varPi _{{\underline{w}}}). \end{aligned}$$

(20)

That is, the risk centrality of the network associated with the Markowitz portfolio is the portfolio variance.

Proposition 2

Let $\underline{w}=(w_1,w_2,\ldots ,w_{N_A})^\prime$ be any vector of non-negative constants which sum to one and let ${\overline{C}}$ be the left-tail-covariance-like matrix in (3), then the left tail risk centrality $r(\varPi _{{\underline{w}}},{\overline{C}})$ is a variability measure in the left tail of portfolio distribution at time t.

See the Appendix for the proof of Proposition 2.

These findings suggest a reinterpretation of the optimal Markowitz portfolio as the portfolio that minimizes the weighted risk centralities of the allocated assets. Thus, choosing C as the extended adjacency matrix (see (20)) is equivalent to changing the way in which the risk is measured, because (20) assigns more risk to assets positively covariant with a high level of volatility. In other words, in (17), risk refers to the volatile, linearly dependent left-hand tails, while in (20), risk refers to the covariance between the asset returns. In analogy with the covariance matrix C, we therefore call $\overline{C}$ the left-tail-covariance-like matrix.

In order to account for the two dimensions of risk expressed by (17) and (20), we introduce a variability measure given by the convex combination of the variability measures in (17), (20), that is,

$$\begin{aligned} r_{\alpha }(\varPi _{{\underline{w}}})=\alpha r(\varPi _{\underline{w}},C)+(1-\alpha ) r(\varPi _{{\underline{w}}},\overline{C}),\,\,0\le \alpha \le 1. \end{aligned}$$

(21)

It is easy to see that

$$\begin{aligned} r_{\alpha }(\varPi _{{\underline{w}}})=r(\varPi _{\underline{w}}\,,C_{\alpha })={\underline{w}}^\prime C_{\alpha }{\underline{w}}, \end{aligned}$$

(22)

where the extended adjacency matrix corresponding to the new variability measure (21) is given by the convex combination of the covariance matrix C and the left-tail-covariance-like matrix ${\overline{C}},$ i.e.,

$$\begin{aligned} C_{\alpha }=\alpha C+(1-\alpha )\overline{C},\,\, 0\le \alpha \le 1. \end{aligned}$$

(23)

According to the interpretation proposed in Diebold and Yılmaz (2014), the matrix $C_{\alpha }$ can be read as a connectedness table and the measure in (21) can be read as a measure of portfolio vulnerability to volatility shocks that hit the assets. In fact, in the connectedness table, the presence of assets with high volatility and high left tail volatility and with high left-hand tail similarity and covariance may imply portfolio vulnerability since a market shock on one asset may cause a cascade.

By minimizing the variability measure in (21) with respect to ${\underline{w}}$ for a given $\alpha$, $0\le \alpha \le 1$, we aim to diversify the portfolio and also reduce the left-hand tail volatility and similarity. As stressed above, like the Markowitz portfolio selection problem, the variability measure $r_\alpha$ is expressed as a quadratic form involving a positive semidefinite matrix (i.e., $C_\alpha$ in Eq. (23)), thereby allowing for a closed-form minimum of $r_\alpha .$

4 Empirical analysis

In this section, we provide empirical evidence that the asset allocation obtained by minimizing the two-dimensional risk defined in Sect. 3 truly acts to increase profits and reduce losses. To this end, we use a dataset of 3173 daily observations of 44 ETF (see Sect. 4.1). We show that the left tail informative set obtained from this dataset is reliable since every variable used to describe the asset tails is weakly or not correlated each other, and the dataset allows us to identify the investment class of the assets using a clustering method. Finally, in Sect. 4.3, we compare portfolio performances when the asset allocation strategy considers different values of $\alpha$ according to Eq. (21).

4.1 Data description

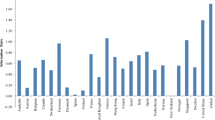
We consider a data set composed of 44 daily ETF price time series traded over the period January 2006 to February 2018 (for $N=3173$ total observations). Table 1 shows the ETFs classified into 5 asset classes according to the classification per investment class provided by the Italian Stock Exchange. Summary statistics of prices for the asset classes—mean, variance, excess kurtosis, and skewness—are described in Table 1. Note that the mean value is different for each asset class as are the values of standard deviation: Emerging equity ETFs are more remunerative and volatile with respect to other classes considered in the analysis.

Table 1 ETF price summary statistics. Summary statistics for exchange traded funds: mean, standard deviation, excess kurtosis, and skewness

Table 2 describes summary statistics for gross returns in Eq. (1). Mean values are equal to 1 and standard deviations are around 0 regardless of the investment class considered.

Table 2 ETF exponential logarithmic centered return summary statistics. Summary statistics for Exchange Traded Funds: mean, standard deviation, excess of kurtosis, and skewness

Figure 1 shows summary plots for each ETF price belonging to the specific investment class. This shows that especially for emerging market classes, ETF prices can be quite different and it explains the higher values of standard deviation in Table 1.

Fig. 1

Summary plots for ETF prices in the specific investment class

Figure 2 shows summary plots for gross returns computed according to Eq. (1). These scaled ETF values allow us to remove the seasonal trend typical of long time-series data.

Fig. 2

Summary plots for ETF gross returns in the specific investment class

4.2 How is the left tail informative set reliable?

We start by motivating our choice to consider all variables in the left tail informative set (see Sect. 2) by implementing the principal component analysis. The results are shown in Table 3.

Table 3 Principal components analysis. Importance of components of left tail informative sets

Note that in Table 3, ten factors are needed to best represent the total variance. Indeed, each component contributes a small amount of variance (about 10%). We have shown that all variables in the left tail informative set contribute to the total variance of the asset returns, so we assess the performance of the left tail informative set when used to determine asset classes. Figure 3 shows the dendrogram according to the complete linkage clustering applied to the Euclidean distance computed from the informative set:

$$\begin{aligned} \overline{d}_{i,j}=({\underline{x}}_i-{\underline{x}}_j)^\prime ({\underline{x}}_i-{\underline{x}}_j),\, i,j=1,2,\ldots ,N_A. \end{aligned}$$

(24)

Despite its sensitivity to outliers, complete linkage clustering avoids the chaining effect suffered by single linkage clustering, so it is usually preferred to single linkage. The results relative to the accuracy of the analysis are shown in Table 4. For the sake of simplicity, emerging classes (Asia and America) were incorporated into a single class (emerging).

Fig. 3

Dendrogram associated with complete linkage clustering based on distance (24)

Table 4 Classification resulting from the complete linkage clustering based on distance (24) (rows and columns represent, respectively, the cluster group c and the asset class)

Figure 3 and Table 4 show that cluster analysis on the informative set correctly classifies ETFs based on their specific investment class. The accuracy is $88.64\%$ with five errors in the classification: two aggregate bonds were classified as corporate bonds and three emerging assets as commodities. The same level of accuracy can be achieved if cluster analysis is applied to the informative set computed by removing outliers through trimming and winsorization using a threshold of 0.005¹.

The accuracy obtained in Table 4 can be improved by choosing the distance

$$\begin{aligned} \tilde{d}_{i,j}=\sqrt{2-2\rho _{i,j}} \end{aligned}$$

(25)

as the distance measure of the clustering procedure, where $\rho _{i,j}$ is the correlation coefficient associated with the i-th and j-th asset returns. The distance (25) is the metric distance based on the correlation proposed by Mantegna in Mantegna (1997). The latter ranges from 0 to 2,  taking the value $\sqrt{2}$ for uncorrelated assets. When the clustering is based on distance (25), the empirical investigation indicates that the single linkage is the most appropriate clustering method (Stanley and Mantegna 2000). Table 5 shows the results relative to the accuracy of single linkage clustering applied to the metric distance (25).

Table 5 Classification resulting from single linkage clustering based on distance (25) (rows and columns represent cluster group c and asset class, respectively)

We observe that a single linkage with distance (25) achieves an accuracy of 95.45%, higher than the level obtained with the informative set (88.64%). In fact, in Table 5, only the two aggregate bonds are misclassified as corporate ones. This misclassification is probably due to low correlations with the other aggregate bond returns and strong correlations with the corporate bond returns. Moreover, it is worth noting that the probability densities of the misclassified aggregate bond returns are also closer to those of corporate bond returns than to those of the other aggregate bond returns. Specifically, they have smaller standard deviations (equal to 0.0019 and 0.0015) than the mean standard deviation of the aggregate bond returns (i.e., 0.003, see Table 2) and comparable to those of the corporate bond returns (i.e., 0.002, see Table 2). This suggests that the informative set on the left-hand tail needs to be combined with the information on asset covariances to obtain complete information on asset returns. To support this intuition, we apply single linkage clustering to the correlation matrix obtained from $C_\alpha$, $\alpha \in [0,1]$ given in Eq. (23). We recall that the matrix $C_\alpha$ equals the covariance matrix for $\alpha =1$ and the left-tail-covariance-like matrix for $\alpha =0$.

We apply single linkage clustering based on distance (25) with the correlation coefficients $\rho _{\alpha ,i,j}=C_{\alpha ,i,j}/\sqrt{C_{\alpha ,i,i}C_{\alpha ,j,j}}$, $i,j,=1,2,\ldots ,N_A$, for $\alpha =0.0005*k$, $k=1,2,\ldots ,2000$. We observe that an accuracy of 95.45% is obtained for any $\alpha \ge 0.001$. Table 6 shows the accuracy of the single linkage classification for $\alpha =0.001$. This result has two main implications. First, the sole use of the left-tail-covariance-like matrix is not enough to capture all the crucial information on asset riskiness. Second, it is sufficient to include a small contribution from the covariance matrix (i.e., $\alpha =0.001$) to capture the information for a correct classification.

Table 6 Classification resulting from the single linkage clustering based on distance (25) with correlation coefficients $\rho _{\alpha ,i,j}$, $\alpha =0.001$ (rows and columns represent cluster group c and asset class, respectively)

From Table 6, we note that a convex combination for a small value of $\alpha$ provides the same classification accuracy as $\alpha =1$ (see Table 5). This highlights how the choice of $\alpha$ plays a crucial role in both clustering and asset allocation strategies, as explained in Sect. 4.3.

4.3 Asset allocation

In this section, we solve the following Markowitz-like asset allocation problem:

$$\begin{aligned}&\min _{{\underline{w}}}{\underline{w}}^\prime C_{\alpha }{\underline{w}},\quad 0\le \alpha \le 1, \nonumber \\&\sum _{i=1}^{N_A}w_i{\log Y_i}=\overline{y},\quad \sum _{i=1}^{N_A}w_i=1,\quad w_i\ge 0, \end{aligned}$$

(26)

where $Y_i$, $i=1,2,\ldots ,N_A$ refers to the 44 ETFs gross returns (i.e., $N_A=44$) and $\overline{y}$ is chosen to be the average of the returns over the time period considered.

The coefficient $\alpha$ allows investors to choose a risk profile by suitably weighting the two risk dimensions of interest: asset covariance risk with left tail similarity and volatility risk (see Eq. (23)).

We compare asset allocation strategies for different values of $\alpha$, including the classical Markowitz selection (i.e., $\alpha =1$) and the new left tail covariance selection (i.e., $\alpha =0$). We stress that only when we consider values of $\alpha$ in the interior of the interval [0, 1] can we make use of the two-dimensional risk.

Specifically, the portfolio analysis is carried out on consecutive overlapping time windows of N consecutive trading days (i.e, $N=1290$, about 5 years) and two consecutive windows differ by six months ($\cong$ 125 consecutive trading days), for a total of 16 windows. We use $\tau _{j-1}=1+125(j-1)$ and $\tau _{j}=1290+125(j-1)$ to denote the first and last observation times of the j-th window, $j=1,2,\ldots ,16$.

For any $\alpha$, we solve sixteen allocation problems in the form (26) using the asset returns observed in the above-mentioned time windows, and $w_{\alpha ,i,j}$ represents the weight of the i-th asset in the portfolio, $i=1,2,\ldots ,N_A$, computed using the asset returns observed over the j-th window.

We compare the portfolio variability measures defined via $\alpha$ looking at the portfolio return up to six months ahead. Specifically, for $j=1,2,\ldots ,16$, we define the portfolio return as

$$\begin{aligned} r_{\alpha ,j,t}=\frac{\left( \sum _{i=1}^{N_A}w_{\alpha , i, j}p_{i, t}\right) -P_{\alpha ,j}}{P_{\alpha ,j}},\,\, t=\tau _{j}+1,\tau _{j}+2,\ldots , \tau _{j}+125. \end{aligned}$$

(27)

Here, $p_{i,t}$ is the price of the i-th asset (see Eq (1)) while $P_{\alpha ,j}$ is the budget necessary to allocate assets, namely, the value of the j-th portfolio on the last date of the j-th window. $P_{\alpha ,j}$ is written as

$$\begin{aligned} P_{\alpha ,j}=\sum _{i=1}^{N_A}w_{\alpha , i, j}\,{p_{i, \tau _{j}}}. \end{aligned}$$

(28)

The portfolio returns $r_{\alpha ,j,t}$ are out-of-sample returns in that they are computed using the portfolio value $\sum _{i=1}^{N_A}w_{\alpha , i, j}\,p_{i, t}$ for $t=\tau _j+1,\tau _j+2,\ldots , \tau _j+125$ out of the windows used to compute the portfolio weights.

We analyze the distribution of portfolio returns $r_{\alpha ,j,t}$, $j=1,2,\ldots ,16$, $t=\tau _j+1,\tau _j+2,\ldots ,\tau _j+125$ for different values of $\alpha$, specifically $\alpha =\alpha _{k} = 0.1k,$ $k=0,1,\dots ,10$. Summary statistics are reported in Table 7.

Table 7 Summary statistics of aggregated portfolio returns

Fig. 4

Summary plots for aggregated portfolio returns

Fig. 5

Portfolio-optimal weights for $\alpha$ equal to 0 (a), 0.70 (b), 1 (c). Ag., comm., corp., em. Asia, and em. America are the abbreviations of investment classes reported in Table 1. Portfolio turnover: 16.7 (a), 13.1, (b) 15.6 (c)

The table shows that investing in the portfolio with $\alpha =0$ performs better with respect to the Markowitz portfolio, i.e., $\alpha =1$. The latter presents a negative mean and median for portfolio returns, which occurs again for $\alpha$ equal to 0.90. This shows that strong exposure to covariance risk increases the probability of losses. Note that the minimum observed losses are obtained only when $\alpha =0$, while the largest profit is achieved on average when $\alpha =0.7$, but the minimum and first quartile worsen. Figure 4 shows summary plots for aggregated portfolio returns with $\alpha =0, 0.7, 1,$ where the black and red lines represent the median and mean values, respectively. For robustness, aggregated portfolio returns associated with $\alpha =1$ are computed by applying the random matrix theory (RMT) filter to the correlation matrix ( Tola et al. 2008) and considering the extreme downside correlation (EDC) of the returns ( Harris et al. 2019; Ahelegbey et al. 2021).

Figure 4 shows higher losses associated with the Markowitz portfolio, i.e., $\alpha =1$ and higher profits for the combined portfolio with $\alpha =0.7.$ Results of the filtered case (RMT) are in line with those of the classical Markowitz portfolio; the EDC portfolio instead shows a positive mean and higher range of variation. Figure 5 shows portfolio weights for each time window and $\alpha =0, 0.7, 1.$ With regard to transaction cost, we refer to the turnover quantity, i.e., the portfolio which shows the best performance in terms of investor wealth (Bodnar et al. 2021). Portfolio turnover is defined as

$$\begin{aligned} Turnover=\sum _{t=t_0+1}^{t_1} \sum _{i=1}^{N_A}|w_{\alpha , i, t}-w_{\alpha , i, t-1}|, \end{aligned}$$

(29)

where $t_0$ and $t_1$ are the first and last times in the rolling window estimation. In Fig. 5, the portfolio turnover is 16.7 when $\alpha =0$, 13.1 when $\alpha =0.7$ and 15.6 when $\alpha =1$.

Fig. 6

Left-hand tail comparison

Fig. 7

Profit and loss curve

Each row in Fig. 5 shows the portfolio asset allocation for the time window considered and the portfolio turnover. Note that the portfolio is more concentrated when investors only consider asset covariance risk with left-hand tail similarity. The same is true for the combined portfolio. Instead, when $\alpha =1$, the portfolio is more balanced between assets. Corporate bonds are predominant assets, regardless of the time window considered. Moreover, looking at Fig. 5, we observe that when $\alpha =0$, emerging assets are preferred to aggregate bonds, despite their higher riskiness. Though this may seem counterintuitive, corporate bonds are the most numerous class in the optimal portfolio, a preference due to the similarity in left-hand tails between corporate and aggregate bonds being larger than the similarity between corporate bonds and emerging assets (see Fig. 6).

We conclude this section with the profit and loss curve. Specifically, Fig. 7 shows the portfolio returns (27) of the five portfolios obtained for $\alpha =0$ (tail: black dotted line), $\alpha =0.7$ (combined: blue solid line), and $\alpha =1$, considering the three cases: classical Markowitz (Markowitz: red dashed line), Markowitz with RMT (RMT: green dashed line), and Markowitz with EDC (EDC: brown solid line) as a function of time. The portfolio returns shown in Fig. 7 are computed out-of-sample up to six months ahead. We can see that the tail portfolio has very limited losses but also limited profits, and the Markowitz and RMT portfolios show several losses even if the tail and combined ones are able to make a profit. Specifically, losses are generated not only during the period of crisis (December 2010 to September 2011), but also in the standard market situation (January 2014–March 2014). This situation worsens for the EDC portfolio. In fact, the high range of variation associated with this portfolio (Fig. 4) increases profits but strongly amplifies losses. The combined portfolio improves profits while reducing losses of the Markowitz portfolio, except for the negative peak in the year 2015, which is probably related to the oil crisis, which also negatively impacted the RMT portfolio. Table 8 shows the sum in absolute value of profits and losses and their difference of portfolios computed under different strategies.

Table 8 Profits and losses (absolute values) of portfolios under different strategies

In Table 8 note that the combined and tail portfolios show higher performances in terms of profits and losses computed out-of-sample, 13.52 and 10.70 respectively, with respect to the Markowitz portfolios (all cases considered).

5 Conclusions

The results of this paper contribute to the recent literature on portfolio optimization in several respects. First, a new informative set on price return distribution is computed using an adaptive algorithm that approximates suitably identified sub-groups of gross returns using log-normal mixtures. Second, a left-tail-covariance-like matrix is introduced. The left-tail correlations are computed as the cosine correlation of the vectors identifying the assets while the left tail volatilities are obtained from suitably weighted volatilities of the leftmost components of the mixtures. Third, a two-dimensional portfolio risk is introduced as the convex combination of the asset and left tail covariance risks. A revisited Markowitz portfolio problem is formulated and solved using ETFs representative of the assets traded via robot advisory. Fourth, the resilience of the portfolio to shock on assets is introduced by defining a weighted centrality of assets in the portfolio. The new portfolio optimization outperforms the classical one by reducing loss and increasing profit. The analysis of the informative set in the case of well known parametric stochastic volatility models deserves further investigation. In fact, it would be interesting to establish some explicit relationships between model parameters and the left tail volatility. Finally, a further line of research is the relationship between risk and resilience measures. Indeed, our findings suggest that a volatile portfolio could be resilient to asset shocks if the leftmost tails of the assets are diversified and not very volatile.

Appendix

In this Appendix, we prove Propositions 1 and 2. First, we prove the following lemma, which will be used to prove Propositions 1 and 2.

Lemma 1

For $i=1,2,\ldots ,N_A$ and $t>0$ denoting ${\underline{y}}_{t,i}=(y_{t,i}, y_{t-1,i},\ldots ,$ $y_{t-N_y+1,i})^\prime$, the vector $N_y$ of consecutive daily returns of asset i at time t,  the left tail informative set associated with asset i at time t:

$$\begin{aligned} {{\underline{x}}^\prime _{t,i}=({\tilde{a}}^1_{t,i}, \tilde{a}^2_{t,i},\pi ^1_{t,i},\pi ^2_{t,i}, F^1_{2,t,i}, F^2_{2,t,i}, 1-F^1_{1,t,i}, \ 1-F^2_{1,t,i}, \sigma ^1_{1,t,i}, \sigma ^2_{1,t,i}), } \end{aligned}$$

(30)

is invariant by translation of $\log {\underline{y}}_{t,i}.$

Proof

For simplicity in the proof, we drop the subscripts t and i in (30) and use, respectively,

$$\begin{aligned} {{\underline{x}}^\prime =({\tilde{a}}^1, {\tilde{a}}^2,\pi ^1,\pi ^2, F^{1}_2, F^2_{2}, 1-F^1_{1}, \ 1-F^2_{1}, \sigma ^1_{1}, \sigma ^2_{1}), } \end{aligned}$$

(31)

and ${\underline{y}}=(y_1,y_2,\ldots ,y_{N_y})^\prime$ to denote the left tail informative set and the vector of daily returns associated with a generic asset.

The components of the vector ${\underline{x}}$ are found applying the expectation maximization (EM) method to ${\underline{y}},$ under the assumption that the latter contains the realizations of a vector of the independent and equally distributed random variables $Y_1,$ $Y_2,$..., $Y_{N_y}\sim Y,$ whose density is given by

$$\begin{aligned} f_Y(y)=\pi _{Y} f_{1,Y}(y)+(1-\pi _Y) f_{2,Y}(y),\quad y\in \mathbb R_+, \end{aligned}$$

(32)

$\pi _Y\in (0,1),$ and

$$\begin{aligned} f_{j,Y}(y)=f_Y(y|Z_{k,Y}=j),\quad y\in {\mathbb {R}}_+,\ j=1,2,\, k=1,2,\ldots ,N_y, \end{aligned}$$

(33)

are log-normal probability densities of parameters $\mu _{1,Y},$ $\sigma _{1,Y},$ $\mu _{2,Y},$ $\sigma _{2,Y}.$ Here, $Z_{k,Y}$ denotes the (latent) random variable representing the mixture component for Y,  defined by

$$\begin{aligned} Z_{k,Y}=j\text { if } Y_k \text { is drawn by the component } j,\quad j=1,2. \end{aligned}$$

(34)

In the context of mixture distribution, the EM algorithm works in the usual way, maximizing the log-likelihood function associated with the observation vector ${\underline{y}}$ via an iterative procedure. The procedure initializes the unknown mixture parameters $\pi _Y,$ $\mu _{1,Y},$ $\mu _{2,Y},$ $\sigma _{1,Y},$ $\sigma _{2,Y},$ and, at any step, evaluates the posterior probabilities (E-step):

$$\begin{aligned} \gamma _{Z_{k,Y}}(1)=&\frac{\pi _Y f_{1,Y}(y_k)}{\pi _Y f_{1,Y}(y_k)+(1-\pi _Y) f_{2,Y}(y_k)}, \end{aligned}$$

(35)

$$\begin{aligned} \gamma _{Z_{k,Y}}(2)=&\frac{(1-\pi _Y) f_{2,Y}(y_k)}{\pi _Y f_{1,Y}(y_k)+(1-\pi _Y) f_{2,Y}(y_k)}. \end{aligned}$$

(36)

It estimates the new mixture parameters ${\hat{\pi }}_Y,$ ${\hat{\mu }}_{1,Y},$ ${\hat{\mu }}_{2,Y},$ ${\hat{\sigma }}_{1,Y},$ ${\hat{\sigma }}_{2,Y}$ (M-step) as follows:

$$\begin{aligned} {\hat{\mu }}_{j,Y}=&\frac{1}{N_{j,Y}}\sum _{k=1}^{N_y}\gamma _{Z_{k,Y}}(j) \log y_k,\quad j=1,2, \end{aligned}$$

(37)

$$\begin{aligned} {\hat{\sigma }}_{j,Y}=&\sqrt{\frac{1}{N_{j,Y}}\sum _{k=1}^{N_y}\gamma _{Z_{k,Y}}(j) (\log y_k-{\hat{\mu }}_{j,Y})^2},\quad j=1,2, \end{aligned}$$

(38)

$$\begin{aligned} {\hat{\pi }}_Y=&\frac{N_{1,Y}}{N_y}, \end{aligned}$$

(39)

where $N_{j,Y}=\sum _{k=1}^{N_y} \gamma _{Z_{k,Y}}(j),$ $j=1,2,$ and computes the log-likelihood in the estimated mixture parameters. The iterative procedure stops when the difference between the log-likelihood obtained in two consecutive steps is less than a small value $\epsilon .$ For more details about the EM procedure, we refer to Dempster et al. (1977).

The left tail informative set ${\underline{x}}$ in (31) is composed of functions of the mixture parameters obtained in the last step by the EM algorithm, so in order to prove the invariance by translation of the left tail informative set, we prove the invariance by translation of the functions of mixture parameters appearing in (31).

Let ${{\underline{\tau }}}=\exp (\log {\underline{y}}+c)=e^c {\underline{y}}$ be the vector of returns obtained shifting the log returns $\underline{y}$ by a constant $c\in {\mathbb {R}}.$ Assuming that the vector ${{\underline{\tau }}}$ contains the realizations of a vector of the independent and equally distributed random variables $T_{1},$ $T_{2},$ ..., $T_{N_y}\sim T={e^c Y},$ the posterior probabilities obtained applying the EM algorithm to ${\underline{\tau }}=(T_1,T_2,\ldots ,T_{N_y})$ are

$$\begin{aligned} \gamma _{Z_{k,T}}(1)=&\frac{\pi _T f_{1,T}(e^cy_k)}{\pi _{T} f_{1,T}(e^c y_k)+(1-\pi _{T}) f_{2,T}(e^c y_k)}, \end{aligned}$$

(40)

$$\begin{aligned} \gamma _{Z_{k,T}}(2)=&\frac{(1-\pi _{T}) f_{2,T}(e^c y_k)}{\pi _{T} f_{1,T}(e^cy_k)+(1-\pi _{T}) f_{2,T}(e^cy_k)}, \end{aligned}$$

(41)

where $f_{1,T},$ $f_{2,T}$ are log-normal probability densities of parameters $\mu _{1,T}{=\mu _{1,Y}+c},$ $\mu _{2,T}{=\mu _{2,Y}+c},$ $\sigma _{1,T}{=\sigma _{1,Y}},$ $\sigma _{2,T}{=\sigma _{2,Y}}$ and $\pi _T=\pi _Y$. Bearing in mind that $f_{1,T}(e^c y_k)=f_{1,Y}(y_k)e^{-c},$ from (40), (41) we have $\gamma _{Z_{k,T}}=\gamma _{Z_{k,Y}}.$ Consequently, from (40), (41) we have

$$\begin{aligned} N_{j,T}=\sum _{k=1}^{N_y} \gamma _{Z_{k,T}}(j)=\sum _{k=1}^{N_y} \gamma _{Z_{k,Y}}(j)=N_{j,Y}, \end{aligned}$$

(42)

and, using (40), (41), (42), we see that the estimates of the mixture parameters associated with ${{\underline{\tau }}}$ are

$$\begin{aligned} {\hat{\mu }}_{j,T}=&\frac{1}{N_{j,T}}\sum _{k=1}^{N_y}\gamma _{Z_{k,T}}(j) (\log y_k+c)={\hat{\mu }}_{j,Y}+c,\quad j=1,2, \end{aligned}$$

(43)

$$\begin{aligned} {\hat{\sigma }}_{j,T}=&\sqrt{\frac{1}{N_{j,T}}\sum _{k=1}^{N_y}\gamma _{Z_{k,T}}(j) (\log y_k+c-{\hat{\mu }}_{j,T})^2}={\hat{\sigma }}_{j,Y},\quad j=1,2, \end{aligned}$$

(44)

$$\begin{aligned} {\hat{\pi }}_{T}=&\frac{N_{1,T}}{N_y}={\hat{\pi }}_Y. \end{aligned}$$

(45)

Now, recalling that the change point of the mixture associated with ${{\underline{\tau }}}$ is the point $a_T$ such that

$$\begin{aligned} \pi _{T} f_{1,T}(a_T)=(1-\pi _{T}) f_{2,T}(a_T), \end{aligned}$$

(46)

we find the estimate of the change point, ${\hat{a}}_{T},$ by solving the following equation:

$$\begin{aligned} {\hat{\pi }}_{T} {\hat{f}}_{1,T}({\hat{a}}_{T})=(1-{{\hat{\pi }}_{T}}) {\hat{f}}_{2,T}({\hat{a}}_{T}), \end{aligned}$$

(47)

where ${\hat{f}}_{1,T},$ ${\hat{f}}_{2,T}$ are log-normal probability densities of parameters ${\hat{\mu }}_{1,T},$ ${\hat{\mu }}_{2,T},$ $\hat{\sigma }_{1,T},$ ${\hat{\sigma }}_{2,T}.$ Now, since $T=e^cY,$ we have

$$\begin{aligned} {\hat{f}}_{j,T}({\hat{a}}_T)={\hat{f}}_{j,Y}( e^{-c}{\hat{a}}_T)e^{-c}, \end{aligned}$$

(48)

and, using the estimates (43), (44), (45) together with (48), equation (47) becomes

$$\begin{aligned} {\hat{\pi }}_{Y} {\hat{f}}_{1,Y}( e^{-c}{\hat{a}}_T)=(1-{{\hat{\pi }}_{Y}}) {\hat{f}}_{2,Y}( e^{-c}{\hat{a}}_T), \end{aligned}$$

(49)

which implies that the change point of the two-component mixture associated with ${{\underline{\tau }}},$ estimated by the EM algorithm, is the point

$$\begin{aligned} {\hat{a}}_{T}=e^c{\hat{a}}_{Y}, \end{aligned}$$

(50)

where ${\hat{a}}_Y$ is the change point of the two-component mixture associated with ${\underline{y}},$ estimated by the EM algorithm.

Moreover, the first and second kinds of errors associated with ${{\underline{\tau }}}$ as estimated by the EM algorithm are equal, respectively, to the estimated first and second kinds of errors associated with ${\underline{y}},$ i.e.,

$$\begin{aligned} {\hat{F}}_{2,T}=&\underbrace{\int _0^{{\hat{a}}_{T}}{\hat{f}}_{2,T}(s) ds={ \int _0^{e^{-c}{\hat{a}}_{T}}{\hat{f}}_{2,T}(e^{c}\xi )d(e^{c}\xi )}}_{s=e^{c}\xi }\nonumber \\ =&{\int _0^{{\hat{a}}_{Y}}{\hat{f}}_{2,Y}(\xi )d\xi }={\hat{F}}_{2,Y}, \end{aligned}$$

(51)

and, likewise,

$$\begin{aligned} 1-{\hat{F}}_{1,T}=1-{\hat{F}}_{1,Y}. \end{aligned}$$

(52)

Equations (43), (44), (45), (50), (51), (52) prove that all components of vector (31) of the first iteration are invariant by translation of $\log {\underline{y}}.$

The remaining components of (31) (i.e., those relative to the second iteration) are obtained applying the EM algorithm to the observations $y_k$ such that $y_k>{\hat{a}}_{Y}$. Thus, the invariance by translation follows as argued above. This concludes the proof.$\Box$ $\square$

Now, using Lemma 1 in analogy with Furman et al. (2017), Gardes and Girard (2021), we introduce the definition of the variability measure and prove Propositions 1and 2.

Definition 4

A set ${\mathcal {X}}$ is a convex cone if $\alpha X + \beta Y\in {\mathcal {X}}$ for all $X, Y\in {\mathcal {X}}$ and $\alpha ,\beta >0.$

Definition 5

(see Furman et al. 2017) With ${\mathcal {X}}$ a convex cone of random variables, a map $\nu :{\mathcal {X}}\rightarrow [0,+\infty )$ is a variability measure if it satisfies the following properties:

• (i) if $X,Y\in {\mathcal {X}}$ have the same distributions ($X\overset{d}{=}Y$), then $\nu (X)=\nu (Y),$

• (ii) $\nu (c)=0$ for all $c\in {\mathbb {R}},$

• (iii) $\nu (X+c)=\nu (X)$ for all $c\in {\mathbb {R}}$ and $X\in {\mathcal {X}}.$

As observed in Furman et al. (2017), the standard deviation of X is a coherent variability measure of X but not a coherent risk measure of X.

Proof of Proposition 1

Let:

$$\begin{aligned} {\mathcal {X}}= & {} \{\log Y\ : \ Y\text { is a random variable approximable by EM algorithm}\nonumber \\&\text {with a two-component log-normal mixture}\}. \end{aligned}$$

(53)

For $i=1,2,\ldots ,N_A$ and $t>0,$

$$\begin{aligned} {\nu _i}:{\mathcal {X}}&\rightarrow [0,+\infty ]\nonumber \\ Y_{t,i}&\rightarrow \sqrt{\frac{\pi _{t,i}^1}{1-\pi _{t,i}^1}}\sigma _{1,t,i}^1 \end{aligned}$$

(54)

is the map associated with any gross return $Y_{t,i}\in {\mathcal {X}}$ and its left tail volatility.

Now we prove that (54) satisfies the three properties (i), (ii), (iii) of Definition 5. This proves property (i).

If two gross returns have the same distributions, they also have the same associated informative set and, as a consequence, the same measure.

When $\log Y_{t,i}=c,$ $c\in {\mathbb {R}},$, $\forall t,i$, by (38) we have the mixture parameters associated with the first components estimated by the EM algorithm are

$$\begin{aligned} {\hat{\mu }_{1,t,i}^1}=&{\hat{\mu }}_{1,e^c}=c, \end{aligned}$$

(55)

$$\begin{aligned} {\hat{\sigma }_{1,t,i}^1}=&{\hat{\sigma }}_{1,e^c}=0. \end{aligned}$$

(56)

Substituting (56) into (54) yields $\nu _i(c)=0.$ This proves property (ii).

The proof of property (iii) follows easily by Lemma 1, observing that the a priori probability $\pi _{1,t,i}^1$ and the mixture volatility $\sigma _{1,t,i}^1,$ estimated by the EM algorithm are both invariant by translation of $\log Y_{t,i}.$ This concludes the proof. $\square$

Now, using Proposition 1, in analogy with Joachim (2017), we prove that the left tail risk centrality $r(\varPi _{{\underline{w}}},{\overline{C}})$ defined in (18) is a variability measure in the left tail of the portfolio distribution at time t.

Proof of Proposition 2

Let $\overline{{{\underline{\xi }}}}_{t}=(w_1{\overline{\sigma }}_{t,1},w_2{\overline{\sigma }}_{t,2},\ldots ,w_{N_A}{\overline{\sigma }}_{t,N_A})^\prime$ be the vector of weighted variability measures associated with assets $1,2\ldots ,N_A$ at time t, and ${{\overline{\varGamma }}}_t$ be the left-tail-correlation-like matrix at time t defined in (8). Following the core of risk aggregation in the Solvency II standard formula (see Parliament 2009, Appendix IV) and in line with Joachim (2017), the left tail risk centrality of portfolio, $r(\varPi _{{\underline{w}}},{\overline{C}})$, at time t in (18) can be rewritten as

$$\begin{aligned} r(\varPi _{{\underline{w}}},\overline{C})=\nu (Y_{t,1},Y_{t_2},\ldots ,Y_{t,N_A})=\Vert \overline{\underline{\xi }}_t\Vert _{{{\overline{\varGamma }}}_t}^2=\overline{{{\underline{\xi }}}}_t^\prime \ {{\overline{\varGamma }}}_t \ \overline{{{\underline{\xi }}}}_t, \end{aligned}$$

(57)

where $\nu :{\mathcal {X}}^{N_A}\rightarrow [0,+\infty )$ and ${\mathcal {X}}$ is given by (53). Let us prove that the map $\nu$ satisfies the properties (i), (ii), (iii) of Definition 5.

If two gross returns have the same distributions, they also have the same associated vector $\overline{{{\underline{\xi }}}}_{t}$ and matrix ${{\overline{\varGamma }}}_t$ and, as a consequence, the same measure. This proves property (i).

We observe that when the portfolio $\varPi _{{\underline{w}}}$ at time t is made by constant log returns $\log Y_{t,i}=c,$ $i=1,2,\ldots ,N_A,$ by virtue of Proposition 1, the corresponding vector of weighted variability measures $\overline{{{\underline{\xi }}}}_t={\underline{0}},$ where ${\underline{0}}$ is the $N_A$-dimension zero vector, therefore the property (ii) follows easily from (57).

Property (iii) follows from the invariance by translation of the vector of weighted variability measures ${{\underline{\xi }}}_{t},$ established in Proposition 1, and by the invariance by translation of the left-tail-correlation-like matrix ${{\overline{\varGamma }}}_t,$ by virtue of Lemma 1. This concludes the proof. $\square$

It is worth noting that the portfolio variance $r(\varPi _{\underline{w}},C),$ defined in (20), can be rewritten as follows:

$$\begin{aligned} r(\varPi _{{\underline{w}}}, C)=\nu (Y_{t,1},Y_{t_2},\ldots ,Y_{t,N_A})=\Vert \underline{\xi }_t\Vert _{\varGamma _t}^2={{\underline{\xi }}}_t^\prime \ \varGamma _t \ {{\underline{\xi }}}_t, \end{aligned}$$

(58)

where $\underline{\xi }_t=(w_1\sigma _{1,t},w_2\sigma _{2,t},\ldots ,w_{N_A}\sigma _{N_A,t})$, $\sigma _{i,t}$ is the standard deviation of the $i-$th asset log-return at time t and $\varGamma _t$ is the correlation matrix at time t. Then, similar to $r(\varPi _{{\underline{w}}},{\overline{C}}),$ $r(\varPi _{{\underline{w}}}, C)$ is the variability measure associated with the Markowitz portfolio.