Introduction

In school mathematics, new concepts of one subject area are usually introduced and practiced in a blocked fashion, i.e., one after another (Rohrer et al., 2020). This also applies to the introduction of subtraction strategies in primary school and especially to the standard written algorithm. The standard written algorithm is usually introduced after practicing number-based strategies, which are rarely discussed in the classroom afterwards. This may explain why numerous studies show that students barely use number-based strategies after the standard written algorithm has been introduced. Instead, they almost exclusively use the standard written algorithm to solve subtraction problems, irrespective of the task characteristics (e.g., Hickendorff, 2020; Selter, 2001; Torbeyns et al., 2017). This lack in flexibility can lead to a non-adaptive use of different subtraction strategies, though the adaptive use of strategies, i.e., choosing efficient strategies based on task characteristics, is a meaningful competence for primary school students (e.g., Baroody & Dowker, 2003; Kilpatrick et al., 2001; National Council of Teachers of Mathematics (NCTM), 2000).

In contrast to the usual blocked learning approach in mathematics classrooms, in which exemplars or tasks of different categories are presented one after another (e.g., AAABBBCCC), interleaved practice intermixes tasks (e.g., ABCBCACBA; Richter et al., 2022b). Research has shown that this approach can promote students’ adaptive use of subtraction strategies (Nemeth et al., 2021). The advantage of interleaved over blocked practice is often traced back to implicit comparison processes (Birnbaum et al., 2013), which explains why interleaved practice might be suitable to foster students’ adaptive use of subtraction strategies: by using different subtraction strategies alternately, students are made aware of the differences between the strategies, that is, for which kinds of subtraction problems which strategy can be used adaptively.

However, students do not automatically compare if they are not explicitly prompted to do so (Durkin et al., 2017). Previous research shows that interleaved practice combined with explicit prompts to compare different tasks and solution methods can better foster students’ accuracy when solving mathematical problems, reduce misconceptions, and lead to more flexible and adaptive use of strategies compared to blocked learning (e.g., Nemeth et al., 2019, 2021; Ziegler & Stern, 2014, 2016), though it is unclear whether all students benefit equally from this teaching approach. The comparison processes evoked by interleaved practice are cognitively demanding. At the same time, they support the learning of relevant processes. Thus, the current study investigates the role of students’ prior knowledge and need for cognition (NFC), i.e., their engagement in and enjoyment of cognitive activities, for the effectiveness of interleaved practice combined with prompts to compare.

Adaptive use of subtraction strategies

There is a broad consensus among mathematics researchers and educators that students should be able to use strategies adaptively to solve problems (e.g., Baroody & Dowker, 2003; Hickendorff et al., 2022; Kilpatrick et al., 2001; NCTM, 2000). Using strategies adaptively represents a part of individuals’ cognitive variability, which leads to faster and more accurate problem solving (Heinze et al., 2009b; Verschaffel et al., 1998). The definition of strategy proficiency by Lemaire and Siegler (1995) illustrates that strategy competence is more than calculating correctly: strategy proficiency comprises strategy repertoire (the repertoire of strategies one uses), strategy distribution (the frequency with which the strategies are used), strategy efficiency (speed and accuracy), and strategy adaptivity (choosing an appropriate strategy based on task characteristics or based on the individual efficiency when applying specific strategies). Star (2005) describes adaptivityFootnote 1 as deep procedural knowledge, which “is associated with comprehension, flexibility, and critical judgement” (p. 408). Thus, the adaptive use of strategies exceeds procedural knowledge, i.e., the ability to execute procedures (Hiebert & Lefevre, 1986). In our study, we take a normative perspective on adaptivity following several other studies (e.g., Blöte et al., 2000; Heinze et al., 2018; Torbeyns et al., 2009) and define adaptivity as the fit between a specific subtraction task and the subtraction strategy used (without considering the accuracy of students’ solutions).

Number-based strategies are based on the specific characteristics of the task and one’s knowledge of the number system and operations (Torbeyns & Verschaffel, 2016). While these strategies are typically performed mentally, students often note solution steps or interim results to relieve their working memory. When using decomposition strategies (stepwise strategy and split strategy, Table 1), the hundreds, tens, and ones of one or both numbers are decomposed before starting to solve the task. When using shortcut strategies (compensation strategy and indirect addition, Table 1), one must adapt the numbers and operations flexibly to task characteristics (Torbeyns et al., 2009). Despite the range of available strategies, numerous studies have shown that primary school students rarely solve subtraction problems adaptively, relying instead on a few standard approaches (e.g., Blöte et al., 2000; Heinze et al., 2009a; Hickendorff, 2020; Selter, 2001). For example, shortcut strategies are rarely used if they have not been taught systematically (De Smedt et al., 2010; Torbeyns et al., 2009; Van der Auwera et al., 2023), although they can accelerate problem-solving and reduce mental effort if used for appropriate tasks. This non-adaptive use of strategies becomes even more pronounced after the introduction of the standard written algorithm (Table 1)—a fixed step-by-step procedure for solving mathematical tasks (Torbeyns & Verschaffel, 2016)—as students often use it by default (e.g., Selter, 2001; Torbeyns & Verschaffel, 2016; Torbeyns et al., 2017).

Table 1 Overview of selected number-based strategies and the standard written algorithm
Full size table

Empirical findings show that explicit teacher-led instruction on how and when to use different subtraction strategies adaptively promotes students’ use of shortcut strategies and enhances their adaptivity (e.g., De Smedt et al., 2010; Heinze et al., 2018; Nemeth et al., 2019, 2021; for an overview, see Heinze et al., 2020). To foster students’ adaptive use of strategies, it seems worthwhile to teach different subtraction strategies in an interleaved fashion, thereby encouraging students to reflect on their strategy choice for different tasks.

Interleaved practice and comparison learning

Despite the fact that teachers usually try to simplify learning for their students, there is large empirical evidence that hampering learning processes can lead to better long-term retention (Dunlosky et al., 2013). These so-called desirable difficulties include, among other instructional approaches, interleaved practice (Bjork & Bjork, 2011; Richter et al., 2022a). While blocked practice facilitates within-comparisons, which can help students to recognize common features of specific categories, it does not encourage students to compare between categories; they usually learn one category after another without comparing (Rohrer et al., 2015). Regarding solution strategies in mathematics, this may result in a lack of understanding of the underlying principles and the specific application conditions of each strategy (Ziegler et al., 2018).

Unlike blocked practice, interleaved practice intermixes learning contents, which hampers learning in the short-term. However, interleaving contents results in better long-term retention, as various studies demonstrate (Dunlosky et al., 2013). One theoretical explanation for this advantage is the discriminative-contrast hypothesis, which states that interleaved practice activates discrimination and comparison processes (Birnbaum et al., 2013). As learners are alternately confronted with different content, they are stimulated to focus on the differences (attentional bias framework; Carvalho & Goldstone, 2015, 2017). Moreover, students must choose a strategy for each problem and are required to reflect on their strategy choice which should benefit their adaptivity. When solving tasks in a blocked fashion, on the contrary, students are likely to assume that the current problem can be solved adaptively with the same strategy used for the previous task (Rohrer & Hartwig, 2020). Therefore, blocked practice does not engage students in reflecting their strategy choice to the same extent as interleaved practice.

Brunmair and Richter (2019) found a moderate interleaving effect in their meta-analysis over all included primary studies (g = 0.42) and a small interleaving effect for mathematics (g = 0.34). However, the included primary studies on interleaving mathematical tasks are inconsistent, yielding both negative and positive effects. The results of this meta-analysis suggest that the concrete implementation of interleaved practice influences its effectiveness. According to the discriminative-contrast hypothesis, comparison processes are expected to be underlying learning mechanisms, explaining the advantage of interleaved over blocked practice. Comparing supports students in learning the principles of each category and in detecting central differences and similarities among them (e.g., Gentner, 1983; Loewenstein et al., 1999). In the case of younger children, empirical studies have shown that they are less likely to focus on the relevant dimension during learning (Cook & Odom, 1992; Thompson & Markson, 1998). However, interleaved practice requires learners to pay attention to the relevant alternating dimension to use the evoked comparison processes. What is more, previous research demonstrates that learning which supports students’ comparison processes by including explicit comparison prompts results in higher learning gains in contrast to only offering opportunities to compare (e.g., Alfieri et al., 2013; Catrambone & Holyoak, 1989; Gentner et al., 2003). Further studies have demonstrated that prompting students to compare different types of tasks or solution strategies can enhance flexibility and adaptivity when learning mathematics (e.g., Durkin et al., 2023; Rittle-Johnson & Star, 2007, 2009). This is supported by research showing that interleaved practice combined with prompts to compare can foster students’ adaptive strategy use (Nemeth et al., 2019, 2021), though it is unclear whether all students benefit equally from this teaching approach.

Prior knowledge and NFC as potential moderators of interleaved practice

Prior arithmetical knowledge affects the adaptive use of subtraction strategies among primary school students (Nemeth et al., 2019; Torbeyns & Verschaffel, 2016). Choosing an adaptive subtraction strategy for a subtraction problem requires demanding cognitive processes: students have to analyze the numbers in the subtraction task and choose an appropriate strategy from their strategy repertoire or invent a strategy appropriate to the task’s characteristics. To meet these challenges, students need a conceptual understanding of numbers, as well as a grasp of the number system and arithmetic operations. As interleaved practice is a desirable difficulty, it is expected that prior knowledge might be even more relevant when interleaved practice and comparison processes are included in the learning process. Blocking learning contents, and thus practicing the same procedure repeatedly, could reduce the demands on working memory. In contrast, when interleaving and comparing subtraction strategies, more interacting elements need to be processed simultaneously, which increases cognitive load (Sweller & Chandler, 1994). Interleaving and comparing various subtraction strategies might thus become an undesirable difficulty when solving subtraction tasks with a given strategy is already challenging for a student (McDaniel & Butler, 2011). Nonetheless, interleaving subtraction strategies can trigger learning mechanisms central to the acquisition of adaptive, task-based use: students are repeatedly prompted indirectly—and in our study also directly through comparison prompts—to compare strategies for different tasks. Compared to blocked learning, this approach should support students more in abstracting the conditions of the application of different subtraction strategies which could especially benefit low-prior-knowledge students.

Following these two contradictory explanations, empirical findings regarding the role of prior knowledge for interleaved practice (e.g., Rau et al., 2010, 2014) and comparison learning in mathematics (Guo et al., 2012, 2014; Rittle-Johnson et al., 2009, 2012; Star & Rittle-Johnson, 2009) are also inconsistent. Researchers, therefore, conclude that the target knowledge type and the aspects of the learning content that are critical for student learning might play a major role if interleaving and comparing are beneficial for low-prior-knowledge students (Guo et al., 2012, 2014; Rau et al., 2014). According to variation theory (Kullberg et al., 2017; Marton & Booth, 1997; Marton & Pang, 2006), learning occurs when individuals discern and focus on the critical aspects of the target phenomenon. To achieve this, the learning content must vary in the specific dimension critical to the target learning goal (Marton & Pang, 2006). When the adaptive use of subtraction strategies is the target learning goal, identifying the characteristics of subtraction tasks, and knowing when to apply which strategy efficiently is critical for learning. To support students in discerning and focusing on the critical aspects, they should be encouraged to contrast different examples, i.e., to compare the efficiency of different subtraction strategies for different subtraction tasks.

Contrasting and comparing are inherent to the learning process regarding the adaptive use of subtraction strategies: students need to analyze the task and weigh and compare the adaptivity of the different strategies to choose the most adaptive one. Interleaved practice and comparing can stimulate these processes repeatedly and may support students in acquiring this kind of deep procedural knowledge (Star, 2005). In particular, it can address aspects critical to the learning of students with lower prior knowledge, i.e., the characteristics of the tasks are systematically varied, and students are repeatedly confronted with the adaptivity of different strategies. High-prior-knowledge students, on the other hand, might already be equipped to compare and abstract the rules over longer periods, and therefore may also benefit from blocked practice (Rau et al., 2014).

NFC refers to an individual’s intrinsic cognitive motivation, i.e., their engagement in and enjoyment of cognitive activities (Cacioppo et al., 1996). Individuals high in NFC process information more deeply, choose strategies more adaptively, and have a more positive attitude towards cognitively challenging tasks (Cacioppo et al., 1996; Evans et al., 2003), which explains why NFC has been associated with academic achievement (von Stumm & Ackermann, 2013), though in studies conducted with primary students, no relation was found (Ginet et al., 2000; Luong et al., 2017). However, there is still a lack of research regarding the impact of NFC when it comes to cognitively demanding tasks in the context of interleaved practice or comparison learning. As mentioned above, interleaved practice, as well as comparing learning contents, require higher cognitive effort from students compared to a blocked or sequential approach. Thus, it can be assumed that low-NFC students may not exploit the learning opportunities offered by these cognitively demanding teaching approaches. Hence, students’ NFC may influence the effectiveness of interleaved practice combined with prompts to compare, while it may be less important for blocked practice, which is less cognitively demanding.

The current study

Several studies show that interleaved practice leads to higher learning gains than blocked practice (Brunmair & Richter, 2019). This is also true in primary school mathematics (Nemeth et al., 2019, 2021; Taylor & Rohrer, 2010). However, research investigating whether all students benefit equally from interleaved practice in the primary mathematics classroom is lacking. Thus, the goal of this study is to investigate whether the effectiveness of interleaved practice combined with prompts to compare is moderated by students’ prior knowledge and NFC.

In the first step, we investigate if students’ prior knowledge moderates the effect of interleaved vs blocked practice (research question 1). Comparing different subtraction strategies for several tasks is critical for learning how to choose adaptive strategies based on task characteristics. Especially low-prior-knowledge students should benefit from interleaved practice including prompts to compare. This is because the critical aspects are explicitly varied, and students are encouraged to contrast and compare, and thus to abstract rules as to when to apply which subtraction strategy. Blocked practice does not explicitly offer these comparison processes and does not directly support students’ focus on and discernment of different task characteristics triggering the use of different subtraction strategies. Students probably need more learning-relevant prior knowledge to abstract the rules without being repeatedly instructed to compare—implicitly through interleaved practice and explicitly through comparison prompts. Therefore, we hypothesize that prior knowledge has a stronger positive effect on students’ learning gains in blocked than in interleaved practice (H1).

We further investigate if students’ NFC has a moderating effect (research question 2). It can be assumed that the higher the students’ NFC, the more they benefit from interleaved practice as a desirable difficulty in learning. This is because they enjoy cognitively demanding activities, leading to deeper information processing. Even though there are currently no studies which investigate the role of NFC for the effectiveness of interleaved practice/comparison learning, we expect that high-NFC students prefer to use the learning opportunities offered by interleaved practice, including comparison prompts. At the same time, NFC should be less important for blocked practice as it is less cognitively demanding. Hence, we expect that students’ NFC has a stronger positive impact on students’ learning gains in interleaved compared to blocked practice (H2).

Material and methods

Participants

The research questions were answered with an experimental classroom study in which 236 German third-graders from 12 classes participated. The students were randomly assigned to either the blocked condition including within-comparison prompts (n = 117) or the interleaved condition including between-comparison prompts (n = 119). The regular class composition was broken up, and new learning groups were formed. The halves of two classes of one school that were randomly assigned to the interleaved condition were combined into the interleaved learning group, and the halves of two classes that were assigned to the blocked condition formed the blocked learning group. The students were not told that the lessons differed between the groups. To participate in this study, addition up to 1000 had to have been introduced in class before the intervention, while subtraction up to 1000 need not have been introduced. Table 2 shows the descriptive statistics of student characteristics for the blocked and interleaved condition. Analyses revealed no significant difference between the two groups with respect to students’ age, t(231) = 0.80, p = 0.43, the proportion of female and male students, χ(1) = 0.00, p = 0.99, and prior arithmetical knowledge, t(219) =  − 0.36, p = 0.72.

Table 2 Overview of student characteristics for the interleaved and the blocked condition
Full size table

Design

The experimental study follows a 2 × 4 design: (group: interleaved vs blocked) × (time: T1: before the intervention, T2: 1 day later, T3: 1 week later, and T4: 5 weeks later; Fig. 1).

Fig. 1
figure 1

Design of the study

Full size image

At T0, prior arithmetical knowledge and NFC were measured. The dependent variable, adaptivity, was measured immediately before the intervention (T1), immediately after the intervention (T2), and at two follow-up tests, i.e., 1 week (T3) and 5 weeks (T4) after the intervention.

The lessons were conducted by four trained staff members using precise lesson scripts for each of the 14 lessons, including teacher explanations and questions, scenarios of potential student behavior during whole-class discussions and individual work, respective teacher reactions (e.g., how to deal with incorrect student answers), and the time expected to be spent on each activity (for examples of a lesson script from the blocked condition, see Supplementary file 1; for the interleaved condition, see Supplementary file 2). The staff members had studied mathematical didactics for primary schools at university for at least six semesters. To be able to disentangle teacher effects from treatment effects, all staff members taught both conditions equally often. During the intervention, no regular mathematics lesson was held, and the students were not assigned any mathematics homework. They were not allowed to take the material home.

Treatment

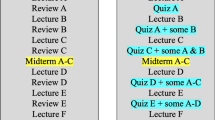
The intervention comprised 14 45-min lessons in which the adaptive use of subtraction strategies when solving three-digit subtraction problems was taught. The first two lessons were equal for both conditions: students’ prior knowledge of numbers was activated and a first approximation of their aptitude at solving subtraction tasks was made at a math conference, i.e., groups of students discussed which strategy is the most appropriate for solving a specific subtraction task. Moreover, the criteria for solving tasks adaptively (number of solution steps, mental effort, error rate) were discussed in both conditions and a poster with these criteria was hung up in class in all following lessons (Supplementary file 3). From the third lesson onwards, the number-based subtraction strategies split strategy, stepwise strategy, compensation strategy, and indirect addition, along with the standard written algorithm (Table 1), were introduced and practiced in class. While the teaching content was the same, the two conditions differed in the order in which the strategies were introduced and practiced. In the blocked condition, the strategies were introduced and practiced one after another, while they were practiced alternately in the interleaved condition (detailed overview of the activities of each lesson for both conditions, see Supplementary file 4). The total time spent on each strategy and the mathematical tasks were nearly identical.

Posters with worked examples of each strategy were hung on the walls during the lessons to assist the students with calculations and with arguing whether a specific strategy is adaptive for a specific task (for an example, see Supplementary file 3). During the lessons, the teacher encouraged the students to use the posters to describe the solution steps of the different strategies (see Supplementary file 1 and 2). In addition, a poster (mathematical lexical storage) with relevant mathematical terms and the corresponding explanations was hung up in class and each student received a printout in A4 format to help the students verbalize explanations and solution steps (Supplementary file 3).

The students in the interleaved condition were explicitly prompted to compare strategies for specific tasks and to explain why a specific strategy is more adaptive than another (between-comparison) during individual work (see Fig. 2) and classroom discussions (e.g., “Which strategy is the cleverest for the task 441 – 297? The squirrel-strategy (compensation strategy), the mouse-strategy (stepwise strategy), or the frog-strategy (indirect addition)? Why do you think that this task can be solved cleverly with the squirrel-/mouse-/frog-strategy?”). In the blocked condition, each lesson focused on one strategy and the students in the blocked condition were not prompted to draw comparisons between strategies. Nevertheless, the specific task characteristics that prompt the use of each subtraction strategy were discussed and the students were asked to decide for several tasks if they can be solved adaptively with that strategy and to explain their decision (within-comparison, e.g., “Can you solve the task 441 – 297 cleverly with the squirrel-strategy or not? Why do you think that you can/cannot solve this task cleverly with the squirrel-strategy?”). Figure 2 illustrates the differences between the two conditions in individual work:

Fig. 2
figure 2

Example worksheet of the blocked condition (left, lesson 7) and the interleaved condition (right, lesson 8). Squirrel-strategy = compensation strategy, mouse-strategy = stepwise strategy, frog-strategy = indirect addition. The tasks were translated from German to English

Full size image

In this example, the students in the blocked condition had to decide for task 532 – 297 (and for several more tasks afterwards) if it can be solved adaptively with the squirrel-strategy (compensation strategy) and, if so, to solve the task with this strategy. The students in the interleaved condition, on the contrary, had to decide for the same task if the squirrel-, mouse-, or frog-strategy, i.e., compensation strategy, stepwise strategy, or indirect addition, is the most adaptive strategy and to solve the task with the most adaptive one.

To ensure that the students do not develop misconceptions, incorrect answers were corrected during whole-class discussion in both conditions. The students checked their answers during individual work with a solution sheet, which was only handed out when the students had solved all the tasks, or the answers were discussed in class (see Supplementary file 1 and 2 for examples).

Measures

Adaptivity

A subtraction strategy test was administered at T1–T4 to assess students’ adaptivity. At each point, the test contained 11 items, of which six were linked across all points of measurement, while the other five items varied (anchor items: 532 – 476, 720 – 269, 534 – 399, 502 – 299, 802 – 797, 475 – 469). Students solved three-digit subtraction problems (exception: two two-digit tasks in the pretest). The tasks evoked the use of number-based strategies and the standard written algorithm. The students were prompted, “Solve the tasks in a clever way. Write down how you solved the tasks.” The test time was 28 min to ensure that the students had sufficient time to reflect on the most adaptive strategy.

For each of the students’ solutions, the used strategies were coded using a detailed coding system comprising 32 subtraction strategiesFootnote 2 (κ ≥ 0.88). Moreover, the adaptivity of students’ solutions was assessed. Two independent raters estimated the adaptivity for each of the 32 strategies on a 3-point scale for each subtraction task with a standardized coding manual (0 = non-adaptive, 1 = partially adaptive, 2 = highly adaptive; Heinze et al., 2018). The following criteria were considered: number of solution steps, mental effort, and error rate (for an example rating, see Supplementary file 5). This rating was independent of the accuracy of the solutions: even if a student solved a subtraction task incorrectly due to a calculation error or inaccurate use of the strategy, the chosen strategy could still be rated as partially or highly adaptive (Heinze et al., 2018). Interrater reliability was calculated for each of the 26 different tasks over the ratings for each of the 32 strategies of both raters and was satisfactory overall (0.63 ≤ κweighted ≤ 1.00, M = 0.87, SD = 0.10). When raters did not agree, a consensus was negotiated. Adaptivity was scaled longitudinally over the four points of measurement using a one-dimensional partial credit model with virtual persons with ConQuest parametrization (Robitzsch et al., 2018). The advantage of using virtual persons to estimate person-parameters longitudinally is that the item difficulties are equated over the different points of measurement. The person-parameters of all points of measurement can be interpreted as values from the same scale. Therefore, the difference of person-parameters between different time-points can be interpreted as the growth or decline of individuals’ abilities (Hartig & Kühnbach, 2006).

Four of the anchor items and nine of the varying items were dichotomized because the intermediate category was represented in less than 10%, whereas the other items remained trichotomous. One anchor item and one of the varying items of T3 were underfitting and thus removed from the model. The remaining items had an acceptable item fit (0.67 < WMNSQ < 1.32). The EAP/PV-reliability of 0.82, as well as the WLE-reliability of 0.79, were satisfactory (σ2WLE = 1.92). Recursive partitioning for partial credit models did not detect DIF between the two groups (Zeileis et al., 2018). The person-parameters were estimated using WLE. Person-parameters do not have an explicit minimum or maximum, and they can reach negative as well as positive values, with higher values representing a higher level of adaptivity.

Prior arithmetical knowledge

Students’ arithmetical knowledge was measured before the intervention (T0). The measurement captured their knowledge of numbers, number relations, and the relation of addition and subtraction, as well as their competencies in addition (for sample tasks, see Supplementary file 6). The test consisted of 25 tasks and was scaled using a 1-PL logistic model for dichotomous data with the R-Package TAM (Robitzsch et al., 2018). The items had acceptable WMNSQ between 0.79 and 1.22. The EAP/PV- (0.82) and WLE-reliability (0.86) were satisfactory (σ2WLE = 1.86). The person-parameters were calculated using WLE (M =  − 0.01, SD = 1.46).

Need for cognition

We administered an NFC scale consisting of 10 items (Keller et al., 2019) before the intervention took place at T0 (Supplementary file 7). The items comprised self-reports about students’ enjoyment of cognitive activities (e.g., “Thinking is fun for me”) and about students’ seeking of cognitively effortful activities (e.g., “I like to solve tricky problems”). The items were read aloud by the test leaders to counter possible reading difficulties of students. Items were answered on a 4-point Likert scale ranging from “Not true at all” to “Very true.” Sample reliability was satisfactory (α = 0.84; M = 3.01, SD = 0.58).

Analyses

All research questions were addressed using multiple-group (interleaved vs blocked) latent growth curve models (LGCMs), which is a suitable statistical approach to evaluate experimental studies and, in particular, to analyze differences in development on the group and the individual level (Hesser, 2015). LGCMs provide the possibility to estimate mean growth trajectories, as well as between-person differences in development and potential moderating effects of covariates on students’ learning trajectories (Duncan & Duncan, 2004; Meredith & Tisak, 1990). The development is modelled by an intercept and slope factor(s). Given that the first time point is fixed to zero, the mean of the intercept represents the mean starting value of individuals, and the associated variance indicates whether there are interindividual differences regarding students’ intercept. LGCMs can be extended by adding a slope factor, e.g., a linear slope, which describes the mean linear trend and interindividual differences in development. However, students do not linearly improve their competencies, and especially in intervention studies, their ability might decrease after the treatment when resuming their regular mathematics lessons. Therefore, we tested whether the inclusion of a quadratic slope factor is more appropriate to describe our data.

To detect the most appropriate LGCM, we compared the following multiple-group LGCM: intercept only; intercept and linear slope; intercept, linear slope, and quadratic slope. To take the different time intervals between the points of measurement into account, we specified the factor loadings of the slope factors under consideration of the weeks between the measures (T1: λ = 0, T2: λ = 3, T3: λ = 4, T4: λ = 8; Preacher et al., 2008). The factor loadings were squared for the quadratic slope factor.

To address our research questions as to whether students’ prior arithmetical knowledge and NFC have a moderating effect on the effectiveness of interleaved/blocked practice on students’ learning gains in using subtraction strategies adaptively, we extended our multiple-group LGCM by including students’ prior arithmetical knowledge and NFC as covariates (Fig. 3). We used likelihood ratio tests to test for interaction effects of the covariates with teaching condition. All analyses were conducted with Mplus Version 8.5 using MLR-estimator and full information maximum likelihood (FIML) to deal with missing values.

Fig. 3
figure 3

Multiple-group LGCM (blocked vs interleaved) with NFC and prior knowledge as covariates

Full size image

Results

Descriptive statistics

Table 3 displays the latent means and standard deviations for students’ adaptivity at the four points of measurement. A descriptive analysis of the development of the adaptive use of subtraction strategies reveals improvements from T1 to T3 and a decline from T3 to T4 in both conditions.

Table 3 Latent means and standard deviations in adaptivity separately for the interleaved and blocked condition
Full size table

Development of the adaptive use of subtraction strategies

We compared different multiple-group LGCMs to detect the optimal growth function over the four points of measurement. Table 4 shows that a quadratic LGCM, which captures an increase as well as a decline in growth, describes students’ learning trajectories best. Therefore, a quadratic LGCM was used for all subsequent analyses.

Table 4 Model comparison for multiple-group (interleaved vs blocked) LGCM
Full size table

Table 5 shows the coefficients, standard errors, and p-values for the means, variances, and covariances of the intercept, slope, and quadratic slope. There was no significant difference between the two groups in the intercept, χ2(1) = 0.03, p = 0.86. The interleaved group exhibited a significant stronger linear growth in adaptivity (linear slope = 0.79) than the blocked group (linear slope = 0.29), χ2(1) = 35.72, p < 0.001. The means of the quadratic slope also differed significantly between the two conditions, χ2(1) = 33.49, p < 0.001, meaning that interleaved learning (quadratic slope =  − 0.07) was accompanied by a slightly stronger inhibition and decline of growth compared to blocked practice (quadratic slope =  − 0.03).

Table 5 LGCM parameters for the interleaved and blocked condition in adaptivity
Full size table

Effects of prior knowledge and NFC

Next, students’ prior arithmetical knowledge (research question 1) and NFC (research question 2) were included in the multiple-group LGCM as predictor variables to investigate whether these variables interact with our learning conditions. The extended multiple-group LGCM had a satisfactory fit, χ2(13) = 15.14, p = 0.30, RMSEA = 0.04, CFI = 1.00, TLI = 0.99, SRMR = 0.03.

Students’ prior arithmetical knowledge had a significant positive effect on the intercept in both the interleaved (β = 0.34, 95% CI (0.16; 0.52), SE = 0.09, p < 0.001) and blocked condition (β = 0.21, 95% CI (0.01; 0.41), SE = 0.10, p < 0.05), meaning that students with greater prior arithmetical knowledge solved the tasks more adaptively at T1. The difference in the parameters between the two groups was not significant (χ2(1) = 2.19, p = 0.14). Regarding linear growth, students’ prior knowledge had a significant positive effect in the blocked condition (β = 0.26, 95% CI (0.01; 0.50), SE = 0.12, p < 0.05) but not in the interleaved condition (β = 0.15, 95% CI (− 0.07; 0.37), SE = 0.11, p = 0.17). However, as the strongly overlapping confidence intervals show, the regression parameters did not differ significantly between the two groups, χ2(1) = 0.26, p = 0.61. Contrary to H1, with respect to linear growth no differential effect of prior knowledge for blocked and interleaved practice was found. Regarding the quadratic slope, prior arithmetical knowledge had no significant influence in both conditions (interleaved: β =  − 0.11, 95% CI (− 0.34; 0.13), SE = 0.12, p = 0.38; blocked: β =  − 0.23, 95% CI (− 0.51; 0.05), SE = 0.14, p = 0.10), and there was no significant difference between the two conditions regarding the effect on the quadratic slope, χ2(1) = 0.34, p = 0.56.

In both groups, students’ NFC did not have a significant impact on intercept (interleaved: β =  − 0.14, 95% CI (− 0.33; 0.04), SE = 0.10, p = 0.13; blocked: β = 0.10, 95% CI (− 0.13; 0.34), SE = 0.12, p = 0.39), and the two conditions did not differ regarding the effect of NFC on intercept, χ2(1) = 1.58, p = 0.21. Students’ NFC affected linear growth only in the interleaved condition (β = 0.21, 95% CI (0.01; 0.41), SE = 0.10, p < 0.05), but not in the blocked condition (β =  − 0.09, 95% CI (− 0.32; 0.13), SE = 0.12, p = 0.41). This result indicates that the higher the students’ NFC in the interleaved condition, the higher their learning gains, while it does not influence linear growth in the blocked condition. However, we have to reject H2 as the difference in the parameters failed to reach significance, χ2(1) = 3.51, p = 0.06. NFC had a significant influence on the quadratic slope in the interleaved condition (β =  − 0.21, 95% CI (− 0.41; − 0.00), SE = 0.11, p < 0.05), but not in the blocked one (β = 0.05, 95% CI (− 0.19; 0.30), SE = 0.13, p = 0.68). Nonetheless, the regression parameters did not differ significantly, χ2(1) = 2.96, p = 0.08).

Discussion

We investigated the role of students’ prior arithmetical knowledge and NFC in the effectiveness of interleaved practice and blocked practice on students’ adaptive use of subtraction strategies in third-grade mathematics. Regarding research question 1, our multiple-group LGCM has shown that students’ prior arithmetical knowledge had a significantly positive influence on learning gains in the blocked condition (research question 1). Thus, a Matthew effect (Merton, 1968; Rigney, 2010; Simonsmeier et al., 2021) was found for blocked learning, meaning that higher prior arithmetical knowledge was accompanied by stronger linear growth in adaptivity. One reason for this result could be that the students in our blocked condition were not explicitly prompted to compare the subtraction strategies (between-comparison). They were only prompted to decide whether tasks can be solved adaptively with a specific strategy (within-comparison). To select the most appropriate strategy for specific subtraction tasks, students need to compare multiple strategies to focus on and discern the central characteristics of the task (Kullberg et al., 2017; Marton & Pang, 2006). Therefore, it can be assumed that students with higher prior knowledge were more capable of engaging in these necessary comparison activities over a longer period and without our instructional support initiating between-comparisons, which we, on the contrary, provided in our interleaved condition. Although prior arithmetical knowledge had a significant impact on linear growth in the blocked but not in the interleaved condition, this difference is negligible as the parameters did not differ significantly. No significant differential effect of prior arithmetical knowledge on students’ learning gains regarding adaptivity between interleaved and blocked practice was found. Therefore, H1, with which we expected that students’ prior knowledge has a stronger impact on learning gains in blocked practice, has to be rejected.

Regarding research question 2, we investigated the role of students’ NFC for interleaved and blocked practice. While students’ NFC had a positive influence on the linear slope in the interleaved condition, meaning that students with a higher NFC had greater learning gains in the adaptive use of subtraction strategies, such an effect was not found in the blocked condition. Because interleaved practice combined with prompts to compare is more cognitively demanding than blocked learning, interleaved practice is more beneficial for students higher in NFC, i.e., with more pronounced enjoyment of and engagement in cognitively demanding activities. Our interleaved teaching approach probably matches these students’ high NFC, leading to deeper information processing and thus higher learning gains (Evans et al., 2003). On the contrary, practicing different subtraction strategies successively, as in our blocked condition, does not urge students to engage in cognitively demanding comparison processes. However, the parameters between the two conditions did not differ significantly, although the confidence intervals were only slightly overlapping. Thus, we have to reject H2, with which we expected differential effects of students’ NFC on interleaved and blocked practice.

The results related to the role of NFC in students’ learning gains when learning subtraction strategies in an interleaved fashion raise the question of how students low in NFC can be supported to benefit more from interleaved practice. One possibility could be to gradually shift from a blocked to an interleaved practice of subtraction strategies, rather than implementing a pure form of interleaved practice. To be able to detect the differences between the tasks and thus decide which strategy is most adaptive, students need sufficient knowledge about when to use which strategy. This could be promoted by an initial blocked learning phase. Through an initial blocked phase, students get the chance to detect similarities between different subtraction tasks that can all be solved adaptively with the same subtraction strategy. The subsequent interleaved learning phase then offers students the chance to distinguish between subtraction tasks that are solved adaptively with different subtraction strategies. Hence, as students’ proficiency increases, contextual interference and thus task difficulty increases as well (Nakata & Suzuki, 2019; Rohrer & Hartwig, 2020). Such an approach could reduce cognitive effort since students would start with a more pronounced prior knowledge regarding the adaptive use of the different subtraction strategies in interleaved practice. Because research on increasing interleaved practice is inconsistent (e.g., Nakata & Suzuki, 2019; Pan et al., 2019; Sorensen & Woltz, 2016; Yan et al., 2017) and lacking for primary school mathematics, further research is required to investigate the assumed benefits of increasing interleaved practice for third-graders’ adaptive use of subtraction strategies—especially for those low in NFC.

There are some limitations regarding our study that must be considered. First, due to our complex statistical models, statistical power was limited. Thus, smaller effects may have remained undiscovered, e.g., a possible differential effect of NFC on interleaved vs blocked practice, as suggested by the slightly overlapping confidence intervals of the two conditions regarding the effect of NFC on students’ learning trajectories. Second, we combined interleaved practice with prompts to compare. Therefore, we cannot conclusively identify which of the instructional approaches is responsible for the impressive learning gains in our interleaved condition. Moreover, we cannot make a conclusive statement on whether prior arithmetical knowledge and NFC interact differently with interleaved/blocked practice and with comparison learning, since our intervention combined both instructional approaches. Third, our results indicate that interleaved practice combined with prompts to compare can promote students' adaptive use of subtraction strategies. However, further research needs to examine whether the positive effects of interleaved practice, including prompts to compare, and the role of prior knowledge and NFC, are transferable to other mathematical topics and other domains.