Efficiency analysis in two-stage structures using fuzzy data envelopment analysis

Abstract

Two-stage data envelopment analysis (TsDEA) models evaluate the performance of a set of production systems in which each system includes two operational stages. Taking into account the internal structures is commonly found in many situations such as seller-buyer supply chain, health care provision and environmental management. Contrary to conventional DEA models as a black-box structure, TsDEA provides further insight into sources of inefficiencies and a more informative basis for performance evaluation. In addition, ignoring the qualitative and imprecise data leads to distorted evaluations, both for the subunits and the system efficiency. We present the fuzzy input and output-oriented TsDEA models to calculate the global and pure technical efficiencies of a system and sub-processes when some data are fuzzy. To this end, we propose a possibilistic programming problem and then convert it into a deterministic interval programming problem using the α-level based method. The proposed method preserves the link between two stages in the sense that the total efficiency of the system is equal to the product of the efficiencies derived from two stages. In addition to the study of technical efficiency, this research includes two further contributions to the ancillary literature; firstly, we minutely discuss the efficiency decompositions to indicate the sources of inefficiency and secondly, we present a method for ranking the efficient units in a fuzzy environment. An empirical illustration is also utilised to show the applicability of the proposed technique.

Appendix 1. Fuzzy sets theory

This appendix reviews some basic definitions of fuzzy sets theory and fuzzy numbers (Zimmermann 1996).

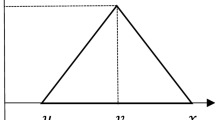
Let U be a universe set. A fuzzy set $\tilde{M}$ in the universe set U is defined by the membership function $\mu_{{\tilde{M}}} \left( x \right) \to \left[ {0,1} \right]$ where $\forall x \in U \to \mu_{{\tilde{M}}} \left( x \right)$ stands for the grade of membership of $\tilde{M}$ in U. A fuzzy subset $\tilde{M}$ is said to be normal and convex if $\mathop {\sup }\limits_{x \in U} \mu_{{\tilde{M}}} \left( x \right) = 1$ and $\mu_{{\tilde{M}}} \left( {\lambda x + \left( {1 - \lambda } \right)y} \right) \ge \left( {\mu_{{\tilde{M}}} \left( x \right) \wedge \mu_{{\tilde{M}}} \left( y \right)} \right), \forall x,y \in U, \forall \lambda \in \left[ {0,1} \right]$, respectively, where $\wedge$ is the minimum operator. A fuzzy number is a normal and convex fuzzy subset with a given membership whose grade varies between 0 and 1. A triangular fuzzy number, denoted as $\tilde{M} = \left( {l,m,u} \right)$, is the most widely used fuzzy numbers in practice and theory with the following membership function:

$$ \mu _{{\tilde{M}}} (x) = \left\{ {\begin{array}{*{20}l} {\frac{{x - l}}{{m - l}},} \hfill & {l \le {\text{x}} \le m} \hfill \\ {\frac{{u - x}}{{u - m}},} \hfill & {m < {\text{x}} \le u} \hfill \\ {0,} \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right. $$

Note that a crisp number M is a special case of the triangular fuzzy number in which $l = m = u.$