Analytical technique for electroelastic field in piezoelectric bodies belonging to point group D _∞

Abstract

To elucidate the electroelastic field in woods, which are piezoelectric bodies belonging to point group D _∞, we construct an analytical technique for general solutions to electroelastic problems in these bodies. First, the constitutive equations are derived considering the microstructures and their combined behaviors. Then, the displacement and electric field are expressed in terms of two types of displacement potential functions and the electric potential function, and their governing equations are obtained using the fundamental equations for the electroelastic field. As a result, the electroelastic field quantities are found to be expressed in terms of four functions, namely two elastic displacement potential functions and two piezoelastic displacement potential functions, each of which satisfies a Laplace equation with respect to the appropriately transformed spatial coordinates. As an application of the technique, the electroelastic field in a semi-infinite body subjected to a prescribed electric potential on its surface is analyzed, and the numerical results are illustrated. This novel technique serves to investigate the electroelastic field inside wooden materials.

Introduction

The concepts of carbon neutrality have attracted considerable attention recently because of an increasing demand for a reduction in environmental loads. From the viewpoint of engineering production, wooden materials are one of the most promising candidates for achieving carbon neutrality.

To ensure the quality of wooden materials, nondestructive evaluation techniques need to be developed. In particular, the detection of local defects such as cracks, knots, and pith is of great importance for ensuring structural integrity. Wood has been known as a piezoelectric material since the middle of the 20th century, when Fukada succeeded in experimentally verifying the direct and converse piezoelectric effects of wood [1]. Using piezoelectric effects, the mechanical behaviors of wood were investigated; the piezoelectric signals were related to the profiles of defects [2–4] and to the deformation [5, 6] and stress–strain relation [7, 8].

Because wooden materials are composed of complicated microstructures, a microscopic approach is preferable to investigate their electroelastic properties in detail, and investigations from such an approach were actually made for elastic [9, 10], dielectric [11, 12], and piezoelectric [13] properties. In the design procedures of engineering applications, however, such an approach requires a considerably high computational cost and is not practical. Therefore, a macroscopic approach is required.

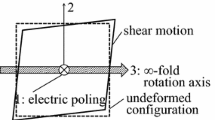
From a macroscopic viewpoint, woods are generally recognized as orthotropic materials with their principal axes in the longitudinal, radial, and tangential directions: the piezoelectric constants as orthotropic materials are actually detected [13, 14]. From a mesoscopic viewpoint, however, woods are considered to belong to point group $D_{\infty }$ [1], which is characterized by an $\infty$-fold rotation axis and a twofold rotation axis perpendicular to it [15]. More specifically, the elastic stiffness constant and dielectric constant exhibit the same symmetry as transverse isotropy, but the nonzero components of the piezoelectric constant are $d_{14}$ and $d_{25} \left( { = - d_{14} } \right)$ only, allowing the $\infty$-fold rotation axis be the third axis, and the pyroelectric constant disappears. In that case, the electric field perpendicular to the $\infty$-fold rotation axis (third axis) induces shear strain in the plane perpendicular to the direction of the electric field, as shown in Fig. 1. In woods, $D_{\infty }$ symmetry appears as follows. Many molecular chains of natural cellulose aggregate into a microcrystalline structure called a micelle, which belongs to point group $C_{2}$ and has the resultant dipole moment in the chain direction; many micelles aggregate into a microfibril and then into a fiber, in a manner that makes the twofold rotation axes of $C_{2}$ randomly parallel or antiparallel to the fiber direction and orients the axes perpendicular to the twofold rotation axes in random directions [1, 8]. As a result, $D_{\infty }$ symmetry appears.

Fig. 1

Piezoelectric effect through $d_{14}$

As stated above, the elastic stiffness constant and dielectric constant of a body belonging to point group $D_{\infty }$ exhibit the same symmetry as those of transversely isotropic bodies. Therefore, elastic problems, which do not involve the piezoelectric constants, of bodies with $D_{\infty }$ symmetry can be regarded as elastic problems of transversely isotropic bodies, which were extensively analyzed for two- or three-dimensional cases, e.g., [16–31]. On the other hand, electroelastic problems of bodies belonging to point group $D_{\infty }$ were investigated experimentally for wood [5–8]. To the best of our knowledge, however, theoretical analyses of electroelastic problems in such bodies do not appear in the literature.

In this study, therefore, we construct an analytical technique for obtaining general solutions to electroelastic problems in bodies belonging to point group $D_{\infty }$. First, the displacement and electric field are expressed in terms of two types of displacement potential functions and the electric potential function. Then, the equations that these potential functions should satisfy are obtained by the equilibrium equations of stresses and the Gauss law. As a result, the electroelastic field quantities, including the displacement, strain, stress, electric potential, electric field, and electric displacement, are found to be expressed in terms of four functions, namely, two elastic displacement potential functions and two piezoelastic displacement potential functions, each of which satisfies a Laplace equation with respect to the spatial coordinates transformed by the material properties of the body. Moreover, as an application of the technique, we analyze the electroelastic field in a semi-infinite body subjected to a prescribed electric potential on its surface, which is one of the most elementary models of nondestructive evaluation by use of the piezoelectric effects, and illustrate the results graphically.

General solution technique

Fundamental equations

We consider a piezoelectric body belonging to point group $D_{\infty }$. The Cartesian coordinate system $(x,y,z)$ is defined so that the $z$ axis is parallel to the $\infty$-fold rotation axis of the body. Let $(u_{x} ,u_{y} ,u_{z} )$, $(\varepsilon_{xx} ,\varepsilon_{yy} ,\varepsilon_{zz} ,\varepsilon_{yz} ,\varepsilon_{zx} ,\varepsilon_{xy} )$, $(\sigma_{xx} ,\sigma_{yy} ,\sigma_{zz} ,\sigma_{yz} ,\sigma_{zx} ,\sigma_{xy} )$, $(E_{x} ,E_{y} ,E_{z} )$, and $(D_{x} ,D_{y} ,D_{z} )$ be the components of the displacement, strain, stress, electric field, and electric displacement, respectively. The displacement–strain relations are given as

$$ \varepsilon_{xx} = \frac{{\partial u_{x} }}{\partial x},\,\,\varepsilon_{yy} = \frac{{\partial u_{y} }}{\partial y},\,\,\varepsilon_{zz} = \frac{{\partial u_{z} }}{\partial z},\,\,2\varepsilon_{yz} = \frac{{\partial u_{y} }}{\partial z} + \frac{{\partial u_{z} }}{\partial y},\,\,2\varepsilon_{zx} = \frac{{\partial u_{z} }}{\partial x} + \frac{{\partial u_{x} }}{\partial z},\,\,2\varepsilon_{xy} = \frac{{\partial u_{x} }}{\partial y} + \frac{{\partial u_{y} }}{\partial x} . $$

(1)

The constitutive equations of the body for an isothermal case are given as

$$ \left\{ {\begin{array}{*{20}c} {\sigma_{xx} } \\ {\sigma_{yy} } \\ {\sigma_{zz} } \\ {\sigma_{yz} } \\ {\sigma_{zx} } \\ {\sigma_{xy} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {c_{11} } & {c_{12} } & {c_{13} } & 0 & 0 & 0 \\ {} & {c_{11} } & {c_{13} } & 0 & 0 & 0 \\ {} & {} & {c_{33} } & 0 & 0 & 0 \\ {} & {} & {} & {c_{44} } & 0 & 0 \\ {} & {} & {} & {} & {c_{44} } & 0 \\ {{\text{sym}} .} & {} & {} & {} & {} & {\frac{{c_{11} - c_{12} }}{2}} \\ \end{array} } \right]\times\left\{ {\begin{array}{*{20}c} {\varepsilon_{xx} } \\ {\varepsilon_{yy} } \\ {\varepsilon_{zz} } \\ {2\varepsilon_{yz} } \\ {2\varepsilon_{zx} } \\ {2\varepsilon_{xy} } \\ \end{array} } \right\} - \left[ {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ {e_{14} } & 0 & 0 \\ 0 & { - e_{14} } & 0 \\ 0 & 0 & 0 \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {E_{x} } \\ {E_{y} } \\ {E_{z} } \\ \end{array} } \right\} , $$

(2)

$$ \left\{ {\begin{array}{*{20}c} {D_{x} } \\ {D_{y} } \\ {D_{z} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & {e_{14} } & 0 & 0 \\ 0 & 0 & 0 & 0 & { - e_{14} } & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{xx} } \\ {\varepsilon_{yy} } \\ {\varepsilon_{zz} } \\ {2\varepsilon_{yz} } \\ {2\varepsilon_{zx} } \\ {2\varepsilon_{xy} } \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} {\eta_{11} } & 0 & 0 \\ {} & {\eta_{11} } & 0 \\ {{\text{sym}}.} & {} & {\eta_{33} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {E_{x} } \\ {E_{y} } \\ {E_{z} } \\ \end{array} } \right\} , $$

(3)

where $c_{ij}$, $\eta_{kl}$, and $e_{kj}$ denote the elastic stiffness constant, dielectric constant, and piezoelectric constant, respectively. Equations (2) and (3) are derived in Appendix 1. The components of stress and electric displacement are chosen as dependent variables in Eqs. (2) and (3) because the governing equations are described in terms of those components as shown later in Eqs. (7) and (8). Here, by denoting

$$ \left. \begin{gathered} \left\{ {\varvec{\upsigma}} \right\} \equiv \left\{ {\begin{array}{*{20}c} {\sigma_{xx} } & {\sigma_{yy} } & {\sigma_{zz} } & {\sigma_{yz} } & {\sigma_{zx} } & {\sigma_{xy} } \\ \end{array} } \right\}^{\text{T}} ,\,\,\,\,\left\{ {\varvec{\varepsilon}} \right\} \equiv \left\{ {\begin{array}{*{20}c} {\varepsilon_{xx} } & {\varepsilon_{yy} } & {\varepsilon_{zz} } & {2\varepsilon_{yz} } & {2\varepsilon_{zx} } & {2\varepsilon_{xy} } \\ \end{array} } \right\}^{\text{T}} , \hfill \\ \left\{ {\mathbf{D}} \right\} \equiv \left\{ {\begin{array}{*{20}c} {D_{x} } & {D_{y} } & {D_{z} } \\ \end{array} } \right\}^{\text{T}} ,\,\,\,\,\left\{ {\mathbf{E}} \right\} \equiv \left\{ {\begin{array}{*{20}c} {E_{x} } & {E_{y} } & {E_{z} } \\ \end{array} } \right\}^{\text{T}} , \hfill \\ \left[ {\mathbf{c}} \right] \equiv \left[ {\begin{array}{*{20}c} {c_{11} } & {c_{12} } & {c_{13} } & 0 & 0 & 0 \\ {} & {c_{11} } & {c_{13} } & 0 & 0 & 0 \\ {} & {} & {c_{33} } & 0 & 0 & 0 \\ {} & {} & {} & {c_{44} } & 0 & 0 \\ {} & {} & {} & {} & {c_{44} } & 0 \\ {{\text{sym}} .} & {} & {} & {} & {} & {\frac{{c_{11} - c_{12} }}{2}} \\ \end{array} } \right], \hfill \\ \left[ {\varvec{\upeta}} \right] \equiv \left[ {\begin{array}{*{20}c} {\eta_{11} } & 0 & 0 \\ {} & {\eta_{11} } & 0 \\ {{\text{sym}} .} & {} & {\eta_{33} } \\ \end{array} } \right],\,\,\,\,\left[ {\mathbf{e}} \right] = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & {e_{14} } & 0 & 0 \\ 0 & 0 & 0 & 0 & { - e_{14} } & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right] \hfill \\ \end{gathered} \right\} , $$

(4)

the energy density stored in the body, $u_{\text{piezo}}$, is defined and calculated from Eqs. (2) and (3) as

$$ u_{\text{piezo}} \equiv \frac{1}{2}\left( {\left\{ {\varvec{\upsigma}} \right\}^{\text{T}} \left\{ {\varvec{\upvarepsilon}} \right\} + \left\{ {\mathbf{E}} \right\}^{\text{T}} \left\{ {\mathbf{D}} \right\}} \right) = \frac{1}{2}\left( {\left\{ {\varvec{\upvarepsilon}} \right\}^{\text{T}} \left[ {\mathbf{c}} \right]\left\{ {\varvec{\upvarepsilon}} \right\} + \left\{ {\mathbf{E}} \right\}^{\text{T}} \left[ {\varvec{\upeta}} \right]\left\{ {\mathbf{E}} \right\}} \right) . $$

(5)

For an equilibrium state to be stable, the quadratic forms $\left\{ {\varvec{\upvarepsilon}} \right\}^{\text{T}} \left[ {\mathbf{c}} \right]\left\{ {\varvec{\upvarepsilon}} \right\}$ and $\left\{ {\mathbf{E}} \right\}^{\text{T}} \left[ {\varvec{\upeta}} \right]\left\{ {\mathbf{E}} \right\}$ in Eq. (5) must be positive definite. They are positive definite if and only if all the principal minors of $\left[ {\mathbf{c}} \right]$ and $\left[ {\varvec{\upeta}} \right]$ are positive [32]. By arranging these conditions, we finally have the conditions required for the material properties:

$$ \left. \begin{gathered} c_{11} > 0,\,\,\,\,c_{33} > 0,\,\,\,\,c_{44} > 0,\,\,\,\,c_{11} - c_{12} > 0,\,\,\,\,c_{11} + c_{12} > 0, \hfill \\ c_{11} c_{33} - c_{13}^{2} > 0,\,\,\,\,\left( {c_{11} + c_{12} } \right)c_{33} - 2c_{13}^{2} > 0,\,\,\,\,\eta_{11} > 0,\,\,\,\,\eta_{33} > 0 \hfill \\ \end{gathered} \right\} . $$

(6)

The equilibrium equations of stresses and the Gauss law are given, respectively, by

$$ \frac{{\partial \sigma_{xx} }}{\partial x} + \frac{{\partial \sigma_{xy} }}{\partial y} + \frac{{\partial \sigma_{zx} }}{\partial z} = 0,\,\,\,\,\frac{{\partial \sigma_{yy} }}{\partial y} + \frac{{\partial \sigma_{yz} }}{\partial z} + \frac{{\partial \sigma_{xy} }}{\partial x} = 0,\,\,\,\,\frac{{\partial \sigma_{zz} }}{\partial z} + \frac{{\partial \sigma_{zx} }}{\partial x} + \frac{{\partial \sigma_{yz} }}{\partial y} = 0 , $$

(7)

$$ \frac{{\partial D_{x} }}{\partial x} + \frac{{\partial D_{y} }}{\partial y} + \frac{{\partial D_{z} }}{\partial z} = 0 . $$

(8)

Governing equations for potential functions

We introduce the displacement potential functions $\varphi$ and $\vartheta$ as

$$ u_{x} = \frac{\partial \varphi }{\partial x} + \frac{\partial \vartheta }{\partial y},\,\,\,\,u_{y} = \frac{\partial \varphi }{\partial y} - \frac{\partial \vartheta }{\partial x},\,\,\,\,u_{z} = k\frac{\partial \varphi }{\partial z} , $$

(9)

where $k$ is an unknown coefficient at present. The components of the electric field are expressed by the electric potential function $\Phi$ as

$$ E_{x} = - \frac{\partial \Phi }{\partial x},\,\,\,\,E_{y} = - \frac{\partial \Phi }{\partial y},\,\,\,\,E_{z} = - \frac{\partial \Phi }{\partial z} . $$

(10)

Substituting Eqs. (1), (9), and (10) into Eqs. (2) and (3) and the results into Eqs. (7) and (8), we have

$$ c_{11} \Delta_{\text{p}} \varphi + \left[ {kc_{13} + \left( {1 + k} \right)c_{44} } \right]\frac{{\partial^{2} \varphi }}{{\partial z^{2} }} = 0 , $$

(11)

$$ \left[ {c_{13} + \left( {1 + k} \right)c_{44} } \right]\Delta_{\text{p}} \varphi + kc_{33} \frac{{\partial^{2} \varphi }}{{\partial z^{2} }} = 0 , $$

(12)

$$ \frac{{c_{11} - c_{12} }}{2}\Delta_{\text{p}} \vartheta + c_{44} \frac{{\partial^{2} \vartheta }}{{\partial z^{2} }} - e_{14} \frac{\partial \Phi }{\partial z} = 0 , $$

(13)

$$ e_{14} \frac{\partial }{\partial z}\left( {\Delta_{\text{p}} \vartheta } \right) + \left( {\eta_{11} \Delta_{\text{p}} \Phi + \eta_{33} \frac{{\partial^{2} \Phi }}{{\partial z^{2} }}} \right) = 0 , $$

(14)

where

$$ \Delta_{\text{p}} \equiv \frac{{\partial^{2} }}{{\partial x^{2} }} + \frac{{\partial^{2} }}{{\partial y^{2} }} . $$

(15)

For the governing Eqs. (11) and (12), which are both for $\varphi$, to be identical, the relation

$$ \frac{{kc_{13} + \left( {1 + k} \right)c_{44} }}{{c_{11} }} = \frac{{kc_{33} }}{{c_{13} + \left( {1 + k} \right)c_{44} }} \equiv \mu $$

(16)

must hold. Solving Eq. (16) for $k$, we have

$$ k = \frac{{c_{11} \mu - c_{44} }}{{c_{13} + c_{44} }} = \frac{{\left( {c_{13} + c_{44} } \right)\mu }}{{c_{33} - c_{44} \mu }} , $$

(17)

which leads to a quadratic equation for $\mu$:

$$ c_{11} c_{44} \mu^{2} - \left( {c_{11} c_{33} - c_{13}^{2} - 2c_{13} c_{44} } \right)\mu + c_{33} c_{44} = 0 . $$

(18)

Therefore, to solve $\mu$ in Eq. (18), Eqs. (11) and (12) both become

$$ \Delta_{p} \varphi + \mu \frac{{\partial^{2} \varphi }}{{\partial z^{2} }} = 0 . $$

(19)

Because the governing equation for the potential function $\varphi$ is found to be independent of the electric potential function $\Phi$ from Eq. (19), we refer to $\varphi$ as an elastic displacement potential function. On the other hand, because the potential function $\vartheta$ is found to be coupled to the electric potential function $\Phi$ through a piezoelectric constant from Eqs. (13) and (14), we refer to $\vartheta$ as a piezoelastic displacement potential function.

Governing equation for elastic displacement potential function

Let us denote the two roots of quadratic Eq. (18) as $\mu_{1}$ and $\mu_{2}$, the corresponding $\varphi$ as $\varphi_{1}$ and $\varphi_{2}$, and the corresponding $k$ as $k_{1}$ and $k_{2}$. Then, from Eq. (19), the governing equations for $\varphi_{1}$ and $\varphi_{2}$ are

$$ \Delta_{\text{p}} \varphi_{i} + \mu_{i} \frac{{\partial^{2} \varphi_{i} }}{{\partial z^{2} }} = 0\,\,\left( {i = 1,\,2} \right) . $$

(20)

From Eq. (17), we have

$$ k_{i} = \frac{{c_{11} \mu_{i} - c_{44} }}{{c_{13} + c_{44} }} = \frac{{\left( {c_{13} + c_{44} } \right)\mu_{i} }}{{c_{33} - c_{44} \mu_{i} }}\,\,\left( {i = 1,\,2} \right) . $$

(21)

When the condition

$$ c_{44} < \frac{{\sqrt {c_{11} c_{33} } - c_{13} }}{2} $$

(22)

holds, in other words, when the stiffness against the shear in the plane containing the $\infty$-fold rotation axis is low relative to the other stiffness components, we can obtain, from Eqs. (6) and (18),

$$ \mu_{1} \ne \mu_{2} ,\,\,\,\,\mu_{1} > 0,\,\,\,\,\mu_{2} > 0 ; $$

(23)

therefore, $\varphi_{1}$ and $\varphi_{2}$ are independent of each other. We treat the case described by Eqs. (22) or (23). The other cases are omitted for brevity.

Governing equation for piezoelastic displacement potential function

From Eqs. (13) and (14), we have

$$ \frac{{2e_{14} }}{{c_{11} - c_{12} }}\frac{\partial \Phi }{\partial z} = \Delta_{\text{p}} \vartheta + \mu_{3} \frac{{\partial^{2} \vartheta }}{{\partial z^{2} }} , $$

(24)

$$ \frac{{e_{14} }}{{\eta_{11} }}\frac{\partial }{\partial z}\left( {\Delta_{\text{p}} \vartheta } \right) + \Delta_{\text{p}} \Phi + \eta \frac{{\partial^{2} \Phi }}{{\partial z^{2} }} = 0 , $$

(25)

and, by substituting Eq. (24) into Eq. (25), we have

$$ \Delta_{\text{p}} \Delta_{\text{p}} \vartheta + \left[ {\mu_{3} \left( {1 + k_{\text{couple}}^{ 2} } \right) + \eta } \right]\Delta_{\text{p}} \left( {\frac{{\partial^{2} \vartheta }}{{\partial z^{2} }}} \right) + \mu_{3} \eta \frac{{\partial^{4} \vartheta }}{{\partial z^{4} }} = 0 , $$

(26)

where

$$ \mu_{3} = \frac{{2c_{44} }}{{c_{11} - c_{12} }},\,\,\,\,\eta = \frac{{\eta_{33} }}{{\eta_{11} }},\,\,\,\,k_{\text{couple}}^{ 2} = \frac{{e_{14}^{2} }}{{c_{44} \eta_{11} }} . $$

(27)

Equation (26) is rewritten as

$$ \left( {\Delta_{\text{p}} + \upsilon_{1} \frac{{\partial^{2} }}{{\partial z^{2} }}} \right)\left( {\Delta_{\text{p}} + \upsilon_{2} \frac{{\partial^{2} }}{{\partial z^{2} }}} \right)\vartheta = 0 , $$

(28)

where $\upsilon_{1}$ and $\upsilon_{2}$ are the two roots of a quadratic equation with respect to $\upsilon$:

$$ \upsilon^{2} - \left[ {\mu_{3} \left( {1 + k_{\text{couple}}^{ 2} } \right) + \eta } \right]\upsilon + \mu_{3} \eta = 0 . $$

(29)

When $e_{14} \ne 0$, we can obtain, from Eqs. (6), (27), and (29),

$$ \upsilon_{1} \ne \upsilon_{2} ,\,\,\,\,\upsilon_{1} > 0,\,\,\,\,\upsilon_{2} > 0 , $$

(30)

a general solution to Eq. (28) is obtained as

$$ \vartheta = \vartheta_{1} + \vartheta_{2} , $$

(31)

where $\vartheta_{1}$ and $\vartheta_{2}$ denote general solutions to

$$ \left( {\Delta_{\text{p}} + \upsilon_{i} \frac{{\partial^{2} }}{{\partial z^{2} }}} \right)\vartheta_{i} = 0\,\,\left( {i = 1,\,2} \right) . $$

(32)

Moreover, by substituting the $\vartheta$ obtained in this manner into Eq. (24), we can obtain the solution of $\Phi$.

General solution of electroelastic field

From Eq. (23) or (30), the governing Eq. (20) or (32) is regarded as a Laplace equation with respect to $\left( {x,\,y,\,{z \mathord{\left/ {\vphantom {z {\sqrt {\mu_{i} } }}} \right. \kern-0pt} {\sqrt {\mu_{i} } }}} \right)$ or $\left( {x,\,y,\,{z \mathord{\left/ {\vphantom {z {\sqrt {\upsilon_{i} } }}} \right. \kern-0pt} {\sqrt {\upsilon_{i} } }}} \right)$, respectively, whose general solutions are well established. By substituting the general solutions for $\varphi_{i}$ and $\vartheta_{i}$ $\left( {i = 1,\,2} \right)$ and the resulting electric potential function $\Phi$ obtained from Eqs. (24) and (31) into Eqs. (9) and (10) and, furthermore, by substituting the results into Eqs. (1)-(3), we have the general solutions for the electroelastic field quantities in the body as follows:

$$ u_{x} = \sum\limits_{i = 1}^{2} {\left( {\frac{{\partial \varphi_{i} }}{\partial x} + \frac{{\partial \vartheta_{i} }}{\partial y}} \right)} ,\,\,\,\,u_{y} = \sum\limits_{i = 1}^{2} {\left( {\frac{{\partial \varphi_{i} }}{\partial y} - \frac{{\partial \vartheta_{i} }}{\partial x}} \right)} ,\,\,\,\,u_{z} = \frac{\partial }{\partial z}\sum\limits_{i = 1}^{2} {k_{i} \varphi_{i} } , $$

(33)

$$ E_{x} = - \frac{\partial \Phi }{\partial x},\,\,\,\,E_{y} = - \frac{\partial \Phi }{\partial y},\,\,\,\,E_{z} = - \frac{\partial \Phi }{\partial z} , $$

(34)

$$ \left. \begin{gathered} \varepsilon_{xx} = \sum\limits_{i = 1}^{2} {\left( {\frac{{\partial^{2} \varphi_{i} }}{{\partial x^{2} }} + \frac{{\partial^{2} \vartheta_{i} }}{\partial x\partial y}} \right)} ,\,\,\,\,\varepsilon_{yy} = \sum\limits_{i = 1}^{2} {\left( {\frac{{\partial^{2} \varphi_{i} }}{{\partial y^{2} }} - \frac{{\partial^{2} \vartheta_{i} }}{\partial x\partial y}} \right)} ,\,\,\,\,\varepsilon_{zz} = \sum\limits_{i = 1}^{2} {k_{i} \frac{{\partial^{2} \varphi_{i} }}{{\partial z^{2} }}} , \hfill \\ 2\varepsilon_{yz} = \sum\limits_{i = 1}^{2} {\left[ {\left( {1 + k_{i} } \right)\frac{{\partial^{2} \varphi_{i} }}{\partial y\partial z} - \frac{{\partial^{2} \vartheta_{i} }}{\partial z\partial x}} \right]} ,\,\,\,\,2\varepsilon_{zx} = \sum\limits_{i = 1}^{2} {\left[ {\left( {1 + k_{i} } \right)\frac{{\partial^{2} \varphi_{i} }}{\partial z\partial x} + \frac{{\partial^{2} \vartheta_{i} }}{\partial y\partial z}} \right]} , \hfill \\ 2\varepsilon_{xy} = \sum\limits_{i = 1}^{2} {\left[ {2\frac{{\partial^{2} \varphi_{i} }}{\partial x\partial y} + \left( { - \frac{{\partial^{2} \vartheta_{i} }}{{\partial x^{2} }} + \frac{{\partial^{2} \vartheta_{i} }}{{\partial y^{2} }}} \right)} \right]} \hfill \\ \end{gathered} \right\} , $$

(35)

$$ \left. \begin{gathered} \sigma_{xx} = \sum\limits_{i = 1}^{2} {\left[ {\left( {c_{11} \frac{{\partial^{2} \varphi_{i} }}{{\partial x^{2} }} + c_{12} \frac{{\partial^{2} \varphi_{i} }}{{\partial y^{2} }} + k_{i} c_{13} \frac{{\partial^{2} \varphi_{i} }}{{\partial z^{2} }}} \right) + \left( {c_{11} - c_{12} } \right)\frac{{\partial^{2} \vartheta_{i} }}{\partial x\partial y}} \right]} , \\ \sigma_{yy} = \sum\limits_{i = 1}^{2} {\left[ {\left( {c_{12} \frac{{\partial^{2} \varphi_{i} }}{{\partial x^{2} }} + c_{11} \frac{{\partial^{2} \varphi_{i} }}{{\partial y^{2} }} + k_{i} c_{13} \frac{{\partial^{2} \varphi_{i} }}{{\partial z^{2} }}} \right) - \left( {c_{11} - c_{12} } \right)\frac{{\partial^{2} \vartheta_{i} }}{\partial x\partial y}} \right]} , \\ \sigma_{zz} = \sum\limits_{i = 1}^{2} {\left( {c_{13} \Delta_{\text{p}} \varphi_{i} + k_{i} c_{33} \frac{{\partial^{2} \varphi_{i} }}{{\partial z^{2} }}} \right)} , \\ \sigma_{yz} = c_{44} \sum\limits_{i = 1}^{2} {\left[ {\left( {1 + k_{i} } \right)\frac{{\partial^{2} \varphi_{i} }}{\partial y\partial z} - \frac{{\partial^{2} \vartheta_{i} }}{\partial z\partial x}} \right]} + e_{14} \frac{\partial \Phi }{\partial x}, \\ \sigma_{zx} = c_{44} \sum\limits_{i = 1}^{2} {\left[ {\left( {1 + k_{i} } \right)\frac{{\partial^{2} \varphi_{i} }}{\partial z\partial x} + \frac{{\partial^{2} \vartheta_{i} }}{\partial y\partial z}} \right]} - e_{14} \frac{\partial \Phi }{\partial y}, \\ \sigma_{xy} = \frac{{c_{11} - c_{12} }}{2}\sum\limits_{i = 1}^{2} {\left[ {2\frac{{\partial^{2} \varphi_{i} }}{\partial x\partial y} + \left( { - \frac{{\partial^{2} \vartheta_{i} }}{{\partial x^{2} }} + \frac{{\partial^{2} \vartheta_{i} }}{{\partial y^{2} }}} \right)} \right]} \\ \end{gathered} \right\} , $$

(36)

$$ \left. \begin{gathered} D_{x} = e_{14} \sum\limits_{i = 1}^{2} {\left[ {\left( {1 + k_{i} } \right)\frac{{\partial^{2} \varphi_{i} }}{\partial y\partial z} - \frac{{\partial^{2} \vartheta_{i} }}{\partial z\partial x}} \right]} - \eta_{11} \frac{\partial \Phi }{\partial x}, \hfill \\ D_{y} = - e_{14} \sum\limits_{i = 1}^{2} {\left[ {\left( {1 + k_{i} } \right)\frac{{\partial^{2} \varphi_{i} }}{\partial z\partial x} + \frac{{\partial^{2} \vartheta_{i} }}{\partial y\partial z}} \right]} - \eta_{11} \frac{\partial \Phi }{\partial y},\,\,\,\,D_{z} = - \eta_{33} \frac{\partial \Phi }{\partial z} \hfill \\ \end{gathered} \right\} . $$

(37)

Application

In this section, the general solution technique presented in "General solution technique" is applied to a concrete boundary value problem. As a first step, we choose one of the most fundamental problems to verify the validity of the proposed technique.

We consider a semi-infinite piezoelectric body $(x > 0)$ belonging to point group $D_{\infty }$, as shown in Fig. 2, where the $z$ axis is parallel to the $\infty$-fold rotation axis of the body. The surface of the body is subjected to the electric potential distribution $\Phi_{s} (y,z)$, which is symmetric with respect to $y$ and $z$, and is free from stresses. It should be noted that this is one of the most elementary models of nondestructive evaluation by use of the piezoelectric effects. The displacements and electric potential are assumed to be zero at infinity.

Fig. 2

Analytical model

Analysis

The boundary conditions are described as

$$ \left. {\begin{array}{*{20}l} {x = 0\,:} \hfill & {\sigma_{xx} = 0,\,\,\sigma_{zx} = 0,\,\,\sigma_{xy} = 0,\,\,\Phi = \Phi_{s} \left( {y,z} \right);} \hfill \\ {\sqrt {x^{2} + y^{2} + z^{2} } \to \infty \,:} \hfill & {u_{x} \to 0,\,\,u_{y} \to 0,\,\,u_{z} \to 0,\,\,\Phi \to 0} \hfill \\ \end{array} } \right\} . $$

(38)

By considering the symmetry of the electroelastic field, it is found that $\varphi_{i}$ is antisymmetric with respect to $y$ and $z$ and that $\vartheta_{i}$ is symmetric and antisymmetric with respect to $y$ and $z$, respectively. Therefore, the Fourier sine transforms with respect to $y$ and $z$ and their inversions [33] are applied to Eq. (20); the Fourier cosine transform with respect to $y$ and its inversion [33], and the Fourier sine transform with respect to $z$ and its inversion are applied to Eq. (32). Then, by considering the conditions at infinity described by Eq. (38), the general solutions to Eqs. (20) and (32) are obtained as

$$ \varphi_{i} = \int\limits_{0}^{\infty } {\int\limits_{0}^{\infty } {A_{i} \left( {\alpha ,\beta } \right)\exp \left( { - \gamma_{\mu i} x} \right)\sin \left( {\alpha y} \right)\sin \left( {\beta z} \right){\text{d}}\alpha {\text{d}}\beta } } \;\;\left( {i = 1,2} \right)\,\,\,\, , $$

(39)

$$ \vartheta_{i} = \int\limits_{0}^{\infty } {\int\limits_{0}^{\infty } {C_{i} \left( {\alpha ,\beta } \right)\exp \left( { - \gamma_{\upsilon i} x} \right)\cos \left( {\alpha y} \right)\sin \left( {\beta z} \right){\text{d}}\alpha {\text{d}}\beta } } \;\;\left( {i = 1,2} \right)\, , $$

(40)

where

$$ \gamma_{\mu i} = \sqrt {\alpha^{2} + \mu_{i} \beta^{2} } ,\,\,\,\,\gamma_{\upsilon i} = \sqrt {\alpha^{2} + \upsilon_{i} \beta^{2} } ; $$

(41)

$A_{i} \left( {\alpha ,\beta } \right)$ and $C_{i} \left( {\alpha ,\beta } \right)$ $\left( {i = 1,2} \right)$ are unknown constants to be determined by the boundary conditions described by Eq. (38). Furthermore, by substituting Eq. (40) into Eqs. (24) and (31) and integrating the result with respect to $z$, the general solution of the electric potential function is obtained as

$$ \Phi = \frac{{c_{44} }}{{e_{14} }}\frac{1}{{\mu_{3} }}\sum\limits_{i = 1}^{2} {\left[ {\int\limits_{0}^{\infty } {\int\limits_{0}^{\infty } {\left( {\mu_{3} - \upsilon_{i} } \right)\beta C_{i} \left( {\alpha ,\beta } \right)\exp \left( { - \gamma_{\upsilon i} x} \right)\cos \left( {\alpha y} \right)\cos \left( {\beta z} \right){\text{d}}\alpha {\text{d}}\beta } } } \right]} . $$

(42)

By substituting Eqs. (39)–(42) into Eqs. (33)–(37), the electroelastic field quantities are obtained as

$$ \left. \begin{gathered} u_{x} = \sum\limits_{i = 1}^{2} {\left\{ {\int\limits_{0}^{\infty } {\int\limits_{0}^{\infty } {\left[ \begin{gathered} - \gamma_{\mu i} A_{i} \left( {\alpha ,\beta } \right)\exp \left( { - \gamma_{\mu i} x} \right) \hfill \\ - \alpha C_{i} \left( {\alpha ,\beta } \right)\exp \left( { - \gamma_{\upsilon i} x} \right) \hfill \\ \end{gathered} \right]\sin \left( {\alpha y} \right)\sin \left( {\beta z} \right){\text{d}}\alpha {\text{d}}\beta } } } \right\},} \hfill \\ u_{y} = \sum\limits_{i = 1}^{2} {\left\{ {\int\limits_{0}^{\infty } {\int\limits_{0}^{\infty } {\left[ \begin{gathered} \alpha A_{i} \left( {\alpha ,\beta } \right)\exp \left( { - \gamma_{\mu i} x} \right) \hfill \\ + \gamma_{\upsilon i} C_{i} \left( {\alpha ,\beta } \right)\exp \left( { - \gamma_{\upsilon i} x} \right) \hfill \\ \end{gathered} \right]\cos \left( {\alpha y} \right)\sin \left( {\beta z} \right){\text{d}}\alpha {\text{d}}\beta } } } \right\}} , \hfill \\ u_{z} = \sum\limits_{i = 1}^{2} {k_{i} \left[ {\int\limits_{0}^{\infty } {\int\limits_{0}^{\infty } {\beta A_{i} \left( {\alpha ,\beta } \right)\exp \left( { - \gamma_{\mu i} x} \right)\sin \left( {\alpha y} \right)\cos \left( {\beta z} \right){\text{d}}\alpha {\text{d}}\beta } } } \right]} \hfill \\ \end{gathered} \right\} , $$

(43)

$$ \left. \begin{gathered} E_{x} = \frac{{c_{44} }}{{e_{14} \mu_{3} }}\sum\limits_{i = 1}^{2} {\left[ {\int\limits_{0}^{\infty } {\int\limits_{0}^{\infty } {\left( {\mu_{3} - \upsilon_{i} } \right)\gamma_{\upsilon i} \beta C_{i} \left( {\alpha ,\beta } \right)\exp \left( { - \gamma_{\upsilon i} x} \right)\cos \left( {\alpha y} \right)\cos \left( {\beta z} \right){\text{d}}\alpha {\text{d}}\beta } } } \right]} , \hfill \\ E_{y} = \frac{{c_{44} }}{{e_{14} \mu_{3} }}\sum\limits_{i = 1}^{2} {\left[ {\int\limits_{0}^{\infty } {\int\limits_{0}^{\infty } {\left( {\mu_{3} - \upsilon_{i} } \right)\alpha \beta C_{i} \left( {\alpha ,\beta } \right)\exp \left( { - \gamma_{\upsilon i} x} \right)\sin \left( {\alpha y} \right)\cos \left( {\beta z} \right){\text{d}}\alpha {\text{d}}\beta } } } \right]} , \hfill \\ E_{z} = \frac{{c_{44} }}{{e_{14} \mu_{3} }}\sum\limits_{i = 1}^{2} {\left[ {\int\limits_{0}^{\infty } {\int\limits_{0}^{\infty } {\left( {\mu_{3} - \upsilon_{i} } \right)\beta^{2} C_{i} \left( {\alpha ,\beta } \right)\exp \left( { - \gamma_{\upsilon i} x} \right)\cos \left( {\alpha y} \right)\sin \left( {\beta z} \right){\text{d}}\alpha {\text{d}}\beta } } } \right]} \hfill \\ \end{gathered} \right\} , $$

(44)

$$ \left. \begin{gathered} \varepsilon_{xx} = \sum\limits_{i = 1}^{2} {\left\{ {\int\limits_{0}^{\infty } {\int\limits_{0}^{\infty } {\left[ \begin{gathered} \gamma_{\mu i}^{2} A_{i} \left( {\alpha ,\beta } \right)\exp \left( { - \gamma_{\mu i} x} \right) \hfill \\ + \gamma_{\upsilon i} \alpha C_{i} \left( {\alpha ,\beta } \right)\exp \left( { - \gamma_{\upsilon i} x} \right) \hfill \\ \end{gathered} \right]\sin \left( {\alpha y} \right)\sin \left( {\beta z} \right){\text{d}}\alpha {\text{d}}\beta } } } \right\}} , \hfill \\ \varepsilon_{yy} = \sum\limits_{i = 1}^{2} {\left\{ {\int\limits_{0}^{\infty } {\int\limits_{0}^{\infty } {\left[ \begin{gathered} - \alpha^{2} A_{i} \left( {\alpha ,\beta } \right)\exp \left( { - \gamma_{\mu i} x} \right) \hfill \\ - \gamma_{\upsilon i} \alpha C_{i} \left( {\alpha ,\beta } \right)\exp \left( { - \gamma_{\upsilon i} x} \right) \hfill \\ \end{gathered} \right]\sin \left( {\alpha y} \right)\sin \left( {\beta z} \right){\text{d}}\alpha {\text{d}}\beta } } } \right\}} , \hfill \\ \varepsilon_{zz} = \sum\limits_{i = 1}^{2} {\left[ {\int\limits_{0}^{\infty } {\int\limits_{0}^{\infty } {\left( { - k_{i} \beta^{2} } \right)A_{i} \left( {\alpha ,\beta } \right)\exp \left( { - \gamma_{\mu i} x} \right)\sin \left( {\alpha y} \right)\sin \left( {\beta z} \right){\text{d}}\alpha {\text{d}}\beta } } } \right]} , \hfill \\ 2\varepsilon_{yz} = \sum\limits_{i = 1}^{2} {\left\{ {\int\limits_{0}^{\infty } {\int\limits_{0}^{\infty } {\left[ \begin{gathered} \left( {1 + k_{i} } \right)\alpha \beta A_{i} \left( {\alpha ,\beta } \right)\exp \left( { - \gamma_{\mu i} x} \right) \hfill \\ + \gamma_{\upsilon i} \beta C_{i} \left( {\alpha ,\beta } \right)\exp \left( { - \gamma_{\upsilon i} x} \right) \hfill \\ \end{gathered} \right]\cos \left( {\alpha y} \right)\cos \left( {\beta z} \right){\text{d}}\alpha {\text{d}}\beta } } } \right\}} , \hfill \\ 2\varepsilon_{zx} = \sum\limits_{i = 1}^{2} {\left\{ {\int\limits_{0}^{\infty } {\int\limits_{0}^{\infty } {\left[ \begin{gathered} - \left( {1 + k_{i} } \right)\gamma_{\mu i} \beta A_{i} \left( {\alpha ,\beta } \right)\exp \left( { - \gamma_{\mu i} x} \right) \hfill \\ - \alpha \beta C_{i} \left( {\alpha ,\beta } \right)\exp \left( { - \gamma_{\upsilon i} x} \right) \hfill \\ \end{gathered} \right]\sin \left( {\alpha y} \right)\cos \left( {\beta z} \right){\text{d}}\alpha {\text{d}}\beta } } } \right\}} , \hfill \\ 2\varepsilon_{xy} = \sum\limits_{i = 1}^{2} {\left\{ {\int\limits_{0}^{\infty } {\int\limits_{0}^{\infty } {{\left[ \begin{gathered} - 2\gamma_{\mu i} \alpha A_{i} \left( {\alpha ,\beta } \right)\exp \left( { - \gamma_{\mu i} x} \right) \hfill \\ - \left( {2\alpha^{2} + \upsilon_{i} \beta^{2} } \right)C_{i} \left( {\alpha ,\beta } \right)\exp \left( { - \gamma_{\upsilon i} x} \right) \hfill \\ \end{gathered} \right]\cos \left( {\alpha y} \right)\sin \left( {\beta z} \right){\text{d}}\alpha {\text{d}}\beta } } } } \right\}} \hfill \\ \end{gathered} \right\} , $$

(45)

$$ \left. \begin{gathered} \sigma_{xx} = \frac{{c_{44} }}{{\mu_{3} }}\sum\limits_{i = 1}^{2} {\left\{ {\int\limits_{0}^{\infty } {\int\limits_{0}^{\infty } {\left[ \begin{gathered} \left( {2\alpha^{2} + \left( {1 + k_{i} } \right)\mu_{3} \beta^{2} } \right)A_{i} \left( {\alpha ,\beta } \right)\exp \left( { - \gamma_{\mu i} x} \right) \hfill \\ + 2\gamma_{\upsilon i} \alpha C_{i} \left( {\alpha ,\beta } \right)\exp \left( { - \gamma_{\upsilon i} x} \right) \hfill \\ \end{gathered} \right]} \, \sin \left( {\alpha y} \right)\sin \left( {\beta z} \right){\text{d}}\alpha {\text{d}}\beta } } \right\}} , \\ \sigma_{yy} = \frac{{c_{44} }}{{\mu_{3} }}\sum\limits_{i = 1}^{2} {\left\{ \begin{gathered} \int\limits_{0}^{\infty } {\int\limits_{0}^{\infty } {\left[ \begin{gathered} \left[ \begin{gathered} - 2\alpha^{2} \hfill \\ + \left( { - 2\mu_{i} + \left( {1 + k_{i} } \right)\mu_{3} } \right)\beta^{2} \hfill \\ \end{gathered} \right]A_{i} \left( {\alpha ,\beta } \right)\exp \left( { - \gamma_{\mu i} x} \right) \hfill \\ - 2\gamma_{\upsilon i} \alpha C_{i} \left( {\alpha ,\beta } \right)\exp \left( { - \gamma_{\upsilon i} x} \right) \hfill \\ \end{gathered} \right]} } \hfill \\ \,\,\,\,\,\,\,\,\,\; \cdot \sin \left( {\alpha y} \right)\sin \left( {\beta z} \right){\text{d}}\alpha {\text{d}}\beta \hfill \\ \end{gathered} \right\}} , \\ \sigma_{zz} = \sum\limits_{i = 1}^{2} {\left\{ {\int\limits_{0}^{\infty } {\int\limits_{0}^{\infty } {\left[ {\left( {c_{13} \mu_{i} - c_{33} k_{i} } \right)\beta^{2} A_{i} \left( {\alpha ,\beta } \right)\exp \left( { - \gamma_{\mu i} x} \right)} \right]\sin \left( {\alpha y} \right)\sin \left( {\beta z} \right){\text{d}}\alpha {\text{d}}\beta } } } \right\}} , \\ \sigma_{yz} = \frac{{c_{44} }}{{\mu_{3} }}\sum\limits_{i = 1}^{2} {\left\{ {\int\limits_{0}^{\infty } {\int\limits_{0}^{\infty } {\left[ \begin{gathered} \mu_{3} \left( {1 + k_{i} } \right)\alpha \beta A_{i} \left( {\alpha ,\beta } \right)\exp \left( { - \gamma_{\mu i} x} \right) \hfill \\ + \upsilon_{i} \gamma_{\upsilon i} \beta C_{i} \left( {\alpha ,\beta } \right)\exp \left( { - \gamma_{\upsilon i} x} \right) \hfill \\ \end{gathered} \right]\cos \left( {\alpha y} \right)\cos \left( {\beta z} \right){\text{d}}\alpha {\text{d}}\beta } } } \right\}} , \\ \sigma_{zx} = \frac{{c_{44} }}{{\mu_{3} }}\sum\limits_{i = 1}^{2} {\left\{ {\int\limits_{0}^{\infty } {\int\limits_{0}^{\infty } {\left[ \begin{gathered} - \mu_{3} \left( {1 + k_{i} } \right)\gamma_{\mu i} \beta A_{i} \left( {\alpha ,\beta } \right)\exp \left( { - \gamma_{\mu i} x} \right) \hfill \\ - \upsilon_{i} \alpha \beta C_{i} \left( {\alpha ,\beta } \right)\exp \left( { - \gamma_{\upsilon i} x} \right) \hfill \\ \end{gathered} \right]\sin \left( {\alpha y} \right)\cos \left( {\beta z} \right){\text{d}}\alpha {\text{d}}\beta } } } \right\}} , \\ \sigma_{xy} = \frac{{c_{44} }}{{\mu_{3} }}\sum\limits_{i = 1}^{2} {\left\{ {\int\limits_{0}^{\infty } {\int\limits_{0}^{\infty } {\left[ \begin{gathered} - 2\gamma_{\mu i} \alpha A_{i} \left( {\alpha ,\beta } \right)\exp \left( { - \gamma_{\mu i} x} \right) \hfill \\ - \left( {2\alpha^{2} + \upsilon_{i} \beta^{2} } \right)C_{i} \left( {\alpha ,\beta } \right)\exp \left( { - \gamma_{\upsilon i} x} \right) \hfill \\ \end{gathered} \right]\cos \left( {\alpha y} \right)\sin \left( {\beta z} \right){\text{d}}\alpha {\text{d}}\beta } } } \right\}} \\ \end{gathered} \right\} , $$

(46)

$$ \left. \begin{gathered} D_{x} = \eta_{11} \frac{{c_{44} }}{{e_{14} \mu_{3} }}\sum\limits_{i = 1}^{2} {\left\{ \begin{gathered} \int\limits_{0}^{\infty } {\int\limits_{0}^{\infty } {\left[ \begin{gathered} \mu_{3} k_{\text{couple}}^{ 2} \left( {1 + k_{i} } \right)\alpha \beta A_{i} \left( {\alpha ,\beta } \right)\exp \left( { - \gamma_{\mu i} x} \right) \hfill \\ + \left( {\mu_{3} \left( {1 + k_{\text{couple}}^{ 2} } \right) - \upsilon_{i} } \right)\gamma_{\upsilon i} \beta C_{i} \left( {\alpha ,\beta } \right)\exp \left( { - \gamma_{\upsilon i} x} \right) \hfill \\ \end{gathered} \right]} } \hfill \\ \,\,\,\,\,\,\,\,\,\, \cdot \cos \left( {\alpha y} \right)\cos \left( {\beta z} \right){\text{d}}\alpha {\text{d}}\beta \hfill \\ \end{gathered} \right\}} , \\ D_{y} = \eta_{11} \frac{{c_{44} }}{{e_{14} \mu_{3} }}\sum\limits_{i = 1}^{2} {\left\{ \begin{gathered} \int\limits_{0}^{\infty } {\int\limits_{0}^{\infty } {\left[ \begin{gathered} \mu_{3} k_{\text{couple}}^{ 2} \left( {1 + k_{i} } \right)\gamma_{\mu i} \beta A_{i} \left( {\alpha ,\beta } \right)\exp \left( { - \gamma_{\mu i} x} \right) \hfill \\ + \left( {\mu_{3} \left( {1 + k_{\text{couple}}^{2} } \right) - \upsilon_{i} } \right)\alpha \beta C_{i} \left( {\alpha ,\beta } \right)\exp \left( { - \gamma_{\upsilon i} x} \right) \hfill \\ \end{gathered} \right]} } \hfill \\ \,\,\,\,\,\,\,\,\,\,\, \cdot \sin \left( {\alpha y} \right)\cos \left( {\beta z} \right){\text{d}}\alpha {\text{d}}\beta \hfill \\ \end{gathered} \right\}} , \\ D_{z} = \eta_{33} \frac{{c_{44} }}{{e_{14} \mu_{3} }}\sum\limits_{i = 1}^{2} {\left[ {\int\limits_{0}^{\infty } {\int\limits_{0}^{\infty } {\left( {\mu_{3} - \upsilon_{i} } \right)\beta^{2} C_{i} \left( {\alpha ,\beta } \right)\exp \left( { - \gamma_{\upsilon i} x} \right)\cos \left( {\alpha y} \right)\sin \left( {\beta z} \right){\text{d}}\alpha {\text{d}}\beta } } } \right]} \\ \\ \end{gathered} \right\} . $$

(47)

For the subsequent analytical procedures, the electric potential distribution on the surface, $\Phi_{s} (y,z)$, is expressed in the Fourier integral form [33] as

$$ \Phi_{s} \left( {y,z} \right) = \int\limits_{0}^{\infty } {\int\limits_{0}^{\infty } {\Phi_{s}^{*} \left( {\alpha ,\beta } \right)\cos \left( {\alpha y} \right)\cos \left( {\beta z} \right){\text{d}}\alpha {\text{d}}\beta } } , $$

(48)

where

$$ \Phi_{s}^{*} \left( {\alpha ,\beta } \right) = \frac{4}{{\pi^{2} }}\int\limits_{0}^{\infty } {\int\limits_{0}^{\infty } {\Phi_{s} (y,z)\cos \;(\alpha y)\cos \;(\beta z){\text{d}}y{\text{d}}z} } . $$

(49)

By substituting Eqs. (42), (46), and (48) into Eq. (38), a set of simultaneous equations for $A_{i} (\alpha ,\beta )$ and $C_{i} (\alpha ,\beta )$ $(i = 1,2)$ is obtained as

$$ \left. \begin{gathered} \sum\limits_{i = 1}^{2} {\left\{ {\left[ {2\alpha^{2} + \left( {1 + k_{i} } \right)\mu_{3} \beta^{2} } \right]A_{i} \left( {\alpha ,\beta } \right) + 2\gamma_{\upsilon i} \alpha C_{i} \left( {\alpha ,\beta } \right)} \right\}} = 0, \hfill \\ \sum\limits_{i = 1}^{2} {\left[ {\mu_{3} \left( {1 + k_{i} } \right)\gamma_{\mu i} \beta A_{i} \left( {\alpha ,\beta } \right) + \upsilon_{i} \alpha \beta C_{i} \left( {\alpha ,\beta } \right)} \right] = 0} , \hfill \\ \sum\limits_{i = 1}^{2} {\left[ {2\gamma_{\mu i} \alpha A_{i} \left( {\alpha ,\beta } \right) + \left( {2\alpha^{2} + \upsilon_{i} \beta^{2} } \right)C_{i} \left( {\alpha ,\beta } \right)} \right]} = 0, \hfill \\ \sum\limits_{i = 1}^{2} {\left( {\mu_{3} - \upsilon_{i} } \right)\beta C_{i} \left( {\alpha ,\beta } \right)} = \frac{{e_{14} \mu_{3} }}{{c_{44} }}\Phi_{s}^{*} \left( {\alpha ,\beta } \right) \hfill \\ \end{gathered} \right\} . $$

(50)

Equation (50) is solved as

$$ \left\{ {\begin{array}{*{20}c} {A_{1} \left( {\alpha ,\beta } \right)} \\ {A_{2} \left( {\alpha ,\beta } \right)} \\ {C_{1} \left( {\alpha ,\beta } \right)} \\ {C_{2} \left( {\alpha ,\beta } \right)} \\ \end{array} } \right\} = \frac{{e_{14} }}{{c_{44} }}\frac{{\Phi_{s}^{*} \left( {\alpha ,\beta } \right)}}{\beta }\frac{1}{{\Delta \left( {\alpha ,\beta } \right)}}\left\{ {\begin{array}{*{20}c} {A_{1}^{*} \left( {\alpha ,\beta } \right)} \\ {A_{2}^{*} \left( {\alpha ,\beta } \right)} \\ {C_{1}^{*} \left( {\alpha ,\beta } \right)} \\ {C_{2}^{*} \left( {\alpha ,\beta } \right)} \\ \end{array} } \right\} , $$

(51)

where

$$ \left. \begin{gathered} \Delta \left( {\alpha ,\beta } \right) \equiv 2\left[ {2\mu_{3} - \left( {\upsilon_{1} + \upsilon_{2} } \right)} \right]\left( {k_{1} - k_{2} } \right)\alpha^{2} \gamma_{\mu 1} \gamma_{\mu 2} \left( {\gamma_{\upsilon 1} - \gamma_{\upsilon 2} } \right) \\ + \left( {\upsilon_{1} - \upsilon_{2} } \right)\left\{ \begin{gathered} 2\left( {k_{1} - k_{2} } \right)\alpha^{2} \left[ {\gamma_{\mu 1} \gamma_{\mu 2} \left( {\gamma_{\upsilon 1} + \gamma_{\upsilon 2} } \right) - \mu_{3} \beta^{2} \left( {\gamma_{\mu 1} + \gamma_{\mu 2} } \right)} \right] \hfill \\ - \mu_{3} \left( {1 + k_{1} } \right)\left( {1 + k_{2} } \right)\left( {2\alpha^{2} + \mu_{3} \beta^{2} } \right)\beta^{2} \left( {\gamma_{\mu 1} - \gamma_{\mu 2} } \right) \hfill \\ - 4\alpha^{4} \left( {k_{1} \gamma_{\mu 1} - k_{2} \gamma_{\mu 2} } \right) \hfill \\ \end{gathered} \right\}, \\ A_{1}^{*} \left( {\alpha ,\beta } \right) \equiv - \alpha \left\{ \begin{gathered} 2\left( {\upsilon_{1} - \upsilon_{2} } \right)\alpha^{2} \left[ {2\alpha^{2} + \left( {1 + k_{2} } \right)\mu_{3} \beta^{2} } \right] \hfill \\ + 2\left[ {2\alpha^{2} - \mu_{3} \left( {1 + k_{2} } \right)\beta^{2} } \right]\gamma_{\mu 2} \left( {\upsilon_{2} \gamma_{\upsilon 1} - \upsilon_{1} \gamma_{\upsilon 2} } \right) \hfill \\ - 4\mu_{3} \left( {1 + k_{2} } \right)\alpha^{2} \gamma_{\mu 2} \left( {\gamma_{\upsilon 1} - \gamma_{\upsilon 2} } \right) \hfill \\ \end{gathered} \right\}, \\ C_{1}^{*} \left( {\alpha ,\beta } \right) \equiv - \left\{ \begin{gathered} 4\left( {k_{1} - k_{2} } \right)\mu_{3} \alpha^{2} \gamma_{\mu 1} \gamma_{\mu 2} \gamma_{\upsilon 2} \hfill \\ + \left( {2\alpha^{2} + \mu_{3} \beta^{2} } \right)\left( {\gamma_{\mu 1} - \gamma_{\mu 2} } \right)\left[ {2\alpha^{2} \left( {\upsilon_{2} - \mu_{3} } \right) - \mu_{3}^{2} \left( {1 + k_{1} } \right)\left( {1 + k_{2} } \right)\beta^{2} } \right] \hfill \\ - 2\mu_{3} \left( {k_{1} - k_{2} } \right)\upsilon_{2} \alpha^{2} \beta^{2} \left( {\gamma_{\mu 1} + \gamma_{\mu 2} } \right) - 4\alpha^{4} \mu_{3} \left( {k_{1} \gamma_{\mu 1} - k_{2} \gamma_{\mu 2} } \right) \hfill \\ \end{gathered} \right\} \\ \end{gathered} \right\} , $$

(52)

and $A_{2}^{*} \left( {\alpha ,\beta } \right)$ and $C_{2}^{*} (\alpha ,\beta )$ are obtained by interchanging subscripts “1” and “2” in $A_{1}^{*} (\alpha ,\beta )$ and $C_{1}^{*} (\alpha ,\beta )$, respectively. By substituting Eqs. (51) and (52) into Eqs. (42)–(47), the electroelastic field quantities are formulated.

Numerical calculations

The electric potential distribution on the surface, $\Phi_{s} \left( {y,z} \right)$, is assumed to have Gaussian distributions with respect to $y$ and $z$ with a maximum value $\Phi_{0}$ and standard deviation $\delta$,

$$ \Phi_{s} \left( {y,z} \right) = \Phi_{0} \exp \left( { - \frac{{y^{2} + z^{2} }}{{\delta^{2} }}} \right) , $$

(53)

for which Eq. (49) is calculated as

$$ \Phi_{s}^{*} \left( {\alpha ,\beta } \right) = \Phi_{0} \frac{{\delta^{2} }}{\pi }\exp \left[ { - \frac{{\left( {\alpha \delta } \right)^{2} + \left( {\beta \delta } \right)^{2} }}{4}} \right] . $$

(54)

As the piezoelectric body, Sitka spruce (Picea sitchensis) is chosen. Because it is hard to find a complete set of its material constants, the required parameters are constructed using data from several sources in the literature [34–36] as

$$ \left. \begin{gathered} c_{11} = 830.84\,\left[ {\text{MPa}} \right],\,\,c_{33} = 12.276\,\left[ {\text{GPa}} \right],\,\,c_{12} = 294.47\,\left[ {\text{MPa}} \right], \\ c_{13} = 472.07\,\left[ {\text{MPa}} \right],\,\,c_{44} = 742.50\,\left[ {\text{MPa}} \right], \\ \eta_{11} = 16.823 \times 10^{ - 12} \,\left[ {\frac{{{\text{C}}^{2} }}{{{\text{N}} \cdot {\text{m}}^{2} }}} \right],\,\,\eta_{33} = 22.490 \times 10^{ - 12} \left[ {\frac{{{\text{C}}^{ 2} }}{{{\text{N}} \cdot {\text{m}}^{2} }}} \right],\,\,e_{14} = - 0.14850 \times 10^{ - 3} \,\left[ {\frac{\text{C}}{{{\text{m}}^{2} }}} \right] \\ \end{gathered} \right\} , $$

(55)

which satisfy Eqs. (6) and (22). The construction of Eq. (55) is described in Appendix 2. To illustrate the numerical results, the following nondimensional quantities are introduced:

$$ \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{z} } \right) \equiv \frac{{\left( {x,y,z} \right)}}{\delta },\,\,\,\,\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{E}_{x} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{E}_{y} } \right) \equiv \frac{{\left( {E_{x} ,E_{y} } \right)}}{{\left( {\frac{{\Phi_{0} }}{\delta }} \right)}},\,\,\,\,\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\sigma }_{yz} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\sigma }_{zx} } \right) \equiv \frac{{\left( {\sigma_{yz} ,\sigma_{zx} } \right)}}{{\left( {\left| {e_{14} } \right|\frac{{\Phi_{0} }}{\delta }} \right)}} . $$

(56)

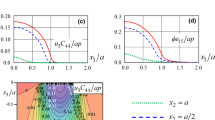
Equation (2) reveals that the shear stress $\sigma_{yz}$ reflects mainly the electric field $E_{x}$ and that the shear stress $\sigma_{zx}$ reflects mainly the electric field $E_{y}$. Figure 3 shows the distributions of the electric fields and the resulting shear stresses. Figure 3a shows that the electric field $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{E}_{x}$ is maximum at the boundary $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} = 0$ and decreases monotonically toward zero with $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x}$ and that the resulting shear stress $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\sigma }_{yz}$ exhibits similar behavior. Figure 3b shows that the electric field $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{E}_{x}$ and shear stress $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\sigma }_{yz}$ are maximum at the center of the surface electric potential and, roughly speaking, decrease toward zero with $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y}$ and that, on the other hand, the electric field $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{E}_{y}$ and the resulting shear stress $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\sigma }_{zx}$ are zero at the origin (because they are antisymmetric with respect to $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y}$), reach their maxima around the periphery of the surface electric potential (namely, $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y} \approx 1$), and decrease toward zero with $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y}$.

Fig. 3

Distributions of electric fields and resulting stresses: a on $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x}$ axis $(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y} = 0,\,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{z} = 0)$, b on $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y}$ axis $(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} = 0,\,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{z} = 0)$

Concluding remarks

In this study, we constructed an analytical technique for obtaining general solutions to electroelastic problems of piezoelectric bodies belonging to point group $D_{\infty }$. We found that the electroelastic field quantities can be expressed in terms of four functions, namely, two elastic displacement potential functions and two piezoelastic displacement potential functions, each of which satisfies a Laplace equation with respect to the appropriately transformed spatial coordinates. Moreover, as an application of the technique, we analyzed the problem of a semi-infinite body subjected to a prescribed electric potential on its surface and illustrated the results graphically. Thus, this novel technique was found to serve to investigate the electroelastic field inside wooden materials.

Appendices

Appendix 1: constitutive equations for body with D _∞ symmetry

As stated in the Introduction, many microcrystalline structures called micelles, each of which belongs to point group $C_{2}$, aggregate into fibers in a manner that makes the twofold rotation axes of $C_{2}$ randomly parallel or antiparallel to the fiber direction and orients the axes perpendicular to the twofold rotation axes in random directions. In this Appendix, the constitutive equations are derived for wood species which are viewed appropriately from such a standpoint.

The constitutive equations for a body with $C_{2}$ symmetry, with its twofold rotation axis parallel to the third of the principal axes of anisotropy $(x_{1} ,\,x_{2} ,\,x_{3} )$, are given as [37]

$$ \left\{ {\begin{array}{*{20}c} {\sigma_{1} } \\ {\sigma_{2} } \\ {\sigma_{3} } \\ {\sigma_{4} } \\ {\sigma_{5} } \\ {\sigma_{6} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {c_{11} } & {c_{12} } & {c_{13} } & 0 & 0 & {c_{16} } \\ {} & {c_{22} } & {c_{23} } & 0 & 0 & {c_{26} } \\ {} & {} & {c_{33} } & 0 & 0 & {c_{36} } \\ {} & {} & {} & {c_{44} } & {c_{45} } & 0 \\ {} & {} & {} & {} & {c_{55} } & 0 \\ {\text{sym.}} & {} & {} & {} & {} & {c_{66} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{1} } \\ {\varepsilon_{2} } \\ {\varepsilon_{3} } \\ {\varepsilon_{4} } \\ {\varepsilon_{5} } \\ {\varepsilon_{6} } \\ \end{array} } \right\} - \left[ {\begin{array}{*{20}c} 0 & 0 & {e_{31} } \\ 0 & 0 & {e_{32} } \\ 0 & 0 & {e_{33} } \\ {e_{14} } & {e_{24} } & 0 \\ {e_{15} } & {e_{25} } & 0 \\ 0 & 0 & {e_{36} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {E_{1} } \\ {E_{2} } \\ {E_{3} } \\ \end{array} } \right\} - \left\{ {\begin{array}{*{20}c} {\beta_{1} } \\ {\beta_{2} } \\ {\beta_{3} } \\ 0 \\ 0 \\ {\beta_{6} } \\ \end{array} } \right\}{T} , $$

(57)

$$ \left\{ {\begin{array}{*{20}c} {D_{1} } \\ {D_{2} } \\ {D_{3} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & {e_{14} } & {e_{15} } & 0 \\ 0 & 0 & 0 & {e_{24} } & {e_{25} } & 0 \\ {e_{31} } & {e_{32} } & {e_{33} } & 0 & 0 & {e_{36} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{1} } \\ {\varepsilon_{2} } \\ {\varepsilon_{3} } \\ {\varepsilon_{4} } \\ {\varepsilon_{5} } \\ {\varepsilon_{6} } \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} {\eta_{11} } & {\eta_{12} } & 0 \\ {} & {\eta_{22} } & 0 \\ {{\text{sym}} .} & {} & {\eta_{33} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {E_{1} } \\ {E_{2} } \\ {E_{3} } \\ \end{array} } \right\} + \left\{ {\begin{array}{*{20}c} 0 \\ 0 \\ {p_{3} } \\ \end{array} } \right\} {T} . $$

(58)

Then, we consider the reference coordinate system $(x_{{1^{\prime}}} ,\,x_{{2^{\prime}}} ,\,x_{{3^{\prime}}} )$, as shown in Fig. 4. By employing the transformation laws for tensors [37], the elastic stiffness constant, dielectric constant, piezoelectric constant, stress–temperature coefficient, and pyroelectric constant in the system $(x_{{1^{\prime}}} ,\,x_{{2^{\prime}}} ,\,x_{{3^{\prime}}} )$ are obtained, respectively, as

Fig. 4

Arbitrary rotation around the third axis

$$ \left. \begin{gathered} c_{{i^{\prime}j^{\prime}}} = f_{{ci^{\prime}j^{\prime}}}^{ + } \left( \theta \right),\,\,\,\,\eta_{{k^{\prime}l^{\prime}}} = f_{{\eta k^{\prime}l^{\prime}}}^{ + } \left( \theta \right),\,\,\,\,e_{{k^{\prime}j^{\prime}}} = f_{{ek^{\prime}j^{\prime}}}^{ + } \left( \theta \right),\,\,\,\,\beta_{{i^{\prime}}} = f_{{\beta i^{\prime}}}^{ + } \left( \theta \right),\,\,\,\,p_{{k^{\prime}}} = f_{{pk^{\prime}}}^{ + } \left( \theta \right) \hfill \\ \left( {i^{\prime},\,j^{\prime} = 1,\,2,\,3,\,4,\,5,\,6;\,\,k^{\prime},\,l^{\prime} = 1,\,2,\,3} \right) \hfill \\ \end{gathered} \right\} , $$

(59)

where

$$ \left. \begin{gathered} f_{{c1^{\prime}1^{\prime}}}^{ + } \left( \theta \right) = \cos^{4} \theta \cdot c_{11} + \sin^{4} \theta \cdot c_{22} + 2\cos^{2} \theta \sin^{2} \theta \cdot c_{12} + 4\cos^{2} \theta \sin^{2} \theta \cdot c_{66} \\ - 4\cos^{3} \theta \sin \theta \cdot c_{16} - 4\cos \theta \sin^{3} \theta \cdot c_{26} , \\ f_{{c1^{\prime}2^{\prime}}}^{ + } \left( \theta \right) = \cos^{2} \theta \sin^{2} \theta \cdot c_{11} + \cos^{2} \theta \sin^{2} \theta \cdot c_{22} + \left( {\cos^{4} \theta + \sin^{4} \theta } \right) \cdot c_{12} \\ - 4\cos^{2} \theta \sin^{2} \theta \cdot c_{66} \\ + 2\cos \theta \sin \theta \left( {\cos^{2} \theta - \sin^{2} \theta } \right) \cdot c_{16} - 2\cos \theta \sin \theta \left( {\cos^{2} \theta - \sin^{2} \theta } \right) \cdot c_{26} , \\ f_{{c1^{\prime}3^{\prime}}}^{ + } \left( \theta \right) = \cos^{2} \theta \cdot c_{13} + \sin^{2} \theta \cdot c_{23} - 2\cos \theta \sin \theta \cdot c_{36} , \\ f_{{c1^{\prime}4^{\prime}}}^{ + } \left( \theta \right) = 0,\,\,\,\,f_{{c1^{\prime}5^{\prime}}}^{ + } \left( \theta \right) = 0, \\ f_{{c1^{\prime}6^{\prime}}}^{ + } \left( \theta \right) = \cos^{3} \theta \sin \theta \cdot c_{11} - \cos \theta \sin^{3} \theta \cdot c_{22} - \cos \theta \sin \theta \left( {\cos^{2} \theta - \sin^{2} \theta } \right) \cdot c_{12} \\ - 2\cos \theta \sin \theta \left( {\cos^{2} \theta - \sin^{2} \theta } \right) \cdot c_{66} \\ + \cos^{2} \theta \left( {\cos^{2} \theta - 3\sin^{2} \theta } \right) \cdot c_{16} + \sin^{2} \theta \left( {3\cos^{2} \theta - \sin^{2} \theta } \right) \cdot c_{26} , \\ f_{{c2^{\prime}2^{\prime}}}^{ + } \left( \theta \right) = \sin^{4} \theta \cdot c_{11} + \cos^{4} \theta \cdot c_{22} + 2\cos^{2} \theta \sin^{2} \theta \cdot c_{12} + 4\cos^{2} \theta \sin^{2} \theta \cdot c_{66} \\ + 4\cos \theta \sin^{3} \theta \cdot c_{16} + 4\cos^{3} \theta \sin \theta \cdot c_{26} , \\ f_{{c2^{\prime}3^{\prime}}}^{ + } \left( \theta \right) = \sin^{2} \theta \cdot c_{13} + \cos^{2} \theta \cdot c_{23} + 2\cos \theta \sin \theta \cdot c_{36} , \\ f_{{c2^{\prime}4^{\prime}}}^{ + } \left( \theta \right) = 0,\,\,\,\,f_{{c2^{\prime}5^{\prime}}}^{ + } \left( \theta \right) = 0, \\ f_{{c2^{\prime}6^{\prime}}}^{ + } \left( \theta \right) = \cos \theta \sin^{3} \theta \cdot c_{11} - \cos^{3} \theta \sin \theta \cdot c_{22} + \cos \theta \sin \theta \left( {\cos^{2} \theta - \sin^{2} \theta } \right) \cdot c_{12} \\ + 2\cos \theta \sin \theta \left( {\cos^{2} \theta - \sin^{2} \theta } \right) \cdot c_{66} \\ + \sin^{2} \theta \left( {3\cos^{2} \theta - \sin^{2} \theta } \right) \cdot c_{16} + \cos^{2} \theta \left( {\cos^{2} \theta - 3\sin^{2} \theta } \right) \cdot c_{26} , \\ f_{{c3^{\prime}3^{\prime}}}^{ + } \left( \theta \right) = c_{33} , \\ f_{{c3^{\prime}4^{\prime}}}^{ + } \left( \theta \right) = 0,\,\,\,\,f_{{c3^{\prime}5^{\prime}}}^{ + } \left( \theta \right) = 0, \\ f_{{c3^{\prime}6^{\prime}}}^{ + } \left( \theta \right) = \cos \theta \sin \theta \cdot c_{13} - \cos \theta \sin \theta \cdot c_{23} + \left( {\cos^{2} \theta - \sin^{2} \theta } \right) \cdot c_{36} , \\ f_{{c4^{\prime}4^{\prime}}}^{ + } \left( \theta \right) = \cos^{2} \theta \cdot c_{44} + \sin^{2} \theta \cdot c_{55} + 2\cos \theta \sin \theta \cdot c_{45} , \\ f_{{c4^{\prime}5^{\prime}}}^{ + } \left( \theta \right) = - \cos \theta \sin \theta \cdot c_{44} + \cos \theta \sin \theta \cdot c_{55} + \left( {\cos^{2} \theta - \sin^{2} \theta } \right) \cdot c_{45} , \\ f_{{c4^{\prime}6^{\prime}}}^{ + } \left( \theta \right) = 0, \\ f_{{c5^{\prime}5^{\prime}}}^{ + } \left( \theta \right) = \sin^{2} \theta \cdot c_{44} + \cos^{2} \theta \cdot c_{55} - 2\cos \theta \sin \theta \cdot c_{45} , \\ f_{{c5^{\prime}6^{\prime}}}^{ + } \left( \theta \right) = 0, \\ f_{{c6^{\prime}6^{\prime}}}^{ + } \left( \theta \right) = \cos^{2} \theta \sin^{2} \theta \cdot c_{11} + \cos^{2} \theta \sin^{2} \theta \cdot c_{22} - 2\cos^{2} \theta \sin^{2} \theta \cdot c_{12} \\ + \left( {\cos^{4} \theta - 2\cos^{2} \theta \sin^{2} \theta + \sin^{4} \theta } \right) \cdot c_{66} \\ + 2\cos \theta \sin \theta \left( {\cos^{2} \theta - \sin^{2} \theta } \right) \cdot c_{16} - 2\cos \theta \sin \theta \left( {\cos^{2} \theta - \sin^{2} \theta } \right) \cdot c_{26} , \\ f_{{cj^{\prime}i^{\prime}}}^{ + } \left( \theta \right) = f_{{ci^{\prime}j^{\prime}}}^{ + } \left( \theta \right)\,\,\,\,\left( {i^{\prime},\,j^{\prime} = 1,\,2,\,3,\,4,\,5,\,6} \right) \\ \end{gathered} \right\} , $$

(60)

$$ \left. \begin{gathered} f_{{\eta 1^{\prime}1^{\prime}}}^{ + } \left( \theta \right) = \cos^{2} \theta \cdot \eta_{11} + \sin^{2} \theta \cdot \eta_{22} - 2\cos \theta \sin \theta \cdot \eta_{12} , \\ f_{{\eta 1^{\prime}2^{\prime}}}^{ + } \left( \theta \right) = \cos \theta \sin \theta \cdot \eta_{11} - \cos \theta \sin \theta \cdot \eta_{22} + \left( {\cos^{2} \theta - \sin^{2} \theta } \right)\eta_{12} , \\ f_{{\eta 1^{\prime}3^{\prime}}}^{ + } \left( \theta \right) = 0, \\ f_{{\eta 2^{\prime}2^{\prime}}}^{ + } \left( \theta \right) = \sin^{2} \theta \cdot \eta_{11} + \cos^{2} \theta \cdot \eta_{22} + 2\cos \theta \sin \theta \cdot \eta_{12} , \\ f_{{\eta 2^{\prime}3^{\prime}}}^{ + } \left( \theta \right) = 0, \\ f_{{\eta 3^{\prime}3^{\prime}}}^{ + } \left( \theta \right) = \eta_{33} , \\ f_{{\eta l^{\prime}k^{\prime}}}^{ + } \left( \theta \right) = f_{{\eta k^{\prime}l^{\prime}}}^{ + } \left( \theta \right)\,\,\,\,\left( {k^{\prime},\,l^{\prime} = 1,\,2,\,3} \right) \\ \end{gathered} \right\} , $$

(61)

$$ \left. \begin{gathered} f_{{e1^{\prime}1^{\prime}}}^{ + } \left( \theta \right) = 0,\,\,\,\,f_{{e1^{\prime}2^{\prime}}}^{ + } \left( \theta \right) = 0,\,\,\,\,f_{{e1^{\prime}3^{\prime}}}^{ + } \left( \theta \right) = 0, \\ f_{{e1^{\prime}4^{\prime}}}^{ + } \left( \theta \right) = \cos^{2} \theta \cdot e_{14} + \cos \theta \sin \theta \cdot e_{15} - \cos \theta \sin \theta \cdot e_{24} - \sin^{2} \theta \cdot e_{25} , \\ f_{{e1^{\prime}5^{\prime}}}^{ + } \left( \theta \right) = - \cos \theta \sin \theta \cdot e_{14} + \cos^{2} \theta \cdot e_{15} + \sin^{2} \theta \cdot e_{24} - \cos \theta \sin \theta \cdot e_{25} , \\ f_{{e1^{\prime}6^{\prime}}}^{ + } \left( \theta \right) = 0, \\ f_{{e2^{\prime}1^{\prime}}}^{ + } \left( \theta \right) = 0,\,\,\,\,f_{{e2^{\prime}2^{\prime}}}^{ + } \left( \theta \right) = 0,\,\,\,\,f_{{e2^{\prime}3^{\prime}}}^{ + } \left( \theta \right) = 0, \\ f_{{e2^{\prime}4^{\prime}}}^{ + } \left( \theta \right) = \cos \theta \sin \theta \cdot e_{14} + \sin^{2} \theta \cdot e_{15} + \cos^{2} \theta \cdot e_{24} + \cos \theta \sin \theta \cdot e_{25} , \\ f_{{e2^{\prime}5^{\prime}}}^{ + } \left( \theta \right) = - \sin^{2} \theta \cdot e_{14} + \cos \theta \sin \theta \cdot e_{15} - \cos \theta \sin \theta \cdot e_{24} + \cos^{2} \theta \cdot e_{25} , \\ f_{{e2^{\prime}6^{\prime}}}^{ + } \left( \theta \right) = 0, \\ f_{{e3^{\prime}1^{\prime}}}^{ + } \left( \theta \right) = \cos^{2} \theta \cdot e_{31} + \sin^{2} \theta \cdot e_{32} - 2\cos \theta \cdot \sin \theta \cdot e_{36} , \\ f_{{e3^{\prime}2^{\prime}}}^{ + } \left( \theta \right) = \sin^{2} \theta \cdot e_{31} + \cos^{2} \theta \cdot e_{32} + 2\cos \theta \cdot \sin \theta \cdot e_{36} , \\ f_{{e3^{\prime}3^{\prime}}}^{ + } \left( \theta \right) = e_{33} , \\ f_{{e3^{\prime}4^{\prime}}}^{ + } \left( \theta \right) = 0,\,\,\,\,f_{{e3^{\prime}5^{\prime}}}^{ + } \left( \theta \right) = 0, \\ f_{{e3^{\prime}6^{\prime}}}^{ + } \left( \theta \right) = \cos \theta \sin \theta \cdot e_{31} - \cos \theta \sin \theta \cdot e_{32} + \left( {\cos^{2} \theta - \sin^{2} \theta } \right) \cdot e_{36} \\ \end{gathered} \right\} , $$

(62)

$$ \left. \begin{gathered} f_{{\beta 1^{\prime}}}^{ + } \left( \theta \right) = \cos^{2} \theta \cdot \beta_{1} + \sin^{2} \theta \cdot \beta_{2} - 2\cos \theta \sin \theta \cdot \beta_{6} , \\ f_{{\beta 2^{\prime}}}^{ + } \left( \theta \right) = \sin^{2} \theta \cdot \beta_{1} + \cos^{2} \theta \cdot \beta_{2} + 2\cos \theta \sin \theta \cdot \beta_{6} , \\ f_{{\beta 3^{\prime}}}^{ + } \left( \theta \right) = \beta_{3} ,\,\,\,\,f_{{\beta 4^{\prime}}}^{ + } \left( \theta \right) = 0,\,\,\,\,f_{{\beta 5^{\prime}}}^{ + } \left( \theta \right) = 0, \\ f_{{\beta 6^{\prime}}}^{ + } \left( \theta \right) = \cos \theta \sin \theta \cdot \beta_{1} - \cos \theta \sin \theta \cdot \beta_{2} + \left( {\cos^{2} \theta - \sin^{2} \theta } \right)\beta_{6} \\ \end{gathered} \right\} , $$

(63)

$$ f_{{p1^{\prime}}}^{ + } \left( \theta \right) = 0,\,\,\,\,f_{{p2^{\prime}}}^{ + } \left( \theta \right) = 0,\,\,\,\,f_{{p3^{\prime}}}^{ + } \left( \theta \right) = p_{3} . $$

(64)

Next, we consider the reference coordinate system $(x_{{1^{\prime}}} ,\,x_{{2^{\prime}}} ,\,x_{{3^{\prime}}} )$, as shown in Fig. 5. In the manner described above, the material properties in the system $(x_{{1^{\prime}}} ,\,x_{{2^{\prime}}} ,\,x_{{3^{\prime}}} )$ are obtained as

Fig. 5

Arbitrary rotation around the third axis and half-rotation around the first axis

$$ \left. \begin{gathered} c_{{i^{\prime}j^{\prime}}} = f_{{ci^{\prime}j^{\prime}}}^{ - } \left( \theta \right),\,\,\,\,\eta_{{k^{\prime}l^{\prime}}} = f_{{\eta k^{\prime}l^{\prime}}}^{ - } \left( \theta \right),\,\,\,\,e_{{k^{\prime}j^{\prime}}} = f_{{ek^{\prime}j^{\prime}}}^{ - } \left( \theta \right),\,\,\,\,\beta_{{i^{\prime}}} = f_{{\beta i^{\prime}}}^{ - } \left( \theta \right),\,\,\,\,p_{{k^{\prime}}} = f_{{pk^{\prime}}}^{ - } \left( \theta \right) \hfill \\ \left( {i^{\prime},\,j^{\prime} = 1,\,2,\,3,\,4,\,5,\,6;\,\,k^{\prime},\,l^{\prime} = 1,\,2,\,3} \right) \hfill \\ \end{gathered} \right\} . $$

(65)

By comparing Fig. 5 with Fig. 4, it is found that the transformation in Fig. 5 consists of the transformation in Fig. 4 and the $180^\circ$-rotation about $x_{1}$-axis. Therefore, $f_{{ci^{\prime}j^{\prime}}}^{ - } \left( \theta \right)$, $f_{{\eta k^{\prime}l^{\prime}}}^{ - } \left( \theta \right)$, $f_{{ek^{\prime}j^{\prime}}}^{ - } \left( \theta \right)$, $f_{{\beta i^{\prime}}}^{ - } \left( \theta \right)$, and $f_{{pk^{\prime}}}^{ - } \left( \theta \right)$ are obtained by replacing $\left( {c_{16} ,\,c_{26} ,\,c_{36} ,\,c_{45} ,\,\eta_{12} ,\,e_{15} ,\,e_{24} ,\,e_{31} ,\,e_{32} ,\,e_{33} ,\,\beta_{16} ,\,p_{3} } \right)$ with $- \left( {c_{16} ,\,c_{26} ,\,c_{36} ,\,c_{45} ,\,\eta_{12} ,\,e_{15} ,\,e_{24} ,\,e_{31} ,\,e_{32} ,\,e_{33} ,\,\beta_{16} ,\,p_{3} } \right)$ in $f_{{ci^{\prime}j^{\prime}}}^{ + } \left( \theta \right)$, $f_{{\eta k^{\prime}l^{\prime}}}^{ + } \left( \theta \right)$, $f_{{ek^{\prime}j^{\prime}}}^{ + } \left( \theta \right)$, $f_{{\beta i^{\prime}}}^{ + } \left( \theta \right)$, and $f_{{pk^{\prime}}}^{ + } \left( \theta \right)$, respectively.

Because wood is considered to be composed of micelles belonging to point group $C_{2}$, as described above, it is considered that their material properties are obtained in terms of the uniform composition given by Eqs. (59) and (65) and a uniform distribution for $- \pi < \theta < \pi$. Thus, we have

$$ \left. \begin{gathered} c_{{i^{\prime}j^{\prime}}} = \frac{1}{2}\left[ {\frac{1}{2\pi }\int_{\,\, - \pi }^{\,\,\pi } {f_{{ci^{\prime}j^{\prime}}}^{ + } \left( \theta \right)d\theta } + \frac{1}{2\pi }\int_{\,\, - \pi }^{\,\,\pi } {f_{{ci^{\prime}j^{\prime}}}^{ - } \left( \theta \right){\text{d}}\theta } } \right], \hfill \\ \eta_{{k^{\prime}l^{\prime}}} = \frac{1}{2}\left[ {\frac{1}{2\pi }\int_{\,\, - \pi }^{\,\,\pi } {f_{{\eta k^{\prime}l^{\prime}}}^{ + } \left( \theta \right)d\theta } + \frac{1}{2\pi }\int_{\,\, - \pi }^{\,\,\pi } {f_{{\eta k^{\prime}l^{\prime}}}^{ - } \left( \theta \right){\text{d}}\theta } } \right], \hfill \\ e_{{k^{\prime}j^{\prime}}} = \frac{1}{2}\left[ {\frac{1}{2\pi }\int_{\,\, - \pi }^{\,\,\pi } {f_{{ek^{\prime}j^{\prime}}}^{ + } \left( \theta \right)d\theta } + \frac{1}{2\pi }\int_{\,\, - \pi }^{\,\,\pi } {f_{{ek^{\prime}j^{\prime}}}^{ - } \left( \theta \right){\text{d}}\theta } } \right], \hfill \\ \beta_{{i^{\prime}}} = \frac{1}{2}\left[ {\frac{1}{2\pi }\int_{\,\, - \pi }^{\,\,\pi } {f_{{\beta i^{\prime}}}^{ + } \left( \theta \right)d\theta } + \frac{1}{2\pi }\int_{\,\, - \pi }^{\,\,\pi } {f_{{\beta i^{\prime}}}^{ - } \left( \theta \right){\text{d}}\theta } } \right], \hfill \\ p_{{k^{\prime}}} = \frac{1}{2}\left[ {\frac{1}{2\pi }\int_{\,\, - \pi }^{\,\,\pi } {f_{{pk^{\prime}}}^{ + } \left( \theta \right)d\theta } + \frac{1}{2\pi }\int_{\,\, - \pi }^{\,\,\pi } {f_{{pk^{\prime}}}^{ - } \left( \theta \right){\text{d}}\theta } } \right] \hfill \\ \left( {i^{\prime},\,j^{\prime} = 1,\,2,\,3,\,4,\,5,\,6;\,\,k^{\prime},\,l^{\prime} = 1,\,2,\,3} \right) \hfill \\ \end{gathered} \right\} . $$

(66)

By substituting Eqs. (60)–(64) and $f_{{ci^{\prime}j^{\prime}}}^{ - } \left( \theta \right)$, $f_{{\eta k^{\prime}l^{\prime}}}^{ - } \left( \theta \right)$, $f_{{ek^{\prime}j^{\prime}}}^{ - } \left( \theta \right)$, $f_{{\beta i^{\prime}}}^{ - } \left( \theta \right)$, and $f_{{pk^{\prime}}}^{ - } \left( \theta \right)$ into Eq. (66), the elastic stiffness constant, dielectric constant, piezoelectric constant, stress–temperature coefficient, and pyroelectric constant in the reference coordinate system $\left( {x_{{1^{\prime}}} ,\,x_{{2^{\prime}}} ,\,x_{{3^{\prime}}} } \right)$ are obtained, respectively, as

$$ \left[ {\begin{array}{*{20}c} {c_{{1^{\prime}1^{\prime}}} } & {c_{{1^{\prime}2^{\prime}}} } & {c_{{1^{\prime}3^{\prime}}} } & {c_{{1^{\prime}4^{\prime}}} } & {c_{{1^{\prime}5^{\prime}}} } & {c_{{1^{\prime}6^{\prime}}} } \\ {} & {c_{{2^{\prime}2^{\prime}}} } & {c_{{2^{\prime}3^{\prime}}} } & {c_{{2^{\prime}4^{\prime}}} } & {c_{{2^{\prime}5^{\prime}}} } & {c_{{2^{\prime}6^{\prime}}} } \\ {} & {} & {c_{{3^{\prime}3^{\prime}}} } & {c_{{3^{\prime}4^{\prime}}} } & {c_{{3^{\prime}5^{\prime}}} } & {c_{{3^{\prime}6^{\prime}}} } \\ {} & {} & {} & {c_{{4^{\prime}4^{\prime}}} } & {c_{{4^{\prime}5^{\prime}}} } & {c_{{4^{\prime}6^{\prime}}} } \\ {} & {} & {} & {} & {c_{{5^{\prime}5^{\prime}}} } & {c_{{5^{\prime}6^{\prime}}} } \\ {{\text{sym}} .} & {} & {} & {} & {} & {c_{{6^{\prime}6^{\prime}}} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {f_{{c1^{\prime}1^{\prime}}} } & {f_{{c1^{\prime}2^{\prime}}} } & {f_{{c1^{\prime}3^{\prime}}} } & 0 & 0 & 0 \\ {} & {f_{{c1^{\prime}1^{\prime}}} } & {f_{{c1^{\prime}3^{\prime}}} } & 0 & 0 & 0 \\ {} & {} & {f_{{c3^{\prime}3^{\prime}}} } & 0 & 0 & 0 \\ {} & {} & {} & {f_{{c4^{\prime}4^{\prime}}} } & 0 & 0 \\ {} & {} & {} & {} & {f_{{c4^{\prime}4^{\prime}}} } & 0 \\ {{\text{sym}} .} & {} & {} & {} & {} & {\frac{{f_{{c1^{\prime}1^{\prime}}} - f_{{c1^{\prime}2^{\prime}}} }}{2}} \\ \end{array} } \right], $$

(67)

$$ \left[ {\begin{array}{*{20}c} {\eta_{{1^{\prime}1^{\prime}}} } & {\eta_{{1^{\prime}2^{\prime}}} } & {\eta_{{1^{\prime}3^{\prime}}} } \\ {} & {\eta_{{2^{\prime}2^{\prime}}} } & {\eta_{{2^{\prime}3^{\prime}}} } \\ {{\text{sym}} .} & {} & {\eta_{{3^{\prime}3^{\prime}}} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {f_{{\eta 1^{\prime}1^{\prime}}} } & 0 & 0 \\ {} & {f_{{\eta 1^{\prime}1^{\prime}}} } & 0 \\ {{\text{sym}} .} & {} & {f_{{\eta 3^{\prime}3^{\prime}}} } \\ \end{array} } \right] , $$

(68)

$$ \left[ {\begin{array}{*{20}c} {e_{{1^{\prime}1^{\prime}}} } & {e_{{1^{\prime}2^{\prime}}} } & {e_{{1^{\prime}3^{\prime}}} } & {e_{{1^{\prime}4^{\prime}}} } & {e_{{1^{\prime}5^{\prime}}} } & {e_{{1^{\prime}6^{\prime}}} } \\ {e_{{2^{\prime}1^{\prime}}} } & {e_{{2^{\prime}2^{\prime}}} } & {e_{{2^{\prime}3^{\prime}}} } & {e_{{2^{\prime}4^{\prime}}} } & {e_{{2^{\prime}5^{\prime}}} } & {e_{{2^{\prime}6^{\prime}}} } \\ {e_{{3^{\prime}1^{\prime}}} } & {e_{{3^{\prime}2^{\prime}}} } & {e_{{3^{\prime}3^{\prime}}} } & {e_{{3^{\prime}4^{\prime}}} } & {e_{{3^{\prime}5^{\prime}}} } & {e_{{3^{\prime}6^{\prime}}} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & {f_{{e1^{\prime}4^{\prime}}} } & 0 & 0 \\ 0 & 0 & 0 & 0 & { - f_{{e1^{\prime}4^{\prime}}} } & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right] , $$

(69)

$$ \left\{ {\begin{array}{*{20}c} {\beta_{{1^{\prime}}} } & {\beta_{{2^{\prime}}} } & {\beta_{{3^{\prime}}} } & {\beta_{{4^{\prime}}} } & {\beta_{{5^{\prime}}} } & {\beta_{{6^{\prime}}} } \\ \end{array} } \right\}^{\text{T}} = \left\{ {\begin{array}{*{20}c} {f_{{\beta 1^{\prime}}} } & {f_{{\beta 1^{\prime}}} } & {f_{{\beta 3^{\prime}}} } & 0 & 0 & 0 \\ \end{array} } \right\}^{\text{T}} , $$

(70)

$$ \left\{ {\begin{array}{*{20}c} {p_{{1^{\prime}}} } & {p_{{2^{\prime}}} } & {p_{{3^{\prime}}} } \\ \end{array} } \right\}^{\text{T}} = \left\{ {\begin{array}{*{20}c} 0 & 0 & 0 \\ \end{array} } \right\}^{\text{T}} , $$

(71)

where

$$ \left. \begin{gathered} f_{{c1^{\prime}1^{\prime}}} = \frac{{3c_{11} + 3c_{22} + 2c_{12} + 4c_{66} }}{8},\,\,\,\,f_{{c1^{\prime}2^{\prime}}} = \frac{{c_{11} + c_{22} + 6c_{12} - 4c_{66} }}{8},\,\,\,\,f_{{c1^{\prime}3^{\prime}}} = \frac{{c_{13} + c_{23} }}{2}, \\ f_{{c3^{\prime}3^{\prime}}} = c_{33} ,\,\,\,\,f_{{c4^{\prime}4^{\prime}}} = \frac{{c_{44} + c_{55} }}{2},\,\,\,\,f_{{\eta 1^{\prime}1^{\prime}}} = \frac{{\eta_{11} + \eta_{22} }}{2},\,\,\,\,f_{{\eta 3^{\prime}3^{\prime}}} = \eta_{33} ,\,\,\,\,f_{{e1^{\prime}4^{\prime}}} = \frac{1}{2}\left( {e_{14} - e_{25} } \right), \\ f_{{\beta 1^{\prime}}} = \frac{{\beta_{1} + \beta_{2} }}{2},\,\,\,\,f_{{\beta 3^{\prime}}} = \beta_{3} \\ \end{gathered} \right\} . $$

(72)

Appendix 2: construction of material constants

In this Appendix, the material constants in Eqs. (2) and (3) are presented for Sitka spruce (Picea sitchensis). Unfortunately, a complete set of its material constants is not found under a common condition or in the form of Eqs. (2) and (3). Therefore, it is constructed using data from several sources in the literature [34–36] as follows.

The constitutive equations whose independent variables are the components of stress and electric field are given as

$$ \left\{ {\begin{array}{*{20}c} {\varepsilon_{xx} } \\ {\varepsilon_{yy} } \\ {\varepsilon_{zz} } \\ {2\varepsilon_{yz} } \\ {2\varepsilon_{zx} } \\ {2\varepsilon_{xy} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {{1 \mathord{\left/ {\vphantom {1 E}} \right. \kern-0pt} E}} & { - {\mu \mathord{\left/ {\vphantom {\mu E}} \right. \kern-0pt} E}} & { - {{\mu_{L} } \mathord{\left/ {\vphantom {{\mu_{L} } {E_{L} }}} \right. \kern-0pt} {E_{L} }}} & 0 & 0 & 0 \\ {} & {{1 \mathord{\left/ {\vphantom {1 E}} \right. \kern-0pt} E}} & { - {{\mu_{L} } \mathord{\left/ {\vphantom {{\mu_{L} } {E_{L} }}} \right. \kern-0pt} {E_{L} }}} & 0 & 0 & 0 \\ {} & {} & {{1 \mathord{\left/ {\vphantom {1 {E_{L} }}} \right. \kern-0pt} {E_{L} }}} & 0 & 0 & 0 \\ {} & {} & {} & {{1 \mathord{\left/ {\vphantom {1 {G_{L} }}} \right. \kern-0pt} {G_{L} }}} & 0 & 0 \\ {} & {} & {} & {} & {{1 \mathord{\left/ {\vphantom {1 {G_{L} }}} \right. \kern-0pt} {G_{L} }}} & 0 \\ {{\text{sym}} .} & {} & {} & {} & {} & {2{{\left( {1 + \mu } \right)} \mathord{\left/ {\vphantom {{\left( {1 + \mu } \right)} E}} \right. \kern-0pt} E}} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\sigma_{xx} } \\ {\sigma_{yy} } \\ {\sigma_{zz} } \\ {\sigma_{yz} } \\ {\sigma_{zx} } \\ {\sigma_{xy} } \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ {d_{14} } & 0 & 0 \\ 0 & { - d_{14} } & 0 \\ 0 & 0 & 0 \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {E_{x} } \\ {E_{y} } \\ {E_{z} } \\ \end{array} } \right\} , $$

(73)

$$ \left\{ {\begin{array}{*{20}c} {D_{x} } \\ {D_{y} } \\ {D_{z} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & {d_{14} } & 0 & 0 \\ 0 & 0 & 0 & 0 & { - d_{14} } & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\sigma_{xx} } \\ {\sigma_{yy} } \\ {\sigma_{zz} } \\ {\sigma_{yz} } \\ {\sigma_{zx} } \\ {\sigma_{xy} } \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} {\eta_{11}^{\sigma } } & 0 & 0 \\ {} & {\eta_{11}^{\sigma } } & 0 \\ {{\text{sym}} .} & {} & {\eta_{33}^{\sigma } } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {E_{x} } \\ {E_{y} } \\ {E_{z} } \\ \end{array} } \right\} , $$

(74)

where $E$ and $\mu$ denote the Young’s modulus and Poisson’s ratio in the isotropic plane, namely the plane perpendicular to the $\infty$-fold rotation axis; $\mu_{\text{L}}$ the ratio of the normal strain in the isotropic plane to that along the $\infty$-fold rotation axis; $G_{L}$ the shear modulus in the plane perpendicular to the isotropic plane; $\eta_{kl}^{\sigma }$ the dielectric constant; $d_{14}$ the piezoelectric constant.

By denoting the longitudinal, radial, and tangential directions of Sitka spruce for an orthotropic material as L, R, and T, respectively, elastic constants are given for approximate 12 % moisture content as [34]

$$ \left. \begin{gathered} E_{L} = 11.880\,\left[ {\text{GPa}} \right],\,\,\,\,E_{R} = 926.64\,\left[ {\text{MPa}} \right],\,\,\,\,E_{T} = 510.84\,\left[ {\text{MPa}} \right], \hfill \\ G_{LR} = 760.32\,\left[ {\text{MPa}} \right],\,\,\,\,G_{LT} = 724.68\,\left[ {\text{MPa}} \right], \hfill \\ \mu_{RT} = 0.435,\,\,\,\,\mu_{TR} = 0.245,\,\,\,\,\mu_{LR} = 0.372,\,\,\,\,\mu_{LT} = 0.467 \hfill \\ \end{gathered} \right\} . $$

(75)

To confirm the properties given by Eq. (75) to those by Eq. (73), the material constants in the isotropic plane are assumed to be the average of those in the radial and tangential directions as

$$ \left. \begin{gathered} E = {{\left( {E_{R} + E_{T} } \right)} \mathord{\left/ {\vphantom {{\left( {E_{R} + E_{T} } \right)} 2}} \right. \kern-0pt} 2} = 718.74\,\left[ {\text{MPa}} \right], \hfill \\ \mu = {{\left( {\mu_{RT} + \mu_{TR} } \right)} \mathord{\left/ {\vphantom {{\left( {\mu_{RT} + \mu_{TR} } \right)} 2}} \right. \kern-0pt} 2} = 0.340, \hfill \\ G_{L} = {{\left( {G_{LR} + G_{LT} } \right)} \mathord{\left/ {\vphantom {{\left( {G_{LR} + G_{LT} } \right)} 2}} \right. \kern-0pt} 2} = 742.50\,\left[ {\text{MPa}} \right], \hfill \\ \mu_{L} = {{\left( {\mu_{LR} + \mu_{LT} } \right)} \mathord{\left/ {\vphantom {{\left( {\mu_{LR} + \mu_{LT} } \right)} 2}} \right. \kern-0pt} 2} = 0.4195 \hfill \\ \end{gathered} \right\} . $$

(76)

The static specific dielectric constants for the longitudinal and tangential directions are given as

$$ \varepsilon_{L} = 2.54,\,\,\,\,\varepsilon_{T} = 1.90 , $$

(77)

respectively, for an absolutely dried condition [35]. By assuming the dielectric constant in the isotropic plane is represented by the value for the tangential direction, the dielectric constants in Eq. (74) are given as

$$ \eta_{11}^{\sigma } = \varepsilon_{T} \varepsilon_{0} = 16.823 \times 10^{ - 12} \left[ {\frac{{{\text{C}}^{2} }}{{{\text{N}} \cdot {\text{m}}^{2} }}} \right],\,\,\,\,\eta_{33}^{\sigma } = \varepsilon_{L} \varepsilon_{0} = 22.490 \times 10^{ - 12} \left[ {\frac{{{\text{C}}^{2} }}{{{\text{N}} \cdot {\text{m}}^{2} }}} \right] , $$

(78)

where $\varepsilon_{0}$ denotes the permittivity of vacuum.

Because the piezoelectric constant $d_{25} ( = - d_{14} )$ for $10\,\left[ {\text{Hz}} \right]$ takes on values around $0.2\,\left[ {\text{pC/N}} \right]$ under a repeated heat treatment between $100\left[ {^\circ {\text{C}}} \right]$ and $220\left[ {^\circ {\text{C}}} \right]$ [36], we make a rough estimate of the value as

$$ d_{14} = - 0.2\,\left[ {\frac{\text{pC}}{\text{N}}} \right] . $$

(79)

Finally, by converting Eqs. (73) and (74) into the forms of Eqs. (2) and (3), $c_{ij}$, $\eta_{kl}$, and $e_{kj}$ are formulated as

$$ \left. \begin{gathered} c_{11} = E\frac{{1 - \mu_{L}^{2} {E \mathord{\left/ {\vphantom {E {E_{L} }}} \right. \kern-0pt} {E_{L} }}}}{{\left( {1 + \mu } \right)\left[ {\left( {1 - \mu } \right) - 2\mu_{L}^{2} {E \mathord{\left/ {\vphantom {E {E_{L} }}} \right. \kern-0pt} {E_{L} }}} \right]}},\,\,\,\,c_{33} = E_{L} \frac{1 - \mu }{{\left( {1 - \mu } \right) - 2\mu_{L}^{2} {E \mathord{\left/ {\vphantom {E {E_{L} }}} \right. \kern-0pt} {E_{L} }}}}, \hfill \\ c_{12} = E\frac{{\mu + \mu_{L}^{2} {E \mathord{\left/ {\vphantom {E {E_{L} }}} \right. \kern-0pt} {E_{L} }}}}{{\left( {1 + \mu } \right)\left[ {\left( {1 - \mu } \right) - 2\mu_{L}^{2} {E \mathord{\left/ {\vphantom {E {E_{L} }}} \right. \kern-0pt} {E_{L} }}} \right]}},\,\,\,\,c_{13} = E\frac{{\mu_{L} }}{{\left( {1 - \mu } \right) - 2\mu_{L}^{2} {E \mathord{\left/ {\vphantom {E {E_{L} }}} \right. \kern-0pt} {E_{L} }}}},\,\,\,\,c_{44} = G_{L} , \hfill \\ \eta_{11} = \eta_{11}^{\sigma } - G_{L} d_{14}^{2} ,\,\,\,\,\eta_{33} = \eta_{33}^{\sigma } ,\,\,\,\,e_{14} = G_{L} d_{14} \hfill \\ \end{gathered} \right\} . $$

(80)

By substituting Eqs. (75), (76), (78), (79) into Eq. (80), the material constants are obtained as shown in Eq. (55).