Disclosure services and welfare gains in matching markets for indivisible assets

Abstract

We present a competitive matching model in which indivisible assets are reallocated among many traders. The model has three features: (i) traders are heterogeneous in their prospects as buyers, sellers, and also in their stand-alone values with endowed assets, (ii) buyers do not know true values of assets sold, (iii) sellers can disclose values of their assets by paying fees. Despite its complexity, the model admits closed-form solutions. Two main results emerge. First, if full Disclosure is facilitated by a monopolist, it captures a large fraction of the welfare gains. Second, adding the option of minimum disclosure, when combined with a cap regulation on price-dependent fees for full disclosure, significantly weakens the monopolist’s power.

1 Introduction

When trying to sell a large, indivisible, and complex asset, credibly disclosing its quality is critical but difficult. Many sellers of such assets rely on professional service providers to disclose their asset quality. In fact, billions of dollars are paid to large professional firms. As an example, consider mergers and acquisitions (M &A) markets. A unit of trading is an entire firm. Golubov et al. (2012) report that in 2007, investment banks advised on over 85% of M &A deals by transaction values and fees are estimated to be $39.7 billion. On the one hand, these professional firms provide socially valuable services. Without their expertise to conduct otherwise impossible or extremely costly disclosure, markets may entirely shut down. On the other hand, their presence—surplus extraction—may reduce and distort the reallocation of assets. This trade-off seems relevant for many other markets, such as real estate markets and labor markets for high-skill professionals, where intermediaries’ information provision is crucial.

We present a matching model that captures three salient features of markets for indivisible assets. First, there are many potential traders that are heterogeneous in their prospects as buyers, sellers, and also in their prospects without trading. Second, buyers do not know the true value of assets sold. Finally, sellers may disclose the values of their assets at some costs, which we model as fees charged by intermediaries. We use this model to answer the following questions: how does the nature of Disclosure technologies and fees affect trading? Should intermediaries be regulated? If so, how should such regulations be designed?

In our competitive matching model with a price mechanism, each trader owns two indivisible factors: a tradeable “asset” and non-tradeable “skill” to manage an asset. Traders are heterogeneous in both dimensions, and complementarity between the two factors creates potential gains from trade. Traders are privately informed about their asset quality and skill. A price mechanism equates demand and supply of assets given disclosure by sellers. Traders take prices as given when choosing their roles in asset trading.

In Sect. 3, we characterize a natural lower bound on the amount of information revelation by assuming that sellers cannot credibly disclose their asset quality at all. In this case, matching between sellers and buyers is random, but traders’ self-selection to sell or buy induced by the price mechanism still reveals some information. We call this equilibrium no disclosure equilibrium. We also study an equilibrium with a minimum disclosure technology. The analysis in this section is used as a building block of our policy proposal in Sect. 5.

In Sect. 4, we analyze a full disclosure equilibrium where sellers pay fees to disclose their asset quality. We first characterize a market-clearing condition as a second-order differential equation. To our knowledge, we are the first to formulate and characterize an equilibrium matching model with two dimensional heterogeneity subject to two sources of distortions: information frictions and transaction costs. After presenting a welfare benchmark without distortions, we solve the differential equation in a closed form under a fixed fee and a fee proportional to prices. Finally, we endogenize fees and show that the intermediary’s surplus extraction is highly distortionary. In fact, traders are made worse off with the full disclosure service than without any disclosure service.

In Sect. 5, we make a novel policy proposal to improve the efficiency of asset trading in the presence of the monopoly intermediary. While an orthodox remedy to this problem may be to promote entries, it may not be the best solution in the current context. First, if large professional firms have long established a business practice of collectively extracting surplus from traders, it might be difficult to promote entries.¹ Second, more entries may not generally lead to socially better outcomes. Without a proper understanding of potential entrants, a policy promoting entries of intermediaries may adversely affect traders.²

Alternatively, we propose an indirect way of regulating the monopoly intermediary. Specifically, we construct hybrid market equilibrium, where the intermediary offers the full disclosure technology (with profit-maximizing fees) in “the upper market”, and the public service provider offers the minimum disclosure technology (for free) in “the lower market”. Traders endogenously select into the two markets. In this equilibrium, sellers in the upper market have better assets than those in the lower market, and buyers in the upper market have better skills than those in the lower market. A price function in the upper market ensures that an asset of better quality is transferred to a trader with a better skill, while matching is random in the lower market.

We first identify conditions on the fees such that asset trading occurs in both markets. In particular, a fixed fee must be positive to make a marginal seller indifferent between full disclosure in the upper market and pooling with other sellers in the lower market. We then show that, without any regulation, the intermediary would only use a proportional fee so that no trade occurs in the lower market. As a result, the welfare gain and traders’ gain change little from the case where only the full disclosure service is offered to traders. Thus, simply making the minimum disclosure service available for free has a limited welfare impact.

Interestingly, we show that, with a cap imposed on the proportional fee, a small but active lower market emerges. The optimal cap brings the welfare gain close to the benchmark level and most of the welfare gain accrues to traders. We also show that, if the same cap is imposed in the absence of the free minimum disclosure technology, the welfare gain is much smaller and traders do not gain much. Thus, it is the cap regulation activating the lower market that significantly improves the welfare and traders’ gain. What is crucial for our policy proposal is that, even though traders in the lower market do not directly contribute to the overall welfare, the hybrid market structure allows them to contribute to it indirectly. While the inefficiency due to random matching remains, its magnitude is minor because traders in the lower market have small gains from trade. Yet, their presence makes the demand for the full disclosure service more elastic, significantly reducing the surplus extraction.

Our policy proposal has three advantages over a standard policy encouraging entries. First, the cap on the proportional fee is relatively easier to implement, compared to the difficulty and the uncertainty associated with encouraging entries. Second, a public service provider is not required to have a disclosure technology comparable to that of existing service providers. The most simple technology—the minium disclosure—is sufficient. Finally and most importantly, this policy benefits traders with larger potential gains more, because the expertise of the incumbent service provider is utilized in the upper market, but its profit is significantly reduced. While the cost of public service provision must be bourne by someone, perhaps by all potential traders, the suggested magnitude of the welfare improvement indicates that it may be justified on the basis of the reallocational efficiency.

The structure of the paper is as follows. After the literature review, Sect. 2 describes a model. Section 3 studies a minimum disclosure technology. Section 4 studies a full disclosure equilibrium with fees. After establishing a welfare benchmark without distortions, we assess the magnitude of welfare loss due to profit-maximizing fees. In Sect. 5 we study a hybrid market equilibrium and make a policy proposal. Section 6 concludes. Appendix A contains additional results. Appendix B contains the proofs.

1.1 Related literature

Our paper is at the intersection of the two literatures, matching and disclosure. Fernandez and Gali (1999) develop a model of distorted matching, in which agents on one side are heterogeneous in two dimensions. They study distortions due to borrowing constraints, while we focus on information frictions and transaction costs. Moreover, they make standard assumptions of two exogenous sides (e.g. schools and students) and zero outside options. In our model, traders have heterogenous outside options (stand-alone values) and choose sides of the market (sellers or buyers), both of which are important features of many asset markets. The complementarity assumption with two-dimensional heterogeneity is also used in two applied works, Jovanovic and Braguinsky (2004) and Nocke and Yeaple (2008). These two works study efficient trading, while we study inefficient trading. More specifically, relative to Jovanovic and Braguinsky (2004), our model features multiple modes of disclosures.³ Also, Nocke and Yeaple (2008) entirely abstract from frictions that constrain asset trading. Motivations are also different. While they use their (efficient) asset trading model as a part of a larger model of foreign direct investment, we focus on inefficiency of asset trading itself. Finally, a minimum disclosure equilibrium studied in Sect. 3 is related to the literature on coarse matching initiated by McAfee (2002). Most works in this literature study matching of unidimensional type of agents between two exogenous sides (Damiano and Li (2007), Hoppe et al. (2009), and Hoppe et al. (2011)). We add to this literature by expanding the scope of the analysis to multi-dimensional types and endogenous sides.

Following Lizzeri (1999), a large literature emerged to study disclosure design by intermediaries. This literature typically studies a general disclosure design in a relatively simple environment.⁴ We take an opposite approach: we focus on simple disclosure technologies, but embed them in a frictional matching environment with two dimensional heterogeneity. This approach allows us to shed a new light on the welfare impact of coarse information provision. In a related work, Harbaugh and Rasmusen (2018) shows that coarse grading (e.g., pass or fail) may generate more information than exact grading because it induces more agents to be certified. A similar force is at work in our model, but our model underlines that, in a matching environment, coarse information provision has a large welfare impact through its competitive effect on the demand for certifiers who provide finer information. The two approaches are complementary and should converge toward disclosure design in a general matching environment, which we believe is a promising area for future works.

2 Model

After describing a model environment in Sect. 2.1, we explain a notion of competitive market-clearing equilibrium in Sect. 2.2 and a welfare measure in Sect. 2.3.

2.1 Environment

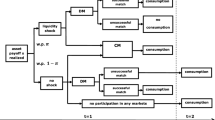
Each trader has two factors. The first factor is tradeable but indivisible, while the second factor is non-tradeable. Traders are heterogeneous in the quality of both factors. We call the tradeable factor an asset, and the non-tradeable factor skill. Without skill, assets do not generate any value. We assume that each trader can manage at most one asset, and that traders cannot act on both sides of the market simultaneously. Hence, three options are available for each trader: (i) sell an endowed asset (seller), or (ii) buy and manage a new asset (buyer ), or (iii) manage its endowed asset (stand-alone). Finally, we assume that a continuum measure one of traders draw A and X independently from a uniform distribution on $\left[ 0,1\right]$. A trader with an asset of quality A and the skill level X can realize a gross value using a common technology $F\left( A,X\right) =AX$.

The assumption that traders cannot act on both sides of the market simultaneously deserves some discussion. First, this naturally occurs if time is also indivisible: to buy and manage a new asset, one must focus on that activity, thereby leaving the endowed asset idle.⁵ Second, the assumption can be micro-founded by adding explicit costs of buying and selling assets simultaneously.⁶ Finally, without these implicit or explicit costs, all traders would be active on both sides of the market, as in Nocke and Yeaple (2008). This feature is undesirable for applications where only a small fraction of potential traders actually trade.⁷

2.2 Equilibrium

Our solution concept is a competitive market-clearing equilibrium, in which traders act taking prices as given, and prices clear markets for assets given some form of disclosure by sellers. More specifically, traders endowed with $\left( A,X\right)$ face the following problem:

$$\begin{aligned} \Pi \left( A,X\right) \equiv \max \left\{ \Pi _{S}\left( A\right) ,\ \Pi _{B}\left( X\right) ,\ AX\right\} , \end{aligned}$$

(1)

where $\Pi _{S}\left( A\right)$ is the payoff as a seller, $\Pi _{B}\left( X\right)$ is the payoff as a buyer, and AX is the payoff as a stand-alone trader. A choice of assets, prices of assets paid by buyers to sellers, and fees for disclosure paid by sellers to intermediaries are all subsumed in $\Pi _{S}\left( A\right)$ and $\Pi _{B}\left( X\right)$. A solution to (1) endogenously determines the supply and demand of assets. A competitive equilibrium is a pair of traders’ strategies and prices such that (i) traders’ strategies solve (1), (ii) prices clear the markets for assets, and (iii) traders’ expectation about the quality of assets for sale is consistent with (i) and (ii). Obviously, $\Pi _{S}\left( A\right)$, $\Pi _{B}\left( X\right)$, and equilibrium prices all depend on the disclosure technology and fees. In Sects. 3, 4, 5, we introduce a specific disclosure technology and fees, and define and characterize an associated equilibrium. We defer further discussion of equilibrium to each section.

2.3 Welfare measure

Our welfare measure is the aggregate values created when trading is allowed, minus the aggregate values created when trading is not allowed. We denote by V the aggregate value generated by the assets sold by sellers and managed by buyers. We denote by $C_{S}$ the aggregate value that would have been created by sellers if there were no trading, i.e., their opportunity costs of trading. Similarly, we denote by $C_{B}$ buyers’ opportunity costs of trading. With the three endogenous variables $\left( V,C_{S},C_{B}\right)$, we define a welfare gain by⁸

$$\begin{aligned} G\equiv V-\left( C_{S}+C_{B}\right) . \end{aligned}$$

As we assume that the intermediary incurs no cost for disclosure,⁹ the aggregate fees paid by all sellers, $\pi$, equal the intermediary’s profit. We define traders’ gain by

$$\begin{aligned} TG\equiv G-\pi . \end{aligned}$$

We characterize G and TG, and compare them across different types of equilibria.

3 Minimum (or no) disclosure

In this section, we study a minimum disclosure technology, which only verifies that an asset quality is above a fixed value $A_{\min }\in \left[ 0,1\right]$. We call $A_{\min }$ a minimum standard. This disclosure technology is important for two reasons. First, it is the most simple disclosure technology. As such, we use it as a policy tool in Sect. 5. Second, when $A_{\min }=0$, only traders’ self-selection reveals information (i.e., no explicit disclosure). This sets a natural lower bound on the amount of information revelation. We call an equilibrium with the minimum disclosure technology minimum disclosure equilibrium (henceforth MD equilibrium), and call an equilibrium with $A_{\min }=0$ no disclosure equilibrium (ND equilibrium).

Because the disclosure “$A\ge A_{\min }$ ” is common for all sellers, assets must be traded at a single price P. Traders’ problem (1) simplifies to

$$\begin{aligned} \Pi ^{MD}\left( A,X\right) =\max \left\{ P,\ aX-P,\ AX\right\} , \end{aligned}$$

(2)

where the expected quality of assets for sale, $a\equiv E\left[ A|A\text { is for sale}\right]$, is endogenous.

Definition

A minimum disclosure equilibrium is a collection of a price $P^{*}$, the expected quality of assets for sale $a^{*}$, and traders’ strategies such that (i) traders’ strategies solve (2) with $\left( P^{*},a^{*}\right)$, (ii) $P^{*}$ clears a market, (iii) $a^{*}$ is consistent with (i) and (ii).

3.1 Equilibrium characterization

We briefly describe how the price mechanism clears the market and relegate details to Appendix B.¹⁰ From (2), a necessary condition for non-zero trading is $0<P<a<1$. Participation constraints as a seller and as a buyer are

$$\begin{aligned}{} & {} \max \left\{ aX-P, AX\right\} \le P, \end{aligned}$$

(3)

$$\begin{aligned}{} & {} \max \left\{ P, AX\right\} \le aX-P. \end{aligned}$$

(4)

In Fig. 1, we assume $A_{\min }=0$ and plot sellers’ participation constraint (3) as a solid blue line, and buyers’ participation constraint (4) as a dashed red line. The intersection of the two lines is $\left( X^{*},A^{*}\right) =\left( \frac{2P}{a}, \frac{a}{2}\right)$. A vertical line below this point represents traders who are indifferent between selling and buying, but strictly prefer trading to not trading.

Fig. 1

Self-selection of traders with $A_{\min }=0$

Sellers are in the area below the solid blue line, and their measure can be computed by integrating their skill. Because sellers of assets $A\in \left[ 0,A^{*}\right]$ have skill $X\le X^{*}$, while sellers of assets $A\in \left[ A^{*},1\right]$ have skill $X\le \frac{P}{A}$, the total supply for a given price P is

$$\begin{aligned} S\left( P\right) =\int _{0}^{A^{*}}X^{*}dA+\int _{A^{*}}^{1}\frac{P }{A}dA. \end{aligned}$$

(5)

Similarly, buyers are in the area below the dashed red line. Because buyers with skill $X\in \left[ X^{*},1\right]$ have initial assets $A\le a- \frac{P}{X}$, the total demand is

$$\begin{aligned} D\left( P\right) =\int _{X^{*}}^{1}\left( a-\frac{P}{X}\right) dX. \end{aligned}$$

(6)

The supply (5) increases in P, while the demand (6 ) decreases in P. We show that, for any conjectured $a\in \left( 0,1\right)$, a market-clearing condition $S\left( P\right) =D\left( P\right)$ has a unique market-clearing price $P\left( a\right) \in \left( 0,a\right)$. With this $P\left( a\right)$, the expected quality of assets for sale is

$$\begin{aligned} \frac{\int _{0}^{A^{*}}\left( AX^{*}\right) dA+\int _{A^{*}}^{1}\left( A\frac{P\left( a\right) }{A}\right) dA}{S\left( P\left( a\right) \right) }\equiv \Gamma \left( a\right) . \end{aligned}$$

We show that $\Gamma \left( a\right) =a$ has a unique solution $a^{*}\in \left( 0,1\right)$. An equilibrium price is $P^{*}=P\left( a^{*}\right)$.

Figure 2 illustrates two qualitatively different cases with $A_{\min }>0$. Because the value of $A^{*}=\frac{a^{*}}{2}$ depends on $A_{\min }$, we write it as $A^{*}\left( A_{\min }\right)$.

Fig. 2

Self-selection of traders with $A_{\min }>0$

When $A_{\min }<A^{*}\left( A_{\min }\right)$ (panel (a)), we say that sellers and buyers are connected. When $A^{*}\left( A_{\min }\right) \le A_{\min }$ (panel (b)), we say that sellers and buyers are separated. Which case occurs depends on $A_{\min }$. Using $\left\{ X^{*},A^{*},a^{*},P^{*}\right\}$, which all depend on $A_{\min }$, we compute the welfare gain $G^{MD}\left( A_{\min }\right)$. This turns out to be a strikingly simple function of $\left( a^{*},P^{*}\right)$.

Proposition 1

(MD equilibrium).

• (a) A unique MD equilibrium exists for all $A_{\min }\in \left[ 0,1\right]$. Sellers and buyers are connected if and only if $A_{\min }<A_{+}$, where $A_{+}\in \left( 0,1\right)$ is a smaller solution to $1=A\left( 1-2\ln A\right)$.

• (b) The welfare gain in the MD equilibrium is $G^{MD}\left( A_{\min }\right) =\left( \frac{a^{*}-P^{*}}{2}\right) ^{2}$.

Figure 3 shows how the minimum standard $A_{\min }$ affects the behavior of traders.

Fig. 3

MD equilibria with different levels of $A_{\min }$

Sellers are in the area $A\in \left[ A_{\min },\frac{P^{*}}{X}\right]$ (colored blue). Buyers are in the area $A\le a^{*}-\frac{P^{*}}{X}$ (colored red). The panel (a) is the case with $A_{\min }=0$ (ND equilibrium). The minimum standard $A_{\min }$ increases from the panel (a) to (d). The MD equilibrium is inefficient for two reasons. On the one hand, buyers with initial assets $A\in \left[ A_{\min },a^{*}-P^{*}\right]$ may end up with worse assets (panel (a)(b)).¹¹ By raising $A_{\min }$, this problem disappears (panel (c)). On the other hand, too high $A_{\min }$ leaves most welfare gains unrealized (panel (d)). A key for the efficiency in MD equilibrium is to make $A_{\min }$ high enough that traders that qualify as sellers do not become buyers, but not too high such that sufficient trading occurs.

Proposition 1 allows us to compute the welfare gain in MD equilibrium as a function of $A_{\min }\in \left[ 0,1\right]$. We denote the welfare gain in ND equilibrium by $\underline{G}\equiv G^{MD}\left( 0\right)$. In Sect. 4, we characterize a benchmark welfare gain $\overline{G}$ in the absence of distortions. To facilitate clear welfare comparison, we numerically evaluate $G^{MD}\left( A_{\min }\right)$ as a percentage of $\overline{G}$.¹²

Claim 1

There is $A_{\min }^{*}\in \left( A_{+},1\right)$ that maximizes $G^{MD}\left( A_{\min }\right)$, and $G^{MD}\left( A_{\min }^{*}\right)$ is 83% of the benchmark welfare gain $\overline{G}$. The welfare gain in ND equilibrium $\underline{G}$ is 29% of $\overline{G}$.

The MD equilibrium with $A_{\min }^{*}\approx 0.562$ is shown in Fig. 3 (c). One may wonder if the welfare can be improved by allowing assets below $A_{\min }$ to be separately traded. In the older version of the paper (Kawakami 2022), we found that this market segmentation is quite effective – with two markets but without optimizing minimum standards, the welfare gain is 88% of $\overline{G}$.¹³ We use this insight for a policy proposal in Sect. 5.

4 Full disclosure and fees

In this section, we study a case where sellers can disclose their asset quality perfectly if they pay fees.¹⁴ In Sect. 4.1, we define a full disclosure equilibrium (henceforth FD equilibrium) and provide general characterization. In Sect. 4.2, we specialize a fee structure to the one commonly used in practice – a fixed fee and a fee proportional to asset prices.¹⁵ In Sect. 4.3, we quantify the welfare loss due to profit-maximizing fees.

4.1 Full disclosure equilibrium and welfare benchmark

Let $\left\{ P\left( A\right) \right\} _{A\in \left( 0,1\right] }$ be a price function for assets. Suppose that sellers who disclose A and sell it at a price P must pay a fee $f\left( A,P\right)$. In equilibrium, the price function depends on f, but we suppress the notation. Traders with $\left( A,X\right)$ solve

$$\begin{aligned} \Pi ^{FD}\left( A,X\right)\equiv & {} \max \left\{ \Pi _{S}^{FD}\left( A\right) ,\ \Pi _{B}^{FD}\left( X\right) ,\ AX\right\} , \nonumber \\ \text {where }\Pi _{S}^{FD}\left( A\right)\equiv & {} P\left( A\right) -f\left( A,P\left( A\right) \right) \! \ \ \text {and }\,\!\Pi _{B}^{FD}\left( X\right) \equiv \underset{A\in \left[ 0,1\right] }{\max }\left\{ AX-P\left( A\right) \right\} .\nonumber \\ \end{aligned}$$

(7)

Definition

A full disclosure equilibrium is a pair of a price function $\left\{ P\left( A\right) \right\} _{A\in \left( 0,1\right] }$ and traders’ strategies such that (i) traders’ strategies solve (7) with $\left\{ P\left( A\right) \right\} _{A\in \left( 0,1\right] }$, (ii) $\left\{ P\left( A\right) \right\} _{A\in \left( 0,1\right] }$ clears a market.

4.1.1 Equilibrium characterization

Because asset quality A is disclosed in FD equilibrium, there is no need to characterize the expected quality of assets for sale. However, a price function in FD equilibrium is more complicated as it must jointly achieve matching and market-clearing. We briefly describe how the price mechanism achieves both, and relegate details to Appendix B.¹⁶ First, consider matching. From buyers’ problem, we define

$$\begin{aligned} \widehat{a}\left( X\right) \equiv \arg \underset{A\in \left[ 0,1\right] }{ \max }\left\{ AX-P\left( A\right) \right\} \end{aligned}$$

and also define a matching function by its inverse.¹⁷ That is, $m\left( A\right) \equiv \widehat{a}^{-1}\left( A\right)$ is the skill level of buyers who demand assets A for a given price function $P\left( A\right)$.

Next, consider market-clearing. We first derive a supply density $S^{FD}\left( A\right)$ for assets A, for a given price function $P\left( A\right)$. For each $A\in \left[ 0,1\right]$, the supply density $S^{FD}\left( A\right)$ is a measure of traders who satisfy sellers’ participation constraint $\max \left\{ \Pi _{B}^{FD}\left( X\right) , AX\right\} \le P\left( A\right) -f\left( A,P\left( A\right) \right)$. We show that this measure equals a measure of traders with skill $X\le \frac{ P\left( A\right) -f\left( A,P\left( A\right) \right) }{A}$. Because the distribution of X is uniform, $S^{FD}\left( A\right) =\frac{P\left( A\right) -f\left( A,P\left( A\right) \right) }{A}$. The derivation of a demand density $D^{FD}\left( A\right)$ is similar. A market-clearing condition is then

$$\begin{aligned} \int _{0}^{A}S^{FD}\left( a\right) da=\int _{0}^{m\left( A\right) }D^{FD}\left( \widehat{a}\left( X\right) \right) dX\ \text {for any }A\in \left( 0,1\right] \ \text {and} \ m\left( 1\right) =1. \end{aligned}$$

(8)

We show that the market-clearing condition (8) can be expressed as a differential equation in $P\left( A\right)$ and used to derive model predictions. This is our technical contribution.

Proposition 2

(FD equilibrium). In any FD equilibrium in which $P^{\prime }\left( A\right) >0$ and $P^{\prime \prime }\left( A\right) >0$,

• (a) A matching function is $m\left( A\right) =P^{\prime }\left( A\right)$. A price function $\left\{ P\left( A\right) \right\} _{A\in \left( 0,1\right] }$ is a solution to the second-order differential equation

  $$\begin{aligned} \left( \frac{\ P^{\prime }\left( A\right) }{P\left( A\right) }A-1\right) \frac{\ P^{^{\prime \prime }}\left( A\right) }{P^{\prime }\left( A\right) } A=1-\frac{f\left( A,P\left( A\right) \right) }{P\left( A\right) }, P^{\prime }\left( 1\right) =1. \end{aligned}$$

  (9)

• (b) Payoffs for matched sellers and buyers satisfy $\Pi _{S}^{FD}\left( A\right) =\Pi _{B}^{FD}\left( m\left( A\right) \right) \frac{ \ m^{\prime }\left( A\right) }{m\left( A\right) }A$.

First, given the symmetry of our environment, without fees, a conjectured efficient matching $m\left( A\right) =A$ immediately yields $P\left( A\right) =\frac{1}{2}A^{2}$.¹⁸ The benefit of deriving (9) arises because with general fees we do not know a priori the form of matching function. Second, (9) can generate testable predictions even when we cannot solve it explicitly. Proposition 2(b) is one such example: any change that increases the elasticity of $m\left( A\right)$ leads to an increase in sellers’ payoff relative to matched buyers’ payoff. This comparative statics holds in any FD equilibria satisfying (9). In Appendix A, we discuss this and other model predictions based on (9) in a specific applied context.

4.1.2 Welfare benchmark

A special case of full disclosure without fees sets the upper bound on the welfare gain. We use this case as our welfare benchmark, and denote the benchmark welfare gain by $\overline{G }$. As already done in Claim 1, all the welfare statements will be presented as a percentage of $\overline{G}$.

Corollary 1

(Welfare benchmark). In FD equilibrium with $f\left( A,P\left( A\right) \right) =0$, $P\left( A\right) = \frac{1}{2}A^{2}$, $m\left( A\right) =A$, $\overline{G}= \frac{1}{16}$, and $\Pi ^{FD}\left( A,X\right) =\left\{ \begin{array}{lll} \frac{1}{2}A^{2} &{} \text {for }\frac{A}{X}\ge 2, &{} \text {{(sellers)}} \\ \frac{1}{2}X^{2} &{} \text {for }\frac{A}{X}\le \frac{1}{2}, &{} \text {(buyers)}\\ AX &{} \text {otherwise.} &{} \text {(others)} \end{array}\right.$

4.2 Fixed and proportional fees

The differential Eq. (9) does not admit a general solution, but fortunately we can make a further progress for important classes of fees. A fixed fee and a fee proportional to asset prices can be expressed as $f=\phi +\tau P$ with fixed numbers $\left( \phi ,\tau \right) \in \left[ 0,1 \right] ^{2}$. With these fees, (9) has a closed-form solution. Corollary 1 follows by setting $\phi =\tau =0$ in the next result.

Proposition 3

(FD equilibrium with fixed and proportional fees). For any $\left( \phi ,\tau \right) \in \left[ 0,1\right] ^{2}$ such that $\phi +\tau <1$, an FD equilibrium with trading exists. The price function, the matching function, and the welfare gain are

$$\begin{aligned} P\left( A;\phi ,\tau \right)= & {} \frac{1}{1+\sqrt{1-\tau }}\left( A^{1+\sqrt{ 1-\tau }}+\frac{\phi }{\sqrt{1-\tau }}\right) \ \ \text {and }\ m\left( A\right) =A^{\sqrt{1-\tau }},\nonumber \\ \end{aligned}$$

(10)

$$\begin{aligned} G^{FD}\left( \phi ,\tau \right)= & {} \frac{\frac{1}{2}\frac{\phi ^{2}}{\sqrt{ 1-\tau }}\ln \frac{\phi }{1-\tau }}{\left( 1+\sqrt{1-\tau }\right) ^{2}}+ \frac{1}{4}\left( \frac{\sqrt{1-\tau }}{1+\sqrt{1-\tau }}\right) ^{2}\nonumber \\{} & {} \quad \times \left( 1-\frac{\phi }{1-\tau }\right) \left\{ \begin{array}{l} 2-\sqrt{1-\tau }+ \\ \left( 3\sqrt{1-\tau }-2\right) \frac{\phi }{1-\tau } \end{array}\right\} . \end{aligned}$$

(11)

We use (10) to draw Fig. 4 that shows matching and self-selection in FD equilibrium.

Fig. 4

FD equilibria with different levels of fees

Sellers are in the top-left area (colored blue). Buyers are in the bottom-right area (colored red). The panel (a) shows the welfare benchmark with $m\left( A\right) =A$. In the other panels, a solid black line is $m\left( A\right) =A^{\sqrt{1-\tau }}$ and dashed blue lines indicate the welfare benchmark. Notice that the proportional fee reduces asset sales by more at higher levels of A (panel (b)), while the opposite holds for the fixed fee (panel (c)). Intuitively, the fixed fee discourages traders with small gains from trade, but it does not distort the matching among participating traders. In contrast, the proportional fee is more taxing for better assets, which makes the matching asymmetric: to clear the market for high quality assets with even higher prices, the demand must come from more skilled buyers.

Figure 5 plots the welfare gain $G^{FD}\left( \phi ,\tau \right)$ given in (11).

Fig. 5

$G^{FD}\left( \phi ,\tau \right)$. Note. $\overline{G}=G^{FD}\left( 0,0\right) =\frac{1}{16} \approx 0.063$

The figure shows that the welfare gain takes the maximum $\overline{G}$ at $\phi =\tau =0$ and decreases in $\left( \phi ,\tau \right)$. Moreover, higher $\phi$ makes a marginal increase in $\tau$ more distortionary, and vice versa. To see why this mutual aggravation of fees occurs, sellers’ payoff is

$$\begin{aligned} \Pi _{S}^{FD}\left( A\right) =\frac{1-\tau }{1+\sqrt{1-\tau }}\left( A^{1+ \sqrt{1-\tau }}-\frac{\phi }{1-\tau }\right) . \end{aligned}$$

The supply density is positive only for A such that $\Pi _{S}^{FD}\left( A\right) >0$. This is equivalent to

$$\begin{aligned} A>\left( \frac{\phi }{1-\tau }\right) ^{\frac{1}{1+\sqrt{1-\tau }}}\equiv \underline{A}\left( \phi ,\tau \right) . \end{aligned}$$

(12)

$\underline{A}\left( \phi ,\tau \right)$ in (12) is the worst quality of assets for sale. With a higher $\phi$, a marginal effect of $\tau$ on (12) is greater. We use this insight in our policy proposal in Sect. 5.

4.3 Profit-maximizing fees

In this subsection, we quantify the welfare effect of profit-maximizing fees. We proceed in two steps. First, we derive the aggregate fees paid by sellers $\pi ^{FD}\left( \phi ,\tau \right)$. We only state the result in Proposition 4(a). Second, we characterize $\left( \phi ,\tau \right)$ that maximize $\pi ^{FD}\left( \phi ,\tau \right)$. To this end, we define two functions $\phi ^{FD}\left( \tau \right) \equiv \arg \underset{\phi }{\max }\ \left\{ \pi ^{FD}\left( \phi ,\tau \right) \right\}$ and $\tau ^{FD}\left( \phi \right) \equiv \arg \underset{\tau }{\max }\left\{ \pi ^{FD}\left( \phi ,\tau \right) \right\}$. Proposition 4(b) characterizes $\phi ^{FD}\left( \tau \right)$ and the associated welfare gain and traders’ gain.

Proposition 4

(Distortions in FD equilibrium).

• (a) The intermediary’s profit for a given $\left( \phi ,\tau \right)$is

  $$\begin{aligned} \pi ^{FD}\left( \phi ,\tau \right)= & {} \frac{\frac{\phi ^{2}}{\sqrt{1-\tau }} \ln \left( \frac{\phi }{1-\tau }\right) }{\left( 1+\sqrt{1-\tau }\right) ^{2} } \nonumber \\{} & {} +\frac{1}{2}\left( \frac{\sqrt{1-\tau }}{1+\sqrt{1-\tau }}\right) ^{2}\left( 1-\frac{\phi }{1-\tau }\right) \left\{ \begin{array}{l} 1-\sqrt{1-\tau } \\ +\left( 3\sqrt{1-\tau }-1\right) \frac{\phi }{1-\tau } \end{array} \right\} .\nonumber \\ \end{aligned}$$

  (13)

• (b) For $\tau <\frac{3}{4}$, $\phi ^{FD}\left( \tau \right) \in \left( 0,1-\tau \right)$ is unique and $\underset{ \tau \uparrow \frac{3}{4}}{\lim }\phi ^{FD}\left( \tau \right) =0$. For $\tau \ge \frac{3}{4}$, $\phi ^{FD}\left( \tau \right) =0$ . With fees $\left( \phi ^{FD}\left( \tau \right) ,\tau \right)$ , the welfare gain and traders’ gain satisfy

  $$\begin{aligned} G^{FD}\left( \phi ^{FD}\left( \tau \right) ,\tau \right)= & {} \frac{1}{4} \left( \frac{\sqrt{1-\tau }}{1+\sqrt{1-\tau }}\right) ^{2}\left( 1-\frac{ \phi ^{FD}\left( \tau \right) }{1-\tau }\right) \nonumber \\{} & {} \times \left\{ 1+\left( 1-\sqrt{1-\tau }\right) \left( 1-\frac{\phi ^{FD}\left( \tau \right) }{1-\tau }\right) \right\} , \end{aligned}$$

  (14)
  $$\begin{aligned} \frac{TG^{FD}\left( \phi ^{FD}\left( \tau \right) ,\tau \right) }{ G^{FD}\left( \phi ^{FD}\left( \tau \right) ,\tau \right) }= & {} \frac{1-\frac{ \phi ^{FD}\left( \tau \right) }{1-\tau }-\left( 1-\sqrt{1-\tau }+\frac{\phi ^{FD}\left( \tau \right) }{\sqrt{1-\tau }}\right) }{1-\frac{\phi ^{FD}\left( \tau \right) }{1-\tau }+\left( 1-\sqrt{1-\tau }+\frac{\phi ^{FD}\left( \tau \right) }{\sqrt{1-\tau }}\right) }. \end{aligned}$$

  (15)

A problem of maximizing $\pi ^{FD}\left( \phi ,\tau \right)$ in (13) is well-behaved for small $\left( \phi ,\tau \right)$.¹⁹ Figure 6 plots $\pi ^{FD}\left( \phi ,\tau \right)$.

Fig. 6

Intermediary’s profit

Proposition 4(b) shows that $\phi ^{FD}\left( \tau \right)$ takes zero for high enough $\tau$. To see this clearly, the panel (b) plots $\pi ^{FD}\left( \phi ,\tau \right)$ as a function of $\phi$ for a fixed $\tau$. Intuitively, $\phi$ and $\tau$ are substitutes for the intermediary’s profit due to their mutual aggravation discussed earlier.

Figure 7a plots $\left\{ \phi ^{FD}\left( \tau \right) ,\tau ^{FD}\left( \phi \right) \right\}$ with profit-maximizing fees $\left( \phi _{FD}^{*},\tau _{FD}^{*}\right)$.

Fig. 7

Profit-maximizing fees $\left( \phi _{FD}^{*},\tau _{FD}^{*}\right)$ and self-selection

The panel (b) shows the self-selection pattern. Dashed blue lines indicate the welfare benchmark. Clearly, asset trading is reduced and matching is distorted. Finally, by substituting $\tau _{FD}^{*}$ into (14) and (15), we compute the welfare gain $G^{FD}\left( \phi _{FD}^{*},\tau _{FD}^{*}\right)$ and traders’ gain $TG^{FD}\left( \phi _{FD}^{*},\tau _{FD}^{*}\right)$. Claim 2 quantities the welfare loss due to profit-maximizing fees.²⁰

Claim 2

With the profit maximizing fees $\left( \phi _{FD}^{*},\tau _{FD}^{*}\right)$, the welfare gain $G^{FD}\left( \phi _{FD}^{*},\tau _{FD}^{*}\right)$ is 74% of the benchmark welfare gain $\overline{G}$. Traders’ gain $TG^{FD}\left( \phi _{FD}^{*},\tau _{FD}^{*}\right)$ is 28% of $\overline{G}$ and it is smaller than the welfare gain $\underline{G}$ in ND equilibrium.

With profit-maximizing fees, despite using the full disclosure technology, traders’ gain is smaller than the welfare gain without any disclosure, $\underline{G}$. Thus, a combination of fixed and proportional fees impose a heavy burden on traders. In the next section, we make a policy proposal that alleviates this problem.

5 Policy proposal: hybrid market structure

In preceding sections, we investigated the MD technology and the FD technology in isolation. Two natural questions are whether they can coexist and whether they should. A short answer is “yes and yes”. In Sect. 5.1, we construct a hybrid market equilibrium (henceforth HM equilibrium) and identify conditions under which both disclosure technologies are used by traders. In Sect. 5.2, we study profit-maximizing fees in HM equilibrium. In Sect. 5.3, we propose a regulation to sustain a welfare gain and traders’ gain.

5.1 Hybrid market equilibrium

In this subsection, we construct an equilibrium where the full disclosure technology and the minimum disclosure technology are both utilized. Suppose that assets $A\ge \overline{A}\in \left( 0,1\right)$ are fully disclosed in one market (the upper market), while assets $A\in \left[ A_{\min },\overline{A}\right)$ are pooled in the other market (the lower market). The marginal asset $\overline{A}$ as well as the minimum standard $A_{\min }$ will be endogenously determined. Prices in the upper market are given by a price function $\left\{ P\left( A\right) \right\} _{A\ge \overline{A}}$. We denote the price and the expected asset quality in the lower market by $\left( P_{0},a_{0}\right)$. In equilibrium, all traders optimally choose which market to participate as well as their roles in each market.

Definition

A hybrid-market equilibrium is a collection of a price function $\left\{ P\left( A\right) \right\} _{A\in \left( 0,1\right] }$ in the upper market, a price $P_{0}$, the expected asset quality $a_{0}$, and the minimum standard $A_{\min }$ in the lower market, and traders’ strategies such that (i) traders’ strategies are optimal, (ii) prices clear all markets, (iii) $a_{0}$ is consistent with (i) and (ii).

5.1.1 Equilibrium characterization

The analysis of MD equilibrium applies in the lower market, while that of FD equilibrium applies in the higher market. Figure 8 shows two examples: $\left( \phi ,\tau \right) =\left( 0.01,0\right)$ and $\left( \phi ,\tau \right) =\left( 0.08,0\right)$.

Fig. 8

HM equilibrium with different values of fees

The two markets are connected by the two indifference conditions. Specifically, sellers of assets $\overline{A}$ must be indifferent between disclosing $\overline{A}$ in the upper market and pooling with lower quality assets $A\in \left[ A_{\min },\overline{A}\right]$ in the lower market. Similarly, buyers with skill $\overline{X}=\overline{A}^{\sqrt{1-\tau }}$ must be indifferent between buying an asset $\overline{A}$ in the upper market (at price $P\left( \overline{A}\right)$) and buying assets with expected value $a_{0}$ (at price $P_{0}$). Combining these two indifference conditions with the two equilibrium conditions in the lower market, we solve for $\left\{ P_{0},a_{0},A_{\min },\overline{A}\right\}$.

The key endogenous variable is the worst asset quality in the upper market

$$\begin{aligned} \overline{A}=\left( \frac{\phi }{1-T\left( \tau \right) }\right) ^{\frac{1}{ 1+\sqrt{1-\tau }}}\equiv \overline{A}\left( \phi ,\tau \right) \text {, where }T\left( \tau \right) \equiv \tau +\kappa \left( \tau \right) \sqrt{1-\tau } \end{aligned}$$

(16)

and $\kappa \left( \tau \right) \in \left( 0,1\right)$ is derived in Appendix B.²¹ Note that $\overline{A}\left( \phi ,\tau \right) \in \left( 0,1\right)$ is necessary for both markets to attract a positive measure of traders. Accordingly, we say that HM equilibrium is non-trivial if $\overline{A}\left( \phi ,\tau \right) \in \left( 0,1\right)$. The expression of $\overline{A}\left( \phi ,\tau \right)$ in (16) should be compared to its FD equilibrium counterpart $\underline{A}\left( \phi ,\tau \right) =\left( \frac{\phi }{ 1-\tau }\right) ^{\frac{1}{1+\sqrt{1-\tau }}}$ in (12). Importantly, $T\left( \tau \right) >\tau$ implies $\overline{A}\left( \phi ,\tau \right) >\underline{A}\left( \phi ,\tau \right)$ whenever $\phi >0$. Moreover, for the same $\tau$, the demand for the full disclosure service becomes more elastic to $\phi$ in HM equilibrium than in FD equilibrium.

The next result characterizes HM equilibrium for a given $\left( \phi ,\tau \right)$. We suppress the dependence of $\kappa \left( \tau \right)$ on $\tau$ in the next result.

Proposition 5

(HM equilibrium for a given $\left( \phi ,\tau \right)$).

• (a) There is $\tau _{\max }\in \left( 0,1\right)$ such that a non-trivial HM equilibrium exists if and only if

  $$\begin{aligned} \tau<\tau _{\max } \ \text {and}\ \ 0<\phi <1-T\left( \tau \right) . \end{aligned}$$

• (b) A welfare gain in the upper market and that in the lower market are

  $$\begin{aligned} G^{U}\left( \phi ,\tau \right)= & {} \frac{\frac{1}{2}\frac{\phi ^{2}}{\sqrt{ 1-\tau }}\ln \frac{\phi }{1-T\left( \tau \right) }}{\left( 1+\sqrt{1-\tau } \right) ^{2}}+\frac{1}{4}\left( \frac{\sqrt{1-\tau }}{1+\sqrt{1-\tau }} \right) ^{2}\left( 1-\frac{\phi }{1-T\left( \tau \right) }\right) \nonumber \\{} & {} \times \left\{ 2-\sqrt{1-\tau }+\left\{ \begin{array}{c} \left( 4-\frac{\sqrt{1-\tau }}{\sqrt{1-\tau }-\kappa }\right) \sqrt{1-\tau }\\ -2\left( 2-\frac{\sqrt{1-\tau }}{\sqrt{1-\tau }-\kappa }\right) \end{array} \right\} \frac{\phi }{1-\tau }\right\} , \nonumber \\ G^{L}\left( \phi ,\tau \right)= & {} \frac{1}{4}\left( \frac{\kappa \frac{\phi }{1-T\left( \tau \right) }}{1+\sqrt{1-\tau }}\right) ^{2}. \end{aligned}$$

  (17)

• (c) The intermediary’s profit for a given $\left( \phi ,\tau \right)$ is

  $$\begin{aligned} \pi ^{HM}\left( \phi ,\tau \right)= & {} \frac{\frac{\phi ^{2}}{\sqrt{1-\tau }} \ln \frac{\phi }{1-T\left( \tau \right) }}{\left( 1+\sqrt{1-\tau }\right) ^{2}} +\frac{1}{2}\left( \frac{\sqrt{1-\tau }}{1+\sqrt{1-\tau }}\right) ^{2}\nonumber \\ {}{} & {} \quad \times \left( 1-\frac{\phi }{1-T\left( \tau \right) }\right) \left\{ \begin{array}{l} 1-\sqrt{1-\tau }+ \\ \left( 3\sqrt{1-\tau }-1+\frac{1-\sqrt{1-\tau }}{\sqrt{1-\tau }-\kappa } \kappa \right) \frac{\phi }{1-\tau } \end{array} \right\} .\nonumber \\ \end{aligned}$$

  (18)

Proposition 5(a) shows the condition on fees for HM equilibrium to be non-trivial. The two upper bounds on fees, $\tau _{\max }$ and $1-T\left( \tau \right)$, naturally arise from $\overline{A}\left( \phi ,\tau \right) <1$, i.e., too high fees reduce demand for the full disclosure service to zero. A more subtle condition, $0<\phi$, follows from $\overline{A}\left( \phi ,\tau \right) >0$. Intuitively, to make sellers with the assets $\overline{A}\left( \phi ,\tau \right)$ indifferent between fully disclosing $\overline{A}\left( \phi ,\tau \right)$ and pooling with lower quality $A\in \left[ A_{\min },\overline{A}\right]$, $\phi$ must be positive. Otherwise, unravelling (i.e., full disclosure by paying $\tau P\left( A\right)$) occurs and pooling in the lower market cannot be sustained. This implies that, conditional on $\phi$ being positive, the intermediary would choose fees to satisfy $\tau <\tau _{\max }$ and $\phi <1-T\left( \tau \right)$.

We use (18) to endogenize fees, and (17) to compute the welfare gain $G^{HM}\left( \phi ,\tau \right) \equiv G^{U}\left( \phi ,\tau \right) +G^{L}\left( \phi ,\tau \right)$. We can build some intuition by comparing (17)(18) with their FD equilibrium counterparts $G^{FD}\left( \phi ,\tau \right)$ and $\pi ^{FD}\left( \phi ,\tau \right)$((11)(13)). First, we can show that $\kappa \left( \tau \right) =\frac{a_{0}}{\overline{A}\left( \phi ,\tau \right) }$ holds in equilibrium. Hence, $\kappa \left( \tau \right)$ measures the relative quality of the lower market. Consistent with this interpretation, exogenously setting $\kappa =0$ (and hence $T\left( \tau \right) =\tau$) in (17)(18) yields $G^{U}\left( \phi ,\tau \right) =G^{FD}\left( \phi ,\tau \right)$, $G^{L}\left( \phi ,\tau \right) =0$, and $\pi ^{HM}\left( \phi ,\tau \right) =\pi ^{FD}\left( \phi ,\tau \right)$.

Second, with $\phi =0$, the indifference condition between the two markets breaks down and the lower market attracts no trader. As a result, the intermediary’s behavior and the associated welfare gain will be the same with those in the FD equilibrium. This is confirmed by observing $\pi ^{HM}\left( 0,\tau \right) =\pi ^{FD}\left( 0,\tau \right)$, $G^{U}\left( 0,\tau \right) =G^{FD}\left( 0,\tau \right)$, and $G^{L}\left( 0,\tau \right) =0$. In the next subsection, we show that the monopoly intermediary optimally chooses $\phi =0$. This means that some regulation on fees is necessary to make HM equilibrium non-trivial.

5.2 Profit-maximizing fees in HM equilibrium

To characterize the profit-maximizing fees in HM equilibrium, we proceed similarly as before by characterizing two functions $\phi ^{HM}\left( \tau \right) \equiv \arg \underset{\phi }{\max }\left\{ \pi ^{HM}\left( \phi ,\tau \right) \right\} \$and $\tau ^{HM}\left( \phi \right) \equiv \arg \underset{\tau }{\max }\left\{ \pi ^{HM}\left( \phi ,\tau \right) \right\}$. We then find the intersection of these two functions, and numerically verify that the profit function (18) is indeed maximized at this point. Figure 9 plots $\pi ^{HM}\left( \phi ,\tau \right)$ and the profit-maximizing fees $\left( \phi _{HM}^{*},\tau _{HM}^{*}\right)$.

Fig. 9

Intermediary’s profit and fees in HM equilibrium. Note. Dashed lines in panels (c) and (d) plot counterparts in FD equilibrium

The panel (a) plots $\pi ^{HM}\left( \phi ,\tau \right)$ with the same scale used for $\pi ^{FD}\left( \phi ,\tau \right)$ in Fig. 6a. The line $\pi ^{HM}\left( 0,\tau \right)$ along the $\tau$-axis is identical to $\pi ^{FD}\left( 0,\tau \right)$, suggesting the discontinuity of $\pi ^{HM}\left( \phi ,\tau \right)$ at $\phi =0$. By choosing a large $\tau$ and $\phi =0$, the intermediary enjoys its monopoly status even in the presence of the free minimum disclosure service. This no longer works with $\phi >0$. No matter how small it is, a positive fixed fee makes the lower market active, which makes setting high $\tau$ not a viable option for the intermediary. The panel (b) plots $\pi ^{HM}\left( \phi ,\tau \right)$ for $\phi >0$ with a magnified scale. For $\phi >0$, $\tau ^{HM}\left( \phi \right) \in \left[ 0,\tau _{\max }\right)$ is unique.

The panel (c) plots $\pi ^{HM}\left( \phi ,\tau \right)$ as a function of $\phi$ for fixed values of $\tau$. Dashed lines are $\pi ^{FD}\left( \phi ,\tau \right)$, with the same color for the same value of $\tau$. Comparing solid lines with dashed lines, the profit is significantly reduced for any $\phi >0$. However, at $\phi =0$, the intermediary will choose $\tau ^{HM}\left( 0\right) =\tau ^{FD}\left( 0\right)$. The panel (d) plots $\phi ^{HM}\left( \tau \right)$ and $\tau ^{HM}\left( \phi \right)$.²² Note that $\tau ^{HM}\left( \phi \right)$ is plotted with red asterisk markers ( $*$) to emphasize the discontinuity of $\tau ^{HM}\left( \phi \right)$ at $\phi =0$.²³ This shows the optimality of $\left( \phi _{HM}^{*},\tau _{HM}^{*}\right) =\left( 0,\tau ^{FD}\left( 0\right) \right)$ (a marker “$\circ$”), which is close to $\left( \phi _{FD}^{*},\tau _{FD}^{*}\right)$ (a marker “$\triangle$”).

Claim 3

The profit-maximizing fees in HM equilibrium are $\left( \phi _{HM}^{*},\tau _{HM}^{*}\right) =\left( 0,\tau ^{FD}\left( 0\right) \right)$. The welfare gain $G^{HM}\left( \phi _{HM}^{*},\tau _{HM}^{*}\right)$ is 74% of the benchmark welfare gain $\overline{G}$ and traders’ gain $TG^{HM}\left( \phi _{HM}^{*},\tau _{HM}^{*}\right)$ is 29% of $\overline{G}$.

When competing with the minimum disclosure technology, the intermediary can use a fixed fee but chooses not to. Comparing Claim 3 to Claim 2, the welfare impact of this change in the intermediary’s behavior is negligible. This is because the intermediary can secure a large profit without the fixed fee. Recall that the force of the lower market works through $\overline{A}\left( \phi ,\tau \right) \equiv \left( \frac{\phi }{1-T\left( \tau \right) }\right) ^{\frac{1}{1+\sqrt{1-\tau }} }>\left( \frac{\phi }{1-\tau }\right) ^{\frac{1}{1+\sqrt{1-\tau }}}= \underline{A}\left( \phi ,\tau \right)$, i.e., by making the demand for the disclosure service more elastic to fees. The intermediary can eliminate this force by setting $\phi =0$, and it does so because optimizing $\tau$ alone (with $\phi =0$) can secure a higher profit than optimizing $\left( \phi ,\tau \right)$ subject to $\phi >0$ (see Fig. 9a).

5.3 Regulation to support a non-trivial HM equilibrium

In the previous subsection we showed that if the intermediary can freely set fees, $\phi =0$ will be chosen to make the HM equilibrium trivial, leading to a limited welfare improvement. However, Fig. 9d shows that the solid blue line (representing $\phi ^{HM}\left( \tau \right)$) lies below asterisks markers (representing $\tau ^{HM}\left( \phi \right)$). This means that $\tau <\tau ^{HM}\left( \phi ^{HM}\left( \tau \right) \right)$ holds for any $\tau <\tau _{\max }$, i.e., the intermediary has an incentive to raise $\tau <\tau _{\max }$. We exploit this observation in a policy proposal. More precisely, if the upper bound $\tau _{c}\in \left[ 0,\tau _{\max }\right)$ (c for cap) is imposed on the proportional fee $\tau$, then the intermediary chooses $\left( \phi ,\tau \right) =\left( \phi ^{HM}\left( \tau _{c}\right) ,\tau _{c}\right)$.²⁴ Proposition 6 characterizes $\phi ^{HM}\left( \tau \right)$ for $\tau <\tau _{\max }$ and the associated welfare gain.

Proposition 6

(Distortions in HM equilibrium). For $\tau <\tau _{\max }$, $\phi ^{HM}\left( \tau \right) \in \left( 0,1-T\left( \tau \right) \right)$ is unique and $\underset{\tau \uparrow \tau _{\max }}{\lim }\phi ^{HM}\left( \tau \right) =0$.

With fees $\left( \phi ^{HM}\left( \tau \right) ,\tau \right)$ , the welfare gain is

$$\begin{aligned} G^{HM}\left( \phi ^{HM}\left( \tau \right) ,\tau \right)= & {} \frac{1}{4} \left( \frac{\sqrt{1-\tau }}{1+\sqrt{1-\tau }}\right) ^{2}\left( 1-\frac{ \phi ^{HM}\left( \tau \right) }{1-\tau }\right) \nonumber \\{} & {} \times \left\{ 1+\left( 1-\sqrt{1-\tau }\right) \left( 1-\frac{\phi ^{HM}\left( \tau \right) }{1-\tau }\right) \right\} . \end{aligned}$$

(19)

There is a complete parallel between $G^{HM}\left( \phi ^{HM}\left( \tau \right) ,\tau \right)$ in (19) and $G^{FD}\left( \phi ^{FD}\left( \tau \right) ,\tau \right)$ in (14), despite that the former includes the welfare gain in the lower market. As a simple example, consider $\tau _{c}=0$, i.e., a ban on the proportional fee. From (19), the welfare gain $G^{HM}\left( \phi ^{HM}\left( 0\right) ,0\right) =\left( 1-\phi ^{HM}\left( 0\right) \right) \overline{G}$ is 93% of $\overline{G}$.²⁵ The corresponding traders’ gain is 81% of $\overline{G}$. Let us compare these numbers with $G^{FD}\left( \phi ^{FD}\left( 0\right) ,0\right)$ and $TG^{FD}\left( \phi ^{FD}\left( 0\right) ,0\right)$, i.e., the effects of the same regulation $\tau _{c}=0$ in the absence of the lower market. $G^{FD}\left( \phi ^{FD}\left( 0\right) ,0\right)$ is 72% of $\overline{G}$ and $TG^{FD}\left( \phi ^{FD}\left( 0\right) ,0\right)$ is only 31% of $\overline{G}$. Thus, while a cap regulation alone does little for traders, in the presence of the lower market it significantly increases traders’ gain.

Figure 10 plots $G^{HM}\left( \phi ^{HM}\left( \tau _{c}\right) ,\tau _{c}\right)$ and $TG^{HM}\left( \phi ^{HM}\left( \tau _{c}\right) ,\tau _{c}\right)$ as we vary $\tau _{c}\in \left[ 0,\tau _{\max }\right)$. For comparison, dashed lines are $G^{FD}\left( \phi ^{FD}\left( \tau _{c}\right) ,\tau _{c}\right)$ and $TG^{FD}\left( \phi ^{FD}\left( \tau _{c}\right) ,\tau _{c}\right)$ for $\tau _{c}<\tau _{FD}^{*}$. These are obtained under the same cap, but in the absence of the lower market.

Fig. 10

$G^{HM}\left( \phi ^{HM}\left( \tau _{c}\right) ,\tau _{c}\right)$ and $TG^{HM}\left( \phi ^{HM}\left( \tau _{c}\right) ,\tau _{c}\right)$

In Fig. 10, a marker “$\triangle$ ” is $\tau _{FD}^{*}\approx 0.603$, and a marker “$\times$” is $\tau _{\max }\approx 0.338$. The panel (a) plots $G^{HM}\left( \phi ^{HM}\left( \tau _{c}\right) ,\tau _{c}\right)$ and $G^{FD}\left( \phi ^{FD}\left( \tau _{c}\right) ,\tau _{c}\right)$. It shows that $G^{HM}\left( \phi ^{HM}\left( \tau _{c}\right) ,\tau _{c}\right)$ is maximized by the interior cap $\tau _{c}^{*}\approx 0.218\in \left( 0,\tau _{\max }\right)$ (a marker “$\circ$”). The associated fixed fee is $\phi ^{HM}\left( \tau _{c}^{*}\right) \approx 0.009$. The panel (b) plots $TG^{HM}\left( \phi ^{HM}\left( \tau _{c}\right) ,\tau _{c}\right)$ and $TG^{FD}\left( \phi ^{FD}\left( \tau _{c}\right) ,\tau _{c}\right)$. The former (a solid line) shows that most of the welfare gain accrues to traders.²⁶ In contrast, the latter (a dashed line) is close to $\underline{G}$ (29%). Without the lower market, the intermediary absorbs almost all the welfare improvement by the disclosure.

Claim 4

With a cap regulation $\tau \le \tau _{c}\in \left[ 0,\tau _{\max }\right)$, the intermediary chooses $\left( \phi ,\tau \right) =\left( \phi ^{HM}\left( \tau _{c}\right) ,\tau _{c}\right)$. There is the optimal cap regulation $\tau _{c}^{*}\in \left( 0,\tau _{\max }\right)$ that maximizes the welfare gain $G^{HM}\left( \phi ^{HM}\left( \tau _{c}\right) ,\tau _{c}\right)$. The maximized welfare gain $G^{HM}\left( \phi ^{HM}\left( \tau _{c}^{*}\right) ,\tau _{c}^{*}\right)$ is 97% of the benchmark welfare gain $\overline{G}$ and traders’ gain $TG^{HM}\left( \phi ^{HM}\left( \tau _{c}^{*}\right) ,\tau _{c}^{*}\right)$ is 75% of $\overline{G}$. With the same cap $\tau _{c}^{*}$ but without the lower market, the welfare gain $G^{FD}\left( \phi ^{FD}\left( \tau _{c}^{*}\right) ,\tau _{c}^{*}\right)$ is 74% and traders’ gain is 31% of $\overline{G}$.

The following back-of-envelope calculation may be useful. At the optimal cap $\tau _{c}^{*}$, the share of the welfare gain for traders is $\frac{75}{ 97}$. Because $\frac{97-75}{75}\in \left( \frac{1}{4},\frac{1}{3}\right)$, if one person can intermediate two transactions (i.e., two sellers and buyers) or more on average, then the intermediation sector gets the larger division of the welfare gain on the per capita basis. In the absence of the lower market, the same cap leads to much more unequal division of the welfare gain ($\frac{74-31}{31}\approx 1.387$).

Figure 11 shows the self-selection pattern of traders with $\left( \phi ,\tau \right) =\left( \phi ^{HM}\left( \tau _{c}^{*}\right) ,\tau _{c}^{*}\right)$.

Fig. 11

HM equilibrium with the optimal cap $\tau _{c}^{*}$

With the optimal cap $\tau _{c}^{*}$, the lower market attracts much smaller mass of traders relative to the upper market. If measured by transaction values, its relative size is even smaller. Nevertheless, these small transactions play a key role in improving the overall welfare. Trading in the lower market is inefficient due to random matching, and a direct welfare contribution of the lower market is small because traders in this market have small gains from trade. Yet, a hybrid market structure allows these traders to contribute to the aggregate welfare indirectly, and its aggregate impact is significant. The welfare analysis with profit-maximizing fees is summarized in Table 1.

Table 1 The welfare gain with profit-maximizing fees

The minimum disclosure technology, although inefficient on its own, is a useful regulatory tool to control non-competitive and/or collusive behaviors of disclosure service providers. While the minimum disclosure service and the cap regulation requires real resources, the magnitude of the welfare gain indicates that the benefit may exceed the cost.

6 Conclusion

We presented a competitive matching model of asset trading subject to information frictions, where traders choose to be sellers or buyers. We showed that the full disclosure service by a monopoly intermediary and the minimum disclosure service by a regulatory body can coexist, if the intermediary’s fees are appropriately regulated. An active market with the free minimum disclosure service raises the demand elasticity for the full disclosure service. As a result, more welfare gains are realized, and more “productive” traders – sellers with better assets and buyers with better skills—benefit more from this policy. The result shows that a minimum disclosure technology, although it is inefficient on its own, is a useful regulatory tool. More generally, our analysis indicates that in a situation where a natural monopoly (or collusion) has been established but its (or their) expertise is valuable, “pseudo” competition induced by a regulatory body may be an indirect but effective measure of regulation.

While the model incorporates many features of markets for large, indivisible, and complex assets (heterogeneity, information frictions, and transaction costs), it remains tractable. In Appendix A, we derive and discuss testable model predictions. Investigating the empirical validity of the model for various applications is an important work to be done.

There are obvious limitations to our model: we remained in a static model, focused on simple disclosure technologies, and ignored strategic interactions among intermediaries. How much do we gain (or lose) by allowing for a second round of trading?²⁷ Does the intermediary have an incentive to provide a more general disclosure service? How do intermediaries with different disclosure technologies compete in our matching environment? How do all these considerations affect traders’ ex ante incentive to improve their asset quality and skill? We believe that our model is a useful first step toward answering these questions.

Appendices

Appendix A: Additional results and applications

This Appendix contains some additional results. In Sect. 7.1, we show that a market-clearing condition can be exploited to characterize matched pairs of traders. In Sect. 7.2, we apply these results to M &A markets.

1.1 Comparative statics in FD equilibrium

We define four empirical measures based on our model, and characterize them using the market-clearing condition (9). First, define a relative seller payoff by

$$\begin{aligned} RS\left( A\right) \equiv \frac{\Pi _{S}^{FD}\left( A\right) }{\Pi _{B}^{FD}\left( m\left( A\right) \right) }. \end{aligned}$$

(20)

Second, define a fee ratio by the amount of fees as a fraction of prices:

$$\begin{aligned} FR\left( A\right) \equiv \frac{f\left( A,P\left( A\right) \right) }{P\left( A\right) }. \end{aligned}$$

(21)

Third, define a skill premium by the difference between the skill of buyers and that of matched sellers divided by the skill of buyers. Because skill of sellers who sell assets of quality A have a non-degenerate distribution in equilibrium, we take an average of sellers’ skill conditional on A. Formally, a skill premium is

$$\begin{aligned} SP\left( A\right) \equiv \frac{m\left( A\right) -E\left[ X|X\in \mathcal {S} \left( A\right) \right] }{m\left( A\right) }. \end{aligned}$$

(22)

We also define a skill gap by $SG\left( A\right) \equiv m\left( A\right) -E\left[ X|X\in \mathcal {S}\left( A\right) \right]$ so that $SG\left( A\right) =m\left( A\right) SP\left( A\right)$.

To state the results, we introduce the following notations. We denote the elasticity of the price function by $\eta _{p}\left( A\right) \equiv \frac{\ P^{\prime }\left( A\right) }{P\left( A\right) }A$. Similarly, we denote the elasticity of the matching function by $\eta _{m}\left( A\right) \equiv$ $\frac{m^{\prime }\left( A\right) }{m\left( A\right) }A$.

Proposition A

(Positive properties of FD equilibrium).

• (a) $RS\left( A\right) =\eta _{m}\left( A\right)$, $FR\left( A\right) =1-\left( \eta _{p}\left( A\right) -1\right) \eta _{m}\left( A\right)$, and $SP\left( A\right) =1-\frac{RS\left( A\right) }{2}\frac{1-FR\left( A\right) }{RS\left( A\right) +1-FR\left( A\right) }$. $SP\left( A\right)$ is decreasing in $RS\left( A\right)$ and increasing in $FR\left( A\right)$.

• (b) If $f\left( A,P\right) =\phi +\tau P$, then $RS\left( A\right) =\sqrt{1-\tau }$, $FR\left( A\right) =1-\sqrt{1-\tau } \frac{1-\tau -\frac{\phi }{A^{1+\sqrt{1-\tau }}}}{\sqrt{1-\tau }+\frac{\phi }{A^{1+\sqrt{1-\tau }}}}$, and $SP\left( A\right) =\frac{1}{2\left( 1+\sqrt{ 1-\tau }\right) }\left\{ 1+\tau +2\sqrt{1-\tau }+\frac{\phi }{A^{1+\sqrt{ 1-\tau }}}\right\}$. $FR\left( A\right)$ decreases in A given $\phi >0$, and increases in $\phi$ and $\tau$ . $SP\left( A\right)$ decreases in A given $\phi >0$, and increases in $\phi$ and $\tau$. $SG\left( A\right)$ increases in A and increases in $\phi$ and $\tau$.

Proof of Proposition A

(a) By multiplying P on both sides of (9), we have $\Pi _{B}^{FD}\left( m\left( A\right) \right) \eta _{m}\left( A\right) =\Pi _{S}^{FD}\left( A\right) \Leftrightarrow RS\left( A\right) =\eta _{m}\left( A\right)$. Substituting $\eta _{p}\left( A\right) =\frac{\ P^{\prime }\left( A\right) }{P\left( A\right) }A$ and $\eta _{m}\left( A\right) =\frac{ P^{^{\prime \prime }}\left( A\right) }{P^{\prime }\left( A\right) }A$ into (9) yields the expression of $FR\left( A\right)$.

Sellers of assets A satisfy the participation constraint $AX\le \Pi _{S}^{FD}\left( A\right) \Leftrightarrow X\le S\left( A\right)$. Therefore, $E\left[ X|X\in \mathcal {S}\left( A\right) \right] =\frac{S\left( A\right) }{2}$. Using $S\left( A\right) =\frac{P\left( A\right) -\ f\left( A,P\left( A\right) \right) }{A}$ and (9), the skill premium can be expressed as $SP\left( A\right) =1-\frac{\eta _{m}\left( A\right) }{2} \frac{\eta _{p}\left( A\right) -1}{\eta _{p}\left( A\right) }$. Substituting $\eta _{m}\left( A\right) =RS\left( A\right)$ and $\eta _{p}\left( A\right) -1=\frac{1-FR\left( A\right) }{\eta _{m}\left( A\right) }$ into this expression yields the result. $\square$

(b) Using (10) in Proposition 3 to compute $\eta _{p}\left( A\right)$ and $\eta _{m}\left( A\right)$ in (20), (21), (22) yields the first set of results.

Comparative statics of $FR\left( A\right)$ with respect to A and $\phi$ is obvious. To show that $FR\left( A\right)$ is increasing in $\tau$, we let $s\equiv \sqrt{1-\tau }$ and show that $FR\left( A\right) =1-s\frac{ s^{2}-\frac{\phi }{A^{1+s}}}{s+\frac{\phi }{A^{1+s}}}$ is decreasing in s. This holds because $\frac{s^{2}-\frac{\phi }{A^{1+s}}}{s+\frac{\phi }{A^{1+s} }}=s\frac{sA^{1+s}-\frac{\phi }{s}}{sA^{1+s}+\phi }$ is increasing in s.

Because $RS\left( A\right) =\sqrt{1-\tau }$ is independent of A and decreasing in $\tau$, results in (a) and comparative statics of $FR\left( A\right)$ imply the comparative statics for $SP\left( A\right)$.

Finally, consider $SG\left( A\right)$. Because $m\left( A\right) =A^{\sqrt{ 1-\tau }}$ is independent of $\phi$, $SG\left( A\right) =m\left( A\right) SP\left( A\right)$ is increasing in $\phi$. To show that $SG\left( A\right)$ is increasing in A for any A such that $\Pi _{S}\left( A\right) >0$, notice that $SG^{\prime }\left( A\right)>0\Leftrightarrow \left( \left( 1+\tau \right) \sqrt{1-\tau }+2\left( 1-\tau \right) \right) A^{1+\sqrt{1-\tau }}>\phi$ is implied by $\Pi _{S}\left( A\right)>0\Leftrightarrow \left( 1-\tau \right) A^{1+\sqrt{1-\tau }}>\phi$.

Finally, to show that $SG\left( A\right) =A^{\sqrt{1-\tau }}SP\left( A\right) =\frac{1}{2\left( 1+\sqrt{1-\tau }\right) }\Big \{ \left( 1+\tau +2 \sqrt{1-\tau }\right) A^{\sqrt{1-\tau }}+\frac{\phi }{A}\Big \}$ is increasing in $\tau$, it suffices to show that $\frac{1+\tau +2\sqrt{1-\tau }}{1+\sqrt{1-\tau }}$ is increasing in $\tau$. Taking a derivative,

$$\begin{aligned} \frac{\left( 1\!-\!\frac{1}{\sqrt{1-\tau }}\right) \left( 1\!+\!\sqrt{1-\tau } \right) \!-\!\left( 1\!+\!\tau \!+\!2\sqrt{1\!-\!\tau }\right) \left( -\frac{1}{2\sqrt{ 1\!-\!\tau }}\right) }{\left( 1\!+\!\sqrt{1\!-\!\tau }\right) ^{2}}=\frac{1\!+\!\frac{1}{2} \sqrt{1-\tau }}{\left( 1\!+\!\sqrt{1-\tau }\right) ^{2}}>0. \end{aligned}$$

$\square$

1.2 Applications to M &A markets

First, we briefly describe how our model can be applied to M &A markets and discuss the existing empirical evidence. In a context of M &As, traders are firms, sellers are target firms, buyers are bidder firms, and each unit of indivisible asset can be interpreted as a collection of tangible assets which remain productive when their ownership changes. Examples of such assets include a large plant (manufacturing), a customer base (retail), and an access to specific locations (services). We interpret skill as a collection of intangible assets within firms which are productive only within the current firm boundary.²⁸ Examples of skill include organization-specific knowledge and team capital embodied in a network of people. These may be called useful “assets”, but various coordination issues make sustaining their productivity after M &As difficult.²⁹

Next, we discuss how to test predictions made in Proposition A. First, the relative value of targets to bidders is less than one, and decreases in the proportional fee. Second, the skill gap is positive, increases in the asset quality across matched pairs, and increases in both types of fees. Thus, our model generates endogenous asymmetry between buyers and sellers in an otherwise symmetric environment, and predicts that the asymmetry between matched buyers and sellers should be greater (i) the higher the quality of assets traded or (ii) the higher the transaction costs.

Empirically, it is well documented that target firms are smaller than matched bidder firms (see Eckbo (2014)). While there can be many reasons behind this asymmetry, our model singles out a new mechanism – a proportional fee. Because this form of fee is common in M &A markets, it could be an important determinant of the relative size of targets. Moreover, with variations in proportional fees across deals, our model predicts that, among deals for which proportional fees are higher, the relative values of targets should be smaller. There are two pieces of suggestive evidence in this context: (i) cross-border deals exhibit a smaller relative size of targets (see Moeller and Schlingemann (2005)), and (ii) privately held targets have a smaller relative size (see Chang (1998)). Our model offers the following explanation. Costs of information production for foreign and/or privately held targets are likely to be higher than average targets. If intermediaries pass on to target firms these higher costs by raising proportional fees, then our model predicts that the relative target size in these deals is smaller.³⁰ It would be interesting to know if, and the extent to which, this prediction is borne out in the data.

Finally, Li et al. (2018) directly measure organization capital and study its role in M &As. They find that high organization capital bidders achieve better post-merger operating performance.³¹ They also find that, while target organization capital does not matter for the deal performance, the gap between bidder and target organization capital does. This is consistent with the skill gap $SG\left( A\right)$ increasing in A in our model. Our model also predicts that (i) the skill premium decreases in A, and (ii) the skill gap and skill premium increase in both types of fees. These predictions about the relationship between fees and the characteristics of matched pairs is unique to our model, and deserves further empirical investigation.

Appendix B: Proofs

This Appendix contains the proofs to the results in the main text.

1.1 Proposition 1

Proposition 1(a) follows from Lemma B1 below.

Lemma B1

Let $A_{+}$ be a smaller solution to $A\left( 1-2\ln A\right) =1$.

• (a) For $A_{\min }\in \left[ 0,A_{+}\right)$, $a^{*}\in \left( 2A_{\min },2A_{+}\right)$ is a unique solution to $a=\Gamma \left( a;A_{\min }\right)$, where

  $$\begin{aligned} \Gamma \left( a;A_{\min }\right) =\frac{1-\frac{a}{4}-\frac{1}{a}A_{\min }^{2}}{1-\ln \frac{a}{2}-\frac{2}{a}A_{\min }}, \end{aligned}$$

  (23)

  and $A_{\min }<A^{*}=\frac{a^{*}}{2}$ holds. A market-clearing price $P^{*}$ is a unique solution to

  $$\begin{aligned} a^{*}=P\left\{ 3-\ln P-\left( 4\frac{A_{\min }}{a^{*}}+\ln \left( 1- \frac{A_{\min }}{a^{*}}\right) \right) \right\} . \end{aligned}$$

  (24)

• (b) For $A_{\min }\in \left[ A_{+},1\right)$, $a^{*}=-\frac{1-A_{\min }}{\ln A_{\min }}\in \left[ 2A_{+},1\right)$ and $A_{\min }\ge A^{*}=\frac{a^{*}}{2}$ holds. A market-clearing price $P^{*}$ is a unique solution to

  $$\begin{aligned} a^{*}=P\left( 1-\ln P+\ln \frac{a^{*}}{A_{\min }}\right) . \end{aligned}$$

  (25)

Proof of Lemma B1

(a) Recall that $0<P<a<1$ must hold in equilibrium. Suppose $A_{\min }<A^{*}=\frac{a}{2}$. We verify later that this occurs if and only if $A_{\min }<A_{+}$. Given $A_{\min }<A^{*}$, the selection pattern (see the left panel in Fig. 2) implies that sellers satisfy $X\le \frac{P}{A}$, $X\le X^{*}$, and $A\ge A_{\min }$. Hence, a supply function is

$$\begin{aligned} S\left( P\right) =\int _{A_{\min }}^{A^{*}}X^{*}dA+\int _{A^{*}}^{1}\frac{P}{A}dA=X^{*}\left( A^{*}-A_{\min }\right) -P\ln A^{*}. \end{aligned}$$

Substituting $A^{*}=\frac{a}{2}$ and $X^{*}=\frac{2P}{a}$,

$$\begin{aligned} S\left( P\right) =P\left( 1+\ln \frac{2}{a}-A_{\min }\frac{2}{a}\right) . \end{aligned}$$

Buyers satisfy $A\le a-\frac{P}{X}$, and additionally, if $A\in \left[ A_{\min },A^{*}\right]$,$\ X>X^{*}$. Note that $a-\frac{P}{X}=0$ defines a skill threshold $X=\frac{P}{a}$ (below which no buyer exists), while $a-\frac{P}{X}=A_{\min }$ defines another threshold $X=\frac{P}{ a-A_{\min }}\in \left( \frac{P}{a},X^{*}\right)$ (above which the minimum standard $A_{\min }$ becomes a binding constraint for some traders). Using these, a demand function is

$$\begin{aligned} D\left( P\right)= & {} \int _{\frac{P}{a}}^{1}\left( a-\frac{P}{X}\right) dX-\int _{\frac{P}{a-A_{\min }}}^{X^{*}}\left( a-\frac{P}{X}-A_{\min }\right) dX \\= & {} P\left\{ \frac{a}{P}-\ln \frac{a}{P}+\ln \left( 2\frac{a-A_{\min }}{a} \right) -2\frac{a-A_{\min }}{a}\right\} . \end{aligned}$$

For $P>0$, a market-clearing condition $S\left( P\right) =D\left( P\right)$ is equivalent to

$$\begin{aligned} a=P\left\{ 3-\ln P-\left( 4\frac{A_{\min }}{a}+\ln \left( 1-\frac{A_{\min }}{ a}\right) \right) \right\} \equiv \Phi _{1}\left( P;a,A_{\min }\right) . \end{aligned}$$

This is (24). A brief inspection of the right hand side $\Phi _{1}$ yields

$$\begin{aligned} \frac{\partial \Phi _{1}}{\partial P}=2\left( 1-2\frac{A_{\min }}{a}\right) +\ln \frac{a}{a-A_{\min }}-\ln P. \end{aligned}$$

This is positive for any $0<P<a<1$ such that $A_{\min }<A^{*}=\frac{a}{2}$, because

$$\begin{aligned} 2\left( 1-2\frac{A_{\min }}{a}\right)>0>\ln P-\ln \frac{a}{a-A_{\min }} . \end{aligned}$$

Also, $\Phi _{1}\left( 0;a,A_{\min }\right) =0$ and $\Phi _{1}\left( a;a,A_{\min }\right) =a\left\{ 3-4\frac{A_{\min }}{a}-\ln \left( a-A_{\min }\right) \right\}$. Note that $\Phi _{1}\left( a;a,A_{\min }\right)>a\Leftrightarrow 2-4\frac{A_{\min }}{a}>\ln \left( a-A_{\min }\right)$ holds because $A_{\min }<A^{*}=\frac{a}{2}$ implies $2\left( 1-2\frac{ A_{\min }}{a}\right)>0>\ln \left( a-A_{\min }\right)$. This establishes a unique solution $P\left( a\right) \in \left( 0,a\right)$ to (24).

Given the selection pattern, the expected quality of assets for sale is

$$\begin{aligned} \frac{\int _{A_{\min }}^{A^{*}}\left( AX^{*}\right) dA+\int _{A^{*}}^{1}\left( A\frac{P}{A}\right) dA}{S\left( P\right) }. \end{aligned}$$

The numerator is $P\left\{ \frac{1}{2}\frac{2}{a}\left( A^{*2}-A_{\min }^{2}\right) +1-A^{*}\right\} =P\left( 1-\frac{a}{4}-\frac{1}{a}A_{\min }^{2}\right)$. Combining this with $S\left( P\right) =P\left( 1+\ln \frac{2 }{a}-A_{\min }\frac{2}{a}\right)$ yields (23).

We prove that, for any $A_{\min }<A_{+}$, $\Gamma \left( a;A_{\min }\right)$ given in (23) satisfies

$$\begin{aligned} \text {(i) }\Gamma \left( 2A_{\min };A_{\min }\right) >2A_{\min }, \quad \text {(ii) }\Gamma \left( 1;A_{\min }\right)<1,\qquad \text { (iii)} \frac{\partial \Gamma \left( a;A_{\min }\right) }{\partial a} |_{a=a*}<1. \end{aligned}$$

The properties (i) - (iii) imply that $\Gamma \left( a;A_{\min }\right) =a$ has a unique solution $a^{*}\in \left( 2A_{\min },1\right)$.

For the property (i),

$$\begin{aligned} \Gamma \left( 2A_{\min };A_{\min }\right) =\frac{1-\frac{A_{\min }}{2}-\frac{ A_{\min }}{2}}{-\ln A_{\min }}>2A_{\min } \Leftrightarrow 1>A_{\min }\left( 1-2\ln A_{\min }\right) \\ \Leftrightarrow A_{\min }<A_{+}. \end{aligned}$$

For the property (ii),

$$\begin{aligned} \Gamma \left( 1;A_{\min }\right) =\frac{\frac{3}{4}-A_{\min }^{2}}{1+\ln 2-2A_{\min }}<1 \Leftrightarrow \frac{3}{4}-\ln 2<\left( 1-A_{\min }\right) ^{2}. \end{aligned}$$

This holds because $\frac{3}{4}-\ln 2=0.057<\left( 1-A_{+}\right) ^{2}=\left( 1-0.285\right) ^{2}=0.511<\left( 1-A_{\min }\right) ^{2}$.

For the property (iii), let $N\equiv 1-\frac{a}{4}-\frac{1}{a}A_{\min }^{2}$ and $D\equiv 1-\ln \frac{a}{2}-\frac{2}{a}A_{\min }$ in (23). Then

$$\begin{aligned}{} & {} \frac{\partial \Gamma \left( a;A_{\min }\right) }{\partial a}<1 \Leftrightarrow \frac{\partial N}{\partial a}D-N\frac{\partial D}{ \partial a}<D^{2} \Leftrightarrow \frac{\partial N}{\partial a }-D<\frac{N}{D}\frac{\partial D}{\partial a}\\{} & {} \quad \Leftrightarrow \left( \frac{A_{\min }}{a}\right) ^{2}-\frac{1}{4}-D<\frac{N }{D}\left( \frac{2A_{\min }}{a}-1\right) \frac{1}{a}. \end{aligned}$$

Because both sides are negative for $A_{\min }<\frac{a}{2}$, this is equivalent to

$$\begin{aligned} \frac{N}{D}=\Gamma \left( a;A_{\min }\right) <a\frac{1-\ln \frac{a}{2}-\frac{ 2}{a}A_{\min }+\frac{1}{4}\left\{ 1-\left( \frac{2A_{\min }}{a}\right) ^{2}\right\} }{1-\frac{2A_{\min }}{a}}. \end{aligned}$$

The right hand side can be written as $a+a\frac{\ln \frac{2}{a}+\frac{1}{4} \left( 1-\frac{2A_{\min }}{a}\right) \left( 1+\frac{2A_{\min }}{a}\right) }{ 1-\frac{2A_{\min }}{a}}$, so

$$\begin{aligned} \frac{\partial \Gamma \left( a;A_{\min }\right) }{\partial a}<1 \Leftrightarrow \frac{\Gamma \left( a;A_{\min }\right) -a}{a}<\frac{ \ln \frac{2}{a}}{1-\frac{2A_{\min }}{a}}+\frac{1}{4}\left( 1+\frac{2A_{\min } }{a}\right) . \end{aligned}$$

Because the right hand side is positive for $A_{\min }<\frac{a}{2}$ while the left hand side is zero at $a=a^{*}$, this implies that $\frac{ \partial \Gamma \left( a;A_{\min }\right) }{\partial a}<1$ holds at $a=a^{*}$.

To show that $a^{*}$ is increasing in $A_{\min }$, it suffices to show that $\frac{\partial \Gamma \left( a;A_{\min }\right) }{\partial A_{\min }} |_{a=a^{*}}>0$.

$$\begin{aligned} \frac{\partial \Gamma \left( a;A_{\min }\right) }{\partial A_{\min }}>0 \Leftrightarrow \frac{\partial N}{\partial A_{\min }}D>N\frac{ \partial D}{\partial A_{\min }}. \end{aligned}$$

Because $\frac{\partial N}{\partial A_{\min }}=-\frac{2A_{\min }}{a}$ and $\frac{\partial D}{\partial A_{\min }}=-\frac{2}{a}$ are both negative,

$$\begin{aligned} \frac{\partial \Gamma \left( a;A_{\min }\right) }{\partial A_{\min }}>0 \Leftrightarrow \frac{N}{D}=\Gamma \left( a;A_{\min }\right) >A_{\min }. \end{aligned}$$

This holds at $a=a^{*}$, because $A_{\min }<\frac{a^{*}}{2}<a^{*}=\Gamma \left( a^{*};A_{\min }\right)$.

Finally, we already know that, for $A_{\min }<1$, $\Gamma \left( 2A_{\min };A_{\min }\right) =2A_{\min }\Leftrightarrow 1=A_{\min }\left( 1-2\ln A_{\min }\right) \Leftrightarrow A_{\min }=A_{+}$. Therefore, $\underset{ A_{\min }\nearrow A_{+}}{\lim }a^{*}=2A_{0}$. $\square$

(b) Suppose $A_{\min }\ge A^{*}=\frac{a}{2}$. We verify later that this occurs if and only if $A_{\min }\ge A_{+}$. A supply function is

$$\begin{aligned} S\left( P\right) =\int _{A_{\min }}^{1}\frac{P}{A}dA=-P\ln A_{\min }. \end{aligned}$$

A demand function is

$$\begin{aligned} D\left( P\right) =\int _{\frac{P}{a}}^{1}\left( a-\frac{P}{X}\right) dX=a-P+P\ln \frac{P}{a}. \end{aligned}$$

A market-clearing condition $S\left( P\right) =D\left( P\right)$ is equivalent to

$$\begin{aligned} a=P\left( 1-\ln P+\ln \frac{a}{A_{\min }}\right) \equiv \Phi _{2}\left( P;a,A_{\min }\right) . \end{aligned}$$

This is (25). A brief inspection of the right hand side $\Phi _{2}$ yields $\frac{\partial \Phi _{2}}{\partial P}=\ln \frac{a}{PA_{\min }}$. This is positive if and only if $\frac{a}{P}>A_{\min }$, which is true for any $A_{\min }<1$ and $P<a$. Also, $\Phi _{2}\left( 0;a,A_{\min }\right) =0$ and $\Phi _{2}\left( a;a,A_{\min }\right) =a\left( 1-\ln A_{\min }\right) >a$ for any $A_{\min }<1$. This establishes a unique solution $P\in \left( 0,a\right)$ to (25).

Given the sorting pattern, the expected quality of assets for sale is

$$\begin{aligned} \frac{\int _{A_{\min }}^{1}\left( A\frac{P}{A}\right) dA}{S\left( P\right) }= \frac{P\left( 1-A_{\min }\right) }{-P\ln A_{\min }}=\frac{A_{\min }-1}{\ln A_{\min }}. \end{aligned}$$

Therefore, given $A_{\min }\ge A^{*}=\frac{a}{2}$, $a^{*}=\frac{ A_{\min }-1}{\ln A_{\min }}$. To verify the conjecture $A_{\min }\ge A^{*}=\frac{a}{2}$,

$$\begin{aligned} A_{\min }\ge \frac{1}{2}\frac{A_{\min }-1}{\ln A_{\min }} \Leftrightarrow 1\le A_{\min }\left( 1-2\ln A_{\min }\right) \Leftrightarrow A_{\min }\ge A_{+}. \end{aligned}$$

That $a^{*}=\frac{A_{\min }-1}{\ln A_{\min }}$ is increasing in $A_{\min }$ is immediate from

$$\begin{aligned} \ln A_{\min }-\frac{A_{\min }-1}{A_{\min }}>0 \Leftrightarrow 1>A_{\min }\left( 1-\ln A_{\min }\right) , \end{aligned}$$

where $A_{\min }\left( 1-\ln A_{\min }\right)$ is increasing in $A_{\min }$ and approaches one as $A_{\min }\nearrow 1$. Note also that $\underset{ A_{\min }\nearrow 1}{\lim }\frac{A_{\min }-1}{\ln A_{\min }}=1$. At $A_{\min }=A_{+}$, $a^{*}=\frac{A_{+}-1}{\ln A_{+}}=2A_{+}$ holds because this is equivalent to $1=A_{+}\left( 1-2\ln A_{+}\right)$. This means that $a^{*}$ is continuous in $A_{\min }\in \left[ 0,1\right)$. $\square$

Proof of Proposition 1(b)

We drop “$*$” from $\left( a^{*},P^{*}\right)$ and proceed in two steps. First, we derive the welfare gain $G^{MD}$ as a function of $\left( a,P,A_{\min }\right)$. Second, we use a market-clearing condition to show $G^{MD}=\left( \frac{a-P}{2}\right) ^{2}$ for any $A_{\min }\in \left[ 0,1\right]$.

• Step 1. The expected welfare gain as a function of $\left( a,P,A_{\min }\right)$.

For $A_{\min }<A_{+}$, the expected value of new production is given by

$$\begin{aligned} V^{MD}= & {} \underset{a\left( \frac{a}{2}-P\right) }{\underbrace{ a\int _{X^{*}}^{1}X\left( a-\frac{P}{X}\right) dX}}+\underset{\frac{P^{2} }{2}\left( \frac{A_{\min }}{a-A_{\min }}\right) ^{2}}{\underbrace{a\int _{ \frac{P}{a}}^{\frac{P}{a-A_{\min }}}X\left( a-\frac{P}{X}\right) dX}}+ \underset{\frac{P^{2}}{2}\frac{A_{\min }}{a}\left( 4-\left( \frac{a}{ a-A_{\min }}\right) ^{2}\right) }{\underbrace{a\int _{\frac{P}{a-A_{\min }} }^{X^{*}}\left( XA_{\min }\right) dX}} \\= & {} a\left( \frac{a}{2}-P\right) +\frac{P^{2}}{2}\frac{A_{\min }}{a}\left( \frac{3-4\frac{A_{\min }}{a}}{1-\frac{A_{\min }}{a}}\right) . \end{aligned}$$

Sellers’ opportunity cost is

$$\begin{aligned} C_{S}^{MD}=\underset{\frac{1}{2}\left( A^{*2}-A_{\min }^{2}\right) \frac{ X^{*2}}{2}}{\underbrace{\int _{A_{\min }}^{A^{*}}\int _{0}^{X^{*}}\left( AX\right) dAdX}}+\underset{-\frac{P^{2}}{2}\ln \frac{a}{2}}{ \underbrace{\int _{A^{*}}^{1}\left( A\int _{0}^{\frac{P}{A}}XdX\right) dA}} =\frac{P^{2}}{2}\left( \frac{1}{2}-\ln \frac{a}{2}\right) -P^{2}\left( \frac{A_{\min }}{a}\right) ^{2}. \end{aligned}$$

Buyers’ opportunity cost is

$$\begin{aligned} C_{B}^{MD}= & {} \underset{\left( \frac{a}{2}-P\right) ^{2}+\frac{P^{2}}{2} \left( \ln \frac{a}{2}-\ln P\right) }{\underbrace{\int _{X^{*}}^{1}\left( X\int _{0}^{a-\frac{P}{X}}AdA\right) dX}}+\underset{\frac{P^{2}}{2}\left[ 2\left( \frac{A_{\min }}{a}\right) ^{2}-\frac{A_{\min }}{a-A_{\min }}+\ln \left( 1+\frac{A_{\min }}{a-A_{\min }}\right) \right] }{\underbrace{\int _{ \frac{P}{a}}^{X^{*}}\left( X\int _{0}^{a-\frac{P}{X}}AdA\right) dX-\int _{ \frac{P}{a-A_{\min }}}^{X^{*}}\left( X\int _{A_{\min }}^{a-\frac{P}{X} }AdA\right) dX}} \\= & {} \left( \frac{a}{2}-P\right) ^{2}+\frac{P^{2}}{2}\left( \ln \frac{a}{2} -\ln P\right) +\frac{P^{2}}{2}\left[ 2\left( \frac{A_{\min }}{a}\right) ^{2}- \frac{A_{\min }}{a-A_{\min }}+\ln \left( 1+\frac{A_{\min }}{a-A_{\min }} \right) \right] . \end{aligned}$$

The welfare gain is

$$\begin{aligned} G^{MD}\left( A_{\min }<A_{+}\right)= & {} V^{MD}-\left( C_{S}^{MD}+C_{B}^{MD}\right) \\= & {} a\left( \frac{a}{2}-P\right) -\left\{ \left( \frac{a}{2}-P\right) ^{2}+ \frac{P^{2}}{2}\left( \frac{1}{2}-\ln P\right) \right\} \\{} & {} +\frac{P^{2}}{2}\frac{A_{\min }}{a}\left( \frac{3-4\frac{A_{\min }}{a}}{1- \frac{A_{\min }}{a}}\right) \\ {}{} & {} \quad -\frac{P^{2}}{2}\left[ \ln \left( 1+\frac{ A_{\min }}{a-A_{\min }}\right) -\frac{A_{\min }}{a-A_{\min }}\right] \\= & {} G_{0}\left( a,P\right) +\frac{P^{2}}{2}\left\{ 4\frac{A_{\min }}{a}+\ln \left( 1-\frac{A_{\min }}{a}\right) \right\} , \end{aligned}$$

where $G_{0}\left( a,P\right)$ in the last line is defined by

$$\begin{aligned} G_{0}\left( a,P\right) \equiv \left( \frac{a}{2}-P\right) \left( \frac{a}{2} +P\right) +\frac{P^{2}}{2}\left( \ln P-\frac{1}{2}\right) . \end{aligned}$$

(26)

For $A_{\min }\ge A_{+}$, the expected value of new production is given by $V^{MD}=a\int _{\frac{P}{a}}^{1}X\left( a-\frac{P}{X}\right) dX=\frac{\left( a-P\right) ^{2}}{2}$. Sellers’ opportunity cost is $C_{S}^{MD}=\int _{A_{\min }}^{1}\left( A\int _{0}^{\frac{P}{A}}XdX\right) dA=-\frac{P^{2}}{2}\ln A_{\min }$. Buyers’ opportunity cost is

$$\begin{aligned} C_{B}^{MD}=\int _{\frac{P}{a}}^{1}\left( X\int _{0}^{a-\frac{P}{X}}AdA\right) dX=\frac{1}{4}\left( a-P\right) \left( a-3P\right) -\frac{P^{2}}{2}\ln \frac{ P}{a}. \end{aligned}$$

Therefore, the welfare gain is

$$\begin{aligned} G^{MD}\left( A_{\min }\ge A_{+}\right)= & {} V^{MD}-\left( C_{S}^{MD}+C_{B}^{MD}\right) \\= & {} \frac{1}{4}\left( a-P\right) \left( a+P\right) +\frac{P^{2}}{2}\ln \left( A_{\min }\frac{P}{a}\right) . \end{aligned}$$

• Step 2. Use a market-clearing condition to show that the welfare gain is always $\left( \frac{a-P}{2}\right) ^{2}$.

For $A_{\min }<A_{+}$, from the market-clearing condition (24) in Lemma B1(a),

$$\begin{aligned} 4\frac{A_{\min }}{a}+\ln \left( 1-\frac{A_{\min }}{a}\right) =3-\ln P-\frac{a }{P}. \end{aligned}$$

(27)

Recall that $G^{MD}\left( A_{\min }<A_{+}\right) =G_{0}\left( a,P\right) + \frac{P^{2}}{2}\left\{ 4\frac{A_{\min }}{a}+\ln \left( 1-\frac{A_{\min }}{a} \right) \right\}$, where $G_{0}\left( a,P\right)$ is given in (26 ). Eliminating $A_{\min }$ using (27) yields

$$\begin{aligned} G^{MD}\left( A_{\min }<A_{+}\right) \!=\!\left( \frac{a}{2}\right) ^{2}-P^{2}\!+\! \frac{P^{2}}{2}\left( \ln P-\frac{1}{2}+3-\ln P-\frac{a}{P}\right) \!=\!\left( \frac{a-P}{2}\right) ^{2}. \end{aligned}$$

For $A_{\min }\ge A_{+}$, from the market-clearing condition (25) in Lemma B1(b),

$$\begin{aligned} \ln \left( A_{\min }\frac{P}{a}\right) =-\frac{a-P}{P}. \end{aligned}$$

(28)

Using (28) in $G^{MD}\left( A_{\min }\ge A_{+}\right) =\frac{1}{4} \left( a-P\right) \left( a+P\right) +\frac{P^{2}}{2}\ln \left( A_{\min } \frac{P}{a}\right)$,

$$\begin{aligned} G^{MD}\left( A_{\min }\ge A_{+}\right) =\frac{1}{4}\left( a^{2}-P^{2}\right) -\frac{P}{2}\left( a-P\right) =\left( \frac{a-P}{2} \right) ^{2}. \end{aligned}$$

$\square$

1.2 Proposition 2

A supply density $S^{FD}\left( A\right)$ and a demand density $D^{FD}\left( A\right)$ for assets A are formulated as follows. First, a set of skill X of sellers of assets A is

$$\begin{aligned} \mathcal {S}\left( A\right) \equiv \left\{ X\in \left[ 0,1\right] |\Pi ^{FD}\left( A,X\right) =\Pi _{S}^{FD}\left( A\right) \right\} \qquad \subset \left[ 0,1\right] . \end{aligned}$$

Recall that, for any A, X is distributed uniformly on $\left[ 0,1\right]$. Using an indicator function $1_{\mathcal {S}\left( A\right) }$ that takes a value of one if and only if $X\in \mathcal {S}\left( A\right)$, a supply density for assets of quality A is $S^{FD}\left( A\right) \equiv \int 1_{ \mathcal {S}\left( A\right) }dX$.

Similarly, a set of asset qualities $\widetilde{A}$ initially owned by buyers with skill $m\left( A\right)$ is

$$\begin{aligned} \mathcal {D}\left( A\right) \equiv \left\{ \widetilde{A}\in \left[ 0,1\right] |\Pi ^{FD}\left( \widetilde{A},m\left( A\right) \right) =\Pi _{B}^{FD}\left( m\left( A\right) \right) \right\} \qquad \subset \left[ 0,1\right] . \end{aligned}$$

A demand density for assets of quality A is $D^{FD}\left( A\right) \equiv \int 1_{\mathcal {D}\left( A\right) }d\widetilde{A}$.

Proof of Proposition 2

(a) $P^{\prime }\left( A\right) >0$ and $P^{\prime \prime }\left( A\right) >0$ ensure that for any $X\in \left( 0,1\right]$ a buyer’s problem has a unique interior solution characterized by $X=P^{\prime }\left( a^{*}\right) \Leftrightarrow \widehat{a}\left( X\right) =P^{\prime -1}\left( X\right)$. This implies that $m\left( A\right) =P^{\prime }\left( A\right)$. The matching $X=m\left( A\right) =P^{\prime }\left( A\right)$ implies $\frac{dX}{dA}=P^{^{\prime \prime }}\left( A\right)$. Then the market-clearing condition (8) can be stated as

$$\begin{aligned} S^{FD}\left( A\right) =D^{FD}\left( A\right) P^{^{\prime \prime }}\left( A\right) \text { for any }A\in \left( 0,1\right] . \end{aligned}$$

(29)

Because buyers who demand assets A have skill $m\left( A\right)$, their participation constraint is $\max \left\{ \Pi _{S}^{FD}\left( \widetilde{A} \right) ,\widetilde{A}m\left( A\right) \right\} \le \Pi _{B}^{FD}\left( m\left( A\right) \right)$, where $\widetilde{A}$ is their initial asset quality. Lemma B2 (a) below shows that this is equivalent to $\widetilde{A} m\left( A\right) \le \Pi _{B}^{FD}\left( m\left( A\right) \right) =Am\left( A\right) -P\left( A\right)$. This implies the demand density

$$\begin{aligned} D^{FD}\left( A\right) =A-\frac{P\left( A\right) }{P^{\prime }\left( A\right) }. \end{aligned}$$

On the other side of the market, sellers’ (who try to sell assets A) participation constraint is $\max \left\{ \Pi _{B}^{FD}\left( X\right) ,AX\right\} \le \Pi _{S}^{FD}\left( X\right)$. Lemma B2 (b) below shows that this is equivalent to $AX\le \Pi _{S}^{FD}\left( X\right) =P\left( A\right) -f\left( A,P\left( A\right) \right)$. This implies the supply density

$$\begin{aligned} S^{FD}\left( A\right) =\frac{P\left( A\right) -\ f\left( A,P\left( A\right) \right) }{A}. \end{aligned}$$

Substituting $D^{FD}\left( A\right)$ and $S^{FD}\left( A\right)$ into the market-clearing condition (29) yields (9).

(b) This follows from Proposition A (a). $\square$

Lemma B2

For any $A\in \left( 0,1\right]$,

• (a) $\forall$ $\widetilde{A}\in \left( 0,1\right]$, $\widetilde{A} m\left( A\right) \le \Pi _{B}^{FD}\left( m\left( A\right) \right) \Rightarrow \Pi _{S}^{FD}\left( \widetilde{A}\right) <\widetilde{A}m\left( A\right)$.

• (b) $\forall$ $X\in \left( 0,1\right]$, $AX\le \Pi _{S}^{FD}\left( A\right) \Rightarrow \Pi _{B}^{FD}\left( X\right) <AX$.

Proof of Lemma B2

For any $A\in \left( 0,1\right]$ such that $\Pi _{B}^{FD}\left( m\left( A\right) \right) >0$, define $A_{B}\left( A\right) \equiv \frac{\Pi _{B}^{FD}\left( m\left( A\right) \right) }{m\left( A\right) }$. This implies that $\widetilde{A}m\left( A\right) \le \Pi _{B}^{FD}\left( m\left( A\right) \right) \Leftrightarrow \widetilde{A}\le A_{B}\left( A\right)$. Because $A_{B}\left( A\right) =A-\frac{P\left( A\right) }{m\left( A\right) } <A$, buyers who demand assets of quality A must have their initial asset quality strictly smaller than A. Similarly, for any $A\in \left( 0,1\right]$ such that $\Pi _{S}^{FD}\left( A\right) >0$, define $X_{S}\left( A\right) \equiv \frac{\Pi _{S}^{FD}\left( A\right) }{A}$. This implies that $AX\le \Pi _{S}^{FD}\left( A\right) \Leftrightarrow X\le X_{S}\left( A\right)$. Because $X_{S}\left( A\right) =\frac{P\left( A\right) -f\left( A,P\left( A\right) \right) }{A}=\frac{\left( A-A_{B}\left( A\right) \right) m\left( A\right) -f\left( A,P\left( A\right) \right) }{A}<m\left( A\right)$, sellers who sell assets of quality A must have their skill strictly lower than $m\left( A\right)$.

To prove (a), we must show that $\forall \widetilde{A}\le A_{B}\left( A\right)$, $\Pi _{S}^{FD}\left( \widetilde{A}\right) <\widetilde{A}m\left( A\right)$. This holds because

$$\begin{aligned} \frac{\Pi _{S}^{FD}\left( \widetilde{A}\right) }{\widetilde{A}}=X_{S}\left( \widetilde{A}\right)<m\left( \widetilde{A}\right) <m\left( A\right) . \end{aligned}$$

The last inequality follows from $\widetilde{A}\le A_{B}\left( A\right) <A$ and the monotonicity of $m\left( A\right)$.

To prove (b), we must show that $\forall X\le X_{S}\left( A\right)$, $\Pi _{B}^{FD}\left( X\right) <AX$. This holds because

$$\begin{aligned} \frac{\Pi _{B}^{FD}\left( X\right) }{X}=\widehat{a}\left( X\right) -\frac{ P\left( \widehat{a}\left( X\right) \right) }{X}<\widehat{a}\left( X\right) < \widehat{a}\left( m\left( A\right) \right) =A. \end{aligned}$$

The last inequality follows from $X\le X_{S}\left( A\right) <m\left( A\right)$ and the monotonicity of $\widehat{a}\left( X\right)$. $\square$

1.3 Proposition 3 and Corollary 1

Proof of Proposition 3

By substituting $f=\phi +\tau P$ into (9),

$$\begin{aligned} \left( \frac{\ P^{\prime }\left( A\right) }{P\left( A\right) }A-1\right) \frac{\ P^{^{\prime \prime }}\left( A\right) }{P^{\prime }\left( A\right) } A=1-\tau -\frac{\phi }{P\left( A\right) },{\qquad }P^{\prime }\left( 1\right) =1. \end{aligned}$$

(30)

Suppressing the argument of P, $P^{\prime }$, $P^{^{\prime \prime }}$, the differential equation (30) is

$$\begin{aligned} \left( P^{\prime }A-P\right) \frac{P^{^{\prime \prime }}}{P^{\prime }} A=\left( 1-\tau \right) P-\phi . \end{aligned}$$

(31)

We find a solution in the class of power functions $P\left( A;\phi ,\tau \right) =\frac{1}{c_{0}}A^{c_{0}}+c_{1}$. Substituting $P^{\prime }A-P=\frac{ c_{0}-1}{c_{0}}A^{c_{0}}-c_{1}$ and $\frac{P^{^{\prime \prime }}}{P^{\prime } }A=c_{0}-1$ into (31) and equating coefficients on both sides,

$$\begin{aligned} \frac{c_{0}-1}{c_{0}}\left( c_{0}-1\right) =\frac{1-\tau }{c_{0}} \qquad \text {and}\qquad \left( c_{0}-1\right) c_{1}=\phi -\left( 1-\tau \right) c_{1}. \end{aligned}$$

This has a unique solution $c_{0}=1+\sqrt{1-\tau }$ and $c_{1}=\frac{\phi }{ c_{0}-\tau }=\frac{\phi }{1-\tau +\sqrt{1-\tau }}$. With these $\left( c_{0},c_{1}\right)$, $P\left( A;\phi ,\tau \right)$ in (10) is obtained.

Next, we derive the welfare gain $G^{FD}$. New values generated by buyers are

$$\begin{aligned} V^{FD}\equiv \int _{0}^{1}\left( \widehat{a}\left( X\right) X\right) D^{FD}\left( \widehat{a}\left( X\right) \right) dX. \end{aligned}$$

Sellers’ opportunity cost and buyers’ opportunity cost are

$$\begin{aligned} C_{S}^{FD}\equiv \int \int \left( AX\right) \varvec{1}_{\mathcal {S} }dAdX\qquad \text {and}\qquad C_{B}^{FD}\equiv \int \int \left( AX\right) \varvec{1}_{\mathcal {D}}dAdX, \end{aligned}$$

where $\mathcal {S}\equiv \underset{A\in \left( 0,1\right] }{\cup }\mathcal {S} \left( A\right)$ and $\mathcal {D}\equiv \underset{A\in \left( 0,1\right] }{ \cup }\mathcal {D}\left( A\right)$. It remains to compute the integrals above to obtain $G^{FD}=V^{FD}-\left( C_{S}^{FD}+C_{B}^{FD}\right)$.

To save space, we work with $s\equiv \sqrt{1-\tau }$. We write $P\left( A;\phi ,s\right)$ to mean $P\left( A;\phi ,\tau \right)$ with $\tau =1-s^{2}$, and similarly for other variables. The price function (10 ) is

$$\begin{aligned} P\left( A;\phi ,s\right) =\frac{1}{1+s}\left( A^{1+s}+\frac{\phi }{s}\right) . \end{aligned}$$

(32)

Sellers’ payoff is

$$\begin{aligned} \Pi _{S}^{FD}\left( A\right) =P\left( A;\phi ,s\right) -\left\{ \phi +\left( 1-s^{2}\right) P\left( A;\phi ,s\right) \right\} =\frac{s^{2}}{1+s}\left( A^{1+s}-\frac{\phi }{s}\right) , \end{aligned}$$

and the supply density at A is

$$\begin{aligned} S^{FD}\left( A;\phi ,s\right) =\frac{\Pi _{S}^{FD}\left( A\right) }{A}=\frac{ s^{2}}{1+s}\left( A^{s}+\frac{\phi }{s^{2}}\frac{1}{A}\right) . \end{aligned}$$

As buyers with skill X are matched with assets $\widehat{a}\left( X\right) =X^{\frac{1}{s}}$, their payoff is

$$\begin{aligned} \Pi _{B}^{FD}\left( X\right) =X^{\frac{1}{s}}\times X-P\left( X^{\frac{1}{s} };\phi ,s\right) =\frac{s}{1+s}\left( X^{\frac{1+s}{s}}-\frac{\phi }{s^{2}} \right) . \end{aligned}$$

The demand density for assets $\widehat{a}\left( X\right)$ is

$$\begin{aligned} D^{FD}\left( \widehat{a}\left( X\right) ;\phi ,s\right) =\frac{\Pi _{B}^{FD}\left( X\right) }{X}=\frac{1}{\left( 1+s\right) s}\left( s^{2}X^{ \frac{1}{s}}-\frac{\phi }{X}\right) . \end{aligned}$$

The new production is

$$\begin{aligned} V^{FD}\left( \phi ,s\right) =\int _{\underline{X}}^{1}X^{\frac{1+s}{s} }D^{FD}\left( \widehat{a}\left( X\right) ;\phi ,s\right) dX,\qquad \text {where }\underline{X}=\underline{A}^{s}=\left( \frac{\phi }{s^{2}}\right) ^{ \frac{s}{1+s}}. \end{aligned}$$

The opportunity costs of sellers and buyers are

$$\begin{aligned} C_{S}^{FD}\left( \phi ,s\right)= & {} \int _{\underline{A}}^{1}\left\{ A\int _{0}^{S^{FD}\left( A;\phi ,s\right) }XdX\right\} dA, \\ C_{B}^{FD}\left( \phi ,s\right)= & {} \int _{\underline{X}}^{1}\left\{ X\int _{0}^{D^{FD}\left( \widehat{a}\left( X\right) ;\phi ,s\right) }AdA\right\} dX. \end{aligned}$$

Computing $V^{FD}\left( \phi ,s\right)$, $C_{S}^{FD}\left( \phi ,s\right)$, $C_{B}^{FD}\left( \phi ,s\right)$,

$$\begin{aligned} V^{FD}\left( \phi ,s\right)= & {} \frac{s^{2}}{\left( 1+s\right) s}\int _{ \underline{X}}^{1}X^{\frac{2+s}{s}}dX-\frac{\phi }{\left( 1+s\right) s}\int _{\underline{X}}^{1}X^{\frac{1}{s}}dX\\{} & {} =\frac{1}{2}\left( \frac{s}{1+s}\right) ^{2}\left( 1-\underline{X}^{\frac{1+s}{s}}\right) ^{2},\\ C_{B}^{FD}\left( \phi ,s\right)= & {} \frac{1}{2}\int _{\underline{X} }^{1}\left\{ X\frac{1}{\left( 1+s\right) ^{2}s^{2}}\left( s^{4}X^{\frac{2}{s} }-2s^{2}\phi X^{\frac{1-s}{s}}+\frac{\phi ^{2}}{X^{2}}\right) \right\} dX \\= & {} \frac{1}{4}\left( \frac{s}{1+s}\right) ^{3}\left( 1-\underline{X}^{\frac{ 1+s}{s}}\right) \left( 1-3\underline{X}^{\frac{1+s}{s}}\right) -\frac{\phi ^{2}\ln \underline{X}}{2\left( 1+s\right) ^{2}s^{2}},\\ C_{S}^{FD}\left( \phi ,s\right)= & {} \frac{1}{2}\int _{\underline{A} }^{1}\left\{ A\left( \frac{s^{2}}{1+s}\right) ^{2}\left( A^{2s}-\frac{2\phi }{s^{2}}A^{s-1}+\frac{\phi ^{2}}{s^{4}}\frac{1}{A^{2}}\right) \right\} dA \\= & {} sC_{B}^{FD}\left( \phi ,s\right) . \end{aligned}$$

Therefore, the welfare gain is

$$\begin{aligned} G^{FD}\left( \phi ,s\right)= & {} V^{FD}\left( \phi ,s\right) -\left( C_{S}^{FD}\left( \phi ,s\right) +C_{B}^{FD}\left( \phi ,s\right) \right) \\= & {} \frac{1}{4}\left( \frac{s}{1+s}\right) ^{2}\left( 1-\underline{X}^{\frac{ 1+s}{s}}\right) \left\{ 2-s+\left( 3s-2\right) \underline{X}^{\frac{1+s}{s} }\right\} +\frac{\frac{\phi ^{2}}{s}\ln \underline{X}^{\frac{1+s}{s}}}{ 2\left( 1+s\right) ^{2}}. \end{aligned}$$

Using $\underline{X}^{\frac{1+s}{s}}=\frac{\phi }{s^{2}}$, we have

$$\begin{aligned} G^{FD}\left( \phi ,s\right) =\frac{1}{4}\left( \frac{s}{1+s}\right) ^{2}\left( 1-\frac{\phi }{s^{2}}\right) \left\{ 2-s+\left( 3s-2\right) \frac{ \phi }{s^{2}}\right\} +\frac{\frac{\phi ^{2}}{s}\ln \frac{\phi }{s^{2}}}{ 2\left( 1+s\right) ^{2}}. \end{aligned}$$

(33)

Substituting $s\equiv \sqrt{1-\tau }$ back yields $G^{FD}\left( \phi ,\tau \right)$. $\square$

Proof of Corollary 1

The first three results are obtained by setting $\phi =\tau =0$ in Proposition 3. For $\Pi ^{FD}\left( A,X\right)$, first compute $\Pi _{S}^{FD}\left( A\right) =P\left( A\right) =\frac{1}{2}A^{2}$ and $\Pi _{B}^{FD}\left( X\right) =X^{2}-\frac{1}{2}X^{2}=\frac{1}{2}X^{2}$. These imply the participation constraints $AX\le \frac{1}{2}A^{2}\Leftrightarrow \frac{A}{X}\ge 2$ and $AX\le \frac{1}{2}X^{2}\Leftrightarrow \frac{A}{X} \le \frac{1}{2}$. $\square$

1.4 Proposition 4 and Claim 2

Proof of Proposition 4

(a) Fees paid by sellers of assets A are

$$\begin{aligned} R^{FD}\left( \phi ,\tau ;A\right) \equiv \left\{ \tau P\left( A;\phi ,\tau \right) +\phi \right\} S^{FD}\left( A\right) . \end{aligned}$$

(34)

The term $\tau P\left( A;\phi ,\tau \right) +\phi$ in (34) is a fee charged for each seller, and $S^{FD}\left( A\right) =\frac{\left( 1-\tau \right) P\left( A;\phi ,\tau \right) -\phi }{A}$ is the supply density of assets A. Recall that the worst asset quality is $\underline{A}\left( \phi ,\tau \right)$ given in (12). Aggregating $R^{FD}\left( \phi ,\tau ;A\right)$ over A yields the total fees $\pi ^{FD}\left( \phi ,\tau \right) =\int _{\underline{A}\left( \phi ,\tau \right) \ }^{1}R^{FD}\left( \phi ,\tau ;A\right) dA$. We compute this integral to derive the expression of $\pi ^{FD}\left( \phi ,\tau \right)$.

For the rest, we work with $s\equiv \sqrt{1-\tau }$ to save space. With abuse of notation, we write $\pi ^{FD}\left( \phi ,s\right)$ to mean $\pi ^{FD}\left( \phi ,\tau \right)$ with $\tau =1-s^{2}$. The intermediary’s profit is

$$\begin{aligned} \pi ^{FD}\left( \phi ,s\right) =\int _{\underline{A}}^{1}\frac{s^{2}P\left( A;\phi ,s\right) -\phi }{A}\left( \left( 1-s^{2}\right) P\left( A;\phi ,s\right) +\phi \right) dA, \ \ \text {where } \underline{A}\equiv \left( \frac{\phi }{s^{2}}\right) ^{\frac{1}{1+s}}. \end{aligned}$$

$\pi ^{FD}\left( \phi ,s\right) >0$ for any $\phi <s^{2}$ and zero otherwise. This equals

$$\begin{aligned} s^{2}\left( 1-s^{2}\right) \int _{\underline{A}}^{1}\frac{\left( P\left( A;\phi ,s\right) \right) ^{2}}{A}dA+\phi \left( 2s^{2}-1\right) \int _{ \underline{A}}^{1}\frac{P\left( A;\phi ,s\right) }{A}dA-\phi ^{2}\int _{ \underline{A}}^{1}\frac{dA}{A}. \end{aligned}$$

(35)

Using the price function (32),

$$\begin{aligned}{} & {} \int _{\underline{A}}^{1}\frac{\left( P\left( A;\phi ,s\right) \right) ^{2}}{A }dA=\frac{1}{\left( 1+s\right) ^{3}}\left[ \left( 1-\frac{\phi }{s^{2}} \right) \left\{ \frac{1}{2}\left( 1+\frac{\phi }{s^{2}}\right) +\frac{2\phi }{s}\right\} -\left( \frac{\phi }{s}\right) ^{2}\ln \frac{\phi }{s^{2}} \right] ,\\{} & {} \int _{\underline{A}}^{1}\frac{P\left( A;\phi ,s\right) }{A}dA=\frac{1}{ \left( 1+s\right) ^{2}}\left[ 1-\frac{\phi }{s^{2}}-\frac{\phi }{s}\ln \frac{ \phi }{s^{2}}\right] . \end{aligned}$$

Substituting these expressions into (35), and simplifying,

$$\begin{aligned} \pi ^{FD}\left( \phi ,s\right) =\frac{1}{2\left( 1+s\right) ^{2}}\left[ \left( 1-\frac{\phi }{s^{2}}\right) \left\{ \left( 1-s\right) s^{2}+\left( 3s-1\right) \phi \right\} +2\frac{\phi ^{2}}{s}\ln \frac{\phi }{s^{2}}\right] . \end{aligned}$$

(36)

Substituting $s\equiv \sqrt{1-\tau }$ back yields $\pi ^{FD}\left( \phi ,\tau \right)$. $\square$

(b) Taking a partial derivative $\frac{\partial \pi ^{FD}\left( \phi ,s\right) }{\partial \phi }$,

$$\begin{aligned} \frac{\partial \pi ^{FD}\left( \phi ,s\right) }{\partial \phi }\ge 0\qquad \Leftrightarrow \qquad \left( 2s-1\right) \left( s^{2}-\phi \right) \ge 2\phi s\ln \frac{s^{2}}{\phi } \end{aligned}$$

Note that $\phi =s^{2}$ does not satisfy the second order condition. Hence, we have

$$\begin{aligned} \frac{\partial \pi ^{FD}\left( \phi ,s\right) }{\partial \phi }\ge 0\qquad \Leftrightarrow \qquad \frac{\frac{s^{2}}{\phi }-1}{\ln \frac{s^{2}}{\phi }} \left( 2s-1\right) \ge 2s. \end{aligned}$$

If $s\le \frac{1}{2}$ ($\Leftrightarrow \tau \ge \widehat{\tau }\equiv \frac{3}{4}$), it is optimal to set $\phi =0$, i.e., $\phi ^{FD}\left( \tau \right) =0$ for $\tau \ge \widehat{\tau }$. For a given $s>\frac{1}{2}$ ($\Leftrightarrow \tau <\widehat{\tau }$), the profit-maximizing $\phi$ must satisfy $\frac{\frac{s^{2}}{\phi }-1}{\ln \frac{s^{2}}{\phi }}=\frac{2\,s}{2\,s-1 }$. This is equivalent to

$$\begin{aligned} \frac{1-\tau }{\phi }-1=\frac{2\sqrt{1-\tau }}{2\sqrt{1-\tau }-1}\ln \frac{ 1-\tau }{\phi }. \end{aligned}$$

(37)

Applying the implicit function theorem, this has a unique solution $\phi ^{FD}\left( \tau \right) \in \left( 0,1-\tau \right)$ decreasing in $\tau < \widehat{\tau }$, that satisfies $\underset{\tau \uparrow \widehat{\tau }}{ \lim }\phi ^{FD}\left( \tau \right) =0$. Also, $\overline{\phi }\equiv \phi ^{FD}\left( 0\right) \approx 0.285$ is defined as a smaller solution to $\phi \left( 1-2\ln \phi \right) =1$.

Finally, rearrange (37) as $\frac{\phi ^{2}}{s}\ln \frac{\phi }{ s^{2}}=\frac{1-2\,s}{2}\phi \left( 1-\frac{\phi }{s^{2}}\right)$ and substitute it into (36) to get

$$\begin{aligned} \pi ^{FD}\left( \phi ^{FD}\left( s\right) ,s\right) =\frac{1}{2}\left( \frac{ s}{1+s}\right) ^{2}\left( 1-\frac{\phi ^{FD}\left( s\right) }{s^{2}}\right) \left( 1-s+\frac{\phi ^{FD}\left( s\right) }{s}\right) . \end{aligned}$$

Substituting $s\equiv \sqrt{1-\tau }$ back, we obtain

$$\begin{aligned} \pi ^{FD}\left( \phi ^{FD}\left( \tau \right) ,\!\tau \right) \!=\!\frac{1}{2} \left( \frac{\sqrt{1\!-\!\tau }}{1\!+\!\sqrt{1-\tau }}\right) ^{2}\left( 1\!-\!\frac{ \phi ^{FD}\left( \tau \right) }{1\!-\!\tau }\right) \left( 1\!-\!\sqrt{1\!-\!\tau }\!+\! \frac{\phi ^{FD}\left( \tau \right) }{\sqrt{1\!-\!\tau }}\right) \end{aligned}$$

Similarly, by substituting $\frac{\phi ^{2}}{s}\ln \frac{\phi }{s^{2}}=\frac{ 1-2\,s}{2}\phi \left( 1-\frac{\phi }{s^{2}}\right)$ into (33),

$$\begin{aligned} G^{FD}\left( \phi ^{FD}\left( s\right) ,s\right) \!=\!\frac{1}{4}\left( \frac{s}{ 1\!+\!s}\right) ^{2}\left( 1\!-\!\frac{\phi ^{FD}\left( s\right) }{s^{2}}\right) \left\{ 1\!+\!\left( 1\!-\!s\right) \left( 1\!-\!\frac{\phi ^{FD}\!\left( s\right) }{s^{2}} \right) \right\} . \end{aligned}$$

Substituting $s\equiv \sqrt{1-\tau }$ back, we obtain $G^{FD}\left( \phi ^{FD}\left( \tau \right) ,\tau \right)$. Because $TG^{FD}\left( \phi ,\tau \right) =G^{FD}\left( \phi ,\tau \right) -\pi ^{FD}\left( \phi ,\tau \right)$, using the results above,

$$\begin{aligned} \frac{TG^{FD}\left( \phi ^{FD}\left( \tau \right) ,\tau \right) }{ G^{FD}\left( \phi ^{FD}\left( \tau \right) ,\tau \right) }= & {} 1-\frac{\pi ^{FD}\left( \phi ^{FD}\left( \tau \right) ,\tau \right) }{G^{FD}\left( \phi ^{FD}\left( \tau \right) ,\tau \right) } \\= & {} 1-\frac{2\left( 1-\sqrt{1-\tau }+\frac{\phi ^{FD}\left( \tau \right) }{ \sqrt{1-\tau }}\right) }{1+\left( 1-\sqrt{1-\tau }\right) \left( 1-\frac{ \phi ^{FD}\left( \tau \right) }{1-\tau }\right) } \\= & {} \frac{1-\frac{\phi ^{FD}\left( \tau \right) }{1-\tau }-\left( 1-\sqrt{ 1-\tau }+\frac{\phi ^{FD}\left( \tau \right) }{\sqrt{1-\tau }}\right) }{1- \frac{\phi ^{FD}\left( \tau \right) }{1-\tau }+\left( 1-\sqrt{1-\tau }+\frac{ \phi ^{FD}\left( \tau \right) }{\sqrt{1-\tau }}\right) }. \end{aligned}$$

$\square$

Analysis behind Claim 2.

We establish the existence of the interior optimum $\left( \phi _{FD}^{*},\tau _{FD}^{*}\right)$. Above, we already showed that $\phi ^{FD}\left( \tau \right) =0$ for $\tau \ge \widehat{\tau }=\frac{3}{4}$ and $\overline{\phi }\equiv \phi ^{FD}\left( 0\right) \approx 0.2855$. Below, we similarly show that $\tau ^{FD}\left( \phi \right) =0$ for $\phi \ge \widehat{\phi }\approx 0.319$ and $\overline{\tau }\equiv \tau ^{FD}\left( 0\right) \approx 0.685$. Then, $\overline{\phi }<\widehat{\phi }$, $\overline{\tau }<\widehat{\tau }$, and the continuity of $\left\{ \phi ^{FD}\left( \tau \right) ,\tau ^{FD}\left( \phi \right) \right\}$ together imply the existence of the interior solution $\left( \phi _{FD}^{*},\tau _{FD}^{*}\right)$. Numerically, this is the unique optimum as shown in Fig. 7a.

Taking a partial derivative of $\pi ^{FD}\left( \phi ,s\right)$ with respect to s,

$$\begin{aligned}{} & {} \frac{\partial \pi ^{FD}\left( \phi ,s\right) }{\partial s}\ge 0\\{} & {} \quad \Leftrightarrow s^{2}\left( 1+s\right) ^{2}\frac{\partial }{\partial s}\left[ \left( s^{2}-\phi \right) \frac{\left( 1-s\right) s^{2}+\left( 3s-1\right) \phi }{2} -s\phi ^{2}\ln \frac{s^{2}}{\phi }\right] \\{} & {} \quad \ge \left[ \left( s^{2}-\phi \right) \frac{\left( 1-s\right) s^{2}+\left( 3s-1\right) \phi }{2}-s\phi ^{2}\ln \frac{s^{2}}{\phi }\right] \frac{ \partial }{\partial s}\left\{ s^{2}\left( 1+s\right) ^{2}\right\} \\ \end{aligned}$$

Because $\frac{\partial }{\partial s}\left\{ s^{2}\left( 1+s\right) ^{2}\right\} =2\,s\left( 1+s\right) \left( 1+2\,s\right)$, this is equivalent to

$$\begin{aligned} \frac{\frac{\partial }{\partial s}\left[ \left( s^{2}-\phi \right) \frac{ \left( 1-s\right) s^{2}+\left( 3s-1\right) \phi }{2}-s\phi ^{2}\ln \frac{ s^{2}}{\phi }\right] }{\left( s^{2}-\phi \right) \frac{\left( 1-s\right) s^{2}+\left( 3s-1\right) \phi }{2}-s\phi ^{2}\ln \frac{s^{2}}{\phi }}\ge \frac{2\left( 1+2s\right) }{s\left( 1+s\right) }\in \left[ 2,3\right] . \end{aligned}$$

Evaluating the numerator of the left hand side,

$$\begin{aligned}{} & {} \frac{\partial }{\partial s}\left[ \left( s^{2}-\phi \right) \frac{\left( 1-s\right) s^{2}+\left( 3s-1\right) \phi }{2}-s\phi ^{2}\ln \frac{s^{2}}{\phi }\right] \\{} & {} \quad =s^{3}\left( 2-\frac{5}{2}s\right) -\frac{7}{2}\phi ^{2}+2\phi s\left( 3s-1\right) -\phi ^{2}\ln \frac{s^{2}}{\phi }. \end{aligned}$$

Therefore, $\frac{\partial \pi ^{FD}\left( \phi ,s\right) }{\partial s}\ge 0$ if and only if

$$\begin{aligned} \frac{s^{4}\left( 2-\frac{5}{2}s\right) -\frac{7}{2}\phi ^{2}s+2\phi s^{2}\left( 3s-1\right) -s\phi ^{2}\ln \frac{s^{2}}{\phi }}{\left( s^{2}-\phi \right) \frac{\left( 1-s\right) s^{2}+\left( 3s-1\right) \phi }{2} -s\phi ^{2}\ln \frac{s^{2}}{\phi }}\ge \frac{2\left( 1+2s\right) }{1+s} . \end{aligned}$$

(38)

For $\phi =0$, the left hand side of (38) becomes $\frac{ s^{4}\left( 2-\frac{5}{2}s\right) }{\frac{\left( 1-s\right) s^{4}}{2}}=\frac{ 4-5\,s}{1-s}$. For this to be positive, we need $s<\frac{4}{5}$. The optimal $\tau$ when $\phi =0$, i.e. $\tau ^{FD}\left( 0\right) \equiv \overline{\tau }$, is given by a solution to

$$\begin{aligned} \left( 4-5s\right) \left( 1+s\right) =2\left( 1+2s\right) \left( 1-s\right) \ \ \Leftrightarrow \ \ s^{2}+3s-2=0. \end{aligned}$$

This has a unique positive solution $s=\frac{-3+\sqrt{17}}{2}\Leftrightarrow \tau =1-\frac{26-6\sqrt{17}}{4}=\frac{3\sqrt{17}-11}{2}=\overline{\tau } \approx 0.685$. Finally, we verify $s=\frac{-3+\sqrt{17}}{2}<\frac{4}{5} \Leftrightarrow \sqrt{17}<\frac{21}{5}$.

For $\phi >0$, rewrite (38) with equality as

$$\begin{aligned} \frac{\frac{s^{2}}{\phi }\left\{ 4\left( 3s-1\right) -\frac{s^{2}}{\phi } \left( 5s-4\right) \right\} -7s-2s\ln \frac{s^{2}}{\phi }}{\left( \frac{s^{2} }{\phi }-1\right) \left\{ \left( 1-s\right) \frac{s^{2}}{\phi }+3s-1\right\} -2s\ln \frac{s^{2}}{\phi }}=\frac{2\left( 1+2s\right) }{1+s}. \end{aligned}$$

(39)

By setting $s=1$ in (39),

$$\begin{aligned} \frac{\frac{1}{\phi ^{2}}\left( -\frac{1}{2}\right) -\frac{7}{2}+\frac{4}{ \phi }-\ln \frac{1}{\phi }}{\frac{1}{\phi }-1-\ln \frac{1}{\phi }}= & {} 3\ \ \Leftrightarrow \ -\frac{1}{2\phi }-\frac{7}{2}\phi +4+\phi \ln \phi =3\left( 1-\phi +\phi \ln \phi \right) \\\Leftrightarrow & {} 1-\frac{1}{2\phi }-\frac{1}{2}\phi =2\phi \ln \phi \\\Leftrightarrow & {} 1=\phi \left( 2-\phi -4\phi \ln \phi \right) . \end{aligned}$$

This has two solutions and the smaller one is $\widehat{\phi }\approx 0.319$. Numerically, (39) has a unique solution $\tau ^{FD}\left( \phi \right)$ decreasing in $\phi$ and satisfies $\underset{\phi \uparrow \widehat{\phi }}{\lim }\tau ^{FD}\left( \phi \right) =0$ and $\tau ^{FD}\left( 0\right) =\overline{\tau }\approx 0.685$. Therefore, $\overline{ \phi }<\widehat{\phi }$ and $\overline{\tau }<\widehat{\tau }$, as shown in Fig. 7a. This establishes the existence of the interior optimum $\left( \phi _{FD}^{*},\tau _{FD}^{*}\right)$.

1.5 Proposition 5

(a) We conjecture that buyers and sellers are separated, and later verify that the conjecture is true, as shown in Fig. 8. For a given $P_{0}$, a supply is $S\left( P_{0}\right) =\int _{A_{\min }}^{ \overline{A}}\frac{P_{0}}{A}dA$ and a demand is $D\left( P_{0}\right) =\int _{ \frac{P_{0}}{a_{0}}}^{\overline{X}}\left( a_{0}-\frac{P_{0}}{X}\right) dX$. A market-clearing condition $S\left( P_{0}\right) =D\left( P_{0}\right)$ yields

$$\begin{aligned} \frac{a_{0}\overline{X}}{P_{0}}-1=\ln \frac{a_{0}\overline{X}}{P_{0}}+\ln \frac{\overline{A}}{A_{\min }}, \end{aligned}$$

(40)

with a unique solution $P_{0}\in \left( 0,a_{0}\overline{X}\right)$ for any $\frac{\overline{A}}{A_{\min }}>1$. The expected quality of assets is

$$\begin{aligned} a_{0}=\frac{\overline{A}-A_{\min }}{\ln \overline{A}-\ln A_{\min }}. \end{aligned}$$

(41)

Sellers with assets $\overline{A}$ and buyers with skill $\overline{X}= \overline{A}^{\sqrt{1-\tau }}$ must be indifferent between the two markets. These two indifference conditions are

$$\begin{aligned} \Pi _{S}^{U}\left( \overline{A}\right) =P_{0}\qquad \text {and}\qquad \Pi _{B}^{U}\left( \overline{A}^{\sqrt{1-\tau }}\right) =a_{0}\overline{A}^{ \sqrt{1-\tau }}-P_{0}, \end{aligned}$$

(42)

where $\Pi _{S}^{U}\left( A\right)$ is sellers’ payoff and $\Pi _{B}^{U}\left( X\right)$ is buyers’ payoff in the upper market. From (40), (41), (42), we derive $\left\{ P_{0},a_{0},A_{\min }, \overline{A}\right\}$.

From the two indifference conditions (42) with $\Pi _{S}^{U}\left( \overline{A}\right) =\frac{1-\tau }{1+\sqrt{1-\tau }}\left( \overline{A}^{1+ \sqrt{1-\tau }}-\frac{\phi }{1-\tau }\right)$ and $\Pi _{B}^{U}\left( \overline{A}^{\sqrt{1-\tau }}\right) =\frac{\sqrt{1-\tau }}{1+\sqrt{1-\tau }} \left( \overline{A}^{1+\sqrt{1-\tau }}-\frac{\phi }{1-\tau }\right)$, we obtain

$$\begin{aligned}{} & {} P_{0}=\frac{\sqrt{1-\tau }}{1+\sqrt{1-\tau }}a_{0}\overline{A}^{\sqrt{1-\tau }}, \end{aligned}$$

(43)

$$\begin{aligned}{} & {} \overline{A}^{1+\sqrt{1-\tau }}-\frac{a_{0}}{\sqrt{1-\tau }}\overline{A}^{ \sqrt{1-\tau }}-\frac{\phi }{1-\tau }=0. \end{aligned}$$

(44)

Substituting (43) into the market-clearing condition in the lower market (40) yields

$$\begin{aligned} A_{\min }=\kappa _{\min }\left( \tau \right) \overline{A},\qquad \text {where }\kappa _{\min }\left( \tau \right) \equiv \frac{1+\sqrt{1-\tau } }{\sqrt{1-\tau }}\exp \left( -\frac{1}{\sqrt{1-\tau }}\right) . \end{aligned}$$

(45)

By substituting (45) into (41) to eliminate $A_{\min }$,

$$\begin{aligned} a_{0}=\kappa \left( \tau \right) \overline{A},\qquad \text {where } \kappa \left( \tau \right) \equiv \frac{1-\kappa _{\min }\left( \tau \right) }{-\ln \kappa _{\min }\left( \tau \right) }\ \in \left( \kappa _{\min }\left( \tau \right) ,1\right) . \end{aligned}$$

(46)

That $\kappa _{\min }<\kappa \left( \tau \right) <1$ implies $A_{\min }<a_{0}<\overline{A}$. Combining (44) and (46) yields $\overline{A}=\left( \frac{\phi }{1-\tau -\kappa \left( \tau \right) \sqrt{ 1-\tau }}\right) ^{\frac{1}{1+\sqrt{1-\tau }}}$, which is (16). We characterized $\left( A_{\min },a_{0},P_{0}\right)$ as functions of $\overline{A}\left( \phi ,\tau \right)$:

$$\begin{aligned} A_{\min }= & {} \kappa _{\min }\left( \tau \right) \overline{A}\left( \phi ,\tau \right) , \nonumber \\ a_{0}= & {} \kappa \left( \tau \right) \overline{A}\left( \phi ,\tau \right) , \nonumber \\ P_{0}= & {} \frac{\sqrt{1-\tau }}{1+\sqrt{1-\tau }}\kappa \left( \tau \right) \left\{ \overline{A}\left( \phi ,\tau \right) \right\} ^{1+\sqrt{1-\tau }}. \end{aligned}$$

(47)

From (16) and (47), both markets attract some traders if and only if $0<\overline{A}\left( \phi ,\tau \right)<1\Leftrightarrow 0<\phi <1-T\left( \tau \right)$. Because $1-T\left( \tau \right) =1-\tau -\kappa \left( \tau \right) \sqrt{1-\tau }$, $0<1-T\left( \tau \right)$ requires $\kappa \left( \tau \right) <\sqrt{1-\tau }$. We show that there is $\tau _{\max }\in \left( 0,1\right)$ such that $\kappa \left( \tau \right) < \sqrt{1-\tau }$ if and only if $\tau <\tau _{\max }$. First, by the definition of $\kappa \left( \tau \right)$ given in (46), $\kappa \left( \tau \right) <\sqrt{1-\tau }$ is equivalent to $1-\kappa _{\min }\left( \tau \right) <-\ln \kappa _{\min }\left( \tau \right) \sqrt{1-\tau }$. Second, using the definition of $\kappa _{\min }\left( \tau \right)$ given in (45) and $s\equiv \sqrt{1-\tau }$ to evaluate this inequality,

$$\begin{aligned} \kappa \left( \tau \right) <\sqrt{1-\tau } \Leftrightarrow \frac{1}{s}\left( 1+\frac{1}{s}\right) >\exp \left( \frac{1}{s}\right) \ln \left( 1+\frac{1}{s}\right) . \end{aligned}$$

At $s=1$ ($\Leftrightarrow \tau =0$), $2>\exp \left( 1\right) \ln 2\approx 1.8842$ holds. For sufficiently small $s>0$, $\frac{1}{s}\left( 1+\frac{1}{s} \right) <\exp \left( \frac{1}{s}\right) \ln \left( 1+\frac{1}{s}\right)$ holds. Therefore, there is $s\in \left( 0,1\right)$ that solves $\frac{1}{s} \left( 1+\frac{1}{s}\right) =\exp \left( \frac{1}{s}\right) \ln \left( 1+ \frac{1}{s}\right)$. To show uniqueness, we let $\widehat{s}\equiv \frac{1}{ s}$ and show that the derivative of $\widehat{s}\left( 1+\widehat{s}\right)$ is smaller than that of $\exp \left( \widehat{s}\right) \ln \left( 1+ \widehat{s}\right)$, whenever $\widehat{s}\left( 1+\widehat{s}\right) =\exp \left( \widehat{s}\right) \ln \left( 1+\widehat{s}\right)$ holds. This is equivalent to $1+2\widehat{s}<\widehat{s}\left( 1+\widehat{s}\right) \frac{ \exp \left( \widehat{s}\right) }{1+\widehat{s}}\Leftrightarrow \left( 1+ \widehat{s}-\widehat{s}^{2}\right) \left( 1+\widehat{s}\right) <\exp \left( \widehat{s}\right)$, which is true for any $\widehat{s}\ge 1$. Below, we plot $\kappa \left( \tau \right)$ and $\sqrt{1-\tau }$ as functions of $\tau$.

Fig. 12

$\kappa \left( \tau \right) <\sqrt{1- \tau }$ implies $\kappa _{\min }\left( \tau \right) >A_{+}$. Note. $\tau _{\max }\approx 0.338$ satisfies $\kappa \left( \tau \right) =\sqrt{1- \tau }$ (a higher red marker “$\circ$”)

Finally, we show $A_{\min }>\frac{a_{0}}{2}$ to verify our conjecture that sellers and buyers are not connected in the lower market. First, $A_{\min }> \frac{a_{0}}{2}\Leftrightarrow 2\kappa _{\min }\left( \tau \right)>\kappa \left( \tau \right) =\frac{1-\kappa _{\min }\left( \tau \right) }{-\ln \kappa _{\min }\left( \tau \right) }\Leftrightarrow \kappa _{\min }\left( \tau \right) \left( 1-2\ln \kappa _{\min }\left( \tau \right) \right)>1\Leftrightarrow \kappa _{\min }\left( \tau \right) >A_{+}$, where $A_{+}$ was defined in Proposition 1. The last inequality is implied by $\tau <\tau _{\max }$, as shown in Fig. 12. $\square$

(b) We work with $s=\sqrt{1-\tau }$. In the upper market, the matching function is $m\left( A\right) =A^{s}\Leftrightarrow \widehat{a} \left( X\right) =X^{\frac{1}{s}}$ and the only difference from the FD equilibrium is that the worst pair $\left( \underline{X},\underline{A} \right)$ is replaced with $\left( \overline{X},\overline{A}\right)$. The new value generated in the upper market is

$$\begin{aligned} V^{U}\left( \phi ,s\right) =\int _{\overline{X}}^{1}\left\{ \widehat{a}\left( X\right) X\right\} D\left( \widehat{a}\left( X\right) ;\phi ,s\right) dX , \ \text {where }\overline{X}=\overline{A}^{s}=\left( \frac{\phi }{s\left( s-\kappa \right) }\right) ^{\frac{s}{1+s}}. \end{aligned}$$

The opportunity costs by sellers and buyers are

$$\begin{aligned} C_{S}^{U}\left( \phi ,s\right)= & {} \int _{\overline{A}}^{1}\left\{ A\int _{0}^{S\left( A;\phi ,s\right) }XdX\right\} dA \ \ \text {and} \\ C_{B}^{U}\left( \phi ,s\right)= & {} \int _{\overline{X}}^{1}\left\{ X\int _{0}^{D\left( \widehat{a}\left( X\right) ;\phi ,s\right) }AdA\right\} dX . \end{aligned}$$

Therefore,

$$\begin{aligned} V^{U}\left( \phi ,s\right)= & {} \frac{1}{2}\left( \frac{s}{1+s}\right) ^{2}\left( 1-\overline{X}^{\frac{1+s}{s}}\right) \left( 1+\overline{X}^{ \frac{1+s}{s}}-2\frac{\phi }{s^{2}}\right) , \\ C_{B}^{U}\left( \phi ,s\right)= & {} \frac{1}{4}\left( \frac{s}{1+s}\right) ^{3}\left( 1-\overline{X}^{\frac{1+s}{s}}\right) \left( 1+\overline{X}^{ \frac{1+s}{s}}-\frac{4\phi }{s^{2}}\right) -\frac{\phi ^{2}\ln \overline{X}}{ 2\left( 1+s\right) ^{2}s^{2}}, \\ C_{S}^{U}\left( \phi ,s\right)= & {} sC_{B}^{U}\left( \phi ,s\right) . \end{aligned}$$

The welfare gain in the upper market is

$$\begin{aligned} G^{U}\left( \phi ,s\right)= & {} V^{U}\left( \phi ,s\right) -\left( C_{S}^{U}\left( \phi ,s\right) +C_{B}^{U}\left( \phi ,s\right) \right) \\= & {} \frac{1}{4}\left( \frac{s}{1+s}\right) ^{2}\left( 1-\overline{X}^{\frac{ 1+s}{s}}\right) \left\{ 2-s+\left\{ \begin{array}{c} \left( 4-\frac{s}{s-\kappa }\right) s \\ -2\left( 2-\frac{s}{s-\kappa }\right) \end{array} \right\} \frac{\phi }{s^{2}}\right\} \\{} & {} +\frac{\phi ^{2}\ln \overline{X}^{\frac{ 1+s}{s}}}{2\left( 1+s\right) ^{2}s}. \end{aligned}$$

Substituting $\overline{X}^{\frac{1+s}{s}}=\frac{\phi }{s\left( s-\kappa \right) }$, $s\equiv \sqrt{1-\tau }$ and $1-T\left( \tau \right) =s\left( s-\kappa \right)$ yields $G^{U}\left( \phi ,\tau \right)$.

In the lower market, we compute $G^{L}\left( \phi ,\tau \right) =V^{L}\left( \phi ,s\right) -\left( C_{S}^{L}\left( \phi ,s\right) +C_{B}^{L}\left( \phi ,s\right) \right)$. These are obtained by replacing the upper bound of 1 with $\overline{X}$ and $\overline{A}$ in the corresponding expressions in the MD equilibrium. The new production is

$$\begin{aligned} V^{L}\left( \phi ,s\right) =a_{0}\int _{\frac{P_{0}}{a_{0}}}^{\overline{X} }X\left( a_{0}-\frac{P_{0}}{X}\right) dX=\frac{\left( a_{0}\overline{X} -P_{0}\right) ^{2}}{2}. \end{aligned}$$

Sellers’ opportunity cost is

$$\begin{aligned} C_{S}^{L}\left( \phi ,s\right) =\int _{A_{\min }}^{\overline{A}}\left( A\int _{0}^{\frac{P_{0}}{A}}XdX\right) dA=\frac{P_{0}^{2}}{2}\ln \frac{ \overline{A}}{A_{\min }}. \end{aligned}$$

Buyers’ opportunity cost is

$$\begin{aligned} C_{B}^{L}\left( \phi ,s\right)= & {} \int _{\frac{P_{0}}{a_{0}}}^{\overline{X} }\left( X\int _{0}^{a_{0}-\frac{P_{0}}{X}}AdA\right) dX\\= & {} \frac{1}{4}\left( a_{0}\overline{X}-P_{0}\right) \left( a_{0}\overline{X}-3P_{0}\right) +\frac{ P_{0}^{2}}{2}\ln \frac{a_{0}\overline{X}}{P_{0}}. \end{aligned}$$

Therefore,

$$\begin{aligned} C_{S}^{L}\left( \phi ,s\right) +C_{B}^{L}\left( \phi ,s\right) =\frac{1}{4} \left( a_{0}\overline{X}-P_{0}\right) \left( a_{0}\overline{X}-3P_{0}\right) +\frac{P_{0}^{2}}{2}\ln \left( \frac{\overline{A}}{A_{\min }}\frac{a_{0} \overline{X}}{P_{0}}\right) . \end{aligned}$$

Because $\overline{X}=\overline{A}^{s}$, from the market-clearing condition of the lower market (40),

$$\begin{aligned} \frac{a_{0}\overline{X}}{P_{0}}-1=\ln \frac{a_{0}\overline{X}}{P_{0}}+\ln \frac{\overline{A}}{A_{\min }}. \end{aligned}$$

Using this, $C_{S}^{L}\left( \phi ,s\right) +C_{B}^{L}\left( \phi ,s\right) = \frac{1}{4}\left( a_{0}\overline{X}-P_{0}\right) ^{2}$. Therefore,

$$\begin{aligned} G^{L}\left( \phi ,\tau \right) =\frac{\left( a_{0}\overline{X}-P_{0}\right) ^{2}}{2}-\frac{1}{4}\left( a_{0}\overline{X}-P_{0}\right) ^{2}=\left( \frac{ a_{0}\overline{X}-P_{0}}{2}\right) ^{2}. \end{aligned}$$

From (43) and (46), $a_{0}\overline{X}-P_{0}=\left( 1-\frac{s}{ 1+s}\right) a_{0}\overline{X}=\frac{1}{1+s}\left( \kappa \overline{X}^{\frac{ 1}{s}}\right) \overline{X}=\frac{\kappa }{1+s}\overline{X}^{\frac{1+s}{s}}$. With $\overline{X}^{\frac{1+s}{s}}=\frac{\phi }{s\left( s-\kappa \right) }$ and $s\equiv \sqrt{1-\tau }$, we obtain $G^{L}\left( \phi ,\tau \right)$. $\square$

(c) We work with $s=\sqrt{1-\tau }$. We start by replacing $\underline{A}$ with $\overline{A}$ in the expression (35) derived for the FD equilibrium.

$$\begin{aligned}{} & {} \int _{\overline{A}}^{1}\frac{\left( P\left( a;\phi ,s\right) \right) ^{2}}{a} da=\frac{1}{\left( 1+s\right) ^{3}}\left\{ \left( 1-\overline{A} ^{1+s}\right) \left( \frac{1+\overline{A}^{1+s}}{2}+\frac{2\phi }{s}\right) -\left( \frac{\phi }{s}\right) ^{2}\ln \overline{A}^{1+s}\right\} ,\\{} & {} \int _{\overline{A}}^{1}\frac{P\left( a;\phi ,s\right) }{a}da=\frac{1}{1+s} \left[ \frac{a^{1+s}}{1+s}+\frac{\phi }{s}\ln a\right] _{\overline{A}}^{1}= \frac{1}{\left( 1+s\right) ^{2}}\left( 1-\overline{A}^{1+s}-\frac{\phi }{s} \ln \overline{A}^{1+s}\right) . \end{aligned}$$

Therefore,

$$\begin{aligned} \pi ^{HM}\left( \phi ,s\right)= & {} \frac{1}{\left( 1+s\right) ^{2}}\left( 1- \overline{A}^{1+s}\right) \left\{ s^{2}\left( 1-s\right) \left( \frac{1+ \overline{A}^{1+s}}{2}+\frac{2\phi }{s}\right) +\phi \left( 2s^{2}-1\right) \right\} \\{} & {} -\left\{ \left( \frac{s}{1+s}\right) ^{2}\left( 1-s\right) \left( \frac{ \phi }{s}\right) ^{2}+\frac{\phi \left( 2s^{2}-1\right) }{\left( 1+s\right) ^{2}}\frac{\phi }{s}-\frac{\phi ^{2}}{1+s}\right\} \ln \overline{A}^{1+s}. \end{aligned}$$

The first term is $\frac{1-s}{2}\left( \frac{s}{1+s}\right) ^{2}\left( 1- \overline{A}^{2\left( 1+s\right) }\right) +\frac{\left( 2\,s-1\right) \phi }{ \left( 1+s\right) ^{2}}\left( 1-\overline{A}^{1+s}\right)$, while the second term is

$$\begin{aligned} -\left\{ \left( \frac{s}{1+s}\right) ^{2}\left( 1-s\right) \left( \frac{\phi }{s}\right) ^{2}+\frac{\phi \left( 2s^{2}-1\right) }{\left( 1+s\right) ^{2}} \frac{\phi }{s}-\frac{\phi ^{2}}{1+s}\right\} \ln \overline{A}^{1+s}=\frac{ \phi ^{2}}{\left( 1+s\right) ^{2}s}\ln \overline{A}^{1+s}. \end{aligned}$$

Therefore,

$$\begin{aligned} \pi ^{HM}\left( \phi ,s\right)= & {} \frac{1}{s^{2}\left( 1+s\right) ^{2}}\left[ s^{4}\frac{1-s}{2}\left( 1-\overline{A}^{2\left( 1+s\right) }\right) +s^{2}\left( 2s-1\right) \phi \left( 1-\overline{A}^{1+s}\right) +s\phi ^{2}\ln \overline{A}^{1+s}\right] \\= & {} \frac{1}{2}\left( \frac{s}{1+s}\right) ^{2}\left( 1-\overline{A} ^{1+s}\right) \left\{ 1-s+\left\{ 3s-1+\frac{\kappa }{s-\kappa }\left( 1-s\right) \right\} \frac{\phi }{s^{2}}\right\} +\frac{\frac{\phi ^{2}}{s}}{ \left( 1+s\right) ^{2}}\ln \overline{A}^{1+s}. \end{aligned}$$

Substituting $\overline{A}^{1+s}=\frac{\phi }{s\left( s-\kappa \right) }$, $s\equiv \sqrt{1-\tau }$ and $1-T\left( \tau \right) =1-\tau -\kappa \sqrt{ 1-\tau }=s\left( s-\kappa \right)$ yields $\pi ^{HM}\left( \phi ,\tau \right)$. $\square$

1.6 Proposition 6

Proof of Proposition 6

We first show that $\phi ^{HM}\left( \tau \right) \in \left( 0,1-T\left( \tau \right) \right)$ is a unique solution to

$$\begin{aligned} \frac{1-T\left( \tau \right) }{\phi }-1=\frac{1}{2\sqrt{1-\tau }-1}\frac{ \kappa \left( 1-\kappa \right) }{\sqrt{1-\tau }-\kappa }+\frac{2\left( \sqrt{ 1-\tau }-\kappa \right) }{2\sqrt{1-\tau }-1}\ln \frac{1-T\left( \tau \right) }{\phi }. \end{aligned}$$

(48)

Define $\Phi \equiv \frac{\phi }{1-T\left( \tau \right) }$. With $s=\sqrt{ 1-\tau }$, $1-T=s\left( s-\kappa \right)$ and $\Phi =\frac{\phi }{s\left( s-\kappa \right) }$. Using $\frac{\partial \Phi }{\partial \phi }=\frac{1}{ s\left( s-\kappa \right) }$, $\frac{\partial \pi ^{HM}}{\partial \phi }\ge 0$ if and only if

$$\begin{aligned} 2\left( 2\phi \ln \Phi +\phi \right) \ge \frac{1}{s-\kappa }\left\{ \left( 1-s\right) s^{2}+\left( 3s-1+\frac{1-s}{s-\kappa }\kappa \right) \phi \right\} -s\left( 1-\Phi \right) \\ \times \left( 3s-1+\frac{1-s}{s-\kappa }\kappa \right) . \end{aligned}$$

Computing the right hand side yields $2\,s\left\{ 1-2\,s+\left( 3\,s-1+\frac{1-s}{ s-\kappa }\kappa \right) \Phi \right\}$, so

$$\begin{aligned} \frac{\partial \pi ^{HM}}{\partial \phi }\ge 0\ \ \Leftrightarrow \ \ 2\phi \ln \Phi \ge s\left\{ \left( 2s-1+\frac{1-\kappa }{s-\kappa }\kappa \right) \Phi -\left( 2s-1\right) \right\} . \end{aligned}$$

At the equality, this can be written as

$$\begin{aligned} \frac{1}{\Phi }-1=\frac{1}{2s-1}\frac{\kappa \left( 1-\kappa \right) }{ s-\kappa }+\frac{2\left( s-\kappa \right) }{2s-1}\ln \frac{1}{\Phi }. \end{aligned}$$

For $s>\kappa$ ($\Leftrightarrow \tau <\tau _{\max }$), this has a unique solution $\Phi \in \left( 0,1\right)$, with which we obtain $\phi ^{HM}\left( s\right) =s\left( s-\kappa \right) \Phi$. Substituting $s\equiv \sqrt{1-\tau }$ back yields (48). Notice that with $\kappa =0$ (48) becomes (37), the equation that determines $\phi ^{FD}\left( \tau \right)$.

By computing $G^{HM}\left( \phi ,\tau \right) =G^{U}\left( \phi ,\tau \right) +G^{L}\left( \phi ,\tau \right)$,

$$\begin{aligned} G^{HM}\left( \phi ,s\right) =\frac{1}{4}\frac{1}{\left( 1+s\right) ^{2}} \Bigg \{ s^{2}\left( 2-s\right) \left( 1-\Phi ^{2}\right) -4\left( 1-s\right) \phi \left( 1-\Phi \right) +\kappa ^{2}\Phi ^{2}\\+\frac{\phi }{s}\left( 2\phi \ln \Phi \right) \Bigg \} . \end{aligned}$$

Using $\frac{\partial \pi ^{HM}}{\partial \phi }=0\Leftrightarrow 2\phi \ln \Phi =s\left\{ \left( 2\,s-1+\frac{1-\kappa }{s-\kappa }\kappa \right) \Phi -\left( 2\,s-1\right) \right\}$ in the curly bracket above yields $s^{2}\left( 2-s\right) -\left( 3-2\,s\right) \phi +\left( 1-s\right) \left( s-\kappa \right) ^{2}\Phi ^{2}$. Therefore,

$$\begin{aligned} G^{HM}\left( \phi ^{HM}\left( s\right) ,s\right)= & {} \frac{1}{4}\frac{1}{ \left( 1+s\right) ^{2}}\Bigg \{ s^{2}\left( 2-s\right) -\left( 3-2s\right) \phi ^{HM}\left( s\right) \\ {}{} & {} \quad +\frac{1-s}{s^{2}}\left\{ \phi ^{HM}\left( s\right) \right\} ^{2}\Bigg \} \\= & {} \frac{1}{4}\left( \frac{s}{1+s}\right) ^{2}\left( 1-\frac{\phi ^{HM}\left( s\right) }{s^{2}}\right) \left( 1+\left( 1-s\right) \left( 1- \frac{\phi ^{HM}\left( s\right) }{s^{2}}\right) \right) . \end{aligned}$$

With $s\equiv \sqrt{1-\tau }$ and $\tau =\tau _{c}$, we obtain $G^{HM}\left( \phi ^{HM}\left( \tau _{c}\right) ,\tau _{c}\right)$. $\square$