Skip to main content
SpringerLink
Log in

Consensus Convergence with Stochastic Effects

  • Published:
Vietnam Journal of Mathematics Aims and scope Submit manuscript

Abstract

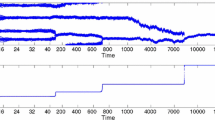
We consider a stochastic, continuous state and time opinion model where each agent’s opinion locally interacts with other agents’ opinions in the system, and there is also exogenous randomness. The interaction tends to create clusters of common opinion. By using linear stability analysis of the associated nonlinear Fokker–Planck equation that governs the empirical density of opinions in the limit of infinitely many agents, we can estimate the number of clusters, the time to cluster formation, and the critical strength of randomness so as to have cluster formation. We also discuss the cluster dynamics after their formation, the width and the effective diffusivity of the clusters. Finally, the long-term behavior of clusters is explored numerically. Extensive numerical simulations confirm our analytical findings.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17

Similar content being viewed by others

References

  1. Baccelli, F., Chatterjee, A., Vishwanath, S.: Stochastic bounded confidence opinion dynamics. In: 2014 IEEE 53rd Annual Conference on Decision and Control (CDC), date 15–17 December 2014, pp 3408–3413 (2014)

  2. Blondel, V.D., Hendrickx, J.M., Olshevsky, A., Tsitsiklis, J.N.: Convergence in multiagent coordination, consensus, and flocking. In: 44th IEEE Conference on Decision and Control, 2005 and 2005 European Control Conference. CDCECC 05. , pp 2996–3000 (2005)

  3. Blondel, V.D., Hendrickx, J.M., Tsitsiklis, J.N.: On the 2R conjecture for multi-agent systems. In: 2007 European Control Conference (ECC), pp 874–881 (2007)

  4. Canuto, C., Fagnani, F., Tilli, P.: An Eulerian approach to the analysis of Krause’s consensus models. SIAM J. Control Optim. 50, 243–265 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  5. Carro, A., Toral, R., San Miguel, M.: The role of noise and initial conditions in the asymptotic solution of a bounded confidence, continuous-opinion model. J. Stat. Phys. 151, 131–149 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  6. Como, G., Fagnani, F.: Scaling limits for continuous opinion dynamics systems. Ann. Appl. Probab. 21, 1537–1567 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  7. Düring, B., Markowich, P., Pietschmann, J., Wolfram, M.-T.: Boltzmann and Fokker–Planck equations modelling opinion formation in the presence of strong leaders. Proc. R. Soc. Lond. A: Math. Phys. Eng. Sci. 465, 3687–3708 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  8. Dawson, D.A.: Critical dynamics and fluctuations for a mean-field model of cooperative behavior. J. Stat. Phys. 31, 29–85 (1983)

    Article  MathSciNet  Google Scholar 

  9. Deffuant, G., Neau, D., Amblard, F., Weisbuch, G.: Mixing beliefs among interacting agents. Adv. Complex Syst. 3, 87–98 (2000)

    Article  Google Scholar 

  10. Gómez-Serrano, J., Graham, C., Le Boudec, J.-Y.: The bounded confidence model of opinion dynamics. Math. Models Methods Appl. Sci. 22, 1150007 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  11. Gärtner, J.: On the McKean–Vlasov limit for interacting diffusions. Math. Nachr. 137, 197–248 (1988)

    Article  MathSciNet  MATH  Google Scholar 

  12. Ha, S.-Y., Tadmor, E.: From particle to kinetic and hydrodynamic descriptions of flocking. Kinet. Relat. Methods 1, 415–435 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  13. Hegselmann, R., Krause, U.: Opinion dynamics and bounded confidence models, analysis, and simulation. J. Artif. Soc. Soc. Simul. 3, 5 (2002)

    Google Scholar 

  14. Hegselmann, R., Krause, U.: Opinion dynamics under the influence of radical groups, charismatic leaders, and other constant signals: a simple unifying model. Netw. Heterog. Media 10, 477–509 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  15. Huang, M., Manton, J.H.: Opinion dynamics with noisy information. In: 2013 IEEE 52nd Annual Conference on Decision and Control (CDC), pp 3445–3450 (2013)

  16. Jabin, P.-E., Motsch, S.: Clustering and asymptotic behavior in opinion formation. J. Differ. Equ. 257, 4165–4187 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  17. Kurtz, T.G., Xiong, J.: Particle representations for a class of nonlinear SPDEs. Stoch. Process. Appl. 83, 103–126 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  18. Lanchier, N., Neufer, J.: Stochastic dynamics on hypergraphs and the spatial majority rule model. J. Stat. Phys. 151, 21–45 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  19. Lorenz, J.: Continuous opinion dynamics under bounded confidence: a survey. Int. J. Mod. Phys. C 18, 1819–1838 (2007)

    Article  MATH  Google Scholar 

  20. Mäs, M., Flache, A., Helbing, D.: Individualization as driving force of clustering phenomena in humans. PLoS Comput. Biol. 6, e1000959 (2010)

    Article  Google Scholar 

  21. Mirtabatabaei, A., Jia, P., Bullo, F.: Eulerian opinion dynamics with bounded confidence and exogenous inputs. SIAM J. Appl. Dyn. Syst. 13, 425–446 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  22. Motsch, S., Tadmor, E.: Heterophilious dynamics enhances consensus. SIAM Rev. 56, 577–621 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  23. Pineda, M., Toral, R., Hernandez-Garcia, E.: Noisy continuous-opinion dynamics. J. Stat. Mech.: Theory Exp. 2009, P08001 (2009)

    Article  Google Scholar 

  24. Pineda, M., Toral, R., Hernandez-Garcia, E.: Diffusing opinions in bounded confidence processes. Eur. Phys. J. D 62, 109–117 (2011)

    Article  Google Scholar 

  25. Pineda, M., Toral, R., Hernandez-Garcia, E.: The noisy Hegselmann–Krause model for opinion dynamics. Eur. Phys. J. B 86, 12 (2013)

    Article  MathSciNet  Google Scholar 

  26. Yang, Y., Dimarogonas, D.V., Hu, X.: Opinion consensus of modified Hegselmann–Krause models. In: 2012 IEEE 51st Annual Conference on Decision and Control (CDC), pp 100–105 (2012)

Download references

Author information

Authors and Affiliations

  1. Laboratoire de Probabilités et Modèles Aléatoires, Laboratoire Jacques-Louis Lions, Université Paris Diderot, Cedex 13, 75205, Paris, France

    Josselin Garnier

  2. Department of Mathematics, Stanford University, Stanford, CA, 94305, USA

    George Papanicolaou

  3. School of Mathematics, University of Minnesota, Minneapolis, MN, 55455, USA

    Tzu-Wei Yang

Authors
  1. Josselin Garnier
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. George Papanicolaou
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Tzu-Wei Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Tzu-Wei Yang.

Additional information

Dedication to Willi Jäger’s 75th Birthday.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Garnier, J., Papanicolaou, G. & Yang, TW. Consensus Convergence with Stochastic Effects. Vietnam J. Math. 45, 51–75 (2017). https://doi.org/10.1007/s10013-016-0190-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10013-016-0190-2

Keywords

Mathematics Subject Classification (2010)

Search

Navigation