Introduction

Density functional theory (DFT) [1] has enjoyed tremendous success in the past few decades as a popular approach to bypass solving the Schrodinger equation. Applications of DFT to understand structural properties and chemical reactivity in a conceptual framework have also seen considerable interest in the literature [2–4]. From the historical viewpoint, there are two separate undertakings in the literature to appreciate and entertain molecular properties related to stability and reactivity: one using frontier molecular orbitals, and the other through density-related quantities. Well-known examples of the former approach are Fukui’s frontier molecular orbital theory [5, 6] and Woodward–Hoffmann rules, [7] whereas for the latter method, examples are conceptual DFT [2–4] and its recent developments, which is often called density functional reactivity theory (DFRT) [8]. The molecular orbital theory of chemical reactivity has been the mainstream for over 50 years. The main issue with the orbital method, however, is the fact that orbitals are human inventions so their general applicability is often questionable. In fact, the more accurate the computational results are, the more ambiguous the orbital’s physical meanings will be. As quoted by Mullikan [9], “with old-fashioned chemical concepts, which at first seemed to have their counterparts in Molecular Quantum Mechanics, the more accurate the calculations became the more the concepts tended to vanish into thin air. So we have to ask, should we try to keep these concepts—do they still have a place—or should they be relegated to chemical history. Among such concepts are electronegativity… hybridization, population analysis, charges on atoms, even the idea of orbitals…”

On the other hand, the approach of chemical reactivity theory using density related quantities is still in the development phase [1]. Much has been accomplished in the past few decades [2–4]. More recent developments have been summarized in a review by one of the present authors [8]. It originates from the chemical application of DFT. Its rigor and validity have been widely outlined and demonstrated. According to DFT, the electron density of a system should determine everything in the ground state, which includes properties related to stability and reactivity. Nevertheless, how to implement this idea and how to make it happen are subject to debate. Different approaches are possible. Conceptual DFT [1–4] is one such effort, where first, second and third orders of partial derivatives of the total energy with respect to system parameters such as the total number of electrons and external potential are conceptualized to quantify chemical reactivity. The introduction of conceptual DFT and quantification of concepts like electronegativity, hardness, Fukui function, and dual descriptors have evidently witnessed the validity and effectiveness of such alternative tools [1–4], even though there have been many challenges and controversies reported in the literature for their general validity and applicability for quite some time [10–13].

Very recently, we advocated using simple density functionals to quantify reactivity properties [8]. Since this approach deviates so much from the original idea of CDFT [1–4], we call this new effort DFRT [8]. Steric effects quantified using the Weizsäcker kinetic energy density functional [14] were the first example [15–29]. Electrophilicity, nucleophilicity, and regioselectivity in terms of information gain or Kullback–Leibler divergence were other examples [30–39], which have enabled us to provide a completely novel understanding about the orth/para/meta group directing phenomena for electrophilic aromatic substitution reactions [32, 33]. Three representations [8] of the theoretical framework using the electron density, shape function, and atoms-in-molecules (AIM) densities with three different atomic partition methods such as Bader’s zero-flux [40], Becke’s fuzzy atom [41], and Hirshfeld’s stock-holder [42] schemes have been established. Three principles [8], the principle of extreme physical information, minimum information gain principle, and information conservation principle, have also been proposed. These earlier results form the foundation of the so-called information-theoretic (IT) approach in DFRT [8].

From the perspective of molecular properties themselves, these two vastly different methods deal with exactly the same subject, just from two distinctive angles, one using the wave function as the basic quantity and the other using electron density as the basic quantity, so they should be closely related to each other. Meanwhile, because of their close relationship, quantities from one approach should be comprehensible, and able to be represented by, the other approach. For example, the molecular orbital is often thought of being as one of essential quantities from the wave function theory (WFT). According to above assertion, one should be able to appreciate and quantify properties of molecular orbitals using density-related quantities from the perspective of DFRT.

Is this last statement really valid? How accurate is it, if so? To provide an answer to such questions was the main purpose of this work. To that end, we made use of five conjugate molecular chains, such as trans-ethylene, benzene, naphthalene, di-thiophene, and phenanthrene chains, with from one to ten repeating units, n = 1–10, and calculated their frontier orbital (HOMO, highest occupied molecular orbital, and LUMO, lowest unoccupied molecular orbital) energies as well as the HOMO/LUMO gap. The properties and changing patterns of these quantities were then correlated with the quantities from the IT approach from DFRT [8], such as Shannon entropy [43], Fisher information [44], Ghosh-Berkowitz-Parr entropy [45], Onicescu information energy [46], Rényi entropy [47], etc. As will be revealed by the results from this work, we find that the answer to the above questions is definitely yes. We witness strong linear correlations between the properties from the frontier orbital method and quantities from the IT approach. We confirm this favorable answer with numerical results for these systems at both the whole molecule level and the atoms-in-molecules (AIM) level. What we have accomplished in this work is the establishment of a bridge between two different approaches, wave-function-based theory (frontier orbital theory) and density-based theory (DFRT), to comprehend and appreciate the same properties of the electronic structure for molecular systems from different perspectives.

This work is dedicated to Prof. Henry Chermette [48], who, among his many contributions, published the first ever review on conceptual DFT as early as 1999.

Information-theoretic approach in DFRT

Central quantities in the IT approach are Shannon entropy [43], Fisher information [44], Ghosh-Berkowitz-Parr (GBP) [45] entropy and Onicescu information energy [46], whose definitions are as follows: Shannon entropy quantifies the uncertainty involved in predicting the value of a distribution function like the electron density, which reads

$$ {S}_S=-\int \rho \left(\mathbf{r}\right) \ln\;\rho \left(\mathbf{r}\right)d\mathbf{r}=\int {s}_S\left(\mathbf{r}\right)d\mathbf{r}, $$
(1)

where s S(r) is the Shannon entropy density and ρ(r) is the total electron density, satisfying the following condition in relation to the total number of electrons, N, of a molecular system,

$$ \int \rho \left(\mathbf{r}\right)d\mathbf{r}=N. $$
(2)

Shannon entropy measures the spatial delocalization of the electronic density. Fisher information is another widely used concept in the IT approach, and is a gauge of the sharpness or concentration of the electron density distribution. Shannon entropy is defined as follows:

$$ {I}_F\equiv \int {I}_F\left(\mathbf{r}\right)d\mathbf{r}=\int \frac{{\left|\nabla \rho \left(\mathbf{r}\right)\right|}^2}{\rho \left(\mathbf{r}\right)}d\mathbf{r}, $$
(3)

where I F(r) is the Fisher information density and ∇ρ(r) is the density gradient. This quantity is closely related to the Weizsäcker kinetic energy [14], which differs from IF by a factor of only one-eighth. The Weizsäcker kinetic energy, which has been employed by one of us to quantify the steric effect [15]—a concept widely used in chemistry—and has been applied to many molecular systems to explain and reinterpret many different phenomena [15–29]. Also, earlier, we proved that there is an equivalent expression for the Fisher information in terms of the Laplacian of the electron density ∇2ρ [49]

$$ I{\prime}_F\equiv \int I{\prime}_F\left(\mathbf{r}\right)d\mathbf{r}=-\int {\nabla}^2\rho \left(\mathbf{r}\right)\kern0.5em \ln \rho \left(\mathbf{r}\right)d\mathbf{r}. $$
(4)

Equations (3) and (4) are equal in the sense that they can be derived by partial integration from one to the other, and the two integrals share the same value. As has been shown earlier, the local behavior of the two integrals, I F(r) and I’F(r), are markedly different. More importantly, for atomic and molecular systems, we proved that the following relationship is rigorous, [49]

$$ {S}_S=\int {s}_S\left(\mathbf{r}\right)d\mathbf{r}=-N+\frac{1}{4\pi}\iint \frac{I_F\left(\mathbf{r}^{\prime}\right)-I{\prime}_F\left(\mathbf{r}^{\prime}\right)}{\left|\mathbf{r}-\mathbf{r}^{\prime}\right|}d\mathbf{r}d\mathbf{r}^{\prime } $$
(5)

The validity of this relationship has been verified and confirmed numerically [49].

The third quantity is the Ghosh-Berkowitz-Parr (GBP) entropy [46],

$$ {S}_{GBP}=\int \frac{3}{2}k\rho \left(\boldsymbol{r}\right)\left[c+ \ln \frac{t\left(\boldsymbol{r};\rho \right)}{t_{TF}\left(\boldsymbol{r};\rho \right)}\right]d\boldsymbol{r} $$
(6)

where t(r,ρ) is the kinetic energy density, which is related to the total kinetic energy T S via \( \int t\left(\boldsymbol{r};\rho \right)d\boldsymbol{r}={T}_{\mathrm{S}} \), and \( {t}_{TF}\left(\mathbf{r};\rho \right)\; is \) the Thomas-Fermi kinetic energy density, \( {t}_{TF}\left(\boldsymbol{r};\rho \right)={c}_K{\rho}^{5/3}\left(\boldsymbol{r}\right) \), with k as the Boltzmann constant (set as unity for convenience in this work), \( c=\frac{5}{3}+ \ln \frac{4\pi {c}_K}{3} \), and \( {c}_K=\frac{3}{10}{\left(3{\pi}^2\right)}^{2/3} \). The GBP entropy originates from the effort to transcribe the ground-state DFT into a local thermodynamics through the phase-space distribution function f(r,p), which is a function of both the electron position r and momentum p as its two basic variables. The conditions of such a recast of DFT into thermodynamics are that the phase-space distribution function is associated with the ground state electron density ρ(r) and kinetic energy density \( t\left(\mathbf{r};\uprho \right) \) through the following relationships, \( \rho \left(\boldsymbol{r}\right)=\int f\left(\boldsymbol{r},\boldsymbol{p}\right)d\boldsymbol{p} \) and \( t\left(\boldsymbol{r};\uprho \right)=\frac{1}{2}\int f\left(\boldsymbol{r},\boldsymbol{p}\right){p}^2d\boldsymbol{p} \), with the specific form of the local kinetic energy \( t\left(\boldsymbol{r};\uprho \right)=\sum_I\frac{1}{8}\frac{\nabla {\rho}_I\bullet \nabla {\rho}_I}{\rho_I}-\frac{1}{8}{\nabla}^2\rho \). This GBP entropy has been found to be good descriptors in describing chemical bond formation and it is closely related to other quantities in the information-theoretic approach [35].

Another quantity in the IT approach is the Onicescu information energy of order n [46]:

$$ {E}_n=\frac{1}{n-1}{\int \rho \left(\mathbf{r}\right)}^nd\mathbf{r} $$
(7)

Onicescu introduced this quantity in an attempt to define a finer measure of dispersion distribution than that of Shannon entropy in information theory. This quantity is closely related to two other quantities in information theory, Rényi entropy [47]

$$ {R}_n=\frac{1}{1-n} \ln \left[{\int \rho \left(\mathbf{r}\right)}^nd\mathbf{r}\right], $$
(8)

and Tsallis entropy [48]

$$ {T}_n=\frac{1}{n-1}\left[1-{\int \rho \left(\mathbf{r}\right)}^nd\mathbf{r}\right], $$
(9)

which were also recently introduced into DFRT by us [38].

Closely related to above quantities are the relative entropies, which are non-symmetric measures of the entropy difference between two probability distribution functions. Examples include the relative Shannon entropy, also called information gain, Kullback–Leibler divergence, or information divergence, defined by [51]

$$ {S}_r=\int \rho \left(\mathbf{r}\right) \ln\;\frac{\rho \left(\mathbf{r}\right)}{\rho_0\left(\mathbf{r}\right)}d\mathbf{r} $$
(10)

and the relative Rényi entropy of order n,

$$ {R}_n^r=\frac{1}{n-1} \ln \left[\int \frac{\rho^n\left(\mathbf{r}\right)}{\rho_0^{n-1}\left(\mathbf{r}\right)}d\mathbf{r}\right] $$
(11)

where ρ 0(r) is the reference state density satisfying the same normalization condition as ρ(r). This reference density can be from the same molecule with different conformation or from the reactant of a chemical reaction when the transition state is investigated.

Equations (1) to (11) as the main result of the IT approach in DFRT employ the electron density ρ(r) as the probability distribution function. There is another distribution function in DFRT, the shape function σ(r), which is related to the electron density ρ(r) and the total number of electrons N through the following relationship,

$$ r(r) = Ns(r) $$
(12)

with the normalization condition \( \int \upsigma \left(\boldsymbol{r}\right)d\boldsymbol{r}=1 \). With σ(r), Eqs. (1) to (11) can be rewritten. We call the set of quantities using the shape function as the shape function representation in DFRT [8]. Also, since ρ(r) and σ(r) are correlated through Eq. (12), it is possible to derive explicit relationships of IT quantities between these two representations. For example, one has [8]

$$ {S}_{\sigma }=\frac{S_S}{N}+\kern0.62em \ln\;N $$
(13)
$$ {I}_F=N{I}_{\sigma } $$
(14)
$$ {E}_n={N}^n\;{E}_n^{\sigma }, $$
(15)

and

$$ {R}_n\kern0.5em -\kern0.5em {R}_n^{\sigma }=\frac{n}{1-n} \ln N $$
(16)

where Sσ, Iσ, En σ , and Rn σ are counterparts of SS, IF, En and Rn in the shape function representation defined through Eqs. (1), (3), (7), and (8), respectively.

An important aspect of the IT approach is to reevaluate the above quantities from the perspective of atoms in molecules (AIM). To consider atomic contributions of an IT quantity in a molecular system, we decided to analyze three approaches to perform atoms-in-molecules’ partitions. They are Becke’s fuzzy atom approach [41], Bader’s zero-flux AIM approach [40], and Hirshfeld’s stockholder approach [42]. The total electron population N of the system is the summation of electron density in each atomic contribution, N A,

$$ N=\sum_A{N}_A=\sum_A\underset{\varOmega_A}{\int }{\rho}_A\left(\mathbf{r}\right)d\mathbf{r} $$
(16)

and the quantities in Eqs. (1), (3), (7), and (10) can be rewritten as [8]

$$ {S}_S=-\sum_A\underset{\varOmega_A}{\int }{\rho}_A\left(\mathbf{r}\right) \ln\;{\rho}_A\left(\mathbf{r}\right)d\mathbf{r} $$
(17)
$$ {I}_F=\sum_A\underset{\varOmega_A}{\int}\frac{{\left|\nabla {\rho}_A\left(\mathbf{r}\right)\right|}^2}{\rho_A\left(\mathbf{r}\right)}d\mathbf{r} $$
(18)
$$ {E}_n=\frac{1}{n-1}\sum_A\underset{\varOmega_A}{\int }{\rho}_A^n\left(\mathbf{r}\right)d\mathbf{r} $$
(19)

and

$$ {S}_r=\sum_A\underset{\varOmega_A}{\int }{\rho}_A\left(\mathbf{r}\right)\frac{\rho_A\left(\mathbf{r}\right)}{\rho_A^0\left(\mathbf{r}\right)}d\mathbf{r}. $$
(20)

We should keep in mind that the AIM IT magnitudes calculated in Eqs. 17–20 are not, in general, equal to their previously defined counterparts. They will have the same numerical values for non-overlapping atoms in molecules (i.e., Bader atoms), but this will not be true for overlapping atomic densities (i.e., Hirshfeld atoms).

Three principles have been established in the IT approach in DFRT [8]. The first is the principle of extreme physical information, proposed by Nagy [52], who showed that the “physical information” K of a system should be extreme,

$$ K = {I}_F\hbox{--}\ J = extreme $$
(21)

where IF is the Fisher information, J is the set of constraints that are to be imposed, and K is the difference between IF and J, called the “physical information”. According to the literature [50], these constraints are three-fold. The first constraint is that the total wave function of the system is antisymmetric, which generates the Pauli potential υ P (r). Secondly, the total density of the noninteracting system should be the same as that of the interacting system. Like the Kohn-Sham equation, this constraints yields the Kohn-Sham potential υ KS (r). Lastly, the total electron density is normalized to N, Eq. (2), which results in a Lagrange multiplier μ, the chemical potential of the system. Minimizing the Fisher information subject to the above three constraints should give us the Euler equation in the orbital-free DFT [1, 53–55],

$$ \left(-\frac{1}{2}{\nabla}^2+{\upsilon}_P\left(\mathbf{r}\right)+{\upsilon}_{KS}\left(\mathbf{r}\right)\right){\rho}^{1/2}\left(\mathbf{r}\right)=\mu {\rho}^{1/2}\left(\mathbf{r}\right). $$
(22)

The second principle was pioneered by Nalewajski and Parr in 2000 [56]. They employed the AIM representation of the relative Shannon entropy, Eq. (20), and minimized it subject to the constraint that atomic densities are always normalized to the total electron N [56–59],

$$ {\sum}_A\int {\rho}_{A\ }\mathrm{d}\boldsymbol{r}={\sum}_A\int {\rho}_A^0\ \mathrm{d}\boldsymbol{r}=N. $$
(23)

What they obtained is the following,

$$ {\rho}_A=\frac{\rho_A^0}{\sum_A{\rho}_A^0}\rho, $$
(24)

which is the well-known “stockholder partition” of the electron density for AIM first proposed by Hirshfeld [42]. That is to say, if one employs the Hirshfeld scheme to partition atoms in a molecule, the information gain due to the formation of the molecule from the composing pieces will be minimal. In other words, AIM partitioned in this manner will preserve the identity (e.g., electrophilic and nucleophilic properties, etc.) of the reference state as much as possible. This nature of minimal information deficiency is the essence of the minimum information gain principle [30].

The third principle was recently established by us as the first-order approximation of the information gain, Eq. (20) [30]. Since AIM tend to keep their identity as much as possible, indicating that ρA and \( {\rho}_A^0 \) should be similar, and the difference between the two densities should be simulated by a perturbation expansion using the Taylor series. We can define a new variable, x = (\( {\rho}_A-{\rho}_A^0\Big)/{\rho}_A \) so the information gain in Eq. (20) becomes

$$ {I}_G={\sum}_A\int {\rho}_A\ \ln \frac{1}{1-x}d\mathrm{r} $$
(25)

Since x is expected to be small, using \( \ln \frac{1}{1-x}\approx x \) as the first-order approximation, we have [30]

$$ {I}_G\approx {\sum}_A\int \left({\rho}_A - {\rho}_A^0\right)d\mathrm{r}=-{\sum}_A{q}_A $$
(26)

where qA is the Hirshfeld charge on atom (or Group) A. This result shows that, under the first-order approximation, the information gain simply gives rise to the Hirshfeld charge distribution. Meanwhile, since \( {\rho}_A \) and \( {\rho}_A^0 \) satisfy the same normalization condition, Eq. (23), the total information gain in Eq. (26) must vanish,

$$ {I}_G\approx -{\sum}_A{q}_A\equiv 0. $$
(27)

suggesting that under the first-order approximation, the information before and after a system is formed should be conserved. We call this result the information conservation principle [8, 30].

Employing the information gain and Hirshfeld charge from above formulations, we successfully correlated them to electrophilicity, nucleophilicity, and regioselectivity [30, 31]. We also applied these ideas to a number of well-studied organic reactions [34–38]. In particular, we provided a completely novel understanding about the origin and nature of the ortho/para/meta group directing phenomena for electrophilic aromatic substitution reactions [32, 33]. In addition, our recent efforts have shown that these quantities from the IT approach are able to adequately accurately describe the total electronic energy and its components for both atoms and molecules [39]. Instead of looking for long-elusive formulas to approximate the universal energy density functional and its components such as the exchange-correlation energy density functional, we proposed to simulate them alternatively using a set of simple density functionals from the IT approach [39].

In this work, continuing our previous efforts to evaluate electronic properties of molecular systems with the IT quantities, we examined their feasibility and applicability to quantify frontier orbital energies and the HOMO/LUMO gap, which are often believed to be unique to WFT. Employing five polymeric systems as illustrative examples, some of which were found responsible for the visible luminescence from low dimensional carbon materials [60], as will be shown below, we observed strong correlations between these properties and IT quantities, providing favorable answers to the questions defined above.

Computational details

The main purpose of this work was to examine whether or not frontier orbital (HOMO and LUMO) energies and the HOMO/LUMO gap can be quantitatively described by quantities from the IT approach. To that end, as illustrative examples, we made use of the following five conjugate molecular chains: trans-ethylene, benzene, naphthalene, di-thiophene, and phenanthrene chains, with from one to up to ten repeating units, i.e., n = 1–10, as shown in Scheme 1. We noted that the quality of the frontier orbitals and the magnitude of the HOMO/LUMO gap were impacted immensely by the quality of the functionals and basis sets. We are also aware of the issues related to approximate functionals on these matters, but these are not what we are concerned in this work. Again, the main purpose of this work was to find connections between quantities in the WFT and the quantities in DFT.

Scheme 1
scheme 1

Repeating units of five conjugate systems with n = 1–10 and terminated by hydrogen atoms. (1) Trans-ethylene chain; (2) benzene chain; (3) naphthalene chain; (4) di-thiophene chain; and (5) phenanthrene chain

Full size image

All electronic wave functions were obtained from the Gaussian 09 package, version D01 [61]. For all atoms and molecules investigated in this work, the B3LYP hybrid density functional was employed [62, 63]. For the choice of basis sets, the standard Pople’s 6-311G(d,p) basis set was used [64]. A total of 50 molecular systems was investigated in this work. For each conjugated system chosen, its monomer, dimer, trimer, …, and up to 10 repeating units were examined. Both molecular and AIM values of the Shannon entropy, Fisher information, GBP entropy, and Onicescu information energy of orders 2 and 3 were calculated by the Multiwfn 3.3 package [65], whose reliability and applicability have extensively been verified previously. To consider atomic contributions at the AIM level, three schemes to perform the atomic partition are possible: Becke’s fuzzy atom approach, Bader’s zero-flux AIM criterion, and Hirshfeld’s stockholder approach. As demonstrated earlier by us, these three approaches yield similar results [36]. In this work, we chose the Hirshfeld’s stockholder approach to partition atoms in molecules. To consider atomic contributions at the AIM level and their correlations with quantities like HOMO, LUMO and HOMO/LUMP gap, we made use of the average of the IT quantities on carbon atoms for each of the systems for the purpose. The IT quantities in the shape function representation can be obtained using the relationships in Eqs. (13) to (15). All molecules were fully optimized. Tight self-consistent field convergence criterion and ultrafine integration grids were employed. Checkpoint files obtained from these Gaussian calculations were used as the input file to obtain numerical values for the IT quantities. It is well known that the energy of the LUMO orbital can be modified dramatically when diffuse functions are used in the basis set. We anticipate that the IT quantities would change accordingly. That is to say, we expect that, though both HOMO/LUMO energies and IT quantities changes with respect to the choice of the basis set, the correlation between the two sets of quantities will be similar.

Results and discussion

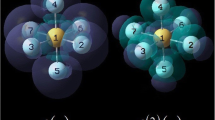
As an example, Fig. 1 shows the optimized structure of the five species studied in this work, each with four repeating units. In most cases, the molecules are in the same plane, highlighting one of the key characteristics of the conjugate system. For the benzene chain (Molecule 2), however, an average dihedral angle of about 40° is seen between benzene rings, indicating that these benzene rings are not in perfect conjugation mode with each other.

Fig. 1
figure 1

Optimized structures of five exemplary systems in this study, each with four repeating units

Full size image

Table 1 lists the computed frontier orbital energies and HOMO/LUMO gap for the species in Scheme 1 with from one to up to ten repeating units. The total number of electrons in each of the systems is also given. As can be seen from Table 1, as the number of repeating units increases, the HOMO energy also increases but the LUMO level decreases, leading to an overall decrease in the HOMO/LUMO gap. This trend is true for all five species studied in this work. We anticipate that this will be the case for all polymeric conjugate systems as well, as reported elsewhere by one of the present authors and coworkers [66]. The reason behind this phenomenon is that, as a conjugate chain becomes longer, it requires more energy, and thus it is more difficult for the HOMO electrons to spread across the entire molecule but easier for them to excite to the LUMO level. Figure 2 displays the simple, but fairly strong, linear correlation of HOMO energy and HOMO/LUMP gap values with the size of the polymeric systems, i.e., the reciprocal of the total number N of electrons in a molecule. As can be seen, the correlation coefficient of HOMO/N vs. 1/N and GAP/N vs. 1/N is 0.988 and 0.948, respectively, suggesting that, as the polymer chain becomes longer, the HOMO energy increases and the gap decreases [66].

Table 1 Numerical results of highest occupied molecular orbital/lowest unoccupied molecular orbital (HOMO/LUMO) energies and their gap values for the five conjugate systems from Scheme 1, with from one to up to ten repeating units, n = 1–10. Units in eV
Full size table
Fig. 2
figure 2

Strong linear correlations between highest occupied molecular orbital (HOMO) and HOMO/lowest unoccupied molecular orbital (LUMO) gap values with 1/N with N as the total number of electrons in a polymeric system for all five systems put together

Full size image

Table 2 shows the calculated IT quantities for Molecule 1 in Scheme 1 with one to up to ten repeating units. These are numerical values of these quantities for the entire molecules. The IT quantities included are Shannon entropy SS and its shape-function counterpart Sσ, Fisher information IF and its shape-function counterpart Iσ, GBP entropy SGBP, information gain IG, Rényi entropy of order 2 R2, its shape-function counterpart R2 σ, and relative Rényi entropy R2 r. Also shown in the table are the total number of electrons of each of the species, and correlation coefficients of these IT quantities with both HOMO/N and gap/N values. It can be readily seen from the table that only Iσ and R2 σ perform better than others, yielding R2 larger than 0.97 in each case.

Table 2 An illustrative example of information-theoretic (IT) quantities using Molecule 1 in Scheme 1 as an example at the molecular level. Also shown are their correlation coefficients with HOMO/N and GAP/N quantities, with N the total number of electrons in each of the systems. Values in atomic units
Full size table

At the AIM level, using the same molecular system as an example, we tabulate the average numerical value of the above IT quantities on the carbon atoms using Hirshfeld’s share-holder partition scheme in Table 3. Also shown in the table is the average Hirshfeld charge on the carbon atom in each system, the correlation coefficient of these IT quantities with HOMO/Nc, and GAP/Nc values, with Nc representing the average total number of electron populations on the carbon atoms in each of the systems, and n as the number of repeating units. Compared to the results at the molecular level (Table 2), it becomes apparent that much better R2 results are obtained at the AIM level, with R2 larger than 0.98 for all the IT quantities. In particular, we find that Iσ and R2 σ out-perform others, yielding R2 larger than 0.99 in both cases. In addition, the Hirshfeld charge is also a reliable descriptor of HOMO/Nc and GAP/Nc values.

Table 3 An illustrative example of IT quantities on the carbon atoms using Molecule 1 in Scheme 1 as an example at the atoms-in-molecules (AIM) level using Hirshfeld’s share-holder partition scheme. Also shown are their correlation coefficients with HOMO/Nc, and GAP/Nc quantities, with Nc representing the average of the total number of electron populations on the carbon atoms in each of the systems, and n as the number of repeating units. Values in atomic units
Full size table

Table 4 summarizes all the correlation coefficient R2 of HOMO/N and GAP/N values for all five species in Scheme 1 with three representative IT quantities, Sσ, SGBP, and R2 σ, at both whole molecular and AIM levels. Note that, at the entire molecule level, the two quantities are HOMO/N and GAP/N with N as the total number of electrons of the molecule, whereas at the AIM level the two quantities are HOMO/Nc and GAP/Nc with NC as the average total electron population on the carbon atom. As observed for Molecule 1 in Tables 2 and 3, again, at the molecular level, the overall correlation of IT quantities with HOMO and HOMO/LUMO gap is not as strong as at the AIM level.

Table 4 Correlation coefficients R2 of HOMO energy and HOMO/LUMO gap with quantities from density functional reactivity theory (DFRT) at both molecular and AIM levels
Full size table

So far, we have considered only the correlation of frontier orbital properties, HOMO and HOMO/LUMO gap, with IT quantities for each individual molecular system. Is it possible to put all the data points together from all five species and examine their overall behavior at both molecular and AIM level? Recall that Fig. 2 displayed this possibility with a simple parameter, 1/N, but the overall correlation was not as strong as one might anticipate. Plus, it does not involve IT quantities. In the spirit of a recent work [39], where we proposed to evaluate electronic properties of a Coulombic system such as the total electronic energy and its components like the exchange-correlation energy with the IT quantities discussed above, we make use of following four quantities and fit them with each of the frontier orbital properties. These four quantities are Shannon entropy, Fisher information, GBP entropy, and Rényi entropy in the electron density representation. Our results are shown in Fig. 3, from which we can see that the correlation between the calculated frontier orbital properties and the fitted results with these four IT quantities are markedly stronger, with R2 better than 0.99 in both cases. Similar results were obtained with these same quantities in the shape-function representation. These results demonstrate that one is able to evaluate frontier orbital properties much more accurately with a few IT quantities.

Fig. 3
figure 3

Least square fitting of HOMO and HOMO/LUMO gap values with four IT quantities, Shannon entropy, Fisher information, Ghosh-Berkowitz-Parr (GBP) entropy, and Rényi entropy with all five systems put together

Full size image

At the AIM level, as shown in Tables 3 and 4, it is not surprising that the results are better than at the whole molecule level. Figure 4 shows some of the results in this category. When all data points for five systems are put together, we still see markedly strong correlation between the frontier orbital properties (HOMO and HOMO/LUMO gap) and IT quantities. Better results are possible if two or more IT quantities are fitted together to simulate frontier orbital properties (results not shown).

Fig. 4
figure 4

Strong linear correlations obtained at the AIM level between frontier orbital properties and IT quantities with all data points from five polymeric systems put together

Full size image

Put together, the results of this work clearly demonstrate that one is able to accurately evaluate frontier orbital properties such as the HOMO energy and HOMO/LUMO gap with IT quantities such as Shannon entropy, Fisher information, GBP entropy, Rényi entropy, Onicescu information energy, etc. This work is consistent with what we have recently proposed in our previous work [39], where we showed that these same IT quantities can be employed to evaluate the electronic properties of a Coulombic system such as the total electronic energy as well as its components like the exchange-correlation energy. Where this work differs from our previous study is in the fact that, as one of the main products in WFT, orbitals are often believed to be unique to that theory. What we have accomplished in this work is not only to present a convincing piece of evidence that orbital properties can be accurately simulated and appreciated by IT quantities, where only the electron density and its associated quantities are involved, but also to establish a bridge between the two vastly different approaches of wave-function-based theory (frontier orbital theory) and density-based theory (DFRT), to comprehend and entertain the same properties of the electronic structure for molecular systems from different perspectives. WFT and DFT share the same origin, deal with the same objective, yet use distinct methodologies and different vocabularies in their language of understanding and appreciating molecular structure and reactivity properties.

Conclusions

As we continue to look into the possibility of employing IT quantities to evaluate and quantify properties related to molecular structure and chemical reactivity, our current work presents numerical results from a different perspective. Using IT quantities such as Shannon entropy, Fisher information, GBP entropy, Onicescu information energy, Rényi entropy, etc., we evaluate and then correlate these quantities with properties such as frontier orbital levels and the HOMO/LUMO gap, which are often believed to be unique to wave function theory. With five polymeric systems as illustrative examples, we have unambiguously demonstrated that these orbital-related properties can be simulated accurately by IT quantities. The wave-function-based theory like molecular orbital theory and density-based theory such as DFRT are complementary to each other, both trying to comprehend and appreciate the same properties of the electronic structure for molecular systems from different perspectives with their own language.