Skip to main content
SpringerLink
Log in

Meta-material beams with magnetostrictive coatings: vibrational characteristics

  • Original Paper
  • Published:
Acta Mechanica Aims and scope Submit manuscript

Abstract

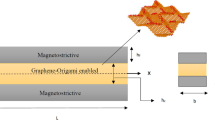
The main objective of this work is to examine the vibrational characteristics of a nanobeam exhibiting auxetic activity, achieved by the incorporation of a magnetostrictive material called Terfenol-D. The nanobeam is postulated to include three distinct layers, whereby the central layer is comprised of a magnetostrictive substance, while the outside layers are formed of auxetic material. On the other hand, the use of higher-order parabolic shear deformation beam theory is utilized to obtain the kinematic relations. Moreover, Eringen’s nonlocal theory is used to include the impact of small-scale phenomena. The governing equations are derived by the application of Hamilton’s principle and then solved using analytical techniques. This work presents a thorough analysis and elucidation of the influence of several parameters, such as auxetic inclination angle, auxetic rib length, and feedback gain, on the investigated system. Based on current research, evidence suggests that adding auxetic facesheets to magnetostrictive beam results in decreasing dimensionless natural frequency. In order to establish the accuracy and dependability of the present study, a comparison examination has been undertaken to juxtapose our results with the existing body of scholarly literature. The results obtained from the present study have the potential to provide a valuable contribution to the advancement and improved understanding of nano-systems, namely nano-sensors and nano-actuators. Furthermore, the conclusions acquired from this study might potentially serve as a fundamental framework for future research.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. Evans, K.E., et al.: Molecular network design. Nature 353(6340), 124–124 (1991)

    Google Scholar 

  2. Novak, N., et al.: Compression and shear behaviour of graded chiral auxetic structures. Mech. Mater. 148, 103524 (2020)

    Google Scholar 

  3. Hou, S., et al.: How does negative Poisson’s ratio of foam filler affect crashworthiness? Mater. Des. 82, 247–259 (2015)

    Google Scholar 

  4. Eghbali, P., Younesian, D., Farhangdoust, S.: Enhancement of the low-frequency acoustic energy harvesting with auxetic resonators. Appl. Energy 270, 115217 (2020)

    Google Scholar 

  5. Amin, F., et al.: Auxetic coronary stent endoprosthesis: fabrication and structural analysis. J. Appl. Biomater. Funct. Mater. 13(2), 127–135 (2015)

    Google Scholar 

  6. Dirrenberger, J., Forest, S., Jeulin, D.: Effective elastic properties of auxetic microstructures: anisotropy and structural applications. Int. J. Mech. Mater. Des. 9, 21–33 (2013)

    Google Scholar 

  7. Steed, A., et al.: A mechatronic shape display based on auxetic materials. Nat. Commun. 12(1), 4758 (2021)

    Google Scholar 

  8. Wang, Z., Zulifqar, A., Hu, H.: Auxetic composites in aerospace engineering. In: Advanced Composite Materials for Aerospace Engineering, pp. 213–240. Elsevier (2016)

    Google Scholar 

  9. Zhao, S., et al.: A functionally graded auxetic metamaterial beam with tunable nonlinear free vibration characteristics via graphene origami. Thin-Walled Struct. 181, 109997 (2022)

    Google Scholar 

  10. Al Mukahal, F., Sobhy, M.: Wave propagation and free vibration of FG graphene platelets sandwich curved beam with auxetic core resting on viscoelastic foundation via DQM. Arch. Civ. Mech. Eng. 22, 1–21 (2022)

    Google Scholar 

  11. Zhao, S., et al.: Vibrational characteristics of functionally graded graphene origami-enabled auxetic metamaterial beams based on machine learning assisted models. Aerosp. Sci. Technol. 130, 107906 (2022)

    Google Scholar 

  12. Murari, B., et al.: Vibrational characteristics of functionally graded graphene origami-enabled auxetic metamaterial beams with variable thickness in fluid. Eng. Struct. 277, 115440 (2023)

    Google Scholar 

  13. Arefi, M., et al.: Free vibrations of functionally graded polymer composite nanoplates reinforced with graphene nanoplatelets. Aerosp. Sci. Technol. 81, 108–117 (2018)

    Google Scholar 

  14. Zargaripoor, A., et al.: Free vibration analysis of nanoplates made of functionally graded materials based on nonlocal elasticity theory using finite element method. J. Comput. Appl. Mech. 49(1), 86–101 (2018)

    Google Scholar 

  15. Phung-Van, P., et al.: An isogeometric approach of static and free vibration analyses for porous FG nanoplates. Eur. J. Mech.-A/Solids 78, 103851 (2019)

    MathSciNet  Google Scholar 

  16. Sobhy, M., Zenkour, A.M.: Porosity and inhomogeneity effects on the buckling and vibration of double-FGM nanoplates via a quasi-3D refined theory. Compos. Struct. 220, 289–303 (2019)

    Google Scholar 

  17. Hoa, L.K., et al.: Bending and free vibration analyses of functionally graded material nanoplates via a novel nonlocal single variable shear deformation plate theory. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 235(18), 3641–3653 (2021)

    Google Scholar 

  18. Singh, P.P., Azam, M.S.: Free vibration and buckling analysis of elastically supported transversely inhomogeneous functionally graded nanoplate in thermal environment using Rayleigh-Ritz method. J. Vib. Control 27(23–24), 2835–2847 (2021)

    MathSciNet  Google Scholar 

  19. Daikh, A.A., et al.: On vibration of functionally graded sandwich nanoplates in the thermal environment. J. Sandwich Struct. Mater. 23(6), 2217–2244 (2021)

    Google Scholar 

  20. Bouafia, H., et al.: Natural frequencies of FGM nanoplates embedded in an elastic medium. Adv. Nano Res. 11(3), 239–249 (2021)

    Google Scholar 

  21. Pourabdy, M., et al.: Analysis of axisymmetric vibration of functionally-graded circular nano-plate based on the integral form of the strain gradient model. J. Appl. Comput. Mech. 7(4), 2196–2220 (2021)

    Google Scholar 

  22. Pham, Q.-H., et al.: A nonlocal quasi-3D theory for thermal free vibration analysis of functionally graded material nanoplates resting on elastic foundation. Case Stud. Therm. Eng. 26, 101170 (2021)

    Google Scholar 

  23. Thang, P.T., Tran, P., Nguyen-Thoi, T.: Applying nonlocal strain gradient theory to size-dependent analysis of functionally graded carbon nanotube-reinforced composite nanoplates. Appl. Math. Model. 93, 775–791 (2021)

    MathSciNet  Google Scholar 

  24. Van Vinh, P.: Nonlocal free vibration characteristics of power-law and sigmoid functionally graded nanoplates considering variable nonlocal parameter. Physica E 135, 114951 (2022)

    Google Scholar 

  25. Sofiyev, A.: Review of research on the vibration and buckling of the FGM conical shells. Compos. Struct. 211, 301–317 (2019)

    Google Scholar 

  26. Bagheri, H., et al.: Free vibration of joined cylindrical–hemispherical FGM shells. Arch. Appl. Mech. 90, 2185–2199 (2020)

    Google Scholar 

  27. Shahmohammadi, M.A., Azhari, M., Saadatpour, M.M.: Free vibration analysis of sandwich FGM shells using isogeometric B-spline finite strip method. Steel Compos. Struct. 34(3), 361–376 (2020)

    Google Scholar 

  28. Liu, Y., Qin, Z., Chu, F.: Nonlinear forced vibrations of FGM sandwich cylindrical shells with porosities on an elastic substrate. Nonlinear Dyn. 104, 1007–1021 (2021)

    Google Scholar 

  29. Zghal, S., Dammak, F.: Vibration characteristics of plates and shells with functionally graded pores imperfections using an enhanced finite shell element. Comput. Math. Appl. 99, 52–72 (2021)

    MathSciNet  Google Scholar 

  30. Alsubaie, A.M., et al.: Porosity-dependent vibration investigation of functionally graded carbon nanotube-reinforced composite beam. Comput. Concr. 32(1), 75–85 (2023)

    Google Scholar 

  31. Zhang, Y.-W., et al.: Wave propagation of CNTRC beams resting on elastic foundation based on various higher-order beam theories. Geomech. Eng. 33(4), 381–391 (2023)

    Google Scholar 

  32. Mangalasseri, A.S., et al.: Vibration based energy harvesting performance of magnetoelectro-elastic beams reinforced with carbon nanotubes. Adv. Nano Res. 14(1), 27–43 (2023)

    Google Scholar 

  33. Huang, Y., et al.: Static stability analysis of carbon nanotube reinforced polymeric composite doubly curved micro-shell panels. Arch. Civ. Mech. Eng. 21(4), 139 (2021)

    Google Scholar 

  34. Arshid, E., et al.: Porosity-dependent vibration analysis of FG microplates embedded by polymeric nanocomposite patches considering hygrothermal effect via an innovative plate theory. Eng. Comput. 38, 1–22 (2021)

    Google Scholar 

  35. Heidari, F., et al.: On the mechanics of nanocomposites reinforced by wavy/defected/aggregated nanotubes. Steel Compos. Struct. Int. J. 38(5), 533–545 (2021)

    Google Scholar 

  36. Garg, A., et al.: Machine learning models for predicting the compressive strength of concrete containing nano silica. Comput. Concr. 30(1), 33 (2022)

    Google Scholar 

  37. Van Vinh, P., Tounsi, A.: Free vibration analysis of functionally graded doubly curved nanoshells using nonlocal first-order shear deformation theory with variable nonlocal parameters. Thin-Walled Struct. 174, 109084 (2022)

    Google Scholar 

  38. Zenkour, A.M., El-Shahrany, H.D.: Hygrothermal effect on vibration of magnetostrictive viscoelastic sandwich plates supported by Pasternak’s foundations. Thin-Walled Struct. 157, 107007 (2020)

    Google Scholar 

  39. Zenkour, A.M., El-Shahrany, H.D.: Vibration suppression of advanced plates embedded magnetostrictive layers via various theories. J. Market. Res. 9(3), 4727–4748 (2020)

    Google Scholar 

  40. Zenkour, A.M., El-Shahrany, H.D.: Hygrothermal vibration of adaptive composite magnetostrictive laminates supported by elastic substrate medium. Eur. J. Mech. A/Solids 85, 104140 (2021)

    MathSciNet  Google Scholar 

  41. Zenkour, A.M., El-Shahrany, H.D.: Quasi-3D theory for the vibration of a magnetostrictive laminated plate on elastic medium with viscoelastic core and faces. Compos. Struct. 257, 113091 (2021)

    Google Scholar 

  42. Ebrahimi, F., Ahari, M.F.: Magnetostriction-assisted active control of the multi-layered nanoplates: effect of the porous functionally graded facesheets on the system’s behavior. Eng. Comput. 39, 1–15 (2021)

    Google Scholar 

  43. Zenkour, A.M., El-Shahrany, H.D.: Hygrothermal vibration of a cross-ply composite plate with magnetostrictive layers, viscoelastic faces, and a homogeneous core. Eng. Comput. 38(Suppl 5), 4437–4456 (2022)

    Google Scholar 

  44. Tounsi, A., et al.: Influences of different boundary conditions and hygro-thermal environment on the free vibration responses of FGM sandwich plates resting on viscoelastic foundation. Int. J. Struct. Stab. Dyn. (2023). https://doi.org/10.1142/S0219455424501177

    Article  Google Scholar 

  45. Zaitoun, M.W., et al.: Influence of the visco-Pasternak foundation parameters on the buckling behavior of a sandwich functional graded ceramic–metal plate in a hygrothermal environment. Thin-Walled Struct. 170, 108549 (2022)

    Google Scholar 

  46. Mudhaffar, I.M., et al.: Impact of viscoelastic foundation on bending behavior of FG plate subjected to hygro-thermo-mechanical loads. Struct. Eng. Mech. 86(2), 167 (2023)

    Google Scholar 

  47. Mudhaffar, I.M., et al.: Hygro-thermo-mechanical bending behavior of advanced functionally graded ceramic metal plate resting on a viscoelastic foundation. In: Structures. Elsevier (2021)

    Google Scholar 

  48. Tounsi, A., et al.: Free vibration investigation of functionally graded plates with temperaturedependent properties resting on a viscoelastic foundation. Struct. Eng. Mech. 86(1), 1 (2023)

    Google Scholar 

  49. Zaitoun, M.W., et al.: An efficient computational model for vibration behavior of a functionally graded sandwich plate in a hygrothermal environment with viscoelastic foundation effects. Eng. Comput. 39(2), 1127–1141 (2023)

    Google Scholar 

  50. Tahir, S.I., et al.: The effect of three-variable viscoelastic foundation on the wave propagation in functionally graded sandwich plates via a simple quasi-3D HSDT. Steel Compos. Struct. 42(4), 501 (2022)

    Google Scholar 

  51. Hebali, H., et al.: Effect of the variable visco-Pasternak foundations on the bending and dynamic behaviors of FG plates using integral HSDT model. Arch. Appl. Mech. 83(2), 177–191 (2022)

    Google Scholar 

  52. Bouafia, K., et al.: Bending and free vibration characteristics of various compositions of FG plates on elastic foundation via quasi 3D HSDT model. Steel Compos. Struct. Int. J. 41(4), 487–503 (2021)

    Google Scholar 

  53. Tounsi, A., et al.: Thermodynamical bending analysis of P-FG sandwich plates resting on nonlinear visco-Pasternak’s elastic foundations. Steel Compos. Struct. 49(3), 307–323 (2023)

    Google Scholar 

  54. Belbachir, N., et al.: A refined quasi-3D theory for stability and dynamic investigation of cross-ply laminated composite plates on Winkler-Pasternak foundation. Struct. Eng. Mech. 85(4), 433 (2023)

    Google Scholar 

  55. Ebrahimi, F., Jafari, A.: A higher-order thermomechanical vibration analysis of temperature-dependent FGM beams with porosities. J. Eng. 2016, 9561504 (2016)

    Google Scholar 

  56. Ebrahimi, F., Sepahvand, M.: Wave propagation analysis of cylindrical sandwich shell with auxetic core utilizing first-order shear deformable theory (FSDT). Mech. Based Des. Struct. Mach. (2022). https://doi.org/10.1080/15397734.2022.2159835

    Article  Google Scholar 

  57. Ebrahimi, F., Ahari, M.F.: Dynamic analysis of meta-material plates with magnetostrictive face sheets. Int. J. Struct. Stab. Dyn. (2023). https://doi.org/10.1142/S0219455424501748

    Article  Google Scholar 

  58. Eringen, A.C., Edelen, D.: On nonlocal elasticity. Int. J. Eng. Sci. 10(3), 233–248 (1972)

    MathSciNet  Google Scholar 

  59. Ebrahimi, F., Dabbagh, A., Rabczuk, T.: On wave dispersion characteristics of magnetostrictive sandwich nanoplates in thermal environments. Eur. J. Mech. A/Solids 85, 104130 (2021)

    MathSciNet  Google Scholar 

  60. Ebrahimi, F., Mollazeinal, A., Ahari, M.F.: Nonlinear vibration analysis of smart truncated conical porous composite shells reinforced with Terfenol-D particles. Acta Mech. (2023). https://doi.org/10.1007/s00707-023-03746-5

    Article  Google Scholar 

  61. Ghorbani, K., et al.: Investigation of surface effects on the natural frequency of a functionally graded cylindrical nanoshell based on nonlocal strain gradient theory. Eur. Phys. J. Plus 135(9), 1–23 (2020)

    Google Scholar 

  62. Ahari, M.F., Ghadiri, M.: Resonator vibration of a magneto-electro-elastic nano-plate integrated with FGM layer subjected to the nano mass-Spring-damper system and a moving load. Waves Random Complex Media (2022). https://doi.org/10.1080/17455030.2022.2053233

    Article  Google Scholar 

  63. Ebrahimi, F., et al.: Hygro-thermal effects on wave dispersion responses of magnetostrictive sandwich nanoplates. Adv. Nano Res. 7(3), 157 (2019)

    Google Scholar 

  64. Ebrahimi, F., Ahari, M.F.: Mechanics of Magnetostrictive Materials and Structures. CRC Press (2023)

    Google Scholar 

  65. Rao, S.S.: Vibration of Continuous Systems. Wiley (2007)

    Google Scholar 

  66. Ebrahimi, F., Farajzadeh Ahari, M.: Dynamic analysis of sandwich magnetostrictive nanoplates with a mass-spring-damper stimulator. Int. J. Struct. Stab. Dyn. (2023). https://doi.org/10.1142/S0219455424501360

    Article  Google Scholar 

  67. Ebrahimi, F., Mollazeinal, A., FarajzadehAhari, M.: Active Vibration Control of Truncated Conical Porous Smart Composite Shells. Int. J. Struct. Stab. Dyn. (2023). https://doi.org/10.1142/S0219455424501323

    Article  Google Scholar 

  68. Ebrahimi, F., Shafiee, M.-S., Ahari, M.F.: Buckling analysis of single and double-layer annular graphene sheets in thermal environment. Eng. Comput. 39, 1–15 (2022)

    Google Scholar 

  69. Ebrahimi, F., Shafiei, M.S., Ahari, M.F.: Vibration analysis of single and multi-walled circular graphene sheets in thermal environment using GDQM. Waves Random Complex Media (2022). https://doi.org/10.1080/17455030.2022.2067370

    Article  Google Scholar 

  70. Rahimi, Y., et al.: Temperature-dependent vibrational behavior of bilayer doubly curved micro-nano liposome shell: simulation of drug delivery mechanism. J. Therm. Stress. 46(11), 1199–1226 (2023)

    Google Scholar 

  71. Mizuji, Z.K., et al.: Numerical modeling of a body vessel for dynamic study of a nano cylindrical shell carrying fluid and a moving nanoparticle. Eng. Anal. Boundary Elem. 152, 362–382 (2023)

    MathSciNet  Google Scholar 

  72. Eltaher, M., Emam, S.A., Mahmoud, F.: Free vibration analysis of functionally graded size-dependent nanobeams. Appl. Math. Comput. 218(14), 7406–7420 (2012)

    MathSciNet  Google Scholar 

  73. Rahmani, O., Pedram, O.: Analysis and modeling the size effect on vibration of functionally graded nanobeams based on nonlocal Timoshenko beam theory. Int. J. Eng. Sci. 77, 55–70 (2014)

    MathSciNet  Google Scholar 

  74. Ebrahimi, F., Ahari, M.F.: Active vibration control of the multilayered smart nanobeams: velocity feedback gain effects on the system’s behavior. Acta Mech. 235, 493–510 (2023)

    MathSciNet  Google Scholar 

Download references

Acknowledgements

The authors would like to thank the reviewers for their comments and suggestions to improve this article’s clarity.

Funding

No funding was received for conducting this study.

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Faculty of Engineering, Imam Khomeini International University, Qazvin, Iran

    Farzad Ebrahimi & Mehrdad Farajzadeh Ahari

Authors
  1. Farzad Ebrahimi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Mehrdad Farajzadeh Ahari
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Farzad Ebrahimi.

Ethics declarations

Conflict of interest

The authors declare that there is no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix 1

Appendix 1

$$ K_{11} = - A_{11} \left( {o^{2} } \right) $$
$$ K_{12} = - B_{11} \left( {o^{2} } \right) + \alpha S_{11} \left( {o^{2} } \right) $$
$$ K_{13} = \alpha S_{11} \left( {o^{3} } \right) $$
$$ K_{21} = - B_{11} \left( {o^{2} } \right) + \alpha S_{11} \left( {o^{2} } \right) $$
$$ K_{22} = - D_{11} \left( {o^{2} } \right) + 2\alpha M_{11} \left( {o^{2} } \right) - \alpha^{2} L_{11} \left( {o^{2} } \right) - A_{55} + 2\beta D_{55} - \beta^{2} M_{55} $$
$$ K_{23} = \alpha M_{11} \left( {o^{3} } \right) - \alpha^{2} L_{11} \left( {o^{3} } \right) + 2\beta D_{55} \left( o \right) - \beta^{2} M_{55} \left( o \right) - A_{55} \left( o \right) $$
$$ K_{31} = \alpha S_{11} \left( {o^{3} } \right) $$
$$ K_{32} = \alpha M_{11} \left( {o^{3} } \right) - \alpha^{2} L_{11} \left( {o^{3} } \right) + 2\beta D_{55} \left( o \right) - \beta^{2} M_{55} \left( o \right) - A_{55} \left( o \right) $$
$$ K_{33} = - \alpha^{2} L_{11} \left( {o^{4} } \right) - \beta^{2} M_{55} \left( {o^{2} } \right) + 2\beta D_{55} \left( {o^{2} } \right) - A_{55} \left( {o^{2} } \right) - K_{w} - K_{g} \left( {o^{2} } \right) - K_{w} \left( {\mu^{2} o^{2} } \right) - K_{g} \left( {\mu^{2} o^{4} } \right) $$
$$ M_{11} = I_{0} \left( {1 + \mu^{2} o^{2} } \right) $$
$$ M_{12} = - \left( {I_{1} - I_{3} \alpha^{ } + \mu^{2} I_{1} o^{2} + I_{3} \alpha^{ } \mu^{2} o^{2} } \right) $$
$$ M_{13} = - \left( { - I_{3} \alpha \left( o \right) - \mu^{2} I_{3} \alpha \left( {o^{3} } \right)} \right) $$
$$ M_{21} = - \left( {I_{1} - I_{3} \alpha^{ } + \mu^{2} I_{1} o^{2} + I_{3} \alpha^{ } \mu^{2} o^{2} } \right) $$
$$ M_{22} = - \left( {I_{2} - 2I_{4} \alpha + I_{6} \alpha^{2} + I_{2} \mu^{2} o^{2} - 2I_{4} \alpha o^{2} + I_{6} \mu^{2} \alpha^{2} o^{2} } \right) $$
$$ M_{23} = - \left( {I_{6} \alpha^{2} o - I_{4} \alpha \left( o \right) + I_{6} \alpha^{2} \mu^{2} o^{3} - I_{4} \alpha \mu^{2} o^{3} } \right) $$
$$ M_{31} = - \left( { - I_{3} \alpha \left( o \right) - \mu^{2} I_{3} \alpha \left( {o^{3} } \right)} \right) $$
$$ M_{32} = - \left( {I_{6} \alpha^{2} o - I_{4} \alpha \left( o \right) + I_{6} \alpha^{2} \mu^{2} o^{3} - I_{4} \alpha \mu^{2} o^{3} } \right) $$
$$ M_{33} = - \left( {I_{0} + I_{6} o^{2} \alpha^{2} + I_{0} \mu^{2} o^{2} + I_{6} \mu^{2} o^{4} \alpha^{2} } \right) $$
$$ A_{11} = \mathop \int \limits_{{\frac{{ - h_{{\text{c}}} }}{2}}}^{{\frac{{h_{{\text{c}}} }}{2}}} C_{11}^{c} {\text{d}}z + \mathop \int \limits_{{ - \frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}}^{{\frac{{ - h_{{\text{c}}} }}{2}}} C_{11}^{f} {\text{d}}z + \mathop \int \limits_{{\frac{{h_{{\text{c}}} }}{2}}}^{{\frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}} C_{11}^{f} {\text{d}}z $$
$$ A_{12} = \mathop \int \limits_{{\frac{{ - h_{{\text{c}}} }}{2}}}^{{\frac{{h_{{\text{c}}} }}{2}}} C_{12}^{c} {\text{d}}z + \mathop \int \limits_{{ - \frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}}^{{\frac{{ - h_{{\text{c}}} }}{2}}} C_{12}^{f} {\text{d}}z + \mathop \int \limits_{{\frac{{h_{{\text{c}}} }}{2}}}^{{\frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}} C_{12}^{f} {\text{d}}z $$
$$ A_{22} = \mathop \int \limits_{{\frac{{ - h_{{\text{c}}} }}{2}}}^{{\frac{{h_{{\text{c}}} }}{2}}} C_{22}^{c} {\text{d}}z + \mathop \int \limits_{{ - \frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}}^{{\frac{{ - h_{{\text{c}}} }}{2}}} C_{22}^{f} {\text{d}}z + \mathop \int \limits_{{\frac{{h_{{\text{c}}} }}{2}}}^{{\frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}} C_{22}^{f} {\text{d}}z $$
$$ A_{44} = \mathop \int \limits_{{\frac{{ - h_{{\text{c}}} }}{2}}}^{{\frac{{h_{{\text{c}}} }}{2}}} C_{44}^{c} {\text{d}}z + \mathop \int \limits_{{ - \frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}}^{{\frac{{ - h_{{\text{c}}} }}{2}}} C_{44}^{f} {\text{d}}z + \mathop \int \limits_{{\frac{{h_{{\text{c}}} }}{2}}}^{{\frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}} C_{44}^{f} {\text{d}}z $$
$$ A_{55} = \mathop \int \limits_{{\frac{{ - h_{{\text{c}}} }}{2}}}^{{\frac{{h_{{\text{c}}} }}{2}}} C_{55}^{c} {\text{d}}z + \mathop \int \limits_{{ - \frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}}^{{\frac{{ - h_{{\text{c}}} }}{2}}} C_{55}^{f} {\text{d}}z + \mathop \int \limits_{{\frac{{h_{{\text{c}}} }}{2}}}^{{\frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}} C_{55}^{f} {\text{d}}z $$
$$ A_{66} = \mathop \int \limits_{{\frac{{ - h_{{\text{c}}} }}{2}}}^{{\frac{{h_{{\text{c}}} }}{2}}} C_{66}^{c} {\text{d}}z + \mathop \int \limits_{{ - \frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}}^{{\frac{{ - h_{{\text{c}}} }}{2}}} C_{66}^{f} {\text{d}}z + \mathop \int \limits_{{\frac{{h_{{\text{c}}} }}{2}}}^{{\frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}} C_{66}^{f} {\text{d}}z $$
$$ B_{11} = \mathop \int \limits_{{\frac{{ - h_{{\text{c}}} }}{2}}}^{{\frac{{h_{{\text{c}}} }}{2}}} zC_{11}^{c} {\text{d}}z + \mathop \int \limits_{{ - \frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}}^{{\frac{{ - h_{{\text{c}}} }}{2}}} zC_{11}^{f} {\text{d}}z + \mathop \int \limits_{{\frac{{h_{{\text{c}}} }}{2}}}^{{\frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}} zC_{11}^{f} {\text{d}}z $$
$$ B_{12} = \mathop \int \limits_{{\frac{{ - h_{{\text{c}}} }}{2}}}^{{\frac{{h_{{\text{c}}} }}{2}}} zC_{12}^{c} {\text{d}}z + \mathop \int \limits_{{ - \frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}}^{{\frac{{ - h_{{\text{c}}} }}{2}}} zC_{12}^{f} {\text{d}}z + \mathop \int \limits_{{\frac{{h_{{\text{c}}} }}{2}}}^{{\frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}} zC_{12}^{f} {\text{d}}z $$
$$ B_{22} = \mathop \int \limits_{{\frac{{ - h_{{\text{c}}} }}{2}}}^{{\frac{{h_{{\text{c}}} }}{2}}} zC_{22}^{c} {\text{d}}z + \mathop \int \limits_{{ - \frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}}^{{\frac{{ - h_{{\text{c}}} }}{2}}} zC_{22}^{f} {\text{d}}z + \mathop \int \limits_{{\frac{{h_{{\text{c}}} }}{2}}}^{{\frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}} zC_{22}^{f} {\text{d}}z $$
$$ B_{44} = \mathop \int \limits_{{\frac{{ - h_{{\text{c}}} }}{2}}}^{{\frac{{h_{{\text{c}}} }}{2}}} zC_{44}^{c} {\text{d}}z + \mathop \int \limits_{{ - \frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}}^{{\frac{{ - h_{{\text{c}}} }}{2}}} zC_{44}^{f} {\text{d}}z + \mathop \int \limits_{{\frac{{h_{{\text{c}}} }}{2}}}^{{\frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}} zC_{44}^{f} {\text{d}}z $$
$$ B_{55} = \mathop \int \limits_{{\frac{{ - h_{{\text{c}}} }}{2}}}^{{\frac{{h_{{\text{c}}} }}{2}}} zC_{55}^{c} {\text{d}}z + \mathop \int \limits_{{ - \frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}}^{{\frac{{ - h_{{\text{c}}} }}{2}}} zC_{22}^{f} {\text{d}}z + \mathop \int \limits_{{\frac{{h_{{\text{c}}} }}{2}}}^{{\frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}} zC_{55}^{f} {\text{d}}z $$
$$ B_{66} = \mathop \int \limits_{{\frac{{ - h_{{\text{c}}} }}{2}}}^{{\frac{{h_{{\text{c}}} }}{2}}} zC_{66}^{c} {\text{d}}z + \mathop \int \limits_{{ - \frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}}^{{\frac{{ - h_{{\text{c}}} }}{2}}} zC_{66}^{f} {\text{d}}z + \mathop \int \limits_{{\frac{{h_{{\text{c}}} }}{2}}}^{{\frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}} zC_{66}^{f} {\text{d}}z $$
$$ D_{11} = \mathop \int \limits_{{\frac{{ - h_{{\text{c}}} }}{2}}}^{{\frac{{h_{{\text{c}}} }}{2}}} z^{2} C_{11}^{c} {\text{d}}z + \mathop \int \limits_{{ - \frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}}^{{\frac{{ - h_{{\text{c}}} }}{2}}} z^{2} C_{11}^{f} {\text{d}}z + \mathop \int \limits_{{\frac{{h_{{\text{c}}} }}{2}}}^{{\frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}} z^{2} C_{11}^{f} {\text{d}}z $$
$$ D_{12} = \mathop \int \limits_{{\frac{{ - h_{{\text{c}}} }}{2}}}^{{\frac{{h_{{\text{c}}} }}{2}}} z^{2} C_{12}^{c} {\text{d}}z + \mathop \int \limits_{{ - \frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}}^{{\frac{{ - h_{{\text{c}}} }}{2}}} z^{2} C_{12}^{f} {\text{d}}z + \mathop \int \limits_{{\frac{{h_{{\text{c}}} }}{2}}}^{{\frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}} z^{2} C_{12}^{f} {\text{d}}z $$
$$ D_{22} = \mathop \int \limits_{{\frac{{ - h_{{\text{c}}} }}{2}}}^{{\frac{{h_{{\text{c}}} }}{2}}} z^{2} C_{22}^{c} {\text{d}}z + \mathop \int \limits_{{ - \frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}}^{{\frac{{ - h_{{\text{c}}} }}{2}}} z^{2} C_{22}^{f} {\text{d}}z + \mathop \int \limits_{{\frac{{h_{{\text{c}}} }}{2}}}^{{\frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}} z^{2} C_{22}^{f} {\text{d}}z $$
$$ D_{44} = \mathop \int \limits_{{\frac{{ - h_{{\text{c}}} }}{2}}}^{{\frac{{h_{{\text{c}}} }}{2}}} z^{2} C_{44}^{c} {\text{d}}z + \mathop \int \limits_{{ - \frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}}^{{\frac{{ - h_{{\text{c}}} }}{2}}} z^{2} C_{44}^{f} {\text{d}}z + \mathop \int \limits_{{\frac{{h_{{\text{c}}} }}{2}}}^{{\frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}} z^{2} C_{44}^{f} {\text{d}}z $$
$$ D_{55} = \mathop \int \limits_{{\frac{{ - h_{{\text{c}}} }}{2}}}^{{\frac{{h_{{\text{c}}} }}{2}}} z^{2} C_{55}^{c} {\text{d}}z + \mathop \int \limits_{{ - \frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}}^{{\frac{{ - h_{{\text{c}}} }}{2}}} z^{2} C_{55}^{f} {\text{d}}z + \mathop \int \limits_{{\frac{{h_{{\text{c}}} }}{2}}}^{{\frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}} z^{2} C_{55}^{f} {\text{d}}z $$
$$ D_{66} = \mathop \int \limits_{{\frac{{ - h_{{\text{c}}} }}{2}}}^{{\frac{{h_{{\text{c}}} }}{2}}} z^{2} C_{66}^{c} {\text{d}}z + \mathop \int \limits_{{ - \frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}}^{{\frac{{ - h_{{\text{c}}} }}{2}}} z^{2} C_{66}^{f} {\text{d}}z + \mathop \int \limits_{{\frac{{h_{{\text{c}}} }}{2}}}^{{\frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}} z^{2} C_{66}^{f} {\text{d}}z $$
$$ S_{11} = \mathop \int \limits_{{\frac{{ - h_{{\text{c}}} }}{2}}}^{{\frac{{h_{{\text{c}}} }}{2}}} z^{3} C_{11}^{c} {\text{d}}z + \mathop \int \limits_{{ - \frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}}^{{\frac{{ - h_{{\text{c}}} }}{2}}} z^{3} C_{11}^{f} {\text{d}}z + \mathop \int \limits_{{\frac{{h_{{\text{c}}} }}{2}}}^{{\frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}} z^{3} C_{11}^{f} {\text{d}}z $$
$$ S_{12} = \mathop \int \limits_{{\frac{{ - h_{{\text{c}}} }}{2}}}^{{\frac{{h_{{\text{c}}} }}{2}}} z^{3} C_{12}^{c} {\text{d}}z + \mathop \int \limits_{{ - \frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}}^{{\frac{{ - h_{{\text{c}}} }}{2}}} z^{3} C_{12}^{f} {\text{d}}z + \mathop \int \limits_{{\frac{{h_{{\text{c}}} }}{2}}}^{{\frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}} z^{3} C_{12}^{f} {\text{d}}z $$
$$ S_{22} = \mathop \int \limits_{{\frac{{ - h_{{\text{c}}} }}{2}}}^{{\frac{{h_{{\text{c}}} }}{2}}} z^{3} C_{22}^{c} {\text{d}}z + \mathop \int \limits_{{ - \frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}}^{{\frac{{ - h_{{\text{c}}} }}{2}}} z^{3} C_{22}^{f} {\text{d}}z + \mathop \int \limits_{{\frac{{h_{{\text{c}}} }}{2}}}^{{\frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}} z^{3} C_{22}^{f} {\text{d}}z $$
$$ S_{44} = \mathop \int \limits_{{\frac{{ - h_{{\text{c}}} }}{2}}}^{{\frac{{h_{{\text{c}}} }}{2}}} z^{3} C_{44}^{c} {\text{d}}z + \mathop \int \limits_{{ - \frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}}^{{\frac{{ - h_{{\text{c}}} }}{2}}} z^{3} C_{44}^{f} {\text{d}}z + \mathop \int \limits_{{\frac{{h_{{\text{c}}} }}{2}}}^{{\frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}} z^{3} C_{44}^{f} {\text{d}}z $$
$$ S_{55} = \mathop \int \limits_{{\frac{{ - h_{{\text{c}}} }}{2}}}^{{\frac{{h_{{\text{c}}} }}{2}}} z^{3} C_{55}^{c} {\text{d}}z + \mathop \int \limits_{{ - \frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}}^{{\frac{{ - h_{{\text{c}}} }}{2}}} z^{3} C_{55}^{f} {\text{d}}z + \mathop \int \limits_{{\frac{{h_{{\text{c}}} }}{2}}}^{{\frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}} z^{3} C_{55}^{f} {\text{d}}z $$
$$ S_{66} = \mathop \int \limits_{{\frac{{ - h_{{\text{c}}} }}{2}}}^{{\frac{{h_{{\text{c}}} }}{2}}} z^{3} C_{66}^{c} {\text{d}}z + \mathop \int \limits_{{ - \frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}}^{{\frac{{ - h_{{\text{c}}} }}{2}}} z^{3} C_{66}^{f} {\text{d}}z + \mathop \int \limits_{{\frac{{h_{{\text{c}}} }}{2}}}^{{\frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}} z^{3} C_{66}^{f} {\text{d}}z $$
$$ M_{11} = \mathop \int \limits_{{\frac{{ - h_{{\text{c}}} }}{2}}}^{{\frac{{h_{{\text{c}}} }}{2}}} z^{4} C_{11}^{c} {\text{d}}z + \mathop \int \limits_{{ - \frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}}^{{\frac{{ - h_{{\text{c}}} }}{2}}} z^{4} C_{11}^{f} {\text{d}}z + \mathop \int \limits_{{\frac{{h_{{\text{c}}} }}{2}}}^{{\frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}} z^{4} C_{11}^{f} {\text{d}}z $$
$$ M_{12} = \mathop \int \limits_{{\frac{{ - h_{{\text{c}}} }}{2}}}^{{\frac{{h_{{\text{c}}} }}{2}}} z^{4} C_{12}^{c} {\text{d}}z + \mathop \int \limits_{{ - \frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}}^{{\frac{{ - h_{{\text{c}}} }}{2}}} z^{4} C_{12}^{f} {\text{d}}z + \mathop \int \limits_{{\frac{{h_{{\text{c}}} }}{2}}}^{{\frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}} z^{4} C_{12}^{f} {\text{d}}z $$
$$ M_{22} = \mathop \int \limits_{{\frac{{ - h_{{\text{c}}} }}{2}}}^{{\frac{{h_{{\text{c}}} }}{2}}} z^{4} C_{22}^{c} {\text{d}}z + \mathop \int \limits_{{ - \frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}}^{{\frac{{ - h_{{\text{c}}} }}{2}}} z^{4} C_{22}^{f} {\text{d}}z + \mathop \int \limits_{{\frac{{h_{{\text{c}}} }}{2}}}^{{\frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}} z^{4} C_{22}^{f} {\text{d}}z $$
$$ M_{44} = \mathop \int \limits_{{\frac{{ - h_{{\text{c}}} }}{2}}}^{{\frac{{h_{{\text{c}}} }}{2}}} z^{4} C_{44}^{c} {\text{d}}z + \mathop \int \limits_{{ - \frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}}^{{\frac{{ - h_{{\text{c}}} }}{2}}} z^{4} C_{44}^{f} {\text{d}}z + \mathop \int \limits_{{\frac{{h_{{\text{c}}} }}{2}}}^{{\frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}} z^{4} C_{44}^{f} {\text{d}}z $$
$$ M_{55} = \mathop \int \limits_{{\frac{{ - h_{{\text{c}}} }}{2}}}^{{\frac{{h_{{\text{c}}} }}{2}}} z^{4} C_{55}^{c} {\text{d}}z + \mathop \int \limits_{{ - \frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}}^{{\frac{{ - h_{{\text{c}}} }}{2}}} z^{4} C_{22}^{f} {\text{d}}z + \mathop \int \limits_{{\frac{{h_{{\text{c}}} }}{2}}}^{{\frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}} z^{4} C_{55}^{f} {\text{d}}z $$
$$ M_{66} = \mathop \int \limits_{{\frac{{ - h_{{\text{c}}} }}{2}}}^{{\frac{{h_{{\text{c}}} }}{2}}} z^{4} C_{66}^{c} {\text{d}}z + \mathop \int \limits_{{ - \frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}}^{{\frac{{ - h_{{\text{c}}} }}{2}}} z^{4} C_{66}^{f} {\text{d}}z + \mathop \int \limits_{{\frac{{h_{{\text{c}}} }}{2}}}^{{\frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}} z^{4} C_{66}^{f} {\text{d}}z $$
$$ L_{11} = \mathop \int \limits_{{\frac{{ - h_{{\text{c}}} }}{2}}}^{{\frac{{h_{{\text{c}}} }}{2}}} z^{6} C_{11}^{c} {\text{d}}z + \mathop \int \limits_{{ - \frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}}^{{\frac{{ - h_{{\text{c}}} }}{2}}} z^{6} C_{11}^{f} {\text{d}}z + \mathop \int \limits_{{\frac{{h_{{\text{c}}} }}{2}}}^{{\frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}} z^{6} C_{11}^{f} {\text{d}}z $$
$$ L_{12} = \mathop \int \limits_{{\frac{{ - h_{{\text{c}}} }}{2}}}^{{\frac{{h_{{\text{c}}} }}{2}}} z^{6} C_{12}^{c} {\text{d}}z + \mathop \int \limits_{{ - \frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}}^{{\frac{{ - h_{{\text{c}}} }}{2}}} z^{6} C_{12}^{f} {\text{d}}z + \mathop \int \limits_{{\frac{{h_{{\text{c}}} }}{2}}}^{{\frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}} z^{6} C_{12}^{f} {\text{d}}z $$
$$ L_{22} = \mathop \int \limits_{{\frac{{ - h_{{\text{c}}} }}{2}}}^{{\frac{{h_{{\text{c}}} }}{2}}} z^{6} C_{22}^{c} {\text{d}}z + \mathop \int \limits_{{ - \frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}}^{{\frac{{ - h_{{\text{c}}} }}{2}}} z^{6} C_{22}^{f} {\text{d}}z + \mathop \int \limits_{{\frac{{h_{{\text{c}}} }}{2}}}^{{\frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}} z^{6} C_{22}^{f} {\text{d}}z $$
$$ L_{44} = \mathop \int \limits_{{\frac{{ - h_{{\text{c}}} }}{2}}}^{{\frac{{h_{{\text{c}}} }}{2}}} z^{6} C_{44}^{c} {\text{d}}z + \mathop \int \limits_{{ - \frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}}^{{\frac{{ - h_{{\text{c}}} }}{2}}} z^{6} C_{44}^{f} {\text{d}}z + \mathop \int \limits_{{\frac{{h_{{\text{c}}} }}{2}}}^{{\frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}} z^{6} C_{44}^{f} {\text{d}}z $$
$$ L_{55} = \mathop \int \limits_{{\frac{{ - h_{{\text{c}}} }}{2}}}^{{\frac{{h_{{\text{c}}} }}{2}}} z^{6} C_{55}^{c} {\text{d}}z + \mathop \int \limits_{{ - \frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}}^{{\frac{{ - h_{{\text{c}}} }}{2}}} z^{6} C_{55}^{f} {\text{d}}z + \mathop \int \limits_{{\frac{{h_{{\text{c}}} }}{2}}}^{{\frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}} z^{6} C_{55}^{f} {\text{d}}z $$
$$ L_{66} = \mathop \int \limits_{{\frac{{ - h_{{\text{c}}} }}{2}}}^{{\frac{{h_{{\text{c}}} }}{2}}} z^{6} C_{66}^{c} {\text{d}}z + \mathop \int \limits_{{ - \frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}}^{{\frac{{ - h_{{\text{c}}} }}{2}}} z^{6} C_{66}^{f} {\text{d}}z + \mathop \int \limits_{{\frac{{h_{{\text{c}}} }}{2}}}^{{\frac{{\left( {h_{{\text{c}}} + h_{f} } \right)}}{2}}} z^{6} C_{66}^{f} {\text{d}}z $$

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ebrahimi, F., Ahari, M.F. Meta-material beams with magnetostrictive coatings: vibrational characteristics. Acta Mech 235, 2495–2512 (2024). https://doi.org/10.1007/s00707-023-03845-3

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00707-023-03845-3

Search

Navigation