An accurate and unified study on non-symmetric tensile and compressive responses of elastoplastic bars and beams until failure

Abstract

A new and unified approach is proposed toward accurately analyzing overall elastoplastic responses of axially loaded bars and finite bending beams until failure. Results are presented for various constituent materials such as metals, reinforced concretes and reinforced composites, etc. Novelties in three respects are incorporated: (a) new uniaxial stress–strain functions are first presented in explicit forms for the purpose of accurately characterizing non-symmetric tensile and compressive behaviors of axially loaded bars from hardening to softening; (b) explicit solutions to both the varying neutral axis and the flexural moment of finite bending beams are then obtained directly in terms of these two uniaxial functions; and, hence, (c) the complex bending problem of various beams until failure is in a unified manner reduced to a simple issue of fitting two uniaxial functions to tension and compression data from uniaxial testing, thus bypassing the analytical and numerical complexity of various existing approaches. Numerical examples of model predictions are provided for typical constituent materials, including aluminium, meso-scopic heterogeneous concrete and ultra-high performance fiber-reinforced concrete with reinforcing rebars. Good agreement is achieved simultaneously with all experimental data for bars and beams made of these materials.

1 Introduction

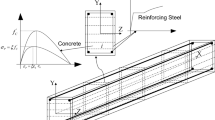
Bars and beams are used as significant structural members subject to axial loading and flexural loading in engineering structures. Various kinds of materials may serve as their constituent materials, such as metals, fiber-reinforced composites, reinforced polymers, and even biological materials, etc., and, moreover, reinforcing rebars may be introduced, such as steel bars and glass fiber-reinforced polymer bars, etc. Beside usual metal bars and metal beams, typical examples are various reinforced concrete columns and reinforced concrete beams. To ensure reliability and safety in service, it is of significance to present a complete and accurate study for full-range elastoplastic responses of such bars and beams until failure.

To accomplish the above objective, complexities in three respects should be effectively treated. Firstly, various constituent materials, such as concretes and composites etc., display much varied elastoplastic features with markedly different uniaxial tensile and compressive behaviors (cf., e.g., [1]). These effects can also be observed for metals and ceramics in the elastic, plastic, and creep ranges (cf., e.g., [2, 3] and the literature therein). In particular, such different features in tension and compression of bars are further complicated with non-symmetric hardening and softening behaviors. Secondly, non-homogeneous stresses over each cross-section of a bending beam accordingly manifest themselves with complex non-symmetric tensile and compressive features. Thirdly, strongly coupling issues are expected with finite strain effects at various stages of softening until failure.

A complete treatment of the first issue above needs to accurately represent complex non-symmetric hardening and softening effects in axially loaded bars until failure, while the second issue above is closely related to the first. In fact, non-symmetric tensile and compressive behaviors imply that the neutral axis over each cross-section of a bending beam is not fixed but constantly varying, and the tension and the compression zone demarcated by this axis are also constantly varying. As such, the varying neutral axis as a moving boundary needs to be first determined toward analyzing the stress distributions over both the tension and the compression zone. Moreover, finite strain effects further bring in coupling complexities in both kinematic and constitutive analyses.

Toward approximately treating the above complexity, various approaches have been established mainly based either on fracture mechanics or on damage mechanics. Representative results are briefly described below.

With fracture-based approaches, various models were introduced towards simulating development of macro-cracks. Reference may be made to, e.g., the crack band model [4], the two-parameter fracture model [5], the equivalent fracture model [6], the size effect model [7], the complete fracture model [8], and many others. On the other hand, various damage variables characterizing evolution of micro-defects were postulated and calculated towards simulating gradual degradation in strength, such as the energy damage mode [9], the geometric damage model [10], the stress- and strain-based damage model [11], the plastic damage model [12, 13], the multi-scale failure model [14], and so on. Such constitutive models have been used in analyzing complex responses of bars and beams. Recent results may be found in, e.g., [15,16,17,18,19,20,21,22], etc.

Usually, cumbersome numerical schemes need to be implemented in treating various complicated constitutive models with damaging and cracking effects, as shown in, e.g., [23,24,25,26]. For each given value of the flexural curvature, the neutral axis position need to be determined in repeatedly performing the sectional analysis (see, e.g., [27, 28]), in which sophisticated models with a number of ad hoc parameters are used toward simulating non-symmetric tensile and compressive behaviors at various stages of cracking, etc.

With various existing approaches, both modeling analyses and numerical procedures are carried out in an approximate sense of the infinitesimal strain analysis, irrespective of the fact that finite strain effects should be taken into account for analyzing full-range responses until failure. It appears that results with finite strain effects are confined to particular cases. Earlier, finite elastoplastic bending of plate strips was studied in [29] for the incompressible perfectly elastoplastic case and in [30] for the compressible perfectly elastoplastic case, as well as in [31] for the power-type work-hardening case. Later on, results were derived in [32] for the linear combined hardening case. Most recently, fatigue failure effects of metal beams under cyclic flexural loading have been studied in [33].

This study is intended for a unified and explicit finite strain analysis for full-range responses of axially loaded bars and finite bending beams until failure. This analysis will be carried out in a broad sense applicable to various elastoplastic constituent materials, such as metals, concretes, reinforced polymers and reinforced composites, etc. New results will be furnished in three respects. First, two uniaxial stress–strain response functions will be presented in explicit forms for the purpose of accurately characterizing non-symmetric tensile and compressive behaviors of axially loaded bars with complex transitions from hardening to softening. Second, explicit solutions to both the varying neutral axis and the flexural moment of finite bending beams will be derived directly from these two uniaxial functions. Third, usual complexities in constitutive modeling and numerical implementation will accordingly be bypassed without simulating either micro-defects or macro-cracks. Moreover, model predictions for three cases of the constituent material will be provided and compared with test data for both bars and beams, including aluminium, meso-scopic heterogeneous concrete, and ultra-high performance fiber-reinforced concrete with glass fiber-reinforced polymer rebars.

The context will be arranged in four sections. In Sect. 2, two uniaxial stress–strain response functions will be presented in explicit forms towards accurately characterizing non-symmetric tensile and compressive responses of axially loaded bars from hardening to softening. In Sect. 3, explicit solutions to both the varying neutral axis and the bending moment will be obtained directly from these two uniaxial functions. In Sects. 3 and 4, numerical examples will be provided towards validating model predictions with comparisons to test data. Finally, results and future studies will be discussed in Sect. 5.

2 Accurate analyses for non-symmetric responses of bars

As mentioned before, stress–strain responses of various axially loaded bars until failure exhibit much varied elastoplastic features with considerable differences in tension and compression. Accordingly, non-symmetric tensile and compressive stress–strain curves are generated with several parts distinct in nature from hardening to softening. In fact, after an initial part of almost linear shape emerges a curvilinear hardening part with the stress going up to a maximum value known as the ultimate strength and then follows a curvilinear softening part with the stress going down to vanish. Moreover, for concretes and composites etc., the softening part contains a nearly flat part with a lower stress value known as the residual strength. Details may be found in Figs. 6 and 7 later.

For constituent materials such as concretes and reinforced composites etc., each feature in the above is distinct in tension and compression, including the shape and the slope of either the hardening or the softening part, the transition from hardening to softening, and, in particular, the ultimate and the residual strength, etc., as shown in Figs. 6 and 7.

In what follows, all such details will be accurately characterized by presenting non-symmetric stress–strain functions in explicit forms. These two forms will be constructed by combining a few hyperbolic tangent functions, which is an extension of the idea in constructing a simple form of the yield strength in [34]. Other types of functions constructed by mechanical and mathematical formalisms are given, e.g., in [3, 35], and the literature therein.

2.1 Stress–strain function in tension

Let $h\ge 0$ and $\sigma \ge 0$ be the axial Hencky strain and the axial Cauchy stress in tension. An explicit form of the stress–strain function in tension is given as follows:

$$\begin{aligned} \displaystyle \sigma = f^*(h)= & {} (a^* h+b^*\textrm{tanh}(\omega ^* h))\frac{1-\textrm{tanh}\alpha ^*\left( \frac{h}{s^*}-1\right) }{1+\textrm{tanh}\alpha ^* }\nonumber \\{} & {} +c^*\frac{\left( \textrm{tanh}\beta ^*+\textrm{tanh}\beta ^* \left( \frac{h}{s^*} - 1 \right) \right) ^2}{({\textrm{tanh}}\beta ^*+1)^2}\,e^{-m^*h},\quad (h\ge 0) \end{aligned}$$

(1)

for the full-range response of an axially loaded bar from hardening to softening until failure. Each parameter therein is positive. The parameters $a^*, b^*, c^*$ are of the same dimension as the stress, while other parameters are dimensionless. Details are explained below.

Equation (1) is intended for a unification in treating metals and concretes. Indeed, it is not on a rational but on an ad hoc basis in essence. It is well designed based on the idea that appropriate combinations of hyperbolic tangent functions with their unique transition features may be used to well represent complex transitions from hardening with positive slopes to softening with negative slopes for various materials such as metals and concretes etc. and, in particular, that would also be the case with additional transitions related to the residual strength at the softening stage. It appears that, with Eq. (1), a unified treatment for elastoplastic response features of both metals and concretes may for the first time be achieved in a sense of ensuring good correlations between model predictions and experimental data. It is this unification that leads to a unified study for non-symmetric tensile and compressive responses of various bars and beams made of metals and concretes, etc.

The geometric features of the tensile stress–strain curve represented by Eq. (1) are controlled by the three hyperbolic tangent functions therein together with given values of the parameters. Of them, the function

$$\begin{aligned} y=\textrm{tanh}(\omega x) \end{aligned}$$

rapidly grows from 0 to 1 and then keeps almost constant, as illustrated in Fig. 1 for $\omega =500,1000,2000$, while the function

$$\begin{aligned} y=\textrm{tanh}\left( \eta \left( \frac{x}{r}-1\right) \right) \end{aligned}$$

rapidly changes from $-1$ to 1 within a narrow interval centered at $x=r$, as shown in Fig. 2 for $\eta =2,3,9$ with $r=0.0025$.

Fig. 1

Three cases of the hyperbolic tangent function $y=\textrm{tanh}(\omega x)$

Fig. 2

Three cases of the hyperbolic tangent function $y=\textrm{tanh}(\eta (x/0.0025-1)))$

With the above properties of the three hyperbolic tangent functions in Eq. (1), various stress–strain curves of the features in the foregoing may be generated with various parameter values. The meanings of the parameters are explained as follows.

The parameters $a^*, b^*, \omega ^*$ jointly prescribe the shape and the slope of the hardening part in tension and, in particular, the initial slope at $h=0$, i.e., Young’s modulus, is given by

$$\begin{aligned} E=\left. \frac{df^*}{dh}\right| _{h=0}=a^*+\omega ^* b^*. \end{aligned}$$

(2)

On the other hand, the parameters $\alpha ^*$ and $s^*$ specify the transition effect from hardening to softening in tension and, in particular, the location of the ultimate tensile strength, while the parameters $\alpha ^*$, $\beta ^*$, $c^*$ determine the shape and the slope of the softening part in tension. Of them, the parameter $c^*$ is the limiting value of Eq. (1) as h exceeds $s^*$, namely, the tensile residual strength. Finally, the parameter $m^*$ ensures that the stress goes to vanish as the strain becomes large, as required by Eq. (12) later on.

2.2 Stress–strain function in compression

Let $h\le 0$ and $\sigma \le 0$ be the axial Hencky strain and the axial Cauchy stress in compression. In parallel with Eq. (1), an explicit form of the stress–strain function in compression is given as follows:

$$\begin{aligned} \displaystyle \sigma =f_*(h)= & {} (a_* h+b_*\textrm{tanh}(\omega _* h))\frac{1+\textrm{tanh}\alpha _*\left( \frac{h}{s_*}+1\right) }{1+\textrm{tanh}\alpha _* }\nonumber \\{} & {} -c_*\frac{\left( \textrm{tanh}\beta _*-\textrm{tanh}\beta _* \left( \frac{h}{s_*} + 1 \right) \right) ^2}{(\textrm{tanh}\beta _*+1)^2}\,e^{m_*h},\quad (h\le 0). \end{aligned}$$

(3)

As in Eq. (1), each parameter in Eq. (3) is positive. The meanings of the parameters may be explained by replacing “tension" with “compression" in the last subsection. In particular, the counterpart of Eq. (2) is as follows:

$$\begin{aligned} E=\left. \frac{df_*}{dh}\right| _{h=0}=a_*+\omega _* b_*. \end{aligned}$$

(4)

This and Eq. (2) together lead to the relationship:

$$\begin{aligned} a^*+\omega ^*b^*=a_*+\omega _*b_*=E. \end{aligned}$$

(5)

2.3 Comparisons with test data

The value of each parameter in Eqs. (1, 3) is determined in fitting sufficient experimental data for uniaxial tension and compression of bar specimens. As illustrative examples and for the calculations to be carried out in the next section, here uniaxial data for three constituent materials are taken into account, including Al 99,5w (cf., [31]), ultra-high-performance fiber-reinforced concrete (UHPFRC) (cf., [18]) and meso-scale heterogeneous concrete (MSHC) (cf., [36]). Two sets of the parameters as given in Eqs. (1, 3) are identified in matching these data and the parameter values are listed in Tables 1, 2, and 3. Comparisons with test data are depicted in Figs. 3, 4, 5, 6, and 7 for tension and compression, respectively.

Table 1 Parameter values in fitting uniaxial data for Al 99,5w in [31]

Table 2 Parameter values in fitting uniaxial data for UHPFRC in [18]

Table 3 Parameter values in fitting uniaxial data for MSHC in [36]

Fig. 3

Fitting uniaxial data for Al 99,5w in [31]

Fig. 4

Fitting uniaxial tension data for UHPFRC in [18]

Fig. 5

Fitting uniaxial compression data for UHPFRC in [18]

Fig. 6

Fitting uniaxial tension data for MSHC in [36]

Fig. 7

Fitting uniaxial compression data for MSHC in [36]

Both hardening and softening parts are depicted in Figs. 6 and 7 with comparisons to data. However, since no softening data are available, the softening parts in Figs. 3, 4, and 5 with the parameter values in Tables 1 and 2 are given in a sense of extrapolation. Here, failure effects with the stress going to vanish are not shown and, hence, values of both $m^*$ and $m_*$ are set to be 0.

2.4 Remarks

The two stress–strain functions may be given in new forms by combining piecewise linear splines [37]. Without involving any unknown parameters, such new forms can accurately and automatically match any given test data, thus bypassing issues both in selecting suitable functional forms and in finding out suitable parameter values. Further remarks will be given in Sect. 5.

3 Explicit solutions to finite bending of beams

As indicated in the introduction section, complexities in both constitutive modeling and numerical implementation are usually involved in analyzing non-elastic bending responses of beams, and that would particularly be the case in the presence of finite strain effects. Here, it will be shown that such complexities may be bypassed by obtaining direct solutions to the varying neutral axis position and the bending moment. Toward this objective, it will be disclosed that, for finite elastoplastic bending of a beam until failure, the stress distributions over the tension and the compression zone can be directly prescribed by the stress–strain functions characterizing uniaxial tensile and compressive behaviors of the constituent material from hardening to softening, as just given in the last section.

The study will be done within a general constitutive framework of finite elastoplastic deformations with failure effects (cf., e.g., [38,39,40]). In so doing, the derived results are of wide applicability for various elastoplastic constituent materials, such as metallic materials, granular materials, reinforced polymers and reinforced composites, etc.

3.1 Elastoplastic formulation with failure effects

We first introduce the Eulerian rate formulation of finite strain elastoplasticity in a broad sense (cf., e.g., [38,39,40]). In what follows, the Cauchy stress, the deformation gradient and the stretching tensor are designated respectively by $\varvec{\sigma }$, ${\varvec{F}}$ and ${\varvec{D}}$ with

$$\begin{aligned} \begin{aligned} {{{{\varvec{D}}}}}=\frac{1}{2}\left( \dot{{{{{\varvec{F}}}}}}\cdot {{{{\varvec{F}}}}}^{-1} +\left( \dot{{{{{\varvec{F}}}}}}\cdot {{{{\varvec{F}}}}}^{-1}\right) ^{\text { T }}\right) . \end{aligned} \end{aligned}$$

Here and in the following, the superimposed dot signifies the material time derivative.

The starting point is the additive separation of the stretching tensor:

$$\begin{aligned} {\varvec{{D}}}={\varvec{{D}}}^e+{\varvec{{D}}}^p. \end{aligned}$$

(6)

Objective Eulerian rate constitutive equations should be formulated for the elastic and the plastic part, ${\varvec{{D}}}^e$ and ${\varvec{{D}}}^p$, in conjunction with a yield function demarcating the elastic and the plastic state. To ensure wide applicability, here the flow rule governing the plastic part ${\varvec{{D}}}^p$ is allowed to be fully general, while the elastic part is governed by (cf., e.g., [41])

$$\begin{aligned} {\varvec{{D}}}^e=\frac{1+\nu }{E}{\mathop {\varvec{\sigma }}\limits ^{\circ }}- \frac{\nu }{E}\,\text{ tr }(\dot{\varvec{\sigma }}){\varvec{I}} \end{aligned}$$

(7)

for small elastic strain. Here and henceforth, E and $\nu$ are Young’s modulus and the Poisson ratio of the constituent material and ${\mathop {\varvec{\sigma }}\limits ^{\circ }}$ is the co-rotational logarithmic stress rate. Details may be found in the foregoing references. With the logarithmic stress rate, Eq. (7) in the elastic unloading case is exactly integrable to really deliver a hyperelastic model, i.e., the Hencky model. The latter can well represent the elastic behavior within a moderate strain range, albeit the elastic strain is small for hard solids such as metals and concretes, etc. Details may be found in [41].

In a broad sense, the yield function is of the general form:

$$\begin{aligned} \varphi =g(\varvec{\sigma })-{\tilde{q}}(\kappa ,\vartheta ). \end{aligned}$$

(8)

In this respect, recent results may be found in, e.g., [42, 43].

In Eq. (8), ${\tilde{q}}(\kappa ,\vartheta )>0$ is the yield strength that is dependent upon both the plastic work $\kappa$ and the stress mode invariant $\vartheta$. Of them, the plastic work $\kappa$ is specified by

$$\begin{aligned} \dot{\kappa }=\varvec{\sigma }: {\varvec{D}}^p, \end{aligned}$$

(9)

while the stress mode invariant $\vartheta$ is given by

$$\begin{aligned} \vartheta =\sqrt{6}\,J_3J_2^{-1.5}, \end{aligned}$$

where $J_n=\text{ tr }\tilde{\varvec{\sigma }}^n,\;(n=2, 3)$ with the deviatoric stress $\tilde{\varvec{\sigma }}$. The invariant $\vartheta$ herein yields 1 and -1 for the uniaxial tension and compression cases, respectively, vanishes for pure shear and, in general, is bound to $-1\le \vartheta \le 1$.

Depending on the particular definition of the invariants of the stress deviator, $\vartheta$ is according to

$$\begin{aligned} \vartheta = - \sin 3\theta \end{aligned}$$

associated with the so-called Lode angle $\theta$, where $\theta$ is the angle between the projection of $\varvec{\sigma }$ on the $\pi$-plane and the nearest pure shear line.

The parameter $\mu$ actually introduced by Lode in his dissertation¹ [44, 45]

$$\begin{aligned} \mu = \frac{2\sigma _2 - \sigma _1 - \sigma _3}{\sigma _1 - \sigma _3}, \quad \sigma _1 \ge \sigma _2 \ge \sigma _3, \quad -1 \le \mu \le 1, \end{aligned}$$

where the $\sigma _i\; (i = 1,2,3)$ are the principal values of $\varvec{\sigma }$, is related to this angle via (refer, e.g., to [46])

$$\begin{aligned} \mu = \sqrt{3} \tan \theta , \quad -\frac{\pi }{6} \le \theta \le \frac{\pi }{6}. \end{aligned}$$

In passing, we note that these special formulas are bound to the sequence $\sigma _1 \ge \sigma _2 \ge \sigma _3$. Similar relations can be given for the other segments of the yield locus. Therefore, we will here refer to $\vartheta$ as a generalized Lode parameter.²

This result can also be achieved if the principal values of the stresses are replaced by cylindrical coordinates. A simple trigonometrical calculation can transform the common invariants into a set of alternative invariants $(\sigma _{\textrm{m}}, \sigma _{\textrm{eq}}, \vartheta )$ (cf, e.g., [43, 49, 50]), where $\sigma _{\textrm{m}}$ is the mean stress and $\sigma _{\textrm{eq}}$ the von Mises equivalent stress.

Instead of the usual plastic work $\kappa$ in Eq. (9), the yield strength ${\tilde{q}}$ may be formulated equivalently in terms of another evolving variable $\xi$, as indicated in [51]. As such, Eq. (8) is recast as follows:

$$\begin{aligned} \varphi =g(\varvec{\sigma })-q(\xi ,\vartheta ). \end{aligned}$$

(10)

Here, the evolving variable $\xi$ is introduced by the following relationship:

$$\begin{aligned} \dot{\kappa }=\frac{q}{E}\left( E-q'\right) \dot{\xi } \end{aligned}$$

(11)

with $q'=\partial q/\partial \xi$. The evolution equation for $\xi$ may be given directly, as is the case for metals in [51].

As indicated in [39, 40], failure effects may be automatically incorporated as inherent response features into finite strain elastoplasticity models, whenever the yield strength tends to vanish with constant development of the plastic flow, as formulated below:

$$\begin{aligned} \lim _{\xi \rightarrow \infty }q(\xi ,\vartheta )=0. \end{aligned}$$

(12)

Both $g(\varvec{\sigma })$ and $q(\xi ,\vartheta )$ in Eq. (10) are allowed to be of fully general forms. A particular form of the yield function for granular materials is the Drucker–Prager function [52]:

$$\begin{aligned} \varphi =\sqrt{J_2}\,+\,\alpha I_1-q(\xi ), \end{aligned}$$

where $\alpha$ is a parameter related to the internal friction angle of granular materials.

3.2 Yield strengths in tension and compression

Now we direct attention to the uniaxial tension and compression cases with $\vartheta =\pm 1$. For these particular cases, we intend to demonstrate that the yield strength $q(\xi ,\vartheta )$ in Eq. (10), designated by

$$\begin{aligned} q^*=q(\xi ,1),\quad q_*=q(\xi ,-1), \end{aligned}$$

(13)

are determined just from the uniaxial tensile and compressive stress–strain response functions of an axially loaded bar of the constituent material.

In fact, let $\lambda$, $\eta$, $\sigma$ be the axial stretch, the lateral stretch and the axial Cauchy stress in an axially loaded bar, respectively, and let ${\varvec{e}}$ be a unit vector in the axial direction. Then, the stretching and the Cauchy stress tensor for an axially loaded bar are of the forms:

$$\begin{aligned} {\varvec{D}}=\frac{\dot{\lambda }}{\lambda }{\varvec{e}}\otimes {\varvec{e}}+\frac{\dot{\eta }}{\eta }({\varvec{I}}-{\varvec{e}}\otimes {\varvec{e}}),\quad \varvec{\sigma }= \sigma {\varvec{e}}\otimes {\varvec{e}}. \end{aligned}$$

(14)

At the yielding state, the condition $\varphi =0$ is met. Without losing generality, the stress function $g(\varvec{\sigma })$ in Eq. (10) is formulated such that it just yields the normal stress $\pm \sigma$ for the uniaxial stress tensor as given in Eq. (14). As such, with Eq. (13) the yield condition $\varphi =0$ produces

$$\begin{aligned} \sigma =q^*(\bar{\xi })\;\text{ for } \text{ tension }\;\sigma \ge 0, \end{aligned}$$

(15)

$$\begin{aligned} \sigma =-q_*(\bar{\xi })\;\text{ for } \text{ compression }\;\sigma \le 0. \end{aligned}$$

(16)

Here, $\bar{\xi }$ is used to denote the value of the evolving variable $\xi$ (cf., Eq. (11)) in the uniaxial loading case.

With Eq. (6), the evolution equation (9) may be recast in a new form below:

$$\begin{aligned} \begin{aligned} \dot{\kappa }={\varvec{\sigma }}:\left( {{{{\varvec{D}}}}}- {{{\varvec{D}}}}^e\right) . \end{aligned} \end{aligned}$$

(17)

Then, the plastic work for an axially loaded bar, signified by $\bar{\kappa }$, is prescribed by

$$\begin{aligned} \dot{\bar{\kappa }}=\sigma (\dot{h}-\dot{\sigma }/E) \end{aligned}$$

(18)

with Young’s modulus, E, of the constituent material and the axial Hencky strain:

$$\begin{aligned} h=\ln \lambda . \end{aligned}$$

(19)

Hence, from Eqs. (11, 15, 16, 18) it may be inferred that the variable $\bar{\xi }$ is just given by the magnitude of the axial Hencky strain h, i.e.,

$$\begin{aligned} \bar{\xi }=|h|. \end{aligned}$$

This and Eqs. (15, 16) jointly produce

$$\begin{aligned} \sigma = q^*(h)\;\text{ for } \text{ tension }\;h\ge 0, \end{aligned}$$

(20)

$$\begin{aligned} \sigma =-q_*(-h)\;\text{ for } \text{ compression }\;h\le 0. \end{aligned}$$

(21)

On the other hand, the axial stress responses $\sigma$ in tension and compression are given by the uniaxial tensile and compressive stress–strain functions (cf., Eqs. (1, 3)) that need to be determined from test data, namely,

$$\begin{aligned} \sigma =f^*(h)\;\text{ for } \text{ tension } \; h\ge 0,\\ \sigma =f_*(h) \; \text{ for } \text{ compression } \; h\le 0, \end{aligned}$$

as in Sect. 2. Thus, from this and Eqs. (20, 21) it follows that

$$\begin{aligned} q^*(h)=f^*(h)\;\text{ for } \text{ tension }\;h\ge 0, \end{aligned}$$

(22)

$$\begin{aligned} q_*(-h)=-f_*(h)\;\text{ for } \text{ compression }\;h\le 0. \end{aligned}$$

(23)

As may be evidenced from the above, finite strain effects are characterized by the axial Hencky strain $h=\ln \lambda$. Essential roles of the Hencky strain may be found in, e.g., [41].

3.3 Stress distributions at finite bending

Now, a beam at finite bending is taken into account, which is of circular sector shape with the height 2a and the width b (cf., Fig. 8 below). Let (${\varvec{{e}}}_1$, ${\varvec{{e}}}_2$, ${\varvec{{e}}}$) be three fixed orthonormal vectors directed respectively in the height, the longitudinal and the width direction of the beam at its initial state and (${\varvec{{e}}}_r$, ${\varvec{{e}}}_{\theta }$, ${\varvec{{e}}}$) be three orthonormal vectors in the current radial, circumferential and width direction, respectively. Each current cross-section at bending is rotated through an angle, $\theta$, around an axis in the ${\varvec{{e}}}$-direction. Then, the following relationships may be established:

$$\begin{aligned} {\varvec{{e}}}_r={\varvec{{e}}}_1\cos \theta + {\varvec{{e}}}_2\sin \theta ,\quad {\varvec{{e}}}_{\theta }= -{\varvec{{e}}}_1\sin \theta + {\varvec{{e}}}_2\cos \theta . \end{aligned}$$

Generally, the deformation gradient at bending is of the form:

$$\begin{aligned} \begin{aligned} {{{{\varvec{F}}}}}=\lambda _r\,{{{{\varvec{e}}}}}_r\otimes {{{{\varvec{e}}}}}_1+ \lambda _{\theta }\,{{{{\varvec{e}}}}}_{\theta }\otimes {{{{\varvec{e}}}}}_2+ \lambda \,{{{{\varvec{e}}}}}\otimes {{{{\varvec{e}}}}}. \end{aligned} \end{aligned}$$

(24)

In the above, $\lambda _{\theta }$, $\lambda _r$, and $\lambda$ are the normal (circumferential), the radial and the lateral stretch at position z (cf., Fig. 8a below) over the current cross-section, respectively. Here, Eq. (24) is given in a broad sense. For pure bending, they are derived from the displacement field as follows:

$$\begin{aligned} \lambda _r=r'(X),\quad \lambda _{\theta }=r\,\theta '(Y),\quad \lambda ={\bar{z}}'(Z), \end{aligned}$$

where the (X, Y, Z) are the Cartesian coordinates in the height, the longitudinal and the width direction of the beam at its initial state, respectively, and the $(r, \theta , {\bar{z}})$³ are the corresponding cylindrical polar coordinates in the radial, circumferential and width direction of the bent beam. Here, the prime denotes differentiation, e.g., $f'(X)=\hbox {d}f/\hbox {d}X$. Since they will play no roles in the sequel, the above relationships derived from the displacement field will no longer be mentioned. In what follows, the stretching tensor

$$\begin{aligned} {\varvec{{D}}}=\frac{\dot{\lambda }_r}{\lambda _r}\, {\varvec{{e}}}_r\otimes {\varvec{{e}}}_r+ \frac{\dot{\lambda }_{\theta }}{\lambda _{\theta }}\, {\varvec{{e}}}_{\theta }\otimes {\varvec{{e}}}_{\theta }+ \frac{\dot{\lambda }}{\lambda }\,{\varvec{{e}}}\otimes {\varvec{{e}}} \end{aligned}$$

(25)

will come into play.

Next, the nature of the stress distributions is analyzed as follows. Both the normal stress $\sigma _{\theta }$ and the radial stress $\sigma _r$ are induced over the beam cross-section. Let $z_0\le 0$ and R be respectively the neutral axis position and the curvature radius at the neutral plane, as shown in Fig. 8. Then, from the equilibrium condition in the radial direction it may be deduced:

$$\begin{aligned} \frac{\hbox {d}\sigma _r}{\hbox {d}r}+\frac{\sigma _r-\sigma _{\theta }}{r}=0. \end{aligned}$$

Hence, the integration over the current cross-section (cf., Fig. 8) from $r=R-a-z_0$ to $r\le R+a-z_0$ yields

$$\begin{aligned} \sigma _r=\dfrac{\int _{R-a-z_0}^r\sigma _{\theta } dr}{r}. \end{aligned}$$

It is noted that $\sigma _r$ attains its maximum value A at the neutral axis position, i.e., at $r=R$. From this it follows that

$$\begin{aligned} |\sigma _r|<\frac{1}{R}\left| \int _{R-a-z_0}^R\sigma _{\theta } \hbox {d}r\,\right|<\frac{a+z_0}{R}\,A<\frac{a}{R}\,A, \end{aligned}$$

with $z_0\le 0$.

From the above, it may be concluded that, whenever the curvature radius is large as compared to the half height a, the radial stress $\sigma _r$ is small for a small ratio a/R. In fact, outside the elastic zone, $\sigma _r$ is negligible (cf., e.g., [30]) as compared to $\sigma _{\theta }$. In a similar way, we can also estimate the influence of the stress $\sigma _{{\bar{z}}}$ in the width direction as small. In fact, the two stresses merely represent the second-order effects and, hence, by neglecting the relatively small radial stress and the stress in the width direction, either of which has no contribution to the bending moment given later in Eq. (35), the Cauchy stress outside the elastic zone is of the form:

$$\begin{aligned} \varvec{\sigma }=\sigma _{\theta }\,{\varvec{{e}}}_{\theta }\otimes {\varvec{{e}}}_{\theta }. \end{aligned}$$

(26)

It is worthwhile to point out that the above results have been derived in a broad sense for various cases of the finite bending. In fact, the three stretches in Eqs. (24, 25) are allowed to be fully general, in which the plane-strain bending with $\lambda =1$ for a wide plate strip is included as a particular case. Furthermore, various cases of thin and medium-thin beams with small ratio a/R may be treated in a unified manner.

Further results may be derived following the same procedures in the last subsection. Firstly, the yield condition $\varphi =0$ produces

$$\begin{aligned} \sigma _{\theta }=q^*(\hat{\xi })\;\text{ for }\;\sigma _{\theta }\ge 0, \end{aligned}$$

(27)

$$\begin{aligned} \sigma _{\theta }=-q_*(\hat{\xi })\;\text{ for }\;\sigma _{\theta }\le 0, \end{aligned}$$

(28)

where $\hat{\xi }$ is used to denote the value of the evolving variable $\xi$ (cf., Eq. (11)) at position z over the current cross-section (cf., e.g., Fig. 8a).

Next, from Eqs. (17, 25, 26) the following may be deduced:

$$\begin{aligned} \dot{\hat{\kappa }}=\sigma _{\theta }(\dot{h}_{\theta }-\dot{\sigma }_{\theta }/E) \end{aligned}$$

(29)

with the normal (circumferential) Hencky strain at position z:

$$\begin{aligned} h_{\theta }=\ln \lambda _{\theta }. \end{aligned}$$

(30)

Moreover, from Eqs. (11, 29) it may be inferred that the variable $\hat{\xi }$ is just given by the magnitude of the normal Hencky strain $h_{\theta }$, i.e., $\hat{\xi }=|h_{\theta }|$. This and Eqs. (27, 28) jointly produce

$$\begin{aligned} \sigma _{\theta }=\left\{ \begin{array}{l} q^*(h_{\theta })\quad \text{ for }\quad h_{\theta }\ge 0,\\ -q_*(-h_{\theta })\quad \text{ for }\quad h_{\theta }\le 0, \end{array}\right. \end{aligned}$$

(31)

Eventually, from Eqs. (21, 22, 30) the following correlation is established:

$$\begin{aligned} \sigma _{\theta }=\left\{ \begin{array}{l} f^*(h_{\theta })\quad \text{ for }\quad h_{\theta }\ge 0,\\ f_*(h_{\theta })\quad \text{ for }\quad h_{\theta }\le 0. \end{array}\right. \end{aligned}$$

(32)

With the yield condition $\varphi =0$, actually the above correlation is first established for the normal stress within the two plastic zones in tension and compression, namely, for $h_{\theta }$ beyond certain elastic limits. Within these limits, i.e., for the elastic zone centered at the neutral axis, the stress is given simply by $\sigma =E h_{\theta }$, which is covered in Eqs. (1, 3) with Eq. (5).

3.4 Explicit solutions

For a uniform rectangular beam with its cross-section of height 2a and width b, a Cartesian coordinate system Oxz over the current beam cross-section at bending is shown in Fig. 8a, where the Oz-axis is in the height-direction and the Ox-axis in the width-direction. In a course of bending, each beam cross-section with its normal rotating keeps planar.

Let $z_0$ and $\gamma$ respectively denote the neutral axis position and the flexural curvature at the neutral plane, as shown in Fig. 8b with $R=\gamma ^{-1}$ the radius of curvature, and, as before, let $\theta$ be the bending angle of the beam cross-section. Then, the normal stretch at position z is given by

$$\begin{aligned} \lambda _{\theta }=\frac{(R+z-z_0)\theta }{R\theta } = 1 + \gamma \left( {z - {z_0}} \right) . \end{aligned}$$

Hence, the normal Hencky strain (cf., Eq. (30)) at position z is as follows:

$$\begin{aligned} {h_{\theta }} =\ln \lambda _{\theta }= {\textrm{ln}}\left( {1 + \gamma \left( {z - {z_0}} \right) } \right) . \end{aligned}$$

(33)

Fig. 8

Bending with varying neutral axis

The rebar reinforcement in the tension zone is taken into consideration. Let $z_{j*}$, $s_j$, $A_{j*}$ be the position, the number, the area of the j-th row of rebars with $j=1,2,\dots ,n$. With the correlation Eq. (32), it may be inferred that the force equilibrium over the cross-section leads to

$$\begin{aligned} b\int _{-a}^{z_0}f_*(h_{\theta }) \hbox {d}z + b\int _{z_0}^{a} f^*(h_{\theta }) \hbox {d}z + \sum \limits _{j = 1}^{\mathrm{{n}}} s_{*j}(E_{*j}h_{*j} - f_*(h_{*j}))A_{*j} \,=\,0. \end{aligned}$$

(34)

In the above, the stress in each rebar is given by Hooke’s law, i.e., $E_{j*}h_{*j}$, in which $E_{j*}$ and $h_{*j}$ are Young’s modulus of the rebar and the Hencky strain at position $z_{*j}$, respectively.

Moreover, again with the correlation Eq. (32), the bending moment M is obtained as follows:

$$\begin{aligned} M =b\int _{-a}^{z_0} (z-z_0)f_*(h_{\theta })\hbox {d}z + b\int _{z_0}^{a} (z-z_0)f^*( h_{\theta })\hbox {d}z + \sum \limits _{j = 1}^{\mathrm{{n}}} s_{*j}(z_{*j}-z_0)(E_*h_{*j} - f_*(h_{*j}))A_{*j}.\nonumber \\ \end{aligned}$$

(35)

With the explicit solutions derived in the above, the neutral axis position $z_0$ is directly determined from Eq. (34) and, then, the bending moment M is directly calculated from Eq. (35).

3.5 Remarks

In a course of bending, both the tension zone and the compression zone over beam cross-section are constantly changing with the varying neutral axis. According to various existing approaches, the stress distributions over such varying zones need to be determined based on various constitutive models with damaging or cracking effects. As such, complexities need to be treated. In fact, the stress function $g(\varvec{\sigma })$ and the yield strength $q(\xi ,\vartheta )$ in Eq. (10) could not be known in exact forms and, in particular, the flow rule for ${\varvec{D}}^p$, which is even non-associated for granular media such as concretes etc., could not be exactly formulated, let alone the fact that either micro-defects or macro-cracks should be simulated. As a result, complicated formulations have to be postulated from different standpoints in various existing approaches.

With the explicit solutions Eqs. (34, 35), now the above uncertainties and complexities are not involved, in which the stress distributions in both the tension and the compression zone are directly calculated from the uniaxial tensile and compressive stress–strain functions of the constituent material until failure, as given in Eqs. (1, 3). Perhaps essentially, forms of the latter may be directly prescribed with experimental data from uniaxial testing of bar specimens, as shown in Sect. 2.3.

4 Model predictions with comparisons to data

A few numerical examples will be provided for bending responses of beams made of Al 99,5w [31], ultra-high-performance fiber-reinforced concrete (UHPFRC) with reinforcing rebars [18], as well as meso-scale heterogeneous concrete [36], respectively. Model predictions are calculated from Eqs. (34, 35) without involving any other adjustable parameters except for those in Tables 1, 2, and 3.

4.1 Plate strip made of Al 99,5w

Results are calculated for a plate strip made of Al 99,5w of the height 1 cm and the width 10 cm. The parameter values are listed in Table 1. Here, the uniaxial behaviors in tension and compression are symmetric and no rebar reinforcement is involved. Predictions for the bending moment are calculated from Eqs. (34, 35) with Eqs. (1, 3) and compared with test data in [31], as depicted in Fig. 9.

Fig. 9

Comparing predictions for bending moment with data in [31]

4.2 UHPFRC beam with GFRP rebars

Results are calculated for UHPFRC beam of the width 200 mm and the height 270 mm with five glass fiber-reinforced polymer (GFRP) rebars in two rows. In this case, the uniaxial behaviors of UHPFRC in tension and compression are of highly non-symmetric nature, as shown in Figs.  4 and 5. The five rebars are arranged in two rows numdered $i=1,2$ with $z_i^*, s_i^*, E_i^*$ and $A_i^*$ the position, the number, Young’s modulus and the area of the rebars in the ith row and details for the two rows of GFRP rebars are as follows:

$$\begin{aligned} \begin{array}{l} z_1^*=70\,\text{ mm },\;s_1^*=2,\;E_1^*=51.3\,\text{ GPa },\;A_1^*=126.7\,\text{ mm}^2,\\ z_2^*=105\,\text{ mm },\;s_2^*=3,\;E_2^*=51.3\,\text{ GPa },\;A_2^*=126.7\,\text{ mm}^2.\\ \end{array} \end{aligned}$$

The parameter values are listed in Table 2. Predictions for the neutral axis position and the bending moment are calculated from Eqs. (34, 35) with Eqs. (1, 3) and compared with test data in [18], as shown in Figs. 10 and 11.

Fig. 10

Comparing predictions for bending moment with data for UH-G5 in [18]

Fig. 11

Comparing predictions for neutral axis position with data for UH-G5 in [18]

4.3 MSHC beam

Results are calculated for meso-scale heterogeneous concrete (MSHC) beam of the width 200 mm and the height 370 mm. Uniaxial softening data are not available for the foregoing two cases. Here, with sufficient data [36] for both hardening and softening, it is evident that the uniaxial behaviors of MSHC in tension and compression are not only highly non-symmetric but display complex softening effects with different residual strengths.

The parameter values are listed in Table 3. Predictions for the neutral axis position and the bending moment are calculated from Eqs. (34, 35) with Eqs. (1, 3) and depicted in Figs. 12 and 13. In the case at issue, test data for bending response are unavailable.

Furthermore, the tensile and compressive stress distributions over beam cross-section with the tension zone and the compression zone are depicted in Fig. 14 for the case at the maximum bending moment. In this case, it may be seen that softening is already induced in a large part of the tension zone. In fact, that may be the case for a bending moment under the maximum value.

Fig. 12

Predictions for bending moment of MSHC beam in [36]

Fig. 13

Predictions for neutral axis position of MSHC beam in [36]

Fig. 14

Stress distributions over tension and compression zones of MSHC beam [36] at maximum moment

5 Concluding remarks

A unified and explicit study has been presented for non-symmetric tensile and compressive responses of both axially loaded bars and flexural beams until failure. Accurate results have been obtained in a direct sense of simulating neither micro-defects nor macro-cracks. As a consequence, the present study bypasses complexities and uncertainties in both constitutive modeling and numerical implementation involved in various existing approaches. Numerical examples suggest that model predictions are in good agreement simultaneously with all data for both uniaxial testing and bending.

Further results may be obtained with unique and unified forms of uniaxial stress–strain functions in [37]. Such new forms are constructed by smoothly combining piecewise linear splines and can accurately and automatically match any given test data, in a direct sense with involving no unknown parameters. Furthermore, full-range bending responses need to be simulated with comparisons to sufficient test data until bending failure. Most recently [33], the correlation in Eq. (33) has been used in a direct approach toward analyzing cyclic fatigue effects of metal beams. Further study needs to be done for cyclic bending behaviors of reinforced composite beams.