Abstract
Critical velocities of a two-layer composite tube under a uniform internal pressure moving at a constant velocity are analytically determined. The formulation is based on a Love–Kirchhoff thin shell theory that incorporates the rotary inertia and material anisotropy. The composite tube consists of two perfectly bonded axisymmetric circular cylindrical layers of dissimilar materials, which can be orthotropic, transversely isotropic, cubic or isotropic. Closed-form expressions for the critical velocities and radial displacement of the two-layer composite tube are first derived for the general case by including the effects of material anisotropy, rotary inertia and radial stress. The formulas for composite tubes without the rotary inertia effect and/or the radial stress effect and with various types of material symmetry for each layer are then obtained as special cases. In addition, it is shown that the model for single-layer, homogeneous tubes can be recovered from the current model as a special case. To illustrate the new model, a composite tube with an isotropic inner layer and an orthotropic outer layer is analyzed as an example. All four critical velocities of the composite tube are calculated using the newly derived closed-form formulas. Six values of the lowest critical velocity of the two-layer composite tube are computed using three sets of the new formulas, which compare fairly well with existing results.
Similar content being viewed by others
1 Introduction
It has been known that dynamic strains in a homogeneous tube under a moving internal pressure can exceed three times of the corresponding static values (e.g., [11, 30,31,32]). This occurs when the velocity of the moving pressure is very close to the lowest critical velocity of the tube. Therefore, it is necessary to find critical velocities of such tubes to ensure safe designs. Critical velocities are also needed in designing other structures subjected to moving loads (e.g., [7, 8, 23, 28, 33]).
Efforts have been made to determine critical velocities of single-layer, homogeneous tubes of materials with various types of symmetry, including isotropic, cubic, transversely isotropic and orthotropic (e.g., [10, 11, 15, 27, 30, 35, 36]). However, for composite tubes containing two or more cylindrical layers of dissimilar materials (e.g., [20, 21, 29]), very few studies have been conducted to find their critical velocities. Jones and Whittier [16] investigated the harmonic wave propagation in an infinitely long two-layered axisymmetric cylindrical shell using a Timoshenko-type shell theory similar to those of Lin and Morgan [19] and Herrmann and Mirsky [14], but they did not include any discussion on critical velocities of the composite cylinder. Chonan [5] studied the steady-state response of a two-layered cylindrical shell to a moving ring load and computed the lowest critical velocity under various bonding conditions at the interface by using the Fourier transform method. The critical velocity of an isotropic tube wrapped with an orthotropic layer was numerically determined by Simkins [29] based on the free vibration model for laminated orthotropic cylindrical shells developed in Dong [6] using a Donnell-type shell theory. However, no closed-form formula has been provided in these and subsequent thin shell theory-based studies on critical velocities of composite tubes containing two or more bonded layers of dissimilar materials. This motivated the current work.
In the present study, closed-form formulas for critical velocities and radial displacement of a composite tube consisting of two cylindrical layers of dissimilar materials subjected to a uniform internal pressure moving at a constant velocity are derived by using a Love–Kirchhoff thin shell theory (e.g., [2, 34, 40]) that incorporates the rotary inertia and material anisotropy. Being based on the general 3D constitutive relations for orthotropic elastic materials, the current formulation provides a unified treatment of composite tubes containing two layers of dissimilar materials, each of which can have a different type of material symmetry, including orthotropic, transversely isotropic, cubic or isotropic. It is shown that the newly derived formulas for two-layer composite tubes recover those for single-layer, homogeneous tubes as special cases.
The rest of this paper proceeds as follows. In Sect. 2, the model for axisymmetric orthotropic cylindrical Love–Kirchhoff thin shells with the rotary inertia effect formulated in Gao and Littlefield [11] is briefly reviewed. In Sect. 3, closed-form formulas for critical velocities and radial displacement of a composite tube consisting of two layers of dissimilar materials under a moving internal pressure are derived by using the Love–Kirchhoff thin shell model reviewed in Sect. 2. In Sect. 4, the general analytical formulas obtained in Sect. 3 are applied to composite tubes made from two layers of dissimilar orthotropic, transversely isotropic, cubic or isotropic materials, leading to four sets of closed-form formulas for critical velocities of two-layer composite tubes. In Sect. 5, a numerical example is provided for a composite tube consisting of an isotropic inner layer and an orthotropic outer layer by directly applying the new formulas derived in Sect. 3. The critical velocity values predicted by the newly obtained analytical formulas are compared with each other and to those computationally determined in Simkins [29]. A summary is presented in Sect. 6.
2 Axisymmetric circular cylindrical shell model with the rotary inertia effect: review
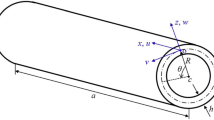
Based on the Love–Kirchhoff kinematic relations, the displacement field in an axisymmetric circular cylindrical thin shell of uniform thickness h and mean radius R in the coordinate system {x, θ, z} shown in Fig. 1 can be written as (e.g., [18, 40])
where ux, uθ and uz are, respectively, the x-, θ- and z-components of the displacement vector u of a point (x, θ, z) in the shell at time t, and u and w are, respectively, the x- and z-displacement components of the corresponding point (x, θ, 0) on the shell middle surface at time t. Note that uθ is identically zero and there is no dependence on θ for all kinematic and kinetic quantities in such an axisymmetric problem (e.g., [11, 14]), which differ from those in general deformations of circular cylindrical shells (e.g., [37, 40]).
From Eq. (1), the components of the infinitesimal strain tensor in the axisymmetric circular cylindrical thin shell can be obtained as (e.g., [11]), with r ≈ R,
The constitutive equations for an orthotropic linear elastic material in the cylindrical coordinate system {x, θ, z} have the general form (e.g., [4, 9, 22, 39]):
where σij (i, j ∈ {x, θ, z}) are the components of the Cauchy stress tensor, and Cij (i, j ∈ {1, 2, 3, 4, 5, 6}) are the components of the elastic stiffness matrix, which contains nine independent components for the orthotropic material, as shown in Eq. (3).
Using Eq. (2) in Eq. (3) gives the stress components in terms of the kinematic variables u(x, t) and w(x, t) in the axisymmetric circular cylindrical thin shell as
The equations of motion in terms of u and w for the axisymmetric circular cylindrical Love–Kirchhoff thin shell satisfying Eqs. (1), (2) and (4) are given by [11]
where fx and fz are, respectively, the x- and z-components of the body force resultant (force per unit area) through the shell thickness acting on the mid-surface. Note that in this axisymmetric case the rotary inertia effect is incorporated through the term “\(\frac{{\rho h^{3} }}{12}\frac{{\partial^{4} w}}{{\partial x^{2} \partial t^{2} }}\)” in Eq. (5b) (e.g., [17, 38]).
3 Critical velocities of a two-layer composite tube under a moving pressure
The critical velocities of a two-layer composite tube subjected to an internal pressure moving at a constant velocity are derived herein using the axisymmetric circular cylindrical Love–Kirchhoff thin shell model reviewed in Sect. 2.
3.1 General case
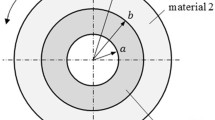
Consider an axisymmetric two-layer composite tube, which consists of an inner cylindrical layer of mean radius R1 and thickness h1 and an outer cylindrical layer of mean radius R2 and thickness h2. The two layers of dissimilar materials are perfectly bonded at the interface r = R1 + h1/2 = R2 − h2/2, and the composite tube is under a uniform internal pressure p0 moving at a constant velocity V, as shown in Fig. 2.
The moving pressure can be represented by
where p0 is the magnitude of the pressure and H(⋅) is the Heaviside step function.
Suppose that each layer is an orthotropic elastic material and satisfies the governing equations in Eqs. (5a) and (5b) for an axisymmetric circular cylindrical Love–Kirchhoff thin shell. Then, applying Eqs. (5a) and (5b) to the inner layer gives, with \(f_{x}^{(1)}\) = 0,
where the superscript “(1)” denotes the inner layer (i.e., material 1) and use has been made of Eq. (6).
Similarly, using Eqs. (5a) and (5b) for the outer cylindrical layer yields, with \(f_{x}^{(2)}\) = 0,
where the superscript “(2)” stands for the outer layer (i.e., material 2).
The continuity conditions at the perfectly bonded interface r = R1 + h1/2 = R2 − h2/2 of the two-layer axisymmetric composite tube read
Substituting Eq. (1) into Eqs. (9a) and (9b) leads to
where use has been made of the approximations \(\frac{{h_{1} }}{2}\frac{{\partial w^{(1)} }}{\partial x} < < u^{(1)} (x,t)\) and \(\frac{{h_{2} }}{2}\frac{{\partial w^{(2)} }}{\partial x} < < u^{(2)} (x,t)\) in reaching Eq. (10a). Note that Eqs. (10a) and (10b) are the same as those obtained in Jones and Whittier [16] by setting z = 0 at the interface.
From Eqs. (7a), (7b), (8a), (8b), (9c) and (10a,b), it follows that
Equations (11a) and (11b) are the equations of motion for the composite tube, which can be solved to obtain u(x, t) and w(x, t). Note that for the current composite tube the rotary inertia effect is included through the term “\(\left[ {\frac{{\rho^{(1)} h_{1}^{3} }}{12} + \frac{{\rho^{(2)} h_{2}^{3} }}{12}} \right]\frac{{\partial^{4} w}}{{\partial x^{2} \partial t^{2} }}\)” in Eq. (11b).
When the tube is homogeneous with \(C_{ij}^{(1)} = C_{ij}^{(2)} = C_{ij} ,\)\(\rho^{(1)} = \rho^{(2)} = \rho\), \(R_{1} \approx R \approx R_{2} ,\) \(h_{1} = h\) and \(h_{2} = 0\), Eqs. (11a) and (11b) reduce to
which are identical to the governing equations for a single-layer axisymmetric orthotropic tube under a uniform internal pressure p0 moving at a constant velocity V [11].
The steady-state solution of Eqs. (11a) and (11b) is derived next by starting with the following transformation (e.g., [15, 30]:
where ξ is a new variable. In terms of ξ, Eqs. (11a) and (11b) become
where all derivatives are with respect to the new variable ξ.
When \(C_{11}^{(1)} + C_{11}^{(2)} - \left[ {\rho^{(1)} + \rho^{(2)} } \right]V^{2} = 0\), Eq. (14a) shows that w is a constant for any value of u. This defines one critical velocity of the composite tube given by
which is also the dilatational wave velocity (denoted by Vd) of the two-layer shell.
When \(C_{11}^{(1)} + C_{11}^{(2)} - \left[ {\rho^{(1)} + \rho^{(2)} } \right]V^{2} \ne 0\), Eq. (14a) can be integrated once with respect to ξ to obtain
where \(\overline{c}\) is an integration constant. Substituting Eq. (15b) into Eq. (14b) then results in
where c \(\left( { \equiv - \left[ {\frac{{C_{12}^{(1)} h_{1} }}{{R_{1} }} + \frac{{C_{12}^{(2)} h_{2} }}{{R_{2} }}} \right]\overline{c}} \right)\) is a constant. The solution of Eq. (16) has the form:
where wp is a particular solution, and wh is the general solution of the homogeneous part of Eq. (16) given by
The solution of Eq. (18) reads
where W and α are constants. Substituting Eq. (19) into Eq. (18) results in
as the characteristic equation, where
The roots of Eq. (20), a quadratic equation in α2, can be readily obtained as, with A ≠ 0,
Equations (21a-c) and (22) show that the four values of α can be real, complex or purely imaginary, depending on the value of V for given material constants (i.e., \(\rho^{(1)} ,\,\,\rho^{(2)} ,\,\,C_{11}^{(1)} ,\,\,C_{22}^{(1)} ,\,\,C_{12}^{(1)} ,\,\,C_{11}^{(2)} ,\,\,C_{22}^{(2)} \,\,{\text{and}}\,\,C_{12}^{(2)}\)) and geometrical parameters (i.e., R1, h1, R2 and h2).
When A = 0, Eq. (20) shows that α2 will be either positive or negative, leading to an exponentially changing or oscillating deflection w according to Eqs. (17) and (19), which is a critical state for tube deformations. Hence, the condition of A = 0 defines a critical velocity for the composite tube, which is given by, upon using Eq. (21a),
as one critical velocity.
When C = 0, α = 0 will be a double repeated root of the characteristic equation in Eq. (20) and the other two roots of Eq. (20) will be either real or purely imaginary, giving an exponentially changing or oscillating deflection w according to Eqs. (17) and (19), which is a critical state. Therefore, the condition of C = 0 defines another critical velocity, which can be readily obtained from Eq. (20c) as
with the quantity in the curly brackets > 0.
From Eqs. (15a) and (24), it is clearly seen that Vcr1 < Vcr3. However, a mathematical comparison of Eq. (15a) with Eq. (23) shows that Vcr2 = Vcr3 when h1 = h2 or \(C_{11}^{(1)} /\rho^{(1)} = C_{11}^{(2)} /\rho^{(2)}\), Vcr2 > Vcr3 when h1 > h2 and \(C_{11}^{(1)} /\rho^{(1)} > C_{11}^{(2)} /\rho^{(2)}\) or h1 < h2 and \(C_{11}^{(1)} /\rho^{(1)} < C_{11}^{(2)} /\rho^{(2)}\), and Vcr2 < Vcr3 when h1 > h2 and \(C_{11}^{(1)} /\rho^{(1)} < C_{11}^{(2)} /\rho^{(2)}\) or h1 < h2 and \(C_{11}^{(1)} /\rho^{(1)} > C_{11}^{(2)} /\rho^{(2)}\).
Finally, when the discriminant of Eq. (20) vanishes, α will be paired real or purely imaginary double roots, yielding an exponentially changing or oscillating deflection w, which is a critical state. Thus, this condition defines one more critical velocity. That is, from Eqs. (21a-c) and (22), it follows that
which can be expanded to obtain the following cubic equation in V 2:
where
It can be readily shown that Eq. (26a), a cubic equation in the standard form, can be reduced to the following depressed cubic equation:
where
The discriminant of Eq. (27) is
When Δd > 0, Eq. (27) has three distinct real roots given by Viète’s trigonometric solution as (e.g., [24, 25]
From Eqs. (30) and (28), the three distinct real roots of Eq. (26a) can be obtained as
Then, the critical velocity Vcr0 in this case can be readily determined as the smallest real value among V1, V2 and V3 calculated from Eq. (31).
When Δd < 0, Eq. (27) has one real root and two conjugated complex roots that are obtainable from the Cardano formula. The three roots of Eq. (26a) in this case can then be determined using the Cardano formula and Eq. (28) as (e.g., [26])
where \(V_{1}^{2}\) in Eq. (32a) is the real root, which defines Vcr0 in this case.
When Δd = 0, Eq. (27) has a triple root of 0 if P = 0 or a single root of \(\omega_{1} = \frac{3Q}{P}\) and a double root of \(\omega_{2} = \omega_{3} = - \frac{3Q}{{2P}}\) if P ≠ 0 (e.g., [25]). Then, it follows from these results and Eq. (28) that the roots of Eq. (26a) in this case are given by
It is clear from Eqs. (33a,b) that Vcr0 = \(\sqrt { - \frac{b}{3a}}\) when P = 0, and Vcr0 is the smaller real value of V1 and V2 (= V3) computed from Eq. (33b) when P ≠ 0.
Note that Eqs. (20) and (21a-c) can also be expressed as
where
Equation (35) can be rewritten as, with the help of Eqs. (15a), (23) and (24),
It is seen from Eq. (36) that p and q each can be positive or negative, depending on the value of V. With the critical velocities Vcr1, Vcr2 and Vcr3 determined, the range of the pressure velocity V can be divided into four segments, for each of which the combination of p and q signs is different, resulting in different forms of the solution of Eq. (16) for the radial displacement w, as shown next.
3.1.1 Segment 1: 0 < V < V cr1
In this case, q > 0 and p > 0, which follows directly from Eq. (36) and the relations Vcr1 < Vcr3 and V < Vcr2.
Then, the solution of Eq. (34) can be readily obtained as
where
Clearly, m > 0 in this case. From Eq. (37), the four roots of the characteristic equation in Eq. (34) or Eq. (20) can be determined as [9, 12]:
where i is the imaginary unit (with i2 = − 1) and the overhead bar represents the conjugate.
From Eqs. (17), (19) and (39), the general solution of Eq. (16) in the current case (with c = 0) can be obtained as
where the superscripts “(I)” and “(II)” represent, respectively, region I (behind the pressure front; ξ < 0) and region II (ahead of the pressure front; ξ > 0), w0 is the static displacement given by
φ, β, τ, χ and κ are parameters defined by
and \(W_{1}^{{({\text{I}})}} \sim W_{4}^{{({\text{I}})}}\) and \(W_{1}^{{({\text{II}})}} \sim W_{4}^{{({\text{II}})}}\) are constants to be determined from the boundary and continuity conditions in the axial direction.
3.1.2 Segment 2: V cr1 < V < V cr2
In this case, q < 0 and p > 0, which follows directly from Eq. (36) and the relation V < Vcr3.
With q < 0, the solution of Eq. (34) has the form:
where
From Eq. (43), the four roots of the characteristic equation in Eq. (34) or Eq. (20) can be obtained as
for both p > 0 and p < 0.
From Eqs. (17), (19) and (45), the general solution of Eq. (16) in this case (with c = 0) can be determined as, for p > 0 and p < 0,
where
3.1.3 Segment 3: V cr2 < V < V cr3
In this case, q > 0 and p < 0, which follows directly from Eq. (36) and the relation Vcr1 < V. Note that the current condition of Vcr2 < Vcr3 corresponds to the cases with h1 > h2 and \(C_{11}^{(1)} /\rho^{(1)} < C_{11}^{(2)} /\rho^{(2)}\) or h1 < h2 and \(C_{11}^{(1)} /\rho^{(1)} > C_{11}^{(2)} /\rho^{(2)}\), as stated right below Eq. (24).
From Eq. (38), it follows that m < 0. Then, the four roots of the characteristic equation in Eq. (34) or Eq. (20) are given by [9, 12]:
Based on Eqs. (17), (19) and (48), the general solution of Eq. (16) in the current case (with c = 0) can be readily obtained as
where
and w0, φ, β and τ are defined in Eqs. (41) and (42).
3.1.4 Segment 4: V > V cr3
In this case, q < 0 and p < 0, which follows directly from Eq. (36) and the relations Vcr1 < Vcr3 and Vcr2 < V.
The four roots of the characteristic equation in this case are given by Eq. (45), and the general solution of Eq. (16) (with c = 0) is provided in Eq. (46).
With the critical velocities Vcr0 – Vcr3 and the radial displacement w(x, t) (\(= w^{(1)} (x,t) = w^{(2)} (x,t)\); see Eq. (10b)) determined for each velocity segment, the axial displacement u(x, t) (\(= u^{(1)} (x,t) = u^{(2)} (x,t)\); see Eq. (10a)) can be obtained from Eq. (11a). Then, all of the displacement, strain and stress components in each layer of the composite tube can be readily computed from Eqs. (1), (2) and (4) for a given value of the pressure velocity V.
3.2 Special cases
3.2.1 Composite tube without the rotary inertia effect
If the rotary inertia effect is neglected, Eq. (11b) reduces to
Similar to what is done in solving Eqs. (11a) and (11b), the characteristic equation for the system of Eqs. (11a) and (50) can be obtained as
which, as a quadratic equation in α2, has the roots:
The critical velocity Vcr0 in this case can be determined from the condition of vanishing discriminant of Eq. (51):
which can be expanded to yield
By following the procedure used in solving Eq. (26a), this cubic equation in V2 can be solved to get the critical velocity Vcr0. It is found that the formulas derived in Eqs. (27)–(33a,b) can be used to obtain Vcr0 in this case except that b and c in Eq. (26b) are now given by
The critical velocities Vcr1 and Vcr3 remain to be given, respectively, by Eqs. (24) and (15a), but Vcr2 is irrelevant in this case.
The radial displacement w continues to be provided by one of those expressions obtained in Sect. 3.1 except that p and q defined in Eq. (35) or Eq. (36) need to be replaced by
which follow directly from Eqs. (34), (51), (24) and (15a).
3.2.2 Composite tube with V/V cr2 < < 1 and V/V cr3 < < 1
With the help of Eqs. (23) and (15a), Eq. (16) can be expressed as
When V/Vcr2 < < 1 and V/Vcr3 < < 1, Eq. (56) simplifies to
It is seen from Eq. (57) that the rotary inertia effect has been precluded under the conditions indicated.
Similar to what is done in solving Eq. (18) in Sect. 3.1, Eq. (57) can be analyzed to get the following characteristic equation:
Note that Eqs. (58) and (51) can both be directly obtained from the general characteristic equation in Eq. (20). Equation (58) will be reached when the pressure velocity V involved in both the first and third terms in Eq. (20) is precluded by enforcing the conditions of V/Vcr2 < < 1 and V/Vcr3 < < 1. On the other hand, Eq. (51) will be generated when the rotary inertia effect is suppressed by removing “\(\left[ {\frac{{\rho^{(1)} h_{1}^{3} }}{12} + \frac{{\rho^{(2)} h_{2}^{3} }}{12}} \right]V^{2}\)” in the first term in Eq. (20), while retaining the velocity V in the third term, which enables the determination of Vcr1.
Solving the quadratic equation in α 2 in Eq. (58) yields
The critical velocity Vcr0 is given by the condition of vanishing discriminant of Eq. (58):
which leads to
This formula is valid for any two-layer composite tube under an internal pressure moving at a constant velocity V < < min(Vcr2, Vcr3), which suppresses the rotary inertia effect. There is no other critical velocity in this case, as indicated in Eq. (58). As a result, 0 < V < Vcr0 (< Vcr1) is the only velocity range to be considered. The expression for w remains the same as one of those given in Eqs. (40a)-(40c) for this velocity range except that p and q defined in Eq. (35) need to be replaced by
4 Applications to composite tubes with layers exhibiting four types of material symmetry
The critical velocity and radial displacement formulas derived in Sect. 3 for composite shells are applied here to tubes consisting of two dissimilar orthotropic, transversely isotropic, cubic or isotropic layers. The general formulas obtained in Sect. 3 can also be directly used for composite tubes containing two layers with a combination of any two of these four types of materials.
4.1 Composite tube with two orthotropic thin layers
The general case of a composite tube made from two dissimilar orthotropic layers with different Cij and ρ has been discussed in detail in Sect. 3.1.
For thin orthotropic cylindrical shells with σzz ≈ 0 and under axisymmetric loading, the elastic stiffness constants are given by [3, 9, 11]
where Exx and Eθθ are, respectively, Young’s moduli in the x- and θ-directions, νxθ and νθx are Poisson’s ratios, and μxz is the shear modulus in the xz-plane.
Applying Eq. (63) to each orthotropic layer and subsequently using Eq. (31), (32a), (33a) or (33b) will lead to the determination of the critical velocity Vcr0 of a composite tube consisting of two dissimilar orthotropic thin layers.
Substituting Eq. (63) into Eqs. (24), (23) and (15a), respectively, yields the critical velocities Vcr1, Vcr2 and Vcr3 as
for a composite tube made from two dissimilar orthotropic thin layers, which incorporate the rotary inertia effect (but exclude the radial stress effect) and have no restriction on the magnitude of the pressure velocity.
With Vcr1 − Vcr3 determined, the expressions of the radial displacement w in regions I and II for a given pressure velocity V belonging to one of the four segments can then be identified from those provided in Sect. 3.1, with C11, C12 and C22 for each layer involved in p and q defined in Eq. (35) now given by Eq. (63).
When V < < Vcr2 and V < < Vcr3, the substitution of Eq. (63) into Eq. (61) yields
as the critical velocity for a composite tube consisting of two dissimilar orthotropic thin layers under an internal pressure moving at a constant velocity V < < min(Vcr2, Vcr3), with both the rotary inertia and radical stress effects precluded. If the tube is homogeneous with \(E_{xx}^{(1)} = E_{xx}^{(2)} = E_{xx} ,\) \(E_{\theta \theta }^{(1)} = E_{\theta \theta }^{(2)} = E_{\theta \theta } ,\) \(\,\nu_{x\theta }^{(1)} = \nu_{x\theta }^{(2)} = \nu_{x\theta } ,\,\,\,\nu_{\theta x}^{(1)} = \nu_{\theta x}^{(2)} = \nu_{\theta x} ,\) \(\rho^{(1)} = \rho^{(2)} = \rho\), \(R_{1} \approx R \approx R_{2} ,\) \(h_{1} = h\) and \(h_{2} = 0\), then Eq. (65) reduces to
which is the same as that reported in Tzeng and Hopkins [36] and derived in Gao and Littlefield [11] for single-layer orthotropic thin tubes without including the rotary inertia effect.
In this case with V < < min(Vcr2, Vcr3), there is no other critical velocity for the composite tube consisting of two dissimilar orthotropic thin layers, and the expression for w remains the same as that given in Eq. (40a), (40b) or (40c) for the velocity range 0 < V < Vcr0 (< Vcr1) except that C11, C12 and C22 for each layer involved in p and q defined in Eq. (35) are now given by Eq. (63).
4.2 Composite tube with two transversely isotropic thin layers
For thin transversely isotropic cylindrical shells with σzz ≈ 0 and under axisymmetric loading, the elastic stiffness constants are given by [3, 11, 13, 41]
where ET and EL are, respectively, the Young’s moduli in the transverse (isotropic) plane and longitudinal direction, νTL and νLT are Poisson’s ratios, and μLT is the shear modulus in the longitudinal direction.
Using Eq. (67) for each transversely isotropic layer and then applying Eq. (31), (32a), (33a) or (33b) will give the critical velocity Vcr0, and substituting Eq. (67) into Eqs. (24), (23) and (15a) will yield the critical velocities Vcr1, Vcr2 and Vcr3 as
for a composite tube consisting of two dissimilar transversely isotropic thin layers, which account for the rotary inertia effect (but exclude the radial stress effect) and have no restriction on the magnitude of the pressure velocity.
With Vcr1 − Vcr3 determined, the expressions of the radial displacement w for a given pressure velocity V can then be identified from those provided in Sect. 3.1, with C11, C12 and C22 for each layer involved in p and q defined in Eq. (35) now given by Eq. (67).
When V < < Vcr2 and V < < Vcr3, substituting Eq. (67) into Eq. (61) gives
as the critical velocity Vcr0 for a composite tube consisting of two dissimilar transversely isotropic thin layers under an internal pressure moving at a constant velocity V < < min(Vcr2, Vcr3), which has precluded the rotary inertia and radial stress effects. If the tube is homogeneous with \(E_{L}^{(1)} = E_{L}^{(2)} = E_{L} ,\)\(E_{T}^{(1)} = E_{T}^{(2)} = E_{T} ,\)\(\,\nu_{LT}^{(1)} = \nu_{LT}^{(2)} = \nu_{LT} ,\,\,\nu_{TL}^{(1)} = \nu_{TL}^{(2)} = \nu_{TL} ,\) \(\rho^{(1)} = \rho^{(2)} = \rho\), R1 ≈ R ≈ R2, h1 = h and h2 = 0, then Eq. (69) simplifies to
which is the same as that first derived in Gao and Littlefield [11] for single-layer transversely isotropic thin tubes without including the rotary inertia effect.
In this case with V < < min(Vcr2, Vcr3), Eq. (58) shows that there is no other critical velocity for the composite tube consisting of two dissimilar transversely isotropic thin layers. In addition, the expression for w remains the same as that given in Eq. (40a), (40b) or (40c) for the velocity range 0 < V < Vcr0 (< Vcr1) except that C11, C12 and C22 for each layer involved in p and q defined in Eq. (35) are now given by Eq. (67).
4.3 Composite tube with two cubic material layers
For cubic materials with three independent elastic constants E, ν and μ, the non-vanishing stiffness components are (e.g., [1, 3]
Applying Eq. (71) to each cubic material layer and then using Eq. (31), (32a), (33a) or (33b) will lead to the determination of the critical velocity Vcr0, and substituting Eq. (71) into Eqs. (24), (23) and (15a), respectively, will yield the critical velocities Vcr1, Vcr2 and Vcr3 as
for a composite tube consisting of two dissimilar cubic material layers, which incorporate both the rotary inertia and radial stress effects and have no restriction on the magnitude of the pressure velocity.
With Vcr1 − Vcr3 determined, the expressions of w for a given pressure velocity V can then be identified from those provided in Sect. 3.1, with C11, C12 and C22 for each layer involved in p and q defined in Eq. (35) now given by Eq. (71).
When V < < Vcr2 and V < < Vcr3, using Eq. (71) in Eq. (61) leads to
as the critical velocity Vcr0 for a composite tube consisting of two dissimilar cubic material layers under an internal pressure moving at a constant velocity V < < min(Vcr2, Vcr3), which has precluded the rotary inertia effect but accounts for the radial stress effect. If the tube is homogeneous with \(E^{(1)} = E^{(2)} = E,\,\,\nu^{(1)} = \nu^{(2)} = \nu ,\)\(\rho^{(1)} = \rho^{(2)} = \rho\), R1 ≈ R ≈ R2, h1 = h and h2 = 0, then Eq. (73) reduces to
which is the same as that first derived in Gao and Littlefield [11] for single-layer cubic material tubes without including the rotary inertia effect.
In this case with V < < min(Vcr2, Vcr3), there is no other critical velocity for the composite tube consisting of two dissimilar cubic material layers, and the expression for w remains the same as that given in Eq. (40a), (40b) or (40c) for the velocity range 0 < V < Vcr0 (< Vcr1) except that C11, C12 and C22 for each layer involved in p and q defined in Eq. (35) are now given by Eq. (71).
For thin cubic material cylindrical shells with σzz ≈ 0 and under axisymmetric loading, the elastic stiffness constants are given by [3, 11]
Using Eq. (75) for each cubic material thin layer and then applying Eq. (31), (32a), (33a) or (33b) will result in the critical velocity Vcr0, and substituting Eq. (75) into Eqs. (24), (23) and (15a), respectively, will lead to the critical velocities Vcr1, Vcr2 and Vcr3 as
for a composite tube consisting of two dissimilar cubic material thin layers, which include the rotary inertia effect (but exclude the radial stress effect) and have no restriction on the magnitude of the pressure velocity.
With Vcr1 − Vcr3 determined, the expressions of w for a given pressure velocity V can then be identified from those provided in Sect. 3.1, with C11, C12 and C22 for each layer involved in p and q defined in Eq. (35) now given by Eq. (75).
When V < < Vcr2 and V < < Vcr3, the use of Eq. (75) in Eq. (61) yields
as the critical velocity Vcr0 for a composite tube consisting of two dissimilar cubic material thin layers under an internal pressure moving at a constant velocity V < < min(Vcr2, Vcr3), which has excluded both the rotary inertia and radial stress effects. If the tube is homogeneous with \(E^{(1)} = E^{(2)} = E,\)\(\nu^{(1)} = \nu^{(2)} = \nu ,\)\(\rho^{(1)} = \rho^{(2)} = \rho\), R1 ≈ R ≈ R2, h1 = h and h2 = 0, then Eq. (77) simplifies to
which is the same as that first derived in Gao and Littlefield [11] for single-layer cubic material thin tubes without including the rotary inertia effect.
In this case with V < < min(Vcr2, Vcr3), there is no other critical velocity for the composite tube consisting of two dissimilar cubic material thin layers. In addition, the expression for w remains the same as that given in Eq. (40a), (40b) or (40c) for the velocity range 0 < V < Vcr0 (< Vcr1) except that C11, C12 and C22 for each layer involved in p and q defined in Eq. (35) are now given by Eq. (75).
4.4 Composite tube with two isotropic layers
For isotropic materials with two independent elastic constants E (Young’s modulus) and ν (Poisson’s ratio), the stiffness components are given by (e.g., [9])
Using Eq. (79) for each isotropic layer and then applying Eq. (31), (32a), (33a) or (33b) will give the critical velocity Vcr0, and substituting Eq. (79) into Eqs. (24), (23) and (15), respectively, will yield the critical velocities Vcr1, Vcr2 and Vcr3 as
for a composite tube consisting of two dissimilar isotropic layers, which incorporate both the rotary inertia and radial stress effects and have no restriction on the magnitude of the pressure velocity.
With Vcr1 − Vcr3 determined, the expressions of w for a given pressure velocity V can then be identified from those provided in Sect. 3.1, with C11, C12 and C22 for each layer involved in p and q defined in Eq. (35) now given by Eq. (79).
When V < < Vcr2 and V < < Vcr3, substituting Eq. (79) into Eq. (61) gives
as the critical velocity for a composite tube consisting of two dissimilar isotropic layers under an internal pressure moving at a constant velocity V < < min(Vcr2, Vcr3), which has precluded the rotary inertia effect but accounts for the radial stress effect. If the tube is homogeneous with \(E^{(1)} = E^{(2)} = E,\,\,\nu^{(1)} = \nu^{(2)} = \nu ,\)\(\rho^{(1)} = \rho^{(2)} = \rho\), R1 ≈ R ≈ R2, h1 = h and h2 = 0, then Eq. (81) reduces to
which is the same as that first derived in Gao and Littlefield [11] for single-layer isotropic tubes without including the rotary inertia effect.
In this case with V < < min(Vcr2, Vcr3), there is no other critical velocity for the composite tube consisting of two dissimilar isotropic layers, as dictated by Eq. (58). In addition, the expression for w remains the same as that given in Eq. (40a), (40b) or (40c) for the velocity range 0 < V < Vcr0 (< Vcr1) except that C11, C12 and C22 for each layer involved in p and q defined in Eq. (35) are now given by Eq. (79).
For the composite tube with two dissimilar isotropic thin layers, σzz ≈ 0 and the expressions of σxx and σθθ in each layer are the same as those for the composite tube with two dissimilar cubic material thin layers. As a result, the expressions for the stiffness components C11, C12, C22 and C55 are also the same as those listed in Eq. (75) except that \(\mu = \frac{E}{2(1 + v)}\) in the current case.
Applying Eq. (75) to each isotropic thin layer and then using Eq. (31), (32a), (33a) or (33b) will lead to the critical velocity Vcr0, and substituting Eq. (75) into Eqs. (24), (23) and (15a), respectively, will yield the critical velocities Vcr1, Vcr2 and Vcr3 that are, respectively, the same as those listed in Eqs. (76a), (76b) and (76c) for the composite tube consisting of two dissimilar cubic material thin layers, which include the rotary inertia effect (but exclude the radial stress effect) and have no restriction on the magnitude of the pressure velocity.
When V < < min(Vcr2, Vcr3), substituting Eq. (75) into Eq. (61) will yield the critical velocity formula Vcr0 for a composite tube consisting of two dissimilar isotropic thin layers under an internal pressure moving at a constant velocity V < < min(Vcr2, Vcr3), which will be the same as that obtained in Eq. (77) for the composite tube with two dissimilar cubic material thin layers without the rotary inertia effect except that \(\mu = \frac{E}{2(1 + v)}\) here. In this case, there is no other critical velocity, as in all other cases with V < < min(Vcr2, Vcr3). That is, when both the rotary inertia and radial normal stress effects are suppressed and the material anisotropy is not considered, the newly derived formulas reduce to those for a composite tube containing two thin layers of dissimilar isotropic materials, which is a special (the simplest) case.
If the tube is homogeneous with \(E^{(1)} = E^{(2)} = E,\,\nu^{(1)} = \nu^{(2)} = \nu ,\)\(\rho^{(1)} = \rho^{(2)} = \rho\), \(R_{1} \approx R \approx R_{2} ,\)\(h_{1} = h\) and \(h_{2} = 0\), then the critical velocity formula for a single-layer isotropic thin tube under an internal pressure moving at a constant velocity V < < Vcr3 (= Vcr2 here) can be obtained from Eq. (77) as a special case, which will be the same as that derived in Eq. (78) for single-layer cubic material thin tubes.
In this case with V < < min(Vcr2, Vcr3), there is no other critical velocity for the composite tube consisting of two dissimilar isotropic thin layers. In addition, the expression for w remains the same as that given in Eq. (40a), (40b) or (40c) for the velocity range 0 < V < Vcr0 (< Vcr1) except that C11, C12 and C22 for each layer involved in p and q defined in Eq. (35) are now given by Eq. (75).
5 Example
To quantitatively illustrate the formulas analytically derived in Sects. 3 and 4, a numerical example is presented herein.
Consider a composite tube consisting of an isotropic steel inner layer with R1 = 31.524 mm, h1 = 3.048 mm, ρ(1) = 7870.9755 kg/m3, E(1) = 208.9111 GPa and ν (1) = 0.3 (or \(C_{11}^{(1)}\) = 229.5726 GPa = \(C_{22}^{(1)}\) and \(C_{12}^{(1)}\) = 68.8718 GPa) and an orthotropic glass/epoxy outer layer with measured values of R2 = 34.9657 mm, h2 = 3.8354 mm, ρ(2) = 2107.4764 kg/m3, \(C_{11}^{(2)}\) = 11.0316 GPa, \(C_{22}^{(2)}\) = 23.3732 GPa and \(C_{12}^{(2)}\) = 6.8051 GPa or predicted values of R2 = 34.8768 mm, h2 = 3.6576 mm, ρ(2) = 2107.4764 kg/m3, \(C_{11}^{(2)}\) = 22.1312 GPa, \(C_{22}^{(2)}\) = 40.2654 GPa and \(C_{12}^{(2)}\) = 9.6527 GPa.
These geometrical and material constants for the inner and outer layers are taken from Simkins [29], where the critical velocity Vcr0 was numerically determined as the minimum phase velocity from a dispersion curve. The other critical velocities Vcr1 – Vcr3 were not discussed in Simkins [29], since the method used there was only capable of predicting Vcr0.
From Eqs. (15a), (23) and (24), the critical velocities Vcr1 – Vcr3 of this two-layer composite tube can be directly obtained as
where the superscripts “M” and “P” denote, respectively, the values based on the measured and predicted material properties and geometrical parameters of the orthotropic outer layer provided in Simkins [29] and listed above.
The critical velocity Vcr0 can be computed using various formulas derived in Sect. 3. For the general case with both the rotary inertia and radial stress effects incorporated, it follows from Eqs. (26b), (28) and (29) that for the current two-layer composite tube,
With Δd > 0 for both cases from Eq. (84), the three distinct real values of \(V^{2}\)(as the roots of the cubic equation in Eq. (26a)) can be readily determined using Eqs. (31) and (84). The critical velocity Vcr0, as the smallest real value of V from the three roots \(V_{k}^{2}\)(k = 1, 2, 3), can then be obtained as
When the rotary inertia effect is suppressed, it follows from Eqs. (26b), (28), (54b) and (29) that for the current two-layer composite tube without the rotary inertia effect,
where the subscript “S” denotes the special case without the rotary inertia effect.
With Δd > 0 from Eq. (86) for both cases, the three distinct real values of \(V^{2}\)(as the roots of the cubic equation in Eq. (26a)) can be calculated from Eqs. (31) and (86). As the smallest real value of V from the three roots \(V_{k}^{2}\)(k = 1, 2, 3), the critical velocity Vcr0 for the composite tube without the rotary inertia effect can then be obtained as
When V < < Vcr2 and V < < Vcr3, the critical velocity Vcr0 of the current two-layer composite tube can be directly computed from Eq. (61) as
where the subscript “SD” represents the special case with the velocity constraints.
The numerical values of Vcr0 of the two-layer composite tube obtained above using various formulas derived in Sect. 3 are listed in Table 1, where they are also compared to the values of Vcr0 for the same composite tube computationally determined in Simkins [29] by plotting the dispersion curves, which read
A comparison of the values of Vcr0 summarized in Table 1 with the values of Vcr1 – Vcr3 listed in Eq. (83) for the two-layer composite tube shows that Vcr0 is much smaller than Vcr1, Vcr2 or Vcr3, which is consistent with what was found for the single-layer isotropic steel tube without the orthotropic outer layer [10, 11].
From Table 1, it is clear that the critical velocity Vcr0 given by the formulas without including the rotary inertia effect is higher than that predicted by the general formulas incorporating the rotary inertia effect, which is true for both the cases with the measured and predicted properties for the orthotropic outer layer. In addition, in both cases the value of Vcr0 obtained using the closed-form formula in Eq. (61), which is derived under the conditions of V < < Vcr2 and V < < Vcr3 that have also precluded the rotary inertia effect, is slightly larger than that predicted by the formulas without the rotary inertia effect. That is, the simplified formulas in the two cases excluding the rotary inertia effect over-predict the critical velocity Vcr0 of the composite tube and may lead to unsafe designs. This finding is consistent with what was observed for single-layer homogeneous tubes [11]. Moreover, the more explicit and simpler formula in Eq. (61) predicts about the same value of Vcr0 as that given by the formulas in Eqs. (31), (28), (26b), (54b) and (29). Hence, Eq. (61) can be used to quickly compute Vcr0 when the rotary inertia effect can be neglected.
Finally, the values of the critical velocity Vcr0 predicted by the three different sets of formulas derived in the current study are seen to agree fairly well with those numerically determined by Simkins [29] from dispersion curves of traveling flexural waves using the laminated orthotropic shell model of Dong [6], especially for the value based on the predicted properties of the orthotropic outer layer. This provides a validation of the newly developed analytical model.
6 Summary
Closed-form formulas are derived for critical velocities and radial displacement of a composite tube consisting of two laminated cylindrical layers of dissimilar materials under a uniform internal pressure moving at a constant velocity. A model for axisymmetric circular cylindrical Love–Kirchhoff thin shells incorporating the rotary inertia effect and general constitutive equations for orthotropic elastic materials is used in the formulation, leading to a unified treatment of composite tubes containing two layers of dissimilar materials, each of which can be orthotropic, transversely isotropic, cubic or isotropic.
The formulas for two-layer composite tubes obtained for the general case include both the rotary inertia and radial stress effects and consider the material anisotropy for each layer, which are reduced to those for the special cases without the rotary inertia effect and/or the radial stress effect and with various types of material symmetry. It is shown that the current new model for two-layer composite tubes recovers the model for single-layer, homogeneous tubes as a special case.
An example for a composite tube with an isotropic inner layer and an orthotropic outer layer is studied by directly applying the new model, which enables the determination of all four critical velocities of the composite tube. The numerical results reveal that six values of the lowest critical velocity given by three sets of the newly derived closed-form formulas are in fairly good agreement with those numerically determined by Simkins [29], thereby validating the current analytical model.
References
Ai, L., Gao, X.-L.: Micromechanical modeling of 3-D printable interpenetrating phase composites with tailorable effective elastic properties including negative Poisson’s ratio. J. Micromech. Mol. Phys. 2, 1750015-1–1750015-21 (2017)
Bert, C.W., Birman, V.: Parametric instability of thick, orthotropic, circular cylindrical shells. Acta Mech. 71, 61–76 (1988)
Bower, A.F.: Applied Mechanics of Solids. CRC Press, Boca Raton, FL (2009)
Cao, R., Li, L., Li, X., Mi, C.: On the frictional receding contact between a graded layer and an orthotropic substrate indented by a rigid flat-ended stamp. Mech. Mater. 158, 103847-1–103847-13 (2021)
Chonan, S.: Moving load on a two-layered cylindrical shell with imperfect bonding. J. Acoust. Soc. Am. 69, 1015–1020 (1981)
Dong, S.B.: Free vibration of laminated orthotropic cylindrical shells. J. Acoust. Soc. Am. 44, 1628–1635 (1968)
Eipakchi, H., Nasrekani, F.M.: Vibrational behavior of composite cylindrical shells with auxetic honeycombs core layer subjected to a moving pressure. Compos. Struct. 254, 112847-1–112847-12 (2020)
Eipakchi, H., Nasrekani, F.M., Ahmadi, S.: An analytical approach for the vibration behavior of viscoelastic cylindrical shells under internal moving pressure. Acta Mech. 231, 3405–3418 (2020)
Gao, X.-L.: Two displacement methods for in-plane deformations of orthotropic linear elastic materials. Z. Angew. Math. Phys. 52, 810–822 (2001)
Gao, X.-L.: Critical velocities of anisotropic tubes under a moving pressure incorporating transverse shear and rotary inertia effects. Acta Mech. 233, 3511–3534 (2022)
Gao, X.-L., Littlefield, A.G.: Critical velocities and displacements of anisotropic tubes under a moving pressure. Math. Mech. Solids 27, 2662–2688 (2022)
Gao, X.-L., Mall, S.: Variational solution for a cracked mosaic model of woven fabric composites. Int. J. Solids Struct. 38, 855–874 (2001)
Gao, X.-L., Mao, C.L.: Solution of the contact problem of a rigid conical frustum indenting a transversely isotropic elastic half-space. ASME J. Appl. Mech. 81, 041007-1–041007-12 (2014)
Herrmann, G., Mirsky, I.: Three-dimensional and shell-theory analysis of axially symmetric motions of cylinders. ASME J. Appl. Mech. 23, 563–568 (1956)
Jones, J.P., Bhuta, P.G.: Response of cylindrical shells to moving loads. ASME J. Appl. Mech. 31, 105–111 (1964)
Jones, J.P., Whittier, J.S.: Axially symmetric motions of a two-layered Timoshenko-type cylindrical shell. ASME J. Appl. Mech. 33, 838–844 (1966)
Labuschagne, A., van Rensburg, N.F.J., van der Merwe, A.J.: Comparison of linear beam theories. Math Comput. Modell. 49, 20–30 (2009)
Leissa, A.W.: Vibration of Shells. NASA SP-288. Scientific and Technical Information Office, National Aeronautics and Space Administration, Washington, DC (1973)
Lin, T.C., Morgan, G.W.: A study of axisymmetric vibrations of cylindrical shells as affected by rotary inertia and transverse shear. ASME J. Appl. Mech. 23, 255–261 (1956)
Littlefield, A.G., Hyland, E.J.: 120 mm prestressed carbon fiber/thermoplastic overwrapped gun tubes. ASME J. Pres. Ves. Tech. 134, 041008-1–041008-9 (2012)
Littlefield, A.G., Hyland, E.J., Andalora, A., Klein, N., Langone, R., Becker, R.: Carbon fiber/thermoplastic overwrapped gun tube. ASME J. Pres. Ves. Tech. 128, 257–262 (2006)
Mirsky, I.: Axisymmetric vibrations of orthotropic cylinders. J. Acous. Soc. Am. 36, 2106–2112 (1964)
Nechitailo, N.V., Lewis, K.B.: Critical velocity for rails in hypervelocity launchers. Int. J. Impact Eng. 33, 485–495 (2006)
Nickalls, R.W.D.: Viète, Descartes and the cubic equation. Math. Gaz. 90(518), 203–208 (2006)
Okereke, O.E., Iwueze, I.S., Ohakwe, J.: Some contributions to the solution of cubic equations. Br. J. Math. Comp. Sci. 4, 2929–2941 (2014)
Okoli, O.C., Laisin, M., Nsiegbe, N.A., Eze, A.C.: Method of solution to cubic equation. COOU J. Phys. Sci. 3, 515–521 (2020)
Prisekin, V.L.: The stability of a cylindrical shell subjected to a moving load. Mekhanika i Mashinostroenie 5, 133–134 (1961)
Ruzzene, M., Baz, A.: Dynamic stability of periodic shells with moving loads. J. Sound Vib. 296, 830–844 (2006)
Simkins, T.E.: Dynamic strains in an orthotropically-wrapped gun tube. Part I – Theoretical. Technical Report ARCCB-TR-93026. Watervliet, NY: U.S. Army Armament Research, Development and Engineering Center, Benét Laboratories (1993)
Simkins, T.E.: Amplification of flexural waves in gun tubes. J. Sound Vib. 172, 145–154 (1994)
Simkins, T.E.: The influence of transient flexural waves on dynamic strains in cylinders. ASME J. Appl. Mech. 62, 262–265 (1995)
Simkins, T.E., Pflegl, G.A., Stilson, E.G.: Dynamic strains in a 60 mm gun tube: An experimental study. J. Sound Vib. 168, 549–557 (1993)
Sofiyev, A.H.: Dynamic response of an FGM cylindrical shell under moving loads. Compos. Struct. 93, 58–66 (2010)
Steigmann, D.J.: On the relationship between the Cosserat and Kirchhoff-Love theories of elastic shells. Math. Mech. Solids 4, 275–288 (1999)
Tang, S.-C.: Dynamic response of a tube under moving pressure. J. Eng. Mech. Div. 91(5), 97–122 (1965)
Tzeng, J.T., Hopkins, D.A.: Dynamic response of composite cylinders subjected to a moving internal pressure. J. Reinf. Plas. Compos. 15, 1088–1105 (1996)
Zhang, G.Y., Gao, X.-L.: A non-classical model for first-order shear deformation circular cylindrical thin shells incorporating microstructure and surface energy effects. Math. Mech. Solids 26, 1294–1319 (2021)
Zhang, G.Y., Gao, X.-L., Bishop, J.E., Fang, H.E.: Band gaps for elastic wave propagation in a periodic composite beam structure incorporating microstructure and surface energy effects. Compos. Struct. 189, 263–272 (2018)
Zhang, G.Y., Gao, X.-L., Guo, Z.Y.: A non-classical model for an orthotropic Kirchhoff plate embedded in a viscoelastic medium. Acta Mech. 228, 3811–3825 (2017)
Zhang, G.Y., Gao, X.-L., Littlefield, A.G.: A non-classical model for circular cylindrical thin shells incorporating microstructure and surface energy effects. Acta Mech. 232, 2225–2248 (2021)
Zhang, G.Y., Qu, Y.L., Gao, X.-L., Jin, F.: A transversely isotropic magneto-electro-elastic Timoshenko beam model incorporating microstructure and foundation effects. Mech. Mater. 149, 103412-1–103412-13 (2020)
Acknowledgements
The author would like to thank Prof. Shaofan Li and two anonymous reviewers for their encouragement and helpful comments on an earlier version of the paper.
Funding
Open access funding provided by SCELC, Statewide California Electronic Library Consortium.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gao, XL. Critical velocities of a two-layer composite tube under a moving internal pressure. Acta Mech 234, 2021–2043 (2023). https://doi.org/10.1007/s00707-023-03476-8
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00707-023-03476-8