Abstract
The impacts of multiple reflection within the interlayer on wave propagation across layered rock masses have remained unclear. To address this, we first derive the governing equations for the wave propagation in time domain based on an equivalent layer model. These equations are validated by comparing them with a previously used method in an idealized case. Subsequently, a systematic investigation is carried out, progressing from idealized to generalized cases, to explore the frequency-dependent characteristics of the transmission and reflection coefficients, as well as energy dissipation rate. The mechanisms behind these frequency-dependent features are thoroughly analyzed, in conjunction with the evolution of waveforms and the effects of multiple reflections. The results indicate that the proposed model and derived equations effectively simulate the multiple reflection effects in the wave propagation behavior of layered rock masses. Multiple reflections within the interlayer result in an oscillatory decay of the transmission coefficient in layered rock masses as wave frequency increases. Interestingly, stress waves with frequencies that are even multiples of the ratio of wave speed to interlayer thickness demonstrate a robust capability to propagate across the interlayer. This phenomenon arises from the superposition of multiple reflected waves in phase within the interlayer, and gradually disappears with a decrease in quality factor of interlayer or an increase in wave frequency. The underlying mechanisms of these features are convincingly explained by combining the effects of multiple wave reflections.
Highlights
-
A wave propagation equation accounting for multiple reflections in layered rock masses was derived.
-
A non-monotonic relationship was revealed between transmission coefficient and wave frequency.
-
A comprehensive analysis was conducted for the underlying mechanisms in frequency dependence.












Similar content being viewed by others
Data availability
The data and code are available by requesting on the corresponding author.
Abbreviations
- x :
-
The number of contact surface
- x −, x + :
-
The downside or upside for the xth contact surface
- u x −, u x + :
-
The displacement at the downside or upside of xth contact surface
- v x −, v x + :
-
The vector velocity at the downside or upside of xth contact surface
- v u x −, v u x + :
-
The velocity of up-traveling wave at the downside or upside of xth contact surface
- v d x −, v d x + :
-
The velocity of down-traveling wave at the downside or upside of xth contact surface
- σ x −, σ x + :
-
The vector stress at the downside or upside of the xth contact surface
- z x −, z x + :
-
The wave impedance for the medium at the downside or upside of xth contact surface
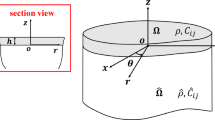
- ρ r, ρ f :
-
The density of rock or thin layer
- c r, c f :
-
The wave speed of rock or thin layer
- N :
-
The total number of thin layers
- E :
-
Modulus of elasticity
- μ :
-
Viscosity coefficient
- k :
-
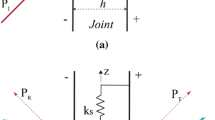
Stiffness coefficient of contact surface
- η :
-
Viscosity coefficient of contact surface
- d :
-
The thickness of thin layer
- h :
-
The thickness of rock interlayer
- t :
-
Time
- Δt :
-
The time step size
- i :
-
Time step
- f :
-
Frequency
- f k :
-
The central frequency for a transient wave of semi-sinusoidal
- v In :
-
The velocity of incident wave
- R :
-
Reflection coefficient
- T :
-
Transmission coefficient
- Δf :
-
Frequency interval
- c :
-
The equivalent wave speed of interlayer
- t 0 :
-
The phase difference between the primary and secondary up-traveling waves
- T :
-
Period
- Q :
-
Quality factor of interlayer
- Q 0 :
-
The true quality factor of the interlayer under the fitting model parameters
- E In, E Re, E Tr :
-
The energy of incident wave, reflected wave, and transmitted wave
- e loss :
-
Energy dissipation rate
- λ :
-
Wave length
References
Brekhovskikh LM (1980) Waves in layered media. Elsevier, Amsterdam
Cai MF (2013) Rock mechanics and engineering. Chinese Science Publishing & Media Ltd., Beijing
Cai JG, Zhao J (2000) Effects of multiple parallel fractures on apparent attenuation of stress waves in rock masses. Int J Rock Mech Min Sci 37(4):661–682. https://doi.org/10.1016/S1365-1609(00)00013-7
Dang WG, Tao K, Chen XF (2022) Frictional behavior of planar and rough granite fractures subjected to normal load oscillations of different amplitudes. J Rock Mech Geotech Eng 14(3):746–756. https://doi.org/10.1016/j.jrmge.2021.09.011
Ding XH, Yang YQ, Zhou W et al (2022) The law of blast stress wave propagation and fracture development in soft and hard composite rock. Sci Rep 12(1):17120. https://doi.org/10.1038/s41598-022-22109-z
Fan LF, Wang LJ, Wu ZJ (2018) Wave transmission across linearly jointed complex rock masses. Int J Rock Mech Min Sci 112:193–200. https://doi.org/10.1016/j.ijrmms.2018.09.004
Fehler M (1982) Interaction of seismic waves with a viscous liquid layer. Bull Seismol Soc Am 72:55–72
Guo JX, Cao CH, Chen XF et al (2023) Effects of intrinsic anisotropy on seismic dispersion, attenuation and frequency-dependent anisotropy. Chin Sci Bull. https://doi.org/10.1360/TB-2022-1039
Huang XL, Qi SW, Xia KW, Shi XS (2018) Particle crushing of a filled fracture during compression and its effect on stress wave propagation. J Geophys Res Solid Earth 123:5559–5587. https://doi.org/10.1029/2018JB016001
Hudson JA (1981) Wave speeds and attenuation of elastic waves in material containing cracks. Geophys J R Astron Soc 64(1):133–150. https://doi.org/10.1111/j.1365-246X.1981.tb02662.x
Johnston DH, Toksoz MN, Timur A (1979) Attenuation of seismic waves in dry and saturated rocks II. Mechanisms. Geophysics 44(4):691–711. https://doi.org/10.1190/1.1440970
Li JC, Ma GW (2010) Analysis of blast wave interaction with a rock joint. Rock Mech Rock Eng 43(6):777–787. https://doi.org/10.1007/s00603-009-0062-0
Li JC, Ma GW, Zhao J (2011) Stress wave interaction with a nonlinear and slippery rock joint. Int J Rock Mech Min Sci 48:493–500. https://doi.org/10.1016/j.ijrmms.2010.11.013
Li JC, Wu W, Li HB et al (2013) A thin-layer interface model for wave propagation through filled rock joints. J Appl Geophys 91:31–38. https://doi.org/10.1016/j.jappgeo.2013.02.003
Lu SW, Zhou CB, Zhang Z, Jiang N (2019) Particle velocity response of surrounding rock of a circular tunnel subjected to cylindrical P-waves. Tunnel Undergr Sp Technol 83:393–400. https://doi.org/10.1016/j.tust.2018.09.020
Pyrak-Nolte LJ (1988) Seismic visibility of fractures. Dissertation: University of California
Rokhlin SI, Wang YJ (1991) Analysis of boundary conditions for elastic wave interaction with an interface between two solids. J Acoust Soc Am 89:503–515
Shen WL, Shi GC, Wang YG et al (2021) Tomography of the dynamic stress coefficient for stress wave prediction in sedimentary rock layer under the mining additional stress. Int J Min Sci Technol 31(4):653–663. https://doi.org/10.1016/j.ijmst.2021.04.003
Sinha UN, Singh B (2000) Testing of rock joints filled with gouge using a triaxial apparatus. Int J Rock Mech Min Sci 37:963–981. https://doi.org/10.1016/S1365-1609(00)00030-7
Tao K, Dang WG (2023) Frictional behavior of quartz gouge during slide-hold-slide considering normal stress oscillation. Int J Coal Sci Technol 10:34. https://doi.org/10.1007/s40789-023-00592-7
Tao K, Dang WG, Li YC (2023) Frictional sliding of infilled planar granite fracture under oscillating normal stress. Int J Min Sci Technol 33(6):687–701. https://doi.org/10.1016/j.ijmst.2022.12.001
Wang ZL, Konietzky H, Shen RF (2010) Analytical and numerical study of P-wave attenuation in rock shelter layer. Soil Dyn Earthq Eng 30(1–2):1–7. https://doi.org/10.1016/j.soildyn.2009.05.004
Wang R, Hu ZP, Zhang D et al (2017) Propagation of the stress wave through the filled joint with linear viscoelastic deformation behavior using time-domain recursive method. Rock Mech Rock Eng 50:3197–3207. https://doi.org/10.1007/s00603-017-1301-4
Wang SW, Li JC, Li X, He L (2022a) Dynamic photoelastic experimental study on the influence of joint surface geometrical property on wave propagation and stress disturbance. Int J Rock Mech Min Sci 149:104985. https://doi.org/10.1016/j.ijrmms.2021.104985
Wang LJ, Fan LF, Du XL (2022b) Non-attenuation behavior of stress wave propagation through a rock mass. Rock Mech Rock Eng 55:3807–3815. https://doi.org/10.1007/s00603-022-02843-6
Wang ZL, Wang SM, Wang JG (2023) Hydro-mechanical coupling behavior and statistical damage constitutive model of deep marble with disturbance. Int J Damage Mech 32(7):889–913. https://doi.org/10.1177/10567895231174630
Wei HX, Wang CZ, Zhu J et al (2023) Propagation characteristics of stress wave in layered rock mass under the impact of high-pressure gas. Proc Inst Civ Eng-Geotech Eng. https://doi.org/10.1680/jgeen.22.00116
Yu J, Cai YY, Song BX et al (2012) A brief review of previous studies on regularity of stress waves propagation in micro-cracks of rock. Appl Mech Mater 170–173(1):511–515. https://doi.org/10.4028/www.scientific.net/AMM.170-173.511
Zhang Y, Zhang N, Dai F et al (2023) Dynamic stress concentration and particle velocity response of a composite lining tunnel with imperfect interfaces subjected to blasting P waves. Int J Geomech 23(11):06023018. https://doi.org/10.1061/IJGNAI.GMENG-8361
Zhou GQ, Liu XM (1996) Viscoelastic theory. University of Science and Technology of China Press, Hefei
Zhu JB, Perino A, Zhao GF et al (2011) Seismic response of a single and a set of filled joints of viscoelastic deformational behavior. Geophys J Int 186:1315–1330. https://doi.org/10.1111/j.1365-246X.2011.05110.x
Zou Y, Li JC, Laloui L et al (2017) Analytical time-domain solution of plane wave propagation across a viscoelastic rock joint. Rock Mech Rock Eng 50(10):2731–2747. https://doi.org/10.1007/s00603-017-1246-7
Acknowledgements
This study was financially supported by the National Natural Science Foundation of China (12272119) and Yalong River Joint Fund of National Natural Science Foundation of China (U1965101).
Funding
The authors are grateful to National Natural Science Foundation of China (NSFC) via projects (12272119; U1965101).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of Interest
The authors declared that they have no conflicts of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Wang, S., Wang, Z. & Wang, J. Analysis of Wave Propagation Across Layered Rock Masses Considering Multiple Reflection Effects. Rock Mech Rock Eng (2024). https://doi.org/10.1007/s00603-024-03941-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00603-024-03941-3