1 Introduction

Hydraulic fracturing techniques have been widely applied in oil/gas extraction, coalbed methane, enhanced geothermal systems, and for pre-conditioning ore bodies ahead of block-caving mining (Guanhua et al. 2019; Ji et al. 2021; Kong et al. 2021; Wu 2018; Zhuang and Zang 2021). The primary purpose of hydraulic fracturing is to improve the permeability of the rock mass, or in the case of block caving to reduce rock integrity and strength, by inducing more cracks, increasing crack density, or enhancing the complexity of existing crack networks. Moreover, the near-wellbore fracture complexity has significant impacts on fracking-related operations, e.g., fluid flow, breakdown pressure, proppant transport, wellbore strengthening and well productivity (Fazio et al. 2021; Feng and Gray 2018; Gordeliy et al. 2016; Zhang et al. 2011). Due to the mineral heterogeneity of the rock matrix and the presence of natural fractures and weak interfaces in the rock mass, hydraulic fracturing involves heterogeneous crack propagation processes. An induced hydraulic fracture may cross, be deflected, or be halted by natural fractures (Lee et al. 2015; Zeng and Wei 2017; Zhang et al. 2009). The interaction between hydraulic fractures (HF) and natural fractures (NF), therefore, plays a fundamental role in the evolution of hydraulic fracture networks.

In the past decades, considerable research has been carried out to investigate the interaction mechanisms between HF and NF (Blanton 1982; Dehghan et al. 2015a, b; Rahman and Rahman 2013; Renshaw and Pollard 1995; Sarmadivaleh and Rasouli 2013; Zhang et al. 2021; Zhou et al. 2008). Blanton (1982) carried out a series of experiments on shale specimens with a single pre-existing fracture and found that hydraulic fractures tended to cross over pre-existing fractures under high differential stresses and high approach angles. Renshaw and Pollard (1995) investigated the interaction modes between the HF and orthogonal NF through experiments and proposed a fracture criterion for predicting whether the HF can cross the orthogonal NF based on linear fracture mechanics. They found that HF was more prone to cross the orthogonal NF with a larger friction coefficient. Furthermore, Sarmadivaleh and Rasouli (2013) modified Renshaw and Pollard’s criterion to predict the interaction mode for a non-orthogonal cohesive NF. They found that the cohesion and friction of the NF significantly changed the interaction mode. Zhou et al. (2008) employed a triaxial fracturing system to investigate fracture patterns for rock-like specimens with natural fractures by inserting three different thicknesses of papers (0.06 mm, 0.11 mm and 0.12 mm in thickness). They found that HF was more prone to cross the NF (paper) with a smaller aperture. Dehghan et al. (2015a; b) investigated the effects of natural fracture dip and strike on hydraulic fracture propagation through triaxial fracturing experiments and found hydraulic fractures were more tortuous for low dip and strike of the pre-existing fractures. Fraser-Harris et al. (2020) carried out hydraulic fracturing experiments of synthetic analogue materials and rock samples under changing polyaxial stress conditions and found fractures propagated in both tensile and shear orientations with respect to the polyaxial stress state. Similar relationships between network complexity and the geometry, approach angle, fracture properties and in situ stress are observed in natural fracture systems where a later set of fractures interacts with earlier features (Soden et al. 2016; Moir et al. 2010) Thus, the interaction between hydraulic and natural fractures is complex and affected by the in situ stress, approach angle, NF shear strength, NF aperture, etc.

Because of the limitations of analytical models on predicting crack interaction and propagation with the fluid flow (Zhang et al. 2021; Sarmadivaleh and Rasouli 2013) and the experimental difficulties of preparing specimens with precise natural fractures (Zhou et al. 2008; Dehghan et al. 2015a, b), the numerical method has brought considerable advantages. Zhang and Jeffrey (2006) developed a numerical method based on stress intensity factors and modelled the interaction between frictional NF and HF in the impermeable rock matrix. They found that the friction coefficient of NF significantly affected the interaction mode and that HF tended to cross the NF for a larger frictional coefficient. Lisjak et al. (2017) and Yan and Zheng (2017) developed a combined finite-discrete element method (FDEM) to investigate hydraulic fracturing in discontinuous rock masses, which can capture cracking and fluid flow through discontinuities and the surrounding permeable rock matrix. Kwok et al. (2019) modelled hydraulic fracturing in a jointed shale formation based on the discrete element model (PFC2D) and found that the formation’s anisotropy promoted fracture growth along the sedimentary bedding. Li et al. (2019a, b) developed a two-dimensional explicit numerical method based on the cohesive crack model and considered the rock formation as impermeable to investigate the interactions between the NF and HF. They found that, compared with NFs without initial hydraulic aperture, NFs with a very small initial hydraulic aperture (0.01–0.05 mm) were more prone to be activated. Zhou et al. (2020) investigated the interaction between NF and HF in a permeable matrix through the extended finite element method (XFEM) employing maximum hoop tensile stress criterion and found the NF was more likely to be dilated in a low permeability matrix.

The fracking treatment is closely related to the near-wellbore fracture. For example, the near-well fracture complexity affects the interpretation of field infectivity tests (e.g., diagnostic fracture injection tests) and the appropriate uses of proppant and lost circulation materials (Feng and Gray 2018; Gordeliy et al. 2016; Zhang et al. 2011). Gordeliy et al. (2016) employed XFEM to simulate the curved fractures near the perforated wellbore and found the fluid injection pressure in the wellbore can change the fracture re-orientation angle. Feng and Gray (2018) modelled the fracture initiation and propagation for a wellbore with perforation in a permeable rock matrix and found a larger permeability of rock matrix resulted in a sharper fracture deflection angle. Fazio et al. (2021) carried out hydraulic fracturing experiments on rock specimens with different permeability, and found that fractures propagated more slowly and episodically in highly permeable sandstones. Reducing the wall permeability of the borehole using an inner sleeve was also shown to promote hydraulic fracturing to occur in highly permeable sandstone (Fazio et al. 2021).

Clearly, for the near-wellbore problem, the stress of rock is redistributed due to the excavation/drilling of the wellbore and the fluid injection pressure also works as a radial pressure on the wellbore surface. These two factors will both unavoidably affect the interaction between HF and NF near the wellbore. For the interaction between HF and NF, the activation of natural fractures is significantly affected by the shearing fracture properties of NF (including cohesion and friction) and that the rock formation should be considered as a permeable medium. However, the shearing fracture mechanism behind the interaction has not been fully understood and a mixed-mode fracture model that considers the crack propagation, frictional effect and the fully hydraulic–mechanical coupling is still lacking. Moreover, the interaction between HF and NF near the wellbore has rarely been investigated so far. Although the cohesive crack model has been widely employed to simulate the fracture of rock, concrete and composite materials (Bazant and Le 2017), the shear fracture properties are normally considered as constant values, which is unable to model the shear fracture propagation in rock under high compressive stress normal to the crack. The interaction between HF and NF normally changes the fracture propagation from tension mode to mixed mode involving compression-dominated shear. A new constitutive model which can account for the compression-induced shear strength enhancement in existing mixed-mode fracture model would be necessary.

This paper aims to develop a mixed-mode fracture model considering the Mohr–Coulomb criterion in the cohesive crack model. The model is implemented into ABAQUS by an in-house subroutine written in FORTRAN. The rock matrix and cohesive crack interfaces are both coupled with fluid flow. A worked example with a wellbore and a natural fracture is established to demonstrate the model and investigate the near-wellbore interaction between HF and NF. The developed numerical method is then verified by comparing the results with analytical solutions and experimental results. Furthermore, the fracture mechanisms behind the near-wellbore interactions are discussed. Finally, the effects of approach angle, NF location, in situ stress, cohesion strength and friction angle of NF, and flow rate on the near-wellbore interaction between the NF and HF are investigated.

2 Mixed-Mode Fracture Model

Since the cohesive crack model was proposed to simulate discrete cracking in the fracture process zone of concrete by Hillerborg et al. (1976), it has been widely employed to model the fracture of quasi-brittle materials including rocks (Bazant and Le 2017; Li et al. 2019a, b; Lisjak et al. 2017; Yan and Jiao 2018; Yang et al. 2018; Yang et al. 2019). Another well-known employment of cohesive crack model is the combined finite-discrete method (Munjiza et al. 1995) which embeds cohesive elements everywhere in the mesh (i.e., every edge of the bulk elements). Normally, the cohesive element is of zero thickness before it is cracked. A traction–separation law is employed to constitutively control the cohesive elements. The traction–separation laws for Mode I (tension) and Mode II (shear) fractures can be expressed as follows:

$$\left\{\begin{array}{c}{\sigma }_{\mathrm{n}}={f}_{\mathrm{n}}\left({\delta }_{\mathrm{n}}\right)\\ {\sigma }_{\mathrm{s}}={f}_{\mathrm{s}}\left({\delta }_{\mathrm{s}}\right)\end{array}\right.,$$
(1)

where \({\sigma }_{\mathrm{n}}\) and \({\sigma }_{\mathrm{s}}\) are the normal and tangential traction stresses, respectively; \({\delta }_{\mathrm{n}}\) and \({\delta }_{\mathrm{s}}\) are the opening and shearing displacements of the cohesive crack. \({f}_{\mathrm{n}}\) and \({f}_{\mathrm{s}}\) are the functions defining the relationships between traction and separation for Mode I and Mode II fractures, respectively.

Before damage or crack initiation, the normal and tangential stress linearly increase as a function of displacement by a penalty stiffness, \({K}_{\mathrm{p}}\), which can be expressed as follows:

$$\left\{\begin{array}{c}{\sigma }_{\mathrm{n}}={K}_{\mathrm{p}}{\delta }_{\mathrm{n}}\\ {\sigma }_{\mathrm{s}}={{K}_{\mathrm{p}}\delta }_{\mathrm{s}}\end{array}.\right.$$
(2)

A quadratic stress criterion f is employed to determine the crack initiation, which can be expressed as follows:

$$f={\left(\frac{\langle {\sigma }_{\mathrm{n}}\rangle }{{\sigma }_{\mathrm{n}}^{0}}\right)}^{2}+{\left(\frac{{\sigma }_{\mathrm{s}}}{{\sigma }_{\mathrm{s}}^{0}}\right)}^{2},$$
(3)

where \({\sigma }_{\mathrm{n}}^{0}\) and \({\sigma }_{\mathrm{s}}^{0}\) are the tensile strength and shear strength of rock, respectively. < > is the Macaulay bracket which ensures the normal compressive stress will not cause rock fracture in Mode I, which is defined as follows:

$$\langle {\sigma }_{\mathrm{n}}\rangle =\left\{\begin{array}{ll} 0 ({\sigma }_{\mathrm{n}} < 0, & {\text{compression}})\\ {\delta }_{\mathrm{n}} ({\sigma }_{\mathrm{n}}\ge 0, & {\text{tension}})\end{array}.\right.$$
(4)

When the fracture criterion f reaches 1, rock crack initiation will occur. The shear strength of rock is determined by the Mohr–Coulomb failure criterion (Mohr 1990; Heyman 1972; Labuz and Zang 2012) as:

$${\sigma }_{\mathrm{s}}^{0}=c+\mathrm{tan}\,\varphi \langle -{\sigma }_{\mathrm{n}}\rangle ,$$
(5)

where \(c\) is the cohesion strength of rock; \(\varphi\) is the friction angle of rock; \(-{\sigma }_{\mathrm{n}}\) is the normal compressive stress of the cohesive crack. The Macaulay bracket makes \(\langle -{\sigma }_{\mathrm{n}}\rangle\) zero for tensile stress.

According to Eqs. (1)–(5), for the cohesive crack in a compressive-shearing mode, rock fracture is caused by the tangential stress and the strength is determined by the cohesion strength, friction angle and normal compressive stress. While for the cohesive crack in a tensile-shearing mode, rock fracture is caused by the normal and tangential stress and the strength is determined by the tensile and cohesion strength.

After damage initiation, the normal and shear stresses gradually decrease while the corresponding displacements continue to increase, which is known as strain softening. For the mixed-mode fracture, an effective displacement which couples tensile and shearing displacements is defined to determine overall damage (Park et al. 2016). The effective displacement \({\delta }_{\mathrm{m}}\) is defined as follows:

$${\delta }_{\mathrm{m}}=\sqrt{{\langle {\delta }_{\mathrm{n}}\rangle }^{2}+{{\delta }_{\mathrm{s}}}^{2}}.$$
(6)

For a linear softening, the overall damage of the cohesive crack can be expressed as follows (Xi et al. 2018):

$$D=\frac{{\delta }_{\mathrm{m}}^{f}({\delta }_{\mathrm{m}}^{\mathrm{max}}-{\delta }_{\mathrm{m}}^{0})}{{\delta }_{\mathrm{m}}^{\mathrm{max}}({\delta }_{\mathrm{m}}^{f}-{\delta }_{\mathrm{m}}^{0})},$$
(7)

where D is the damage value of the cohesive crack varying from 0 to 1; \({\delta }_{\mathrm{m}}^{\mathrm{max}}\) is the maximum effective relative displacement during the loading history; \({\delta }_{\mathrm{m}}^{0}\) is the critical effective relative displacement when the damage starts (i.e., D = 0); \({\delta }_{\mathrm{m}}^{\mathrm{f}}\) is the effective relative displacement when complete failure occurs (i.e., D = 1). \({\delta }_{\mathrm{m}}^{\mathrm{f}}\) can be determined by the mixed-mode fracture B–K criterion as follows (Kenane and Benzeggagh 1997; Xi et al. 2018):

$${\delta }_{\mathrm{m}}^{\mathrm{f}}=\frac{2}{{K}_{\mathrm{p}{\delta }_{\mathrm{m}}^{0}}}\left[{G}_{\mathrm{I}}+({G}_{\mathrm{II}}-{G}_{\mathrm{I}}){\left(\frac{{G}_{\mathrm{s}}}{{G}_{\mathrm{s}}+{G}_{\mathrm{n}}}\right)}^{2}\right],$$
(8)

where \({G}_{\mathrm{I}}\) and \({G}_{\mathrm{II}}\) are the fracture energy (critical energy release rate) of Mode I and Mode II fractures, respectively; \({G}_{\mathrm{n}}\) and \({G}_{\mathrm{s}}\) are the work done by the tractions and their conjugate relative displacements in the normal and shear directions, respectively.

The mixed-mode fracture energy can be expressed as follows:

$${G}_{\mathrm{m}}=\left[{G}_{\mathrm{I}}+({G}_{\mathrm{II}}-{G}_{\mathrm{I}}){\left(\frac{{G}_{\mathrm{s}}}{{G}_{\mathrm{s}}+{G}_{\mathrm{n}}}\right)}^{2}\right].$$
(9)

The Mode I fracture energy of rock can be measured by standard mechanical tests including the closed-loop direct tensile test (Vasconcelos et al. 2008), three-point bending test (Tarokh et al. 2016), compact tensile test (Yang et al. 2019), etc. However, it is very challenging to obtain the Mode II fracture energy of rock, because Mode II fractures are impacted by the normal stress and it is relatively difficult to induce pure Mode II fracture propagation even in shearing tests (Backers and Stephansson 2012; Lin et al. 2019). Experimental results have found that the Mode II fracture energy of rock increases with the normal compressive stress (Choo et al. 2021). Here, for considering the effect of normal compressive stress on Mode II fracture energy, based on the work of (Choo et al. 2021), a normal stress-dependent Mode II fracture energy of rock is defined as follows:

$${G}_{\mathrm{II}}={G}_{\mathrm{II}}^{0}\times \frac{c+\mathrm{tan}\,\varphi \langle -{\sigma }_{\mathrm{n}}\rangle }{c},$$
(10)

where \({G}_{\mathrm{II}}^{0}\) is the Mode II fracture energy under zero normal stress. This treatment can be interpreted as the Mode II fracture energy proportionally increasing with the shear strength for different normal compressive stress.

Furthermore, the residual normal and shear stresses can be obtained by:

$$\left\{\begin{array}{c}{\sigma }_{\mathrm{n}}={(1-D)K}_{\mathrm{p}}{\delta }_{\mathrm{n}}\\ {\sigma }_{\mathrm{s}}={{(1-D)K}_{\mathrm{p}}\delta }_{\mathrm{s}}\end{array}.\right.$$
(11)

Figure 1 illustrates the response model for the mixed-mode fracture. It can be seen that, before damage initiation, the normal, shearing and effective stresses linearly increase by a slope equivalent to the penalty stiffness. The shear strength is dependent on the normal compressive stress. When the fracture criterion f reaches 1, damage initiation occurs and the stresses gradually decrease. The deep red area is the mixed-mode fracture energy while the mapping areas in the normal and shearing plane are the work contributed by Mode I and Mode II fractures, respectively.

Fig. 1
figure 1

Mixed-mode fracture model considering Mohr–Coulomb failure criterion. The stress-displacement curves in normal and shearing planes represent pure mode I and pure mode II fractures, respectively. The shear strength \({\sigma }_{\mathrm{s}}^{0}\) is determined by cohesion strength, compressive normal stress and friction angle. The dark red area represents the mixed-mode fracture energy, while the mapping areas in the normal and shearing planes are the work contributed by mode I and mode II fractures, respectively. Damage initiation occurs when fracture criterion f reaches 1 and the residual strength gradually decreases in the mixed-mode plane

Full size image

3 Coupled Mechanical-Fluid Flow Model

3.1 Flow for Rock Matrix

The rock matrix is assumed to be an elastic porous medium fully saturated with a single-phase fluid. The fluid flow in the porous rock matrix is described by Darcy's law (Darcy 1856):

$${\varvec{q}}=-\frac{k}{\mu }\nabla p,$$
(12)

where \(k\) is the permeability coefficient in unit m2. \(\mu\) the viscosity of the fluid, and p the pore fluid pressure.

The mechanical behaviour of poroelastic rock is described by the effective stress principle (Terzaghi 1943; Alam et al. 2010), as follows:

$${{\varvec{\sigma}}}^{^{\prime}}={\varvec{\sigma}}+p{\varvec{I}},$$
(13)

where \({{\varvec{\sigma}}}^{^{\prime}}\) and \({\varvec{\sigma}}\) are the effective stress tensor and total stress tensor, respectively; \({\varvec{I}}\) is the unit tensor; \(p\) is the pore fluid pressure.

3.2 Flow for Cohesive Crack Element

Figure 2a illustrates the structure of a fluid-filled cohesive crack element which contains four nodes at the top and bottom for displacement and pore pressure and two middle nodes only for pore pressure. Before crack initiation, the fluid flow law for the cohesive element is not activated, which makes the same fluidic performance in rock matrix as that of no cohesive element existing. Once crack initiation occurs, the tangential flow within the cohesive element is expressed as a Newtonian fluid following the Poiseuille's law. The relationship between the pressure gradient and fluid flux is formulated as follows (Xi et al. 2021):

$${\varvec{q}}=-\frac{{{d}_{\mathrm{n}}}^{3}}{12\mu }\nabla p,$$
(14)

where \({\varvec{q}}\) is the fluid flux of the tangential flow; \(\nabla p\) is the fluid pressure gradient along the cohesive zone. \(\mu\) is the fluid viscosity. \({d}_{\mathrm{n}}\) is the crack opening displacement, which equals the true crack opening displacement under mechanical response.

Fig. 2
figure 2

Illustration of fluid cohesive elements and the intersection approach: a fluid cohesive elements with six nodes, of which two middle nodes only have pore pressure DOF (i.e., degrees of freedom) and four side nodes have pore pressure and displacement DOF; b intersection of cohesive elements which share a common middle node for ensuring the fluid flow continuity

Full size image

Fluid flow exists between the cohesive element and bulk element if there is pressure difference between them. The normal flow is described by defining a fluid leak-off coefficient for the cohesive zone surface, presented as follows:

$$\left\{\begin{array}{c}{q}_{\mathrm{t}}={c}_{\mathrm{t}}({p}_{\mathrm{f}}-{p}_{\mathrm{t}})\\ {q}_{\mathrm{b}}={c}_{\mathrm{b}}({p}_{f}-{p}_{\mathrm{b}})\end{array}\right.,$$
(15)

where \({q}_{\mathrm{t}}\) and \({q}_{\mathrm{b}}\) are the flow rates into both top and bottom of the element surface, respectively; \({c}_{\mathrm{t}}\) and \({c}_{\mathrm{b}}\) are the corresponding leak-off coefficients, for the top and bottom surface of the cohesive element, respectively; \({p}_{\mathrm{f}}\) is the fluid pressure at the element gap; \({p}_{\mathrm{t}}\) and \({p}_{\mathrm{b}}\) are the pore pressures of the adjacent pore-containing elements on the top and bottom surfaces, respectively. The fluid leak-off coefficient is related to fluid velocity, fluid viscosity, porosity and permeability of the formation, the reservoir fluid compressibility, etc. In this paper, the leak-off coefficient is assumed as a constant parameter as was the case in other studies (Carrier and Granet 2012; Feng and Gray 2018).

To model the interaction between HF and NF, the intersection point should be specifically processed. Figure 2b illustrates the approach for the intersection between cohesive elements. The four zero-thickness cohesive elements share a common pore pressure middle node, which ensures the fluid flow continuity for the intersection. The intersected cohesive elements share the same displacement and pore pressure node for ensuring the displacement and fluid flow continuity. The zero-thickness cohesive elements are connected with the bulk elements for the permeable rock matrix.

The inner fluid pressure in the cohesive elements acts as traction on the surfaces of the fracture and drives the opening of the fracture. The general stress field of the cohesive zones is balanced by its fluid pressure and external effective stress of adjacent bulk element. Thus, a coupled fluid pressure–traction–separation relationship exists between the cohesive zone defined by the mixed-mode stress–displacement law and the lubrication equation model (Detournay 2016; Xi et al. 2021). Convergence is usually a problem in the execution of FE programs for quasi-brittle materials (e.g., rock and concrete) exhibiting softening behaviour under implicit scheme. We implemented the developed model into ABAQUS by an in-house FORTRAN subroutine and utilize the non-linear solver ability of ABAQUS to address the near-wellbore interaction of HF and NF.

4 Worked Example

A two-dimensional model with a diameter of 2 m is established as a worked example to demonstrate the developed numerical method (Fig. 3). Considering the near-wellbore interaction between HF and NF, the distance between the intersection point and the wellbore surface is equivalent to the wellbore diameter (0.1 m). According to the symmetry, only a half of the geometry is established to reduce the computational time and the y-axis is the symmetric plane. In this model, HF is assumed to propagate through the direction of the maximum principal stress before it approaches the NF. Once the HF has approached the NF, it has options to cross, deflect or offset, subject to a number of underlying factors to be investigated in the parametric study. For near-wellbore problem, the effects of wellbore on the stress re-distribution should be considered. The fluid injection is achieved through a borehole/pipe element connecting with all the nodes on the wellbore surface. Through the tie contacts, the fluid flow continuity is ensured between the borehole element and wellbore, which is a necessary procedure for considering the existence of wellbore. Moreover, the fluid pressure in the wellbore is modelled as a surface radial pressure with the same magnitude of injection pressure, which is implicitly applied to the wellbore surface through ABAQUS keyword “PORMECH”. There are 26,736 bulk elements for the rock matrix and 3953 cohesive elements in the model. The mesh is refined in the potential crack zone, in which the element size is 2.5 mm. It should be noted that the very first cohesive element near the wellbore surface is set as an initial element for fluid entering, while it is also an intact element with a damage value of 0.

Fig. 3
figure 3

Mesh grid of the worked example. Geometric parameters are: model diameter 2 m; natural fracture at angle 45°; wellbore diameter 0.1 m; distance between the NF and wellbore surface 0.1 m. Cohesive elements for HF are inserted into rock matrix along the maximum in-situ principal stress direction. Fluid is injected into a pipe/borehole element connecting with nodes for wellbore surface through tied contacts that ensure the fluid continuity between the pipe element and wellbore surface

Full size image

There are three steps for the modelling: (1) the in situ stress equilibrium is made for the whole rock formation; (2) the elements representing the wellbore are removed, simulating drilling, and the stress field equilibrium is made again; (3) a constant flow rate of fluid is injected into the wellbore/pipe element for fracture initiation, propagation and interaction. The maximum and minimum in-situ stresses are 30 MPa and 20 MPa, respectively. For the half model, the injection flow rate is 2.5 × 10–5 m2 s−1. All the basic geometric, mechanical and fluid parameters and their resources are listed in Table 1.

Table 1 Values for basic variables used in the worked example after Guo et al. (2017); Li et al. (2019a, b)
Full size table

By considering the mixed-mode fracture, wellbore geometry and wellbore surface pressure, the developed numerical method is able to model the near-wellbore interaction of HF and NF. Figure 4 illustrates the fracture propagation and pore pressure distribution with increasing injection time. It can be seen that the pore pressure is the highest in the injection borehole element and at the wellbore surface. With increasing injection time, a fracture propagates along the direction of maximum in situ principal stress, then deflects along the natural fracture away from the wellbore. After the fracture propagates along the natural fracture for a certain distance, it deflects again towards the direction of maximum in situ principal stress. This interaction mode is defined as “offset” (Dahi Taleghani et al. 2016). The fluid pressure in the cracked cohesive elements are much higher than the adjacent bulk element for rock matrix. This is because the fluid flow of cohesive element before crack initiation follows the Darcy’s law for rock matrix while the permeability of cracked cohesive element determined by Poiseuille's law is much higher than that of the adjacent bulk element.

Fig. 4
figure 4

Fracture development and pore pressure distributions as fluid injection time increases: a injection time 0.1 s; b injection time 0.2 s; c injection time 0.35 s; d injection time 0.45 s. The fluid pressures scale is in kPa

Full size image

The mixed-mode ratio (i.e., the contribution of shear on the development of mixed-mode fracture) during the fracture development is obtained by the average of the two integrated points of the cohesive element. Figure 5 shows the injection pressure development and mixed-mode ratios for several typical cohesive elements ordered by fracture propagation. It can be seen that the injection pressure increases to the peak (about 35 MPa) at 0.14 s and then gradually decreases as the fracture propagates. The hydraulic fracture starts to propagate at about 0.1 s when a slight drop of injection pressure occurs. Before crack deflection into the NF, hydraulic fracture propagation is tension-dominated: the fracture mixed-mode ratio for the initial hydraulic fracture (Element 1) is almost zero and for the last element before fracture deflection into NF is smaller than 0.05. The initial fracture propagation can thus be regarded as a Mode I fracture. The fracture deflects into the NF at 0.23 s when the injection pressure has decreased to about 31 MPa. The mixed-mode ratio for the start of NF (Element 3) suddenly increases to about 0.86, then gradually decreases to about 0.75 concordant with crack opening. The mixed-mode ratio for the end of NF (Element 4) grows to about 1 and then subsequently decreases to about 0.95. Therefore, the reactivation of natural fractures is a mixed-mode fracture mechanism dominated by shearing. With fluid entering into the cracked NF and opening the fracture, the normal stress changes from compression to tension and the contribution of shear slightly decreases. Furthermore, the mixed-mode ratios for elements 5 and 6 at the offset crack are smaller than 0.5, which means that the offset fracture is tensile stress dominated. Therefore, the existence of NF or a weak interface in rock formation can significantly change the fracture paths where the HF is deflected to run along a NF that exhibits a typical mixed-mode fracture propagation behaviour.

Fig. 5
figure 5

Mixed-mode ratio (contribution of shear on the fracture element) and injection pressure development through time. For pure mode I and pure mode II fracture, the values of Gs/(Gn + Gs) are 0 and 1, respectively. Elements 1–6 are the typical elements at the crack path: (1) HF start; (2) before NF activation; (3) start of NF activation; (4) end of NF activation; (5) start of offsetting HF and (6) end of offsetting HF

Full size image

5 Verification

A typical KGD (Kristianovich–Geertsma–de Klerk) radial model is established to verify the developed numerical method due to the implementation of a new cohesive constitutive model in ABAQUS. The KGD problem concerns the propagation of a single fracture under a constant flow rate. The fluid is injected into a point representing the wellbore which is very small compared with the length of both the fracture and model. Therefore, following Geertsma and Haafkens (1979), the analytical solutions for fracture length, fracture width at the injection point and injection pressure are given by:

$$\left\{\begin{array}{c}l\left(t\right)=0.68{\left[\frac{G{Q}_{0}^{3}}{\mu (1-v)}\right]}^{1/6}{t}^{2/3} \\ p\left(t\right)=1.38{\left[\frac{{G}^{3}{Q}_{0}^{3}\mu }{{\left(1-v\right)}^{3}{l(t)}^{2}}\right]}^{1/4}+{\sigma }_{h}\\ w\left(t\right)=1.87{\left[\frac{\mu (1-v){Q}_{0}^{3}}{G}\right]}^{1/6}{t}^{1/3} \end{array},\right.$$
(16)

where \(l\left(t\right)\) is the fracture length as a function of injection time; \(p\left(t\right)\) is the fluid pressure at the injection point; \(w\left(t\right)\) is the fracture width at the injection point. \(v\) is the Poisson’s ratio; \({\sigma }_{\mathrm{h}}\) is the minimum in situ principal stress perpendicular to the fracture propagation direction; \(G\) is the shear modulus expressed as \(E/(2\left(1+v\right))\); \({Q}_{0}\) is the injection flow rate; \(\mu\) is the fluid viscosity; and t is the injection time;

Figure 6a shows the mesh for the KGD problem with dimensions of 45 by 60 m. The mesh is refined for the fracture zone. Zero-thickness cohesive elements are inserted into the potential fracture path. There are 24,673 bulk elements and 799 cohesive elements in the model. According to the assumptions of the analytical solution for the KGD problem, the rock formation is regarded as impermeable and fluid leak-off is not considered. The fluid with a flow rate of 1 × 10–3 m2 s−1 is injected into the middle node of the very first cohesive element. All the basic parameters are listed in Table 2. Figure 6b–d shows the good agreement between numerical results and analytical solutions. The injection pressure from the numerical simulation is slightly larger than that from the analytical solutions. It should be mentioned that the analytical model corresponds to the storage-viscosity regime, i.e., the energy expended in fracturing the rock is negligible compared to viscous dissipation and the evolution of the fracture during fluid injection does not depend on the rock toughness or fracture energy(Detournay 2016; Nguyen et al. 2017). Compared with the analytical solutions, this difference makes a slightly larger injection pressure, a slower fracture propagation, and a larger fracture width for the numerical results.

Fig. 6
figure 6

Comparisons of numerical results with analytical solutions for KGD problem: a numerical model; b fracture length development; c fracture width at the injection point; d injection pressure development

Full size image
Table 2 Values of basic variables used for comparison with the analytical solutions after Geertsma and Haafkens (1979); Nguyen et al. (2017)
Full size table

Furthermore, experimental results (Dehghan et al. 2015a, b) on the interaction between HF and NF were used to verify the developed numerical method. Two-dimensional plane strain models for the specimens with a natural fracture with a dip angle 90° were established, and approach angles of 30° 60° and 90° were tested. Half models with dimensions 150 by 300 mm were established due to symmetry. The wellbore diameter in the experiment is 10 mm and the distance between the natural fracture and hydraulic fracture is 75 mm. Figure 7a illustrates one of the numerical models for the approach angle 60°. The basic parameters for the comparisons are listed in Table 3. Figure 7b shows the comparisons between numerical and experimental results (Dehghan et al. 2015a, b) on the intersection mode. The NF opening and slippage were observed from experiments. It can be seen that the numerical results have a good agreement with the experimental results of Dehghan et al. (2015a, b). Moreover, the smaller the approach angle, the less likely the hydraulic fracture is to cross the natural fracture, and the more likely it is to reactivate. The verification of the developed numerical method with the KGD analytical solutions and experimental results support its accuracy in predicting fracture propagation and interaction.

Fig. 7
figure 7

Comparisons of the numerical model with the experimental results on the interaction mode after Dehghan et al. (2015b, a): a mesh example for the specimen with demensions of 150 by 300 mm and natural fracture angle 60°; b numerical and experimental results; the interaction modes under different approach angles and in-situ stresses from numerical models have a good aggreement with those from experiments

Full size image
Table 3 Values of basic variables used for comparison with experimental results after Dehghan et al. (2015a, b)
Full size table

6 Parametric Study and Discussion

6.1 Effect of Approach Angle

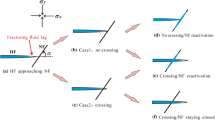
Natural fractures are widely distributed in rock masses, therefore, it is important to investigate the effect of approach angles on near-wellbore interaction with existing fractures during hydraulic stimulation. Figure 8 shows the fracture patterns for approach angles of 30°, 45°, 60°, 75° and 90°. The distance between the intersection point and wellbore is two times the wellbore radius. All the other parameters are the same as those in the worked example (Table 1). It can be seen that there are three modes for the interaction between HF and NF: (1) Deflection—the fracture deflects into the NF and propagates along with the NF until the tip of the NF, then deflects again along the maximum in-situ principal stress direction (approach angle of 30°); (2) Offset—The fracture deflects into the NF and propagates along with the NF, but offsets to the maximum in situ principal stress direction before the tip of the NF (45°, 60°); (3) Cross—the HF crosses the NF without deflection (75°, 90°). The larger the approach angle, the more prone the HF is to cross the NF, matching observations from experiments and fracking practices (Dehghan 2020; Kolawole and Ispas 2019; Zhang et al. 2021).

Fig. 8
figure 8

Fracture propagation patterns for different angles of approach of the hydraulic fracture to the natural fracture: a approach angle 30°—deflect, the fracture deflects into the NF and propagates along with the NF until the tip of the NF, then deflects again along the maximum in-situ principal stress direction; b approach angle 45°—offset, the fracture deflects into the NF and propagates along with the NF, but offsets to the maximum in-situ principal stress direction before the tip of the NF; c approach angle 60°—offset; d approach angle 75°—cross, the HF crosses the NF without deflection; e approach angle 90°—cross. The fluid pressures scale is in kPa

Full size image

To investigate the fracture mechanism behind the interaction, the mixed-mode fracture criterion f (Eq. 3) of the first intersecting element in the NF for crossing cases is obtained as a function of injection time (Fig. 9a). When the fracture criterion f reaches 1, the crack initiation of NF occurs. For the crossing cases, the NF element is not cracked and hence f is smaller than 1. The closer f is to 1, the NF is more likely to be cracked. It can be seen that for the approach angles 60°, 75°, and 90°, f are 0.64, 0.36 and 0.27, respectively, which demonstrates larger approach angles make the HF easier to cross the NF. A sudden jump in fracture criterion occurs when the HF crosses the NF. For larger approach angles, less deformation can be transferred to the tangential deformation of the NF, resulting in a longer time for NF deformation. Furthermore, the contribution of shear on the mixed-mode fracture of NF for the deflecting (30°) and offsetting (45°) cases are obtained as a function of injection time in Fig. 9b. It can be seen that the shear contribution for the 45° approach angle jumps earlier than that for the 30° approach angle. This is because the shear stress on the 45° plane is larger. The mixed-mode ratio for the 45° approach angle is larger than that for the 30° approach angle but both of them are larger than 0.5. Therefore, the deflection and offset of NF for the approach angles 30° and 45° are the shear-dominated mixed-mode fractures.

Fig. 9
figure 9

Fracture evolution of the interaction between HF and NF for different approach angles: a fracture criterion values; the smaller the value is, the less likely the NF is to be reactivated. b Mixed-mode ratios; the larger the ratio is, the larger the contribution of shear on fracturing

Full size image

Figure 10a shows the injection pressure development for different approach angles. It can be seen that injection pressures gradually increase to about 36 MPa and then gradually decrease to 30 MPa as the fractures propagate. The effect of approach angles on pressure development is limited. In the numerical models, the fluid is injected into all the nodes at the wellbore surface. Therefore, the pressure is affected by the permeable rock formation following Darcy’s law and the fracture opening following Poiseuille's law; this is one of the key advantages of the developed numerical model. Furthermore, the fracture length development as a function of injection time is obtained by calculating the total length of cracked cohesive elements with a damage value larger than 0.99, which is achieved by an in-house Python script that iteratively searches the damaged elements and counts the total crack lengths in the outputs. Figure 10b illustrates the fracture length development for different approach angles. The fracture lengths gradually increase with injection time, but the propagation speeds are affected by the interactions between HF and NF. For the crossing cases (approach angles 60°, 75° and 90°), the fracture propagation prior to crossing is slower for larger approach angles, but the final fracture lengths are almost the same after crossing. This phenomenon is because, as discussed in the previous discussion on fracture criterions (Fig. 9a), the fracture propagation prior to crossing contributes to less shear deformation for a larger approach angle. Moreover, the fracture length is smaller for the offsetting case with the approach angle 45°, because the mixed-mode ratio for the approach angle 45° is larger, and more energy is consumed during fracture deflection.

Fig. 10
figure 10

Injection pressure and fracture length developments for different approach angles of a HF interacting with a NF: a injection pressure; b fracture length. The points in b are the deflection or crossing points during cracking. The part between two deflection points in a curve represents the NF activation. The fracture propagation speed (slope of the curves in panel b) during NF activation is relatively slower due to the mixed-mode nature of the fracture

Full size image

6.2 Effects of Natural Fracture Location and In Situ Stress

The near-wellbore disturbance zone is about three times the wellbore radius based on the hole stress concentration principle (Kirsch 1898; Timoshenko and Goodier 1951). According to numerous in situ stress measurement data (Li et al. 2019a, b; Zang et al. 2012), the ratio of maximum to minimum in situ principal stress is usually smaller than 3. Therefore, the NF is modelled in the range of three times wellbore radius for the near-wellbore problem, and the in-situ stress ratios are set as 1.1–2.8 in the simulations. The other parameters are the same as those in the worked example (see Table 1). Figure 11 summarises the interaction modes for different NF locations and in-situ stresses. The offset ratio is defined as the ratio of the activated length of the NF to the half length of the NF. The offsetting ratios for deflecting and crossing modes are 1 and 0, respectively. The three interaction modes (deflect, offset, cross) result from the different combinations of natural fracture locations and in-situ stresses. Interestingly, for the NF very close to the wellbore (d/R = 0.5), the fracture is more prone to cross the NF when the in-situ stress ratio is smaller. But when the in situ stress ratio becomes larger, offsetting occurs. For other near-wellbore cases (1 < d/R < 3), with increasing in situ stress ratio, the interaction mode changes from deflecting to offsetting and the offsetting ratio becomes smaller. In the range of 1 < d/R < 3, the location of NF has little effect on the interaction mode when the in situ stress ratio is smaller. For a larger stress ratio (> 2.5), the further away the NF is from the wellbore within d/R < 1.5R, the smaller the offset ratio. Therefore, crossing NF is more likely to occur if NF is very close to the wellbore and the in situ stress ratios are small; otherwise NF is more likely to be activated.

Fig. 11
figure 11

Fracture patterns for different combinations of NF location and in-situ stress. d is the distance the intersection point and the wellbore surface; R is the wellbore radius which is 50 mm; \({\sigma }_{\mathrm{H}}\) is the maximum in-situ principal stress; \({\sigma }_{\mathrm{h}}\) is the minimum in-situ principal stress which keeps 20 MPa. L is the half length of the natural fracture; l is the activated length of natural fracture. l/L is the offset ratio which is 100% for deflection interaction and 0% for crossing interaction

Full size image

To investigate the fracture mechanism for the abnormal case where the NF is very close to the wellbore (d/R = 0.5), we compare the injection pressure development under different in-situ stress ratios (Fig. 12). The smaller the in situ stress ratio, the longer it takes to reach the breakdown pressure and the larger the breakdown pressure is. However, for in situ stress ratios of 2.5 and 2.8, injection pressures continue to increase after breakdown, because the volume of fluid being injected is more than can be accommodated by the induced fracture. Moreover, the smaller the in situ stress ratio, the larger the pressure at the point of interaction is (see the black square points in Fig. 12). A larger fluid pressure in the wellbore includes a larger radial pressure on the wellbore surface, contributing to rock tangential tensile fracturing along the maximum in-situ principal stress direction. The radial pressure-induced stress in rock decreases as a quadratic function of the distance away from the wellbore (i.e., \({\sigma }_{\theta }=\frac{{R}^{2}}{{d}^{2}}P\)). Therefore, the HF is more likely to cross a NF if the NF is near the wellbore and the injection pressure is high.

Fig. 12
figure 12

Effects of in-situ stress on the injection pressure for d/R = 0.5. d is the distance between the intersection point and the wellbore surface and R is the wellbore radius. \({\sigma }_{\mathrm{H}}\) and \({\sigma }_{\mathrm{h}}\) are the maximum and minimum in-situ principal stresses, respectively. The points show the interaction points between the HF and NF. The smaller the stress ratio is, the later the interaction occurs

Full size image

Figure 13a illustrates the effect of the in situ stress ratio on the fracture length development for d/R = 0.5. The larger the in situ stress, the earlier the fracture length starts to increase. For the crossing cases, the larger the in situ stress ratio is, the faster the fracture propagates. For the offsetting cases, the fracture propagation between the two deflection points is mixed-mode fracture for the NF when the fracture growth speed is slow. Figure 13b shows the effect of NF location on the fracture length development for \({\sigma }_{\mathrm{H}}/{\sigma }_{\mathrm{h}}\)=2. It can be seen that the fracture propagates fastest for the crossing interaction of d/R = 0.5. For the offsetting cases, the fracture propagation is slow when the fracture runs along the NF. The farther the NF from the wellbore, the later the fracture deflects towards NF. Because the injection pressure becomes smaller with the fracture propagation, NF propagation time becomes longer for a NF further from the wellbore.

Fig. 13
figure 13

Fracture length development affected by the in-situ stress and NF location: a d/R = 0.5; b \({\sigma }_{\mathrm{H}}/{\sigma }_{\mathrm{h}}\)=2. d is the distance between the intersection point and the wellbore surface and R is the wellbore radius. \({\sigma }_{\mathrm{H}}\) and \({\sigma }_{\mathrm{h}}\) are the maximum and minimum in-situ principal stresses, respectively. The points in figures show the crossing or deflection points for the interaction between the HF and NF. The part between two deflection points in a curve represents the NF activation. The fracture propagation is slower (curve slope) during NF activation, and NF propagation time becomes longer and slower for NFs further from the wellbore

Full size image

6.3 Effect of Cohesion Strength and Friction Angle of NF

Since the reactivation of natural fractures is a shear-dominated mixed-mode fracture, it is necessary to investigate the effects of cohesion strength and friction angle of NF on the interaction. Figure 14 shows the fracture patterns for natural fracture cohesion strengths of 2, 4, 6 and 8 MPa. The other parameters are the same as those in the worked example (see Table 1). The cohesion strength of NF significantly affects the interaction modes: the smaller the cohesion strength, the larger the offset ratio, which means that longer portions of natural fractures will be activated when they have lower cohesion. In our simulations, when the cohesion strength of a NF is 8 MPa, the hydraulic fracture will cross the natural fracture. Figure 15 illustrates the development of fracture length for different natural fracture cohesive strengths. The cohesion strength has almost no effect on the fracture length development before the interaction. The fracture propagates fastest for the crossing case with the highest cohesion strength. When the fracture offsets into the NF, the larger the cohesion strength, the slower the fracture propagates and the earlier the fracture offsets back out to the direction of maximum in situ principal stress.

Fig. 14
figure 14

Fracture patterns for different cohesion strengths of natural fractures with NF cohesion of a 2 MPa; b 4 MPa; c 6 MPa; d 8 MPa. The offsetting ratio decreases with increasing NF cohesion, until the NF is crossed without being activated

Full size image
Fig. 15
figure 15

Fracture length development for different cohesion strengths of natural fractures shown in Fig. 14. The fracture propagates fastest for the crossing case with the highest cohesion strength. When the fracture offsets into the NF, the larger the cohesion strength, the slower the fracture propagates and the earlier the fracture offsets back out to the direction of maximum in-situ principal stress

Full size image

Figure 16 shows the fracture patterns for different friction angles. The other parameters are the same as those in the worked example (see Table 1). The larger the friction angle, the smaller the offset ratio is. When the friction angle is 40°, the hydraulic fracture crosses the natural fracture. Due to the crack initiation of NF as a compressive-shearing fracture, the friction angle affects the shear strength. Therefore, the friction angle of NF must be considered for accurately predicting the interaction between HF and NF. Figure 17 illustrates the fracture length development for different friction angles. Similar to the previous discussions on the effect of cohesion strength, the fracture propagates fastest for the crossing case. However, the friction angle of NF has little impact on the fracture propagation speed along the NF. This is because once crack initiation occurs, the reactivation of the NF becomes a tensile-shearing fracture due to the fluid entering the fracture. The larger the friction angle, the earlier the fracture offsets to the direction of maximum in-situ principal stress. For offsetting cases, the fracture propagation becomes relatively slower when deflecting into the NF.

Fig. 16
figure 16

Fracture patterns under different friction angles of natural fractures: a friction angle 25°; b friction angle 30°; c friction angle 35°; d friction angle 40°. The offsetting ratio decreases with increasing NF friction angle, until the NF is crossed without being activated

Full size image
Fig. 17
figure 17

Fracture length development for different friction angles of natural fractures shown in Fig. 16. The fracture propagates fastest for the crossing case. However, the friction angle of NF has little impact on the fracture propagation speed along the NF. The fracture propagation becomes faster after offsetting into the direction of maximum in-situ principal stress

Full size image

6.4 Effect of Flow Rate

Figure 18 shows the fracture patterns for the injection flow rate 2.5, 5.0, 7.5 and 10.0 × 10–5 m2 s−1 in the half 2D models. If the fracture height is 1 m, these flow rates are 3, 6, 9, 12 l/min which are at the same magnitude with those in (Zhang et al. 2011; Feng and Gray 2018). The distance from the intersection point to the wellbore is the same as the wellbore radius. Other parameters are the same as those in the worked example (Table 1). For a higher flow rate, the HF is more prone to cross the NF. Figure 19a illustrates the fracture length development under different flow rates. Higher flow rates result in faster fracture propagation. Increasing the flow rate four times from 2.5 × 10–5 m2 s−1to 10 × 10–5 m2 s−1, shortens the time for the fracture to reach 0.2 m from 0.45 to 0.1 s. Figure 19b illustrates the injection pressure development for different flow rates. At higher flow rates, the breakdown pressure is reached faster and the injection pressure is larger. A higher injection flow rate promotes the HF to cross the NF through a larger radial pressure on the wellbore. The obtained results can provide a reference for the optimization of hydraulic fracturing strategies. For instance, fluid injection with high flow rates can make hydraulic fractures propagate further away from the wellbore, whilst lower flow rate injection can be employed to activate natural fractures closer to the wellbore/perforation hole. It is thus likely that during well stimulation, an approach which integrates the use of multiple flow rates may be most effective.

Fig. 18
figure 18

Fracture patterns under different injection flow rates: a 2.5 × 10–5 m2 s−1; b 5.0 × 10–5 m2 s−1; c 7.5 × 10–5 m2 s−1; d 10 × 10–5 m2 s−1. The NF near the wellbore is more likely to be activated by low flow rates

Full size image
Fig. 19
figure 19

Fracture length and injection pressure developments under different injection flow rates: a fracture length development; b injection pressure for the flow rates shown in Fig. 18

Full size image

7 Conclusions

A new mixed-mode fracture model incorporating Mohr–Coulomb failure criterion has been developed to investigate the interaction between hydraulic fractures and natural fractures. The developed model is implemented into ABAQUS through subroutines, in which the shear fracture properties in the mixed-mode fracture are dependent on the normal stress and frictional coefficient. Near-wellbore interaction between HF and NF was modelled by considering the effects of wellbore on stress re-distribution and radial fluid pressure on the wellbore. The numerical model was first validated by comparing against available analytical and experimental results and followed by an extensive parametric study. Three interaction modes including crossing, deflecting and offsetting were demonstrated and analysed. In the case of deflecting and offsetting hydraulic fractures, the portion of the NF that is reactivated slips as a shear-dominated mixed-mode fracture. The larger the approach angle, the hydraulic fracture is more prone to cross the natural fracture. A high injection pressure in the wellbore tends to drive the HF to cross NF located close to the wellbore through the radial pressure on the wellbore surface. When the intersection point is close to the wellbore, the smaller the in-situ stress ratio, the more likely the HF will cross NF. In addition, the smaller cohesion strength and friction angle of NF leads to the larger offsetting ratio. Moreover, even a low flow rate can activate the natural fractures near the wellbore. It can be concluded that the developed numerical method can reliably model the near-wellbore interaction between HF and NF. The results in this study can form useful guidance for the practising engineers and asset managers with regards to the activation of natural fractures, fracture network optimisation and hydraulic stimulation strategies.

Despite all the success in simulating the interactive mechanisms between HF and NF, the numerical method has limitations that the cracking trajectory can only follow the predefined crack paths where cohesive elements are embedded. The deviation of HF before its tip reaching the NF possibly due to local stress re-distribution is not captured. It thus cannot account for arbitrary cracking typically in considering rock as a heterogeneous material. A potential solution to achieve arbitrary cracking is to embed cohesive elements everywhere in the mesh (Xi et al. 2018) or combined finite-discrete element method (Lisjak et al. 2017). The mixed-mode nature should be considered for the arbitrary cracking and complex trajectories, which is under investigation by the authors.