Multi-scale Coupled Processes Modeling of Fractures as Porous, Interfacial and Granular Systems from Rock Images with the Numerical Manifold Method

Abstract

The greatest challenges of rigorously modeling coupled hydro-mechanical processes in fractured rocks at different scales are associated with computational geometry. In addition, selections of continuous or discontinuous models, physical laws, and coupling priorities at different scales based on different geometric features determine the applicability of a numerical model for a certain type of problem. In this study, we present our multi-scale modeling capabilities that have been developed based on the numerical manifold method for analyzing coupled hydro-mechanical processes in fractured rocks. Based on their geometric features, the fractures are modeled as continua—finite-thickness porous zones, and discontinua—discontinuous interfaces and microscale asperities and granular systems. Different governing equations, physical laws, coupling priorities, and approaches for addressing fracture intersections and shearing are then applied to describe these. We applied these models to simulate coupled processes in fractured rocks using realistic geometry obtained from rock images at different scales. We first calculated shearing of a single fracture with different models and demonstrated the impacts of asperities on shearing. We then applied the continuous and discontinuous models to simulate a network of rough fractures, demonstrating that contact dynamics contribute significantly to the geometric, multi-physical evolution of systems where rough fractures are not mineral filled. For a discrete fracture network, our coupled processes modeling demonstrates that shearing of the discrete fractures can have a major impact on stress and pore pressure distribution. Lastly, we applied the discontinuous granular model to simulate evolution of a complex granular system with a deformation band, demonstrating that the deformation band can dominate contact dynamics, the structural and the stress evolution of the granular system.

FormalPara Highlights

Unique capabilities to simulate coupled processes in fractures as continuous porous zones, discrete interface networks, and microscale granular systems

Realistic geometry from rock images at different scales, with differing physical laws, coupling priorities, and solutions for fracture intersections and shearing

Comparison of different models for analyzing shearing of single planar and non-planar fractures, and analyzes compaction of a network of rough fractures

Demonstration from discrete fracture network modeling that stress and pore pressure evolution are majorly impacted by shearing in a network of discrete thin fractures

Demonstration from microscale modeling that contact dynamics, evolution of stress, and porosity loss in a complex granular system are dominated by a deformation band

1 Introduction

Fractures play key roles in the geosciences. Fractures are dynamic results of rock failure, with sizes ranging from microns to kilometers. They divide intact rock into different parts, thus, having an important impact on the mechanical behavior of geological systems as well as providing permeability for fluid and heat transport. Thus, fractures are the key that provide permeability for production in subsurface energy recovery applications (such as hydrocarbon and geothermal energy production). In energy storage and geologic disposal of nuclear waste as well as geologic carbon sequestration, fractures and faults are the major concern for hazards such as leakage of fluid, erosion and seismic events (Rutqvist 2012; 2020; Rutqvist et al. 2020). Thus, understanding coupled processes in fractured geological media is essential for effective control of energy recovery and storage (Rutqvist and Stephansson 2003).

At the reservoir scale, fractures appear to be very thin (relative to their lengths), and they typically form networks. In these networks, alteration of individual fractures in terms of their dimension and physical properties, and creation of new fractures may dynamically occur as a result of coupled processes. Numerical modeling of coupled hydro-mechanical (HM) processes in fractured rock, including equivalent continuum, dual-continuum, and discontinuous models has been an ongoing research topic since the 1980s. The network of fractures may influence the deformation and fluid distribution in the geosystems in a complex way that cannot be simplified as a continuum. Thus, the ability to explicitly consider discrete fractures in a numerical model with full coupling capability is of great importance. Inspired by the increasing demands for engineering solutions such as in nuclear waste disposal and geothermal energy, a number of computer codes for modeling HM and (thermal-hydro-mechanical) THM behavior of fractured rock at various levels of sophistication have been developed (Rutqvist et al. 2001). Most of the earlier models were based on the finite element method (Noorishad et al. 1982, 1992). With the development of discontinuous methods, fractures could be explicitly represented as displacement discontinuities (i.e., interfaces between contacting individual blocks). These models include those based on the Distinct Element Method (DEM): e.g., the commercially available UDEC (Itasca Consulting Group 2011) and 3DEC (Itasca Consulting Group 2013; Mas Ivars 2006), bonded particle model (BPM, Potyondy and Cundall 2004; Mas Ivars et al. 2011), and clumped particle models (Yoon et al. 2012). Meanwhile, discontinuous models based on Discontinuous Deformation Analysis (DDA) were developed for coupled fluid flow and deformation in discrete fractures where the rock matrix is assumed impermeable (Kim et al. 1999; Jing et al. 2001). In addition, hybrid models were developed to combine finite element with discrete element methods for integrating continuum and discontinuum mechanical analysis. One example is the finite-discrete element method that has been applied to coupled processes in discrete fracture networks (Lisjak et al. 2017; Lei et al. 2020).

Models that explicitly account for discrete fractures can be categorized depending on the geometric representation of the fractures in fluid flow and mechanics calculations. For fluid flow in fractures, three types of models can be identified: n-dimensional (i.e., for 2D models, fractures are represented by 2D elements), n-1 dimensional ((i.e., for 2D models, fractures are represented by 1D elements)), and zero-dimensional models where fractures are treated as boundaries of the adjacent rock matrix, thus, without additional degrees of freedom (DOFs) introduced for fractures (Hu et al. 2016, 2017b). For modeling mechanics of fractures, there are two types of models: n-dimensional solid-element models (Rutqvist et al. 2009), and discontinuous interface models where fractures are modeled as interfaces between discontinuous rock blocks (Park et al. 2020; Rutqvist et al. 2020). For both fluid flow and mechanics analyses, the n-dimensional solid-element models (Rutqvist et al. 2009) are excellent for representing fractures with unignorable apertures, but when fracture apertures are far less than their lengths, the use of n-dimensional solid elements becomes computationally too expensive. As for the n-1 dimensional fluid flow models where the fracture thickness is neglected by definition, there are two potential issues: (1) the neglect of flux exchange between the n-1 dimensional fractures and the rock matrix, and (2) the inaccuracy introduced when these flow models are coupled with mechanical models that have different fracture dimensions. As a result, n-1 dimensional fluid flow models are limited to solving couplings with mechanics where contact dynamics and indirect coupling can be quite significant. By comparison, the zero-dimensional fluid model coupled with a discontinuous mechanical interface model for discrete fractures have been proven to be promising for analyzing coupled HM processes in fractured porous media where flow and mechanics are fully coupled in both fractures and rock matrix, and all the coupling components between fracture contact dynamics (dynamic changes of contact locations and contact states) and the fracture flow and permeability are rigorously considered (Hu et al. 2016, 2017b, 2020a).

Modeling of coupled HM processes in fractures at the microscale has only been attempted in recent years. For example, modeling coupled processes in a single fracture was a part of the international DECOVALEX project (Bond et al. 2017; Birkholzer et al. 2019). The models were categorized into 2D simplified models, statistical models, and homogenized models. These include a combined numerical (for flow)-analytical (for chemical–mechanical) model where contacts are assumed to be only parallel edge-to-edge contacts for simulating coupled chemo-hydro-mechanical processes (McDermott et al. 2015), and an elasto-plastic cellular automaton model using grids with different apertures to represent voids but without considering mechanics and contact alteration of the fracture (Pan et al. 2016). In these models, geometric features (such as asperities along fractures and grains) are either not represented explicitly, or they are approximated by spheres or rectangular grids. Thus, contacts along rough surfaces cannot be accurately captured. Because of these limitations, numerical modeling of coupled processes has to the authors’ knowledge never been attempted at the microscopic scale. To overcome these limitations so as to enable microscale understanding of fracture dynamics, a microscale model has been recently developed by the authors and applied for analyzing fractures at the micro-asperity scale as well as in granular systems (Hu and Rutqvist 2020a, b).

The numerical manifold method (NMM, Shi 1992, 1996), based on the theory of mathematical manifolds is a promising method for analyzing both continuous and discontinuous media. In the past two decades, NMM has been successfully applied to analyze mechanical processes in geologic media (Ma et al. 2010) involving higher order interpolation (Chen et al. 1998), fracture propagation (Zheng and Xu 2014), wave propagation across fractured media (Fan et al. 2013), slope stability (Ning et al. 2011; He et al. 2013), fracturing of sandstone (Wu et al. 2017) and microscale mechanics of deformable geomaterials with dynamic contacts (Hu & Rutqvist, 2020b). For fluid flow analysis, NMM also has been successfully applied for analyzing moving interface problems such as free surface flow (Wang et al. 2014, 2016; Zheng et al. 2015). For analyzing flow and fully coupled processes of fractured porous media at different scales, the authors have previously developed a series of models (Hu et al. 2016, 2017a, 2017b, 2020a).

In this paper, we present multi-scale modeling capabilities based on NMM that successfully overcome the limitations discussed above and enable the simulation of coupled processes at multiple scales. In Sect. 2, we describe the modeling capabilities for modeling fractures as finite-thickness porous zones, discontinuous interface networks, and discontinuous asperities and granular systems. We summarize the governing equations, physical laws, coupling aspects and approaches that are used to address the challenges associated with intersections and shearing of fractures for models at different scales. In Sect. 3, we present a few simulation examples, including (1) a comparison of different models for a single fracture shearing, (2) a comparison of the continuous and discontinuous models for simulating a rough fracture network from an image, (3) an example of coupled HM analysis of a discrete fracture network from an image, and (4) an example to investigate the impact of a deformation band on the dynamic evolution of a granular system at the microscale from an image.

2 Modeling Fractures as Porous, Interfacial and Granular Systems

2.1 Geometric Features and Governing Equations

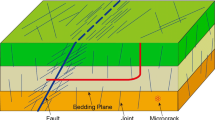
Depending on the scales under consideration, fractures show different geometric and physical features. Figure 1a–d shows a discrete fracture network at reservoir (m–10 km), a rough fracture network (mm–m), a dominant fracture at the core scale (mm–cm, Ajo-Franklin et al. 2018), and a damage zone at the micro-grain scale (μm–mm, Cheng and Wong 2018).

Fig. 1

Fractures at different scales: a a discrete fracture network (m–10 km), b dominant rough fractures (mm–m), c a dominant fracture at the core scale (mm–cm, Ajo-Franklin et al. 2018), and (d) a damage zone at micro-grain scale (μm–mm, Cheng and Wong 2018)

At the reservoir and outcrop scales (Fig. 1a), fractures appear to be very thin relative to their lengths, forming a network. Zooming into a smaller scale (Fig. 1b), the fractures are no longer straight lines—they appear to be quite rough. In some cases when these rough fractures have mineral fillings, these fractures can be categorized as porous zones. At the core scale for a single fracture (Fig. 1c), the asperities of the fractures may have any type of shapes, corners, or distribution that may not be described by any type of statistical functions. Continuing to zoom into the micro-grain scale, a fracture as a damage zone can be considered as a granular system in which grain boundaries may or may not be cemented. Therefore, fractures can be categorized in three types based on geometrical features: (1) dominant fractures with unignorable widths and mineral fillings (finite-thickness porous zones), (2) discrete thin fractures forming networks, and (3) rough interfaces and granular systems.

Regardless of the scales of the fractures, in a fluid-saturated porous medium (e.g., rock matrix or a porous fracture zone), coupled HM processes should satisfy conservation of momentum and mass, described by Biot’s general theory of 3D consolidation (Biot 1941):

$$\nabla \cdot {\varvec{\upsigma}}+\mathbf{f}=\rho \frac{{\partial }^{2}\mathbf{u}}{\partial {t}^{2}}$$

(1)

$$\nabla \cdot \mathbf{v}+\alpha \frac{\partial {\varepsilon }_{v}}{\partial t}+\frac{1}{M}\frac{\partial p}{\partial t}=0$$

(2)

where ${\varvec{\upsigma}}$ is total stress tensor, $\mathbf{f}$ is body force vector, $\rho$ is the density of the solid mass and ${\varvec{u}}$ is the solid displacement vector, $\mathbf{v}$ is the fluid velocity vector, $\alpha$ is the Biot–Willis coefficient (usually ranges between 0 and 1), ${\varepsilon }_{v}$ is the volumetric strain of the porous media, $M$ is Biot`s modulus, and $p$ is the fluid pressure. The Biot–Willis coefficient as a factor multiplied to fluid pressure in Eq. (1) signifies a modification and generalization of Terzaghi’s effective stress law to:

$${\varvec{\upsigma}}={{\varvec{\upsigma}}}^{\mathbf{^{\prime}}}-{\varvec{m}}\alpha p$$

(3)

where σ′ is the effective stress tensor, m^T = [1, 1, 0] for 2D.

For mechanical analysis of linear elastic porous media with small-deformation, we have

$${{\varvec{\upsigma}}}^{\mathbf{^{\prime}}}=\mathbf{E}{\varvec{\upvarepsilon}}$$

(4)

$${\varvec{\upvarepsilon}}=\mathbf{A}\mathbf{u}$$

(5)

where $\mathbf{E}$ is the elastic constitutive tensor, ${\varvec{\upvarepsilon}}$ is the strain tensor, $\mathbf{A}={\left[\begin{array}{ccc}\frac{\partial }{\partial x}& 0& \frac{\partial }{\partial y}\\ 0& \frac{\partial }{\partial y}& \frac{\partial }{\partial x}\end{array}\right]}^{\mathbf{T}}$ is the strain–displacement matrix.

In porous media, we assume that the fluid flow satisfies Darcy`s law:

$$\mathbf{v}=-\mathbf{K}\nabla h$$

(6)

where $\mathbf{K}$ is the tensor of permeability coefficient, and $h$ is the hydraulic head, as the sum of the pressure head $p/\gamma$ and the elevation head.

Two types of couplings between fluid flow and mechanics exist: direct and indirect couplings (Fig. 2, as a concept presented by Rutqvist and Stephansson in 2003). Direct couplings (i.e., pore-volume coupling) refer to solid deformation impact on conservation of mass, while fluid pressure impacts the effective stress. Direct couplings are expressed in the equations of conservation of mass and momentum (Eqs. (1)–(3)), i.e., the Biot’s general theory. When volumetric strain is negligible, however, direct coupling can be reduced to one way. Indirect couplings including hydraulic or mechanical properties change as results of deformation and/or fluid pressure. One typical example is that the fracture permeability is very sensitive to deformation, thus, it requires accurate calculation of this indirect coupling effect.

Fig. 2

Hydro-mechanical direct (I) and indirect (II) couplings (Rutqvist and Stephansson 2003)

For different scales of fractures, different governing equations as well as fracture constitutive behavior and HM coupling apply.

2.1.1 Fractures as Finite-Thickness Porous Zones

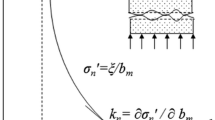
For dominant fractures that can be modeled as finite-thickness porous zones (Hu and Rutqvist 2020a; Hu et al. 2017a), to account for the nonlinear behavior of a fracture that may be partially mineral filled, a reformulation of Bandis’ (1983) equation (Rutqvist et al. 1998, 2000) is used to describe the nonlinear relationship of the fracture effective normal stress ${\upsigma }_{n}^{^{\prime}}$ with the mechanical aperture ${b}_{m}$:

$${\sigma }_{n}^{^{\prime}}=\frac{\xi }{{b}_{m}}+{\sigma }_{n0}^{^{\prime}}$$

(7)

where ${\sigma }_{n0}^{^{\prime}}$ is user-defined and $\xi$ is a constant defined as follows:

$$\xi ={b}_{mi}({{\sigma }_{ni}^{^{\prime}}-\sigma }_{n0}^{^{\prime}})$$

(8)

The behavior of fracture shear displacement under shear stress satisfies:

$${\sigma }_{s}^{^{\prime}}=\frac{\Delta {u}_{s}}{\zeta +\psi \Delta {u}_{s}}$$

(9)

where $\zeta$ and $\psi$ are constants. When $\psi =0$, linear relationship between shear stress and shear displacement is retained.

For fluid flow in fractures, the hydraulic conductivity ${k}_{f}$ of a fracture is related to a hydraulic fracture aperture ${b}_{h}$, which can be defined according to Witherspoon et al. (1980):

$${k}_{f}=\frac{{b}_{h}^{2}{\rho }_{f}g}{12{\mu }_{f}}$$

(10)

where ${\rho }_{f}$ and ${\mu }_{f}$ are the fluid density and dynamic viscosity, respectively, $g$ is the gravitational acceleration. ${b}_{h}$, is the hydraulic aperture assumed to be:

$${b}_{h}={b}_{hr}+f{b}_{m}$$

(11)

where ${b}_{hr}$ is the residual hydraulic aperture when the fracture is mechanically closed, and $f$ reflects the difference from the mechanical and hydraulic apertures by accounting for roughness of a natural fracture.

With the above concepts and equations, the deformation behavior of the finite-thickness porous zone is controlled by two effects: the linear poro-elastic deformation of the solid fracture fillings and adjacent host rock, and the nonlinear behavior of the fracture described in Eq. (7). Correspondingly, the HM couplings include direct pore-volume coupling, as well as indirect coupling with changes of mechanical and hydraulic properties induced by flow and deformation, respectively.

2.1.2 Fractures as Discrete Interfaces

For discrete fracture networks where fractures are boundaries of the adjacent rock matrix, we assume the following boundary constraints apply for fluid flow and mechanical fields.

Since the fractures in this case are very thin relative to their lengths, the hydraulic head within the fracture can be assumed uniform across its thickness:

$$\varphi \left(s\right)={\varphi }_{f}\left(s\right)=\varphi {^{\prime}}\left(s\right)$$

(12)

where φ and φ' denote the hydraulic head on the two sides of rock elements that are divided by the fracture. Thus, fluid flux along a very thin fracture is represented by flow along its two surfaces:

$${q}_{s}^{f}=-{\alpha }_{f}\frac{\partial \varphi }{\partial s}=-{\alpha }_{f}\frac{\partial \varphi {^{\prime}}}{\partial s}$$

(13)

where $\alpha$ _f is the permeability coefficient. Here, we assume parallel plate flow in fractures as given in Eq. (10).

To represent fracture–matrix interaction, i.e., flux exchange normal to a fracture, two Dirichlet boundaries are used to represent the two surfaces of a fracture:

$$\left\{\begin{array}{c}{\varphi }_{0}\left(s\right)=\varphi \left(s\right) \cap {\varphi }_{f}\left(s\right)={\varphi }^{^{\prime}}(s)\\ {\varphi }_{0}\left(s\right)={\varphi }^{^{\prime}}\left(s\right) \cap {\varphi }_{f}\left(s\right)=\varphi (s)\end{array}\right.$$

(14)

Such a simplification is valid because the fractures are assumed to be thin and unfilled, the distribution of hydraulic head on each surface of a fracture and within a fracture is uniform in the direction normal to the fracture surfaces.

Equations (12–14) include all the possibilities of fluid flow in a fracture, which may act as a fluid conduit or seal.

In contrast, the mechanical state of a fracture is more complicated. A fracture may have several segments and every segment from the two sides of this fracture (a contact pair) have three possible contact states: open, bonded, or sliding. When sliding or shearing occurs, contact pairs (i.e., the locations of where contacts occur) may be altered. Meanwhile, the contact pairs and contact states may be impacted by fluid flow and mechanical deformation dynamically.

Corresponding to these three contact states for each contact pair, different boundary constraints are applied. When a fracture segment (a contact pair) is open, a linear constitutive behavior is assumed:

$$\delta {{\varvec{\upsigma}}}_{{\varvec{f}}}^{\boldsymbol{^{\prime}}}={\mathbf{k}}_{{\varvec{f}}} [{\mathbf{u}}_{{\varvec{f}}}]$$

(15)

where ${{\varvec{\upsigma}}}_{{\varvec{f}}}^{\boldsymbol{^{\prime}}}$ denotes a tensor of effective stress in both normal and tangential directions of a segment of a fracture, ${\mathbf{k}}_{{\varvec{f}}}$ is the stiffness tensor of the segment, and $[{\mathbf{u}}_{{\varvec{f}}}]$ is the jump of displacements in both normal and tangential directions of the fracture segment. When ${\mathbf{k}}_{{\varvec{f}}}$ is set as zero, a mechanically open fracture can be described.

When a segment of a fracture is bonded, the distance and relative shear displacement between the two sides of the segment should be zero, satisfying:

$${\varvec{d}}=0\cap[{{\varvec{u}}}_{{\varvec{s}}}]=0$$

(16)

where ${\varvec{d}}$ is the time-dependent normal distance between the two surfaces of the fracture segment, and $[{{\varvec{u}}}_{{\varvec{s}}}]$ is the relative displacement between the two surfaces in the direction along the contacting face.

When a segment of a fracture is sliding, Coulomb’s law of friction is satisfied in the tangential direction, while the normal distance between the two surfaces of the fracture segment should be zero:

$${\varvec{d}}=0 \cap {{\varvec{F}}}_{{\varvec{s}}}={{\varvec{F}}}_{{\varvec{n}}}^{\boldsymbol{^{\prime}}}\mathrm{tan}\varphi \mathrm{sgn}([{{\varvec{u}}}_{{\varvec{s}}}])$$

(17)

where ${{\varvec{F}}}_{{\varvec{s}}}$ is the contact force in the direction of the sliding face, ${{\varvec{F}}}_{{\varvec{n}}}^{\boldsymbol{^{\prime}}}$ is the effective normal contact force by considering fluid pressure, $\varphi$ is the friction angle, and $\mathrm{sgn}\left([{{\varvec{u}}}_{{\varvec{s}}}]\right)$ denotes the direction of ${{\varvec{F}}}_{{\varvec{s}}}$ that depends on the direction of relative shear displacement. When sliding occurs along the two surfaces of a fracture, the locations of contacts change with time, possibly leading to changes of contact pairs as well as contact states among several segments of this fracture (Hu & Rutqvist, 2020a).

Equations (15)–(17) cover all possible states of contact between the two surfaces on each segment of a fracture. Together with the governing equations and the elastic constitutive law described by Eqs. (1), (3)–(5), both continuous and discontinuous behavior of discrete fractured rocks can be described.

For discrete fractured rocks, Biot’s equation can be used for describing fluid mass conservation and conservation of momentum in the rock matrix and the associated direct coupling. However, the discrete fractures, which may be oriented or intersected arbitrarily, are very thin and may be open, bonded or sliding dynamically. Fluid flow in these fractures is highly sensitive to mechanical changes such as changes of apertures induced by contact dynamics. Meanwhile, the contact dynamics (i.e., the changes of contact pairs and/or contact states) and mechanical properties (i.e., the shear strength) are highly sensitive to the fluid flow, thus, establishing a two-way indirect coupling.

2.1.3 Fractures at the Microscale: Asperities and Grains

At the microscale, Darcy’s law is not sufficient to describe flow in the open channels of fractures or the voids between pores and grains. For these cases, the Navier–Stokes equation is typically used to describe conservation of momentum of fluid:

$$\frac{\partial \mathbf{v}}{\partial t}+\left(\mathbf{v}\cdot \nabla \right)\mathbf{v}+\nabla p=\nu\Delta \mathbf{v}$$

(18)

For mechanics at the microscale (Hu and Rutqvist 2020b), the force term includes not only loading (${{\varvec{F}}}_{{\varvec{l}}}$), but also the contact force, ${{\varvec{F}}}_{{\varvec{c}}{\varvec{o}}{\varvec{n}}{\varvec{t}}{\varvec{a}}{\varvec{c}}{\varvec{t}}}$ between discontinuous interfaces (rough fractures) and material bodies (in granular systems):

$$\mathbf{F}={{\varvec{F}}}_{{\varvec{l}}}+{{\varvec{F}}}_{{\varvec{c}}{\varvec{o}}{\varvec{n}}{\varvec{t}}{\varvec{a}}{\varvec{c}}{\varvec{t}}}$$

(19)

Accordingly, displacement include the term that is contributed by deformation $\int{\varvec{\varepsilon}}d{\varvec{s}}$, as well as the translational ${{\varvec{u}}}_{{\varvec{t}}{\varvec{r}}}$ and rotational ${{\varvec{u}}}_{{\varvec{r}}}$ displacements:

$${\varvec{u}}=\int{\varvec{\varepsilon}}\mathrm{d}{\varvec{s}}+{{\varvec{u}}}_{{\varvec{t}}{\varvec{r}}}+{{\varvec{u}}}_{{\varvec{r}}}$$

(20)

Using Eq. (20), continuum and discontinuum mechanics are integrated.

Similar to the contact force calculated for discrete fractures, the contact force ${{\varvec{F}}}_{{\varvec{c}}{\varvec{o}}{\varvec{n}}{\varvec{t}}{\varvec{a}}{\varvec{c}}{\varvec{t}}}$ between discontinuous material bodies is computed based on the contact state of each identified contact pair. With or without considering motion or deformation of material bodies, there are three possible contact states between two material bodies: separated (no contact), bonded, and sliding.

When the discontinuous material bodies are separated, in most cases, there are no contact forces between them. Thus, we have:

$${{\varvec{F}}}_{\mathbf{c}\mathbf{o}\mathbf{n}\mathbf{t}\mathbf{a}\mathbf{c}\mathbf{t}}=0$$

(21)

When the material bodies are bonded or sliding, Eqs. (16) and (17) that are used to describe discrete fractures can be applied here. However, a significant difference between these two types of calculations is that contact pairs and contact states can change more rapidly and significantly when the contact pairs are no longer straight lines as in discrete fracture networks. A recently published paper by the authors (Hu and Rutqvist 2020b) explained the challenges of capturing these features in detail and developed a rigorous model with multi-step contact calculations that tackled these challenges.

At the microscale, direct coupling may exist in the poro-elastic grains. However, in the voids and channels of fractures, couplings between fluid flow and mechanics is mostly one way: mechanical deformation leads to structural changes of fluid channels. When the system is undrained (i.e., the fluid pressure cannot dissipate rapidly), fluid pressure may have an impact on contact pairs, contact states or shear strength of interfaces of discontinuous bodies.

2.2 Numerical Implementation in the Numerical Manifold Method

2.2.1 Numerical Manifold Method

The numerical manifold method (NMM) (Shi 1992) is based on the concept of a “manifold” in topology. In NMM, independent meshes for interpolation and integration are defined. A mathematical cover is a set of connected patches that cover the entire computation domain. The choices of density and shape of these mathematical patches impact the interpolation precision. The physical patches are mathematical patches divided by boundaries, interfaces and discontinuities that determine the integration fields. The union of all the physical patches forms a physical cover.

Based on the dual-cover definition, the global approximation on each element is defined as the weighted average of the local physical cover function:

$$\varphi ={\mathbf{w}}^{\mathbf{T}}{\mathbf{\varphi }}_{\mathbf{p}\mathbf{c}}$$

(22)

where $\mathbf{w}$ and ${\mathbf{\varphi }}_{\mathbf{p}\mathbf{c}}$ are the weight and physical patch functions, respectively.

On each physical patch, the local function ${\mathbf{\varphi }}_{\mathbf{p}\mathbf{c}}$ can be constant, linear, or any function that is able to capture the behavior of the solution on the patch. Using linear local functions, a global second-order approximation is achieved (Fig. 3a, Wang et al. 2016). Using a local function with a jump of the first derivative, material interfaces can cross-patches and elements (Fig. 3b, Hu et al. 2015a). Using discontinuous local functions, material interfaces can be modeled by introducing continuity constraints (Hu et al. 2015b) and fractures can be naturally simulated (Fig. 3c, Hu et al. 2016, 2017b). In this way, NMM is capable of simulating both continua and discontinua with flexible numerical approximation. In the models that are presented in this paper, constant patch functions and linear weight functions with triangular mathematical meshes are used to approximate hydraulic head and displacements.

Fig. 3

Flexible choices of local approximation functions: a a linear function (Wang et al. 2016), b a jump junction for a weak discontinuity (Hu et al. 2015b), c a discontinuous function for a fracture (Hu et al. 2016, 2017b)

NMM can be related to other numerical methods in terms of interpolation, as shown in Fig. 4. If the weight function is bilinear on rectangles and the physical patch function is a constant, NMM can be related to the finite element method (Zheng et al. 2020). If the weight function is piecewise linear in each direction and the physical patch function is a constant, NMM can be related to the finite volume method (Hu and Rutqvist 2020c). If the weight function is a constant as 1 (meaning there is no overlap between physical patches) and the physical patch function is a constant, NMM can be related to the discrete element method. If the weight function is a constant as 1 and the patch function is linear (or higher order), NMM can be related to the DDA.

Fig. 4

Relating NMM to other numerical methods in terms of interpolation

2.2.2 Overview of Multi-scale Models for Coupled Process Analyses

Based on NMM, we developed comprehensive model capabilities to simulate coupled processes in fractured rocks by considering fractures as finite-thickness porous zones, discrete interface networks and granular systems at different scales. The modeling capabilities involving governing equations, constitutive relationships, HM couplings, and challenges associated with intersections and shearing of fractures are summarized in Table 1.

Table 1 Multi-scale coupled processes models for fractured rocks

For dominant fractures, which can be equivalent to finite-thickness porous zones, Biot’s equations are used to describe the poro-elastic behavior. Nonlinearity of fracture normal stiffness as well as shear stiffness associated with shearing can appear. In these porous zones, both direct coupling in rock matrix and fractures, and indirect coupling in fractures are involved. We developed a finite-thickness porous zone model (Hu et al. 2017a; Hu and Rutqvist 2020a) to represent these fractures with solid elements. Thus, calculation of intersections of fractures is straightforward; and calculation of shearing of these fractures is conducted with the linear and nonlinear constitutive fracture laws. To accurately represent linear and nonlinear behavior, an implicit approach that accounts for their strain energy was developed and verified (Hu et al. 2017a).

For discrete fractured rocks, Biot’s equations are used to describe the poro-elastic behavior in the porous rock matrix. These discrete fractures may be oriented or intersected arbitrarily. The mechanical contact state of a fracture segment may be open, bonded or sliding and may change dynamically. In addition, fluid along the fractures may have flux exchange with the surrounding rock matrix. Permeability of these fractures, described by a reformulated cubic law as a function of hydraulic aperture, is highly sensitive to deformation and contact dynamics of the fractures. Meanwhile, the contact pairs and contact states as well as shear strength can be highly sensitive to the fluid pressure, thus, establishing a two-way indirect coupling. To account for such complex behavior in discrete fractured rocks, we developed a zero-dimensional fracture model (Hu et al. 2017b; Hu and Rutqvist 2020a) by considering fractures as boundaries of adjacent solid-rock matrix. Fluid flow in fractures and flux exchange with the rock matrix are implicitly considered. Permeability is updated each time as a function of mechanical aperture depending on the mechanical states. The mechanical states of each fracture segment are rigorously considered in the three contact states: open, bonded and sliding with different constraints. The challenges to simulate these network systems are to simulate intersections and shearing of these discrete fractures. Using a tree-cutting algorithm with discontinuous surfaces approximating each fracture, we are able to calculate each intersection of two fractures considering contacts between each two sides around the intersection. Shearing along a fracture segment is explicitly calculated by updating contact pairs (two surfaces of each fracture segment) while Coulomb’s law of friction is satisfied. Since each fracture is discretized into several line segments and these segments may have different contact states, complex behavior such as shear dilation or uneven opening of a fracture can be calculated.

At the microscale where the asperities of fractures are explicit or the fracture becomes a damaged granular system, the challenge of modeling such microscale behavior is to capture when and where contacts occur between the discontinuous asperities and grains which are moving and deforming as a result of coupled processes. For an open channel bounded by rough fracture surfaces or the pores and voids in a granular system, the Navier–Stokes equation in combination with conservation of mass is needed to represent fluid flow. For a drained system, coupling in these channels, pores and voids majorly exists in one way: mechanical deformation and contact dynamics impact the geometry of the system (i.e., the structure of the channels, pores and voids where fluid flow takes place). We developed a rigorous model with multi-step contact calculations to simulate dynamic contacts with possible large deformation and large displacements with explicit geometric representation of the complex structures (Hu and Rutqvist 2020a, b). On the other hand, fluid flow in the open channels and voids in a drained system may have very limited impact on mechanical deformation. Because of the one-way coupling feature, the flexible choice of decoupling is enabled. With rigorous detection of contact pairs, enforcement of contact constraints and iteration for contact state convergence within each time step, intersections of fractures and shearing of fractures at the asperities or along discontinuous grain boundaries can be rigorously simulated.

Note that for all the described scales, the dynamic processes of both mechanics and fluid flow as described by Biot’s equations are accounted for in our numerical model. To account for dynamic mechanical processes, acceleration is represented as a function of the displacement at the current time step and the velocity of the previous time step, leading to an implicit approach. By assigning different coefficients related to the velocity, damping is considered (Shi 1992). The transient changes of mass conservation caused by the volumetric strain and changes of pore pressure are calculated implicitly as well (Hu et al. 2017a).

A high-level summary of the modeling capabilities for simulating fractures as finite-thickness porous zones, discrete fracture networks as well as microscale asperities and grains is shown in Fig. 5. Radiating from the direct coupling of conservation of solid momentum and conservation of fluid mass, discontinuum mechanics with calculation of dynamic contacts is applied for the two discontinuous scales, i.e., the discrete fracture networks and microscale asperities and grains. In addition, different and indirect couplings apply with different constitutive behavior and physical laws.

Fig. 5

Overview of the multi-scale coupled processes models based on the NMM

3 Examples and Applications

The models described in Sect. 2 have been verified step by step for each component (Hu et al. 2016, 2017a, b; Hu and Rutqvist 2020a, b). In this section, we present several simulation examples involving realistic representation of fracture geometry from images of rough fractures, discrete fracture networks and a deformation band in a granular system at the microscale. We first compare different models for a single fracture shearing and a network of rough non-planar fractures from an image. Then, we show an example of coupled hydro-mechanical analysis of a discrete fracture network from an image of an outcrop. In the last example, we extract an image that contains a soft cataclastic deformation zone and a number of grains to investigate the impact of the cataclastic deformation zone on the dynamic evolution of the granular system at the microscale.

3.1 Modeling a Single Fracture Shearing with Continuous and Discontinuous Models

In the first example, shearing of a single fracture in a rectangular domain exposed to a differential (shear) load is simulated and the results are compared with the analytical solution by Pollard and Segall (1987). This is a part of Task G of the international DECOVALEX¹-2023 model comparison project where Safety ImplicAtions of Fluid Flow, Shear, Thermal and Reaction Processes within Crystalline Rock Fracture NETworks (SAFENET) is the theme. In this example, shearing of smooth and rough fractures is simulated and compared with the analytical solution. The shear strength of the fracture is assumed to be zero, meaning that the shear offset deformation across the fracture will depend on the imposed differential (shear) load and elastic properties of the rock matrix surrounding the fracture.

We simulate a fracture dipping 45° in a 0.5 m × 0.5 m domain. The fracture is 0.17 m long. The Young’s modulus of the rock matrix is 49.74 GPa and the Poisson’s ratio is 0.26. The bottom of the domain is fixed, while a vertical loading of 10 MPa is applied on the top. On the left and right boundaries, horizontal loadings of 5 MPa are applied. We used three different geometric representations to simulate the shearing of the fracture: (1) a continuous model to represent the fracture as a finite-thickness porous and deformable zone (Fig. 6a), (2) a discontinuous model to represent a smooth and planar fracture (Fig. 6b) and (3) a discontinuous model to represent a rough, non-planar fracture with asperities (Fig. 6c). The geometry of the rough, non-planar fracture is defined at discrete points as shown by the focused view of the fracture in Fig. 6c. There are still two simplifications from a real fracture: (1) the roughness at smaller scales is neglected, and (2) it is assumed that the upper and lower fracture surfaces are identical and perfectly mated. Nevertheless, the example is useful for showing the effect of non-planar fracture geometry on the shear behavior of a single fracture. The meshes that are used for the calculations are shown in Fig. 6.

Fig. 6

Modeling a single fracture slip with three different geometric representations: a a finite-thickness porous and deformable zone of a planar fracture, b discontinuous interfaces of a planar and smooth fracture and c discontinuous interfaces and asperities of a non-planar and rough fracture

In the continuous model of a planar fracture, we used a linear elastic model to represent the fracture mechanical behavior using a finite-thickness porous and deformable zone with different material properties from the rock matrix. This assumption is valid based on the fact that the analytical solution considers a smooth and planar fracture. The Young’s modulus is the same as that of the rock matrix whereas the Poisson’s ratio is set as 0.35, leading to a reduced shear modulus of the finite-thickness zone. As a result of the low shear modulus within the fracture, the shear deformation across the fracture is dominated by the elastic shear resistance in the rock matrix surrounding the fracture.

The discontinuous model is used to represent both the smooth, planar fracture and the rough, non-planar fracture. The friction angle and cohesion are both set as zero, leading to a shear strength of zero for the smooth, planar fracture. In the case of the rough and non-planar fracture, the asperities introduce certain friction that may impact the shear displacements at the local contacts between the two opposing fracture surfaces.

We calculated the profile of shear displacements of the fracture and compared it with the analytical solution. The comparisons with analytical solution are shown in Fig. 7. Here we plot the shear displacements along the fracture with a localized 1D coordinate system of the crack. In this localized 1D coordinate system, the crack center is the origin. The negative and positive values denote the distances to the center from the upper left and lower right regions, respectively. In the first two models, shear displacements are calculated as the relative shear offset across the fracture, which is equal to the relative displacements on the two sides of the fracture in the direction along the fracture (45°). For the rough fracture model, we calculated the shear displacements using two approaches. In the first approach, the non-planar fracture was approximated with three straight line segments, which have different orientation angles. We project the relative displacement on the two sides of the fracture within each segment along the direction of that segment. The result is shown in red (Fig. 7c). In the second approach, we projected the relative displacements on the two sides of the fracture in the 45° direction, shown in green. As we can see, good agreement was achieved for both the continuous finite-thickness model (Fig. 7a) and the discontinuous interface model (Fig. 7b) of a planar fracture. For the discontinuous model of the rough, non-planar fracture, some expected larger deviations from the analytical solution are observed (Fig. 7c). Considering the fixed bottom and loading from the top, the reduced shearing seen from the left end of the fracture can be attributed to the lower dip angle of that left section of the fracture. Comparing the results calculated by the two approaches, we find the relative displacements in 45° direction cannot represent localized shear displacements associated with the local contacts pairs between asperities of the two opposing fracture surfaces.

Fig. 7

Calculated shear displacements and comparison with the analytical solution by three different models: a the continuous finite-thickness porous zone model, b the discontinuous planar interface model, and c the discontinuous rough interface model

To further study the impact of asperities on shearing, we compare the stress calculated for the perfectly smooth and planar fracture with that of the rough, non-planar fracture as shown in Fig. 8. In the case of the perfectly planar frictionless fracture, the stresses are concentrated at the two ends of the fractures, whereas in the case of non-planar (rough) fracture some shear stress is transmitted across the fracture at asperity contact points/areas. In the case of a non-planar rough fracture, the stress disturbance affects a wider area around the crack tips and across the fracture as a result of local asperity contacts. Locally, the asperities introduce concentration of both vertical and shear stresses. In general, these concentrated contact stresses could cause formation of new cracks, fracture plasticity, or pressure solution when fluid chemistry condition is satisfied. If considering non-zero friction, local highly stressed asperity contacts could be interpreted as a result of high frictional resistance significantly impacting the overall fracture shear deformations.

Fig. 8

Impact of asperities on shearing: comparison of vertical and shear stresses (Unit: Pa) calculated by the discontinuous planar interface model (a, b) and by the discontinuous rough interface model (c, d)

3.2 Modeling Discrete Rough Fractures with Continuous and Discontinuous Models

We extracted an image of a network of discrete open fractures with rough fracture surfaces (Fig. 9a) for accurate geometric representation in the models. Two different models were applied to simulate its mechanical behavior induced by compaction: (1) a continuous model where the fractures are represented as porous and deformable zones with a softer material than the rock matrix (Fig. 9b), and (2) a discontinuous model where the fractures are represented as discontinuous rough surfaces (Fig. 9c). Since the rough fractures are all connected, the discrete rough fractures divide the domain into a blocky system. In both models, the asperities are explicitly represented. The goal of this simulation is to understand the relationship and differences of the two different models that are used to represent dominant rough fractures which are not filled with minerals.

Fig. 9

Geometric representation of discrete rough fractures from an image (a) with porous zones (b) and with discontinuous rough interfaces (c)

The model domain for this example is 10 m × 8 m. For each model, a vertical loading of 0.42 MPa is applied on the top. The other three boundaries are fixed. In the second model, to prevent the blocky system from falling apart, we use columns outside the blocky system to apply loading on the top and confinement on the left, right and bottom boundaries. For both models, the Young’s modulus is set to 4 GPa and the Poisson’s ratio is 0.3. In the continuous model, the solid material within the fractures surfaces is assumed to have a Young’s modulus of 4 MPa, which is three orders of magnitude lower than the surrounding rock matrix. This could either be seen as a way to represent a fracture with a finite-thickness porous zone with a fracture normal stiffness approximately by E/b, where the b is the thickness of the fracture zone, or it could represent a fracture filled with soft mineral filling. The Poisson’s ratio is the same as the rock matrix. In the discontinuous model, the loading and confinement columns have a Young’s modulus of 4 GPa. The fractures, represented as rough interfaces, have a friction angle of 30°. The meshes that are used for the two different models are shown in Fig. 10. In the first model, the rough fracture surfaces become material interfaces between the finite-thickness thickness zones and the rock matrix (Fig. 10a). These material interfaces divide the mathematical patches that are formed by evenly distributed triangles into discontinuous physical patches. Across each material interface, continuity of stress and displacement for mechanics and continuity of hydraulic head and normal flux for flow should be satisfied, respectively. We used the penalty method for mechanics (Hu et al. 2017a) and the Lagrange multiplier method for fluid flow to realize these continuity constraints, respectively. In the second model, the unfilled fracture channels become gaps between the rock matrix, and the rock matrix is discretized with triangular meshes (Fig. 10b).

Fig. 10

Meshes of (a) the continuous porous zone model and (b) the discontinuous rough interface model

The results of vertical and shear stresses that are calculated by the two different models are shown in Fig. 11. With the fractures represented by soft solid material, high compressive and shear stresses are developed in some fracture zones as well as in the matrix just above each of the fractures in upper right corner of the model as a result of vertical loading on steeply dipping fractures in this area (Fig. 11a, b). Because of the asperities, localized stress concentration can be found at those asperities with relatively sharper corners.

Fig. 11

Calculated vertical and shear stresses (Unit: Pa) with the porous model (a, b) and with the discontinuous rough interface model (c, d)

Looking at the results by the discontinuous model (Fig. 11c, d), we find that larger displacements occur on the right because of the open space available to accommodate these displacements. This phenomenon is consistent with the results shown by the continuous model. However, with these large displacements, the loading is gradually redistributed and concentrated more on the right side and on the center block of the sample. We see that high compressive stress is developed at the contacting areas between the center block and the outer columns, and between the center block with the neighboring blocks.

Comparing these results from the two different models, major differences of stress distribution can be found within the center block. The results calculated by the continuous model suggest that there is not much localized high stress within the center block (Fig. 11a, b). But based on the calculation by the discontinuous model, high compressive stress develops at the contacting areas after motion and deformation are maximized (Fig. 11c, d). In addition, tensile stress is developed in a block on the right, due to confinement on the right and bending toward the center block (Fig. 11c, d).

From this example, we conclude that because the discontinuous model captures the dynamical changes of contacts with large displacements on the right and the stress redistribution as a result of the dynamic changes of contacts, the results appear to be quite different than those obtained by the continuous model. We show that when rough fractures are not filled with minerals and when a number of rough fractures form a blocky system, dynamic contacts play an important role for the geometric, multi-physical evolution of the system.

3.3 Modeling a Discrete Fracture Network

We extracted a network of discrete thin fractures from an outcrop image (Fig. 12a) and conducted modeling for analyzing coupled hydro-mechanical processes in this system. The geometric representation and the mesh that we constructed are shown in Fig. 12b. This domain contains 126 thin fractures, and a number of them are well connected to form a major non-planar fracture running through the domain from the left boundary to the bottom boundary. We set the domain size as 10 m × 8 m.

Fig. 12

A discrete fracture network: a original image and b the generated mesh

Initially, the effective stress is 10 MPa in the horizontal direction and 5 MPa in the vertical direction, and the fluid pressure is 1.5 MPa. All boundaries are fixed mechanically in both directions. A constant injection pressure of 2 MPa is applied on the left boundary, while the pressure on the right boundary is kept constant at 1.5 MPa. The other boundaries are no-flux boundaries. The time step that we used for the calculation is 20 µs. The purpose of this simulation is to investigate how fluid and mechanics interact with a network of densely populated discrete thin fractures. The material parameters in Table 2 are selected with low values of fracture stiffness and shear strength to induced complex shear activation response in the model with significant stress redistribution and HM changes.

Table 2 Computation parameters

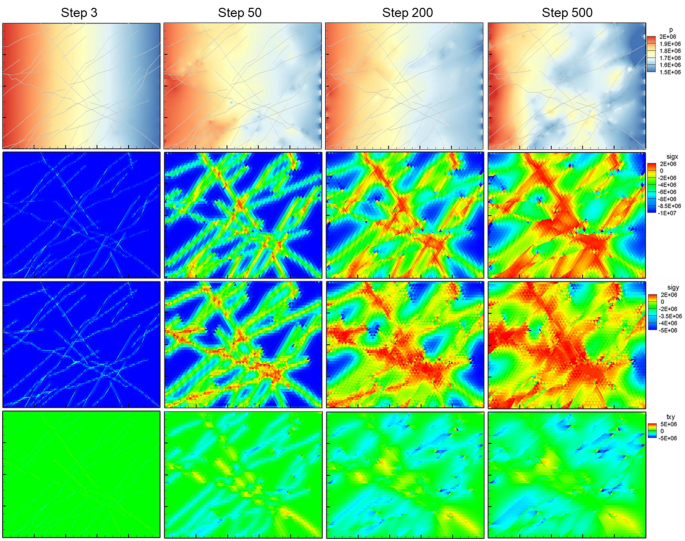
The calculated fluid pressure is shown in Fig. 13 (top row). As can be seen, from the beginning (step 3), a gradient is generated in the domain from the left to the right. At step 50, the fluid flows preferentially along the major fracture paths where intersections are denser in the horizontal direction. At step 200, the fluid pressure begins to dissipate, indicating opening of some fractures occur. At step 500, the pressure increases in a preferential direction, especially along the long non-planar fracture formed with a number of fracture segments. This distribution at step 500 can be correlated with the stress distribution shown below the pore pressure distribution in Fig. 13.

Fig. 13

From top to bottom: calculated pore pressure (Unit: MPa), effective horizontal and vertical stresses and shear stress (Unit: Pa) at steps 3, 50, 200 and 500

In terms of mechanical changes, from Fig. 13, we can see that at step 3, the effective and shear stresses in the domain are quite uniform except for localized areas near the discrete fractures. At this point, shear stress has not accumulated yet. At step 50, a significant stress redistribution has taken place as a result of shear and normal displacement in fractures. This fracture deformation was triggered as a result of an initial shear stress and zero fracture shear strength that induces shear activation. The fracture deformation along with fixed outer boundaries tends to relax stresses within the model, especially in areas of several intersecting fractures. The stress relaxation and redistribution increase with further steps and shear stress develops adjacent fractures undergoing shear, especially apparent around shallowly dipping fractures. The stress relaxes to such a degree that effective stress becomes tensile in the matrix between intersecting fractures especially near the center for the model. If we compare the pore pressure distribution with the shear stress distribution, we find similar patterns of distribution, suggesting shearing occurs with increased permeability.

3.4 Modeling a Grain Pack with a Cataclastic Deformation Zone

In this example, we extract an image of a sandstone with a cataclastic deformation band/zone (Fig. 14a) from the paper by Rotevatn et al. (2008) and investigate the compaction of the system with our microscale model. In our model (Fig. 14b), the 5 mm × 8 mm domain is represented with three different materials: grains with a Young’s modulus of 4 GPa and a Poisson’s ratio of 0.2 (in blue), fragmented grains with a Young's modulus of 0.2 GPa and a Poisson’s ratio of 0.2 (in yellow), and a cataclastic deformation band/zone with a Young’s modulus of 0.2 GPa and a Poisson’s ratio of 0.2 (in grey). The mesh that is used for the calculation is shown in Fig. 14c. To apply boundary constraints, we use four columns outside the domain with a Young’s modulus of 4 GPa and a Poisson’s ratio of 0.3. On the left, right and bottom boundaries, the sample is confined. On the top, a vertical loading of 7.5 MPa is applied. We assume the friction angle is zero because of the fluid. The system is drained so that there is no sufficient fluid pressure built up rapidly to impact the compaction process. The time step that we use for the calculation is 400 µs.

Fig. 14

a An image of a sandstone with a cataclastic deformation zone (Rotevatn et al. 2008), b approximated representation of the image in NMM, and c the generated mesh

Figure 15 shows the evolution of the vertical stress during the dynamic compaction of the granular system. We can see that the compressive stress develops from the top to the bottom, including the small particles on the upper left, the large particle on the upper right and the deformation zone (Fig. 15a). When the upper left and upper right particles make contacts with the lower particles, the compressive stress in the deformation zone continues to propagate from the top to the bottom. Meanwhile, the soft deformation zone makes contacts with neighboring particles (Fig. 15b–d). When the compressive stress is high enough in the entire deformation zone, the upper left and right particles still have a large portion of voids to accommodate their motion. At this point, the deformation band starts to bend (Fig. 15e, f), resulting in a tensile stress area. With the deformation and bending of the deformation band, the compressive stress begins to relocate from the center deformation band to the left and right particles, driving these groups of particles to move downward (Fig. 15g). At the end (Fig. 15h), the deformation band bends to maximum and all particles are in contact with high stress, resulting in a system with a minimized porosity.

Fig. 15

Evolution of vertical stress (unit: Pa) at steps 500 (a), 1000 (b), 2000 (c), 4000 (d), 7000 (e), 10,000 (f), 20,000 (g), 30,000 (h)

The horizontal, vertical and shear stresses when reaching equilibrium are shown in Fig. 16. We can see high compressive horizontal and vertical stress bands are formed in both directions. At the bending area in the center, all stress components reach very high values, indicating a high possibility of fragmentation in this region.

Fig. 16

Calculated horizontal, vertical and shear stresses (unit: Pa) when reaching equilibrium

This example confirms a conclusion in the earlier paper by the authors (Hu and Rutqvist 2020b): the sequential evolution of geomaterials as responses to stress is motion, deformation and accumulation of high stress at local contacting areas (especially at sharp corners). In addition, through this example, we find the fact that the damage zone with softer material can accommodate larger deformations, and therefore, dominate contact evolution and redistribution of stress of a granular system toward a system with minimized porosity.

4 Conclusions

In this study, we presented our multi-scale modeling capabilities to simulate coupled HM processes in fractured rocks. Based on the geometric features, the fractures are modeled as continua—finite-thickness porous zones, and discontinua—discontinuous interfaces and microscale discontinuous asperities and granular systems. Correspondingly, different governing equations, physical laws, coupling priorities and approaches to address intersections and shearing of fractures are applied. By taking advantages of the NMM dual-cover systems, the continuum model with linear and nonlinear fracture models have been implemented, and a rigorous multi-step contact calculation algorithm has been developed for the discontinuous interfaces and microscale asperities and granular systems. With these capabilities, the direct pore-volume coupling in both continuous and discontinuous models (rock matrix and the finite-thickness porous fracture zone), and indirect couplings associated with changes of permeability, contact pairs and contact states, and interfacial strength were implemented in these models.

To highlight the importance of asperities in the fracture contact mechanics, we simulated the same single-fracture shearing problem defined in the DECOVALEX Task G using three different models with different geometric representations where the fracture is represented as a finite-thickness porous zone, a smooth and planar interface, and a rough and non-planar interface, respectively. We compared the displacement profile with the analytical solution and achieved good agreement with the analytical solution using all three models. Expected larger deviations occur with the rough interface model, which is explained by the fact that the analytical solution is based on a smooth fracture surface. But using the rough interface model, we were able to capture stress concentration at the local asperities that may cause dynamic contacts evolution such as propagation of fractures, fracture plasticity, or pressure solution when fluid chemistry conditions are satisfied.

To demonstrate the importance of choosing a reasonable model based on the geometric features, we used two different models to simulate compaction of a discrete rough fracture network: a continuous model with a number of porous zones with a softer material, and a discontinuous model with a number of rough surfaces. Based on the simulation, we found that the discontinuous model was able to adequately capture the dynamic changes of contacts and stress redistribution as a result of the contact dynamics, which resulted in a different stress distribution from that calculated by the continuous model. We conclude that accurate calculation of contact dynamics is important for analyzing the geometric and multi-physical evolution of systems when rough fractures are not filled with minerals and when a number of rough fractures form a blocky system.

The discontinuous interface model was applied to simulate coupled fluid and mechanics of a discrete fracture network consisting of 126 fractures from a rock image. We show a special case in which shearing of discrete fractures can have a major impact of the distribution of pore pressure as well as stress distribution over the domain.

Finally, we used the discontinuous microscale model to simulate evolution of a granular system with a deformation band. We were able to capture the sequential evolution of the system as a response to stress: large displacement, large deformation and accumulation of high stress. We also found the fact that a deformation band with a softer material can accommodate larger deformations, and therefore, dominate contact evolution, structural changes and redistribution of stress of a granular system toward a system with minimized porosity.

In conclusion, using realistic geometric representation from rock images, by applying reasonable physical laws and coupling priorities, and by successfully tackling the challenges associated with calculation of dynamic contacts in deformable discontinuous materials, the multi-scale modeling capabilities presented here have shown to be promising for analyses of a number of geosciences activities, including basic understanding of geosystems evolution, as well as effective and safe design and control of injection and production in the reservoirs. As 3D modeling of coupled processes in fractured systems is still relatively rare at discrete fracture or micro-grain scale, these modeling capabilities will be extended to 3D in the future by addressing the challenges of computational geometry involving geometric representation of discrete fractures and dynamic contacts of fracture planes and micro-grains.