Investigation of the motion of magnetic nanoparticles in microfluidics with a micro domain model

Abstract

In this paper the magnetic nanoparticle (MNP) dynamics in a microfluidic device is investigated in the presence of an external magnetic field. The nanoparticles are used for enzyme-substrate reaction measurements, where the enzyme is immobilized to the surface of the nanoparticles. During the measurements the microreactors, called microchambers are filled up with the MNPs where the distribution of the nanoparticles significantly influences the results of the further reaction measurements. In this paper the procedure of the nanoparticle aggregation is investigated numerically in the microchamber in a micro domain simulation space. First the acting forces on the MNPs are examined from the different phenomena. An in-house numerical model is presented where the dynamics of several MNPs are simulated in the micro-size domain. This model is also embedded in the open source CFD software OpenFOAM. The theoretical calculations and the simulations show that the particle-particle interaction due to magnetization plays an important role during the aggregation procedure. The particles in the magnetic field cluster over the time into chains, which phenomenon is in good agreement with the literature. A theoretical model of the chain dynamics is also established, which is compared to the simulation results. The presented micro domain model was later used to improve an Eulerian-Eulerian based two-phase CFD model and solver, which is able to model the complete MNP aggregation procedure in the magnetic field in macroscopic domains.

1 Introduction

Magnetic nanoparticles are widely used in biomedical applications, such as in drug delivery, hyperthermia treatment or chemotherapy (Mohammed et al. 2017). MNPs are also used in enzyme-substrate reactions by immobilizing the enzyme to the nanoparticle surface. This technique offers re-usability of the enzyme, low cost and potential increase in thermal and pH stability (Ansari and Husain 2012). Investigating the enzyme-substrate reactions in microreactors with MNPs offers additional benefits due to the reduced size. The microreactor size is usually between the sub-micron and the sub-millimetre ranges (Wolfgang et al. 2000). The small volume of a reactor - e.g. $1\,\upmu \hbox {l}$ - requires small amount of the expensive reagents (Kerby et al. 2006), enables precise temperature control (Kikutani et al. 2002) and leads to high surface-to-volume ratio.

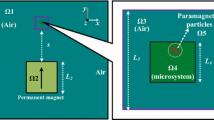
In our research group enzyme-substrate reactions have been investigated in serially connected microchambers filled with magnetic nanoparticles (Ender et al. 2016; Weiser et al. 2015; Pálovics et al. 2018b). The sketch of the measurement is shown in Fig. 1. The diameter of the magnetic nanoparticles were a few hundred nanometers and the enzyme was immobilized to their surface. The cloud of the particles in the fluid, i.e. the nanoparticle suspension was transported into the chambers with a continuous fluid flow and anchored there by the help of external neodymium magnets. These magnets were positioned precisely over the center of each chamber, see in Fig. 2. Then, after all the chambers were filled with the MNP suspension, the substrate was forced to flow through the chambers as an aqueous solution. When the substrate met with the enzyme in the chambers, the reaction occurred and a product was generated. The product concentration then was measured at the outlet with an appropriate detector, see in Fig. 1.

Fig. 1

Enzyme substrate reaction measurement with the MNPs. The nanoparticle aggregate fills each chamber, while the enzyme is immobilized on the MNP surface. The substrate flows through the structure. The generated product solution concentration is measured at the outflow, providing information about the enzyme kinetics (Ender et al. 2016; Pálovics et al. 2018b)

The measured enzyme-substrate reactions showed flow rate dependent parameters (Ender et al. 2016; Pálovics et al. 2018b). This phenomenon was also reported by other authors both in packed beds (Lilly et al. 1966) and in microfluidic devices (Seong et al. 2003; Kerby et al. 2006). To investigate this dependence, recently we have designed microfluidic chambers with optimized shape (see in Fig. 2), where the flow field was aimed to be more homogeneous than in the original chambers with cylindrical shape. The optimization was mainly done with CFD simulations (Pálovics et al. 2018a). During the measurements with the new structures, it was found that the final shape of the MNP aggregate in the chamber was different from what was previously expected, as a small gap remained between the aggregate and the chamber wall, see in Fig. 3. This was an undesired effect, because some parts of the substrate bypassed the aggregate without making any reaction with the enzyme, therefore the gap reduced the microreactor’s efficiency.

Fig. 2

a Microfluidic chip layout with 6 serially connected chambers. The chamber shapes were optimized with CFD simulations. The chamber diameter is $D = 2.8\,\hbox {mm}$ while the channel width is $d=300\,\upmu \hbox {m}$. b The cylindrical neodymium magnet is positioned over the center over the chamber to anchor the incoming MNPs (Pálovics et al. 2018a)

Fig. 3

Photo of the MNP filled enhanced chamber during an enzyme-substrate reaction measurement. The fluid flew from the left to the right. The MNP aggregate’s border is highlighted with a white line. It can be seen the chamber is only partially filled (Pálovics et al. 2018b)

Based on this, and the flow rate dependence of the reaction it was realized that a numerical model is needed, which can predict the aggregation of the nanoparticles in the chamber and the final shape of the MNP aggregate. A detailed model would also be able to estimate the flow velocity in the aggregate, which is an important factor in the flow rate dependent reaction.

This paper focuses on the micro domain modelling of the magnetic nanoparticle dynamics, as a first step in achieving the desired goals. The presented model and simulations give a possible explanation of the MNP aggregation procedure in the chamber. First, the acting forces on the nanoparticles and their magnitudes from the different physical phenomena are investigated in details with calculations. Then an in-house numerical simulator for the particle movement is presented. The problem is also investigated with the open-source CFD solver OpenFOAM by extending one of its solver and the corresponding libraries. The work at some parts relies on recent works from the literature (Han et al. 2010; Karvelas et al. 2017). In Han et al. (2010) magnetorheological (MR) fluid is investigated with the Lattice-Boltzmann method. Although in their work the numerical technique and the investigated cases are different from our case, the theoretical part is found to be a good base for our work. In Karvelas et al. (2017) magnetic particle aggregations are investigated with OpenFOAM. Their theoretical part was found to be useful and at some part similar to (Han et al. 2010). However, their numerical results, like the particle chain length dependence on the magnetic field cannot be applied to our case, because of the different range of the particle size. Moreover, in their case they do not examine the effect of the fluid flow, which will be covered in this paper. Based on the presented micro domain model recently we improved an Eulerian-Eulerian based two-phase CFD model and solver, which is capable to simulate the MNP aggregation in the magnetic field, see the details in Pálovics et al. (2020). In this model one phase is the fluid, while the other is denoted for the MNPs. The benefit of tretating the MNPs as a continous phase is the lower computational demand, as this way the modelling of the individual particles is not needed. This makes the simulation of the complete MNP aggregate possible.

2 Measurement background

In this section the details about the microfluidic flow and MNPs are summarized based on our previous papers, because these data are necessary for the creation of the numerical model.

2.1 Fluid flow

During the MNP filling procedure the fluid was the mix of isopropanol and water [20 % isopropanol–80 % water, as volumetric ratios (Pálovics et al. 2018b)]. The density and dynamic viscosity of this mixture is calculated as $\rho _f = 973\,\hbox {kg/m}^{3}$ and $\mu = 1.87 \cdot 10^{-3} \hbox {Pa s}$ based on (Ngo et al. 2013). The flow was laminar at the used flow rate was $Q= 600\,\upmu \hbox {l min}^{-1}$. At this flow rate the maximum velocities of the fluid in the empty (only fluid filled) chamber are assumed to be in the range of $0.05-0.1\,\hbox {m s}^{-1}$. It should be noted that in the measurements besides the MNPs a small amount polyethylene-glycol (PEG) was also added to avoid the possible self-aggregation of the MNP suspension without the magnetic field. In the current work however the effect of the polyethylene-glycol is not yet included.

2.2 Magnetic nanoparticles

The magnetic nanoparticles were made of a magnetite $\hbox {Fe}_{3}\hbox {O}_{4}$ core with silicone dioxide coating (Ender et al. 2017). The enzyme was immobilized to the surface of the coating. The core had a diameter of $210\,\hbox {nm}$, while the coating width was $10\,\hbox {nm}$ and the enzyme had a length of $\approx 10\,\hbox {nm}$, i.e. the final particle size was 250 nm. In the further calculations we set the $\hbox {Fe}_{3}\hbox {O}_{4}$ density to $\rho = 5250\,\hbox {kg/m}^{3}$ (Roy and Frank 1986), and the silicon-dioxide density as $\rho = 2196\,\hbox {kg/m}^{3}$. The mass of the enzyme was calculated as 15 % of the mass of the core and the silicone-dioxide (Ender et al. 2017). Based on these data, the calculated mass of one particle with the enzyme on its surface is $m_p = 3.312 \cdot 10^{-17}\,\hbox {kg}$, while its moment of inertia is $I_p = 1.809 \cdot 10^{-31}\,\hbox {kgm}^{2}$.

2.3 Neodymium magnets

The referred measurements were done with the MagneFlow device, which contains neodymium magnets over each chamber to fix the MNP suspension in them against the flow (Pálovics et al. 2018b). Each magnet was of N48 type with a cylindrical shape, the diameter was $D = 3\,\hbox {mm}$, and the height was $h = 4\,\hbox {mm}$. The magnet had a remanent magnetization of $B_{T} = 1.4\,\hbox {T}$, and the relative permeability was estimated to $\mu _r \approx 1$. The arrangement and a side view-sketch are shown in Figs. 2, 4.

Fig. 4

Side view sketch of the microfluidic chip and the neodymium magnet over the chamber. The red and blue dashed lines show the position of the magnetic field plots presented in Fig. 5. Both lines start at the centre of the chamber, under the symmetry axis of the magnet

Fig. 5

The calculated magnetic field of the neodymium magnet. The figure shows the vertical and radial components at the chamber top and bottom. The red and blue dashed lines in Fig. 4 represent the sampling positions of the graphs with the corresponding colour

The magnetic field of the magnet is calculated with the open source CFD software OpenFOAM v7 (Weller et al. 1998) with the solver magneticFoam. The field of the magnet is noted as $\mathbf {B}_0$ or $\mathbf {H}_0$. The components of $\mathbf {H}_0$ at the top and bottom of the microfluidic chamber are shown in Fig. 5.

3 Theoretical calculations for modelling the MNP dynamics

3.1 Modelling aspects

In this section we show the main aspects of MNP dynamics modelling. Each nanoparticle is treated as an individual particle. This is an important criterion, because this way we will be able to get a detailed model about the dynamics, by including the particle-particle forces, modelling the collisions, etc. It should be noted however, that this criterion causes that the modelling of the whole chamber will be computationally too expensive, because of the high number of particles $(n\approx{10^{9}-10^{9}})$. To overcome this problem recently we tried to treat the problem with the MP-PIC method (Snider 2001) in OpenFOAM, where one computational parcel meant more particles at the same location with the same velocity (Pálovics and Rencz 2018). Although with this model the particle movement, and the particle-fluid interaction seemed to be appropriate, we have lost the correct modelling of the particle-particle interactions. This is a problem, as it will be shown later, the attractive force between the magnetized particles is one of the main reason of the MNP suspension formulation.

3.2 Drag force on the MNP

When the velocity of the nanoparticle is different velocity from that of the surrounding fluid, the evolving Stokes-drag force is:

$$\begin{aligned} \mathbf {F}_S = - 6 \pi \mu r_p (\mathbf {v}_p - \mathbf {v}_f ), \end{aligned}$$

(1)

where the $\mu$ is the dynamic viscosity of the fluid and $\mathbf {v}_p$ and $\mathbf {v}_r$ are the particle and the local fluid velocity, respectively. If the MNP rotates, the fluid also acts a decelerating torque on the particle:

$$\begin{aligned} \pmb {\tau } = - 8 \pi r_p^3 \mu \cdot \pmb {\omega }, \end{aligned}$$

(2)

where $\mu$ is the dynamic viscosity and $\pmb {\omega }$ is the angular velocity (Etienne et al. 2001).

3.3 MNP magnetization

The particles get magnetized from the external magnetic field. The fluid's relative permeability is assumed to be $\mu_r \,=\,1$. In this case the particle core magnetization $\mathbf {M}_i$ is:

$$\begin{aligned} \mathbf {M}_i = \frac{3 \chi }{3 + \chi } \mathbf {H}_0, \end{aligned}$$

(3)

where $\chi$ is the magnetic susceptibility and the $\mathbf {H}_0$ is the magnetic field of the neodymium magnet (Jackson 2012). This formula is only valid if the $\mathbf {M}(\mathbf {H})$ curve is linear. The magnetization curve of the magnetite nanoparticles have been reported by several authors (Rajput et al. 2016; Goya et al. 2003; Daoush 2017). Generally, the results show that the saturation magnetization value of the nanoparticles can be smaller than the bulk magnetite’s saturation magnetization, which is $\mathbf {M}_{s\_bulk} = 92\,\hbox {emu g}^{-1} = 483\,\hbox {kA m}^{-1}$ (Roy and Frank 1986). Showing an example, in Goya et al. (2003) the $\mathbf {M}_s$ is $75.6\,\hbox {emu g}^{-1}$ and $65.4\,\hbox {emu g}^{-1}$ at $T = 300\,\hbox {K}$ for $\hbox {Fe}_{3}\hbox {O}_{4}$ nanoparticles with a diameter of 150 nm and 50 nm, respectively. It should be noted however, that in our case the particles are far from being fully magnetized, even at the centre of the chamber, where they are closest to the magnet. This means that the actual value of $\mathbf {M}_s$ - assuming that it is being around the listed values - does not affect our calculations.

In our model, Eq. (3) is used to calculate the magnetization. The susceptibility is set to $\chi = 2.8$ (Roy and Frank 1986). The remanent magnetization of the particles is considered to be negligible. After calculating the value of the magnetization inside the particle, the magnetic moment of the particle i is calculated as:

$$\begin{aligned} \mathbf {m}_i = V_{core} \mathbf {M}_i, \end{aligned}$$

(4)

where the $V_{core}$ is the volume of the particle magnetite core ($d_{core} = 210\,\hbox {nm}$).

Treating the particles as magnetic dipoles, the field of particle i at the location $\mathbf {r}$ is

$$\begin{aligned} \mathbf {H}_i (\mathbf {r}) = \frac{1}{4 \pi } \frac{1}{r^3} \left[ 3(\mathbf {m}_i \hat{\mathbf {r}} ) \hat{\mathbf {r}} - \mathbf {m}_i \right] , \end{aligned}$$

(5)

where $r = | \mathbf {r} |$, and $\hat{\mathbf {r}}$ is the unit vector to the given direction $\hat{\mathbf {r}}=\mathbf {r}/r$ (Jackson 2012). The particles close enough to each other can modify each other’s magnetic moment due to their own field. This means, that Eq. (3) should be modified to include the close particles’ field:

$$\begin{aligned} \mathbf {m}_i = V_{core} \frac{3 \chi }{\chi + 3} \left( \mathbf {H}_0 + \sum _{j \ne i} \mathbf {H}_j \right) , \end{aligned}$$

(6)

where $\mathbf {H}_0$ is the field of the neodymium magnet and $\sum \mathbf {H}_j$ is the net field of the surrounding particles.

3.4 Magnetic forces on the MNP

The non-uniform net magnetic field $\mathbf {B}$ acts with a force on a dipole $\mathbf {F} = \nabla (\mathbf {m} \mathbf {B})$. In the following the force is separated to the effect of the field of the magnet and the effect of the surrounding particles. In the non-uniform field of the permanent magnet, the field interacts with the magnetized MNP particle with:

$$\begin{aligned} \mathbf {F}_{M\_field} = \mu _0 (\mathbf {m}_i \nabla ) \mathbf {H}_0 = \mu _0 \mathbf {m}_i \cdot \nabla \mathbf {H}_0 \end{aligned}$$

(7)

where $\mu _0$ is the vacuum permeability as the fluid’s relative permeability. The equality of the second and third part is based on the fact that $\nabla \times \mathbf {H}_0 = 0$.

As the close magnetized particle i is in the non-uniform dipole field of particle j, the force between the two particles is:

$$\begin{aligned} \begin{aligned} \mathbf {F}_{M\_ij}&= \frac{3 \mu _0 m_i m_j}{4 \pi r_{ij}^4 } [ \hat{\mathbf {r}}_{ij} ( \hat{\mathbf {m}}_i \hat{\mathbf {m}}_j ) \\&\quad +\hat{\mathbf {m}}_i ( \hat{\mathbf {r}}_{ij} \hat{\mathbf {m}}_j ) + \hat{\mathbf {m}}_j ( \hat{\mathbf {r}}_{ij} \hat{\mathbf {m}}_i) - 5 \hat{\mathbf {r}}_{ij} ( \hat{\mathbf {r}}_{ij} \hat{\mathbf {m}}_i) ( \hat{\mathbf {r}}_{ij} \hat{\mathbf {m}}_j)], \end{aligned} \end{aligned}$$

(8)

where $m_i$ and $m_j$ are the magnitudes of the magnetic moments, $\mathbf {r}_{ij}$ is the distance vector between the two particle centres and $r_{ij}$ is its magnitude (Han et al. 2010). The $\hat{}$ symbol represents the unit vector to the representative directions, therefore $\hat{\mathbf {r}}_{ij}$ is the unit vector to the direction of the $\mathbf {r}_{ij}$ vector.

The presented mutual dipole model is often used in this type of problems (Han et al. 2010; Karvelas et al. 2017). It should be noted however, that the model can be inaccurate when the particles are really close to each other. In Keaveny and Maxey (2008) the dipole approximation has been compared with other, more precise methods in some basic particle pair configurations. Nevertheless, in paper (Han et al. 2010) it was concluded, that for high number of particles the more advanced methods are hard to be generalized, and therefore they still used the dipole model. The dipole model is more exact when the distance between the particles is increasing. Favourably in our case only the particle cores can be magnetized, which means that when two particles touch each other their distance is $d = 2.4 r_{core}$. At this distance the error of the force between the particles with the mutual dipole approximation is estimated to be less than 10 % in the most of the investigated configurations in Keaveny and Maxey (2008).

3.5 Other forces

The gravity and buoyancy also act on the particle, as

$$\begin{aligned} \mathbf {F}_g + \mathbf {F}_b = (m_p - \rho _f V_p) \mathbf {g}, \end{aligned}$$

(9)

where $\rho _f$ is the fluid density, $V_p$ is the total particle volume and $\mathbf {g}$ is the gravitational acceleration. The pressure gradient force on the particle is

$$\begin{aligned} \mathbf {F}_{gp} = V_p \rho _f \frac{\mathrm {D} \mathbf {u}_f}{\mathrm {D} t}, \end{aligned}$$

(10)

where the last term is the material derivative of $\mathbf {u}_f$, i.e. $\frac{\mathrm {D} \mathbf {u}_f}{\mathrm {D} t} = \frac{\partial \mathbf {u}_f}{\partial t} + \mathbf {u}_f \cdot \nabla \mathbf {u}_f$.

The Brownian force is estimated to negligible in the model. This approximation is based on the fact, that the magnetic interaction energy of two close particles is much higher than kT [further details can be found in Bossis et al. (2002)].

3.6 Particle collision

One should also treat the case, when the particles collide with each other. From the various models in the literature we had chosen the spring-slider-dashpot model, which is a soft-sphere model for the collision based on the Hertzian contact theory (Tsuji et al. 1992; Crowe et al. 2011). The detailed description of this model is out of scope of this paper, but it is well explained in Crowe et al. (2011). Our implementation relies on the corresponding model of the OpenFOAM CFD solver (class SpringSliderDashpot in v7). Here only the main idea of the method is presented. The sketch of a collision of two particles is shown in Fig. 6. According to the model the two particles can be slightly overlapped during the collision. The normal force of the collision to particle i is (normal direction: unit vector in the line which connects the centres of the colliding particles):

$$\begin{aligned} \mathbf {F}_{n\_ij} = \left( -k_n \delta _{n\_ij}^{\frac{3}{2}} - \eta _n \mathbf {v}_{rel\_ij} \cdot \mathbf {n} \right) \cdot \mathbf {n}, \end{aligned}$$

(11)

where $k_n$ is the stiffness in the normal direction, $\delta _{n\_ij}$ is the overlap in the normal direction, $\eta _n$ is the normal damping coefficient and $\mathbf {v}_{rel\_ij}$ is the relative velocity of particle i to particle j and $\mathbf {n}$ is the normal vector of the collision, see in Fig. 6. At the same time in the tangential direction the force is:

$$\begin{aligned} \mathbf {F}_{t\_ij} = -k_t \delta _{t\_ij} - \eta _t \mathbf {v}_{c\_ij}, \end{aligned}$$

(12)

where $k_t$ and $\mathbf {F}_{t\_ij}$ are the tangential stiffness and force, and $\mathbf {v}_{c\_ij}$ is the slip velocity of the contact point. The more detailed description, i.e. the calculation of the stiffness, damping parameters and $\delta _t$ can be found in Crowe et al. (2011). It should be noted, that the tangential force also acts as a torque, i.e. the colliding particles are also changing each other’s angular momentum.

Fig. 6

Spring-dashpot model to the normal direction based on Crowe et al. (2011). The particles are overlapping in the normal direction by $\delta _{n\_ij}$

In the following section, we compare the magnitudes of the presented forces in a simplified case.

3.7 Force comparison

Let us investigate the following case. Two MNPs are placed in the centre of the microchamber, where the fluid velocity is approximately $v_f = 0.05\,\hbox {m s}^{-1}$. The two MNPs are fixed, they are in contact with each other and the second MNP is over the first one (see in Fig. 7). In the followings the magnitude of the previously discussed forces are calculated for this simple case.

Fig. 7

The sketch of the investigated case with two MNPs in the centre of the chamber. The particles are in contact with each other. The fluid flows from the left to right, i.e. to the direction x with a homogeneous velocity of $v_f = 0.05\,\hbox {m s}^{-1}$. The magnet over the chamber creates at the centre a z directional vertical magnetic field

The magnitude of the Stokes-force is

$$\begin{aligned} F_S \approx 2.2 \cdot 10^{-10}\hbox {N}. \end{aligned}$$

(13)

based on Eq. (1). It should be noted, that this calculation is not fully correct, because the neighbouring particle also modifies the fluid field around the investigated particle. Nevertheless, we still use the Stokes-force as an estimation. Moreover the presented value is an over-prediction in most of the cases, because the fluid velocity is smaller closer to the chamber walls, and the aggregated particles also slow down the fluid locally (see later).

To calculate the force of the magnetic field gradient (Eq. (7)) and the particle-particle force (Eq. (8)) first the particle magnetizations have to be computed. To achieve this, the pre-calculated field of the neodymium magnet is used. At the centre of the chamber the magnetic field is almost vertical and its value reaches $180\,\hbox {kA m}^{-1}$ (see Fig. 5). In the following calculations therefore we use that value $\mathbf {H}_0 = 180\,\hbox {kA m}^{-1} \mathbf {e}_z$. Substituting this value to Eq. (3) $\mathbf {M} \approx 261\,\hbox {kA m}^{-1} \mathbf {e}_z$, which means that the nanoparticles are far from the saturation. This results in a magnetic moment of $\mathbf {m}_i \approx 1.27 \cdot 10^{-15}\,\hbox {Am}^{2} \cdot \mathbf {e}_z$ for the particles.

In case of close particles they modify each other’s magnetic moment due to the short distance. Investigating the particles in Fig. 7, the magnetic field for particle i due to particle j is changed by [see Eq. (5) and (6)]:

$$\begin{aligned} \mathbf {H}_i^* = \mathbf {H}_0 + \frac{1}{4 \pi d_p^3} \left[ 3 \left( \mathbf {m}_j \mathbf {e}_z \right) \mathbf {e}_z - \mathbf {m}_j \right] \approx \mathbf {H}_0 + 12.9\, \hbox {kA m}^{-1} \cdot \mathbf {e}_z , \end{aligned}$$

(14)

where $\mathbf {e}_z$ is the z directional unit vector. As $\mathbf {H}_0 = {180}\,\hbox {kA m}^{-1} \cdot \mathbf {e}_z$, this means, that the particle j increased the magnetic field at particle i by approximately 7 %. The magnetic moment of particle i is also changed according to the increased magnetic field, noted with $\mathbf {m}_i^*$. The same procedure can be done by swapping the particles in the previous equation, i.e. the magnetic moment of the particle j is also increased due to the magnetic field of particle i. The corrected magnetic moment values are $\mathbf {m}_j^* = \mathbf {m}_i^* \approx 1.35 \cdot 10^{-15}\,\hbox {Am}^{2} \cdot \mathbf {e}_z$. The magnetic moment values can now be substituted back to the previous equation to calculate a second correction of the magnetic field $\mathbf {H}_i^{**}$ and $\mathbf {H}_j^{**}$ and the magnetic moments. This step is not necessary in practice, as the change of the field with the second correction is small (lower than 1 %). It can be also shown, that any further iteration will not modify significantly the magnetic moment values [see more detailed in Han et al. (2010)]. It should be noted however, that in case of several closely packed particles using only this first correction can be inaccurate due to the numerous magnetic interactions between the particles.

The attractive force of the neodymium magnet over the chamber is determined from Eq. (7). The calculation needs the corrected magnetic moment of the particle and the corresponding components of the magnetic field gradient tensor $\nabla \mathbf {H}_0$, which is defined as $\left( \nabla \mathbf {H}_0 \right) _{ij}=\frac{\partial (H_{0_j})}{\partial x_i}$. This term can be calculated from the magnetic field in OpenFOAM. In the centre of the chamber, at the symmetry axis of the magnet $\frac{\partial (H_{0_z})}{\partial z}\approx1.6\cdot 10^{8} \hbox {Am}^{2}$. Using this value and the increased magnetic moment $\mathbf {m}_i^*$ the attractive force of the magnet is approximately:

$$\begin{aligned} \mathbf {F}_{M\_field} \approx 2.7 \cdot 10^{-13}\,\hbox {N} \cdot \mathbf {e}_z. \end{aligned}$$

(15)

Finally the force between the two particles due to the magnetization is also considered. Both particles magnetic moment’s are increased due to the cross-effects as it was shown before, see Eq. (14). The force is calculated with Eq. (8), where $r_{ij} = 2 \cdot r_p$ (see Fig. 7), and all the unit-vectors are pointing up to the z direction, i.e. they are parallel to each other (the magnetic moment vectors $\mathbf {m}_i^*$ and $\mathbf {m}_j^*$ are still parallel to $\mathbf {e}_z$). Based on this the attractive force can be easily calculated as

$$\begin{aligned} F_{M\_ij} \approx 2.8 \cdot 10^{-10}\, \hbox {N}. \end{aligned}$$

(16)

The magnitude of the force of the gravity minus the buoyancy to one MNP is:

$$\begin{aligned} F_g + F_b \approx 2.5 \cdot 10^{-16} \hbox {N}. \end{aligned}$$

(17)

To calculate the pressure gradient force in Eq. (10) the $\frac{\mathrm {D} u_f}{\mathrm {D} t}$ term around the particle has to be estimated. In a 1D case assuming that $\frac{\partial u_f}{\partial t} = 0$ and $\nabla u_f < u_f / d_p$:

$$\begin{aligned} \mathbf {F}_{gp} < V_p \rho _f u_f \frac{u_f}{d_p} \approx 8 \cdot 10^{-14} \hbox {N}. \end{aligned}$$

(18)

The result of these calculations show us the followings:

• The gravitational force $F_g$ and the buoyancy $F_b$ can be neglected compared to the other forces. The pressure gradient force in a steady case is also quite small.

• The dominant forces are the drag force $F_S$ and the particle-particle force $F_{M\_{ij}}$ because of the magnetization.

• The net attractive force of the neodymium magnet $F_{M\_{field}}$ is approximately 3 orders of magnitude lower than the drag and particle-particle forces. This means, that in this micro domain model it can be also neglected, or it can be relevant only where the fluid flow is really slow, i.e. close to the chamber/channel walls. It should be noted however, that this statement is not generally true for a bigger simulation domain, where a lot of particles are already aggregated.

Interestingly, these pre-calculations show that the nanoparticle aggregation under the neodymium magnet is mainly caused by the particle-particle attractive forces due to the magnetic moments. In the further sections this effect will be examined with a numerical model.

3.8 Chain formulation

As the close particles are attracting each other, they are arranging themselves into chains in the magnetic field. The direction of the chain is parallel to the magnetic field in the absence of other forces. This phenomenon will be shown in the results section. To get macroscopic parameters of the nanoparticle aggregate it is worth to investigate what happens with the chain in a fluid flow with strain rate. A detailed discussion of the problem is presented in Martin and Anderson (1996), where the chain formulation of electrorheological fluids are investigated. Although in their case there are no magnetic forces, the form of the dipolar interaction is similar. Our following discussion relies on this work.

In our case the chain arrangement is shown in Fig. 8.

Fig. 8

A linear chain of particles in a vertical magnetic field. The attractive magnetic particle-particle force holds the chain together. The chain is bent due to the non-homogeneous velocity field of the fluid with the strain rate $\dot{\gamma }$

As the chain starts to rotate due to the inhomogeneous drag force its direction will be non-vertical. Note that in this theoretical model the bent chain is considered to be linear, which assumption will be revisited in the results section. In the rotated chain a magnetic counter torque appears between the neighbouring particle pairs. The presence of this counter torque becomes more clear if the the particle-particle force is rewritten as:

$$\begin{aligned} \mathbf {F}_{M\_ij} = - \frac{3 \mu _0 m_i m_j}{4 \pi r_{ij}^4 } \left[ (3 \cos ^2{\Theta } -1 ) \cdot \mathbf {e}_n + \sin {2 \Theta } \cdot \mathbf {e}_t \right] \end{aligned}$$

(19)

where $\Theta$ is the angle between the chain and the magnetic field, while $\mathbf {e}_n$ and $\mathbf {e}_t$ are unit direction vectors between the neighbouring particles to the normal and tangential directions, as it is shown in Fig. 8. The couple of the tangential forces $F_{ij_t}$,$F_{ji_t}$ causes a net torque on the particle pair. If the chain consists of N particles, there are $N-1$ neighbouring pairs, which means that the overall magnetic torque is

$$\begin{aligned} M_{m} = (N-1) \cdot d_p \cdot \frac{3 \mu _0 m_i m_j}{4 \pi (2r_p)^4 } \sin {2 \Theta }. \end{aligned}$$

(20)

To calculate the torque of the inhomogeneous drag force, the centre of the chain is positioned to the origin, like in Martin and Anderson (1996). Note that in the following equations the problem is solved first when N is odd, i.e. there is a centre particle. Using the Stokes formula, the torque of the ith particle’s drag from the centre is:

$$\begin{aligned} M_{d_i} = (i \cdot d_p) \cdot \left[ 6 \pi \mu r_p (\dot{\gamma } \cdot i \cdot d_p \cos {\Theta } ) \right] \cos {\Theta }. \end{aligned}$$

(21)

As N is odd, there are $(N-1)/2$ particles over the centre particle. The overall torque of the drag is therefore

$$\begin{aligned} M_d = 2 \cdot \sum _{i=1}^{(N-1)/2} 6 r_p^3 \pi \mu \dot{\gamma } \cdot (2i)^2 \cdot \cos ^2{\Theta } \end{aligned}$$

(22)

If the chain is in balance the two torques cancel out each other, $M_m = M_d$. This gives an equation for the rotation angle:

$$\begin{aligned} \tan {\Theta } = \frac{64 \pi ^2 \mu \dot{\gamma } r_p^6}{\mu _0 m_i m_j} \cdot \frac{1}{N-1}\sum _{i=1}^{\frac{N-1}{2}} (2i)^2 \end{aligned}$$

(23)

If the particle number N is even, there is no centre particle, and Eq. 21 should be modified: the term $i d_p$ has to be changed to $i d_p - r_p$ and the summation goes to N/2. This results in, that the tangent of the angle when N is even will be

$$\begin{aligned} \tan {\Theta } = \frac{64 \pi ^2 \mu \dot{\gamma } r_p^6}{\mu _0 m_i m_j} \cdot \frac{1}{N-1}\sum _{i=1}^{\frac{N}{2}} (2i-1)^2 \end{aligned}$$

(24)

These equations show the following:

• The rotation angle $\Theta$ is higher in flows with higher strain rate $\dot{\gamma }$. It is also higher in the same fluid flow with a longer chain.

• The rotation angle decreases if the magnetic field is increased. The reason of this is, that the magnetic moments $m_i$,$m_j$ are approximately linear with $\mathbf {H}$ [see Eq. (3)], and the higher moments represent stronger magnetic torque.

• If the strain rate is known, and the particle moments the rotation angle can be calculated.

In the possession of the rotation angle, the magnetic torque $M_m$ can be determined with Eq. (20). Using the following approximation $\sin {2\Theta } \approx 2 \Theta \approx 2 \tan {\Theta }$ and Eq. (23), (24) in the magnetic torque Eq. (20) we obtain

$$\begin{aligned} M_m \approx 12 \pi \mu \dot{\gamma } r_p^3 \sum _{i=1}^{\frac{N-1}{2}}(2i)^2, \quad M_m \approx 12 \pi \mu \dot{\gamma } r_p^3 \sum _{i=1}^{\frac{N}{2}}(2i-1)^2 \end{aligned}$$

(25)

for the magnetic torque when N is odd or even, respectively. Interestingly, the equation shows that the magnetic torque can be calculated from the chain length, and does not need the exact values of the magnetic moments. As $\sum _{i=1}^{N}i^2 = \frac{1}{6}(2N^3+3N^2+N)$, the torque increases rapidly with N.

In a macroscopic model, the magnetic torque can be handled as an increased viscosity. Let us take as an example a small domain of fluid containing several particle chains with different lengths. Their overall magnetic torque-density is

$$\begin{aligned} \tau _m = \frac{1}{V_{domain}} \sum _{i=1}^{n_{chains}} M_{m_i} \end{aligned}$$

(26)

where $M_{m_i}$ is the magnetic torque of the ith chain. This torque-density can be embedded into a macroscopic CFD model, as an increased viscosity, see more details in our recent work Pálovics et al. (2020).

In Martin and Anderson (1996) the normal forces in the direction of the chain are also investigated. To get a stable chain, the normal component of the attractive magnetic pair force $F_{{ij}_n}$ between the centre particle and its neighbour should be larger than the sum of the normal components of the drag in the half-chain:

$$\begin{aligned} \frac{3 \mu _0 m_i m_j}{4 \pi (2 r_p)^4 } (3 \cos ^2{ \Theta - 1}) \ge 6 \pi \mu r_p \sum _{i=1}^{N^*}(d_p \cdot i \cos {\Theta } \cdot \dot{\gamma }) \sin {\Theta }, \end{aligned}$$

(27)

where $(N^*=(N^*-1)/2$ denotes the particle number in the half-chain. Expressing the $\mu _0 m_i m_j$ term on the left side from the torque balance equation Eq. (23) we obtain the following equation:

$$\begin{aligned} \begin{aligned} 3 \cos ^2{\Theta } -1&\ge \sin ^2{\Theta } \frac{6(N^*)}{2N^*+1}\\&\approx 6 \cos ^2{\Theta } \ge 4 \end{aligned} \end{aligned}$$

(28)

which means that the angle should be less than $\Theta _{crit} = 35.26^{\circ }$ to get a stable chain. Similar deduction can be found in Martin and Anderson (1996) for the electrorehological chain at the part called rigid chain model.

Finally we note that in Martin and Anderson (1996) the tangential force balance is also investigated, which gives a slightly different result for the rotation angle than the torque balance model (the critical chain is also different by a few degrees). We think that the difference is caused by the fact that the bent chain is not exactly linear, as it will be shown in the Results section.

4 Numerical model

In the following sections we present the numerical model of the investigated problem, which was written in C++ language. In the solver the leapfrog algorithm is built with the equations described above. The idea to use this algorithm is originated from the discrete particle modelling (DPM) solver of the OpenFOAM CFD software.

The need for a specialized solver arises from the complexity of the problem. Implementing an in-house solver offered numerous benefits during the developing process. By including the different phenomena in the algorithm, we could understand their effect better than by using a complex simulator package. At the same time during the development the numerous pitfalls in the simulations could be more easily detected and avoided. Thirdly, our solver code could be flexibly handled and modified as it was tailored specifically for this problem.

In addition to our solver the final model was also embedded in the open source CFD solver OpenFOAM by extending one of its solvers and the corresponding libraries. The OpenFOAM solver offered additional benefits, such as the detailed modelling of the fluid field, or in case of the high number of particles a faster computation due the parallelization possibilities.

4.1 Movement algorithm

In the solver the motion of several particles are modelled over the time, where each particle has its own coordinate and velocity. At every time step the forces affecting the nanoparticles are calculated. The movement of the particles follows the steps of the leapfrog algorithm (Benedict et al. 1996). The steps of it are summarized here for one particle, but of course the same procedure is done for the whole particle cloud.

• (1) At time $t_i$ we know the particle’s location $\mathbf {x}_i$ and velocity $\mathbf {v}_i$, the corrected magnetic moment $\mathbf {m}_i^*$ and the sum of the acting forces $\mathbf {F}_i$. The velocity at the half of the next time step is calculated as

  $$\begin{aligned} \mathbf {v}_{i+\frac{1}{2}} = \mathbf {v}_i + \frac{\mathbf {F_i}}{m_p} \cdot \frac{\Delta t }{2}. \end{aligned}$$

  (29)

• (2) The particle is moved with the half-step velocity to the new position:

  $$\begin{aligned} \mathbf {x}_{i+1} = \mathbf {x}_i + \mathbf {v}_{i+\frac{1}{2}} \cdot {\Delta t }. \end{aligned}$$

  (30)

• (3) The corrected magnetic moment $\mathbf {m}_i^*$ is calculated at the new position based on Eq. (6). In the equation the field $\mathbf {H}_j$ of the surrounding particles are set by Eq. (5) with their magnetic moment values from the previous time step. Moreover, at the current time step additional corrections are possible, i.e. calculate $\mathbf {m}_i^{**}$ with the already corrected neighbour moment values $\mathbf {m}_j^*$. The presented technique is similar to the method in Han et al. (2010), although in the correction step of $\mathbf {m}_i$ they use the already updated neighbour moment $\mathbf {m}_{j}^*$ if the particle j was updated before the i. It should be also noted, that in our case only the effects of the close particles are considered, which are closer than a pre-defined cutoff distance $r_c$.

• (4) The force at the new position is determined: $\mathbf {F}_{i+1}$. The velocity at the new position is then calculated as

  $$\begin{aligned} \mathbf {v}_{i+1} = \mathbf {v}_{i+\frac{1}{2}} + \frac{\mathbf {F}_{i+1}}{m_p} \cdot \frac{\Delta t }{2}. \end{aligned}$$

  (31)

  This means that in the new position $\mathbf {x}_{i+1}$ the velocity $v_{i+1}$ and force $\mathbf {F}_{i+1}$ are all calculated, so one can move to the new time step, starting from the first step of the algorithm.

The rotation of the particles were also calculated. The rotation becomes important, when the particles are colliding in each other. In this case the interacting particles can modify their angular velocity $\varvec{\omega }$ due to the calculated torque during the collision using the soft sphere model (Crowe et al. 2011). The angular acceleration is $\varvec{\beta } = \frac{\mathrm {d}{\varvec{\omega }}}{\mathrm {d}{t}} = \frac{\varvec{\tau }}{I_p}$, where the torque $\varvec{\tau }$ is calculated during the collisions based on the soft-sphere model. Moreover on the rotating MNP the torque caused by the viscous fluid is continuously evaluated implicitly in every time step based on Eq. (2).

During the magnetic moment calculation the first estimation is always set based on the external field of the neodymium magnet. Then the correction of the moment $\mathbf {m}_i^*$ is calculated by accounting the effect of the surrounding particles in the same way as it was shown in Eq. (6).

Based on the previous section, the following terms are included in the force calculation:

• Stokes-force, which depends on the particle velocity (see Eq. (1). It is calculated implicitly, which was useful to work with bigger time steps. The viscous torque in Eq. (2) is also calculated implicitly.

• Magnetic attractive force between the particles.

• Collision force and torque when two particles are overlapping based on the spring-slider-dashpot soft-sphere model.

• Magnetic force of the neodymium magnet.

It is important to note, that in our algorithm only the effect of the close particles are investigated during the magnetic moment correction step and the particle-particle force calculation. This is done in order to save computational power. In Han et al. (2010) the cutoff distance of close particles was selected to be $d_c = 6 r$. In our work the cutoff distance for the force and the magnetization correction was set to $d_{c} = 2 \,\upmu \hbox {m}>> 6 r_{core}$.

4.2 Solver implementation

The algorithm was created with the object-oriented C++ v11. The visualisation was done with OpenGL 3.3. In C++ classes have been defined to the particle, particle cloud, collision model etc. Using this object oriented technique the problem can be treated with a relatively easy to see-through code, which is flexibly extendable.

Although the algorithm was written for 3D, the simulations were run only in a 2D domain due to limit the number of the particles, as the higher number of particles in 3D were numerically too expensive. The simulations ran on one core under a 64 bit OpenSUSE Linux.

The algorithm generally performs the previously presented steps of the leap-frog algorithm simultaneously. The particle cloud is stored in a dynamic std::Vector class, where the particles can be added to or released from the cloud representing the incoming and leaving particles at the inlet or outlet by the fluid flow.

4.3 OpenFOAM implementation

The problem was also investigated with the OpenFOAM CFD solver v7 based on the presented model. In the program the discrete particle modelling solver DPMFoam was selected which is capable to simulate the fluid flow and the particles at the same time. A detailed description of the solver can be found in Fernandes et al. (2018). In our case the solver libraries were modified and extended for our purposes. The used particles in OpenFOAM belong to the CollidingParcel class and the particle cloud CollidingCloud. For these classes the magnetic moment calculation was added, including the presented cross-effect correction between the close particles, i.e. the mutual dipole model. Then the magnetic force between the close particles are also calculated. The collision model was the spring-slider-dashpot model (class SpringSliderDashpot). The particle properties were selected with their previously discussed values.

The drag force to the particles is calculated by the Wen-Yu model (Yu and Wen. 1966) with the class WenYuDragForce, which is practically equal to the Stokes-force at the used low velocities and low volume fraction of the particles. Although it is not relevant, but the pressure gradient force shown in Eq. (10) is also included with the class of PressureGradientForce. The virtual mass force is also included with the class VirtualMassForce. The post processing of OpenFOAM based simulations are done with the open source software ParaView (Utkarsh 2015).

The main benefit to use OpenFOAM is that beside the particle movement it calculates also the fluid flow with considering the decelerating effect of the particles. The other advantage is the ability of the parallelization between the computer cores which enables to simulate the high number of particles.

5 Simulation results

In this section different types of simulations are presented based on the new model. First the randomly placed particle aggregation is investigated in the fluid without any external flow. These simulations are performed with our C++ and then with the OpenFOAM based solver. In the next simulation the chain formulation is investigated in a flow with homogeneous strain similar, what was shown in Fig. 8. The linear chain model is compared then with the simulation results. Finally the aggregation is investigated in the presence of a fluid flow with a parabolic velocity profile with the OpenFOAM based solver. The aggregation is tested with different flow velocities.

5.1 Simulation settings

The following collision parameters were set based on Karvelas et al. (2017), where a similar soft-sphere model was used for ${\hbox {Fe}_{3}\hbox {O}_{4}}$ nanoparticles: the coefficient of restitution and Poisson-ratio were set both to 0.5. The coefficient of friction was not mentioned in the cited article and here it is set to 0.5 heuristically. The Young-modulus in our case is artificially reduced to $5 \cdot 10^{6}\, \hbox {Pa}$, which was done in order to increase the time step size. Based on the equations of the soft-sphere model, with this reduced modulus the overlap between the neighbouring particles due to the attractive magnetic force will be approximately 3 % of the particle radius. Other, non-mentioned parameters like particle mass or the viscosity of the fluid are set to their previously presented values. In our solver the relatively low time step $\Delta t= 1 \cdot 10^{-8} \hbox {s}$ was needed to accurately model the particle movement and collisions, even with the reduced Young-modulus. In the OpenFOAM based solver the time step size was dynamically adjusted based on the estimated duration of the particle collisions.

In our solver the field of the neodymium magnet is set to $\mathbf {H}_0 = 180\,\hbox {kA m}^{-1} \cdot \mathbf {e}_z$ for the magnetic moment calculations, the same as in the theoretical part. This field strength can be found at the centre of the chamber under the magnet. The magnetic field is therefore always vertical in all simulations. The gradient tensor of the magnetic field was also evaluated in the magnetic simulation and it is fed into the solver at the given location. In case of the OpenFOAM-based particle simulations the mesh was generated with the blockMesh program. The magnetic field and its gradient were interpolated from the magnetic simulation with OpenFOAM’s interpolation tool mapFields.

5.2 Zero flow case

The aggregation was investigated first without external flow. In our solver, 200 particles were put randomly in a 2D $10\times {10}\,\upmu \hbox {m}$ closed domain. The results can be seen in Fig. 9/a.

In OpenFOAM 8556 particles have been placed randomly in a ${10}\times {10}\times {10}\,\upmu \hbox {m}$ domain, see in Fig. 9/b. We used here more particles, because the core paralellization with OpenMPI enabled higher computational power. The simulation was run on 8 cores in parallel. The given particle number results in an average volume fraction of 7 %, which was the estimated volume fraction of the MNP suspension in the measurements. All domain boundaries were closed also in this case for the particles.

In both simulations the particles are aggregated into chains, which are parallel to the vertical external magnetic field. This is in good agreement with the literature (Han et al. 2010; Karvelas et al. 2017). In Fig. 9/b. the particles are colourized with their magnetic moment. As one can see, the moments are increasing during the aggregation. The reason of this was discussed in the two-particle case: if the close particles are over/under each other, their magnetic field further increases the neighbour’s moment. One can also see, that at the top wall, where the chains end, the moment values are lower than at the middle of the chain. This is also true for the few single particles, which are not aggregated in the chains.

Fig. 9

a Aggregation procedure with our solver with 200 particles in a ${10}\times {10}\,\upmu \hbox {m}$ domain in the zero flow case. b MNP aggregation modelling with OpenFOAM in a ${10}\times {10}\times {10}\,\upmu \hbox {m}$ domain. The particles are colourized with their magnetic moment values

5.3 Chain investigation

The chain dynamics in a fluid flow with constant strain rate was investigated, as it was discussed in the theoretical section, see in Fig. 8. In the simulation we set a horizontal flow with constant strain rate which is 0 at $z=0$, i.e. $\mathbf {v}=\dot{\gamma } \cdot z \cdot \mathbf {e}_x$.

Fig. 10

Steady-state simulation results with the chain. It contains 41 particles in a horizontal flow with the profile $\mathbf {v}=\dot{\gamma } \cdot z \cdot \mathbf {e}_x$, where $\dot{\gamma } = 500\,\hbox {s}^{-1}$. The centre particle is at the origin

A test simulation has been done for a chain with 41 particles. The horizontal flow has the profile $\mathbf {v}=500\,\hbox {s}^{-1} \cdot z \cdot \mathbf {e}_x$, and the centre particle is placed at the origin. The bent shape is shown in Fig. 10.

As it can be seen the chain is nearly, but not perfectly linear. The reason of this, that at the centre sections of the chain the magnetic torque between the neighbouring particle pairs has to be higher to counterbalance the drag torque $M_d$ originated from the particles at the chain ends, which requires a higher rotation angle. Indeed, the angle $\Theta$ monotonously increases from the chain ends towards the centre ($\Theta$ is measured against the vertical magnetic field). The average of the 40 particle pair angles is $\Theta _{avg} = 12.2^{\circ }$. The magnetic moment is higher inside the chain than in a single particle due to the strengthening effect of the neighbouring particles, which was discussed before. Inside the chain the maximum values are around $m \approx 1.5 \cdot 10^{-15} Am^{2}$, except the two particles at the chain ends. Substituting this value to the linear chain model Eq. (23) and $N=41$, the result is $\Theta \approx 12.9^{\circ }$, which is close to average angle in the simulation.

The sum of the magnetic torque was also calculated in the program $M_m \approx 7.1 \cdot 10^{-16}\,\hbox {N m}$. To compare it with the linear chain model Eq. (20) is used with $\Theta _l$ and the increased magnetic moments, which results in $M_m \approx 7.5 \cdot 10^{-16}\,\hbox {N m}$. The error of the equation compared to the simulation is 6 %. Finally the more simple formula for the total torque is checked in Eq. (25), in which only the value of N is needed. The equation gives $M_m \approx 7.9 \cdot 10^{-16}\,\hbox {N m}$, i.e. the error is 11 %. These values confirm, that the linear chain model can be used as an approximation, even with the second formula to find the total magnetic torque on the chain. It should be noted however, that the error of the second formula increases at higher rotation angles.

As it was mentioned above, the benefit of the linear chain model is that it can be used to approximate the average magnetic torque-density in a domain by using Eq. (26). The equation requires the chain length distribution, which can be identified with additional simulations in different particle concentrations. Finally the magnetic torque-density can be handled as an increased viscosity in the macroscopic fluid flow (Pálovics et al. 2020).

5.4 Aggregation in case of fluid flow

The aggregation was also investigated in fluid flow next to the top wall of the chamber. In this case we used the OpenFOAM based solver. This was done because of the high computational demand, due to the high number of particles. Moreover, in this case we are interested about the exact fluid flow field and the effect of the particle aggregate on the flow. The sketch of the simulation domain is shown in Fig. 11. The dimensions are $60\times 24\times {20} \upmu \hbox {m}$, where the top wall of the domain represents the top wall of the chamber, i.e. the flow velocity is 0 there. The fluid has a parabolic velocity profile at the inlet, which is the left plane of the domain. The velocity profile is set in accordance with the measurements. At the top wall the fluid velocity is 0, while $v_f \approx {0.028}\,\hbox {m s}^{-1}$ at the bottom of the domain, at $20 \upmu \hbox {m}$ from the wall. At the side walls and at the bottom of the domain the same parabolic velocity conditions are used as at the inlet. The particles are injected randomly only at the middle third section of the inlet, i.e. a $8 \upmu \hbox {m}$ wide plane, see in Fig. 11. The particle injection rate was selected to an average particle volumetric fraction of $\alpha _p = 1 \cdot 10^{-5}$. In the middle of the top wall some “seed” particles are positioned initially at a $40\times {8} \upmu \hbox {m}$ area, see Fig. 11. These particles’ positions are fixed during the simulation, and they help to start the aggregation procedure in the simulation domain. It should be noted however, that their usage is heuristic. Our guess is that adhesive forces between the wall and MNP appear when they are contacted, but this phenomenon should be further investigated.

Fig. 11

The sketch of fluid flow case simulation domain. The fluid flows into the domain at the left plane of the domain with a parabolic velocity profile. Meanwhile particles are injected into the domain only at the middle third section of the inlet. Seed particles are fixed at the centre section of the top wall

The simulated aggregation procedure can be seen in Fig. 12. The particles are sorting into chains over the time. As the chains are growing, they capture additional particles which are coming from the inlet. This represents a possible explanation of the particle aggregation in the chamber. The chains are skewed, as the fluid flow tries to brush away the particles from the chain with the flow, i.e. to the x direction. Over a certain length the chains can break or be released from the seed particles due to the drag. The broken part is travelling through the domain and might be attached to the next seed particle.

The fixed chains are bent due to the drag, while as a counter-effect the aggregated particles decelerates the fluid locally. The decreased local fluid velocity permits growing longer chains. Moreover, the reduced velocity also facilitates the aggregation of other chains.

Note, that some of the longest chains in Fig. 12 can be held by more than one fixed particle, and these are estimated to be a more stable structure against the flow. Nevertheless the weaker chains over a certain particle number can be broken or be released from the seed particles. This phenomenon usually occurred in the following way: a shorter free particle chain was moving with the flow and suddenly collided and attached to a longer fixed chain. The longer chain was then released due to the increased momentum and drag.

Fig. 12

Simulation result with OpenFOAM. The sketch of the simulation is shown in Fig. 11, and this figure shows the results at $t={132} \hbox {ms}$. The fluid flows from the left to the right with a parabolic profile at the inlet. The domain is colourized with the magnitude of the flow velocity. The particles are injected at the left domain only at the middle part in a ${8} \upmu \hbox {m}$ wide section. The particles are aggregated under the top wall into chains. These chains are bent due to the drag of the flow. The particle chains decrease the fluid velocity locally. The particles are colourized with their magnetic moment values

5.5 Aggregation with different flow velocities

It is worth to investigate the aggregation with different flow velocities. Simulations have been created with 5 times slower, and also 5, as well as 10 times higher velocities compared to the default case. These simulations have been performed with the OpenFOAM based solver, the results are shown in Fig. 13. Note, that in the low velocity case a lot of particles are aggregating into chains. The chains are long and nearly vertical because of the reduced drag. In contrast to this, at the high flow rate simulations (Fig. 13b, c) the chains are significantly bent. Moreover many of the chains are already released by the seed particles i.e. they are travelling with the flow. The chain lengths are much shorter than in the original case, which suggests that the aggregation is limited to a narrow section next the top wall.

Fig. 13

Aggregation at different flow rates with the OpenFOAM based solver. The figure shows the centre part of the domain in three different cases. a 5 times slower velocity than in the default case. The particle chains are nearly vertical in the simulation domain due to the reduced drag. b 5 times higher velocity. c 10 times higher velocity. Note that in case of these higher velocities many bent chains are already released from the seed particles

5.6 Further work

The current model is capable to present the particle aggregation tracking all particles separately. The advantage of this method is that the aggregation procedure can be investigated in details, which was shown in the previous section. The weakness of it is however that it cannot be scaled up to the whole chamber domain due to the high computational demand. As it was mentioned before, the total number of MNPs in the actual chamber is around ${10^{9}}-{10^{10}}$, which is several orders of magnitude bigger than in our investigated cases (10–10000 particles). Thus, our next goal was to create a CFD solver, which models the MNP filling procedure of the chambers without modelling all the particles separately. We improved an Eulerian-Eulerian based two-phase solver, where the nanoparticle aggregate is modelled as a phase and its viscosity depends on its volume fraction and the magnetic field (Pálovics et al. 2020). The viscosity model was implemented based on the linear chain model and the chain length distributions at the different concentrations of the nanoparticles. The chain length distributions were determined by making several micro-domain simulations at the different particle concentrations using the presented technique. Applying the two-phase model we were able to simulate the whole MNP aggregate in the microfluidic structure, where the simulation results were in accordance with the measurements.

6 Summary and conclusion

In this paper the micro-domain numerical model of the magnetic nanoparticle aggregation is investigated in the presence of an external magnetic field in a microfluidic structure. First the problem was presented based on our previous measurement results (Pálovics et al. 2018a, b). Then the acting forces on the MNP were examined based on the different interactions. The magnitude of each force was estimated with a simple example of two close nanoparticles, which were positioned at the centre of the chamber. This calculation showed, that the dominant forces on the MNPs are the Stokes-drag force and the particle-particle attractive force due to the particle magnetization. The particle magnetic moment calculation and correction is shown by taking into account the magnetic field of the close particles.

An in-house numerical simulator is presented, written in C++ to mimic the particle aggregation procedure. In this simulator each particle is modelled individually and their movement is simulated by the leapfrog algorithm. The model was also implemented in OpenFOAM by extending its libraries and the DPMFoam solver. Our solver was capable to investigate the problem in a relatively simple and flexible way. Its usage was beneficial to investigate the fundamental processes during the aggregation, like the particle chain formulation or the bent chain shape in a non-homogeneous flow. The OpenFOAM implementation meanwhile lead to a more exact calculation, e.g. by including to effect of the particles on the flow. Moreover, OpenFOAM can be also used with high number of particles by parallel computation.

The simulations are ran in micro-size domains, where the model parameters were set to be in accordance with our previous measurements. Simulations have been created with both models first without the fluid flow. The results show, that the particles in the fluid cluster aggregate with the time into chains, directed parallel to the external field. These chain formulation is in good agreement with the literature (Han et al. 2010; Karvelas et al. 2017).

A theoretical linear chain model for the particle cluster was established based on Martin and Anderson (1996). The shape of the chain in a flow with homogeneous strain was tested with simulation. The linear chain model was then compared to the detailed simulation results.

Finally the aggregation was investigated in case of a fluid flow with the OpenFOAM based solver. The result shows the particle aggregation procedure, which was detected in the measurements. In the simulations fixed particles were positioned next to the top wall helping to start the aggregation. Their usage was heuristic, and needs to be reconsidered in the future. The aggregation was also investigated at different flow velocities with the OpenFOAM based solver.

The presented micro domain model of the nanoparticles was used to improve a two-phase CFD model and solver, which is able to model the complete MNP aggregation procedure in macroscopic domains (Pálovics et al. 2020).