Abstract
We study weak solutions and minimizers u of the non-autonomous problems \({\text {div}} A(x, Du)=0\) and \(\min _v \int _\Omega F(x,Dv)\,dx\) with quasi-isotropic (p, q)-growth. We consider the case that u is bounded, Hölder continuous or lies in a Lebesgue space and establish a sharp connection between assumptions on A or F and the corresponding norm of u. We prove a Sobolev–Poincaré inequality, higher integrability and the Hölder continuity of u and Du. Our proofs are optimized and streamlined versions of earlier research that can more readily be further extended to other settings. Connections between assumptions on A or F and assumptions on u are known for the double phase energy \(F(x, \xi )=|\xi |^p + a(x)|\xi |^q\). We obtain slightly better results even in this special case. Furthermore, we also cover perturbed variable exponent, Orlicz variable exponent, degenerate double phase, Orlicz double phase, triple phase, double variable exponent as well as variable exponent double phase energies and the results are new in most of these special cases.
Similar content being viewed by others
1 Introduction
We consider the divergence form, quasilinear elliptic equation

and the corresponding F-energy minimization

where A and F have quasi-isotropic (p, q)-growth (see Definition 4.1). Since we allow A and F to depend on x, these are non-autonomous problems. The strategy for dealing with non-autonomous problems is often the reduction to and approximation with autonomous problems, such as the p-power energy \(F(\xi ):=|\xi |^p\), \(p\in (1,\infty )\), and the p-Laplace equation with \(A(\xi ):=|\xi |^{p-2}\xi \). The maximal regularity of weak solutions already to the p-Laplace equation when \(p\ne 2\) is \(C^{1,\alpha }\) for some \(\alpha \in (0,1)\) (e.g., [23, 29, 43, 46, 52]) and this is the objective also in more general cases, including in this article. The approximation technique is often used to deal with Marcellini’s [47] (p, q)-growth energies, \(|\xi |^p \lesssim F(\xi )\lesssim |\xi |^q+1\) and \(1<p\leqslant q\), provided that \(\frac{q}{p}\) is close to 1, see, e.g., [9, 10, 21, 22, 48].
To explain the objective of the current paper we consider the double phase functional \(F(x,\xi ):= |\xi |^p + a(x) |\xi |^q\) with \(1<p\leqslant q\) and \(a:\Omega \rightarrow [0, L_\omega ]\), which is a special case of (p, q)-growth. This model was first studied by Zhikov [53, 54] in the 1980’s and has recently enjoyed a resurgence after a series of papers by Baroni, Colombo and Mingione [6,7,8, 15,16,17]. They studied the relationship between the parameters p and q and the Hölder-exponent \(\alpha \) of a and established maximal regularity of the minimizer u in the following three cases of a priori information:
-
(ap1)
\(u\in W^{1,p}(\Omega )\) and \(q-p\leqslant \frac{p}{n} \alpha \)
-
(ap2)
\(u\in L^\infty (\Omega )\) and \(q-p\leqslant \alpha \)
-
(ap3)
\(u\in C^{0,\gamma }(\Omega )\) and \(q-p< \frac{1}{1-\gamma } \alpha \)
Furthermore, in the first two cases the inequality is sharp in the sense that there exist counter-examples to regularity which fail the inequality arbitrarily little [5, 28]. The case of equality in (ap3) is an open problem. Ok [50] added to these a fourth, likewise sharp, case:
-
(ap4)
\(u\in L^{s^*}(\Omega )\) and \(q-p\leqslant \frac{s}{n} \alpha \)
In view of the Sobolev embedding when \(s<n\), \(s=n\) and \(s>n\), this suggests the unifying, albeit slightly stronger, assumption \(u\in W^{1,s}(\Omega )\) and \(q-p\leqslant \frac{s}{n} \alpha \).
While the relationship between a priori information on u and the conditions for double phase F are quite well understood, this is not the case for the wide range of recently introduced double phase variants, which extend it or combine it with the variable exponent case \(F(x,\xi )=|\xi |^{p(x)}\) [24, 51]. These variants include perturbed variable exponent, Orlicz variable exponent, degenerate double phase, Orlicz double phase, triple phase, double variable exponent and variable exponent double phase. See Corollary 1.1 for the corresponding expressions F and Table 1 for examples of our assumptions in some of these cases. We refer to [41] for references up to 2020 and [3, 4, 18, 20, 30, 32, 45, 49] for some more recent advances on variants of the variable exponent and double phase models.
In most of the special cases, both lower and maximal regularity remain unstudied under assumptions (ap2)–(ap4). Recently, Baasandorj and Byun [2] proved maximal regularity of the Orlicz triple phase case in a massive paper. Rather than study each case individually, we introduced an approach based on generalized Orlicz spaces in [41] and proved maximal regularity for minimizers when \(F(x,\xi )=F(x,|\xi |)\) has so-called Uhlenbeck structure. In [42] we extended the results to weak solutions and minimizers of problems with (p, q)-growth without the Uhlenbeck restriction. In both articles we only considered the assumption \(u\in W^{1,\varphi }(\Omega )\) corresponding to case (ap1). In this article we cover all the different assumptions from cases (ap1)–(ap4), including as special cases all the double phase variants listed in the previous paragraph.
We build on the harmonic approximation approach from [8]. Our method is more streamlined and we are even able to improve the results in the double phase case slightly by introducing the following version of (ap2), which is natural to expect based on the intuition of the Sobolev embedding, and a version of (ap3) with equality provided we have vanishing Hölder continuity:
-
(ap2\('\)) \(u\in BMO(\Omega )\) and \(q-p\leqslant \alpha \)
-
(ap3\('\)) \(u\in VC^{0,\gamma }(\Omega )\) and \(q-p\leqslant \frac{1}{1-\gamma } \alpha \)
This article represents a substantial generalization and unification of prior theory. We expect that our optimized methods can more readily be further extended to other settings.
In recent years, many papers consider bounded weak solutions or minimizers (i.e. Case (ap2)), see for instance [2, 12, 16, 34]. The boundedness can be naturally obtained from the maximum principle for bounded Dirichlet boundary value problems, and is thus a fundamental assumption. The following special case of Corollary 5.14 showcases our results for \(L^\infty \). We emphasize that even many of these special case results are new and that our main results, Theorems 5.3 and 5.11 and Corollary 5.14, also cover other a priori assumptions and structures.
Corollary 1.1
(Bounded minimizers in special cases) Let \(1<p< \min \{q,r\}\), the variable exponents p(x) and q(x) with \(p(x)\leqslant q(x)\) be Hölder continuous and bounded away from 1 and \(\infty \), and \(a\in C^{0,\alpha _a}\) and \(b\in C^{0,\alpha _b}\) be non-negative and bounded. Assume that \(F(x,\xi )=f(x,|\xi |)\) equals one of following functions with corresponding additional conditions hold:
Model | f(x, t) | Additional condition |
|---|---|---|
Perturbed double phase | \(t^p + a(x) t^q\log (e+t)\) | \(\alpha _a\geqslant q-p\) |
Triple phase | \(t^p + a(x) t^q + b(x) t^r\) | \(\alpha _a\geqslant q-p\) & \(\alpha _b\geqslant r-p\) |
Variable exponent double phase | \(t^{p(x)} + a(x) t^{q(x)}\) | \(\alpha _a(x)\geqslant q(x)-p(x)\) |
Then every minimizer \(u\in W^{1,1}_{\textrm{loc}}(\Omega )\cap L^\infty (\Omega )\) of (\(\min F\)) satisfies \(u\in C^{1,\alpha }_{\textrm{loc}}(\Omega )\) for some \(\alpha \in (0,1)\) independent of \(\Vert u\Vert _{L^\infty (\Omega )}\).
Remark 1.2
The previous corollary holds also with the weaker, but more difficult to check, assumption \(u\in W^{1,1}_{\textrm{loc}}(\Omega )\cap BMO(\Omega )\). Without the additional a priori information \(u\in BMO(\Omega )\), the additional conditions are
These are stronger assumptions when \(p<n\) as expected, since if \(p\geqslant n\), then \(W^{1,p}_\textrm{loc}(\Omega ) \subset BMO_\textrm{loc}(\Omega )\), so the a priori assumption \(u\in BMO(\Omega )\) actually contains no additional information.
Remark 1.3
Our results also apply in the following cases with the same assumptions as in Corollary 1.1.
Model | f(x, t) |
|---|---|
Perturbed variable exponent | \(t^{p(x)} \log (e+t)\) |
Orlicz variable exponent | \(\varphi (t)^{p(x)}\) or \(\varphi (t^{p(x)})\) |
Double variable exponent | \(t^{p(x)}+t^{q(x)}\) |
Degenerate double phase | \(t^p + a(x) t^p \log (e+t)\) |
However, in these cases the a priori information does not give any improvement in the result. The reason is that for these energies, a calculation shows that  holds if and only if the
holds if and only if the  condition holds, see Sect. 3. In other words, for these cases we obtain a new proof of results previously obtained in [42].
condition holds, see Sect. 3. In other words, for these cases we obtain a new proof of results previously obtained in [42].
On the other hand, a priori information does matter for the Orlicz double phase \(\varphi (t) + a(x) \psi (t)\), where \(a\in C^{0,\lambda }\) and \(\psi /\varphi \) is almost increasing, but the conditions get a bit messy. The main condition is that for each \(\varepsilon >0\) there exists \(\beta >0\) such that
The detailed calculations are left to the interested reader, cf. [41, Corollary 8.4].
We study regularity of weak solutions or minimizers u with the additional information that they belong to \(L^{s^*}\), BMO, \(L^\infty \) or \(C^{0,\gamma }\), and study sharp conditions on A or F corresponding to restrictions on u. See Definition 3.1 for these sharp conditions and Example 3.2 for their interpretation in the double phase case. The functions \(A:\Omega \times \mathbb {R} ^n\rightarrow \mathbb {R} ^n\) from (\({\text {div}}A\)) and \(F:\Omega \times \mathbb {R} ^n \rightarrow \mathbb {R} \) from (\(\min F\)) have quasi-isotropic (p, q)-growth structure, given in Definition 4.1. We briefly explain the strategy and structure of the paper.
In Sect. 3, we consider lower order regularity in cases of generalized Orlicz growth and a priori information. We prove \(C^{0,\alpha }\)-regularity for some \(\alpha \in (0,1)\) and higher integrability for quasiminimizers (Theorems 3.12 and 3.14). These are based on Sobolev–Poincaré type inequalities with a priori information, which are obtained in Theorem 3.4 with Lemma 3.8.
In Sect. 5 we prove the main results, maximal regularity of weak solutions and minimizers for cases (ap2)–(ap4). We prove \(C^{0,\alpha }\)-regularity for every \(\alpha \in (0,1)\) and \(C^{1,\alpha }\)-regularity for some \(\alpha \in (0,1)\) assuming a priori \(C^{0,\gamma }\)-information (Theorems 5.3 and 5.11). Other cases follow as corollaries by the lower order regularity results. The crucial step of the proofs is approximating the original problem (\({\text {div}}A\)) and (\(\min F\)) with a suitable autonomous problem and obtaining a comparison estimate between solutions to the original problem and the autonomous problem. For the approximation we use tools from [42], but the comparison is achieved quite differently from our earlier papers. In this paper, we use harmonic approximation in Lemma 4.13 generalizing the double phase case from [8]. The main innovations are inventing assumptions and formulating results optimally to cover all special cases while also being sharp, see comments before Theorem 5.3 for details.
We start in Sect. 2 by recalling notation, definitions and basic results on generalized Orlicz spaces.
2 Preliminaries and notation
Throughout the paper we always assume that \(\Omega \) is a bounded domain in \({\mathbb {R}^n} \) with \(n \geqslant 2\). For \(x_0\in {\mathbb {R}^n} \) and \(r>0\), \(B_r(x_0)\) is the open ball with center \(x_0\) and radius r. If its center is clear or irrelevant, we write \(B_r=B_r(x_0)\). The characteristic function \(\chi _E\) of \(E\subset \mathbb {R} ^n\) is defined as \(\chi _E(x)=1\) if \(x\in E\) and \(\chi _E(x)=0\) if \(x\not \in E\).
Let \(f,g:E \rightarrow \mathbb {R} \) be measurable in \(E\subset {\mathbb {R}^n} \). We denote the integral average of f over E with \(0<|E|<\infty \) by  . The gradient of f is denoted Df. If \(E\subset \mathbb {R} \), then f is said to be almost increasing with constant \(L\geqslant 1\) if \(f(s)\leqslant L f(t)\) whenever \(s\leqslant t\). If \(L=1\), f is increasing. Similarly, we define an almost decreasing or decreasing function. We write \(f\lesssim g\), \(f\approx g\) and \(f\simeq g\) if there exists \(C\geqslant 1\) such that \(f(y)\leqslant Cg(y)\), \(C^{-1}f(y)\leqslant g(y) \leqslant Cf(y)\) and \(f(C^{-1}y)\leqslant g(y) \leqslant f(Cy)\) for all \(y\in E\), respectively. We use c as a generic constant whose value may change between appearances.
. The gradient of f is denoted Df. If \(E\subset \mathbb {R} \), then f is said to be almost increasing with constant \(L\geqslant 1\) if \(f(s)\leqslant L f(t)\) whenever \(s\leqslant t\). If \(L=1\), f is increasing. Similarly, we define an almost decreasing or decreasing function. We write \(f\lesssim g\), \(f\approx g\) and \(f\simeq g\) if there exists \(C\geqslant 1\) such that \(f(y)\leqslant Cg(y)\), \(C^{-1}f(y)\leqslant g(y) \leqslant Cf(y)\) and \(f(C^{-1}y)\leqslant g(y) \leqslant f(Cy)\) for all \(y\in E\), respectively. We use c as a generic constant whose value may change between appearances.
A modulus of continuity \(\omega :[0,\infty )\rightarrow [0,\infty )\) is concave and increasing with \(\omega (0)=\lim _{r\rightarrow 0^+}\omega (r)=0\). We define the Hölder seminorm by
Vanishing Hölder continuity \(VC^{0,\gamma }(\Omega )\) means that \(u\in C^{0,\gamma }(\Omega )\) and \(\lim _{r\rightarrow 0^+}[u]_{\gamma ,r}=0\). The spaces \(C^{0,\gamma (\cdot )}(\Omega )\) and \(C^{0,\log }(\Omega )\), as well as their vanishing versions, are defined similarly with \(|x-y|^{\gamma (x)}\) and \(\log (e+\frac{1}{|x-y|})\) instead of \(|x-y|^\gamma \) in the denominator.
We refer to [33, Chapter 2] for the following definitions and properties.
Definition 2.1
We define some conditions for \(\varphi :\Omega \times [0,\infty ]\rightarrow [0,\infty )\) and \(\gamma \in \mathbb {R} \) related to regularity with respect to the second variable, which are supposed to hold for all \(x\in \Omega \) and a constant \(L\geqslant 1\) independent of x.
-
(aInc)\(_\gamma \) \(t\mapsto \varphi (x,t)/t^\gamma \) is almost increasing on \((0,\infty )\) with constant L.
-
(Inc)\(_\gamma \) \(t\mapsto \varphi (x,t)/t^\gamma \) is increasing on \((0,\infty )\).
-
(aDec)\(_\gamma \) \(t\mapsto \varphi (x,t)/t^\gamma \) is almost decreasing on \((0,\infty )\) with constant L.
-
(Dec)\(_\gamma \) \(t\mapsto \varphi (x,t)/t^\gamma \) is decreasing on \((0,\infty )\).
-
(A0) \(L^{-1}\leqslant \varphi (x,1)\leqslant L\).
We write  or
or  if
if  or
or  holds for some \(\gamma > 1\).
holds for some \(\gamma > 1\).
We can rewrite  or
or  with \(p,q>0\) and constant \(L\geqslant 1\) as
with \(p,q>0\) and constant \(L\geqslant 1\) as
for all
\((x,t)\in \Omega \times [0,\infty )\) and \(0\leqslant \lambda \leqslant 1 \leqslant \Lambda \). From these inequalities one sees that  and
and  are equivalent to the \(\nabla _2\)- and \(\Delta _2\)-conditions, respectively. The definition of
are equivalent to the \(\nabla _2\)- and \(\Delta _2\)-conditions, respectively. The definition of  above differs slightly from [33] but the two definitions are equivalent when
\(\varphi \) satisfies
above differs slightly from [33] but the two definitions are equivalent when
\(\varphi \) satisfies  . If \(\varphi (x,\cdot )\in C^1((0,\infty ))\), then for \(0<p \leqslant q\),
. If \(\varphi (x,\cdot )\in C^1((0,\infty ))\), then for \(0<p \leqslant q\),

Suppose \(\varphi ,\psi : [0,\infty )\rightarrow [0,\infty )\) are increasing, \(\varphi \) satisfies  and
and  , and \(\psi \) satisfies
, and \(\psi \) satisfies  . Then there exist a convex \({\tilde{\varphi }}\) and a concave \({\tilde{\psi }}\) such that \(\varphi \approx {\tilde{\varphi }}\) and
\(\psi \approx {\tilde{\psi }}\) [33, Lemma 2.2.1]. Therefore, by Jensen’s inequality for \({\tilde{\varphi }}\) and \({\tilde{\psi }}\),
. Then there exist a convex \({\tilde{\varphi }}\) and a concave \({\tilde{\psi }}\) such that \(\varphi \approx {\tilde{\varphi }}\) and
\(\psi \approx {\tilde{\psi }}\) [33, Lemma 2.2.1]. Therefore, by Jensen’s inequality for \({\tilde{\varphi }}\) and \({\tilde{\psi }}\),

for every \(f\in L^1(\Omega )\) with implicit constants depending on L from  and
and  or
or  (via the constants from the equivalence relation).
(via the constants from the equivalence relation).
We next introduce classes of \(\Phi \)-functions and generalized Orlicz spaces following [33]. We are mainly interested in convex functions for minimization problems and related PDEs, but the class \({\Phi _{\textrm{w}}}(\Omega )\) is very useful for approximating functionals.
Definition 2.2
Let \(\varphi :\Omega \times [0,\infty ]\rightarrow [0,\infty )\). Assume \(x\mapsto \varphi (x,|f(x)|)\) is measurable for every measurable function f on \(\Omega \), \(t\mapsto \varphi (x,t)\) is increasing for every \(x\in \Omega \), and \(\varphi (x,0)=\lim _{t\rightarrow 0^+}\varphi (x,t)=0\) and \(\lim _{t\rightarrow \infty }\varphi (x,t)=\infty \) for every \(x\in \Omega \). Then \(\varphi \) is called a
-
(1)
\(\Phi \)-function, denoted \(\varphi \in {\Phi _{\textrm{w}}}(\Omega )\), if it satisfies
 ;
; -
(2)
convex \(\Phi \)-function, denoted \(\varphi \in {\Phi _{\textrm{c}}}(\Omega )\), if \(t\mapsto \varphi (x,t)\) is left-continuous and convex for every \(x\in \Omega \).
If \({\bar{\varphi }}\) is independent of x and \(\varphi (x,t):= {\bar{\varphi }}(t)\) satisfies \(\varphi \in {\Phi _{\textrm{w}}}(\Omega )\) or \(\varphi \in {\Phi _{\textrm{c}}}(\Omega )\), we write \({\bar{\varphi }}\in {\Phi _{\textrm{w}}}\) or \({\bar{\varphi }}\in {\Phi _{\textrm{c}}}\).
Note that \({\Phi _{\textrm{c}}}(\Omega )\subset {\Phi _{\textrm{w}}}(\Omega )\) since convexity implies  . For \(\varphi ,\psi \in {\Phi _{\textrm{w}}}(\Omega )\) the relation \(\simeq \) is weaker than \(\approx \), but they are equivalent if \(\varphi \) and
\(\psi \) satisfy
. For \(\varphi ,\psi \in {\Phi _{\textrm{w}}}(\Omega )\) the relation \(\simeq \) is weaker than \(\approx \), but they are equivalent if \(\varphi \) and
\(\psi \) satisfy  . We write
. We write
The (left-continuous) inverse function with respect to t is defined by
If \(\varphi \) is strictly increasing and continuous in t, then this is just the normal inverse. We define the conjugate function of \(\varphi \in {\Phi _{\textrm{w}}}(\Omega )\) by
The definition directly implies Young’s inequality
If \(\varphi \) satisfies  or
or  for some
\(p, q>1\), then \(\varphi ^*\) satisfies
for some
\(p, q>1\), then \(\varphi ^*\) satisfies  or
or  , respectively; the prime denotes the Hölder conjugate, \(p'=\frac{p}{p-1}\). We also note that \((\varphi ^*)^*=\varphi \) if \(\varphi \in {\Phi _{\textrm{c}}}(\Omega )\) by [24, Theorem 2.2.6].
, respectively; the prime denotes the Hölder conjugate, \(p'=\frac{p}{p-1}\). We also note that \((\varphi ^*)^*=\varphi \) if \(\varphi \in {\Phi _{\textrm{c}}}(\Omega )\) by [24, Theorem 2.2.6].
If \(\varphi \in {\Phi _{\textrm{c}}}(\Omega )\), then there exists an increasing and right-continuous \(\varphi ':\Omega \times [0,\infty )\rightarrow [0,\infty )\) such that
We collect some results about this (right-)derivative \(\varphi '\).
Proposition 2.3
(Proposition 3.6, [41]) Let \(\gamma >0\) and \(\varphi \in {\Phi _{\textrm{c}}}(\Omega )\).
-
(1)
If \(\varphi '\) satisfies
 ,
,  ,
,  or
or  , then \(\varphi \) satisfies
, then \(\varphi \) satisfies  ,
,  ,
,  or
or  , respectively, with the same constant \(L\geqslant 1\).
, respectively, with the same constant \(L\geqslant 1\). -
(2)
If \(\varphi \) satisfies
 , then \((2^{\gamma +1}L)^{-1}t \varphi '(x,t) \leqslant \varphi (x,t)\leqslant t \varphi '(x,t)\).
, then \((2^{\gamma +1}L)^{-1}t \varphi '(x,t) \leqslant \varphi (x,t)\leqslant t \varphi '(x,t)\). -
(3)
If \(\varphi '\) satisfies
 and
and  with constant \(L\geqslant 1\), then \(\varphi \) also satisfies
with constant \(L\geqslant 1\), then \(\varphi \) also satisfies  , with constant depending on L and \(\gamma \).
, with constant depending on L and \(\gamma \). -
(4)
\(\varphi ^*(x,\varphi '(x,t))\leqslant t\varphi '(x,t)\).
Let \(L^0(\Omega )\) be the set of the measurable functions on \(\Omega \). For \(\varphi \in {\Phi _{\textrm{w}}}(\Omega )\), the generalized Orlicz space (also known as the Musielak–Orlicz space) is defined as
with the (Luxemburg) norm
We denote by
\(W^{1,\varphi }(\Omega )\) the set of functions \(f\in W^{1,1}(\Omega )\) with \(\Vert f\Vert _{W^{1,\varphi }(\Omega )}:=\Vert f\Vert _{L^\varphi (\Omega )}+\big \Vert |Df|\big \Vert _{L^\varphi (\Omega )}<\infty \). Note that if \(\varphi \) satisfies  , then \(f\in L^\varphi (\Omega )\) if and only if
\(\varrho _\varphi (f)<\infty \), and if \(\varphi \) satisfies
, then \(f\in L^\varphi (\Omega )\) if and only if
\(\varrho _\varphi (f)<\infty \), and if \(\varphi \) satisfies  ,
,  and
and  , then \(L^\varphi (\Omega )\) and
\(W^{1,\varphi }(\Omega )\) are reflexive Banach spaces. We denote by \(W^{1,\varphi }_0(\Omega )\) the closure of \(C^\infty _0(\Omega )\) in \(W^{1,\varphi }(\Omega )\). For more information about generalized Orlicz and Orlicz–Sobolev spaces, we refer to the monographs [14, 33] and also [24, Chapter 2].
, then \(L^\varphi (\Omega )\) and
\(W^{1,\varphi }(\Omega )\) are reflexive Banach spaces. We denote by \(W^{1,\varphi }_0(\Omega )\) the closure of \(C^\infty _0(\Omega )\) in \(W^{1,\varphi }(\Omega )\). For more information about generalized Orlicz and Orlicz–Sobolev spaces, we refer to the monographs [14, 33] and also [24, Chapter 2].
3 Lower regularity with a priori assumptions
3.1 Continuity assumptions
The condition  , introduced in [39] (see also [44]), is a “almost continuity” assumption, which allows the function to jump, but not too much. It implies the Hölder continuity of solutions and (quasi)minimizers [11, 36, 37]. For higher regularity, we introduced in [41] a “vanishing
, introduced in [39] (see also [44]), is a “almost continuity” assumption, which allows the function to jump, but not too much. It implies the Hölder continuity of solutions and (quasi)minimizers [11, 36, 37]. For higher regularity, we introduced in [41] a “vanishing  ” condition, denoted
” condition, denoted  , and a weak vanishing version,
, and a weak vanishing version,  and generalized them to the quasi-isotropic situation in [42]. The anisotropic condition was further studied in [13, 40]. These previous studies applied to the “natural” energy assumption \(u\in W^{1,\varphi }(\Omega )\), called Case (ap1) in the introduction. The
and generalized them to the quasi-isotropic situation in [42]. The anisotropic condition was further studied in [13, 40]. These previous studies applied to the “natural” energy assumption \(u\in W^{1,\varphi }(\Omega )\), called Case (ap1) in the introduction. The  and
and  conditions for a priori energy assumptions were developed in [36] and [11] for functions in
\(L^\infty \) and \(W^{1,\psi }\), respectively. Here we generalize and unify all the conditions for a priori information; the most important one for this article is
conditions for a priori energy assumptions were developed in [36] and [11] for functions in
\(L^\infty \) and \(W^{1,\psi }\), respectively. Here we generalize and unify all the conditions for a priori information; the most important one for this article is  .
.
Definition 3.1
Let \(M,N\in {\mathbb {N}}\), \(G:\Omega \times \mathbb {R} ^M \rightarrow \mathbb {R} ^N\), \(\psi :\Omega \times \mathbb {R} ^M\rightarrow [0,\infty )\), \(L_\omega >0 \), \(r\in (0,1]\) and \(\omega :[0,1]\rightarrow [0,L_\omega ]\). We consider the claim
for all \(x,y\in B_r\cap \Omega \) and \(\xi \in \mathbb {R} ^M\). We say that G satisfies:
-
(A1-\(\psi \)) if there exists \(L_\omega \) such that the claim holds with \(\omega \equiv L_\omega \).
-
(VA1-\(\psi \)) if there exists \(L_\omega \) and a modulus of continuity \(\omega \) such that the claim holds.
-
(wVA1-\(\psi \)) if it satisfies
 for every \(\varepsilon >0\), with possibly different functions \(\omega _\varepsilon \) but a common \(L_\omega \) independent of \(\varepsilon \).
for every \(\varepsilon >0\), with possibly different functions \(\omega _\varepsilon \) but a common \(L_\omega \) independent of \(\varepsilon \).
When \(\psi (x,\xi )=|\xi |^s\) with \(s>0\) we use the abbreviations  ,
,  and
and  and in the case \(\psi =|G|\) we write
and in the case \(\psi =|G|\) we write  ,
,  and
and  . We also use the definition for
\(\psi :\Omega \times [0,\infty )\rightarrow [0,\infty )\) with the understanding that \(\psi (x,\xi )=\psi (x,|\xi |)\).
. We also use the definition for
\(\psi :\Omega \times [0,\infty )\rightarrow [0,\infty )\) with the understanding that \(\psi (x,\xi )=\psi (x,|\xi |)\).
It can be easily seen that  \(\Longrightarrow \)
\(\Longrightarrow \) \(\Longrightarrow \)
\(\Longrightarrow \) and
and  \(\Longrightarrow \)
\(\Longrightarrow \) if \(s'\leqslant s\), similarly for
if \(s'\leqslant s\), similarly for  and
and  . In the case
\(M=N=1\), these conditions are somewhat differently formulated than in earlier papers, but we showed in [42] that the formulations are are equivalent to previous versions under natural assumptions on G.
. In the case
\(M=N=1\), these conditions are somewhat differently formulated than in earlier papers, but we showed in [42] that the formulations are are equivalent to previous versions under natural assumptions on G.
The next example shows the relevance of the parameter s in  in the double phase case. Similar relations for other cases are summarized in Table 1.
in the double phase case. Similar relations for other cases are summarized in Table 1.
Example 3.2
Consider two double phase energies for \(1<p \leqslant q\) and \(a:\Omega \rightarrow [0,L]\).
-
Let \(\varphi _1(x, t):= t^p + a(x)t^q\), \(a\in VC^{0,\alpha }(\Omega )\) for some \(\alpha \in (0,1]\).
If \(q-p \leqslant \tfrac{s}{n} \alpha \), then \(\varphi _1\) satisfies
 with \(\omega \) proportional to the modulus of continuity of a.
with \(\omega \) proportional to the modulus of continuity of a. -
Let \(\varphi _2(x, t):= t^p + a(x)^\alpha t^q\), where \(\alpha >0\) and \(a\in C^{0,1}(\Omega )\).
If \(q-p\leqslant \tfrac{s}{n} \alpha \), then \(\varphi _2\) satisfies
 and
and  with \(\omega _\varepsilon (r) = c r^{\{\alpha -\frac{n(q-p)}{(1+\varepsilon )s}\}\min \{1,\frac{1}{\alpha }\}}\);
with \(\omega _\varepsilon (r) = c r^{\{\alpha -\frac{n(q-p)}{(1+\varepsilon )s}\}\min \{1,\frac{1}{\alpha }\}}\);If \(q-p< \tfrac{s}{n} \alpha \), then \(\varphi _2\) satisfies
 with \(\omega (r) = c r^{(\alpha -\frac{n(q-p)}{s})\min \{1,\frac{1}{\alpha }\}}\).
with \(\omega (r) = c r^{(\alpha -\frac{n(q-p)}{s})\min \{1,\frac{1}{\alpha }\}}\).
Note that these conditions can hold for \(\frac{q}{p}\) arbitrarily large. We show the second case only since the first case can be obtained in the same way as the second case with \(\alpha <1\). We will use the elementary inequality
which holds for any \(a, b \geqslant 0\) and \(\delta \in (0,1]\); here \(c_\alpha >0\) is a constant depending on \(\alpha \). The second inequality (\(\alpha >1\)) follows from Young’s inequality applied to the right-hand side of \(b^\alpha -a^\alpha \leqslant \alpha b^{\alpha -1}(b-a)\) when \(b\geqslant a \geqslant 0\).
Suppose that \(q-p\leqslant \frac{s}{n}\alpha \) and let \(x,y\in B_r\) with \(r\in (0,1]\) and \(t \in (0,|B_r|^{-\frac{1}{s(1+\varepsilon )}}]\) with \(\varepsilon \geqslant 0\). Applying the preceding inequality with \(a=a(x)\) and \(b=a(y)\), we obtain that
when \(0<\alpha \leqslant 1\); in the case \(\alpha > 1\), we choose \(\delta :=r^{\{\alpha -\frac{n(q-p)}{(1+\varepsilon )s}\}\frac{1}{\alpha }}\) and find that
These inequalities imply the desired
 ,
,  and
and  -conditions.
-conditions.
Let us show how to use the smallness of \(\omega \) to obtain the inequality from  for a slightly larger range. Intuitively, we shift some power from the coefficient to the range. In this proof it is important that the range of \(\xi \) in the condition is independent of x, so the result does not generalize to
for a slightly larger range. Intuitively, we shift some power from the coefficient to the range. In this proof it is important that the range of \(\xi \) in the condition is independent of x, so the result does not generalize to  easily, unless \(\psi (x,t)=\psi (t)\).
easily, unless \(\psi (x,t)=\psi (t)\).
Proposition 3.3
Let \(G:\Omega \times \mathbb {R} ^M \rightarrow \mathbb {R} ^N\) satisfy  , \(\theta \in [0,1]\) and \(r\in (0,1]\). If \(\omega (r)^{1-\theta }\leqslant \tfrac{1}{3}\), then for every \(x,y \in B_r\cap \Omega \),
, \(\theta \in [0,1]\) and \(r\in (0,1]\). If \(\omega (r)^{1-\theta }\leqslant \tfrac{1}{3}\), then for every \(x,y \in B_r\cap \Omega \),
Proof
Note by the concavity of \(\log \) that \(t\log 2\leqslant \log (1+t)\leqslant t\) when \(t\in [0,1]\), and set
where \(\lfloor \tau \rfloor \) is the largest integer less than or equal to \(\tau \in \mathbb {R} \). Suppose \(x,y\in B_r\cap \Omega \) and \(3^n\omega (r)^{n(1-\theta )} |\xi |^s \leqslant |B_r|^{-1}\). Then \(|\xi |^s\leqslant k^n |B_r|^{-1}\) since \(1\leqslant (3k)^n\omega (r)^{n(1-\theta )}\). We split the segment [x, y] into k equally long subsegments \([x_i, x_{i+1}]\) with \(x_0=x\) and \(x_k=y\) so that \(x_i, x_{i+1}\in B_{r/k}\). Since
\(|\xi |^s\leqslant |B_{r/k}|^{-1}\), we can use  to estimate
to estimate
We use this estimate with the triangle inequality and  :
:
This gives the desired estimate, since by the definition of k,
\(\square \)
3.2 Sobolev–Poincaré inequality
We derive a modular Sobolev–Poincaré-type inequality in generalized Orlicz spaces assuming a priori information. We first state the inequality with an abstract condition, which is explored further in Lemma 3.8 and Example 3.9. The example shows that the conditions in Lemma 3.8 are essentially sharp for the Sobolev–Poincaré inequality, at least when \(s\leqslant n\). This approach is inspired by [11].
Theorem 3.4
(Sobolev–Poincaré inequality) Let \(\varphi \in {\Phi _{\textrm{w}}}(B_r)\) satisfy  ,
,  and
and  with \(1\leqslant p\leqslant q\), and let \(u\in W^{1,1}(B_r)\). If
with \(1\leqslant p\leqslant q\), and let \(u\in W^{1,1}(B_r)\). If

and some \(b_0,\theta >0\), then

for \(\frac{1}{\theta _0} = 1-\min \{\frac{p}{n},\kappa \}+\frac{1}{\theta }\) with any \(\kappa \in (0,1)\) and some \(c=c(n,p,q,L,\kappa ,b_0)>0\).
Remark 3.6
In the previous theorem we can choose \(\theta _0>1\) if and only if \(\theta >\max \{1,\frac{n}{p}\}\). The choice \(\theta _0=1\) is additionally possible when \(\theta =\frac{n}{p} > 1\). These are the most important cases, but the theorem allows also for \(\theta _0\in (0,1)\) in cases with small \(\theta \).
Remark 3.7
Let \(1<p \leqslant q\). Suppose that \(\varphi \) satisfies (3.5) with \(\theta \) such that \(\theta _0>1\). Then so does \(\varphi ^{1/\tau }\) with \(\theta ':=\theta \tau \) and \(\tau \in (1,p)\). Theorem 3.4 for \(\varphi ^{1/\tau }\) implies that

where \(\frac{1}{\theta _0'} = 1-\min \{\frac{p}{n},\kappa \}+\frac{1}{\theta \tau }\). Note that \(\theta _0'\rightarrow \theta _0>1\) when \(\tau \rightarrow 1\) so we can choose \(\tau \) with \(\frac{\theta _0'}{\tau }>1\). Thus there exists \(\theta _1>1\) depending n, p and \(\theta \) such that

Proof of Theorem 3.4
To obtain a differentiable function, we define \(\psi \in {\Phi _{\textrm{c}}}\) by
From  of \(\varphi \) we see that \(\frac{\varphi ^-_{B_r}(t)}{t} \leqslant \psi '(t) \leqslant L \frac{\varphi ^-_{B_r}(t)}{t}\); with
of \(\varphi \) we see that \(\frac{\varphi ^-_{B_r}(t)}{t} \leqslant \psi '(t) \leqslant L \frac{\varphi ^-_{B_r}(t)}{t}\); with  and
and  we conclude that \(\varphi _{B_r}^-\approx \psi (t)\). Choose \(s:=\min \{p,\kappa n\}\in [1,n)\) and \(\theta _0\in (0, \theta )\) with \(\frac{s}{n} = 1-\frac{1}{\theta _0}+\frac{1}{\theta }\). Note that \(\frac{s^*}{\theta _0s}=((1-\frac{s}{n})\theta _0)^{-1}=(1-\frac{\theta _0}{\theta })^{-1}>1\). By Hölder’s inequality with exponents \(\frac{s^*}{\theta _0s}\) and \((\frac{s^*}{\theta _0s})'=\frac{\theta }{\theta _0}\) and the assumption (3.5),
we conclude that \(\varphi _{B_r}^-\approx \psi (t)\). Choose \(s:=\min \{p,\kappa n\}\in [1,n)\) and \(\theta _0\in (0, \theta )\) with \(\frac{s}{n} = 1-\frac{1}{\theta _0}+\frac{1}{\theta }\). Note that \(\frac{s^*}{\theta _0s}=((1-\frac{s}{n})\theta _0)^{-1}=(1-\frac{\theta _0}{\theta })^{-1}>1\). By Hölder’s inequality with exponents \(\frac{s^*}{\theta _0s}\) and \((\frac{s^*}{\theta _0s})'=\frac{\theta }{\theta _0}\) and the assumption (3.5),

We use the Sobolev–Poincaré inequality in \(L^s\) and \(\psi '(t)\approx \psi (t)/t\) to conclude that

Since \(\psi \) satisfies  and \(s\leqslant p\), \(\psi _s(t):=\psi (t^{1/s})\) satisfies
and \(s\leqslant p\), \(\psi _s(t):=\psi (t^{1/s})\) satisfies  . Therefore Young’s inequality for \(\psi _s\) and \(\psi _s^*(\frac{\psi _s(t)}{Lt})\leqslant \psi _s(t)\) [35, Lemma 3.1] with \(t:=v^s\) give \(\frac{\psi (v)}{v^s} |\nabla u|^s \lesssim \psi (v) + \psi (|\nabla u|)\). Continuing the previous estimate with the
\(L^{s^*}\)-triangle inequality and \(\psi \approx \varphi ^-_{B_r}\), we find that
. Therefore Young’s inequality for \(\psi _s\) and \(\psi _s^*(\frac{\psi _s(t)}{Lt})\leqslant \psi _s(t)\) [35, Lemma 3.1] with \(t:=v^s\) give \(\frac{\psi (v)}{v^s} |\nabla u|^s \lesssim \psi (v) + \psi (|\nabla u|)\). Continuing the previous estimate with the
\(L^{s^*}\)-triangle inequality and \(\psi \approx \varphi ^-_{B_r}\), we find that

By Hölder’s inequality, \((\psi (v)^{\frac{1}{s}})_{B_r}^s\leqslant (\psi (v))_{B_r}\) and by the modular Poincaré inequality in the Orlicz space \(L^\psi \) [33, Corollary 7.4.1], \((\psi (v))_{B_r}\) can be estimated by the first term on the right-hand side. Combined with the inequality from the previous paragraph, this gives the claim. \(\square \)
Let us derive some sufficient conditions for the assumption of the previous theorem by complementing [11, Proposition 4.2]. Also the cases \(u\in L^{\psi ^\#}(B_r)\) and \(u\in W^{1,\psi }(B_r)\) for \(\psi \in {\Phi _{\textrm{w}}}(B_r)\) and  are covered by [11], and could likewise be considered here. We define the bounded mean oscillation semi-norm as
are covered by [11], and could likewise be considered here. We define the bounded mean oscillation semi-norm as

Note that in case (3) of the following lemma we need \(s>n(1-\frac{p}{q})\) in order that \(\theta _0>1\) in Theorem 3.4, cf. Remark 3.6.
Lemma 3.8
Let \(\varphi \in {\Phi _{\textrm{w}}}(B_r)\) satisfy  ,
,  ,
,  and
and  with \(1\leqslant p \leqslant q\) and let \(u\in L^1(B_r)\). Assume one of the following holds:
with \(1\leqslant p \leqslant q\) and let \(u\in L^1(B_r)\). Assume one of the following holds:
-
(1)
\(s>n\) and \([u]_{\gamma , B_r} \leqslant b\) with \(\gamma := 1-\frac{n}{s}\).
-
(2)
\(s=n\) and \([u]_{BMO(B_r)}\leqslant b\).
-
(3)
\(s\in [1, n)\) and \(\Vert u\Vert _{L^{s^*}(B_r)} \leqslant b\).
Then (3.5) holds for any \(\theta >0\) in Cases (1)–(2) and for \(\theta =\frac{s^*}{q-p}\) in Case (3). The constant \(b_0\) depends only on n, p, q, L, \(L_\omega \) and b.
Proof
If \([u]_{\gamma }\leqslant b\), then \(v\leqslant 2|B_1|^{\frac{1}{n}} b |B_r|^{\frac{\gamma -1}{n}}\) and \(\varphi ^+_{B_r}(v)\lesssim \varphi ^-_{B_r}(v)+1\) by  , so the claim holds in Case (1). For the same reason and
, so the claim holds in Case (1). For the same reason and  , the integrand in (3.5) in Case (2) is bounded at points with \(v\leqslant \max \{|B_r|^{-1/n},1\}\). On the other hand, at points with \(v>\max \{|B_r|^{-1/n},1\}\) we estimate, by
, the integrand in (3.5) in Case (2) is bounded at points with \(v\leqslant \max \{|B_r|^{-1/n},1\}\). On the other hand, at points with \(v>\max \{|B_r|^{-1/n},1\}\) we estimate, by  ,
,  ,
,  and
and  ,
,
We obtain for any exponent \(\theta >0\) that

where in the last inequality we use the well-known reverse Hölder type inequality for mean oscillations in \(L^{\theta (q-p)}\)-space and BMO (cf. [26, Lemma A.1]). Case (3) was proved in [11, Proposition 4.2]. \(\square \)
The estimates for the Sobolev–Poincaré inequality may seem crude, but the following example shows that the end result is sharp, i.e. the claim is false if  is replaced by
is replaced by  for any \(s'<s\). See also [11, Section 5] for a one-dimensional example.
for any \(s'<s\). See also [11, Section 5] for a one-dimensional example.
Example 3.9
Let \(n=2\) and denote the quadrants by \(Q_k\subset \mathbb {R} ^2\), \(k\in \{1,2,3,4\}\). Let \(\eta :[0,4]\rightarrow [0,1]\) be the piecewise linear, 3-Lipschitz function with \(\eta _{[\frac{1}{3}, \frac{2}{3}]}=\eta _{[\frac{7}{3}, \frac{8}{3}]}=1\) and \(\eta _{[1,2]}=\eta _{[3,4]}=0\). We define \(a:\mathbb {R} ^2\rightarrow [0,\infty )\) in polar coordinates as \(a(r,\theta ):=r^\alpha \eta (\frac{2}{\pi }\theta )\). Thus a equals 0 in \(Q_2\) and \(Q_4\) and \(a(x)=|x|^\alpha \) in the sectors with \(\frac{\pi }{6}<\theta <\frac{\pi }{3}\) in \(Q_1\) and with \(\frac{7\pi }{6}<\theta <\frac{4\pi }{3}\) in \(Q_3\). Consider the double phase functional \(H(x,t)=t^p + a(x)t^q\) with \(p<2\) and the function \(u:\mathbb {R} ^2\rightarrow \mathbb {R} \) which equals 1 in \(Q_1\), \(-1\) in \(Q_3\) and is linear in the polar coordinate \(\theta \) in \(Q_2\) and \(Q_4\). By symmetry, \(u_{B_r}=0\) for every ball \(B_r\) centered at the origin and \(v:=\frac{1}{r} |u-(u)_{B_r}| = \frac{1}{r}\) in the sectors in \(Q_1\) and \(Q_3\). The derivative of u equals zero in \(Q_1\) and \(Q_3\); in the other quadrants the radial derivative is zero, and in the tangential derivative equals \(\frac{4}{\pi r}\). For a constant \(k>0\) we estimate, based on the sectors in \(Q_1\) and \(Q_3\),

and, since the support of the derivative is \(Q_2 \cup Q_4\) where \(a=0\),

If the modular Poincaré inequality from Theorem 3.4 holds with \(\theta _0=1\) (the weakest relevant case), then
Suppose that we want the constant in the inequality to depend on the \(L^{s^*}\)-norm of ku. We calculate \(\Vert ku\Vert _{L^{s^*}(B_r)}=ckr^{2/s^*}\). Thus \(k = c r^{-2/s^*}\) and so
This remains bounded as \(r\rightarrow 0\) when \(\alpha \geqslant \frac{2}{s}(q-p)\) which is exactly the  condition when \(n=2\) and shows the sharpness of Case (3). If \(s=n=2\), this shows the sharpness of Case (2), even if we allow the constant to depend on the \(L^\infty \)-norm. Similarly, we see that if the constant is allowed to depend on \(\rho _H(|\nabla u|)\), then \(\alpha \geqslant \frac{2}{p}(q-p)\) which is
condition when \(n=2\) and shows the sharpness of Case (3). If \(s=n=2\), this shows the sharpness of Case (2), even if we allow the constant to depend on the \(L^\infty \)-norm. Similarly, we see that if the constant is allowed to depend on \(\rho _H(|\nabla u|)\), then \(\alpha \geqslant \frac{2}{p}(q-p)\) which is  . Unfortunately, Case (1) is not covered, since the counter-example is discontinuous.
. Unfortunately, Case (1) is not covered, since the counter-example is discontinuous.
3.3 Quasiminimizers
In this subsection, we derive regularity results for quasiminimizers with a priori information. Let \(\varphi \in {\Phi _{\textrm{w}}}(\Omega )\). We say that \(u\in W^{1,\varphi }_{\textrm{loc}}(\Omega )\) is a (local) quasiminimizer if there exists \(Q\geqslant 1\) such that
for every \(v\in W^{1,\varphi }_{\textrm{loc}}(\Omega )\) with \({\text {supp}}\,(u-v)\Subset \Omega \). Quasiminimizers of energy functionals with generalized Orlicz growth have been studied e.g. in [11, 12, 36,37,38]. If \(\varphi \) satisfies  , then the quasiminimizer u satisfies the Caccioppoli inequality
, then the quasiminimizer u satisfies the Caccioppoli inequality
for some \(c=c(n,q,L,Q)\geqslant 1\) and every \(B_{2r}\Subset \Omega \), see [36, Lemma 4.6].
If \(\varphi \) satisfies  , then a bounded qusiminimizer satisfies a Harnack-type inequality and so is locally Hölder continuous [36, Theorem 4.1]. The main ingredients of the proof are the Caccioppoli estimate (3.10) and the Sobolev–Poincaré inequality (Theorem 3.4). In Lemma 3.8, we derived several sufficient conditions for the Sobolev–Poincaré inequality. Therefore, we obtain the Hölder continuity under these conditions from almost the same proof as [36, Theorem 4.1]. We start with local boundedness of quaisiminimizers. The proof is exactly the same as [36, Proposition 5.5] and is hence omitted.
, then a bounded qusiminimizer satisfies a Harnack-type inequality and so is locally Hölder continuous [36, Theorem 4.1]. The main ingredients of the proof are the Caccioppoli estimate (3.10) and the Sobolev–Poincaré inequality (Theorem 3.4). In Lemma 3.8, we derived several sufficient conditions for the Sobolev–Poincaré inequality. Therefore, we obtain the Hölder continuity under these conditions from almost the same proof as [36, Theorem 4.1]. We start with local boundedness of quaisiminimizers. The proof is exactly the same as [36, Proposition 5.5] and is hence omitted.
Lemma 3.11
Let \(\varphi \in {\Phi _{\textrm{w}}}(\Omega )\) satisfy  ,
,  ,
,  and
and  with \(1<p \leqslant q\), and \(s\in (1,n]\). Assume that \(u\in W^{1,\varphi }_{\textrm{loc}}(\Omega )\) is a quasiminimizer and \(u\in BMO(\Omega )\) with \(s=n\), or \(u\in L^{s^*}(\Omega )\) with \(s\in (n(1-\frac{p}{q}), n)\). Then \(u\in L^{\infty }_{\textrm{loc}}(\Omega )\).
with \(1<p \leqslant q\), and \(s\in (1,n]\). Assume that \(u\in W^{1,\varphi }_{\textrm{loc}}(\Omega )\) is a quasiminimizer and \(u\in BMO(\Omega )\) with \(s=n\), or \(u\in L^{s^*}(\Omega )\) with \(s\in (n(1-\frac{p}{q}), n)\). Then \(u\in L^{\infty }_{\textrm{loc}}(\Omega )\).
Theorem 3.12
Let \(\varphi \in {\Phi _{\textrm{w}}}(\Omega )\) satisfy  ,
,  ,
,  and
and  with \(1<p \leqslant q\), and \(s\in (1,n]\). Assume that \(u\in W^{1,\varphi }_{\textrm{loc}}(\Omega )\) is a quasiminimizer and one of the following holds:
with \(1<p \leqslant q\), and \(s\in (1,n]\). Assume that \(u\in W^{1,\varphi }_{\textrm{loc}}(\Omega )\) is a quasiminimizer and one of the following holds:
-
(1)
\(s=n\) and \(u\in BMO(\Omega )\).
-
(2)
\(s\in (n(1-\frac{p}{q}), n)\) and \(u\in L^{s^*}(\Omega )\).
For every \(\Omega '\Subset \Omega \) there exists \(\gamma \in (0,1)\) depending only on n, p, q, L, \(L_\omega \), Q and \(\Omega '\) such that \(u\in C^{0,\gamma }(\Omega ')\).
Proof
Assume first that \(\varphi \) satisfies  and \(u\in W^{1,\varphi }_{\textrm{loc}}(\Omega )\cap L^\infty (\Omega )\). Then local Hölder continuity follows directly from the Harnack inequality in [36, Theorem 4.1]. We consider then assumptions (1) and (2) and note that Lemma 3.11 implies that \(u\in L^{\infty }_{\textrm{loc}}(\Omega )\). Furthermore,
and \(u\in W^{1,\varphi }_{\textrm{loc}}(\Omega )\cap L^\infty (\Omega )\). Then local Hölder continuity follows directly from the Harnack inequality in [36, Theorem 4.1]. We consider then assumptions (1) and (2) and note that Lemma 3.11 implies that \(u\in L^{\infty }_{\textrm{loc}}(\Omega )\). Furthermore,  implies
implies  when \(s<n\). Therefore, we obtain the local Hölder continuity from the result for bounded solutions. \(\square \)
when \(s<n\). Therefore, we obtain the local Hölder continuity from the result for bounded solutions. \(\square \)
We end the section with a higher integrability result for Hölder continuous quasiminimizers. We first observe that if \(u\in C^{0,\gamma }(B_{2r})\) for some \(\gamma \in (0,1)\) and \(\varphi \) satisfies  , then by Jensen’s inequality and the Caccioppoli inequality (3.10)
, then by Jensen’s inequality and the Caccioppoli inequality (3.10)

which implies

Here c depends on n, p, q, L, \(L_\omega \) and Q, and is independent of \(\gamma \).
Theorem 3.14
(Reverse Hölder inequality) Let \(\varphi \in {\Phi _{\textrm{w}}}(\Omega )\) satisfy  ,
,  ,
,  and
and  with \(1<p\leqslant q\) and \(\gamma \in (0,1)\). If \(u\in W^{1,\varphi }_{\textrm{loc}}(\Omega )\cap C^{0,\gamma }(B_{4r})\) is a quasiminimizer in \(B_{4r}\Subset \Omega \), then \(|Du|\in L^{\varphi ^{1+\sigma }}(B_r)\) for some \(\sigma >0\) with the estimate
with \(1<p\leqslant q\) and \(\gamma \in (0,1)\). If \(u\in W^{1,\varphi }_{\textrm{loc}}(\Omega )\cap C^{0,\gamma }(B_{4r})\) is a quasiminimizer in \(B_{4r}\Subset \Omega \), then \(|Du|\in L^{\varphi ^{1+\sigma }}(B_r)\) for some \(\sigma >0\) with the estimate

The constants \(\sigma \) and c depend only on n, p, q, L, \(L_\omega \), Q and \([u]_{\gamma , B_{2r}}\).
Proof
By the Caccioppoli estimate (3.10) and the Sobolev–Poincaré inequality (from Remark 3.7 and Lemma 3.8(1)), we obtain

for every ball \(B_{2\rho }\subset B_{2r}\), where \(\theta _1\) and \(c_1\) depend on the parameters listed in the statement. By Gehring’s Lemma (e.g. [31, Theorem 6.6]), there exists \(\sigma >0\) depending on \(\theta _1\) and \(c_1\) such that

for every ball \(B_{2\rho }\subset B_{2r}\). Moreover, using the technique from [41, Lemma 4.7] with  instead of
instead of  and with (3.13) in \(B_\rho \), we obtain for every ball \(B_{2\rho }\subset B_{2r}\) that
and with (3.13) in \(B_\rho \), we obtain for every ball \(B_{2\rho }\subset B_{2r}\) that

\(\square \)
4 Growth functions and autonomous problems
Let us precisely define our solutions and minimizers. Since we only consider local versions we will drop the word “local” later on, as indicated by the parentheses. We say that \(u\in W^{1,1}_{\textrm{loc}}(\Omega )\) is a (local) weak solution to (\({\text {div}}A\)) if \(|Du|\,|A(\cdot ,Du)|\in L^1_{\textrm{loc}}(\Omega )\) and
for all \(\zeta \in W^{1,1}(\Omega )\) with \({\text {supp}}\zeta \Subset \Omega \) and \(|D\zeta |\,|A(\cdot , D\zeta )| \in L^1(\Omega )\). We say that \(u\in W^{1,1}_{\textrm{loc}}(\Omega )\) is a (local) minimizer if \(F(\cdot ,Du)\in L^1_{\textrm{loc}}(\Omega )\) and
for every \(v\in W^{1,1}_{\textrm{loc}}(\Omega )\) with \({\text {supp}}(u-v)\Subset \Omega \). Note that if (\({\text {div}}A\)) is an Euler–Lagrange equation, that is, if \(A=D_\xi F\) for some a function F, then the weak solution to (\({\text {div}}A\)) is a minimizer of (\(\min F\)).
We introduce fundamental assumptions on \(A:\Omega \times {\mathbb {R}^n} \rightarrow {\mathbb {R}^n} \) or \(F:\Omega \times {\mathbb {R}^n} \rightarrow [0,\infty )\) with respect to the gradient variable \(\xi \) from [41, 42], so-called (p, q)-growth and quasi-isotropy conditions (parts (Aii) and (Aiii) of the definition, respectively). Here, “quasi-isotropic” indicates that A or F can be estimated by a non-autonomous isotropic \(\Phi \)-function, the so-called growth function.
Definition 4.1
We say that \(A:\Omega \times \mathbb {R} ^n\rightarrow \mathbb {R} ^n\) or \(F:\Omega \times \mathbb {R} ^n\rightarrow [0,\infty )\) has quasi-isotropic (p, q)-growth if conditions (Ai)–(Aiii) or (Fi)–(Fii) hold, respectively.
-
(Ai)
For every \(x\in \Omega \), \(A(x, 0)= 0\) and \(A(x,\cdot )\in C^{1}(\mathbb {R} ^n{\setminus }\{ 0\}; \mathbb {R} ^n)\) and for every \(\xi \in \mathbb {R} ^n\), \(A(\cdot ,\xi )\) is measurable.
-
(Aii)
There exist \(L\geqslant 1\) and \(1<p\leqslant q\) such that the radial function \(t\mapsto | D_\xi A(x,te)|\) satisfies
 ,
,  and
and  with the constant L, for every \(x\in \Omega \) and \(e\in \partial B_1(0)\).
with the constant L, for every \(x\in \Omega \) and \(e\in \partial B_1(0)\). -
(Aiii)
There exists \(L\geqslant 1\) such that
$$\begin{aligned} | D_\xi A(x,\xi ')|\,|{\tilde{\xi }}|^2 \leqslant L\, D_\xi A(x,\xi ){\tilde{\xi }} \cdot {\tilde{\xi }} \end{aligned}$$for all \(x\in \Omega \), \(\xi ,\xi ', {\tilde{\xi }}\in {\mathbb {R}^n} {\setminus }\{0\}\) with \(|\xi |=|\xi '|\).
-
(Fi)
For every \(x\in \Omega \), \(F(x, 0)=|D_\xi F(x,0)|= 0\) and \(F(x,\cdot )\in C^{2}(\mathbb {R} ^n{\setminus }\{ 0\})\) and for every \(\xi \in \mathbb {R} ^n\), \(F(\cdot ,\xi )\) is measurable.
-
(Fii)
The derivative \(A:=D_\xi F\) satisfies conditions (Aii) and (Aiii).
The assumptions (Aii) and (Aiii) for \(A:=D_\xi F\) impose the two crucial conditions on the Hessian matrix \(D^2_\xi F\). The former means that \(|\xi |^2 D^2_{\xi }F(x,\xi )\) satisfies a (p, q)-growth condition which is a variant of (p, q)-growth of F. The latter is equivalent to the existence of \({\tilde{L}}\geqslant 1\) such that
Note that all examples in Table 1 satisfy this condition, but not
which holds for \(F(x,\xi )\approx a(x)\psi (|\xi |)\) with \(0<\nu \leqslant a \leqslant L\). We remark (4.2) and (4.3) are called the pointwise and global uniform ellipticity condition. Here, “uniform” is concerned with the variable \(|\xi |\). For more discussion about this uniform ellipticity condition, we refer to [22].
Definition 4.4
Let \(A:\Omega \times {\mathbb {R}^n} \rightarrow {\mathbb {R}^n} \) or \(F:\Omega \times \mathbb {R} \rightarrow [0,\infty )\) have quasi-isotropic (p, q)-growth. We say that \(\varphi \in {\Phi _{\textrm{c}}}(\Omega )\) is its growth function if there exist \(1<p_1\leqslant q_1\) and \(0<\nu \leqslant \Lambda \) such that \(\varphi (x,\cdot )\in C^1([0,\infty ))\) for every \(x\in \Omega \) and \(\varphi '\) satisfies  ,
,  and
and  as well as
as well as
for all \(x\in \Omega \) and \(\xi , {\tilde{\xi }}\in {\mathbb {R}^n} {\setminus }\{ 0\}\); in the case of F we assume that the the inequalities hold for \(A:=D_\xi F\).
In this paper we always use the growth function from the following proposition. Thus the additional parameters \(p_1\), \(q_1\), \(\nu \) and \(\Lambda \) only depend on the original parameters p, q and L.
Proposition 4.5
(Proposition 3.3, [42]) Every \(A:\Omega \times {\mathbb {R}^n} \rightarrow {\mathbb {R}^n} \) and \(F:\Omega \times \mathbb {R} \rightarrow [0,\infty )\) with quasi-isotropic (p, q)-growth has a growth function \(\varphi \in {\Phi _{\textrm{c}}}(\Omega )\) with \(p_1=p\), \(q_1\geqslant q\), \(\nu \) and \(\Lambda \) depending only on p, q and L.
By Proposition 2.3, the growth function \(\varphi \) satisfies  ,
,  ,
,  as well as \(\varphi ^*(x,\varphi '(x,t))\leqslant \varphi '(x,t)t\approx \varphi (x,t)\). Furthemore, by [42, Remark 3.4] we have the strict monotonicity condition
as well as \(\varphi ^*(x,\varphi '(x,t))\leqslant \varphi '(x,t)t\approx \varphi (x,t)\). Furthemore, by [42, Remark 3.4] we have the strict monotonicity condition
as well as the equivalences
where the implicit constants depend on only p, q and L.
Let \(A:\Omega \times {\mathbb {R}^n} \rightarrow {\mathbb {R}^n} \) have quasi-isotropic (p, q)-growth and growth function \(\varphi \) and let \(u\in W^{1,1}_{\textrm{loc}}(\Omega )\) be a weak solution to (\({\text {div}}A\)). We showed in [42, Section 4.1] that u is a quasiminimizer of the \(\varphi \)-energy for some \(Q=Q(p,q,L)\geqslant 1\); in the reference we assumed that smooth functions are dense in the Sobolev space \(W^{1,\varphi }\), which is reasonable if \(\varphi \) satisfies  . But this is not needed here due to our changed test function class in the definition of weak solution. Thus we can apply the regularity results for quasiminimizers from Sect. 3 to weak solutions.
. But this is not needed here due to our changed test function class in the definition of weak solution. Thus we can apply the regularity results for quasiminimizers from Sect. 3 to weak solutions.
We next show how the  -type condition of A or F transfers to the growth function \(\varphi \). Based on Part (2), we can say that
-type condition of A or F transfers to the growth function \(\varphi \). Based on Part (2), we can say that  and
and  are weaker in the minimization case than in the PDE case. This justifies studying minimizers separately.
are weaker in the minimization case than in the PDE case. This justifies studying minimizers separately.
Proposition 4.8
Let \(A:\Omega \times {\mathbb {R}^n} \rightarrow {\mathbb {R}^n} \) or \(F:\Omega \times \mathbb {R} \rightarrow [0,\infty )\) have quasi-isotropic (p, q)-growth and growth function \(\varphi \), and let \(\psi :\Omega \times {\mathbb {R}^n} \rightarrow [0,\infty )\).
-
(1)
A or F satisfies
 if and only if \(\varphi \) satisfies
if and only if \(\varphi \) satisfies  .
. -
(2)
If \(A:= D_\xi F\) satisfies
 , then so does F, with the same \(\omega \) up to a constant depending on p, q and L.
, then so does F, with the same \(\omega \) up to a constant depending on p, q and L. -
(3)
If A or F satisfies
 , \(s>0\), and \(\theta \in (0,1]\), then $$\begin{aligned} |A(x,\xi )-A(y,\xi )| \leqslant c\, \omega (r)^\theta \big (\varphi '(y,|\xi |)+1\big ) \end{aligned}$$
, \(s>0\), and \(\theta \in (0,1]\), then $$\begin{aligned} |A(x,\xi )-A(y,\xi )| \leqslant c\, \omega (r)^\theta \big (\varphi '(y,|\xi |)+1\big ) \end{aligned}$$or
$$\begin{aligned} |F(x,\xi )-F(y,\xi )| \leqslant c\, \omega (r)^\theta \big (\varphi (y,|\xi |)+1\big ) \end{aligned}$$for \(B_r\) with \(r\in (0,1]\), \(x,y\in B_r\cap \Omega \) and \(\xi \in \mathbb {R} ^n\) with \(3^n\omega (r)^{n(1-\theta )} |\xi |^s\in [0,|B_r|^{-1}]\). The constant \(c>0\) depends only on p, q and L.
Proof
We present only the proofs for A, as the ones for F are similar but simpler. All implicit constants in the proof depend only on p, q and L. Fix \(x,y\in B_r\cap \Omega \) and \(\xi \in {\mathbb {R}^n} \) with \(\psi (y,\xi )\in [0,|B_r|^{-1}]\).
We first prove (1). Suppose that A satisfies  and abbreviate \(t:=|\xi |\). By
and abbreviate \(t:=|\xi |\). By  of A and the equivalence (4.7),
of A and the equivalence (4.7),
in the last inequality we used  and
and  of \(\varphi \) when \(t>1\). Thus \(\varphi \) satisfies
of \(\varphi \) when \(t>1\). Thus \(\varphi \) satisfies  . Conversely, suppose \(\varphi \) satisfies
. Conversely, suppose \(\varphi \) satisfies  . Then we see, using also
. Then we see, using also
 and
and  , that
, that
Hence A satisfies  .
.
We omit the proof of (2) which is essentially the same as [42, Proposition 3.8].
To prove (3), we note by  and Proposition 3.3 that \( |A(x,\xi )-A(y,\xi )| \leqslant \omega (r)^\theta (|A(y,\xi )|+1) \approx \omega (r)^\theta (\varphi '(y,|\xi |) +1)\) when \(|\xi |\) satisfies the condition. \(\square \)
and Proposition 3.3 that \( |A(x,\xi )-A(y,\xi )| \leqslant \omega (r)^\theta (|A(y,\xi )|+1) \approx \omega (r)^\theta (\varphi '(y,|\xi |) +1)\) when \(|\xi |\) satisfies the condition. \(\square \)
When considering equations with nonlinearity A it is natural to assume  for the function \(A^{(-1)}(x,\xi ):=|\xi | A(x,\xi )\). This is the route we took in [42]. However, the next result shows that the conditions for A and \(A^{(-1)}\) are equivalent, up to an exponent which does not affect the conclusion of the main results in the next section. Thus we will in the rest of article use the assumptions directly for A.
for the function \(A^{(-1)}(x,\xi ):=|\xi | A(x,\xi )\). This is the route we took in [42]. However, the next result shows that the conditions for A and \(A^{(-1)}\) are equivalent, up to an exponent which does not affect the conclusion of the main results in the next section. Thus we will in the rest of article use the assumptions directly for A.
Proposition 4.9
Let \(A:\Omega \times {\mathbb {R}^n} \rightarrow {\mathbb {R}^n} \) have quasi-isotropic (p, q)-growth. Then A satisfies  if and only if \(A^{(-1)}\) does. If the original modulus continuity is \(\omega \), then the new modulus continuity can be taken as \(c\,\omega ^{\frac{1}{p'}}\) for some \(c=c(p,q,L,L_\omega )>0\).
if and only if \(A^{(-1)}\) does. If the original modulus continuity is \(\omega \), then the new modulus continuity can be taken as \(c\,\omega ^{\frac{1}{p'}}\) for some \(c=c(p,q,L,L_\omega )>0\).
Proof
Let \(x,y\in B_r\cap \Omega \) and \(\psi (y,\xi )\in (0,|B_r|^{-1}]\). Assume A satisfies  . Since \(|\xi | \leqslant c |\xi | |A(y,\xi )|+1\),
. Since \(|\xi | \leqslant c |\xi | |A(y,\xi )|+1\),
This gives  of \(A^{(-1)}\), with modulus of continuity \(c\omega \).
of \(A^{(-1)}\), with modulus of continuity \(c\omega \).
We prove opposite implication through three cases. If \(|\xi |\geqslant 1\), then
Hence we suppose that \(|\xi | < 1\). If further \(|A(x,\xi )|,|A(y,\xi )|\leqslant \omega (r)^\frac{1}{p'}\), then
Otherwise, we use  and
and  to deduce \(c|\xi |^{p-1} \geqslant \max \{|A(x,\xi )|,|A(y,\xi )|\}\geqslant \omega (r)^\frac{1}{p'}\). Thus \(1\leqslant c |\xi |\omega (r)^{-\frac{1}{p}}\) so that
to deduce \(c|\xi |^{p-1} \geqslant \max \{|A(x,\xi )|,|A(y,\xi )|\}\geqslant \omega (r)^\frac{1}{p'}\). Thus \(1\leqslant c |\xi |\omega (r)^{-\frac{1}{p}}\) so that
Dividing both sides by \(|\xi |\) gives the desired estimate. \(\square \)
Remark 4.10
In [42, Proposition 3.8] we assumed that \(A^{(-1)}\) satisfies  but in the proof we used the condition for A. This mistake can be corrected by means of the previous proposition.
but in the proof we used the condition for A. This mistake can be corrected by means of the previous proposition.
Having defined the structure conditions, we first consider quasi-isotropic (p, q)-growth for an autonomous function \({\bar{A}}:{\mathbb {R}^n} \rightarrow {\mathbb {R}^n} \) via its trivial extension \({\bar{A}}(x,\xi ):= {\bar{A}}(\xi )\). It has a growth function \({\bar{\varphi }}\in {\Phi _{\textrm{c}}}\cap C^1([0,\infty ))\), cf. [42]. For such \({\bar{A}}\) and \({\bar{\varphi }}\), we present regularity results of weak solutions to

Note that we use the bar-symbol to indicate the autonomous versions of A, F, \(\varphi \) and corresponding solutions or minimizers u. In the Uhlenbeck case \({\bar{A}}(\xi )=\frac{{\bar{\varphi }}'(|\xi |)}{\xi }\xi \), we proved the next result in [41] and in [42] we sketched how to extend the proof to the quasi-isotropic case. Since the result is independent of the  -type assumptions, it applies directly also to this paper.
-type assumptions, it applies directly also to this paper.
Lemma 4.11
(\(C^{1,\alpha }\)-regularity, Lemma 4.4, [42]) Let \({\bar{A}}:\mathbb {R} ^n\rightarrow \mathbb {R} ^n\) have quasi-isotropic (p, q)-growth and \({\bar{\varphi }}\in {\Phi _{\textrm{c}}}\) be its growth function. If \({\bar{u}}{}\in W^{1,{\bar{\varphi }}}(B_r)\) is a weak solution to (\({\text {div}}{\bar{A}}\)), then \(D{\bar{u}}\in C^{0,{\bar{\alpha }}}_{\textrm{loc}}(B_r,{\mathbb {R}^n} )\) for some \({\bar{\alpha }}\in (0,1)\) with the following estimates:

for every \(B_\rho \subset B_r\) and \(\tau \in (0,1)\). Here \({\bar{\alpha }}\) and \(c>0\) depend only on n, p, q and L.
Next, we derive a harmonic approximation lemma for weak solutions and minimizers of autonomous problems. We start by recalling a Lipschitz truncation lemma, which is a formulation from [27, Theorem 3.2] and [8, Theorem 5.2] of the result in [1], see also [19, 25].
Lemma 4.12
For \(w\in W^{1,1}_0(B_r)\) and \(\lambda >0\) there exist \(w_\lambda \in W^{1,\infty }_0(B_r)\) and a zero-measure set N such that \(\Vert Dw_\lambda \Vert _{L^\infty (B_r)}\leqslant c \lambda \) for some \(c>0\) depending only on n and
where M is the Hardy–Littlewood maximal operator,  .
.
Part (1) of the next lemma, on almost solutions, was considered in [27, Lemma 1.1] and [8, Lemma 5.1] in the Orlicz and double phase case, respectively. We streamline and generalize their argument and include also almost minimizers in Part (2). The more precise estimates will allow us to omit the re-scaling step in the proofs of the main theorems.
Lemma 4.13
(Harmonic approximation) Let \({\bar{A}}:{\mathbb {R}^n} \rightarrow {\mathbb {R}^n} \) or \({\bar{F}}:{\mathbb {R}^n} \rightarrow [0,\infty )\) have quasi-isotropic (p, q)-growth, \({\bar{\varphi }}\in {\Phi _{\textrm{c}}}\) be its growth function and \({\bar{u}}\in u+W^{1,{\bar{\varphi }}}_0(B_r)\) be a weak solution to (\({\text {div}}{\bar{A}}\)), for \({\bar{A}}:=D_\xi {\bar{F}}\) in the case of \({\bar{F}}\). Suppose that there exist \(b, \sigma >0\) and \(\delta \in (0,1)\) for which

and one of the following conditions holds for all \(\eta \in W^{1,\infty }_0(B_r)\):
-
(1)
 for \(\mu :=1\).
for \(\mu :=1\). -
(2)
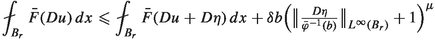 for some \(\mu >0\).
for some \(\mu >0\).
Then there exist \(c=c(n,p,q,L,\sigma )>0\) and \(\bar{\sigma }:=\frac{\sigma p}{\mu +\sigma p}\) such that

Proof
All implicit constants in this proof depend only on n, p, q, L and \(\sigma \). Let \(w:= u-{\bar{u}}\in W^{1,{\bar{\varphi }}}_0(B_r)\) and let \(\lambda \geqslant 1\) be a constant to be chosen. With these w and \(\lambda \) we consider \(w_\lambda \in W^{1,\infty }_0(B_r)\) from Lemma 4.12 so that \(\Vert Dw_\lambda \Vert _{L^\infty (B_r)}\lesssim \lambda \). Denote
Since \({\bar{\varphi }}\) is independent of x, we have  by a Calderón–Zygmund-type estimate in the Orlicz setting, see for instance [42, Lemma 4.5] with \(\theta (x,t)\equiv t^{1+\sigma }\). This and the integrability assumption on Du imply that
by a Calderón–Zygmund-type estimate in the Orlicz setting, see for instance [42, Lemma 4.5] with \(\theta (x,t)\equiv t^{1+\sigma }\). This and the integrability assumption on Du imply that

To estimate \(\frac{|W|}{|B_r|}\), we use \(W\subset \{M(|Dw|)>\lambda \}\cup N\) from Lemma 4.12 and the maximal estimate in \(L^{{\bar{\varphi }}^{1+\sigma }}\) [33, Corollary 4.3.3]:

where, in the last step we used \({\bar{\varphi }}(|Dw|)\lesssim {\bar{\varphi }}(|D{\bar{u}}|)+{\bar{\varphi }}(|Du|)\) and the earlier integrablilty estimates for Du and \(D{\bar{u}}\). Using Hölder’s inequality and these estimates, we find that

We first assume (1). Using monotonicity (4.6) and that \({\bar{u}}\) is a weak solution to (\({\text {div}}{\bar{A}}\)), we find that

For the first term we use assumption (1) with \(\eta =w_\lambda \), and for the second we use that growth functions satisfy \(|{\bar{A}}|\lesssim {\bar{\varphi }}'\). Continuing using Young’s inequality, \({\bar{\varphi }}^*({\bar{\varphi }}'(t))\lesssim {\bar{\varphi }}(t)\) and \( \Vert Dw_\lambda \Vert _{L^\infty (B_r)}\lesssim \lambda \), we find that

In W, we use \({\mathcal {V}}\lesssim {\bar{\varphi }}(|Du|)+{\bar{\varphi }}(|D{\bar{u}}|)\) and obtain the same integral as on the right-hand side, above. With these estimates and (4.14), we obtain that

We choose \(\lambda :={\bar{\varphi }}^{-1}(b\delta ^{-\kappa })\leqslant \delta ^{-\kappa /p}{\bar{\varphi }}^{-1}(b)\) with \(\kappa :=\frac{p}{1+\sigma p}\), and find that

This is the desired upper bound with \(\bar{\sigma }:= \frac{\sigma p}{1+\sigma p}\) and concludes the proof in Case (1).
Assume next that \({\bar{A}}:=D_\xi {\bar{F}}\) and (2) holds. We showed in [42, Lemma 6.3] that
Using this with \({\bar{A}}=D_\xi {\bar{F}}\), the weak form of (\({\text {div}}{\bar{A}}\)), \({\bar{u}}=u+w_\lambda \) in \(W^c\), \({\bar{F}}\approx {\bar{\varphi }}\), assumption (2), \(|{\bar{A}}|\lesssim {\bar{\varphi }}'\) and Young’s inequality with \({\bar{\varphi }}^*({\bar{\varphi }}'(t))\lesssim {\bar{\varphi }}(t)\), we have

In W we use the estimate \({\mathcal {V}}\lesssim {\bar{\varphi }}(|Du|)+{\bar{\varphi }}(|D{\bar{u}}|)\) as before. With (4.14) and the choice \(\lambda :={\bar{\varphi }}^{-1}(b\delta ^{-\kappa })\lesssim \delta ^{-\kappa /p} {\bar{\varphi }}^{-1}(b)\) for \(\kappa :=\frac{p}{\mu +\sigma p}\), we obtain that

This is the desired upper bound with \({\bar{\sigma }}:= \frac{\sigma p}{\mu +\sigma p}\) and concludes the proof in Case (2). \(\square \)
5 Maximal regularity
Let \(B_r\Subset \Omega \) with \(|B_r|\leqslant 1\), \(\gamma \in (0,1)\) and
For \(\varphi \in {\Phi _{\textrm{c}}}(\Omega )\) with \(\varphi '\) satisfying  ,
,  and
and  with \(1<p\leqslant q_1\) we define
with \(1<p\leqslant q_1\) we define
where \(x_0\) is the center of \(B_r=B_r(x_0)\). The relationship between \(\varphi \) and \({\bar{\varphi }}\) is analogous to that in [41, Section 5] with \(t_1=0\) and \(t_2=t_K\). Due to our improved tools, we are able to simplify the argument concerning small values of t by removing the case \(t\in [0,t_1]\).
Proposition 5.2
Let \(t_K\), \(\varphi \) and \({\bar{\varphi }}\) be as above. Suppose that \(\varphi ^+_{B_r}(t)\leqslant L_K \varphi ^-_{B_r}(t)\) for some \(L_K\geqslant 0\) and all \(t \in [1, t_K]\).
-
(1)
\({\bar{\varphi }}\in C^1([0,\infty ))\) and \({\bar{\varphi }}'\) satisfies
 and
and  .
. -
(2)
\({\bar{\varphi }}(t)= \varphi (x_0,t)\) for all \(t\leqslant t_K\).
-
(3)
\({\bar{\varphi }}(t) \leqslant \frac{q_1}{p} L_K\varphi (x,t)+L\) for all \((x,t)\in B_r\times [0,\infty )\) and \(W^{1,\varphi }(B_r) \subset W^{1,{\bar{\varphi }}}(B_r)\).
Proof
Parts (1) and (2) follow directly from the definition of \({\bar{\varphi }}\) and the inclusion in (3) follows from the inequality. If \(t\leqslant 1\), then the inequality in (3) follows from  and when \(t\in [1,t_K]\), it follows from \(\varphi ^+_{B_r}(t)\leqslant L_K \varphi ^-_{B_r}(t)\) and (2). If \(t > t_K\), we calculate
and when \(t\in [1,t_K]\), it follows from \(\varphi ^+_{B_r}(t)\leqslant L_K \varphi ^-_{B_r}(t)\) and (2). If \(t > t_K\), we calculate
We prove our main theorem on Hölder continuous weak solutions to (\({\text {div}}A\)). The major novelties as follows: We use Proposition 3.3 to deal with large values of the derivative; this allows us to handle the borderline double phase case \(q-p=\frac{\alpha }{1-\gamma }\) with \(a\in VC^{0,\alpha }\). Second, this is the first time that harmonic approximation from [8] has been applied in the generalized Orlicz case. Third, optimizations in the formulations allow us to avoid many steps in previous proofs and present a much more streamlined argument. Fourth, we obtain \(C^{1,\alpha }\)-regularity with exponent \(\alpha \) independent of the a priori information \([u]_\gamma \).
Theorem 5.3
Let \(A:\Omega \times {\mathbb {R}^n} \rightarrow {\mathbb {R}^n} \) have quasi-isotropic (p, q)-growth and \(u\in W^{1,1}_{\textrm{loc}}(\Omega )\cap C^{0,\gamma }(\Omega )\) be a weak solution to (\({\text {div}}A\)) with \(\gamma \in (0,1)\).
-
(1)
If A satisfies
 , then \(u\in C^{0,\alpha }_{\textrm{loc}}(\Omega )\) for every \(\alpha \in (0,1)\).
, then \(u\in C^{0,\alpha }_{\textrm{loc}}(\Omega )\) for every \(\alpha \in (0,1)\). -
(2)
If A satisfies
 with \(\omega (r)\lesssim r^{\beta }\) for some \(\beta >0\), then \(u\in C^{1,\alpha }_{\textrm{loc}}(\Omega )\) for some \(\alpha =\alpha (n,p,q,L,\gamma ,\beta )\in (0,1)\).
with \(\omega (r)\lesssim r^{\beta }\) for some \(\beta >0\), then \(u\in C^{1,\alpha }_{\textrm{loc}}(\Omega )\) for some \(\alpha =\alpha (n,p,q,L,\gamma ,\beta )\in (0,1)\).
Proof
We prove the result in three steps. All implicit constants in the following estimates depend only on n, p, q, L and \([u]_\gamma \).
Step 1, setting and approximating equation. For \(\omega \) from  we fix \(B_{4r}\Subset \Omega \) with
we fix \(B_{4r}\Subset \Omega \) with
where \(\theta \in (0,1)\) is given in Step 2, below. Since we always consider \(B_r\) with \(\omega (4r)\leqslant 1\), we assume without loss of generality that A satisfies  with \(L_\omega =1\). We set
with \(L_\omega =1\). We set
Let \(\varphi \in {\Phi _{\textrm{c}}}(\Omega )\) be the growth function of A from Proposition 4.5 so that \(\varphi (x,\cdot )\in C^1([0,\infty ))\) and \(\varphi '\) satisfies  ,
,  and
and  . By Proposition 4.8(1) &(3), \(\varphi \) satisfies
. By Proposition 4.8(1) &(3), \(\varphi \) satisfies  with \(L_\omega \) depending only on p, q and L and
with \(L_\omega \) depending only on p, q and L and
By  of \(\varphi '\), \(|A|\approx \varphi '\) and \(\omega (r)\leqslant 1\) we conclude that
of \(\varphi '\), \(|A|\approx \varphi '\) and \(\omega (r)\leqslant 1\) we conclude that
for every \(t\in [1, t_K]\) and \(x,y\in B_r\). Thus we can apply Proposition 5.2 with \(L_K>0\) depending only on p, q and L.
Let \({\bar{\varphi }}\in {\Phi _{\textrm{c}}}\) be from (5.1). By [42, Lemma 5.2] with \(t_1=0\) and \(t_2=t_K\) there exists an autonomous nonlinearity \({\bar{A}}\in C({\mathbb {R}^n} ,{\mathbb {R}^n} )\cap C^{1}({\mathbb {R}^n} {\setminus }\{ 0\},{\mathbb {R}^n} )\) having quasi-isotropic \((p,q_1)\)-growth such that \({\bar{\varphi }}\) is its growth function and
The exact form of \({\bar{A}}\) is given in [42, (5.2)].
By Theorem 3.14, \(\varphi (\cdot ,|Du|)\in L^{1+\sigma }(B_r)\) for some \(\sigma >0\) depending only on n, p, q, L, and by (3.13) in \(B_{2r}\),

Let \({\bar{u}}\in W^{1,{\bar{\varphi }}}(B_r)\) be the weak solution to (\({\text {div}}{\bar{A}}\)) in \(B_r\) with boundary value u. Then \({\bar{u}}\) is a quasiminimizer of the \({\bar{\varphi }}\)-energy and so the results of Sect. 3 can be applied. By Jensen’s inequality, the minimization property and Proposition 5.2(3),

Then we use the reverse Hölder inequality (Theorem 3.14),  , Proposition 5.2(2) with (5.5) and
, Proposition 5.2(2) with (5.5) and  of \(\varphi \) to conclude that
of \(\varphi \) to conclude that

It follows that

Next we set

By the reverse Hölder inequality (Theorem 3.14) and the earlier estimate (5.6),

and, since \(J\gtrsim 1\),

Step 2, harmonic approximation. We prove that u is an almost weak solution to (\({\text {div}}{\bar{A}}\)) in the sense that

for some \(c\geqslant 1\) depending on n, p, q, L and \([u]_{\gamma ,4r}\) and all \( \eta \in W^{1,\infty }_0(B_r)\).
It suffices to consider \(\eta \) with \(\Vert D\eta \Vert _\infty \leqslant 1\) by scaling. Since u is a weak solution to (\({\text {div}}A\)),

where \(\displaystyle E_1:=\left\{ x\in B_r: |Du| \leqslant \tfrac{1}{2} t_K\right\} \) and \(\displaystyle E_2:= \left\{ x\in B_r: |Du|> \tfrac{1}{2} t_K\right\} \).
We first consider \(E_1\) so that \({\bar{A}}=A(x_0,\cdot )\). By Proposition 4.8(3) with \(s:=\frac{n}{1-\gamma }\),

We abbreviate \({\hat{\varphi }}:=\varphi ^+_{B_{r}}\) and estimate the integral on the right-hand side by \(\varphi '(x,t)\approx \varphi (x,t)/t\), Jensen’s inequality for \({\hat{\varphi }}^*\), \({\hat{\varphi }}^*( \varphi (x,t)/t) \leqslant \varphi (x,t)\), Hölder’s inequality and estimate (5.8) for J:

Since \(1\lesssim \tfrac{{\bar{\varphi }}(J)}{J}\), the whole integral over \(E_1\) can be bounded by \(\omega (r)^\theta \tfrac{{\bar{\varphi }}(J)}{J}\).
In \(E_2\) we estimate

Since \(\frac{{\bar{\varphi }}(J)}{{\bar{\varphi }}(\frac{1}{2} t_K)} \lesssim \frac{{\bar{\varphi }}(r^{\gamma -1})}{{\bar{\varphi }}( Kr^{\gamma -1})} \leqslant K^{-p}\) by (5.7) and  , we obtain
, we obtain

By Proposition 5.2(3) and  , \({\bar{\varphi }}(t)\lesssim \varphi (x,t)\) when \(t\geqslant 1\). Using this, the \({\hat{\varphi }}^*\)-Jensen inequality as in \(E_1\), the previous estimate and
, \({\bar{\varphi }}(t)\lesssim \varphi (x,t)\) when \(t\geqslant 1\). Using this, the \({\hat{\varphi }}^*\)-Jensen inequality as in \(E_1\), the previous estimate and  of \(({\hat{\varphi }}^*)^{-1}\), we find that
of \(({\hat{\varphi }}^*)^{-1}\), we find that

where we used \(({\hat{\varphi }}^*)^{-1}({\hat{\varphi }}(t))\approx {\hat{\varphi }}(t)/t\) and (5.8) in the last step. The desired estimate follows when we combine the estimates in \(E_1\) and \(E_2\), recall that \(K\geqslant 3^{-1} \omega (r)^{-(1-\theta )(1-\gamma )} \) and choose \(\theta :=\frac{(1-\gamma )\sigma (p-1)}{(1-\gamma )\sigma (p-1)+1}\).
Step 3, conclusion. Applying Lemma 4.13(1) with \(b:={\bar{\varphi }}(J)\) to the inequality from Step 2, we obtain that

where \(\bar{\sigma }=\frac{\sigma p}{1+\sigma p}\). By well-known techniques (see, e.g., [41, Corollary 6.3] for details) this implies an \(L^1\)-estimate for the difference of the gradients of u and \({\bar{u}}\) from Step 1:

with \(c\geqslant 1\) depending on n, p, q, L and \([u]_{\gamma , 4r}\) and \(\bar{\omega }\) from Step 2. Note that we can make \(\bar{\omega }(r)^{\frac{\bar{\sigma }}{2q_1}}\) as small as we want by choosing r small. Therefore, this inequality and the Lipschitz regularity of the \({\bar{A}}\)-solutions \({\bar{u}}\) (the first estimate in Lemma 4.11) with (5.6) imply local \(C^{0,\alpha }\)-regularity for every \(\alpha \in (0,1)\) by known methods, see, e.g., [41, Theorem 7.2].
We next assume that \(\omega (r)\lesssim r^{\beta }\) for some \(\beta >0\). Fix \(\Omega '\Subset \Omega \). From Part (1) we obtain \(u\in C^{0, \gamma '}(\Omega ')\) for any \(\gamma '\in (\gamma ,1)\), and consider \(B_{4r}\subset \Omega '\) with r satisfying (5.4) and \([u]_{\gamma ,4r,\Omega '}\leqslant 1\). Then we obtain (5.10) with \(\bar{\omega }(r)^{\frac{\bar{\sigma }}{2q_1}}\lesssim r^{\beta _0}\) for \(\beta _0\) depending only n, p, q, L, \(\gamma \) and \(\beta \). This inequality and the Hölder regularity of the gradient of the \({\bar{A}}\)-solution \({\bar{u}}\) (the second estimate in Lemma 4.11) with (5.6) imply \(u\in C^{1,\alpha }_{\textrm{loc}}(\Omega ')\) for any \(\alpha \in (0, \min \{\beta _0,1-\gamma '\})\) by known methods, see, e.g., [41, Theorem 7.4]. Since \(\beta _0\) and \(1-\gamma '\) are independent of the arbitrary set \(\Omega '\Subset \Omega \), this implies that \(u\in C^{1,\alpha }_{\textrm{loc}}(\Omega )\) for some \(\alpha \in (0,1)\) depending only on n, p, q, L, \(\gamma \) and \(\beta \). \(\square \)
Next we prove maximal regularity for Hölder continuous minimizers of (\(\min F\)). This is our second main result.
Theorem 5.11
Let \(F:\Omega \times {\mathbb {R}^n} \rightarrow \mathbb {R} \) have quasi-isotropic (p, q)-growth and \(u\in W^{1,1}_{\textrm{loc}}(\Omega )\cap C^{0,\gamma }(\Omega )\) be a minimizer of (\(\min F\)) with \(\gamma \in (0,1)\).
-
(1)
If F satisfies
 , then \(u\in C^{0,\alpha }_{\textrm{loc}}(\Omega )\) for every \(\alpha \in (0,1)\).
, then \(u\in C^{0,\alpha }_{\textrm{loc}}(\Omega )\) for every \(\alpha \in (0,1)\). -
(2)
If F satisfies
 with \(\omega (r)\lesssim r^{\beta }\) for some \(\beta >0\), then \(u\in C^{1,\alpha }_{\textrm{loc}}(\Omega )\) for some \(\alpha =\alpha (n,p,q,L,\gamma ,\beta )\in (0,1)\).
with \(\omega (r)\lesssim r^{\beta }\) for some \(\beta >0\), then \(u\in C^{1,\alpha }_{\textrm{loc}}(\Omega )\) for some \(\alpha =\alpha (n,p,q,L,\gamma ,\beta )\in (0,1)\).
Proof
The methodology is similar to Theorem 5.3 except for the application of harmonic approximation. Hence we will take advantage many parts of that proof.
Step 1, setting and approximating functional. We use the same choice of r and K as in Theorem 5.3 and define J in the same way. Let \(\varphi \in \Phi _c(\Omega )\) be the growth function of F from Proposition 4.5; it satisfies the same properties as in Theorem 5.3. In [42, Lemma 5.3] we constructed an autonomous function \({\bar{F}}:{\mathbb {R}^n} \rightarrow [0,\infty )\) such that \({\bar{\varphi }}\in {\Phi _{\textrm{c}}}\) from (5.1) is its growth function and
By Theorem 3.14, \(\varphi (\cdot ,|Du|)\in L^{1+\sigma }(B_r)\) for some \(\sigma =\sigma (n,p,q,L,[u]_{\gamma ,4r})\in (0,1)\). Let \({\bar{u}}\in W^{1,{\bar{\varphi }}}(B_r)\) be the minimizer of
or, equivalently, the weak solution to (\({\text {div}}{\bar{A}}\)) in \(B_r\) with \({\bar{A}}:=D_\xi {\bar{F}}\) and boundary value given by u.
Step 2, harmonic approximation. We prove that u is an almost minimizer of (5.12) in the sense that there exists \(c=c(n,p,q,L,[u]_{\gamma ,4r})\geqslant 1\) such that

for every \(\eta \in W^{1,\infty }_0(B_r)\), where \(\bar{\omega }(r):= \omega (r)^{\frac{(1-\gamma )\sigma p}{(1-\gamma )\sigma p+1}}\).
Let \(E_1\) and \(E_2\) be the sets from Step 2 of the proof of Theorem 5.3. By \({\bar{F}}\approx {\bar{\varphi }}\) (4.7), the definition of \({\bar{F}}\), Propositions 5.2(3) and 4.8(3), and the definition of J,

where the estimate for the term in \(E_2\) is from (5.9).
Next we obtain a similar estimate for \(v:=u+\eta \in u + W^{1,\infty }_0(B_r)\). We define sets \(E_i'\) like \(E_i\) but with |Du| replaced by |Dv|. Since u is an F-minimizer and \(F\approx \varphi \) (4.7),

In \(E_1'\) we use Proposition 4.8(3) with \({\bar{F}}=F(x_0,\cdot )\):

For the second term on the right-hand side, we use \(v=u+\eta \) and \(\varphi (x,|Dv|)\lesssim \varphi (x,|Du|)+\varphi (x,|D\eta |)\). Thus

We use  of \(\varphi \) along with (5.8) to handle the integral with \(D\eta \):
of \(\varphi \) along with (5.8) to handle the integral with \(D\eta \):

In \(E_2'\) we estimate

With the estimate for \(D\eta \) from the previous paragraph, this and \(\frac{{\bar{\varphi }}(J)}{{\bar{\varphi }}(\frac{1}{2} t_K)} \lesssim K^{-p}\) give

Collecting the estimates from this and the previous paragraph, we arrive at

Combining this with the previous paragraphs, the estimate \(K\geqslant 3^{-1}\omega (r)^{-(1-\theta )(1-\gamma )}\) and the choice of \(\theta :=\frac{(1-\gamma )\sigma p}{(1-\gamma )\sigma p+1}\), we complete this step.
Step 3, conclusion. We apply Lemma 4.13(2) with \(b:={\bar{\varphi }}(J)\) and \(\mu :=(1+\sigma )q_1\) to conclude that

where \(\bar{\sigma }:=\frac{\sigma p}{(1+\sigma )q_1 +\sigma p}\) and \(\bar{\omega }\) is from Step 2. The estimate

follows from this as in [41, Corollary 6.3]. We complete the proof as in Step 3 of the proof of Theorem 5.3. Hence we omit details. \(\square \)
We apply the previous theorem to the double phase energies from Example 3.2.
Corollary 5.13
Let \(1<p\leqslant q\), \(a\geqslant 0\) and \(\gamma \in (0,1)\). Assume that either
-
\(F(x,\xi ):=|\xi |^p + a(x) |\xi |^q\), where \(a\in VC^{0,\alpha }(\Omega )\), \(\alpha \in (0,1)\) and \(q-p \leqslant \frac{1}{1-\gamma }\alpha \); or
-
\(F(x,\xi ):= |\xi |^p + a(x)^\alpha |\xi |^q\), where \(a\in C^{0,1}(\Omega )\), \(\alpha >1\) and \(q-p < \frac{1}{1-\gamma }\alpha \).
If \(u\in W^{1,1}_{\textrm{loc}}(\Omega )\cap C^{0,\gamma }(\Omega )\) is a minimizer of (\(\min F\)), then \(u\in C^{1,\beta }_{\textrm{loc}}(\Omega )\) for some \(\beta \) depending only on n, p, q, \(\alpha \) and \(\gamma \).
Proof
Consider first the case with \(\alpha <1\). By Example 3.2, F satisfies  . Therefore \(u\in C^{0,\beta }_{\textrm{loc}}(\Omega )\) for every \(\beta \in (0,1)\) by the previous theorem. Fix \(\gamma _1\in (\gamma ,1)\). Then F satisfies
. Therefore \(u\in C^{0,\beta }_{\textrm{loc}}(\Omega )\) for every \(\beta \in (0,1)\) by the previous theorem. Fix \(\gamma _1\in (\gamma ,1)\). Then F satisfies  with \(\omega (r)\lesssim r^{\alpha -(q-p)(1-\gamma _1)}\) and \(\alpha -(q-p)(1-\gamma _1)> \alpha -(q-p)(1-\gamma )\geqslant 0\). Since \(u\in C^{0,\gamma _1}_\textrm{loc}(\Omega )\), the previous theorem yields that \(u\in C^{1,\beta }_{\textrm{loc}}(\Omega )\) for some \(\beta \in (0,1)\) depending on n, p, q, L, \(\alpha \) and \(\gamma \). In the case \(\alpha >1\) we can directly apply the theorem since the strict inequality \(q-p < \frac{1}{1-\gamma }\alpha \) implies that the condition
with \(\omega (r)\lesssim r^{\alpha -(q-p)(1-\gamma _1)}\) and \(\alpha -(q-p)(1-\gamma _1)> \alpha -(q-p)(1-\gamma )\geqslant 0\). Since \(u\in C^{0,\gamma _1}_\textrm{loc}(\Omega )\), the previous theorem yields that \(u\in C^{1,\beta }_{\textrm{loc}}(\Omega )\) for some \(\beta \in (0,1)\) depending on n, p, q, L, \(\alpha \) and \(\gamma \). In the case \(\alpha >1\) we can directly apply the theorem since the strict inequality \(q-p < \frac{1}{1-\gamma }\alpha \) implies that the condition  holds with a \(\omega \) of power-type (cf. Example 3.2). \(\square \)
holds with a \(\omega \) of power-type (cf. Example 3.2). \(\square \)
Finally, combining Theorems 3.12, 5.3 and 5.11, we obtain regularity results for BMO and \(L^{s^*}\) weak solutions and minimizers. Note that the case \(L^{s^*}\) with \(s\leqslant (n(1-\frac{p}{q})\) remains open, due to a lack of a Sobolev–Poincaré inequality.
Corollary 5.14
Let \(A:\Omega \times {\mathbb {R}^n} \rightarrow {\mathbb {R}^n} \) or \(F:\Omega \times {\mathbb {R}^n} \rightarrow \mathbb {R} \) have quasi-isotropic (p, q)-growth and satisfy  . Suppose that \(u\in W^{1,1}_{\textrm{loc}}(\Omega )\) is a weak solution to (\({\text {div}}A\)) or a minimizer of (\(\min F\)) and that one of the following holds:
. Suppose that \(u\in W^{1,1}_{\textrm{loc}}(\Omega )\) is a weak solution to (\({\text {div}}A\)) or a minimizer of (\(\min F\)) and that one of the following holds:
-
(1)
\(s=n\) and \(u\in BMO(\Omega )\),
-
(2)
\(s\in (n(1-\frac{p}{q}), n)\) and \(u\in L^{s^*}(\Omega )\).
Then \(u\in C^{0,\alpha }_{\textrm{loc}}(\Omega )\) for every \(\alpha \in (0,1)\).
Furthermore, if  holds with \(\omega (r)\lesssim r^{\beta }\) for some \(s'>s\) and \(\beta >0\), then \(u\in C^{1,\alpha }_{\textrm{loc}}(\Omega )\) for some \(\alpha \in (0,1)\) depending on n, p, q, L, s, \(s'\) and \(\beta \).
holds with \(\omega (r)\lesssim r^{\beta }\) for some \(s'>s\) and \(\beta >0\), then \(u\in C^{1,\alpha }_{\textrm{loc}}(\Omega )\) for some \(\alpha \in (0,1)\) depending on n, p, q, L, s, \(s'\) and \(\beta \).
Proof
Note that  implies
implies  and fix \(\Omega '\Subset \Omega \). Since u is a quasiminimizer of the isotropic problem, Theorem 3.12 implies that \(u\in C^{0,\gamma }(\Omega ')\) for some \(\gamma \in (0,1)\). The condition
and fix \(\Omega '\Subset \Omega \). Since u is a quasiminimizer of the isotropic problem, Theorem 3.12 implies that \(u\in C^{0,\gamma }(\Omega ')\) for some \(\gamma \in (0,1)\). The condition  with \(s<\frac{n}{1-\gamma }\) implies
with \(s<\frac{n}{1-\gamma }\) implies  . By Theorem 5.3 or 5.11, we obtain \(u\in C^{0,\alpha }_{\textrm{loc}}(\Omega ')\) so that \(u\in C^{0,\alpha }_{\textrm{loc}}(\Omega )\) for every \(\alpha \in (0,1)\).
. By Theorem 5.3 or 5.11, we obtain \(u\in C^{0,\alpha }_{\textrm{loc}}(\Omega ')\) so that \(u\in C^{0,\alpha }_{\textrm{loc}}(\Omega )\) for every \(\alpha \in (0,1)\).
Next, we suppose that \(\omega (r)\lesssim r^{\beta }\) in  and fix \(\Omega '\Subset \Omega \). By the previous part, \(u\in C^{0,\gamma }(\Omega ')\) for any \(\gamma \in (0,1)\). Furthermore,
and fix \(\Omega '\Subset \Omega \). By the previous part, \(u\in C^{0,\gamma }(\Omega ')\) for any \(\gamma \in (0,1)\). Furthermore,  holds with \(\omega (r)\lesssim r^{\beta }\) when \(\gamma \) is chosen so large that \(\frac{n}{1-\gamma }\geqslant s'\). Therefore, by Theorem 5.3 or 5.11, we obtain \(u\in C^{1,\alpha }_{\textrm{loc}}(\Omega ')\) so that \(u\in C^{1,\alpha }_{\textrm{loc}}(\Omega )\) for some \(\alpha \in (0,1)\) depending only on n, p, q, L, \(\gamma \) and \(\beta \). \(\square \)
holds with \(\omega (r)\lesssim r^{\beta }\) when \(\gamma \) is chosen so large that \(\frac{n}{1-\gamma }\geqslant s'\). Therefore, by Theorem 5.3 or 5.11, we obtain \(u\in C^{1,\alpha }_{\textrm{loc}}(\Omega ')\) so that \(u\in C^{1,\alpha }_{\textrm{loc}}(\Omega )\) for some \(\alpha \in (0,1)\) depending only on n, p, q, L, \(\gamma \) and \(\beta \). \(\square \)
Remark 5.15
For \(C^{1,\alpha }\)-regularity, the obtained exponent \(\alpha \) is independent of the a priori information on weak solutions or minimizers.
Data availability
Data sharing is not applicable to this article as obviously no datasets were generated or analyzed during the current study.
References
Acerbi, E., Fusco, N.: An approximation lemma for \(W^{1, p}\) functions, Material instabilities in continuum mechanics (Edinburgh, 1985–1986), 1–5. Oxford Univ. Press, New York (1988)
Baasandorj, S., Byun, S.S.: Regularity for Orlicz phase problems, Memoirs of American Mathematical Society, to appear. arXiv:2106.15131
Baasandorj, S., Byun, S.S., Lee, H.-S.: Gradient estimates for Orlicz double phase problems with variable exponents. Nonlinear Anal. 221, 112891 (2022)
Baasandorj, S., Byun, S.S., Oh, J.: Gradient estimates for multi-phase problems. Calc Var. Partial Differential Equ. 60, 104 (2021)
Balci, AKh., Diening, L., Surnachev, M.: New examples on Lavrentiev gap using fractals. Calc Var. Partial Differential Equ. 59, 180 (2020)
Baroni, P., Colombo, M., Mingione, G.: Harnack inequalities for double phase functionals. Nonlinear Anal. 121, 206–222 (2015)
Baroni, P., Colombo, M., Mingione, G.: Nonautonomous functionals, borderline cases and related function classes. St. Petersburg Math. J. 27(3), 347–379 (2016)
Baroni, P., Colombo, M., Mingione, G.: Regularity for general functionals with double phase. Calc. Var. Partial Differential Equ. 57(2), 62 (2018)
Beck, L., Mingione, G.: Lipschitz bounds and non-uniform ellipticity. Comm. Pure Appl. Math. 73, 944–1034 (2020)
Bella, P., Schäffner, M.: On the regularity of minimizers for scalar integral functionals with \((p, q)\)-growth. Anal. PDE 13(7), 2241–2257 (2020)
Benyaiche, A., Harjulehto, P., Hästö, P., Karppinen, A.: The weak Harnack inequality for unbounded supersolutions of equations with generalized Orlicz growth. J. Differential Equ. 275, 790–814 (2021)
Benyaiche, A., Khlifi, I.: Harnack inequality for quasilinear elliptic equations in generalized Orlicz-Sobolev spaces. Pot. Anal. 53, 631–643 (2020)
Borowski, M., Chlebicka, I.: Modular density of smooth functions in inhomogeneous and fully anisotropic Musielak-Orlicz-Sobolev spaces. J. Funct. Anal. 283(12), 109716 (2022)
Chlebicka, I., Gwiazda, P., Świerczewska-Gwiazda, A., Wróblewska-Kamińska, A.: Partial Differential Equations in Anisotropic Musielak-Orlicz Spaces. Springer Monographs in Mathematics, Springer, Cham (2021)
Colombo, M., Mingione, G.: Regularity for double phase variational problems. Arch. Ration. Mech. Anal. 215(2), 443–496 (2015)
Colombo, M., Mingione, G.: Bounded minimisers of double phase variational integrals. Arch. Ration. Mech. Anal. 218(1), 219–273 (2015)
Colombo, M., Mingione, G.: Calderón-Zygmund estimates and non-uniformly elliptic operators. J. Funct. Anal. 270(4), 1416–1478 (2016)
Crespo-Blanco, Á., Gasiński, L., Harjulehto, P., Winkert, P.: A new class of double phase variable exponent problems: existence and uniqueness. J. Differential Equ. 323, 182–228 (2022)
Cruz-Uribe, D., Diening, L.: Sharp \({\cal{A} }\)-harmonic approximation. Appl. Anal. 98(1–2), 374–380 (2019)
De Filippis, C.: Optimal gradient estimates for multi-phase integrals. Math. Eng. 4(5), 1–36 (2022)
De Filippis, C., Mingione, G.: Lipschitz bounds and nonautonomous integrals. Arch. Ration. Mech. Anal. 242, 973–1057 (2021)
De Filippis, C.,Mingione, G.: Nonuniformly elliptic schauder theory, Invent. Math. (to appear)
DiBenedetto, E.: \(C^{1+\alpha }\) local regularity of weak solutions of degenerate elliptic equations. Nonlinear Anal. 7(8), 827–850 (1983)
Diening, L., Harjulehto, P., Hästö, P., Růžička, M.: Lebesgue and Sobolev Spaces with Variable Exponents. Lecture Notes in Mathematics, vol. 2017. Springer, Heidelberg (2011)
Diening, L., Málek, J., Steinhauer, M.: On Lipschitz truncations of Sobolev functions (with variable exponent) and their selected applications. ESAIM Control Optim. Calc. Var. 14(2), 211–232 (2008)
Diening, L., Kaplický, P., Schwarzacher, S.: BMO estimates for the \(p\)-Laplacian. Nonlinear Anal. 75(2), 637–650 (2012)
Diening, L., Stroffolini, B., Verde, A.: The \(\varphi \)-harmonic approximation and the regularity of \(\varphi \)-harmonic maps. J. Differential Equ. 253(7), 1943–1958 (2012)
Esposito, L., Leonetti, F., Mingione, G.: Sharp regularity for functionals with \((p, q)\) growth. J. Differential Equ. 204(1), 5–55 (2004)
Evans, L.C.: A new proof of local \(C^{1,\alpha }\) regularity for solutions of certain degenerate elliptic p.d.e. J. Differential Equ. 45(3), 356–373 (1982)
Fang, Y., Rădulescu, V., Zhang, C., Zhang, X.: Gradient estimates for multi-phase problems in Campanato spaces. Indiana Univ. Math. J. 71(3), 1079–1099 (2022)
Giusti, E.: Direct Methods in the Calculus of Variations. World Scientific, River Edge (2003)
Hadzhy, O.V., Skrypnik, I.I., Voitovych, M.V.:Interior continuity, continuity up to the boundary and Harnack’s inequality for double-phase elliptic equations with non-logarithmic conditions, Math. Nachr., to appear. https://doi.org/10.1002/mana.202000574
Harjulehto, P., Hästö, P.: Orlicz Spaces and Generalized Orlicz Spaces. Lecture Notes in Mathematics, vol. 2236. Springer, Cham (2019)
Harjulehto, P., Hästö, P.: Double phase image restoration. J. Math. Anal. Appl. 501(1), 123832 (2021)
Harjulehto, P., Hästö, P., Juusti, J.: Bloch estimates in non-doubling generalized Orlicz spaces. Math. Eng. 5(3), 1–21 (2023). ((Giuseppe Mingione Anniversary SI))
Harjulehto, P., Hästö, P., Lee, M.: Hölder continuity of \(\omega \)-minimizers of functionals with generalized Orlicz growth, Ann. Sc. Norm. Super. Pisa Cl. Sci. XXII (2), 549–582 (2021)
Harjulehto, P., Hästö, P., Toivanen, O.: Hölder regularity of quasiminimizers under generalized growth conditions. Calc. Var. Partial Differential Equ. 56(2), 22 (2017)
Harjulehto, P., Hästö, P., Karppinen, A.: Local higher integrability of the gradient of a quasiminimizer under generalized Orlicz growth conditions. Nonlinear Anal. 177(part B), 543–552 (2018)
Hästö, P.: The maximal operator on generalized Orlicz spaces. J. Funct. Anal. 269(12), 4038–4048 (2015)
Hästö, P.: A fundamental condition for harmonic analysis in anisotropic generalized Orlicz spaces. J. Geom. Anal. 33, 7 (2023)
Hästö, P., Ok, J.: Maximal regularity for local minimizers of non-autonomous functionals. J. Eur. Math. Soc. (JEMS) 24(4), 1285–1334 (2022)
Hästö, P., Ok, J.: Regularity theory for non-autonomous partial differential equations without Uhlenbeck structure. Arch. Ration. Mech. Anal. 245(3), 1401–1436 (2022)
Lewis, J.: Regularity of the derivatives of solutions to certain degenerate elliptic equations. Indiana Univ. Math. J. 32(6), 849–858 (1983)
Maeda, F.Y., Mizuta, Y., Ohno, T., Shimomura, T.: Boundedness of maximal operators and Sobolev’s inequality on Musielak-Orlicz-Morrey spaces. Bull. Sci. Math. 137, 76–96 (2013)
Maeda, F.Y., Mizuta, Y., Ohno, T., Shimomura, T.: Trudinger’s inequality for double phase functionals with variable exponents. Czechosolvak Math. J. 71(2), 511–528 (2021)
Manfredi, J. J.: Regularity of the gradients for a class of nonlinear possibly degenerate elliptic equations, Thesis (Ph.D.) Washington University in St. Louis. 58 pp (1986)
Marcellini, P.: Regularity of minimizers of integrals of the calculus of variations with non standard growth conditions. Arch. Ration. Mech. Anal. 105, 267–284 (1989)
Marcellini, P.: Regularity and existence of solutions of elliptic equations with \((p, q)\)-growth conditions. J. Differential Equ. 90, 1–30 (1991)
Mizuta, Y., Ohno, T., Shimomura, T.: Boundedness of fractional maximal operators for double phase functionals with variable exponents. J. Math. Anal. Appl. 501(1), 124360 (2021)
Ok, J.: Regularity for double phase problems under additional integrability assumptions. Nonlinear Anal. 194, 111408 (2020)
Rădulescu, V.: Nonlinear elliptic equations with variable exponent: old and new. Nonlinear Anal. 121, 336–369 (2015)
N.N. Uralćeva: Degenerate quasilinear elliptic systems (Russian), Zap. Naučn. Sem. Leningrad. Otdel. Mat. Inst. Steklov. (LOMI) 7 (1968), 184–222
Zhikov, V.V.: Averaging of functionals of the calculus of variations and elasticity theory. Izv. Akad. Nauk SSSR Ser. Mat. 50, 675–710 (1986)
Zhikov, V.V.: On Lavrentiev’s phenomenon. Russian J. Math. Phys. 3(2), 249–269 (1995)
Acknowledgements
Peter Hästö was supported in part by the Jenny and Antti Wihuri Foundation and Jihoon Ok was supported by the National Research Foundation of Korea by the Korean Government (NRF-2022R1C1C1004523). We thank the referee for comments.
Funding
Open Access funding provided by University of Turku (including Turku University Central Hospital).
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Laszlo Szekelyhidi.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hästö, P., Ok, J. Regularity theory for non-autonomous problems with a priori assumptions. Calc. Var. 62, 251 (2023). https://doi.org/10.1007/s00526-023-02587-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00526-023-02587-3



 ;
; ,
,  ,
,  or
or  , then
, then  ,
,  ,
,  or
or  , respectively, with the same constant
, respectively, with the same constant  , then
, then  and
and  with constant
with constant  , with constant depending on L and
, with constant depending on L and  for every
for every  with
with  and
and  with
with  with
with  ,
,  and
and  with the constant L, for every
with the constant L, for every  if and only if
if and only if  .
. , then so does F, with the same
, then so does F, with the same  ,
,  for
for 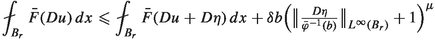 for some
for some  and
and  .
. , then
, then  with
with  , then
, then  with
with