Abstract
We study variational models for dislocations in three dimensions in the line-tension scaling. We present a unified approach which allows to treat energies with subquadratic growth at infinity and other regularizations of the singularity near the dislocation lines. We show that the asymptotics via Gamma convergence is independent of the specific choice of the energy and of the regularization procedure.
Similar content being viewed by others
1 Introduction
Variational models depending on fields that can have topological singularities are of particular interest in materials science. The asymptotic analysis of such models is often based on tools from geometric measure theory and permits to derive effective energies concentrated on sets of lower dimension. Important examples range from the study of vortices in superconductors, to grain boundaries, fractures and other interfaces in solids, as well as line defects and disclinations in liquid crystals. Here we consider the codimension-two case, and in particular integral energies in three dimensions for fields that are curl-free away from a one-dimensional set, having in mind the important application of the study of dislocations in crystals.
Dislocations are the main mechanism for plastic deformation in metals. They are one-dimensional singularities of the strain field, with discrete multiplicity arising from the structure of the underlying crystal lattice. We treat dislocation models of the type
where \(\Omega \subseteq \mathbb {R}^3\), \(W:\mathbb {R}^{3\times 3}\rightarrow [0,\infty )\) is an elastic energy density, \(\beta :\Omega \rightarrow \mathbb {R}^{3\times 3}\) characterizes the strain field and obeys \(\mathop {\textrm{curl}}\beta =\mu \). In turn, \(\mu \) is the density of dislocations; which is a divergence-free finite measure of the form  , with \(\gamma \subset \Omega \) a one-rectifiable curve, \(\theta \in L^1(\gamma ,{\mathcal {H}}^1;{\mathcal {B}})\) the discrete, vectorial multiplicity, \(\tau \in L^\infty (\gamma , {\mathcal {H}}^1; S^{2})\) tangent to \(\gamma \). Here \({\mathcal {B}}\) is a three dimensional Bravais lattice which describes the underlying crystalline structure and the small parameter \({\varepsilon }\) represents the ratio between the atomic distance and the size of the sample. In a finite setting we understand \(\Omega \) as the deformed configuration, and \(\beta \) as the inverse of the elastic strain; the energy density W is then invariant under the action of \({\textrm{SO}}(3)\) on the right. In the entire paper \(\mathop {\textrm{curl}}f\), for f a distribution taking values in \(\mathbb {R}^{3\times 3}\), denotes the rowwise distributional curl, which is also a distribution taking values in \(\mathbb {R}^{3\times 3}\).
, with \(\gamma \subset \Omega \) a one-rectifiable curve, \(\theta \in L^1(\gamma ,{\mathcal {H}}^1;{\mathcal {B}})\) the discrete, vectorial multiplicity, \(\tau \in L^\infty (\gamma , {\mathcal {H}}^1; S^{2})\) tangent to \(\gamma \). Here \({\mathcal {B}}\) is a three dimensional Bravais lattice which describes the underlying crystalline structure and the small parameter \({\varepsilon }\) represents the ratio between the atomic distance and the size of the sample. In a finite setting we understand \(\Omega \) as the deformed configuration, and \(\beta \) as the inverse of the elastic strain; the energy density W is then invariant under the action of \({\textrm{SO}}(3)\) on the right. In the entire paper \(\mathop {\textrm{curl}}f\), for f a distribution taking values in \(\mathbb {R}^{3\times 3}\), denotes the rowwise distributional curl, which is also a distribution taking values in \(\mathbb {R}^{3\times 3}\).
If W has quadratic growth, the energy (1.1) is infinite whenever \(\mu \ne 0\). In reality, the discrete nature of crystals shows that the appropriate model would be discrete. The divergence is a nonphysical result due to the fact that one uses a continuum approximation which in the region close to the singularity is not appropriate. Therefore a number of regularizations of the continuum model have been proposed. They include a subquadratic growth of W at infinity, the replacement of \(\mu \) by a mollified version at scale \({\varepsilon }\), and the elimination of a core region from the integration domain. For example, the latter corresponds to
where \((\gamma )_{\varepsilon }\) denotes an \({\varepsilon }\)-neighbourhood of the curve \(\gamma \). The above models are all considered semi-discrete models, in the sense that they are continuum models that still contain the discrete parameter \({\varepsilon }\) and some discrete effects, namely, the quantization of the measure and the regularization, both at scale \({\varepsilon }\). In turn, the energy density W can be treated in a geometrically linear setting, or with finite kinematics. Ultimately, all these variants have the same leading-order behaviour.
In this paper, we provide a unified treatment of the three-dimensional continuum models which covers many different regularizations, as for example the one with mixed growth conditions, and clarifies the equivalence of all these possible approximations and corresponding regularizations. Our general approach produces also a simpler and more direct proof of some results from the literature [18, 27]; we expect that this unified approach will prove helpful in further future generalizations. We assume that dislocations are dilute, in the sense that the curve \(\gamma \) on which \(\mu \) is supported has some regularity, which may however degenerate in the limit. Our mechanical model includes frame indifference and is formulated in the deformed (spatial) configuration \(\Omega \). As a measure of elastic strain at a point \(x\in \Omega \), we use \(\beta (x)\in \mathbb {R}^{3\times 3}\), which maps directions in the spatial configuration to directions in the lattice configuration; in the language of continuum mechanics this is the inverse elastic strain seen as a spatial field, \(\beta =(F_e)^{-1}_s\), as discussed in Sect. 3.1 below (the subscript s indicates that the field depends on the spatial coordinates).
The topological singularity leads to a logarithmic divergence of the energy in the regularization parameter \({\varepsilon }\). After rescaling by \(\log \frac{1}{{\varepsilon }}\), we show \(\Gamma \)-convergence to an energy which depends on a constant rotation Q, a measure  representing the dislocation density, and a curl-free field \({{\eta }}\) representing the elastic strain. The limiting energy takes the form
representing the dislocation density, and a curl-free field \({{\eta }}\) representing the elastic strain. The limiting energy takes the form
The second term represents the line-tension energy, which can be obtained as the relaxation of
where \(\psi _\mathbb {C}\) is the line-tension energy per unit length of infinite straight dislocations and can be computed from the matrix of elastic constants \(\mathbb {C}\) by a one-dimensional variational problem (see [18] and Sect. 2 below for details). The first term involves the elasticity matrix \(\mathbb {C}\), rotated by Q.
We remark that our kinematic treatment of dislocations in finite kinematics is different from the one used in recent related mathematical literature, as for example [27, 41]. Indeed, we work in the deformed configuration and our limiting energy has the integrand \(\psi _\mathbb {C}(\theta ,Q\tau )\), whereas the cited literature works in the reference configuration and obtains a functional containing (in our notation) \(\psi _\mathbb {C}(Q^T\theta ',\tau ')\). The two can be made to coincide if \(\theta '=Q\theta \), \(\tau '=Q\tau \); as \(\theta \) takes value in the lattice \({\mathcal {B}}\) this suggests that the expression \(\psi _\mathbb {C}(Q^T\theta ',\tau ')\) needs the multiplicity \(\theta '\) to take values in the rotated lattice \(Q{\mathcal {B}}\). We remark that our approach closely matches the one presented in [35, (7.6)–(7.11)].
In Sect. 3 we state the main \(\Gamma \)-convergence result for the energies with mixed growth, we discuss the other models for alternative regularizations in the nonlinear and linear setting, which have the same \(\Gamma \)-limit, and we give a sketch of the main ideas of our approach. The proofs of the \(\Gamma \)-convergence results are then collected in Sect. 7.
In Sect. 4 we show that for a single straight dislocation the leading-order term of the energy can be characterized by a cell problem under general assumptions for the energy density W. After rescaling, this term leads to (1.4). Therefore the linearization of a nonlinear elastic energy arises naturally in the limit. In particular this provides (Sect. 5) the lower bound for the \(\Gamma \)-limit of a nonlinear elastic model with energy densities of mixed growth, i.e., that behave as the minimum between \({\textrm{dist}}^2(\cdot , {\textrm{SO}}(3))\) and \({\textrm{dist}}^p(\cdot , {\textrm{SO}}(3))\) for some \(p\in (1,2)\). For this model we also obtain a compactness statement, that asserts that sequences \(\beta _{\varepsilon }\) with uniformly bounded energy have a converging subsequence in the relevant topology.
Moreover in Sect. 6 we show that the upper bound can be obtained by a pointwise limit. This proves that there is indeed a complete separation of scales between the relaxation, which happens at the line-tension level and only involves the line-tension energies \(\psi _\mathbb {C}\) and \(\psi _\mathbb {C}^{\textrm{rel}}\), and the concentration, which relates the elastic energy W integrated on a three-dimensional volume to the line-tension energy \(\psi _\mathbb {C}\) integrated on one-dimensional sets. This was already apparent in the two-dimensional Nabarro–Peierls setting of [13].
The general approach presented here will also allow, in a forthcoming paper [17], to treat a discrete model, confirming that the semi-discrete models are a good description of discrete ones outside the core region.
In two dimensions dislocations are point singularities, and a similar analysis for dilute configurations was performed for linear models in [19, 25] and for nonlinear models in [35, 41], both in the energy regimes scaling as \(\log \frac{1}{{\varepsilon }}\) and as \(\log ^2\frac{1}{{\varepsilon }}\). These results were extended in [20, 23, 24] to general configurations, exploiting the connection between models for dislocations and Ginzburg–Landau models for vortices [3] and refining the ball construction due to Sandier and Jerrard [31, 38, 39] to the context of elasticity in order to obtain compactness and optimal lower bounds. Similar techniques have been used first in [36] and then in [4] in order to study a discrete two-dimensional model for screw dislocations, see also [30]. Similar problems arise in the context of spin systems, see for instance [7]. The two scales mentioned above give rise to mesoscopic limits where dislocations are identified with points (with energy scaling as \(\log \frac{1}{{\varepsilon }}\)) or with densities (\(\log ^2\frac{1}{{\varepsilon }}\)). Results which obtain a characterization of grain boundaries in polycrystals exhibit a different scaling. Lauteri and Luckhaus [32] characterized the optimal scaling for the elastic energies of small-angle grain boundaries in nonlinear kinematics and gave a rigorous derivation of the Read–Shockley formula (see [28] for the proof of the corresponding \(\Gamma \)-convergence result and [22] for the result in the context of linear elasticity with diluteness assumptions).
The extension from two dimensions to three dimensions in the context of Ginzburg–Landau models is based on a slicing argument [2, 8] which cannot be directly used for the anisotropic vectorial problem of elasticity, also because of the degeneracy arising from frame indifference and the relaxation of the line-tension energy. Therefore the question whether our asymptotic analysis can also be obtained without the diluteness condition in dimension three may be very difficult. An intermediate step in this direction is the case in which the kinematics is restricted to a plane. Here the model reduces to a nonlocal phase-field model and was studied without diluteness assumptions in both regimes in [11, 13, 15, 16, 26].
2 Line dislocations in linear elasticity
We first collect some results concerning the continuum study of dislocations in linear elasticity. Precisely, we recall the definition of the strain field in the presence of defects and its properties, then we give a characterization of the strain field for a straight infinite dislocation and of the associated line tension per unit length.
As usual, we assume that \(\mathbb {C}\in \mathbb {R}^{3\times 3\times 3\times 3}_{\textrm{sym}}\) is degenerate on linearized rotations and is coercive on symmetric matrices, in the sense that
Working in \(\mathbb {R}^3\), dislocations are measures concentrated along one-dimensional sets. More precisely a distribution of dislocations in \(\Omega \subset \mathbb {R}^3\) is a measure \(\mu \) in the set \( {\mathcal {M}}^1(\Omega )\) defined below.
Definition 2.1
We denote by \({\mathcal {M}}(\Omega ;V)\), with V a finite-dimensional vector space, the set of finite V-valued Radon measures on the open set \(\Omega \subseteq \mathbb {R}^3\). We write \({\mathcal {M}}^1(\Omega )\) for the set of \(\mu \in {\mathcal {M}}(\Omega ;\mathbb {R}^{3\times 3})\) which obey \(\mathop {\textrm{div}}\mu =0\) distributionally and have the form

for some 1-rectifiable set \(\gamma \subseteq \Omega \), \(\theta :\gamma \rightarrow \mathbb {R}^3\), \(\tau :\gamma \rightarrow S^2\).
The condition \(\mathop {\textrm{div}}\mu =0\) automatically implies that \(\tau \) is tangent to \(\gamma \) \(\mu \)-almost everywhere. We refer to the multiplicity \(\theta \) in (2.2) as the Burgers vector of the dislocation line \(\gamma \).
2.1 Construction of the strain field
Let \(\mu \in {\mathcal {M}}(\mathbb {R}^3;\mathbb {R}^{3\times 3})\) with \(\mathop {\textrm{div}}\mu =0\). Within linear elasticity, the corresponding equilibrium strain is a distributional solution \(\beta \in L^1_{\textrm{loc}}(\mathbb {R}^3;\mathbb {R}^{3\times 3})\) to
with \(\mathbb {C}\) as in (2.1). Existence and uniqueness of solutions to (2.3) were proven in [18, Theorem 4.1]. We recall here this result in \(\mathbb {R}^3\).
Theorem 2.2
Let \(\mathbb {C}\) be as in (2.1). For any bounded measure \(\mu \in {\mathcal {M}}(\mathbb {R}^3;\mathbb {R}^{3\times 3})\) with \(\mathop {\textrm{div}}\mu =0\) the following holds.
-
(i)
There is a unique \({{\beta }}\in L^{3/2}(\mathbb {R}^3;\mathbb {R}^{3\times 3})\) such that
$$\begin{aligned} \mathop {\textrm{div}}\mathbb {C}{{\beta }}=0 \quad \text { and }\quad \mathop {\textrm{curl}}{{\beta }}=\mu \end{aligned}$$(2.4)distributionally. The solution \({{\beta }}\) satisfies
$$\begin{aligned} \Vert {{\beta }}\Vert _{L^{3/2}(\mathbb {R}^3)} \le c |\mu |(\mathbb {R}^3). \end{aligned}$$ -
(ii)
There is a function \(N\in C^\infty (\mathbb {R}^3{\setminus }\{0\};\mathbb {R}^{3\times 3\times 3\times 3})\) which depends only on \(\mathbb {C}\), is positively \(-2\) homogeneous, in the sense that
$$\begin{aligned} N(\lambda x)=\lambda ^{-2} N(x) \text { for all } x\in \mathbb {R}^3,\lambda \in (0,\infty ), \end{aligned}$$(2.5)and such that the unique solution \({{\beta }}\) satisfies
$$\begin{aligned} {{\beta }}_{ij}(x)=\sum _{k,l=1}^3\int _{\mathbb {R}^3} N_{ijkl}(x-y) d\mu _{kl}(y) \end{aligned}$$(2.6)for \(x\not \in \mathop {\textrm{supp}}\mu \).
-
(iii)
If additionally \(\mu \in {\mathcal {M}}^1(\mathbb {R}^3)\) and
 for countably many segments \(\gamma _i\), then for \(x\not \in \mathop {\textrm{supp}}\mu \)$$\begin{aligned} |{{\beta }}(x)|\le c \sum _i \frac{|b_i|}{{\textrm{dist}}(x, \gamma _i)}. \end{aligned}$$(2.7)
for countably many segments \(\gamma _i\), then for \(x\not \in \mathop {\textrm{supp}}\mu \)$$\begin{aligned} |{{\beta }}(x)|\le c \sum _i \frac{|b_i|}{{\textrm{dist}}(x, \gamma _i)}. \end{aligned}$$(2.7)If the number of segments is finite then \({{\beta }}\in L^p(\mathbb {R}^3;\mathbb {R}^{3\times 3})\) for all \(p\in [3/2,2)\).
The constant c depends only on \(\mathbb {C}\).
We remark that in point (iii) of [18, Theorem 4.1] the vectors \(b_i\) were required to be in a lattice. This assumption was never used in the proof. Assertion (ii) is proven in (4.7) and the following equations of [18].
2.2 Characterization of the strain for straight dislocations
From the representation formula (2.6) one also obtains a representation for the strain field of an infinite straight dislocation of Burgers vector b along the line \(\mathbb {R}t\), for some \(t\in S^2\) and \(b\in \mathbb {R}^3\), which is then a distributional solution of

In the entire paper we denote by \(B_r(x)\) and \(B'_r(x)\) the balls of radius \(r>0\) centered at x in \(\mathbb {R}^3\) and \(\mathbb {R}^2\) respectively. For \(x=0\) we simply write \(B_r\) and \(B'_r\).
Lemma 2.3
Let \(N\in C^{\infty }(\mathbb {R}^3{\setminus }\{0\};\mathbb {R}^{3\times 3\times 3\times 3})\) be as in Theorem 2.2(ii). For any \(b\in \mathbb {R}^3\) and \(t\in S^2\) the function
(for \(x\not \in \mathbb {R}t\)) is in \(L^1_{\textrm{loc}}(\mathbb {R}^3;\mathbb {R}^{3\times 3})\) and satisfies (2.8) in the sense of distributions.
Proof
For \(R>0\) we define \(\mu _R\) by

where \(\gamma _R\) is the union of the segment \([-Rt, Rt]\) with a half-circle which has \([-R t,R t]\) as diameter and \(\tau :\gamma _R\rightarrow S^2\) is a tangent vector to \(\gamma _R\), oriented so that it coincides with t in \([-Rt, Rt]\). One easily checks that \(\mu _R\in {\mathcal {M}}^1(\mathbb {R}^3)\) and \(\mu _R{\displaystyle \mathop {\rightharpoonup }^*}\mu \) as \(R\rightarrow \infty \).
We define \({{\beta }}_R:=N *\mu _R\), where \(*\) denotes convolution as in (2.6). By Theorem 2.2, it satisfies
Let  be defined as in (2.9). We remark that the integral exists for all \(x\not \in \mathbb {R}t\) since the integrand is continuous and decays as \(|y|^{-2}\) at infinity.
be defined as in (2.9). We remark that the integral exists for all \(x\not \in \mathbb {R}t\) since the integrand is continuous and decays as \(|y|^{-2}\) at infinity.
We show that \({{\beta }}_R\rightarrow {\hat{{{\beta }}}}\) in \(L^1_{\textrm{loc}}(\mathbb {R}^3;\mathbb {R}^{3\times 3})\). Fix \(r>0\), and assume that \(R\ge 2r\). Then for almost every \(x\in B_r{\setminus } \mathbb {R}t\) we have
which implies, since \(|x|\le \frac{1}{2} R\) and \(|y|\ge R\),
Therefore \({\hat{{{\beta }}}}-{{\beta }}_R\) converges to zero uniformly on compact sets, as \(R\rightarrow \infty \), and hence in \(L^1_{\textrm{loc}}(\mathbb {R}^3;\mathbb {R}^{3\times 3})\). By (2.11), we obtain (2.8) distributionally in \(\mathbb {R}^3\). \(\square \)
The strain field \({\hat{\beta }}\) in (2.9) can be characterized with a variational argument and it is given by a two-dimensional profile \({{\beta }}_{b,t}\). In order to do this, as in [18], for any \(t\in S^2\) we fix a rotation \(Q_t\in {\textrm{SO}}(3)\) such that \(Q_te_3=t\), define the map
and the orthonormal basis
We recall that in [18, Lemma 5.1], for any \(b\in \mathbb {R}^3\) and \(t\in S^2\) we defined \({{\beta }}_{b,t}\in L^1_{\textrm{loc}}(\mathbb {R}^3;\mathbb {R}^3)\) as the unique function of the form
for some \(f\in L^2((0,2\pi );\mathbb {R}^3)\) with \(\int _0^{2\pi } f(\theta ) d\theta =b\) and \(g\in \mathbb {R}^3\) which minimizes the variational problem
Lemma 2.4
Let \(N\in C^\infty (\mathbb {R}^3{\setminus }\{0\};\mathbb {R}^{3\times 3\times 3\times 3})\) be as in Theorem 2.2(ii). For any \(b\in \mathbb {R}^3\) and \(t\in S^2\) the solution \({{\beta }}_{b,t}\) of the one-dimensional problem in (2.14–2.15) is
(for \(x\not \in \mathbb {R}t\)). On the same set it obeys
where c depends only on \(\mathbb {C}\).
Equation (2.16) in particular shows that \(\beta _{b,t}\) does not depend on the choice of the matrix \(Q_t\).
Proof
We need to prove that \({\hat{{{\beta }}}}\) as defined in (2.9) coincides with \({{\beta }}_{b,t}\). This involves two steps: we first show that \({\hat{{{\beta }}}}\) has the same structure as \({{\beta }}_{b,t}\), and then that it obeys the Euler-Lagrange equations of the variational problem that defines \({{\beta }}_{b,t}\), which has a unique solution by [18, Lemma 5.1].
We claim that the definition of \({\hat{{{\beta }}}}\) implies that there is \(G\in C ^1_\text {per}([0,2\pi ];\mathbb {R}^{3\times 3})\) such that for any \(r>0\), \(\theta \) and z, with \(\Phi _t\) as in (2.12),
To see this, we observe that by definition \(\Phi _t(r,\theta ,z)=rQ_te_r(\theta )+zt\), so that the definition of \({\hat{{{\beta }}}}\) yields
where we used the change of variables \(s':=(s-z)/r\) and (2.5). As the integral depends only on \(\theta \), and the dependence is smooth, (2.18) is proven.
Next we show that the condition that \({\hat{{{\beta }}}}\) is locally curl free away from \(\mathbb {R}t\) implies that G has a special structure. We compute
Therefore
By (2.18), \({\hat{{{\beta }}}}\circ \Phi _t=G(\theta )/r\), and
Away from \(\mathbb {R}t\) we have \(\mathop {\textrm{curl}}{\hat{{{\beta }}}}=0\) and therefore \(D{\hat{{{\beta }}}}=(D{\hat{{{\beta }}}})^T\), in the sense that \(\partial _j{\hat{\beta }}_{ki}=\partial _i{\hat{\beta }}_{kj}\). This implies
which gives \(G(\theta )Q_te_3=0\) for all \(\theta \). Further,
We define \(f,g,h:(0,2\pi )\rightarrow \mathbb {R}^3\) by
The condition \(GQ_te_3=0\) implies \(h=0\). We compute, using \(\partial _\theta e_\theta =-e_r\) and \(\partial _\theta e_r=e_\theta \),
Inserting in (2.20) leads to
which implies that g is constant. We conclude that
By the condition  we obtain \(\int _0^{2\pi } f(\theta ) d\theta =b\).
we obtain \(\int _0^{2\pi } f(\theta ) d\theta =b\).
It remains to show that (f, g) are the unique minimizers of the variational problem in (2.15). Let \({{\tilde{f}}}\in L^\infty ((0,2\pi );\mathbb {R}^3)\) with \(\int _0^{2\pi } {{\tilde{f}}}(\theta )d\theta =0\), and \({{\tilde{g}}}\in \mathbb {R}^3\). We define
and
If we can show that \(A=B=0\), by convexity of the functional in (2.15) we are done.
We start from A. Fix \(h,R\ge 2\), let \(\psi _3\in C^\infty _c(\mathbb {R};[0,1])\) such that \(\int _\mathbb {R}\psi _3 dz=1\), and \(\psi _R\in C^\infty _c((0,\infty );[0,1])\) such that \(\int _0^\infty \psi _R dr=1\). We define \({{\tilde{u}}}\in W^{1,\infty }_0(\mathbb {R}^3;\mathbb {R}^3)\) by
We differentiate and obtain
The three derivatives on the left can be easily computed from the definition. Recalling (2.19),
Since \(\mathop {\textrm{div}}\mathbb {C}{\hat{{{\beta }}}}=0\) distributionally and \({\hat{{{\beta }}}}\in L^1_{\textrm{loc}}(\mathbb {R}^3;\mathbb {R}^{3\times 3})\), we have
We write this equation in cylindrical coordinates, writing the three terms separately and using (2.18). Since \(\int _\mathbb {R}\psi _3 dz=1\) and \(\int _\mathbb {R}\psi _3'dz=0\), this reduces to
The second term vanishes since \(\int _0^\infty \psi _R'(r)dr=0\). We are left with the first term, which recalling (2.22) takes the form
Since \(\int _0^\infty \psi _R(r)dr=1\), the integral is positive, and we conclude that \(A=0\).
We now turn to B. We fix \(\psi _3\) as above, choose \(\Psi _R\in C_c^\infty (\mathbb {R};[0,1])\), such that \(\Psi _R(0)=1\), and define
As above, we compute
and, computing again the integral and recalling that \(\int _\mathbb {R}\psi _3'dz=0\) and \(\int _0^\infty \Psi _R' dr=-1\), we obtain
Therefore \(B=0\) and the proof of the first assertion is concluded.
It remains to prove (2.17). This follows immediately from the fact that N is \(-2\)-homogeneous and continuous,
\(\square \)
2.3 Line tension energy of straight dislocations
The variational problem that characterizes \(\beta _{b,t}\) provides the energy per unit length of the straight infinite dislocation, \(\psi _\mathbb {C}(b,t)\), which we will call the unrelaxed line-tension energy density. Indeed using \(\beta _{b,t}\) we can compute the elastic energy induced by a straight dislocation along \(\mathbb {R}t\) in a cylinder with axis \(\mathbb {R}t\). Precisely given \(r,R,h\in (0,\infty )\) with \(r<R\) we define the hollow cylinders
and the full cylinders
We recall that \(B'_\rho \) denotes the 2-dimensional disk of radius \(\rho >0\), \(B'_\rho :=\{(x_1,x_2): x_1^2+x_2^2<\rho ^2\}\), and that before (2.12) we introduced \(Q_t\) as a fixed rotation with \(Q_te_3=t\). Therefore using the radial structure of \(\beta _{b,t}\), from (2.15) we have
(see also [18, Lemma 5.1(iv)]).
With this energy density one can associate to any \(\mu \in {\mathcal {M}}^1(\Omega )\) the line-tension energy
As shown in [14], this functional may not be lower semicontinuous and needs to be relaxed (see Sect. 3.3 formula (3.42) below). A variational characterization of \(\psi _\mathbb {C}\), in which the elastic energy is minimized over cylinders, has been obtained in [18, Lemma 5.5]. To explain it, for \(\mathbb {C}\) as in (2.1), \(b\in \mathbb {R}^3\), \(t\in S^2\), \(h\ge R>r>0\) we define
Then \(\psi _\mathbb {C}\) arises as limit of \(\Theta \) for \(r\rightarrow 0\). We improve over [18, Lemma 5.5] removing one error term, and prove the following.
Lemma 2.5
Assume that \(\mathbb {C}\) obeys (2.1).
-
(i)
Let \(b\in \mathbb {R}^3\), \(t\in S^2\), \(h\ge R>0\). Then
$$\begin{aligned} \lim _{r\rightarrow 0}\Theta (\mathbb {C},b,t,h,R,r)=\psi _\mathbb {C}(b,t). \end{aligned}$$(2.33) -
(ii)
There is \(c>0\), depending only on \(\mathbb {C}\), such that
$$\begin{aligned} \frac{1}{c}|b|^2\le \psi _\mathbb {C}(b,t)\le c|b|^2 \end{aligned}$$(2.34)and
$$\begin{aligned} \psi _\mathbb {C}(b,t)\le \left( 1+\frac{|b-b'|}{|b|+|b'|}\right) \psi _\mathbb {C}(b',t)+c|b-b'| (|b|+|b'|) \end{aligned}$$(2.35)for all b, \(b'\in \mathbb {R}^3\), \(t\in S^2\).
-
(iii)
There is \(c>0\), depending only on \(\mathbb {C}\), such that for all \(b\in \mathbb {R}^3\), \(t,t'\in S^2\), we have
$$\begin{aligned} \psi _\mathbb {C}(b,t)\le (1+c|t-t'|)\psi _\mathbb {C}(b,t'). \end{aligned}$$(2.36)
Proof
(i): Since any function \(u\in W^{1,1}(Q_tT^{R,r}_h;\mathbb {R}^3)\) can be extended to a function in \(W^{1,1}(Q_tT^{R}_h;\mathbb {R}^3)\), we have

By [18, Lemma 5.5] we get
Moreover for \(R>R'>r\) it holds
Taking the limit as \(r\rightarrow 0\), since \(\lim _{r\rightarrow 0} \frac{\log \frac{R'}{r}}{\log \frac{R}{r}}=1\) from (2.38) we infer
for all \(R'>0\), and therefore for \(R'=0\). At the same time, by (2.30) we obtain \(\Theta (b,t,h,R,r)\le \psi _\mathbb {C}(b,t)\) for all \(r\in (0,R)\), and the proof of (2.33) is concluded.
(ii): The bounds in (2.34) follow from [18, Lemma 5.1(iii)] (the upper bound can be also easily proven inserting the bound in (2.17) into (2.30) and integrating). The remaing bound (Eq. (2.35)) is proven using Lemma 2.4 and (2.30). We first observe that by (2.16) we have \(\beta _{b,t}=\beta _{b',t}+\beta _{b-b',t}\). Therefore for any \(\delta >0\), fixing some \(r<R\le h\) from (2.30) we obtain
In turn, by the upper bound in (2.34) we have
Setting \(\delta :=|b-b'|/(|b|+|b'|)\in (0,1]\) concludes the proof of (2.35).
(iii): follows from [18, Lemma 5.7]. \(\square \)
3 Model and main results
3.1 Dislocations in finite kinematics
We work within the general framework of continuum mechanics, using finite kinematics. In the presence of dislocations, there is no smooth bijection between the reference configuration and the deformed configuration. Therefore any choice of a reference configuration includes a high degree of arbitrariness. We use spatial variables, with an energy obtained integrating over the deformed configuration \(\Omega \), and focus on the strain \(\beta :\Omega \rightarrow \mathbb {R}^{3\times 3}\), with \(\beta (x)\) seen as a linear map from the tangent space to the deformed configuration to the tangent space to the reference configuration, or the so-called (fictitious) “intermediate configuration” or “lattice configuration”. Precisely, for \(x\in \Omega \) (a point in the physical space occupied by the material) and \(t\in S^2\) a direction in the same space, \(\beta (x)t\) is the corresponding vector in the intermediate configuration, as illustrated in Fig. 1. It is then natural to expect that the line integral of \(\beta \) over a closed (spatial) curve results in a lattice vector, the Burgers vector. Therefore we consider the distributional rotation \(\mathop {\textrm{curl}}\beta \) as a measure of the density of dislocations. Indeed, this is the usual Burgers circuit argument, see for example [29, Fig. 1.19], [1, (7)], or [33] for a mathematical treatment.
We can relate \(\mathop {\textrm{curl}}\beta \) to the dislocation density tensor as used in continuum mechanics. Within the customary multiplicative decomposition of the strain into an elastic and a plastic part \(F=F_eF_p\), the density of dislocations (in the sense of the Nye tensor) is given by
where \(\mathop {\textrm{curl}}\) denotes the rotation in the spatial configuration, whereas \(\mathop {\textrm{Curl}}\) denotes the rotation in the material configuration. We refer for example to [10, 34, 37, 40] for these formulas and their equivalence (to compare formulas it is useful to keep in mind that in [10] curl is defined columnwise instead of rowwise as it is here, and that \(\mathop {\textrm{cof}}F=F^{-T}\det F\) for any invertible matrix F). In this language, the variable \(\beta \) we use corresponds to \(F_e^{-1}\), expressed in terms of the spatial coordinates. Whereas \(\alpha \) measures the density of (geometrically necessary) dislocations seen as the total Burgers vector crossing a certain area in the reference configuration, \(\mathop {\textrm{curl}}\beta \) measures the total Burgers vector crossing a certain area in the deformed configuration. We prefer this version for consistency with the fact that we work in the spatial representation, and because \(\mathop {\textrm{curl}}\beta \) (at variance with \(\mathop {\textrm{curl}}\beta \mathop {\textrm{cof}}\beta ^{-1}\)) can be easily understood distributionally.
In order to correctly formulate the variational model it is important to understand how frame indifference acts in this setting. In the usual material formulation of (dislocation-free) nonlinear elasticity, one considers a (bijective) deformation field \(u:\omega \rightarrow \Omega \), with \(\omega \subseteq \mathbb {R}^3\) the reference configuration and \(\Omega \subseteq \mathbb {R}^3\) the deformed (spatial) configuration. In this simple setting, \(\beta :\Omega \rightarrow \mathbb {R}^{3\times 3}\) is defined by \(\beta (u(x))=(Du(x))^{-1}\), and it is the gradient of the map \(v:\Omega \rightarrow \omega \) which is the inverse to u. Superimposing a rotation amounts to replacing u by \(u^Q(x):=Qu(x)\), \(u^Q:\omega \rightarrow Q\Omega \), so that the deformation gradient Du(x) gets replaced by \(Du^Q(x)=QDu(x)\). The inverse \(v^Q\) of \(u^Q\) is given by \(v^Q(u^Q(x))=x\), which is the same as \(v^Q(Qy)=v(y)\). Differentiating this expression one obtains \(Dv^Q(Qy)Q=Dv(y)\), which is the same as
This expression shows the action of rotations on the field \(\beta \). The above computation based on the chain rule shows that the multiplication of \(\beta \) by a rotation on the right is naturally coupled to a change of variables by the same rotation. An hyperelastic material can then be modeled by the energy
and material frame indifference leads to the requirement
With a change of variables, one can relate this expression to the usual integration over the reference configuration:
where \({{\hat{W}}}(F)=W(F^{-1})\det F\). One immediately sees that (3.4) is equivalent to the usual right-invariance \({{\hat{W}}}(QF)={{\hat{W}}}(F)\), and the requirement that \(\{ W=0\} \cap \{\det >0\}={\textrm{SO}}(3)\) is equivalent to \(\{{{\hat{W}}}=0\} \cap \{\det >0\}={\textrm{SO}}(3)\).
If the bijective map u does not exist globally, the same procedure can be performed locally, away from the dislocation cores (or using the intermediate configuration). In the spatial formulation, we consider \(\beta :\Omega \rightarrow \mathbb {R}^{3\times 3}\). It maps directions t in the spatial configuration (in \(\Omega \)) onto directions \(\beta t\) in the (fixed) lattice configuration. If we insert a rotation, mapping \(\Omega \) to \(Q\Omega \), the direction t becomes Qt, and a point \(y\in \Omega \) becomes \(Qy\in Q\Omega \). However, the vector in the lattice configuration is not modified, therefore necessarily \(\beta ^Q(Qy)Qt=\beta (y)t\) for all \(t\in \mathbb {R}^3\), which is the same as (3.2).
We next address how the distribution of dislocations, understood as \(\mathop {\textrm{curl}}\beta \), transforms under rotations, and how the line energy \(\psi _\mathbb {C}\) transforms. The key fact, in terms of the field introduced in (3.2), is
We remark that this equation, written in terms of Nye’s tensor \(\alpha =\mathop {\textrm{curl}}\beta \mathop {\textrm{cof}}\beta ^{-1}\), leads to \(\alpha ^Q(Qy)=\alpha (y)\), i.e., the Nye tensor is invariant under changes of coordinates.
A Burgers circuit in finite elasticity. Left: spatial (deformed) configuration. A closed path goes around the dislocation. The path is composed of finitely many segments \(t_i\) that join an atom to a neighbour. Right: representation in the reference (more precisely, intermediate) configuration. Here the atoms are exactly on the reference Bravais lattice, each of the segments \(t_i\) is mapped to a corresponding lattice vector which (in the continuum limit) is \(\beta t_i\). The path does not close, the sum of the segments is the Burgers vector, which is naturally an element of the (undeformed) crystal lattice. Therefore the contour integral of \(\beta \) equals the Burgers vector of the dislocation
Lemma 3.1
-
(i)
Let \(Q\in {\textrm{SO}}(3)\), \(F\in \mathbb {R}^{3\times 3}\), \(\lambda \in (0,\infty )\), \(v\in \mathbb {R}^3\), \(\Omega \subseteq \mathbb {R}^3\) open. Given \(\beta \in L^1_{\textrm{loc}}(\Omega ;\mathbb {R}^{3\times 3})\) we define \({\hat{\beta }}\in L^1_{\textrm{loc}}({\frac{1}{\lambda }Q^T(\Omega -v)};\mathbb {R}^{3\times 3})\) by
$$\begin{aligned} {\hat{\beta }}(x):=F\beta (\lambda Qx+v) Q. \end{aligned}$$(3.7)Then
$$\begin{aligned} (\mathop {\textrm{curl}}{\hat{\beta }})(x):=\lambda F(\mathop {\textrm{curl}}\beta )(\lambda Qx+v) Q. \end{aligned}$$(3.8) -
(ii)
If \(\mathop {\textrm{curl}}\beta \) is a (matrix-valued) measure, then so is \(\mathop {\textrm{curl}}{\hat{\beta }}\), and for any Borel set A one has \((\mathop {\textrm{curl}}{\hat{\beta }})(A)=\frac{1}{\lambda ^2} F((\mathop {\textrm{curl}}\beta )(\lambda QA+v))Q\). In particular, if
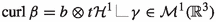 then
then 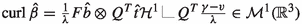 , where \({{\hat{b}}}(x):=b(\lambda Qx+v)\) and \({{\hat{t}}}(x):=t(\lambda Qx+v)\).
, where \({{\hat{b}}}(x):=b(\lambda Qx+v)\) and \({{\hat{t}}}(x):=t(\lambda Qx+v)\). -
(iii)
For any \(\mathbb {C}\) which obeys (2.1) and any \(Q\in {\textrm{SO}}(3)\) the line-tension energy \(\psi _\mathbb {C}\) obeys
$$\begin{aligned} \psi _\mathbb {C}(b,t)=\psi _{\mathbb {C}_Q}(Q^Tb,Q^Tt) \end{aligned}$$(3.9)where \(\mathbb {C}_Q\) is defined by
$$\begin{aligned} \mathbb {C}_Q A\cdot A = \mathbb {C}(QAQ^T)\cdot (QAQ^T). \end{aligned}$$(3.10)
We remark that (3.7) is the same as
Proof
(i): We first observe that (summing over repeated indices)
Indeed, the left-hand side is the i-th component of \((Q^Te_h)\wedge (Q^Te_p)=Q^T(e_h\wedge e_p)\), and \(e_i\wedge e_{i+1}=e_{i+2}\) (with indices taken modulo 3). We now compute (again with implicit sums) \({\hat{\beta }}_{ak}(x)=F_{ab}\beta _{bp}(\lambda Qx+v)Q_{pk}\) and
This proves (3.8).
(ii): If \(\beta \) is regular, by (i)
the general case follows by density. Further,

and \(F({{\hat{b}}}\otimes {{\hat{t}}})Q=(F{{\hat{b}}})\otimes (Q^T{{\hat{t}}})\).
(iii): We recall (2.32), which can be equivalently written as

For any \(\beta \) as above we define \({\hat{\beta }}\) by
Obviously \({\hat{\beta }}\in L^{1}(Q^TQ_t T_h^R;\mathbb {R}^{3\times 3})\), and by (ii) we have

With a change of variables
Then using that \(Q^T Q_t T^{R,r}_h=Q_{Q^Tt} T^{R,r}_h\) and taking the infimum over all choices of \(\beta \) gives
Taking the limit \(r\rightarrow 0\) with Lemma 2.5 (i) we obtain
and an analogous computation proves the converse inequality. \(\square \)
We remark that in the geometrically linear setting one identifies the reference with the deformed configuration, hence the discussion above becomes largely irrelevant. The linearization procedure is based on considering deformations u close to the identity, in the sense that \(u(x)=x+\delta v(x)\), with v the scaled displacement and \(\delta \) the linearization parameter. One then introduces the strain measure \(\xi (x):=Dv(x)\), computes \(F_e(x)={\textrm{Id}}+\delta \xi (x)\) and \(\beta (x+\delta v(x))=({\textrm{Id}}+\delta \xi (x))^{-1}\). A Taylor series for \(\delta \rightarrow 0\), if all fields are regular, gives \(\beta (x)={\textrm{Id}}-\delta \xi (x)+O(\delta ^2)\), and in the linear theory the strain measure is identified with \(\xi (x)= -\frac{\beta (x)-{\textrm{Id}}}{\delta }\). In the presence of dislocations, the passage through u and v can only be done locally, but linearization still amounts to \(\xi =-\frac{\beta -{\textrm{Id}}}{\delta }\). Obviously \(\mathop {\textrm{curl}}\xi =-\frac{1}{\delta }\mathop {\textrm{curl}}\beta \) is then the easiest measure of the dislocation density. If one uses a quadratic energy the prefactor \(\delta \) can be dropped, and the minus sign amounts to a minor change in the definition of the Burgers vector.
In this paper we provide a unified mathematical approach for the linear and the nonlinear setting, using different assumptions on the energy density W presented in the next section.
3.2 Main assumptions
We introduce the class of dilute dislocations identified with a class of divergence-free measures concentrated on polyhedral curves.
Definition 3.2
Given two positive parameters \(\alpha ,h>0\) and an open set \(\Omega \subseteq \mathbb {R}^3\) we say that a polyhedral curve \(\gamma \subset {\overline{\Omega }}\) is \((h,\alpha )\)-dilute if it is the union of finitely many closed segments \(s_j\subset {\overline{\Omega }}\) such that
-
(i)
each \(s_j\) has length at least h;
-
(ii)
if \(s_j\) and \(s_i\) are disjoint then their distance is at least \(\alpha h\);
-
(iii)
if the segments \(s_j\) and \(s_i\) are not disjoint then they share an endpoint, and the angle between them is at least \(\alpha \);
-
(iv)
\(\gamma \) does not have endpoints inside \(\Omega \).
The set of \((h,\alpha )\)-dilute polyhedrals is denoted by \(P(h,\alpha )\).
The diluteness condition given in the Definition 3.2 allows to define the set of compatible configurations. The asymptotic analysis will be performed assuming that the diluteness parameters h and \(\alpha \) are much larger than the lattice spacing \({\varepsilon }\), in a sense made precise in (3.38) below.
Definition 3.3
A \((h,\alpha )\)-dilute dislocation distribution is a measure \(\mu \in {\mathcal {M}}^1(\Omega )\) of the form  such that \(\gamma \in P(h,\alpha )\).
such that \(\gamma \in P(h,\alpha )\).
Given a Bravais lattice \({\mathcal {B}}\) (i.e., a set of the form \({\mathcal {B}}=F\mathbb {Z}^3\) for some invertible matrix \(F\in \mathbb {R}^{3\times 3}\)), we denote by \({\mathcal {M}}^1_{\mathcal {B}}(\Omega )\) the set of measures \(\mu \in {\mathcal {M}}^1(\Omega )\) such that \(\theta \in {\mathcal {B}}\) \({\mathcal {H}}^1\)-almost everywhere on \(\gamma \).
We consider an elastic energy density W in one of two natural frameworks. To simplify notation in the presence of a mixed growth condition we define for \(p\in [1,2]\) the function \(\Phi _p:[0,\infty )\rightarrow [0,\infty )\), by
Assumption \(H^{\textrm{W}}_{\textrm{Finite}}\): In a geometrically nonlinear setting, \(W:\mathbb {R}^{3\times 3}\rightarrow [0,\infty )\) is minimized at the identity and is invariant under the right action of \({\textrm{SO}}(3)\),
We assume also that W is Borel, twice differentiable in a neighbourhood of \({\textrm{Id}}\), and
for some \(p\in (1,2]\) and \(c>0\).
Remark. If \(H^{\textrm{W}}_{\textrm{Finite}}\) holds, then the tensor
satisfies condition (2.1), and there is a modulus of continuity \(\omega :[0,\infty )\rightarrow [0,\infty )\) with \(\omega (\delta )\rightarrow 0\) as \(\delta \rightarrow 0\) such that
For any \(Q\in {\textrm{SO}}(3)\), using \(W(Q({\textrm{Id}}+A))=W(Q({\textrm{Id}}+A)Q^T)\) one obtains
where \(\mathbb {C}_Q\in \mathbb {R}^{3\times 3\times 3\times 3}_{\textrm{sym}}\) is defined from \(\mathbb {C}\) and Q by
It is easy to see that it also obeys condition (2.1).
Assumption \(H^{\textrm{W}}_{\textrm{Lin}}\): In a geometrically linear setting, \(W:\mathbb {R}^{3\times 3}\rightarrow [0,\infty )\) is minimized at zero and only depends on the symmetric part of its argument,
We assume also that W is Borel, twice differentiable in a neighbourhood of 0, and
for some \(p\in (1,2]\) and \(c>0\).
Remark. If \(H^{\textrm{W}}_{\textrm{Lin}}\) holds, then the tensor
satisfies condition (2.1).
It will be useful to have some properties of \(\Phi _p\). We denote by \(\Phi _p^{**}\) its convex envelope, which obeys
for some \(c_p>0\).
Remark 3.4
(i) The function \(\Phi _p\) for every \(\delta >0\) satisfies
In particular, with \(\delta =1\) we obtain
To prove (3.33), we distinguish two cases. If \(|a|\le 1\) and \(|b|\le 1\), then
Otherwise, we write
We recall that \(p-2\le 0\), and that in this case \(|a|+|b|\ge 1\). If \(|a|\le 1\), then \(|a|^2(|a|+|b|)^{p-2}\le |a|^2=\Phi _p(|a|)\). If \(|a|> 1\), then \(|a|^2(|a|+|b|)^{p-2}\le |a|^2|a|^{p-2}=|a|^p=\Phi _p(|a|)\). Therefore \(|a|^2(|a|+|b|)^{p-2}\le \Phi _p(|a|)\), and the same for b. This concludes the proof.
(ii) For any \(f\in L^p(\Omega ;\mathbb {R}^{3\times 3})\) there are \(a,b\in L^p(\Omega ;\mathbb {R}^{3\times 3})\) with \(|a|\le 1\) everywhere, \(|b|\ge 1\) wherever \(b\ne 0\), \(f=a+b\), and
To see this, it suffices to set \(a:=f\chi _{\{|f|\le 1\}}\), and \(b:=f-a\).
3.3 \(\Gamma \)-convergence to a line tension model
We now introduce a small parameter \({\varepsilon }>0\), which in this semidiscrete model represents the lattice spacing, and (given an open set \(\Omega \subseteq \mathbb {R}^3\) and a Bravais lattice \({\mathcal {B}}\subset \mathbb {R}^3\)) the class of admissible configurations
For a Borel set \(A\subseteq \Omega \) we define
and write briefly \(F_{\varepsilon }[\beta ]:=F_{\varepsilon }[\beta ,\Omega ]\). The asymptotic analysis will be performed for any diluteness parameters \(\alpha _{\varepsilon }\) and \(h_{\varepsilon }\) that obey
For pairs in the set of admissible configurations \({\mathcal {A}}^*_{\varepsilon }\) we shall use the following notion of convergence.
Definition 3.5
We say that \((\mu _{\varepsilon },\beta _{\varepsilon })\in {\mathcal {M}}_{{\varepsilon }{\mathcal {B}}}^1(\Omega )\times L^1(\Omega ;\mathbb {R}^{3\times 3})\) converges to \((\mu ,\eta ,Q) \in {\mathcal {M}}^1_{{\mathcal {B}}}(\Omega )\times L^1_{\textrm{loc}}(\Omega ;\mathbb {R}^{3\times 3}) \times {\textrm{SO}}(3) \) in finite kinematics with p growth if \(\frac{1}{{\varepsilon }}\mu _{\varepsilon }\) locally weak-* converges to \(\mu \), in the sense that
and there are \(Q_{\varepsilon }\in {\textrm{SO}}(3)\) such that \(Q_{\varepsilon }\rightarrow Q\) and
for \(q:=\frac{3}{2}\wedge p\).
We say that \((\mu _{\varepsilon },\beta _{\varepsilon })\in {\mathcal {M}}_{{\varepsilon }{\mathcal {B}}}^1(\Omega )\times L^1(\Omega ;\mathbb {R}^{3\times 3})\) converges to \((\mu ,\eta ) \in {\mathcal {M}}^1_{\mathcal {B}}(\Omega )\times L^1_{\textrm{loc}}(\Omega ;\mathbb {R}^{3\times 3}) \) in infinitesimal kinematics with p growth if (3.39) holds and there are skew-symmetric matrices \(S_{\varepsilon }\in \mathbb {R}^{3\times 3}_{\textrm{skew}}\) such that
The local weak-\(*\) convergence in (3.39) can be equivalently defined testing with elements of \(C^0_c(\Omega )\).
In what follows, for \(b\in {\mathcal {B}}\) and \(t\in S^2\), the function \(\psi _\mathbb {C}^{\textrm{rel}}(b,t)\) denotes the \({\mathcal {H}}^1\)-elliptic envelope of \(\psi _\mathbb {C}(b,t)\) and it is given by

In [14] it is proven that \(\psi _\mathbb {C}^{\textrm{rel}}\) provides the energy density of the relaxation of the line tension energy given in (2.31). By a change of variables, one easily sees that the same holds for the function \({\hat{\psi }}(b,t):=\psi (b,Qt)\), for any \(Q\in {\textrm{SO}}(3)\).
The main result of the paper is then the following compactness and \(\Gamma \)-convergence statement in the subcritical regime \(p<2\).
Theorem 3.6
Let \(\Omega \subset \mathbb {R}^3\) be a bounded Lipschitz set with connected boundary and assume that \((h_{\varepsilon },\alpha _{\varepsilon })\) obeys (3.38). Assume also that W obeys \(H^{\textrm{W}}_{\textrm{Finite}}\) for some \(p\in (1,2)\). Then the functionals
\(\Gamma \)-converge, with respect to the convergence in finite kinematics with p growth in the sense of Definition 3.5, to
if \((\mu ,\eta ,Q)\in {\mathcal {M}}^1_{{\mathcal {B}}}(\Omega )\times L^2(\Omega ;\mathbb {R}^{3\times 3}) \times {\textrm{SO}}(3)\),  and \(\mathop {\textrm{curl}}\eta =0\), and \(\infty \) otherwise, \(\mathbb {C}_Q\) as in (3.25) and (3.28), \(\psi _\mathbb {C}^{\textrm{rel}}\) as in (3.42).
and \(\mathop {\textrm{curl}}\eta =0\), and \(\infty \) otherwise, \(\mathbb {C}_Q\) as in (3.25) and (3.28), \(\psi _\mathbb {C}^{\textrm{rel}}\) as in (3.42).
Further, any sequence with \(F_{\varepsilon }^\textrm{subcr}[\mu _{\varepsilon },\beta _{\varepsilon }]\) bounded has a subsequence that converges in the same topology.
If instead W obeys \(H^{\textrm{W}}_{\textrm{Lin}}\), then the corresponding assertions hold with respect to convergence in infinitesimal kinematics with p growth, with (3.44) replaced by
if \((\mu ,\eta )\in {\mathcal {M}}^1_{{\mathcal {B}}}(\Omega )\times L^2(\Omega ;\mathbb {R}^{3\times 3})\),  and \(\mathop {\textrm{curl}}\eta =0\), and \(\infty \) otherwise, with \(\mathbb {C}\) as in (3.31).
and \(\mathop {\textrm{curl}}\eta =0\), and \(\infty \) otherwise, with \(\mathbb {C}\) as in (3.31).
We remark that there are several equivalent ways of treating the sequence of rotations \(Q_{\varepsilon }\rightarrow Q\). One simple observation is that by Lemma 3.1(iii), \(\psi _\mathbb {C}^{\textrm{rel}}(b,Qt)=\psi _{\mathbb {C}_Q}^{\textrm{rel}}(Q^Tb,t)\), which can be inserted in the second term of (3.44). One can also replace \(\mathbb {C}_Q\) by \(\mathbb {C}\) in the first term, if the fields are redefined accordingly; in order to keep the differential constraints one should also rotate the domain of integration. Specifically, given a sequence \((\mu _{\varepsilon },\beta _{\varepsilon }) \in {\mathcal {A}}^*_{\varepsilon }(\Omega )\) (defined as in (3.36)) that converges as above, for each \({\varepsilon }\) one considers the pair \(({\hat{\mu }}_{\varepsilon },{\hat{\beta }}_{\varepsilon })\in {\mathcal {A}}^*_{\varepsilon }(Q_{\varepsilon }\Omega )\) defined by
Then \(F_{\varepsilon }^\textrm{subcr}[{\hat{\mu }}_{\varepsilon },{\hat{\beta }}_{\varepsilon },Q_{\varepsilon }\Omega ]= F_{\varepsilon }^\textrm{subcr}[\mu _{\varepsilon },\beta _{\varepsilon },\Omega ]\),  , with \({{\hat{t}}}(y):=Q t(Q^Ty)\), and setting \({\hat{\eta }}(y):=Q\eta (Q^Ty)Q^T\) condition (3.40) becomes
, with \({{\hat{t}}}(y):=Q t(Q^Ty)\), and setting \({\hat{\eta }}(y):=Q\eta (Q^Ty)Q^T\) condition (3.40) becomes
(the fact that the domain changes along the sequence is not a problem for \(L^q_{\textrm{loc}}\) convergence since \(Q_{\varepsilon }\rightarrow Q\)). The limiting functional in (3.44) then takes the form
with  and \({{\hat{t}}}\) the unit tangent to \({\hat{\gamma }}:=Q\gamma \). For simplicity we stick to the formulation in which the integration domain \(\Omega \) is fixed.
and \({{\hat{t}}}\) the unit tangent to \({\hat{\gamma }}:=Q\gamma \). For simplicity we stick to the formulation in which the integration domain \(\Omega \) is fixed.
Related results have been proven before in [18, 27]. We present here a more general argument that permits to prove Theorem 3.6 in a unified way for finite and infinitesimal kinematics. Our argument also provides the \(\Gamma \)-convergence result for different types of core regularizations, which are needed in the case \(p=2\) and are discussed in Sect. 3.4.
In Sect. 4 we give a unified treatment for the cell problem formula. Building on this, compactness and lower bound are then proven in Sect. 5. In particular, we shall introduce in (5.21) an auxiliary functional, for which we will prove the lower bound result. The auxiliary functional is chosen so that, after rescaling, it is below \(F_{\varepsilon }^\textrm{subcr}\), with corresponding bounds holding for other regularizations as discussed below, and then all results follow at once. Analogously, in Sect. 6, the upper bound will be proven for a second auxiliary functional defined in (6.32), which after rescaling is larger than \(F_{\varepsilon }^\textrm{subcr}\), up to a small error term which can be controlled. Moreover we show that the recovery sequence needed for this upper bound has a good decay near the dislocation line, so that different types of core regularization do not change its energy asymptotically.
In Sect. 7 we will collect the proofs of the \(\Gamma \)-convergence results (Theorems 3.6 and 3.10 below) that are obtained as straightforward consequences of the results proved in Sects. 4, 5 and 6. All proofs are given explicitly in the case \(H^{\textrm{W}}_{\textrm{Finite}}\). The case \(H^{\textrm{W}}_{\textrm{Lin}}\) is very similar therefore we only point out a few relevant differences.
3.4 Extension to different core regularizations
In the case of quadratic growth (in the sense \(p=2\)) one needs a different regularization and possibly a different set of admissible configurations. This requires different convergence properties and compactness results. The \(\Gamma \)-convergence result instead can be obtained as a consequence of the arguments developed to prove Theorem 3.6.
In the literature one considers configurations \((\mu , \beta )\in {\mathcal {M}}^1(\Omega )\times L^1(\Omega ;\mathbb {R}^{3\times 3})\) with \(\mathop {\textrm{curl}}\beta = \mu \) and the associated energy
where \((\mathop {\textrm{supp}}\mu )_{\varepsilon }:=\{x\in \Omega :{\textrm{dist}}(x,\mathop {\textrm{supp}}\mu )<{\varepsilon }\}\). This is known as the core-region approach. Alternatively, one can replace the condition \(\mathop {\textrm{curl}}\beta =\mu \) with a different condition that only involves the behavior of \(\beta \) away from the singularity, that we will call \(\rho \)-compatibility of the pair \((\mu ,\beta )\), see Definition 3.7 below. Since the energy (3.49) does not depend on the value of \(\beta \) inside the core region, one can show that the asymptotics of the rescaled energy does not depend on the set of admissible configurations chosen. Nevertheless for the compactness result an extension argument is needed, which goes beyond the scope of the present work. A third option is a regularization via mollification of the measure, which smears out the singularity on a scale \({\varepsilon }\).
Definition 3.7
Let \(\Omega \subset \mathbb {R}^3\) be a bounded Lipschitz set, with connected boundary, \(\rho >0\). A pair \((\mu ,\beta )\in {\mathcal {M}}^1(\Omega )\times L^1(\Omega {\setminus } (\mathop {\textrm{supp}}\mu )_\rho ;\mathbb {R}^{3\times 3})\) is \(\rho \)-compatible if there are an extension \({\tilde{\mu }}\in {\mathcal {M}}^1(\mathbb {R}^3)\) of \(\mu \) and \(\beta _0\in L^{1}(\Omega ;\mathbb {R}^{3\times 3})\) such that \(\mathop {\textrm{curl}}\beta _0=0\) in \(\Omega \) and \(\beta =\beta ^{{\tilde{\mu }}}+\beta _0\) in \(\Omega {\setminus } (\mathop {\textrm{supp}}{\tilde{\mu }})_\rho \), where \(\beta ^{{\tilde{\mu }}}\) is the solution obtained from \({\tilde{\mu }}\) via Theorem 2.2.
We recall that by [14, Lemma 2.3]) for any \(\mu \in {\mathcal {M}}_{{\varepsilon }{\mathcal {B}}}^1(\Omega )\) there exists an extension \({\tilde{\mu }}\in {\mathcal {M}}_{{\varepsilon }{\mathcal {B}}}^1(\mathbb {R}^3)\) such that  and \(|{\tilde{\mu }}|(\mathbb {R}^3)\le c(\Omega )|\mu |(\Omega )\). We remark that the construction in the proof of [14, Lemma 2.3] uses, without stating it, that the complement of \(\Omega \) is connected. This is equivalent to connectedness of the boundary. The assumption is necessary, as the example \(\Omega =B_2{\setminus } B_1\), with
and \(|{\tilde{\mu }}|(\mathbb {R}^3)\le c(\Omega )|\mu |(\Omega )\). We remark that the construction in the proof of [14, Lemma 2.3] uses, without stating it, that the complement of \(\Omega \) is connected. This is equivalent to connectedness of the boundary. The assumption is necessary, as the example \(\Omega =B_2{\setminus } B_1\), with  shows.
shows.
We define, for \({\varepsilon }>0\) and \(\rho >0\),
and
Here \(\varphi _{\varepsilon }(x):={\varepsilon }^{-3}\varphi (x/{\varepsilon })\) is a fixed mollifier at scale \({\varepsilon }\); as usual \(\varphi \in C^\infty _c(B_1;[0,\infty ))\) and \(\Vert \varphi \Vert _{L^1}=1\).
Lemma 3.8
For any bounded Lipschitz set \(\Omega \) with connected boundary and \({\varepsilon }>0\),
-
(i)
\({\mathcal {A}}^{\textrm{core}}_{\rho ,{\varepsilon }}\subseteq {\mathcal {A}}^{\textrm{core}}_{\rho ',{\varepsilon }}\) for every \(\rho '\ge \rho \);
-
(ii)
\({\mathcal {A}}_{\varepsilon }^\textrm{moll}\subseteq {\mathcal {A}}^{\textrm{core}}_{\rho ,{\varepsilon }}\) for every \(\rho \ge {\varepsilon }\);
-
(iii)
\({\mathcal {A}}^*_{\varepsilon }\subseteq {\mathcal {A}}^{\textrm{core}}_{\rho ,{\varepsilon }}\) for every \(\rho >0\).
Proof
(i) is immediate from the definition.
(ii): Let \((\mu ,\beta )\in {\mathcal {A}}_{\varepsilon }^\textrm{moll}\), and select an extension \({\tilde{\mu }}\) as in the definition of \({\mathcal {A}}_{\varepsilon }^\textrm{moll}\). We define \(\beta _1:=\beta ^{{\tilde{\mu }}*\varphi _{\varepsilon }}- \beta ^{{\tilde{\mu }}}\), and fix \({\varepsilon }'\in (0,{\varepsilon })\) such that \(\mathop {\textrm{supp}}\varphi _{\varepsilon }\subset B_{{\varepsilon }'}\). By the integral representation in (2.6) we have that \(\beta _1\in C^\infty (\mathbb {R}^3{\setminus } (\mathop {\textrm{supp}}{\tilde{\mu }})_{{\varepsilon }'};\mathbb {R}^{3\times 3})\). We show that \(\beta _1\) is exact, in the sense that the circulation on every closed curve \(\gamma \subset \mathbb {R}^3{\setminus } (\mathop {\textrm{supp}}{\tilde{\mu }})_{{\varepsilon }'}\) vanishes,
To see this, we observe that (again by (2.6)) \(\beta ^{{\tilde{\mu }}*\varphi _{\varepsilon }}=\beta ^{{\tilde{\mu }}}*\varphi _{\varepsilon }\), which implies
Since \(\mathop {\textrm{curl}}\beta ^{{\tilde{\mu }}}=0\) in \(\mathbb {R}^3{\setminus } \mathop {\textrm{supp}}{\tilde{\mu }}\), and \(\gamma -z\subset \mathbb {R}^3{\setminus } \mathop {\textrm{supp}}{\tilde{\mu }}\) for all \(z\in B_{{\varepsilon }'}\), the last integrand does not depend on z. Therefore
which proves (3.52). In turn, this implies that there is \(u_1\in C^\infty (\mathbb {R}^3{\setminus } ({\mathop {\textrm{supp}}{\tilde{\mu }}})_{{\varepsilon }'};\mathbb {R}^3)\) such that \(\beta _1=Du_1\) in this set. We now select \(\theta \in C^\infty _c([0,{\varepsilon }))\) such that \(\theta =1\) on \([0,{\varepsilon }']\), and define \(u_0\in W^{1,\infty }_{\textrm{loc}}(\mathbb {R}^3;\mathbb {R}^3)\) by
At this point we define \(\beta _0:=Du_0+\beta -\beta ^{{\tilde{\mu }}*\varphi _{\varepsilon }} {\in L^1(\Omega ;\mathbb {R}^{3\times 3})}\). From \(\mathop {\textrm{curl}}\beta =\varphi _{\varepsilon }*{\tilde{\mu }}\) in \(\Omega \) we obtain \(\mathop {\textrm{curl}}\beta _0=0\) in \(\Omega \); from \(Du_0=Du_1= \beta ^{{\tilde{\mu }}*\varphi _{\varepsilon }}- \beta ^{{\tilde{\mu }}}\) in \(\Omega {\setminus } (\mathop {\textrm{supp}}{\tilde{\mu }})_{\varepsilon }\) we obtain \(\beta =\beta ^{{{\tilde{\mu }}}}+\beta _0\) in \(\Omega {\setminus } (\mathop {\textrm{supp}}{\tilde{\mu }})_{\varepsilon }\). Hence \(\beta \in {\mathcal {A}}^{\textrm{core}}_{{\varepsilon },{\varepsilon }}\subseteq {\mathcal {A}}^{\textrm{core}}_{\rho ,{\varepsilon }}\) for all \(\rho \ge {\varepsilon }\).
(iii): Let \((\mu ,\beta )\in {\mathcal {A}}^*_{\varepsilon }\), and let \({\tilde{\mu }}\in {\mathcal {M}}^1(\mathbb {R}^3)\) be an extension of \(\mu \). Setting \(\beta _0:=\beta -\beta ^{{\tilde{\mu }}}\), one sees that \(\mathop {\textrm{curl}}\beta _0=\mathop {\textrm{curl}}(\beta -\beta ^{{\tilde{\mu }}})=0\) in \(\Omega \), which concludes the proof. \(\square \)
In the set of admissible configurations \({\mathcal {A}}^\textrm{core}_{\rho _{\varepsilon },{\varepsilon }}\) (with \(\rho _\varepsilon \rightarrow 0\)) we introduce the following convergence, which is a variant of the one in Definition 3.5. The key difference is that now the value of \(\beta _{\varepsilon }\) in the core region \((\mathop {\textrm{supp}}\mu _{\varepsilon })_{\rho _{\varepsilon }}\) is ignored.
Definition 3.9
We say that \((\mu _{\varepsilon },\beta _{\varepsilon })\in {\mathcal {M}}_{{\varepsilon }{\mathcal {B}}}^1(\Omega )\times L^1(\Omega ;\mathbb {R}^{3\times 3})\) converges to \((\mu ,\eta ,Q) \in {\mathcal {M}}^1_{\mathcal {B}}(\Omega )\times L^1_{\textrm{loc}}(\Omega ;\mathbb {R}^{3\times 3}) \times {\textrm{SO}}(3) \) in finite kinematics with p growth and radius \(\rho _{\varepsilon }\) if \(\rho _{\varepsilon }\rightarrow 0\),
and there are \(Q_{\varepsilon }\in {\textrm{SO}}(3)\) such that \(Q_{\varepsilon }\rightarrow Q\) and
for \(q:=\frac{3}{2}\wedge p\).
We say that \((\mu _{\varepsilon },\beta _{\varepsilon })\in {\mathcal {M}}_{{\varepsilon }{\mathcal {B}}}^1(\Omega )\times L^1(\Omega ;\mathbb {R}^{3\times 3})\) converges to \((\mu ,\eta ) \in {\mathcal {M}}^1_{\mathcal {B}}(\Omega )\times L^1_{\textrm{loc}}(\Omega ;\mathbb {R}^{3\times 3}) \) in infinitesimal kinematics with p growth and radius \(\rho _{\varepsilon }\) if \(\rho _{\varepsilon }\rightarrow 0\), (3.56) holds, and there are skew-symmetric matrices \(S_{\varepsilon }\in \mathbb {R}^{3\times 3}_{\textrm{skew}}\) such that
We then have the following \(\Gamma \)-convergence result which includes the critical case \(p=2\).
Theorem 3.10
Let \(\Omega \subset \mathbb {R}^3\) be a bounded Lipschitz set with connected boundary and assume that \((h_{\varepsilon },\alpha _{\varepsilon })\) obeys (3.38). Assume also that W obeys \(H^{\textrm{W}}_{\textrm{Finite}}\) for some \(p\in (1,2]\). Let \(\rho _{\varepsilon }\rightarrow 0\) be such that \(\rho _{\varepsilon }\ge {\varepsilon }\) and
-
(i)
The functionals
$$\begin{aligned} F_{\varepsilon }^*[\mu ,\beta ]:= {\left\{ \begin{array}{ll} F_{\varepsilon }[\beta ,\Omega {\setminus }{(\mathop {\textrm{supp}}\mu )_{\rho _{\varepsilon }}}], &{} \text { if}\, (\mu ,\beta )\in {\mathcal {A}}_{\varepsilon }^*,\ \mu \,\text {is}\, (h_{\varepsilon },\alpha _{\varepsilon })\text {-dilute,}\\ \infty , &{} \text { otherwise,} \end{array}\right. } \end{aligned}$$(3.60)\(\Gamma \)-converge to the functional \(F^{\textrm{Finite}}\) defined in (3.44) with respect to the convergence in finite kinematics with p growth and radius \(\rho _{\varepsilon }\) in Definition 3.9.
-
(ii)
The same holds also for the functionals
$$\begin{aligned} F_{\varepsilon }^\textrm{core}[\mu ,\beta ]:= {\left\{ \begin{array}{ll} F_{\varepsilon }[\beta ,\Omega {\setminus }{(\mathop {\textrm{supp}}\mu )_{\rho _{\varepsilon }}}], &{} \text { if}\, (\mu ,\beta )\in {\mathcal {A}}^\textrm{core}_{{\rho _{\varepsilon },{\varepsilon }}}\\ &{}\text { and }\,\mu \,\text {is}\, (h_{\varepsilon },\alpha _{\varepsilon })\,\text {-dilute},\\ \infty , &{} \text { otherwise}. \end{array}\right. } \end{aligned}$$(3.61) -
(iii)
The same holds also for the functionals
$$\begin{aligned} F_{\varepsilon }^\textrm{moll}[\mu ,\beta ]:= {\left\{ \begin{array}{ll} F_{\varepsilon }[\beta ,\Omega ], &{} \text { if}\, (\mu ,\beta )\in {\mathcal {A}}^\textrm{moll}_{\varepsilon },\ \mu \,\text {is}\, (h_{\varepsilon },\alpha _{\varepsilon })\,\text {-dilute,}\\ \infty , &{} \text { otherwise} \end{array}\right. } \end{aligned}$$(3.62)with respect to the convergence of Definition 3.5.
If instead W obeys \(H^{\textrm{W}}_{\textrm{Lin}}\), then the corresponding assertions hold with respect to convergence in infinitesimal kinematics, with \(F^{\textrm{Finite}}\) replaced by \(F^{\textrm{Lin}}\) defined in (3.45).
We remark that this result does not contain a compactness statement. This requires different arguments and will be addressed elsewhere. Only in the case of assertion (iii) compactness can be obtained from the rigidity estimate as in the case of Theorem 3.6.
4 Straight dislocations in a cylinder
This section deals with the cell problem, which describes a single straight dislocation in a cylinder. We first present in Lemma 4.1 a rigidity estimate with mixed growth for an hollow cylinder, then in Lemma 4.2 the standard coercivity statement which shows the origin of the logarithmic divergence. Afterwards, in Proposition 4.3, we prove a lower bound, relating the energy in a cylinder around a straight dislocation to the line-tension energy \(\psi _\mathbb {C}\) defined in (2.15).
4.1 Rigidity and coercivity
The first result shows that the constant in the rigidity estimate with mixed growth from [9, Theorem 1.1] for domains \(T_h^{R,r}\) with \(r\le \frac{1}{2} R\) and \(R\le h\) can be estimated with \(h^2/R^2\), and in particular does not depend on r. We recall the definition of the tubes in (2.28) and (2.29), and the definition of the function \(\Phi _p\) in (3.22) and its properties (see Remark 3.4).
Lemma 4.1
For any \(p\in (1,2]\) there is \(c=c(p)>0\) such that for any \(r,R,h>0\) with \(2r\le R\le h\), any \(Q'\in {\textrm{SO}}(3)\), and any \(\beta \in L^1(Q'T_h^{R,r};\mathbb {R}^{3\times 3})\) with \(\mathop {\textrm{curl}}\beta =0\) there are \(Q\in {\textrm{SO}}(3)\) such that
and \(S\in \mathbb {R}^{3\times 3}_{\textrm{skew}}\) such that
Proof
We first show that it suffices to prove both assertions for \(Q'={\textrm{Id}}\). Indeed, given \(\beta \in L^1(Q'T_h^{R,r};\mathbb {R}^{3\times 3})\) one defines \({\hat{\beta }}\in L^1(T_h^{R,r};\mathbb {R}^{3\times 3})\) by
Then (by Lemma 3.1(i)) \(\mathop {\textrm{curl}}{\hat{\beta }}=0\), \({\textrm{dist}}({\hat{\beta }}(x),{\textrm{SO}}(3))={\textrm{dist}}(\beta (Q'x),{\textrm{SO}}(3))\), \(|{\hat{\beta }}+{\hat{\beta }}^T|(x) =|\beta +\beta ^T|({Q'x})\), and \(|{\hat{\beta }}-A|(x)=|\beta -Q'AQ'^T|(Q'x)\) for any \(A\in \mathbb {R}^{3\times 3}\). Therefore the assertions for \({\hat{\beta }}\) translate in the desired estimates for \(\beta \). In the rest of the proof we deal with \(Q'={\textrm{Id}}\).
By scaling we can assume \(R=1\). We next show that it suffices to prove both assertions for \(h=1\). Indeed, given \(h>1\) we fix \(0=z_0<z_1<\dots <z_N=h-1\) such that \(z_{i}\le z_{i-1}+\frac{1}{2}\) for \(1\le i\le N\), \(z_{i}\ge z_{i-2}{+ \frac{1}{2}}\) for \(2\le i\le N\), and \(N= \lceil 2h-2\rceil \) (for example, \(z_i=i/2\) for \(i<N\), and \(z_N=h-1\)). We then apply (4.1) to each cylinder \(T_1^{1,r}+z_ie_3\) and obtain matrices \(Q_i\in {\textrm{SO}}(3)\) such that
By (3.34),
for every \(\xi \in \mathbb {R}^{3\times 3}\). From \(r\le \frac{1}{2}\) and \(z_i\le z_{i-1}+\frac{1}{2}\) we obtain \({\mathcal {L}}^3((T_1^{1,r}+z_ie_3)\cap (T_1^{1,r}+z_{i-1}e_3))\ge \frac{3}{8}\pi \), so that
Using \(z_{i}\ge z_{i-2}{+ \frac{1}{2}}\) we see that the overlap is finite, hence
By (3.33) with \(\delta =1/N\), for \(1\le i\le N\) we have
and iterating
Therefore, using \(i\le N\) and (4.7),
for each \(i\in \{0,\dots , N\}\) and, since \(N\le 2h\), we conclude, applying (3.34), (4.10) and (4.4),
It remains to prove (4.1) in the case \(R=h=1\), \(Q'={\textrm{Id}}\). Assume first that \(r=2^{-N}\) for some integer \(N\ge 1\). If \(N=1\) then, since \(\mathop {\textrm{curl}}\beta =0\), using [9, Theorem 1.1] on two overlapping simply connected subsets of \(T_1^{1,1/2}\) and then (3.34) one obtains that there is \(Q\in {\textrm{SO}}(3)\) such that
The argument is the same in the linear case, using [9, Theorem 2.1]. For the same reason, for any \(\rho >0\) and any \(\beta \in L^1(T_\rho ^{\rho ,\rho /4};\mathbb {R}^{3\times 3})\) with \(\mathop {\textrm{curl}}\beta =0\) there is \(Q\in {\textrm{SO}}(3)\) with
by scaling the constant does not depend on \(\rho \).
If instead \(N\ge 2\) we divide \(T_1^{1,r}\) into dyadic sets \(C_{i,j}\) of the form \( T_\rho ^{\rho ,\rho /4}\). More precisely we set
with \(R_i:=2^{-i}\), \(i=1,\dots , N-2\) and \(j=0,\dots ,2^i-1\). We now apply (4.13) to each \(C_{i,j}\) and find \(Q_{i,j}\in {\textrm{SO}}(3)\) such that
with an universal constant. Notice that \({\mathcal {L}}^3(C_{i,j}\cap C_{i-1,k_j})\ge c R_i^3\) for \(i\ge 1\) and
and \(j=0,\dots ,2^i-1\). Then by (3.34), arguing as in (4.5)–(4.6)
so that from (3.34) we have
For every i let
Obviously \(a_0=0\). Moreover by (4.15)
In each sum, \(k_j\) takes twice each value in \(\{0,\dots , 2^{i-1}-1\}\). Recalling that \(R_{i-1}=2R_i\), for \(i\ge 1\) we obtain
with \(E_i:=\sum _{j=0}^{2^i-1}E_{i,j}\), for every \(i\ge 0\). By induction we obtain
for every \(i\ge 1\). We conclude that
By (3.34), (4.16), (4.14) and (4.18) we obtain
with \(E:=\sum _{i=0}^{N-2}E_i\). Again by scaling the above inequality holds with the same constant in \(T_{2^{N}\rho }^{2^N\rho ,\rho }\) for any \(\rho >0\) and \(N\in \mathbb {N}\).
Finally if \(r\in (0,\frac{1}{2}]\) is arbitrary we select \(N\in \mathbb {N}\) such that \(\frac{1}{2} <2^Nr\le 1\). Since \(r\le \frac{1}{2}\), we have \(N\ge 1\), and therefore \(2^{-N}\le \frac{1}{2}< 2^Nr\). This implies
For the same reason,
Therefore
We apply the rigidity estimate to each of these three cylinders separately and obtain rotations \(Q^1\), \(Q^2\), \(Q^3\). As the overlap between them is not uniformly controlled we introduce a fourth cylinder. We let \(\rho :=\frac{2^{-N}+r}{2}\) be the average between the two values of the inner radius and set
We then apply the rigidity estimate also to \(C^4\), and obtain another rotation \(Q^4\). From \(\frac{1}{2}<2^Nr\le 1\) we obtain \(\frac{3}{4}<2^N\rho \le 1\) hence \(2^N\rho -2^{-N}>\frac{1}{4}\). This implies \({\mathcal {L}}^3(C^1\cap C^4)\ge c >0\). Similarly, \(2^Nr-\rho \ge \frac{1}{8}\) and \(2^Nr-(\frac{1}{2}-2^{N-1}\rho )\ge \frac{1}{8}\) show that \({\mathcal {L}}^3(C^i\cap C^4)\ge c >0\) for \(i=2,3\). Therefore we can conclude using the triangular inequality (3.34). \(\square \)
Lemma 4.2
Assume that W satisfies \(H^{\textrm{W}}_{\textrm{Finite}}\) or \(H^{\textrm{W}}_{\textrm{Lin}}\) for some \(p\in (1,2]\). There is \(c>0\) such that for any \(0<{\varepsilon }\le r<R\le h\), with \(2r\le R\), \(b\in {\mathcal {B}}\), \(t\in S^2\), and \(\beta \in L^1(Q_t {T}^{R}_h;\mathbb {R}^{3\times 3})\) such that

we have
The constant depends only on W, p, and \({\mathcal {B}}\).
Proof
We prove the statement for the case \(h=R\). If \(h> R\), it suffices to apply this bound on each of the \(\lfloor h/R\rfloor \) disjoint subsets of \(T_h^{R,r}\) which have the same shape as \(T_R^{R,r}\), and then to use that \(h/R\le 2\lfloor h/R\rfloor \). For \(b=0\) there is nothing to prove. Recalling that \(b\in {\mathcal {B}}\), we see that we can assume \(|b|\ge c>0\).
Since \(\mathop {\textrm{curl}}\beta =0\) in \(T_R^{R,r}\), by \(H^{\textrm{W}}_{\textrm{Finite}}\) and Lemma 4.1 there is a rotation \(Q\in {\textrm{SO}}(3)\) such that
In the linear case the same holds with \(S\in \mathbb {R}^{3\times 3}_{\textrm{skew}}\).
Moreover by condition (4.19), for every circle C with radius \(\rho \in (r,R)\), centered in a point of the segment (0, Rt), and contained in the plane orthogonal to t,
By monotonicity and Jensen’s inequality, we then have
where \(\Phi _p^{**}\) is the convex envelope of \(\Phi _p\). Integrating over all circles C by Fubini’s theorem we easily get
If \(p=2\) then \(\Phi _2^{**}(t)=\Phi _2(t)=|t|^2\) and integrating the left-hand side concludes the proof.
It remains to estimate the left-hand side of (4.24) for \(p<2\). By (3.32) there are \(\eta \), \(\eta '>0\) such that
If \({\varepsilon }|b|\le 2r \), we obtain
If \({\varepsilon }|b|\ge R\), we have
We observe that \(s^{2-p}\ge (2-p)\log s\) for all \(s>0\). Using that \({\varepsilon }\le r<R\),
Combining these two concludes the proof in this case.
Finally we consider the case \(2r<{\varepsilon }|b|< R\). We have
Estimating the two integrals as in (4.25) and (4.26) and observing that for some \(c_p>0\) it holds, since \(|b|\ge \log |b|\),
with \({\varepsilon }\le r\) we conclude. \(\square \)
4.2 Lower bound for a cylinder
We present in Proposition 4.3 the key estimate for the lower bound. We work in a unified framework able to treat jointly the case of finite and infinitesimal kinematics and therefore frame the problem via a generic energy density V. In the rest of the paper we use the results of this section only via Corollary 4.4.
Proposition 4.3
Assume that W satisfies \(H^{\textrm{W}}_{\textrm{Finite}}\) or \(H^{\textrm{W}}_{\textrm{Lin}}\) for some \(p\in (1,2]\). Define \(V(F):=W({\textrm{Id}}+{{{\tilde{Q}}}}F{{{\tilde{Q}}}}^T)\) for some \({{{\tilde{Q}}}}\in {\textrm{SO}}(3)\) in the first case, and \(V:=W\) in the second case. Let \(\mathbb {C}^V:=D^2V(0)\), \(c_K>0\), and \(\ell _0>0\). There is a nondecreasing function \(\sigma :(0,\infty )\rightarrow (0,\infty )\), with \(\lim _{s\rightarrow 0}\sigma (s)=0\), depending only on V, p, \(c_K\) and \(\ell _0\) with the following property: if \(0<2r\le R\le h\), \({\varepsilon }>0\), \(b\in \mathbb {R}^3\), \(t\in S^2\), \(\xi \in L^1(Q_t {T}^{R}_h;\mathbb {R}^{3\times 3})\) obey \(|b|\ge \ell _0\),
and

then necessarily
Corollary 4.4
Assume that W satisfies \(H^{\textrm{W}}_{\textrm{Finite}}\) for some \(p\in (1,2]\). Let \(\mathbb {C}:=D^2W({\textrm{Id}})\) and let \({\mathcal {B}}\) be a Bravais lattice. There is a nondecreasing function \({\tilde{\sigma }}:(0,\infty )\rightarrow (0,\infty )\), with \(\lim _{s\rightarrow 0}{\tilde{\sigma }}(s)=0\), depending only on W, \({\mathcal {B}}\) and p, with the following property: if \(0<2r\le R\le h\), \({\varepsilon }>0\), \(b\in {\mathcal {B}}\), \(t\in S^2\), \(\beta \in L^1(Q_t {T}^{R,r}_h;\mathbb {R}^{3\times 3})\) such that

(in the sense of Definition 3.7, for the domain \(Q_tT^R_h\)) and \(Q\in {\textrm{SO}}(3)\) then
Assume that W satisfies \(H^{\textrm{W}}_{\textrm{Lin}}\) for some \(p\in (1,2]\) and let \(\mathbb {C}:=D^2W(0)\). Then the same holds by replacing (4.32) with
Proof
Assume \(H^{\textrm{W}}_{\textrm{Finite}}\) holds. Without loss of generality, \(R\le h\le 2R\). Otherwise we decompose the cylinder in \(\lfloor h/R\rfloor \) pieces with height \(h'\in [R,2R)\), apply the result to each of them and sum. By r-compatibility, there are an extension \({\tilde{\mu }}\in {\mathcal {M}}^1(\mathbb {R}^3)\) of \(\mu \) and \(\beta _0\in L^{1}(Q_t T^{R}_h;\mathbb {R}^{3\times 3})\) with \(\mathop {\textrm{curl}}\beta _0=0\) in \(Q_t T^{R}_h\) and \(\beta =\beta ^{{\tilde{\mu }}}+\beta _0\) in \(Q_t T^{R,r}_h\). We use \(\beta ^{{\tilde{\mu }}}+\beta _0\) to define an extension \(\beta \in L^1(Q_t T^{R}_h;\mathbb {R}^{3\times 3})\) such that

By Lemma 2.5 there is \(c_u>0\) such that \(\psi _\mathbb {C}(b,t)\le c_u |b|^2\) for all b and t. If \(\int _{Q_t {T}^{R,r}_h} W(\beta ) dx\ge c_u {\varepsilon }^2\,h |b|^2 \log \frac{R}{r}\), we are done. Therefore we can assume the converse inequality holds. By the rigidity estimate in Lemma 4.1 and (3.24), there is a rotation \(Q_*\in {\textrm{SO}}(3)\) such that
We define
so that \(V(\xi )= W(\beta Q_*^T)=W(\beta )\) and \(D^2V(0)=\mathbb {C}_{Q^*}\), which was defined from \(\mathbb {C}=D^2W({\textrm{Id}})\) in (3.28). We observe that (4.34) gives

which is (4.29) with \(Q_*^Tb\) in place of b. Equation (4.35) implies (4.28) with \(c_K:=cc_u\), which depends only on \(\mathbb {C}\). By Proposition 4.3 with \(\ell _0:=\min \{|b|: b\in {\mathcal {B}}{\setminus }\{0\}\}\) and the above estimates we obtain
By Lemma 3.1(iii), \(\psi _{\mathbb {C}_{Q^*}}(Q_*^Tb,t)=\psi _\mathbb {C}(b,Q_*t)\). By Lemma 2.5(iii) there is \(c>0\), depending only on \(\mathbb {C}\), such that
which implies
Therefore
From (4.35), treating separately the part with \(|\beta -Q_*|<1\) and the one with \(|\beta -Q_*|\ge 1\), we have
where \(p'\) is the conjugate of p (i.e., \(p'=\frac{p}{p-1}\)). Therefore, recalling that \(h\in [R,2R]\) and that \(\log t\le t^2\) for all \(t>0\),
Plugging (4.43) into (4.41) we easily obtain (4.32).
The proof of (4.33) is similar but simpler. Indeed, one obtains from Lemma 4.1 a matrix \(S_*\in \mathbb {R}^{3\times 3}_{\textrm{skew}}\) with the property corresponding to (4.35). One then sets \(\xi :=\beta -S_*\), which obeys \(\mathop {\textrm{curl}}\xi =\mathop {\textrm{curl}}\beta \). Therefore Proposition 4.3 gives, using \(V(\xi )=W(\xi )=W(\beta )\), (4.38) with \(\psi _\mathbb {C}(b,t)\) instead of \(\psi _{\mathbb {C}_{Q^*}}(Q_*^Tb,t)\), and (4.33) follows. \(\square \)
Proof of Proposition 4.3
We first show that there is \(c\ge 1\) such that
To prove this, assume first \(H^{\textrm{W}}_{\textrm{Finite}}\), and to shorten notation let \(a':={{{\tilde{Q}}}}a{{{\tilde{Q}}}}^T\), \(b':={{{\tilde{Q}}}}b{{{\tilde{Q}}}}^T\). From (3.24) we obtain
Using \({\textrm{dist}}({\textrm{Id}}+a'+b',{\textrm{SO}}(3))\le {\textrm{dist}}({\textrm{Id}}+a',{\textrm{SO}}(3))+|b'|\), monotonicity of \(\Phi _p\), (3.34) and then (3.24) again we have
and then (4.44) follows.
If \(H^{\textrm{W}}_{\textrm{Lin}}\) holds, one similarly computes using (3.30) and (3.34)
This concludes the proof of (4.44).
We reason by contradiction and assume that there exist \(\rho >0\) and sequences \(r_j\), \(R_j\), \(h_j\), \({\varepsilon }_j\), \(b_j\), \(t_j\), \(\xi _j\) as in the statement such that, writing \(Q_j:=Q_{t_j}\),
and
Since \(\psi _{\mathbb {C}^V}\) is positively two-homogeneous in the first argument (see (2.15) and (2.16), or [18, Lemma 5.1(iii)]),
After passing to a subsequence, we can assume that \(\frac{b_j}{|b_j|}\rightarrow b_*\) and \(Q_j\rightarrow Q_*\), for some \(b_*\in S^2\), \(Q_*\in {\textrm{SO}}(3)\); this implies \(t_j=Q_je_3\rightarrow t_*:=Q_*e_3\). By continuity of \(\psi _{\mathbb {C}^V}\) (which follows from (2.15) and (2.16)),
Choose now \(\lambda >0\) such that \(\lambda c_K\le \rho \psi _{\mathbb {C}^V}(b_*, t_*)\). By (4.52) and (4.49),
Let \(\delta \in (0,\frac{1}{2}]\) be fixed. We observe that the sets
for \(k\in \mathbb {N}\cap [1, (1-\delta )\frac{\log R_j/r_j}{\log 1/\delta }-1]\), \(i\in \mathbb {N}\cap [0, \frac{h_j}{\delta ^k R_j}-1]\) are disjoint and contained in \({Q_j} {T}^{R_j,r_j }_{h_j}\). In particular for any such k we have
We choose \(k_j\) (depending on j) such that
and then \(i_j\) (depending on j) with
Inserting (4.57) in (4.53) and taking the limit, using \(R_j/r_j\rightarrow \infty \) and that \(h_j\ge R_j\) and \(k_j\ge 1\) imply \(\lfloor \frac{h_j}{\delta ^{k_j} R_j} \rfloor \ge \frac{h_j}{\delta ^{k_j} R_j} (1-\delta )\), we obtain
We now rescale to a fixed tube \({T}_1^{1,\delta }\). As in the entire proof, the maps are defined and integrable over the entire cylinder \(T^1_1\), but the estimates are only on the restriction to the tube \(T^{1,\delta }_1\). Precisely, we define \({\bar{\xi }}_j\in L^1({T}_1^{1};\mathbb {R}^{3\times 3})\) by
and observe that it obeys (see Lemma 3.1(ii), and recall that \(Q_j^Tt_j=e_3\))

Using (4.58), with a change of variables we obtain
and, for sufficiently large j,
In the rest of the argument we shall use (4.60), (4.61), (4.62) and the definition of \(\psi _{\mathbb {C}^V}\) to reach a contradiction.
By Remark 3.4(ii) and (4.62) there are \(A_j,B_j:{T}_1^{1,\delta }\rightarrow \mathbb {R}^{3\times 3}\) such that
\(|A_j|\le 1\) everywhere, \(|B_j|\ge 1\) on the set \(\{B_j\ne 0\}\), and for sufficiently large j
Recalling that \({\varepsilon }_j|b_j|/r_j\rightarrow 0\) and that \(r_j/R_j\rightarrow 0\), we compute with (4.55)
From (4.64) we obtain \(A_j\rightarrow 0\) in \(L^2(T_1^{1,\delta };\mathbb {R}^{3\times 3})\) and \(B_j\rightarrow 0\) in \(L^p(T_1^{1,\delta };\mathbb {R}^{3\times 3})\). We define \({{\hat{A}}}_j, {{\hat{B}}}_j\in L^1({T_1^{1,\delta }};\mathbb {R}^{3\times 3})\) by
With (4.64) and (4.65) we obtain that
Passing to a further subsequence, \({{\hat{A}}}_j\mathop {\rightharpoonup }{{\hat{A}}}_*\) weakly in \(L^2(T_1^{1,\delta };\mathbb {R}^{3\times 3})\). Let \(\eta \in (0,1)\) be fixed and set
We recall that \(A_j\rightarrow 0\) in \(L^2\) and \(B_j\rightarrow 0\) in \(L^p\). In particular, they converge to zero in measure, and therefore \({\mathcal {L}}^3(T^{1,\delta }_1{\setminus } E^\eta _j)\rightarrow 0\). On \(E^\eta _j\) we have \(B_j=0\) and in particular by (4.67) \({{\hat{B}}}_j ={{\hat{B}}}_j \chi _{T_1^{1,\delta }{\setminus } E^\eta _j} \mathop {\rightharpoonup }0\) in \(L^p(T_1^{1,\delta };\mathbb {R}^{3\times 3})\). By the differentiability of V in a neighbourhood of the origin, if \(\eta \) is sufficiently small we have
where \(\mathbb {C}^V:=D^2V(0)\) and \(\omega :[0,\infty )\rightarrow [0,\infty )\) is monotone, continuous, with \(\omega (0)=0\). We shall use this estimate with \(F={Q_j}A_jQ_j^T\) on \(E^\eta _j\). As \(F=0\) is a minimizer of V, \(V(0)=0\) and \(DV(0)=0\), so that
which is the same as
We recall that \({\mathcal {L}}^3(T^{1,\delta }_1{\setminus } E^\eta _j)\rightarrow 0\), which together with \( {{\hat{A}}}_j\mathop {\rightharpoonup }{{\hat{A}}}_*\) and \(Q_j\rightarrow Q_*\) implies
As \({{\hat{A}}}_j\) is bounded in \(L^2(T_1^{1,\delta };\mathbb {R}^{3\times 3})\)
for every \(\eta \in (0,1)\) sufficiently small and therefore for \(\eta =0\). Hence recalling (4.61), and with \(\mathbb {C}^V_{Q^*}\) defined from \(\mathbb {C}^V\) as in (3.28), for any \(\delta \in (0,\frac{1}{2}]\) we have
To conclude it remains to relate the left-hand side to \(\psi _{\mathbb {C}^V}\). We shall show below that there is \(u_*\in W^{1,1}(T_1^{1,\delta };\mathbb {R}^3)\) such that
with \(\beta _{b,t}\) defined as in Lemma 2.4. We recall the definition of \(\Theta \) in (2.32), and see that \(Du_*+\beta _{Q_*^Tb_*,e_3}\) is an admissible test field, so that (4.74) implies
Taking the limit \(\delta \rightarrow 0\) with Lemma 2.5, we obtain
Recalling that by Lemma 3.1(iii) one has \(\psi _{\mathbb {C}^V_{Q_*}}(Q_*^Tb_*,Q_*^Tt_*)= \psi _{\mathbb {C}^V}(b_*,t_*)\) and that \(Q_*e_3=t_*\) gives the desired contradiction.
It remains to prove (4.75). We define \({\bar{\beta }}_j\in L^1(T_1^1;\mathbb {R}^{3\times 3})\) as the strain field associated to the Burgers vector \(Q_j^Tb_j/|b_j|\) appearing (after scaling) in (4.60),
By (4.60) we have \(\mathop {\textrm{curl}}(\frac{\delta ^{k_j}R_j}{{\varepsilon }_j|b_j|}{\bar{\xi }}_j- {{\bar{\beta }}}_j)=0\) in \(T_1^1\) and there is \(v_j\in W^{1,1}(T_1^1;\mathbb {R}^3)\) such that \( \frac{\delta ^{k_j}R_j}{{\varepsilon }_j|b_j|}{\bar{\xi }}_j ={{\bar{\beta }}_j}+Dv_j\). Inserting (4.63) and (4.66) we obtain
We recall that \({{\hat{A}}}_j\mathop {\rightharpoonup }A_*\) in \(L^2(T_1^{1,\delta };\mathbb {R}^{3\times 3})\) and \({{\hat{B}}}_j\mathop {\rightharpoonup }0\) in \(L^p(T_1^{1,\delta };\mathbb {R}^{3\times 3})\). Further, \(b_j/|b_j|\rightarrow b_*\), \(Q_j\rightarrow Q_*\), \(t_j\rightarrow t_*\), and \(\beta _{b,t}\) depends continuously on b and t away from the singularity, which implies that \({\bar{\beta }}_j\) converges uniformly in \(T^{1,\delta }_1\) to
Therefore the sequence \(v_j\) (possibly after adding a constant to each of them) is bounded in \(W^{1,p}(T_1^{1,\delta };\mathbb {R}^3)\) and there is \( v_*\in W^{1,1}(T_1^{1,\delta };\mathbb {R}^3)\) with
This concludes the proof of (4.75) and of the proposition. \(\square \)
The cell problems from [18, 27] are all immediate consequences of Proposition 4.3, via Corollary 4.4. As an easy consequence one can also prove a lower bound when the dislocation is straight.
Proposition 4.5
Assume that W satisfies \(H^{\textrm{W}}_{\textrm{Finite}}\) for some \(p\in (1,2]\). Let \(\mathbb {C}:=D^2W({\textrm{Id}})\). For any \(0<R\le h\), \(b\in {\mathcal {B}}\), \(t\in S^2\), let \((\mu _{\varepsilon },\beta _{\varepsilon })\in {\mathcal {M}}^1(Q_t{T}^{R}_h)\times L^1(Q_t {T}^{R}_h;\mathbb {R}^{3\times 3})\) be \(\rho _{\varepsilon }\)-compatible, with \(\rho _{\varepsilon }\ge {\varepsilon }\), in the sense of Definition 3.7, with  . Assume that
. Assume that
and
for some \(Q\in {\textrm{SO}}(3)\). Then
Assume that W satisfies \(H^{\textrm{W}}_{\textrm{Lin}}\) for some \(p\in (1,2]\). Let \(\mathbb {C}:=D^2W(0)\). Then the same holds by replacing (4.84) with
Proof
The proof follows by applying Corollary 4.4 with \(r=r_{\varepsilon }:=\rho _{\varepsilon }\log \frac{1}{\rho _{\varepsilon }}\). \(\square \)
5 Compactness and lower bound
In this section we provide the proofs of the compactness and the lower bound needed to prove Theorem 3.6. The proof is similar to the one of [18, Prop. 6.6] using Proposition 4.3 (via Corollary 4.4) instead of [18, Lemma 5.8]. We discuss the various arguments separately in order to be able to reuse them.
5.1 Rigidity
We first recall a rigidity result from [12], which is based on the Friesecke–James–Müller geometric rigidity [21] and on the Bourgain-Brezis critical integrability bound [6], and extend it to smaller exponents.
Proposition 5.1
(From [12]) Let \(\Omega \subset \mathbb {R}^3\) be a bounded connected Lipschitz set, \(q\in [1,\frac{3}{2}]\). Then there is a constant \(c=c(\Omega ,q)\) such that for any \({{\beta }}\in L^q(\Omega ;\mathbb {R}^{3\times 3})\) such that \(\mathop {\textrm{curl}}\beta \) is a finite measure there are \(Q\in {\textrm{SO}}(3)\) such that
and \({S}\in \mathbb {R}^{3\times 3}_{\textrm{skew}}\) such that
Proof
The important case is the critical exponent \(q=\frac{3}{2}\), which was proven in [12]. The case \(q\in [1,\frac{3}{2})\) follows from the same argument, using \(s=q\) in the proof of Theorem 1 in [12], and using Hölder’s inequality in (8). Then after scaling Eq. (11) becomes
the factor \(({\mathcal {L}}^3(Q_r))^{\frac{1}{q}-\frac{2}{3}}=r^{\frac{3}{q}-2}\) is uniformly bounded since \(Q_r\subseteq \Omega \). We remark that the second term in [12, Eq. (11)] incorrectly contains Du instead of \(\beta \). The rest of the argument does not make use of the specific value of s and is unchanged. The modification in the linear case is the same. \(\square \)
5.2 Compactness
We recall the definition of the class \({\mathcal {A}}^*_{\varepsilon }\) of admissible pairs in (3.36) and that of the elastic energy \(E^{\textrm{elast}}[\beta ,A]\) in (3.37) for fields \(\beta \in L^1(\Omega ;\mathbb {R}^{3\times 3})\) and Borel sets \(A\subseteq \Omega \).
Proposition 5.2
Let \(\Omega \subset \mathbb {R}^3\) be a bounded Lipschitz set. Assume W obeys \(H^{\textrm{W}}_{\textrm{Finite}}\) or \(H^{\textrm{W}}_{\textrm{Lin}}\) for some \(p\in (1,2]\). Let \((\mu _{\varepsilon },\beta _{\varepsilon })\in {\mathcal {A}}^*_{\varepsilon }\) be such that \(\mu _{\varepsilon }\) is \((h_{\varepsilon },\alpha _{\varepsilon })\)-dilute in the sense of Definition 3.3, where \((h_{\varepsilon },\alpha _{\varepsilon })\) obeys (3.38), and
for some \(E>0\) and for some \(\rho _{\varepsilon }\ge {\varepsilon }\) such that
Then there is \({c}>0\) such that for any \(\Omega '\subset \subset \Omega \)
Moreover there are \(\mu \in {\mathcal {M}}_{{\mathcal {B}}}^1(\Omega )\) and a subsequence \({\varepsilon }_k\) such that
Remark 5.3
If \(\partial \Omega \) is connected then Proposition 5.2 still holds true if we replace \({\mathcal {A}}^*_{\varepsilon }\) with \({\mathcal {A}}^\textrm{core}_{\rho _{\varepsilon },{\varepsilon }}\) or with \({\mathcal {A}}^\textrm{moll}_{\varepsilon }\) defined in (3.50) and (3.51) respectively. Indeed, in both cases is suffices to extend (separately for each i) the restriction \(\beta _{\varepsilon }|_{T^i_{\varepsilon }{\setminus } {{\hat{T}}}^i_{\varepsilon }}\) to a function \({\tilde{\beta }}_{\varepsilon }\) in \(L^1(T^i_{\varepsilon };\mathbb {R}^{3\times 3})\) with  as was done at the beginning of the proof of Corollary 4.4.
as was done at the beginning of the proof of Corollary 4.4.
Proof
Since \(\mu _{\varepsilon }\) is dilute, we have that  , where \(\gamma ^i_{\varepsilon }\subset {\overline{\Omega }}\) are finitely many closed segments satisfying the diluteness conditions (i)–(iv) of Definition 3.2. Possibly subdividing the segments into smaller ones, we can assume that they have length in \([h_{\varepsilon }, 2h_{\varepsilon }]\). We set \(\gamma _{\varepsilon }:=\cup _i\gamma _{\varepsilon }^i\). We fix \(\Omega '\subset \subset \Omega \) and set \(I_{\varepsilon }:=\{i: \gamma ^i_{\varepsilon }\cap \Omega '\ne \emptyset \}\). We choose \(r_{\varepsilon }=\rho _{\varepsilon }\), \(R_{\varepsilon }:=(\alpha _{\varepsilon }h_{\varepsilon })^2\), \(\delta _{\varepsilon }:=\alpha _{\varepsilon }h_{\varepsilon }\). We let \(S_{\varepsilon }^i\subset \mathbb {R}\) be a segment of length
, where \(\gamma ^i_{\varepsilon }\subset {\overline{\Omega }}\) are finitely many closed segments satisfying the diluteness conditions (i)–(iv) of Definition 3.2. Possibly subdividing the segments into smaller ones, we can assume that they have length in \([h_{\varepsilon }, 2h_{\varepsilon }]\). We set \(\gamma _{\varepsilon }:=\cup _i\gamma _{\varepsilon }^i\). We fix \(\Omega '\subset \subset \Omega \) and set \(I_{\varepsilon }:=\{i: \gamma ^i_{\varepsilon }\cap \Omega '\ne \emptyset \}\). We choose \(r_{\varepsilon }=\rho _{\varepsilon }\), \(R_{\varepsilon }:=(\alpha _{\varepsilon }h_{\varepsilon })^2\), \(\delta _{\varepsilon }:=\alpha _{\varepsilon }h_{\varepsilon }\). We let \(S_{\varepsilon }^i\subset \mathbb {R}\) be a segment of length
\(A_{\varepsilon }^i\) an affine isometry that maps \(S_{\varepsilon }^ie_3\) into \(\gamma _{\varepsilon }^i\) and the midpoint of \(S_{\varepsilon }^ie_3\) to the midpoint of \(\gamma _{\varepsilon }^i\). We define the cylinders
Disjoint segments in the family \(\{\gamma _{\varepsilon }^i\}_i\) are separated by \(\alpha _{\varepsilon }h_{\varepsilon }\gg R_{\varepsilon }\). Since the angle between two non-disjoint segments is at least \(\alpha _{\varepsilon }\), and for small \({\varepsilon }\) we have \(\delta _{\varepsilon }\tan \frac{1}{2}\alpha _{\varepsilon }> R_{\varepsilon }\) we obtain that the sets \(\{T_{{\varepsilon }}^i\}_i\) are pairwise disjoint and \(T^i_{\varepsilon }\cap \gamma ^j_{\varepsilon }=\emptyset \) for all \(j\ne i\). Further, for \({\varepsilon }\) sufficiently small we have \(2h_{\varepsilon }+R_{\varepsilon }\le {\textrm{dist}}(\Omega ',\partial \Omega )\) which implies \(T_{\varepsilon }^i\subseteq \Omega \) for all \(i\in I_{\varepsilon }\). Therefore
By Lemma 4.2,
By the diluteness condition (3.38) and (5.4),
Since \({\mathcal {H}}^1(S^i_{\varepsilon }) \ge (1-2\alpha _{\varepsilon }) {\mathcal {H}}^1(\gamma ^i_{\varepsilon }) \), we conclude that for small \({\varepsilon }\)
Therefore there is a subsequence such that \({\varepsilon }^{-1}\mu _{\varepsilon }\) converges to a limiting measure \(\mu \in {\mathcal {M}}(\Omega ';\mathbb {R}^{3\times 3})\), with \(|\mu |(\Omega ')\le c E\). Since \(\Omega '\) was arbitrary, we have \(\mu \in {\mathcal {M}}(\Omega ;\mathbb {R}^{3\times 3})\), and there is a diagonal subsequence such that \({\varepsilon }_k^{-1}\mu _{{\varepsilon }_k}{\displaystyle \mathop {\rightharpoonup }^*}\mu \) in all \(\Omega '\subset \subset \Omega \). By [14] the limit also belongs to \({\mathcal {M}}_{\mathcal {B}}^1(\Omega )\). This concludes the proof of (5.5) and (5.6). \(\square \)
Proposition 5.4
Let \(\Omega \subset \mathbb {R}^3\) be a bounded Lipschitz set with connected boundary. Assume W obeys \(H^{\textrm{W}}_{\textrm{Finite}}\) or \(H^{\textrm{W}}_{\textrm{Lin}}\) for some \(p\in (1,2)\). Let \((\mu _{\varepsilon },\beta _{\varepsilon })\in {\mathcal {A}}^*_{\varepsilon }\) be such that \(\mu _{\varepsilon }\) is \((h_{\varepsilon },\alpha _{\varepsilon })\)-dilute in the sense of Definition 3.3, where \((h_{\varepsilon },\alpha _{\varepsilon })\) obeys (3.38), and
for some \(E>0\).
Then there are a subsequence \({\varepsilon }_k\rightarrow 0\), \({{\eta }}\in L^{1}_{\textrm{loc}}(\Omega ;\mathbb {R}^{3\times 3})\) with \(\mathop {\textrm{curl}}{{\eta }}=0\), \(\mu \in {\mathcal {M}}_{\mathcal {B}}^1(\Omega )\) and \(Q_*\in {\textrm{SO}}(3)\) such that \((\mu _{{\varepsilon }_k},\beta _{{\varepsilon }_k})\) converges to \((\mu ,\eta , Q_*)\) in finite kinematics with p growth if \(H^{\textrm{W}}_{\textrm{Finite}}\) holds, and to \((\mu ,\eta )\) in infinitesimal kinematics with p growth if \(H^{\textrm{W}}_{\textrm{Lin}}\) holds, in the sense of Definition 3.5.
Proof
We first remark that Proposition 5.2 holds for this sequence (with \(\rho _{\varepsilon }={\varepsilon }\)). Fix a connected Lipschitz set \(\Omega '\subset \subset \Omega \). Then by (5.5) for \({\varepsilon }\) small enough we have
Let
From \(H^{\textrm{W}}_{\textrm{Finite}}\) we obtain the pointwise bound \(d_{\varepsilon }^2\wedge d_{\varepsilon }^p=\Phi _p(d_{\varepsilon })\le c W(\beta _{\varepsilon })\). Since \(q:=\frac{3}{2}\wedge p<2\),
Using first \(q\le p\) and then \(q< 2\), for \({\varepsilon }\) small
Combining these two estimates,
By Proposition 5.1 and (5.13), there is \(Q_{\varepsilon }\in {\textrm{SO}}(3)\) such that for small \({\varepsilon }\)
where c may depend on \(\Omega '\). The rotation \(Q_{\varepsilon }\), however, may be chosen not to depend on \(\Omega '\). Passing to a further subsequence we can assume \(Q_{{\varepsilon }_k}\rightarrow Q_*\) for some \(Q_*\in {\textrm{SO}}(3)\).
From (5.18) we see that, after extracting a further subsequence, there is \(\eta \in L^q(\Omega ';\mathbb {R}^{3\times 3})\) such that
Again, after taking a diagonal subsequence this holds for all \(\Omega '\). In order to prove \(\mathop {\textrm{curl}}\eta =0\), we write
As \(|\mu _{\varepsilon }|(\Omega ')\le c {\varepsilon }\), \(\mathop {\textrm{curl}}\eta _{\varepsilon }\rightarrow 0\) distributionally in \(\Omega '\).
The proof in the geometrically linear case is analogous. \(\square \)
5.3 Lower bound
We define, given a pair \((\mu ,\beta )\in {\mathcal {M}}_{{\varepsilon }{\mathcal {B}}}^1(\Omega )\times L^1(\Omega ;\mathbb {R}^{3\times 3})\) and \(\rho ,{\varepsilon }>0\),
We recall that the class \({\mathcal {A}}^\textrm{core}_{\rho ,{\varepsilon }}\) of admissible pairs was defined in (3.50). As \({\mathcal {A}}_{\varepsilon }^*\subseteq {\mathcal {A}}_{\rho ,{\varepsilon }}^\textrm{core}\) for every \(\rho >0\) by Lemma 3.8(iii), for any \((\mu ,\beta )\in {\mathcal {M}}^1_{{\varepsilon }{\mathcal {B}}}(\Omega )\times L^1(\Omega ;\mathbb {R}^{3\times 3})\) and all \(\rho >0\) we have
This will permit (in Sect. 7) to prove the lower bound in Theorem 3.6 by means of a lower bound on \(E^{\textrm{lb}}_{\rho _{\varepsilon },{\varepsilon }}\) for a good choice of \(\rho _{\varepsilon }\). Precisely, we assume that \(\rho _{\varepsilon }\rightarrow 0\) is such that
Theorem 5.5
Let \(\Omega \subset \mathbb {R}^3\) be open, bounded, Lipschitz, with connected boundary. Let \(\rho _{\varepsilon }\rightarrow 0\) be such that (5.23) holds true. Let \((\mu _{\varepsilon },\beta _{\varepsilon })\in {\mathcal {A}}^\textrm{core}_{\rho _{\varepsilon },{\varepsilon }}\) be such that \(\mu _{\varepsilon }\) is \((h_{\varepsilon },\alpha _{\varepsilon })\)-dilute, where \((h_{\varepsilon },\alpha _{\varepsilon })\) obeys (3.38).
Assume that W obeys \(H^{\textrm{W}}_{\textrm{Finite}}\) for some \(p\in (1,2]\). Assume that there are a sequence \({\varepsilon }_k\rightarrow 0\) and \((\mu ,\eta ,Q)\in {\mathcal {M}}^1_{{\mathcal {B}}}(\Omega )\times L^1_{\textrm{loc}}(\Omega ;\mathbb {R}^{3\times 3})\times {\textrm{SO}}(3)\), with  and \(\mathop {\textrm{curl}}{{\eta }}=0\), such that \((\mu _{{\varepsilon }_k},\beta _{{\varepsilon }_k})\) converges to \((\mu ,\eta ,Q)\) in finite kinematics with p growth and radius \(\rho _{{\varepsilon }_k}\) in the sense of Definition 3.9.
and \(\mathop {\textrm{curl}}{{\eta }}=0\), such that \((\mu _{{\varepsilon }_k},\beta _{{\varepsilon }_k})\) converges to \((\mu ,\eta ,Q)\) in finite kinematics with p growth and radius \(\rho _{{\varepsilon }_k}\) in the sense of Definition 3.9.
Then
with \(\mathbb {C}:=D^2W({\textrm{Id}})\), \(\mathbb {C}_Q\) as in (3.10), and \(\psi _\mathbb {C}^{\textrm{rel}}\) defined as in (3.42). Further, if the right-hand side of (5.24) is finite then \(\eta \in L^2(\Omega ;\mathbb {R}^{3\times 3})\).
Assume W obeys \(H^{\textrm{W}}_{\textrm{Lin}}\) for some \(p\in (1,2]\). Then the same holds with respect to the convergence in infinitesimal kinematics with p growth and radius \(\rho _{{\varepsilon }_k}\) in the sense of Definition 3.9 with \(\psi _\mathbb {C}^{\textrm{rel}}(b,Qt)\) replaced by \(\psi _\mathbb {C}^{\textrm{rel}}(b,t)\) and \(\mathbb {C}_Q\) by \(\mathbb {C}=D^2W(0)\).
Proof
We discuss the proof in the finite case, the linear case is similar. For notational simplicity we write \({\varepsilon }\) for \({\varepsilon }_k\). Without loss of generality we can assume that the \(\liminf \) is finite and, possibly passing to a further subsequence, that it is a limit; in particular
for some \(E>0\). During the proof we shall extract further subsequences, which are not made explicit in the notation.
By hypothesis on \((\mu _{\varepsilon },\beta _{\varepsilon })\) we have that
and there is \(Q_{\varepsilon }\in {\textrm{SO}}(3)\) such that \(Q_{\varepsilon }\rightarrow Q\) and
for \(q:=\frac{3}{2}\wedge p\).
Fix a connected Lipschitz set \(\Omega '\subset \subset \Omega \). The key idea in the proof is to use Proposition 4.3 and the double differentiability of W near the identity to show that, writing  , there are \(\sigma _{\varepsilon }\rightarrow 0\) and two disjoint subsets \(\Omega '_{\varepsilon }, \omega '_{\varepsilon }\subset \Omega {\setminus } (\gamma _{\varepsilon })_{\rho _{\varepsilon }}\) such that \({\mathcal {L}}^3(\Omega '{\setminus }\Omega '_{\varepsilon })\rightarrow 0\),
, there are \(\sigma _{\varepsilon }\rightarrow 0\) and two disjoint subsets \(\Omega '_{\varepsilon }, \omega '_{\varepsilon }\subset \Omega {\setminus } (\gamma _{\varepsilon })_{\rho _{\varepsilon }}\) such that \({\mathcal {L}}^3(\Omega '{\setminus }\Omega '_{\varepsilon })\rightarrow 0\),
and
We start by showing (5.28), following the setting in the proof of Proposition 5.2. Since \(\mu _{\varepsilon }\) is dilute we can write  , with \(\gamma _{\varepsilon }=\cup _i \gamma _{\varepsilon }^i\) \((h_{\varepsilon },\alpha _{\varepsilon })\)-dilute, and we can assume \({\mathcal {H}}^1(\gamma _{\varepsilon }^i)\in [h_{\varepsilon },2h_{\varepsilon }]\). We define \(R_{\varepsilon }\), \(S_{\varepsilon }^i\), \(T_{\varepsilon }^i\), \( {\hat{T}}^i_{\varepsilon }\), \(I_{\varepsilon }\) as in the proof of Proposition 5.2 where now \(r_{\varepsilon }:=\max \{\rho _{\varepsilon },{\varepsilon }h_{\varepsilon }^{-2}\}\). We set
, with \(\gamma _{\varepsilon }=\cup _i \gamma _{\varepsilon }^i\) \((h_{\varepsilon },\alpha _{\varepsilon })\)-dilute, and we can assume \({\mathcal {H}}^1(\gamma _{\varepsilon }^i)\in [h_{\varepsilon },2h_{\varepsilon }]\). We define \(R_{\varepsilon }\), \(S_{\varepsilon }^i\), \(T_{\varepsilon }^i\), \( {\hat{T}}^i_{\varepsilon }\), \(I_{\varepsilon }\) as in the proof of Proposition 5.2 where now \(r_{\varepsilon }:=\max \{\rho _{\varepsilon },{\varepsilon }h_{\varepsilon }^{-2}\}\). We set
Clearly \(\Omega '\cap \gamma _{\varepsilon }\subseteq \gamma _{\varepsilon }'\). As in Proposition 5.2, for \({\varepsilon }\) sufficiently small the \(T^i_{\varepsilon }\) are disjoint and \(T^i_{\varepsilon }\subseteq \Omega \) for all \(i\in I_{\varepsilon }\). By Corollary 4.4 with \(h={\mathcal {H}}^1(S_{\varepsilon }^i)\), \(R=R_{\varepsilon }\), \(r=r_{\varepsilon }\), for every index \(i\in I_{\varepsilon }\) we get
where
and \({\tilde{\sigma }}:(0,\infty )\rightarrow (0,\infty )\) nondecreasing and such that \(\lim _{s\rightarrow 0}{\tilde{\sigma }}(s)=0\). We show that the argument of \({\tilde{\sigma }}\) converges uniformly in i to zero. From the definitions of \(R_{\varepsilon }\) and \(r_{\varepsilon }\), the diluteness condition (3.38) and (5.23) we obtain \(r_{\varepsilon }/R_{\varepsilon }\rightarrow 0\). By (5.27) we have that \(\sup _{\varepsilon }\Vert \eta _{\varepsilon }\Vert _{L^1(\Omega ')}<\infty \), and recalling the definition of \(R_{\varepsilon }\) and the diluteness assumption,
We remark that (5.5) implies that for sufficiently small \({\varepsilon }\) one has
and using \({\mathcal {H}}^1(\gamma _i^{\varepsilon }) \ge h_{\varepsilon }\) and \(r_{\varepsilon }\ge {\varepsilon }h_{\varepsilon }^{-2}\), we obtain
Therefore for all \({i\in I_{\varepsilon }}\)
with \({\hat{\sigma }}_{\varepsilon }\rightarrow 0\). In turn, summing (5.31) over \(i\in I_{\varepsilon }\) and using (5.7) we obtain
By
the factor in front of the integral converges to 1. Therefore (5.28) follows. In turn, from (5.28) we obtain
By \(Q_{\varepsilon }\rightarrow Q\), (2.36) and the relaxation result of [14, Theorem 3.1], this implies
We next show (5.29). Since W is twice differentiable at the identity, there is \(\omega :[0,\infty )\rightarrow [0,\infty )\), monotone and continuous in 0, with \(\omega (0)=0\), such that for any \(\delta >0\) sufficiently small we have
We shall apply this with \(F=(Q_{\varepsilon }^T\beta _{\varepsilon }(x)-{\textrm{Id}})\chi _{\Omega {\setminus } (\gamma _{\varepsilon })_{\rho _{\varepsilon }}} {(x)}={\varepsilon }\log ^{1/2}\frac{1}{{\varepsilon }}\eta _{\varepsilon }(x)\), away from the boundary, the singularity, and the parts where \(\eta _{\varepsilon }\) is exceptionally large. To make this precise, we first define
As \(\Omega '\) is Lipschitz, \(\gamma _{\varepsilon }\) is dilute and \({\mathcal {H}}^1(\gamma ^i_{\varepsilon })\in [h_{\varepsilon }, 2h_{\varepsilon }]\), using (5.34) and \(|b_i|\ge c>0\) we obtain
We then choose \(L_{\varepsilon }\rightarrow \infty \) such that \(L_{\varepsilon }{\varepsilon }\log ^{1/2}\frac{1}{{\varepsilon }}+ L_{\varepsilon }^2 \omega (L_{\varepsilon }{\varepsilon }\log ^{1/2}{\frac{1}{{\varepsilon }}})\rightarrow 0\) and define
Since \(\eta _{\varepsilon }\) is bounded in \(L^q(\Omega ';{\mathbb {R}^{3\times 3}})\), \({\mathcal {L}}^3({\hat{\Omega }}'_{\varepsilon }{\setminus } \Omega '_{\varepsilon })\rightarrow 0\), and recalling (5.43) we obtain \({\mathcal {L}}^3(\Omega '{\setminus } \Omega '_{\varepsilon })\rightarrow 0\). For any \(x\in \Omega '_{{\varepsilon }}\) we have
Therefore
which is (5.29). Moreover by (5.27) and \({\mathcal {L}}^3(\Omega '{\setminus } \Omega '_{\varepsilon })\rightarrow 0\) we obtain that
and, by lower semicontinuity and \(\mathbb {C}_{Q_{\varepsilon }}\rightarrow \mathbb {C}_Q\),
Combining (5.40) and (5.48), recalling that \(\omega '_{\varepsilon }\cap \Omega '_{\varepsilon }=\emptyset \), we obtain
for all Lipschitz sets \(\Omega '\subset \subset \Omega \); as the right-hand side does not depend on \(\Omega '\) the same holds on \(\Omega \). This proves (5.24).
If the right-hand side is finite, then \(\eta +\eta ^T\in L^2(\Omega ;\mathbb {R}^{3\times 3})\). By Korn’s inequality, recalling that \(\mathop {\textrm{curl}}\eta =0\), this implies \(\eta \in L^2(\Omega ;\mathbb {R}^{3\times 3})\). \(\square \)
6 Upper bound
A key technical result of this section, which permits a refinement of the argument used for the upper bound in [18, 27] is the following statement. It shows that the upper bound for the unrelaxed problem can be taken at constant \(\beta \).
Proposition 6.1
Let \(\mathbb {C}\) obey (2.1). Let  be polygonal, and let \({{\beta }}\in L^{3/2}(\mathbb {R}^3;\mathbb {R}^{3\times 3})\) be the solution to
be polygonal, and let \({{\beta }}\in L^{3/2}(\mathbb {R}^3;\mathbb {R}^{3\times 3})\) be the solution to
Let \(\nu _{\varepsilon }\) be the positive measure defined by

Then \(\nu _{\varepsilon }\) converges weakly-\(*\) to

In particular, if \(\Omega \subset \mathbb {R}^3\) is an open set with \(|\mu |(\partial \Omega )=0\), then
Further, the positive measures

are uniformly locally bounded, in the sense that for all \(R>0\) one has
and for any \(s\in (0,1)\) obey
Proof
Since \(\mu \) is polygonal, we have that \(\gamma =\cup _i\gamma _i\), with the \(\gamma _i\) being finitely many pairwise disjoint segments in \(\mathbb {R}^3\). For the same reason, \(b\in L^\infty (\gamma ,{\mathcal {H}}^1;{\mathcal {B}})\). By Theorem 2.2(iii), for any \(x\not \in {\overline{\gamma }}\) we have
where
In particular, this shows that

where

We fix an index i and estimate \(\nu _{\varepsilon }^i\) separately near \(\gamma _i\) and far away. Let \(\delta ,R>0\). Since \(f_i\le 1/\delta \) outside \((\gamma _i)_\delta \),
We recall that we denote by \(B_r(x)\) and \(B'_r(x)\) the balls of radius \(r>0\) centered at x in \(\mathbb {R}^3\) and \(\mathbb {R}^2\) respectively; for \(x=0\) we simply write \(B_r\) and \(B'_r\). Let now \(x\in \overline{\gamma _i}\), \(r>0\). Then
Note that the first integral in the first inequality of (6.10) is needed to estimate \(\nu _{\varepsilon }^i(B_r(x))\) in the case that x is near the endpoints of \(\gamma _i\). For any \(\delta \in (0,{\mathcal {H}}^1(\gamma _i))\) we can cover \((\gamma _i)_\delta \) with at most \(3{\mathcal {H}}^1(\gamma _i)/\delta \) balls \(B_{2\delta }(x^k)\), with \(x^k\in {\overline{\gamma }}_i\). Therefore, using (6.10) with \(r=2\delta \) and (6.9),
which implies
for all \(R>0\). Recalling (6.8), this proves (6.5).
For any \(s\in (0,1)\) the same computation, using \(\delta ={\varepsilon }^s\) in (6.10), shows that
and similarly \(\limsup _{{\varepsilon }\rightarrow 0} \nu _{\varepsilon }^i((\gamma _j)_{{\varepsilon }^s})=0\) for \(j\ne i\). This proves (6.6).
By (6.11), after taking a subsequence we can assume that for each i \(\nu _{\varepsilon }^i{\displaystyle \mathop {\rightharpoonup }^*}\nu _0^i\) for some Radon measure \(\nu _0^i\). By (6.9) we obtain \(\nu _0^i(B_R{\setminus } (\gamma _i)_\delta )=0\) for any \(\delta \) and R; taking \(\delta \rightarrow 0\) and \(R\rightarrow \infty \) this gives \(\nu ^i_0(\mathbb {R}^3{\setminus } \overline{\gamma _i})=0\). By (6.10) we obtain
Therefore  . Summing over i (and possibly taking a further subsequence), \(\nu _{\varepsilon }\mathop {\rightharpoonup }\nu _0\) with
. Summing over i (and possibly taking a further subsequence), \(\nu _{\varepsilon }\mathop {\rightharpoonup }\nu _0\) with  .
.
In order to conclude the proof it suffices to show that for any i we have

where we recall that \(b_i\in {\mathcal {B}}\) and \(t_i\in S^2\) are defined by  .
.
For \(x\in \gamma _i\) we denote by \(T_r^x\) a cylinder with axis parallel to \(t_i\), radius \(r>0\) and height 2r centered at x,
where as usual \(Q_{t_i}\) is an element of \({\textrm{SO}}(3)\) with \(Q_{t_i}e_3=t_i\). By the Radon-Nikodým theorem, for \({\mathcal {H}}^1\)-almost every \(x\in \gamma _i\) there is a sequence \(r_k\rightarrow 0\) such that \(\nu _0(\partial T^x_{r_k})=0\) and

We can assume that x is not an endpoint of \(\gamma _i\) and that it does not belong to \({\overline{\gamma }}_j\) for \(i\ne j\). For sufficiently large k, \({\mathcal {H}}^1(\gamma _i\cap T_{r_k}^x)=2r_k\). Recalling that \(\nu _{\varepsilon }(T_{r_k}^x)\rightarrow \nu _0(T_{r_k}^x)\), the definition of \(\nu _{\varepsilon }\), and \({\textrm{dist}}(x,\gamma _j)>0\) for \(j\ne i\),

By Theorem 2.2(ii)
Assume first \(j\ne i\), so that \({\textrm{dist}}(x,\gamma _j)>0\). Since \(|N(z)|\le c/|z|^2\), we have \(|{{\beta }}_j|\le c\) in \(T_{r_k}^x\) for sufficiently large k. The term \(\beta _i\) instead is compared with \({{\beta }}_{b_i, t_i}\). By Lemma 2.4 we have that
which implies, using again \(|N(z)|\le c/|z|^2\),
for sufficiently large k (with c depending on x and i).
As for any \(\delta \in (0,1]\)
we obtain, recalling (2.30) in order to evaluate the integral,
Therefore (6.14) gives

for any \(\delta >0\), so that

In order to prove the converse bound we start from (6.14) and notice that \(\beta \) is an admissible test function in (2.37) for \(\Theta (\mathbb {C},b_i, t_i, {2r_k}, r_k,{\varepsilon })\). Therefore

where in the last step we used Lemma 2.5(i). This concludes the proof. \(\square \)
Remark 6.2
The same argument also yields
To see this, we observe that \(|\beta |\le c\sum _i f_i\) implies \(|\beta *\varphi _{\varepsilon }|\le c\sum _i (f_i*\varphi _{\varepsilon })\). With (6.7) we obtain \(|f_i*\varphi _{\varepsilon }|\le c/{\varepsilon }\) everywhere, and therefore \(\Vert \beta *\varphi _{\varepsilon }\Vert _{L^\infty } \le c/{\varepsilon }\). For each segment \(\gamma _i\) one computes \({\mathcal {L}}^3((\gamma _i)_{\varepsilon })= \pi {\varepsilon }^2{\mathcal {H}}^1(\gamma _i)+\frac{4\pi }{3}{\varepsilon }^3\), and since there are finitely many of them we have \({\mathcal {L}}^3((\gamma )_{2{\varepsilon }})\le c {\varepsilon }^2 + c {\varepsilon }^3\). Condition (6.16) follows.
We next deal with a technical issue related to the intersection of \(\gamma \) and the boundary of \(\Omega \). Indeed, in the above proposition one has integrated over the complement of an \({\varepsilon }\)-neighbourhood of the entire curve \(\gamma \subset \mathbb {R}^3\), whereas in \(E^{\textrm{ub}}_{\varepsilon }\) one integrates over the complement of an \({\varepsilon }\)-neighbourhood of the part of \(\gamma \) which is contained within \(\Omega \). It is apparent that this may generate difficulties if \(\gamma \) is tangential to \(\partial \Omega \), including the extreme case in which one of the segments composing \(\gamma \) is contained in \(\partial \Omega \). This situation is obviously not generic, and indeed we show in the next result that in the generic situation this boundary effect vanishes in the limit.
Let \(\Omega \subseteq \mathbb {R}^3\) be open and Lipschitz, \(\gamma \subset \mathbb {R}^3\) a finite union of closed segments. We say that \(\gamma \) is transversal to \(\partial \Omega \) if \(\gamma \cap \partial \Omega \) consists of finitely many points, each of them belongs to only one of the segments, is in its interior, is a point where \(\partial \Omega \) has a normal, and the normal is not orthogonal to \(\gamma \).
Lemma 6.3
Let \(\Omega \subseteq \mathbb {R}^3\) be an open Lipschitz set, \(\gamma \subset \mathbb {R}^3\) a finite union of closed segments.
-
(i)
For \({\mathcal {L}}^3\)-almost all \(a\in \mathbb {R}^3\) the curve \(a+\gamma \) is transversal to \(\partial \Omega \).
-
(ii)
If \(\gamma \) is transversal to \(\partial \Omega \), then in the setting of Proposition 6.1
$$\begin{aligned} \limsup _{{\varepsilon }\rightarrow 0} \frac{1}{\log \frac{1}{{\varepsilon }}} \int _{\Omega \cap (\gamma )_{{\varepsilon }}{\setminus }(\Omega \cap \gamma )_{\varepsilon }}|\beta |^2 dx =0. \end{aligned}$$(6.17)
The proof of the second part uses the following geometric fact.
Lemma 6.4
Let \(\Omega \subseteq \mathbb {R}^n\) be an open Lipschitz set, \(x\in \partial \Omega \) with outer normal \(\nu \in S^{n-1}\), \(v\in S^{n-1}\) with \(v\cdot \nu >0\). Then there are \(c,c',\rho >0\) such that
and
Proof
After a change of variables we can assume that \(x=0\), \(\nu =e_n\), \(v_n>0\), and there is a Lipschitz function \(f:\mathbb {R}^{n-1}\rightarrow \mathbb {R}\) with \(f(0)=0\), \(Df(0)=0\), and
for some \(r>0\). We write \(y=(y',y_n)\), with \(y'\in \mathbb {R}^{n-1}\) and \(y_n\in \mathbb {R}\), and the same for the other vectors. As \(Df(0)=0\) and \(v_n>0\), we can choose \(\rho \in (0,\frac{1}{2}r]\) such that \(|f(y')|\le \frac{1}{2}v_n|y'|\) for all \(|y'|\le \rho \). For \(t\in [-\rho ,\rho ]\) we have \(tv\in B_r{\setminus } \Omega \) iff \(t\ge 0\), and in this case
which implies
We then estimate \(|y'|\le t+|y'-tv'|\) and, with \(|v'|\le 1\),
for all \(t\in [0,\rho ]\), which together with (6.22) implies
which is (6.18) with \(c=4/v_n\).
To prove (6.19), let \(y\in \Omega \), \(t\in [0,\rho ]\). Then \(|v|=1\), (6.18) and \({\textrm{dist}}(x+tv,\Omega )\le |x+tv-y|\) give
which proves (6.19). \(\square \)
Proof of Lemma 6.3
(i): There are finitely many points in \(\gamma \) which are either endpoints or belong to more than one segment, and for almost all choices of a none of them belongs to the 2-dimensional set \(\partial \Omega \). For the rest of the argument we can consider each of the segments composing \(\gamma \) individually. Analogously, since \(\partial \Omega \) is covered by finitely many Lipschitz graphs, it suffices to prove the assertion for one of them. Therefore it suffices to show the following: if \(v\in S^{2}\), \(F:\mathbb {R}^{2}\rightarrow \mathbb {R}^3\) is Lipschitz, and \(r>0\), then for \({\mathcal {L}}^3\)-almost every \(a\in \mathbb {R}^3\) the following holds: the equation
with \(y'\in B_r'\) has finitely many solutions \(y'_1,\dots , y'_K\), at each \(y_k'\) the function F is differentiable, with v not contained in the space spanned by \(\partial _1F(y'_k)\) and \(\partial _2F(y'_k)\). We remark that one can replace \({\mathcal {L}}^3\)-almost every \(a\in \mathbb {R}^3\) with \({\mathcal {H}}^2\)-almost every \(a\in v^\perp \).
To see this, one considers the Lipschitz function \(G:B_r'\rightarrow v^\perp \subseteq \mathbb {R}^3\) defined by \(G(y'):=P_vF(y')\), where \(P_v:={\textrm{Id}}-v\otimes v\) is the projection onto the space \(v^\perp \). For \(a\in v^\perp \), equation (6.26) can be rewritten as \(G(y')=a\). As F is Lipschitz, it is almost everywhere differentiable, and \(G(\{y'\in B_r': DF(y') \text { does not exist}\})\) is an \({\mathcal {H}}^2\)-null set. By Sard’s Lemma, \(G(\{y'\in B_r': \mathrm{rank\,} DG(y')\le 1\})\) is also an \({\mathcal {H}}^2\)-null set. We observe that, since \(DG=({\textrm{Id}}-v\otimes v)DF\), DG has full rank exactly when v is not contained in the space spanned by \(\partial _1F\) and \(\partial _2F\). By the area formula [5, Th. 2.71] applied to the function G we obtain
so that \(B_r'\cap G^{-1}(a)\) is a finite set for \({\mathcal {H}}^2\)-almost all a. This proves the claim.
(ii): Let \(\{x_1,\dots , x_M\}=\gamma \cap \partial \Omega \). By Lemma 6.4 there are \(c'\), \(\rho >0\) such that (6.19) holds for all of them. Possibly reducing \(\rho \), \(\gamma \cap B_{\rho }(x_i)\) is a diameter of \(B_{\rho }(x_i)\) for all i. Pick \(c_*\in (0,1)\) with \(c_*c'<1\). We claim that for \({\varepsilon }\) sufficiently small one has
We prove (6.28) by contradiction. If not, there are \({\varepsilon }_k\rightarrow 0\), \(y_k\in \Omega \), \(z_k\in \gamma \) with \(|y_k-z_k|< c_*{\varepsilon }_k\) and \({\textrm{dist}}(y_k, \Omega \cap \gamma )\ge {\varepsilon }_k\). As \(c_*<1\) the last two conditions imply \(z_k\in \gamma {\setminus }\Omega \). By compactness of \({\bar{\Omega }}\), passing to a subsequence we can assume that \(y_k\) and \(z_k\) converge to the same limit, which belongs to \({\overline{\Omega }}\cap (\gamma {\setminus }\Omega )=\partial \Omega \cap \gamma \). Therefore there is \(i\in \{1,\dots , M\}\) with \(z_k\rightarrow x_i\), which means that for sufficiently large k we have \(z_k\in \gamma \cap B_\rho (x_i)\) and therefore \(z_k=x_i+t_kv_i\) for some \(t_k\rightarrow 0\), as \(z_k\in \Omega \) we have \(t_k\ge 0\). By (6.19) we have
This contradicts \({\varepsilon }_k\le {\textrm{dist}}(y_k,\Omega \cap \gamma )\le |y_k-x_i|\) and concludes the proof of (6.28).
We now observe that (6.28) implies \( \Omega {\setminus }(\Omega \cap \gamma )_{\varepsilon }\subseteq \Omega {\setminus }(\gamma )_{c_*{\varepsilon }}\) and therefore
For any \(s\in (0,1)\), if \({\varepsilon }\) is sufficiently small then \((c_*{\varepsilon })^s\ge {\varepsilon }\). Using first (6.4) and then (6.6),
As \(s\in (0,1)\) was arbitrary, this concludes the proof of (6.17). \(\square \)
We next come to the key construction for the proof of the upper bound. We define, given a pair \((\mu ,\beta )\in {\mathcal {M}}^1_{{\varepsilon }{\mathcal {B}}}(\Omega )\times L^1(\Omega ;\mathbb {R}^{3\times 3})\),
where \(E^{\textrm{elast}}\) and \({\mathcal {A}}^*_{\varepsilon }\) are defined in (3.37) and (3.36) respectively.
Theorem 6.5
Let \(\Omega \subseteq \mathbb {R}^3\) be a bounded Lipschitz set with connected boundary. Assume that W obeys \(H^{\textrm{W}}_{\textrm{Finite}}\) for some \(p\in (1,2]\). Let \((\mu ,\eta ,Q)\in {\mathcal {M}}_{\mathcal {B}}^1(\Omega )\times L^2(\Omega ;\mathbb {R}^{3\times 3})\times {\textrm{SO}}(3)\) with  and \(\mathop {\textrm{curl}}\eta =0\). Then for every sequence \({\varepsilon }_k\rightarrow 0\) and any \((h_{{\varepsilon }_k},\alpha _{{\varepsilon }_k})\) satisfying (3.38) there is \((\mu _k,\beta _k)\in {\mathcal {A}}_{{\varepsilon }_k}^*\), with \(\mu _k\) \((h_{{\varepsilon }_k},\alpha _{{\varepsilon }_k})\)-dilute, such that
and \(\mathop {\textrm{curl}}\eta =0\). Then for every sequence \({\varepsilon }_k\rightarrow 0\) and any \((h_{{\varepsilon }_k},\alpha _{{\varepsilon }_k})\) satisfying (3.38) there is \((\mu _k,\beta _k)\in {\mathcal {A}}_{{\varepsilon }_k}^*\), with \(\mu _k\) \((h_{{\varepsilon }_k},\alpha _{{\varepsilon }_k})\)-dilute, such that
and
for all \(q\in [1,2)\). Moreover
where \(\mathbb {C}:=D^2W({\textrm{Id}})\), \(\psi _\mathbb {C}^{\textrm{rel}}\) is defined as in (3.42), \(\mathbb {C}_Q\) as in (3.28) and
for all \(q\in [1,2)\).
Assume W obeys \(H^{\textrm{W}}_{\textrm{Lin}}\) for some \(p\in (1,2]\). Let \((\mu ,\eta )\in {\mathcal {M}}_{\mathcal {B}}^1(\Omega )\times L^2(\Omega ;\mathbb {R}^{3\times 3})\) with  and \(\mathop {\textrm{curl}}\eta =0\). Then the same holds with
and \(\mathop {\textrm{curl}}\eta =0\). Then the same holds with
in place of (6.34), \(\psi _\mathbb {C}^{\textrm{rel}}(b,t)\) in place of \(\psi _\mathbb {C}^{\textrm{rel}}{(b,Qt)}\) and \(\mathbb {C}\) in place of \(\mathbb {C}_Q\) in (6.35) and \(|\beta _k+\beta _k^T|^q\) in place of \({\textrm{dist}}^q(\beta _k,{\textrm{SO}}(3))\) in (6.36).
Proof
We prove the thesis in the finite case as the linear case can be treated similarly. As in [18, Proposition 6.8], the proof is divided in two steps. In the first one we provide an explicit construction attaining the unrelaxed limiting energy, and under the additional assumption that \(\eta \) is essentially bounded. In the second step we conclude by using a diagonal argument.
Step 1: We assume additionally that  is polyhedral, transversal to \(\partial \Omega \) in the sense of Lemma 6.3, which implies \(|\mu |(\partial \Omega )=0\), and that \(\eta \in L^\infty (\mathbb {R}^3;\mathbb {R}^{3\times 3})\) with \(\mathop {\textrm{curl}}\eta =0\). We first sketch the treatment of the rotation Q, ignoring \(\eta \) at first. Our aim is to define \(\beta _k\) as \(Q({\textrm{Id}}+{\varepsilon }_k\xi )\) for some matrix-valued field \(\xi \), and then to expand the energy, using the invariance (3.23) and then a Taylor series, as
is polyhedral, transversal to \(\partial \Omega \) in the sense of Lemma 6.3, which implies \(|\mu |(\partial \Omega )=0\), and that \(\eta \in L^\infty (\mathbb {R}^3;\mathbb {R}^{3\times 3})\) with \(\mathop {\textrm{curl}}\eta =0\). We first sketch the treatment of the rotation Q, ignoring \(\eta \) at first. Our aim is to define \(\beta _k\) as \(Q({\textrm{Id}}+{\varepsilon }_k\xi )\) for some matrix-valued field \(\xi \), and then to expand the energy, using the invariance (3.23) and then a Taylor series, as
with \(\mathbb {C}_Q\) defined as in (3.28). In particular, \(\xi \) should be chosen to solve the linear problem with coefficients \(\mathbb {C}_Q\), and to obey \(\mathop {\textrm{curl}}(Q\xi )=\mu \).
We now start the construction. Let \(\xi \in L^{3/2}(\mathbb {R}^3;\mathbb {R}^{3\times 3})\) be the solution to
as in Theorem 2.2. Clearly  is also transversal to \(\partial \Omega \). We define
is also transversal to \(\partial \Omega \). We define

Then clearly (6.33) holds and \((\mu _k,\beta _k)\in {\mathcal {A}}^*_{{\varepsilon }_k}\). Since \(\mu \) is polyhedral, by Theorem 2.2(iii) for all \(q\in [1,2)\) we have \(\xi \in L^q(\Omega ;\mathbb {R}^{3\times 3})\) which implies
and in particular (6.34) holds. Similarly,
The fist equality above is true since \(\eta \in L^\infty \) and \(|(\gamma )_{{\varepsilon }_k}|\le C{\varepsilon }_k^2\). The last one is a consequence of (2.7) in Theorem 2.2(iii) for \(\xi \), that satisfies (6.39).
Let \(s\in (0,1)\) be fixed. By the growth condition on W it holds
By Theorem 2.2(iii) and \(\eta \in L^\infty (\Omega ;\mathbb {R}^{3\times 3})\), for any \(x\in \Omega {\setminus }(\gamma )_{{\varepsilon }_k^s}\) we have
By frame indifference and Taylor expansion near the identity there is \(\omega \) with \(\omega (\delta )\rightarrow 0\) as \(\delta \rightarrow 0\) such that
pointwise, and
Now (6.3) in Proposition 6.1 yields
where in the last step we used Lemma 3.1(iii). Since \(\eta \in L^\infty (\Omega ;\mathbb {R}^{3\times 3})\) and \(\xi \in L^1(\Omega ;\mathbb {R}^{3\times 3})\) we derive that
Additionally, recalling (6.5)
As \( \omega (\delta _k)\rightarrow 0\), also the last error term in (6.43) vanishes in the limit.
Finally, again from \(\eta \in L^\infty (\Omega ;\mathbb {R}^{3\times 3})\) and (6.6) in Proposition 6.1 we obtain
By Lemma 6.3(ii) the same holds with the integration domain \({\Omega \cap (\gamma )_{{\varepsilon }_k^s}{\setminus } (\gamma \cap \Omega )_{{\varepsilon }_k}}\). Gathering together (6.42)–(6.47), we infer
for all \(s\in (0,1)\), and hence for \(s=1\).
Step 2: Let  , \(\eta \in L^2(\Omega ;\mathbb {R}^{3\times 3})\) with \(\mathop {\textrm{curl}}\eta =0\). We first approximate \(\eta \), and then \(\mu \).
, \(\eta \in L^2(\Omega ;\mathbb {R}^{3\times 3})\) with \(\mathop {\textrm{curl}}\eta =0\). We first approximate \(\eta \), and then \(\mu \).
We first show that we can construct a smooth sequence \(\eta _j\) with \(\mathop {\textrm{curl}}\eta _j=0\) such that \(\eta _j\rightarrow \eta \) strongly in \(L^2(\Omega ;\mathbb {R}^{3\times 3})\). To see this, observe that since \(\Omega \) is Lipschitz there are an open set \(\omega \) with \(\partial \Omega \subset \omega \) and a bilipschitz map \(\Phi :\omega \rightarrow \omega \) such that \(\Phi (x)=x\) for \(x\in \partial \Omega \) and \(\Phi (\Omega \cap \omega )=\omega {\setminus }{\overline{\Omega }}\). We extend \(\eta \) to \(\Omega \cup \omega \) by
Obviously \(\eta \in L^2(\Omega \cup \omega ;\mathbb {R}^{3\times 3})\). For every ball \(B\subset \omega \) such that \(B\cap \Omega \) is simply connected there is \(u\in W^{1,2}(B\cap \Omega ;\mathbb {R}^3)\) such that \(\eta =Du\) in \(B\cap \Omega \), and \(u\circ \Phi \) gives an extension of u to \(W^{1,2}(B\cup \Phi (B);\mathbb {R}^3)\). As \(\eta =D(u\circ \Phi )\) on \(\Phi (B){\setminus }\Omega \) we obtain \(\mathop {\textrm{curl}}\eta =0\) on \(\Omega \cup \omega \). We then define \(\eta _j\) as the mollification on scale 1/j of the extension. For every j we have \(\eta _j\in C^\infty (\overline{\Omega };\mathbb {R}^{3\times 3})\), \(\mathop {\textrm{curl}}\eta _j=0\), and
which implies
We now turn to the measure \(\mu \). By [14, Theorem 3.1 and Lemma 2.3] (see also [18, Theorem 6.5 and Lemma 6.2]) we can find a sequence  such that
such that  ,
,
and
By [18, Lemma 6.4], which we can apply by Lemma 2.5(iii), for every j there are a polyhedral measure  and a bijective map \(f^j\in C^1(\mathbb {R}^3;\mathbb {R}^3)\) such that
and a bijective map \(f^j\in C^1(\mathbb {R}^3;\mathbb {R}^3)\) such that
and, for some \(r_j>0\),
where \((\Omega )_{r_j}=\{x:{\textrm{dist}}(x,\Omega )<r_j\}\). Here \(f^j_\sharp \mu _j\) denotes the push-forward of the current corresponding to the measure \(\mu _j\), in the sense that

By Lemma 6.3(i) we can choose \(f_j\) and \(\mu _j\) such that \(\mu _j\) is transversal to \(\partial \Omega \) (possibly replacing \(f_j\) by \(f_j+a_j\), for some \(a_j\rightarrow 0\)). In particular it turns out that \(\mu _j{\displaystyle \mathop {\rightharpoonup }^*}\mu \) in \(\Omega \). Moreover since \(\mu _j\) is polyhedral it is \((h_{{\varepsilon }_k},\alpha _{{\varepsilon }_k})\)-dilute for sufficiently large k. By step 1 for every j there is \((\mu _k^j,\beta _k^j)\in {\mathcal {A}}_{{\varepsilon }_k}^*\) constructed as in (6.40) such that \({\varepsilon }_k^{-1}\mu _k^j=\mu _j\) and
for all \(q\in [1,2)\). Moreover
and
Further, from (6.49), (6.53) and (6.52) it follows that
To conclude it remains to construct a diagonal sequence. Notice first that for any fixed j there is \(k_j\in \mathbb {N}\) such that for \(k\ge k_j\) the following properties are satisfied:
-
(i)
 is \((h_{{\varepsilon }_k},\alpha _{{\varepsilon }_k})\)-dilute;
is \((h_{{\varepsilon }_k},\alpha _{{\varepsilon }_k})\)-dilute; -
(ii)
$$\begin{aligned}\left\| \frac{Q^T\beta _k^j-{\textrm{Id}}}{{\varepsilon }_k\log ^{1/2}\frac{1}{{\varepsilon }_k}} -{{\eta }}_j \right\| _{L^q(\Omega ;\mathbb {R}^{3\times 3})}\le \frac{1}{j} \quad \text { for all } q\in [1,2-\frac{1}{j}]; \end{aligned}$$
-
(iii)
$$\begin{aligned} \frac{1}{{\varepsilon }_k^2\log \frac{1}{{\varepsilon }_k}}\int _{\Omega \cap (\mathop {\textrm{supp}}\mu _k^j)_{{\varepsilon }_k}}{\textrm{dist}}^q(\beta ^j_k,{\textrm{SO}}(3)){\,dx}\le \frac{1}{j}\quad \text { for all } q\in [1,2-\frac{1}{j}]; \end{aligned}$$
-
(iv)
$$\begin{aligned} \frac{1}{{\varepsilon }_k^2\log \frac{1}{{\varepsilon }_k}}E^{\textrm{ub}}_{{\varepsilon }_k}[\mu _k^j,\beta ^j_k]\le \int _\Omega \frac{1}{2}\mathbb {C}_Q{{\eta }}_j\cdot {{\eta }}_j{\,dx}+ \int _{\Omega \cap \gamma _j}\psi _\mathbb {C}(b_j,Qt_j)d{\mathcal {H}}^1+\frac{1}{j}. \end{aligned}$$
Without loss of generality, \(k_j>k_{j-1}\). Finally for every \(k>0\) we take \({\tilde{\mu }}_k:=\mu _k^j\) and \({\tilde{\beta }}_k:=\beta _k^j\) if \(k\in [k_j,k_{j+1})\cap \mathbb {N}\), and this concludes the proof. \(\square \)
Remark 6.6
The same result as in Theorem 6.5 holds if \(E^{\textrm{ub}}_{\varepsilon }\) is replaced by
where \(E^{\textrm{elast}}\) and \({\mathcal {A}}^\textrm{moll}_{\varepsilon }\) are defined in (3.37) and (3.51) respectively. To see this, it suffices to replace the definition of \(\beta _k\) in (6.40) with
The computation leading to (6.43) is unchanged, with \(\xi *\varphi _{\varepsilon }\) in place of \(\xi \). Then one applies (6.3) in Proposition 6.1 to a larger set \((\Omega )_{r}\), for some \(r>0\). For almost all r we have \(|\mu |(\partial ((\Omega )_r))=0\), so that one obtains instead of (6.44)
By convexity this gives
for almost all \(r>0\), and since \(|\mu |(\partial \Omega )=0\) also with the integral over \(\Omega \cap \gamma \) in the right-hand side. In the rest of the estimates we need to use \(2{\varepsilon }_k^s\) instead of \({\varepsilon }_k^s\), without any significant change. For the estimate in (6.47) we separate the two terms. The first one is unchanged, since \(\eta \in L^\infty \). For the second one we use (6.6) in Proposition 6.1 on some \(\Omega _r\), so that by convexity we obtain (6.47) on \(\Omega \cap (\gamma )_{{\varepsilon }_k^s}{\setminus } (\gamma )_{2{\varepsilon }_k}\). It remains to deal with \((\gamma )_{2{\varepsilon }_k}\). This is treated by Remark 6.2, which shows that
Step 2 is unchanged.
7 Proofs of the main results
We start with the proof of our main result, Theorem 3.6.
Proof of Theorem 3.6
Compactness follows from Proposition 5.4. For the lower bound we use Theorem 5.5 with \(\rho _{\varepsilon }={\varepsilon }\) and (5.22). For the upper bound we use Theorem 6.5, observing that
The geometrically linear case is proven analogously. \(\square \)
We now turn to Theorem 3.10.
Proof of Theorem 3.10
(i): As in the proof of Theorem 3.6, the lower bound follows from Theorem 5.5 and the fact that
for every \(\rho \ge \rho _{\varepsilon }\) which follows as above from \({\mathcal {A}}_{\varepsilon }^*\subseteq {\mathcal {A}}_{\rho ,{\varepsilon }}^\textrm{core}\) for every \(\rho >0\).
For the upper bound we use Theorem 6.5, observing that \(\rho _{\varepsilon }\ge {\varepsilon }\) implies
(ii): For the lower bound we observe that
Hence the thesis follows again by Theorem 5.5.
For the upper bound we use Theorem 6.5, observing that
which again is a consequence of \({\mathcal {A}}^*_{\varepsilon }\subseteq {{\mathcal {A}}_{\rho _{\varepsilon },{\varepsilon }}^\textrm{core}}\) (see Lemma 3.8(iii)).
(iii): For lower bound we use Theorem 5.5 and the fact that
for every \(\rho \ge {\varepsilon }\) which follows from \({\mathcal {A}}_{\varepsilon }^\textrm{moll}\subseteq {\mathcal {A}}_{\rho ,{\varepsilon }}^\textrm{core}\) (see Lemma 3.8(ii)).
For the upper bound we use the same argument as in Theorem 6.5, as discussed in Remark 6.6 observing that
\(\square \)
Data Availability
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
References
Acharya, A., Bassani, J.L.: Lattice incompatibility and a gradient theory of crystal plasticity. J. Mech. Phys. Solids 48, 1565–1595 (2000)
Alberti, G., Baldo, S., Orlandi, G.: Variational convergence for functionals of Ginzburg–Landau type. Indiana Univ. Math. J. 54, 1411–1472 (2005)
Alicandro, R., Cicalese, M., Ponsiglione, M.: Variational equivalence between Ginzburg–Landau, XY-spin systems and screw dislocations energies. Indiana Univ. Math. J. 60, 171–208 (2011)
Alicandro, R., De Luca, L., Garroni, A., Ponsiglione, M.: Metastability and dynamics of discrete topological singularities in two dimensions: a \(\Gamma \)-convergence approach. Arch. Ration. Mech. Anal. 214, 269–330 (2014)
Ambrosio, L., Fusco, N., Pallara, D.: Functions of Bounded Variation and Free Discontinuity Problems. Mathematical Monographs, Oxford University Press, Oxford (2000)
Bourgain, J., Brezis, H.: New estimates for elliptic equations and Hodge type systems. J. Eur. Math. Soc. (JEMS) 9, 277–315 (2007)
Badal, R., Cicalese, M., Luca, L.D., Ponsiglione, M.: \(\Gamma \)-convergence analysis of a generalized XY model: fractional vortices and string defects. Commun. Math. Phys. 358, 1705–739 (2018)
Baldo, S., Jerrard, R.L., Orlandi, G., Soner, H.M.: Vortex density models for superconductivity and superfluidity. Commun. Math. Phys. 318, 131–171 (2013)
Conti, S., Dolzmann, G., Müller, S.: Korn’s second inequality and geometric rigidity with mixed growth conditions. Calc. Var. PDE 50, 437–454 (2014)
Cermelli, P., Gurtin, M.E.: On the characterization of geometrically necessary dislocations in finite plasticity. J. Mech. Phys. Solids 49, 1539–1568 (2001)
Cacace, S., Garroni, A.: A multi-phase transition model for the dislocations with interfacial microstructure. Interfaces Free Bound. 11, 291–316 (2009)
Conti, S., Garroni, A.: Sharp rigidity estimates for incompatible fields as a consequence of the Bourgain–Brezis div-curl result. C. R. Math. 359, 155–160 (2021)
Conti, S., Garroni, A., Müller, S.: Singular kernels, multiscale decomposition of microstructure, and dislocation models. Arch. Rat. Mech. Anal. 199, 779–819 (2011)
Conti, S., Garroni, A., Massaccesi, A.: Modeling of dislocations and relaxation of functionals on 1-currents with discrete multiplicity. Calc. Var. PDE 54, 1847–1874 (2015)
Conti, S., Garroni, A., Müller, S.: Dislocation microstructures and strain-gradient plasticity with one active slip plane. J. Mech. Phys. Solids 93, 240–251 (2016)
Conti, S., Garroni, A., Müller, S.: Derivation of strain-gradient plasticity from a generalized Peierls-Nabarro model. J. Eur. Math. Soc. (JEMS) 25, 2487–2524 (2023)
Conti, S., Garroni, A., Ortiz, M.: Derivation of a line-tension dislocation model starting from discrete crystal elasticity in 3D. In preparation
Conti, S., Garroni, A., Ortiz, M.: The line-tension approximation as the dilute limit of linear-elastic dislocations. Arch. Ration. Mech. Anal. 218, 699–755 (2015)
Cermelli, P., Leoni, G.: Renormalized energy and forces on dislocations. SIAM J. Math. Anal. 37, 1131–1160 (2005)
De Luca, L., Garroni, A., Ponsiglione, M.: \(\Gamma \)-convergence analysis of systems of edge dislocations: the self energy regime. Arch. Ration. Mech. Anal. 206, 885–910 (2012)
Friesecke, G., James, R.D., Müller, S.: A theorem on geometric rigidity and the derivation of nonlinear plate theory from three-dimensional elasticity. Commun. Pure Appl. Math. 55, 1461–1506 (2002)
Fanzon, S., Paolombaro, M., Ponsiglione, M.: Derivation of linearised polycrystals from a two-dimensional system of edge dislocations. SIAM J. Math. Anal. 51, 3956–3981 (2020)
Ginster, J.: Plasticity as the \(\Gamma \)-limit of a two-dimensional dislocation energy: the critical regime without the assumption of well-separateness. Arch. Ration. Mech. Anal. 233, 1253–1288 (2019)
Ginster, J.: Strain-gradient plasticity as the \(\Gamma \)-limit of a nonlinear dislocation energy with mixed growth. SIAM J. Math. Anal. 51, 3424–3464 (2019)
Garroni, A., Leoni, G., Ponsiglione, M.: Gradient theory for plasticity via homogenization of discrete dislocations. JEMS J. Eur. Math. Soc. 12, 1231–1266 (2010)
Garroni, A., Müller, S.: A variational model for dislocations in the line tension limit. Arch. Ration. Mech. Anal. 181, 535–578 (2006)
Garroni, A., Marziani, R., Scala, R.: Derivation of a line-tension model for dislocations from a nonlinear three-dimensional energy: the case of quadratic growth. SIAM J. Math. Anal. 53, 4252–4302 (2021)
Garroni, A., Spadaro, E.: Asymptotic analysis of Luckhaus–Lauteri energy for grain boundaries in polycrystals. In preparation. preprint arXiv:2306.07742
Hull, D., Bacon, D.J.: Introduction to Dislocations, 5th edn. Butterworth-Heinemann, Oxford (2011)
Hudson, T., Ortner, C.: Analysis of stable screw dislocation configurations in an antiplane lattice model. SIAM J. Math. Anal. 47, 291–320 (2015)
Jerrard, R.L.: Lower bounds for generalized Ginzburg–Landau functionals. SIAM J. Math. Anal. 30, 721–746 (1999)
Lauteri, G., Luckhaus, S.: An energy estimate for dislocation configurations and the emergence of Cosserat-type structures in metal plasticity. arXiv:1608.06155 (2017)
Luckhaus, S., Mugnai, L.: On a mesoscopic many-body Hamiltonian describing elastic shears and dislocations. Contin. Mech. Thermodyn. 22, 251–290 (2010)
Mielke, A., Müller, S.: Lower semicontinuity and existence of minimizers in incremental finite-strain elastoplasticity. ZAMM Z. Angew. Math. Mech. 86, 233–250 (2006)
Müller, S., Scardia, L., Zeppieri, C.I.: Gradient theory for geometrically nonlinear plasticity via the homogenization of dislocations. In: Conti, S., Hackl, K. (eds.) Analysis and Computation of Microstructure in Finite Plasticity, pp. 175–204. Springer, Berlin (2015)
Ponsiglione, M.: Elastic energy stored in a crystal induced by screw dislocations: from discrete to continuous. SIAM J. Math. Anal. 39, 449–469 (2007)
Reina, C., Conti, S.: Kinematic description of crystal plasticity in the finite kinematic framework: a micromechanical understanding of \(F=F^e F^p\). J. Mech. Phys. Solids 67, 40–61 (2014)
Sandier, E.: Lower bounds for the energy of unit vector fields and applications. J. Funct. Anal. 152, 379–403 (1998)
Sandier, E., Serfaty, S.: Vortices in the Magnetic Ginzburg–Landau Model. Progress in Nonlinear Differential Equations and Their Applications, vol. 70. Birkhäuser Boston, Inc., Boston (2007)
Svendsen, B.: Continuum thermodynamic models for crystal plasticity including the effects of geometrically-necessary dislocations. J. Mech. Phys. Solids 50, 1297–1329 (2002)
Scardia, L., Zeppieri, C.: Line-tension model for plasticity as the \(\Gamma \)-limit of a nonlinear dislocation energy. SIAM J. Math. Anal. 44, 2372–2400 (2012)
Acknowledgements
We thank Malte Borken for pointing out the mistake in [14, Lemma 2.3] mentioned after Definition 3.7 and the counterexample. This work was partially funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) via project 211504053 - SFB 1060, project 390685813 - GZ 2047/1 - HCM3, and project 2044-390685587 - “Mathematics Münster: Dynamics–Geometry–Structure” and by PRIN 2017BTM7SN_004 “Variational methods for stationary and evolution problems with singularities and interfaces”.
Funding
Open access funding provided by Università degli Studi di Roma La Sapienza within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Andrea Mondino.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Conti, S., Garroni, A. & Marziani, R. Line-tension limits for line singularities and application to the mixed-growth case. Calc. Var. 62, 228 (2023). https://doi.org/10.1007/s00526-023-02552-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00526-023-02552-0




 for countably many segments
for countably many segments 
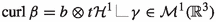 then
then 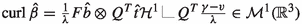 , where
, where  is
is