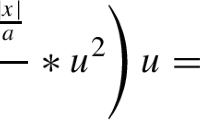Abstract
We prove a multiplicity result for
where (M, g) is a smooth and compact 3-dimensional Riemannian manifold without boundary, \(p\in (4,6)\), \(a,m,q\ne 0\), \(\varepsilon >0\) small enough. The proof of this result relies on Lusternik–Schnirellman category. We also provide a profile description for low energy solutions.
Similar content being viewed by others
Data availibility
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
Notes
Without the normalization of the constants, our results hold for every \(\omega ,q>0\) and \(2am<1\).
For completeness, in “Appendix A” we give some details.
Without the normalization of the constants assumed at the beginning of Sect. 2, we get \(u_{\varepsilon }(P)\ge \omega ^{\frac{1}{p-2}}\).
References
Ambrosetti, A., Malchiodi, A.: Nonlinear Analysis and Semilinear Elliptic Problems. Cambridge Studies in Advanced Mathematics, vol. 104. Cambridge University Press, Cambridge (2007)
Bahri, A., Coron, J.-M.: On a nonlinear elliptic equation involving the critical Sobolev exponent: the effect of the topology of the domain. Commun. Pure Appl. Math. 41, 253–294 (1988)
Benci, V., Bonanno, C., Micheletti, A.M.: On the multiplicity of solutions of a nonlinear elliptic problem on Riemannian manifolds. J. Funct. Anal. 252, 464–489 (2007)
Benci, V., Cerami, G.: The effect of the domain topology on the number of positive solutions of nonlinear elliptic problems. Arch. Ration. Mech. Anal. 114, 79–93 (1991)
Benci, V., Cerami, G., Passaseo, D.: On the number of the positive solutions of some nonlinear elliptic problems, 93–107. In: Ambrosetti, A., Marino, A. (eds.) Nonlinear Analysis. A tribute in honour of G. Prodi, Quaderni Sc. Norm. Super. di Pisa, Scuola Norm. Sup., Pisa (1991)
Bopp, F.: Eine Lineare Theorie des Elektrons. Ann. Phys. 430, 345–384 (1940)
Chen, S., Li, L., Rădulescu, V.D., Tang, X.: Ground state solutions of the non-autonomous Schrödinger–Bopp–Podolsky system. Anal. Math. Phys. 12, 32 (2022)
Chen, S., Tang, X.: On the critical Schrödinger–Bopp–Podolsky system with general nonlinearities. Nonlinear Anal. 195, 111734 (2020)
d’Avenia, P., Siciliano, G.: Nonlinear Schrödinger equation in the Bopp–Podolsky electrodynamics: solutions in the electrostatic case. J. Differ. Equ. 267, 1025–1065 (2019)
de Figueiredo, D.G.: Lectures on the Ekeland variational principle with applications and detours. In: Tata Institute of Fundamental Research Lectures on Mathematics and Physics, vol. 81. Springer, Berlin (1989)
Figueiredo, G.M., Siciliano, G.: Existence and asymptotic behaviour of solutions for a quasi-linear Schrödinger–Poisson system under a critical nonlinearity. Z. Angew. Math. Phys. 71, 130 (2020)
Figueiredo, G.M., Siciliano, G.: Multiple solutions for a Schrödinger–Bopp–Podolsky system with positive potentials. arXiv:2006.12637
Gidas, B., Ni, W.M., Nirenberg, L.: Symmetry of positive solutions of nonlinear elliptic equations in \({\mathbb{R}}^{n}\). In: Mathematical Analysis and Applications, Part A, Advances in Mathematics Supplementary Studies, vol. 7a, pp. 369–402. Academic Press, New York (1981)
Gilbarg, D., Trudinger, N.S.: Elliptic Partial Differential Equations of Second Order, 2nd edn. Springer, Berlin (1983)
Ghimenti, M., Micheletti, A.M.: Number and profile of low energy solutions for singularly perturbed Klein–Gordon–Maxwell systems on a Riemannian manifold. J. Differ. Equ. 256, 2502–2525 (2014)
Hebey, E.: Electro-magneto-static study of the nonlinear Schrödinger equation coupled with Bopp–Podolsky electrodynamics in the Proca setting. Discrete Contin. Dyn. Syst. 39, 6683–6712 (2019)
Hebey, E.: Strong convergence of the Bopp–Podolsky–Schrödinger–Proca system to the Schrödinger–Poisson–Proca system in the electro-magneto-static case. Calc. Var. Partial Differ. Equ. 59, 25 (2020)
Hebey, E.: Schrödinger–Poisson–Proca systems in EMS regime. Commun. Contemp. Math. 24, 2150038 (2022)
Hebey, E.: Blowing-up solutions to Bopp–Podolsky–Schrödinger–Proca and Schrödinger–Poisson–Proca systems in the electro-magneto-static case. Adv. Differ. Equ. 27, 253–332 (2022)
Kwong, M.K.: Uniqueness of positive solutions of \(\Delta u-u+u^p=0\) in \({\mathbb{R} }^n\). Arch. Ration. Mech. Anal. 105, 243–266 (1989)
Li, L., Pucci, P., Tang, X.: Ground state solutions for the nonlinear Schrödinger–Bopp–Podolsky system with critical Sobolev exponent. Adv. Nonlinear Stud. 20, 511–538 (2020)
Mascaro, B., Siciliano, G.: Positive Solutions For a Schrödinger–Bopp–Podolsky system in \({\mathbb{R}}^{3}\). arXiv:2009.08531
Peng, X., Jia, G.: Existence and concentration behavior of solutions for the logarithmic Schrödinger–Bopp–Podolsky system. Z. Angew. Math. Phys. 72, 198 (2021)
Podolsky, B.: A generalized electrodynamics. Phys. Rev. 62, 68–71 (1942)
Schoen, R., Yau, S.-T.: Lectures on Differential Geometry, International Press, 2010 by International Press, Somerville (1994)
Silva, K.: On an abstract bifurcation result concerning homogeneous potential operators with applications to PDEs. J. Differ. Equ. 269, 7643–7675 (2020)
Zheng, P.: Existence and finite time blow-up for nonlinear Schrödinger equations in the Bopp–Podolsky electrodynamics. J. Math. Anal. Appl. 514, 126346 (2022)
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by A. Neves.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The authors are members of GNAMPA (INdAM).
Pietro d’Avenia is partially supported by PRIN 2017JPCAPN Qualitative and quantitative aspects of nonlinear PDEs and by GNAMPA project Modelli EDP nello studio problemi della fisica moderna.
Marco G. Ghimenti is partially supported by GNAMPA project Modelli matematici con singolarità per fenomeni di interazione and by PRA 2022 Nonlinear dispersive equations and dynamics of fluids
Appendices
Appendix A. Ekeland principle
In this Appendix we want to show that (4.12) holds.
To this end, we proceed as in [3, Lemma 5.4], applying the Ekeland Principle (see [10, Chapter 4]) as follows:
for every \(\theta ,\iota >0\) and \(u\in J_\varepsilon ^{m_\varepsilon +\theta /2}\), there exists \(u_\iota \in {\mathcal {N}}_\varepsilon \) such that
Thus, for every k, taking \(\theta =4\delta _k\) and \(\iota =4\sqrt{\delta _k}\), there exists \({\tilde{u}}_k\in {\mathcal {N}}_{\varepsilon _{k}}\) such that
The boundedness of \(\{\Vert u_k\Vert _{\varepsilon _{k}}\}\) and (A.1) implies that \(\{\Vert {\tilde{u}}_k\Vert _{\varepsilon _{k}}\}\) is bounded too.
Observe, moreover, that, for every \(\xi \in T_{{\tilde{u}}_k}{\mathcal {N}}_{\varepsilon _{k}}\), there exists a smooth curve \(\gamma :[a,b]\rightarrow {\mathcal {N}}_{\varepsilon _{k}}\), with \(a<0<b\), such that
(see e.g. [1]).
Let \(\{t_n\}\subset {\mathbb {R}}\) such that \(t_n \rightarrow 0\).
Since
and
by the Ekeland Variational Principle, we get
Considering the left and right limits as \(t_n\rightarrow 0\) we can conclude that
Let now \(\varphi \in H^1(M)\) be arbitrary.
Since \({\tilde{u}}_k\in {\mathcal {N}}_{\varepsilon _{k}}\), by (iii) in Lemma 3.1,
Then \({\tilde{u}}_k\notin T_{{\tilde{u}}_k} {\mathcal {N}}_{\varepsilon _{k}}\). Thus there exists \(\lambda ,\mu \in {\mathbb {R}}\) and \(\xi \in T_{{\tilde{u}}_k} {\mathcal {N}}_{\varepsilon _{k}}\) such that \(\varphi =\lambda \xi + \mu {\tilde{u}}_k\).
Observe that, by (A.3), there exists \(C\in (0,1)\) such that for all \(u\in {\mathcal {N}}_{\varepsilon _{k}}, \xi \in T_u {\mathcal {N}}_{\varepsilon _{k}}\), \( |\langle \xi ,u\rangle _{\varepsilon _{k}}|\le C\Vert \xi \Vert _{\varepsilon _{k}} \Vert u\Vert _{\varepsilon _{k}}\). Then a straightforward calculation shows that there exists \(C>0\) such that \(\Vert \lambda \xi \Vert _{\varepsilon _k} \le C\Vert \varphi \Vert _{\varepsilon _k}\).
Then, by (A.2), we get that for every \(\varphi \in H^1(M)\)
Hence, we can conclude. Indeed, since
by (A.4), it is enough to prove that
This follows observing that
Then, by Hölder inequality and (A.1),
Moreover
Considering the first term in the right hand side of (A.6), by Lemma 2.1, Sobolev embedding \(H^2(M)\subset C^0(M)\), Hölder inequality, (2.1), the boundedness of \(\{\Vert u_k\Vert _{\varepsilon _{k}}\}\), and (A.1),
To estimate the second term in the right hand side of (A.6), first observe that
Then, using also Sobolev and Hölder inequalities, (2.1), (A.1), and the boundedness of \(\{\Vert u_k\Vert _{\varepsilon _{k}}\}\) and \(\{\Vert {\tilde{u}}_k\Vert _{\varepsilon _{k}}\}\),
Thus, using also Sobolev imbeddings, Hölder inequality, and (A.1),
Finally, by Lagrange Theorem, Hölder inequality, (2.1), boundedness of \(\{\Vert u_k\Vert _{\varepsilon _{k}}\}\) and \(\{\Vert {\tilde{u}}_k\Vert _{\varepsilon _{k}}\}\), (A.1), we have
completing the proof of (A.5).
Appendix B. Bootstrap argument
In this section, through a classical bootstrap argument, we prove that \(\{{\bar{v}}_{j}^{1}\} \subset C^{2}(B(0,R/2))\) and that it is bounded in \(C^{2}(B(0,R/2))\).
Let \(R>0\).
Observe that, arguing as in (5.1), for j large,
Thus, in B(0, R), since \(u_{\varepsilon _{j}}\) is a solution of (2.3), we have
But, since
(B.2) reads as
where
and \({\bar{\phi }}_j(z):=\phi _{u_{\varepsilon _j}} \big (\exp _{P^{1}}(Q_{\varepsilon _{j}}^{1}+\varepsilon _{j}z)\big )\).
Let us show that \({\bar{v}}_j^1 \in C^{0,\alpha }(B(0,R))\) for some \(\alpha \in (0,1)\).
Let us consider equation (B.3) in B(0, R) and let \(q_0:=6\). Since \(p \in (4, 6)\), then \(q_0/(p-1)\in (6/5,2)\). Thus
and so, using the boundedness of \(\{{\bar{v}}_j^1\}\) in \(H^1({\mathbb {R}}^3)\) and of \(\{\Vert u_{\varepsilon _{j}}\Vert _{\varepsilon _{j}}\}\), (B.1), and Lemma 2.1, \(f_j \in L^{q_0/(p-1)} (B(0,R))\) and
Hence, by (B.3),
and so, by a classical interpolation inequality, \({\bar{v}}_j^1 \in W^{2, q_0/(p-1)} (B(0,R))\) and
If \(q_0/(p-1)>3/2 \), namely if
we get that \({\bar{v}}_j^1\) is continuous and, by the previous arguments, \(\{{\bar{v}}_j^1\}\) is bounded in \(C^{0,\alpha }(B(0,R))\) for some \(\alpha \in (0,1)\).
If, instead, \(q_0/(p-1) \le 3/2\), namely if
or, equivalently, \( 5 \le p < 6\), then \(W^{2, q_0/(p-1)} (B(0,R))\) embeds in \(L^{q_1} (B(0,R))\) with
Then we consider
and we iterate the procedure.
So, at the nth step we take
and we consider
We can conclude if
which occurs in a finite number of steps since
namely for
Observe that, at each step, whenever
arguing as before we get that \(\{{\bar{v}}_j^1\}\) is bounded in \(C^{0,\alpha }(B(0,R))\) for some \(\alpha \in (0,1)\).
Now, let us write (B.3) as
The continuity of \({\bar{v}}_j^1\) implies that the right hand side of (B.4) is in \(L^2(B(0,R))\). In addition, also \(|\nabla ({\bar{v}}_j^1)^{p-1}| \in L^2(B(0,R))\) and so the right hand side of (B.4) is in \(H^1(B(0,R))\). Thus, [14, Theorem 8.10] implies that \({\bar{v}}_j^1\in W_\mathrm{loc}^{3,2}(B(0,2R/3))\) and so, by classical embeddings, \({\bar{v}}_j^1\in C^{1,\alpha }(B(0,2R/3))\) for some \(\alpha \in (0,1)\). Then, repeating the procedure we get that \({\bar{v}}_j^1\in C^{2,\alpha }(B(0,R/2))\) for some \(\alpha \in (0,1)\) and, by Schauder estimate [14, page 93],
Rights and permissions
Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
d’Avenia, P., Ghimenti, M.G. Multiple solutions and profile description for a nonlinear Schrödinger–Bopp–Podolsky–Proca system on a manifold. Calc. Var. 61, 223 (2022). https://doi.org/10.1007/s00526-022-02341-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00526-022-02341-1