1 Introduction

The aircraft landing gear is the most important part of the aircraft in terms of safety on land due to its functional mission. The first task of the landing gear is to absorb the horizontal and vertical kinetic energy, ensuring stability and safety on the runway. For this reason, with the advent of modern aircraft, more efficient landing gears have been developed. Due to the increasing weight and landing speeds of aircraft, energy dissipation has become necessary to protect the fuselage from ground loads on the runway.

Shimmy dampers are passive solutions for unwanted roll vibrations in the aircraft landing gear. Although they dampen vibrations substantially, when added to existing landing gear systems, they can bring weight, cost and safety issues. Li et al. [1] have been designed a device to dampen the shimmy vibrations that occur in the main landing gear. They developed a nonlinear mathematical model to represent the landing gear dynamics. As a result of the analysis, it has been seen that the proposed device is more efficient than conventional dampers. Rahmani and Behdinan [2] have been presented a new damper concept. The designed damper is suitable for installation on the existing landing gear and includes damping units. In another study, they have been investigated the effect of torque link Freeplay on the Coulomb frictions that occur in the nose landing gear [3]. Tourajizedeh and Zare [4] have been performed robust and optimal control of shimmy vibrations in the nose landing gear.

Vibration in the aircraft's landing gear causes fatigue tension in its mechanical elements. This causes high wear and damage to the landing gear components. Orlando [5] has been proposed an adaptive controller that damps vibrations under disturbing effects to prevent this security problem. Laporte et al. [6] has designed a landing gear free from the dynamic behaviour of shimmy vibrations. Huynh et al. [7] have been presented a new active controller to prevent roll oscillations occurring in the nose landing gear. Simulations have shown that the controller can effectively dampen shimmy vibrations for different scenarios. Wang et al. [8] have been developed a mathematical model to control aircraft vibrations occurring due to disturbances in the runway. According to the results of the simulation, the impact loads and the vertical displacement of the aircraft formed instantly reduced with the use of the active controller. Luong et al. [9] have been used genetic algorithm and artificial neural networks (ANN) controllers for the control of MR damper landing gear. Analysis results have been revealed the effectiveness of the designed controller. Jo et al. [10] have been developed a two degree of freedom model to validate the performance of MR dampers for light aircraft landing gear. Lee et al. [11] have been used a different approach in their study and modelled the behaviour of the MR damper landing gear under irregular impacts during taxiing with Monte Carlo analysis. Viet et al. [12] have been researched sliding mode control for MR damper landing gear.

The stability of the aircraft during taxiing, as well as during landing and take-off, is one of the important issues in the development of aircraft. Sivakumar and Haran [13] have been examined the vibrations occurring in the landing gear of unmanned aerial vehicles in their study. They investigated the optimization of aircraft mass and torsional damping under the influence of shimmy vibrations. Thus, it is aimed to extend the life of the landing gear and prevent potential risks related to oscillations. In another study, they have been analysed random vibrations in the random ground profile of passive and active landing gear [14]. The results obtained in the study showed that the vibration level in the active landing gear was lower than in the conventional landing gear. Yazıcı and Sever [15] have been performed active vibration control for a full aircraft model with 11 degrees of freedom. They designed an observation-based optimal controller with the linear matrix inequities approach to dampen the vibrations originating from the ground during taxiing. Simulation results showed that the proposed controller reduces vibration amplitudes in the aircraft fuselage. Quang-Ngoc et al. [16] have been controlled the aircraft landing gear equipped with MR damper with intelligent control and model predictive control approach. They used these two different control approaches to solve the nonlinear behaviour and delay time problems in the MR tipper semi-active landing gear.

In the literature, it is possible to come across many studies aimed at dampening the vibrations called shimmy that aircrafts are exposed to. In this sense, in addition to the existing suspension systems of the landing gear, ER and MR dampers were integrated to dampen vibrations. In this study, it is aimed to contribute to the literature by controlling the angular position variables of the landing gear mechanism, in addition to the semi-active suspension systems in the passenger aircraft landing gear. Simulations were made for two different landing speeds and different runway pavement surfaces. The equations of the angular joint variables of the six-linked landing gear mechanism were obtained, and transfer functions and state-spaces were created. The landing gear system was modelled in the Simulink environment under the influence of disturbances (aerodynamic and reaction forces). While analysing the landing gear subject to the study, the A320 model aircraft of Airbus company, which is the most popular passenger aircraft in the fleets of airline companies around the world, was taken as reference.

The motivation in this study is that the aircraft is exposed to very big vibrations during landing, and this is an undesirable situation for both aircraft equipment and passengers in terms of comfort and safety. Unlike other studies, the novelty of this article is that the angular displacement of the landing gear mechanism is controlled by the proposed controller. In this study, a neural network control system for aircraft landing gear’s vibration control is proposed. The paper firstly explains the dynamic of the landing gear mechanism. Then, the proposed neural controller and PID controller are defined. The results of proposed neural control system and PID control system are presented and debated. In conclusion, the efficiency of proposed control method is determined.

2 Dynamic of the landing gear mechanism

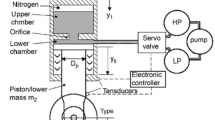
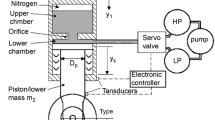
To explain the dynamics of a landing gear mechanism, four degrees of freedom (DOF) mathematical model is used and is presented in Fig. 1. The model, containing the link lengths (L2, L3, L4, L5 and L6), angular joint variables (θ2, θ3, θ4, θ5 and θ6), link mass (m2, m3, m4, m5 and m6) and external forces (Ff, N) of the landing gear mechanism.

Fig. 1
figure 1

a Landing gear mechanism axis and angular joint variables and b physical model of the landing gear system

Full size image

As shown in Fig. 1, Link 2 and Link 3 represent the side-stay strut. Link 4 and Link 5 denote the unlock mechanism, and Link 6 is the main strut. The main strut contains the support shaft and shock absorber. The strut, which is described as the leg of the landing gear, supports the shaft together with the shock absorber. Structural parameters of the Airbus A320 aircraft main landing gear are given in Table 1.

Table 1 Landing gear mechanism structural parameters [17]
Full size table

The dynamics of the landing gear mechanism is derived using Lagrangian equations.

$$\mathcal{L}={K}_{E}-{P}_{E}.$$
(1)

The Euler–Lagrangian equations can be solved by taking partial derivatives of the kinetic energy and potential energy properties of the system. Thus, the equation of motion of the system is obtained.

$$\frac{{\text{d}}}{{\text{d}}(t)}=\left(\frac{\partial \mathcal{L}}{\partial {\dot{\theta }}_{n}}\right)-\frac{\partial \mathcal{L}}{\partial {\dot{\theta }}_{n}}={\tau }_{n}.$$
(2)

where θn is the angular joint variable of joints, and τn is the torque applied to the links. The positions of the links are calculated as a function of the angular joint variables in the Y–Z coordinate plane using the forward kinematic equations.

$${y}_{2}={L}_{2}\cdot {\text{cos}}{\theta }_{2},$$
(3)
$${z}_{2}=-{L}_{2}\cdot \sin{\theta }_{2},$$
(4)
$${y}_{3}={L}_{2}\cdot \cos{\theta }_{2}+{L}_{3}\cdot \cos\left({\theta }_{2}+{\theta }_{3}\right),$$
(5)
$${z}_{3}=-{L}_{2}\cdot \sin{\theta }_{2}-{L}_{3}\cdot {\text{sin}}\left({\theta }_{2}+{\theta }_{3}\right),$$
(6)
$${y}_{4}={L}_{2} \cdot \cos{\theta }_{2}+{L}_{4}\cdot {\text{cos}}\left({\theta }_{4}+{\theta }_{2}\right),$$
(7)
$${z}_{4}=-{L}_{2}\cdot \sin{\theta }_{2}-{L}_{4}\cdot {\text{sin}}\left({\theta }_{4}+{\theta }_{2}\right),$$
(8)
$${y}_{5}={L}_{6}\cdot \cos{\theta }_{6}+{L}_{5} \cdot {\text{cos}}\left({\theta }_{5}+{\theta }_{6}\right),$$
(9)
$${z}_{5}=-{L}_{6}\cdot \sin{\theta }_{6}-{L}_{5}\cdot {\text{sin}}\left({\theta }_{5}+{\theta }_{6}\right),$$
(10)
$${y}_{6}={L}_{6}\cdot \cos{\theta }_{6},$$
(11)
$${z}_{6}=-{L}_{6}\cdot \sin{\theta }_{6}.$$
(12)

Kinetic and potential energy equations of L2 link;

$${K}_{E2}=\frac{1}{2}{m}_{2}{{L}_{2}}^{2}{\dot{\theta }}_{2}^{2},$$
(13)
$${P}_{E2}={m}_{2}g{L}_{2}\sin{\theta }_{2}.$$
(14)

Kinetic and potential energy equations of L3 link;

$${K}_{E3}=\frac{1}{2}{m}_{3}{L}_{2}^{2}{\dot{\theta }}_{2}^{2}+\frac{1}{2}{m}_{3}{L}_{3}^{2}{({\dot{\theta }}_{2}+{\dot{\theta }}_{3})}^{2}+{m}_{3}{L}_{2}{L}_{3}\left({\dot{\theta }}_{2}^{2}+{\dot{\theta }}_{2}{\dot{\theta }}_{3}\right)\cos{\theta }_{3},$$
(15)
$${P}_{E3}=-{m}_{3}g{L}_{2}\sin{\theta }_{2}-{m}_{3}g{L}_{3}\sin\left({\theta }_{2}+{\theta }_{3}\right).$$
(16)

Kinetic and potential energy equations of L4 link;

$${K}_{E4}=\frac{1}{2}{m}_{4}{L}_{2}^{2}{\dot{\theta }}_{2}^{2}+\frac{1}{2}{m}_{4}{L}_{4}^{2}{({\dot{\theta }}_{2}+{\dot{\theta }}_{4})}^{2}+{m}_{4}{L}_{2}{L}_{4}\left({\dot{\theta }}_{2}^{2}+{\dot{\theta }}_{2}{\dot{\theta }}_{4}\right)\cos{\theta }_{4},$$
(17)
$${P}_{E4}=-{m}_{4}g{L}_{2}\sin{\theta }_{2}-{m}_{4}g{L}_{4}\sin\left({\theta }_{2}+{\theta }_{4}\right).$$
(18)

Kinetic and potential energy equations of L5 link;

$${K}_{E5}=\frac{1}{2}{m}_{5}{L}_{6}^{2}{\dot{\theta }}_{6}^{2}+\frac{1}{2}{m}_{5}{L}_{5}^{2}{({\dot{\theta }}_{5}+{\dot{\theta }}_{6})}^{2}+{m}_{5}{L}_{2}{L}_{5}\left({\dot{\theta }}_{6}^{2}+{\dot{\theta }}_{5}{\dot{\theta }}_{6}\right)\cos{\theta }_{5},$$
(19)
$${P}_{E5}=-{m}_{5}g{L}_{6}\sin{\theta }_{5}-{m}_{5}g{L}_{5}\sin\left({\theta }_{6}+{\theta }_{5}\right).$$
(20)

Kinetic and potential energy equations of L6 link;

$${K}_{E6}=\frac{1}{2}{m}_{6}{{L}_{6}}^{2}{\dot{\theta }}_{6}^{2},$$
(21)
$${P}_{E6}={m}_{6}g{L}_{6}\sin{\theta }_{6}.$$
(22)

These energy equations are created to the Lagrangian equations, and the following nonlinear equations of the landing gear mechanism are obtained.

$${\mathcal{L}}_{23}={K}_{E2}+{K}_{E3}-{P}_{E2}-{P}_{E3},$$
(23)
$${\mathcal{L}}_{23}=\frac{1}{2}{m}_{2}{{L}_{2}}^{2}{\dot{\theta }}_{2}^{2}+\frac{1}{2}{m}_{3}{L}_{2}^{2}{\dot{\theta }}_{2}^{2}+\frac{1}{2}{m}_{3}{L}_{3}^{2}{\left({\dot{\theta }}_{2}+{\dot{\theta }}_{3}\right)}^{2}$$
$$+{m}_{3}{L}_{2}{L}_{3}\left({\dot{\theta }}_{2}^{2}+{\dot{\theta }}_{2}{\dot{\theta }}_{3}\right)\cos{\theta }_{3}-{m}_{3}g{L}_{2}\sin{\theta }_{2}-{m}_{3}g{L}_{3}\sin\left({\theta }_{2}+{\theta }_{3}\right)$$
$$-{m}_{2}g{L}_{2}\sin{\theta }_{2}+{m}_{3}g{L}_{2}\sin{\theta }_{2}+{m}_{3}g{L}_{3}\sin\left({\theta }_{2}+{\theta }_{3}\right).$$
(24)
$${\mathcal{L}}_{24}={K}_{E2}+{K}_{E4}-{P}_{E2}-{P}_{E4},$$
(25)
$${\mathcal{L}}_{24}=\frac{1}{2}{m}_{2}{{L}_{2}}^{2}{\dot{\theta }}_{2}^{2}+\frac{1}{2}{m}_{4}{L}_{2}^{2}{\dot{\theta }}_{2}^{2}+\frac{1}{2}{m}_{4}{L}_{4}^{2}{\left({\dot{\theta }}_{2}+{\dot{\theta }}_{4}\right)}^{2}+{m}_{4}{L}_{2}{L}_{4}\left({\dot{\theta }}_{2}^{2}+{\dot{\theta }}_{2}{\dot{\theta }}_{4}\right)\cos{\theta }_{4}-{m}_{2}g{L}_{2}\sin{\theta }_{2}+ {m}_{3}g{L}_{2}\sin{\theta }_{2}+{m}_{3}g{L}_{3}\sin\left({\theta }_{2}+{\theta }_{3}\right).$$
(26)
$${\mathcal{L}}_{65}={K}_{E6}+{K}_{E5}-{P}_{E6}-{P}_{E5},$$
(27)
$${\mathcal{L}}_{65}=\frac{1}{2}{m}_{6}{{L}_{6}}^{2}{\dot{\theta }}_{6}^{2}+\frac{1}{2}{m}_{5}{L}_{6}^{2}{\dot{\theta }}_{6}^{2}+\frac{1}{2}{m}_{5}{L}_{5}^{2}{({\dot{\theta }}_{5}+{\dot{\theta }}_{6})}^{2}+{m}_{5}{L}_{2}{L}_{5}\left({\dot{\theta }}_{6}^{2}+{\dot{\theta }}_{5}{\dot{\theta }}_{6}\right)\cos{\theta }_{5}-{m}_{6}g{L}_{6}\sin{\theta }_{6}+{m}_{5}g{L}_{6}\sin{\theta }_{5}+{m}_{5}g{L}_{5}\sin\left({\theta }_{6}+{\theta }_{5}\right).$$
(28)

Using the Lagrangian equation, the torque forces of the five links are obtained as follows.

$${\tau }_{2}=\left(\left({m}_{2}+{m}_{3}\right){L}_{2}^{2}+{m}_{3}{L}_{3}^{2}+2{m}_{3}{L}_{2}{L}_{3}\cos{\theta }_{3}\right){\ddot{\theta }}_{2}+\left({m}_{3}{L}_{3}^{2}+{m}_{3}{L}_{2}{L}_{3}\cos{\theta }_{3}\right){\ddot{\theta }}_{3}-{m}_{3}{L}_{2}{L}_{3}\left(2{\dot{\theta }}_{2}{\dot{\theta }}_{3}+{\dot{\theta }}_{3}^{2}\right)\sin{\theta }_{3}+\left({m}_{2}-{m}_{3}\right)g{L}_{2}\cos{\theta }_{2}-{m}_{3}g{L}_{3}{\text{cos}}\left({\theta }_{2}+{\theta }_{3}\right),$$
(29)
$${\tau }_{3}={m}_{3}{L}_{3}^{2}{\ddot{\theta }}_{3}+\left({m}_{3}{L}_{3}^{2}+{m}_{3}{L}_{2}{L}_{3}\cos{\theta }_{3}\right){\ddot{\theta }}_{2}+{m}_{3}{L}_{2}{L}_{3}{\ddot{\theta }}_{2}^{2}\sin{\theta }_{3}-{m}_{3}g{L}_{3}{\text{cos}}\left({\theta }_{2}+{\theta }_{3}\right),$$
(30)
$${\tau }_{4}={m}_{4}{L}_{4}^{2}{\ddot{\theta }}_{4}+\left({m}_{4}{L}_{4}^{2}+{m}_{4}{L}_{2}{L}_{4}\cos{\theta }_{4}\right){\ddot{\theta }}_{2}+{m}_{4}{L}_{2}{L}_{4}{\ddot{\theta }}_{2}^{2}\sin{\theta }_{4}-{m}_{4}g{L}_{4}{\text{cos}}\left({\theta }_{2}+{\theta }_{4}\right),$$
(31)
$${\tau }_{5}={m}_{5}{L}_{5}^{2}{\ddot{\theta }}_{5}+\left({m}_{5}{L}_{5}^{2}+{m}_{5}{L}_{6}{L}_{5}\cos{\theta }_{5}\right){\ddot{\theta }}_{6}+{m}_{5}{L}_{6}{L}_{5}{\ddot{\theta }}_{6}^{2}\sin{\theta }_{5}-{m}_{5}g{L}_{5}{\text{cos}}\left({\theta }_{6}+{\theta }_{5}\right),$$
(32)
$${\tau }_{6}=\left(\left({m}_{6}+{m}_{5}\right){L}_{6}^{2}+{m}_{5}{L}_{5}^{2}+2{m}_{5}{L}_{6}{L}_{5}\cos{\theta }_{5}\right){\ddot{\theta }}_{6}+\left({m}_{5}{L}_{5}^{2}+{m}_{5}{L}_{6}{L}_{5}\cos{\theta }_{5}\right){\ddot{\theta }}_{5}-{m}_{5}{L}_{6}{L}_{5}\left(2{\dot{\theta }}_{6}{\dot{\theta }}_{5}+{\dot{\theta }}_{5}^{2}\right)\sin{\theta }_{5}+\left({m}_{6}-{m}_{5}\right)g{L}_{6}\cos{\theta }_{6}-{m}_{5}g{L}_{5}{\text{cos}}\left({\theta }_{6}+{\theta }_{5}\right).$$
(33)

The second-order differential equations describing the movement of the landing gear mechanism are given as follows.

$${\ddot{\theta }}_{2}=\frac{1}{\left(\left({m}_{2}+{m}_{3}\right){L}_{2}^{2}+{m}_{3}{L}_{3}^{2}+2{m}_{3}{L}_{2}{L}_{3}\cos{\theta }_{3}\right)}[{\tau }_{1}-\left({m}_{3}{L}_{3}^{2}+{m}_{3}{L}_{2}{L}_{3}\cos{\theta }_{3}\right){\ddot{\theta }}_{3}+{m}_{3}{L}_{2}{L}_{3}\left(2{\dot{\theta }}_{2}{\dot{\theta }}_{3}+{\dot{\theta }}_{3}^{2}\right)\sin{\theta }_{3}-\left({m}_{2}-{m}_{3}\right)g{L}_{2}\cos{\theta }_{2}+{m}_{3}g{L}_{3}{\text{cos}}\left({\theta }_{2}+{\theta }_{3}\right),$$
(34)
$${\ddot{\theta }}_{3}=\frac{1}{{m}_{3}{L}_{3}^{2}}[{\tau }_{3}-\left({m}_{3}{L}_{3}^{2}+{m}_{3}{L}_{2}{L}_{3}\cos{\theta }_{3}\right){\ddot{\theta }}_{2}-{m}_{3}{L}_{2}{L}_{3}{\ddot{\theta }}_{2}^{2}\sin{\theta }_{3}+{m}_{3}g{L}_{3}{\text{cos}}\left({\theta }_{2}+{\theta }_{3}\right),$$
(35)
$${\ddot{\theta }}_{4}=\frac{1}{{m}_{4}{L}_{4}^{2}}[{\tau }_{4}-\left({m}_{4}{L}_{4}^{2}+{m}_{4}{L}_{2}{L}_{4}\cos{\theta }_{4}\right){\ddot{\theta }}_{2}-{m}_{4}{L}_{2}{L}_{4}{\ddot{\theta }}_{2}^{2}\sin{\theta }_{4}+{m}_{4}g{L}_{4}{\text{cos}}\left({\theta }_{2}+{\theta }_{4}\right),$$
(36)
$${\ddot{\theta }}_{5}=\frac{1}{{m}_{5}{L}_{5}^{2}}[{\tau }_{5}-\left({m}_{5}{L}_{5}^{2}+{m}_{5}{L}_{6}{L}_{5}\cos{\theta }_{5}\right){\ddot{\theta }}_{6}-{m}_{5}{L}_{6}{L}_{5}{\ddot{\theta }}_{6}^{2}\sin{\theta }_{5}+{m}_{5}g{L}_{5}{\text{cos}}\left({\theta }_{6}+{\theta }_{5}\right),$$
(37)
$${\ddot{\theta }}_{6}=\frac{1}{\left(\left({m}_{6}+{m}_{5}\right){L}_{6}^{2}+{m}_{5}{L}_{5}^{2}+2{m}_{5}{L}_{6}{L}_{5}\cos{\theta }_{5}\right)}[{\tau }_{6}-\left({m}_{5}{L}_{5}^{2}+{m}_{5}{L}_{6}{L}_{5}\cos{\theta }_{5}\right){\ddot{\theta }}_{5}+{m}_{5}{L}_{6}{L}_{5}\left(2{\dot{\theta }}_{6}{\dot{\theta }}_{5}+{\dot{\theta }}_{5}^{2}\right)\sin{\theta }_{5}-\left({m}_{6}-{m}_{5}\right)g{L}_{6}\cos{\theta }_{6}+{m}_{5}g{L}_{5}{\text{cos}}\left({\theta }_{6}+{\theta }_{5}\right).$$
(38)

External forces acting on the landing gear mechanism can be defined as friction force and ground reaction force. The torque that occurs in the joints due to the effect of external forces can be calculated using the inverse of the Jacobian matrix.

$${F}_{f}={\mu }_{k}\cdot N,$$
(39)
$${\tau }_{T}=\tau +{J}^{T}\cdot {F}_{ex},$$
(40)
$${J}^{T}\cdot {F}_{ex}= \left[\begin{array}{cc}\frac{\partial {y}_{3}}{\partial {\theta }_{2}}& \frac{\partial {z}_{3}}{\partial {\theta }_{2}}\\ \frac{\partial {y}_{3}}{\partial {\theta }_{3}}& \frac{\partial {z}_{3}}{\partial {\theta }_{3}}\end{array}\right]\cdot \left[\begin{array}{c}{F}_{f}\\ N\end{array}\right].$$
(41)

where Ff is the friction force, N is the ground reaction force, Fex is the external forces, µk is the friction coefficient of the ground, τT is the total torque and JT is the transpose of the Jacobian matrix.

3 Control systems

In this study, angular joint variables of the landing gear mechanism are controlled, and different control organs are used to approximate the variables to the reference value. The transfer functions and state-spaces of the angular joint variables, which are detailed in Sect. 2, are presented below. Angular joint variable transfer function and state-space of L2 link;

$$\frac{{\theta }_{2}\left(s\right)}{{\tau }_{2}(s)}=\frac{-148{s}^{2}+1275s+5574}{250{s}^{4}+288{s}^{3}+354.5{s}^{2}+11.5s+8.054},$$
(42)
$${\varvec{A}}=\left[\begin{array}{cccc}-1.1528& -1.4188& -0.0460& -0.0324\\ 1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\end{array}\right], {\varvec{B}}=\left[\begin{array}{c}1\\ 0\\ 0\\ 0\end{array}\right],$$
$${\varvec{C}}=\left[\begin{array}{cccc}0& -0.5919& 50.9968& 22.2962\end{array}\right],{\varvec{D}}=0.$$
(43)

Angular joint variable transfer function and state-space of L3 link;

$$\frac{{\theta }_{3}\left(s\right)}{{\tau }_{3}(s)}=\frac{-137{s}^{2}+1135s+5244}{230{s}^{4}+271{s}^{3}+334.5{s}^{2}+10.5s+7.154},$$
(44)
$${\varvec{A}}=\left[\begin{array}{cccc}-1.1326& -1.3842& -0.0360& -0.0221\\ 1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\end{array}\right], {\varvec{B}}=\left[\begin{array}{c}1\\ 0\\ 0\\ 0\end{array}\right],$$
$${\varvec{C}}=\left[\begin{array}{cccc}0& -0.4819& 47.9458& 18.2232\end{array}\right], {\varvec{D}}=0.$$
(45)

Angular joint variable transfer function and state-space of L4 link;

$$\frac{{\theta }_{4}\left(s\right)}{{\tau }_{4}(s)}=\frac{-9.8{s}^{3}+268{s}^{2}+13.28s-8.587}{210{s}^{4}+204{s}^{3}+214.5{s}^{2}+9.5s+7.054},$$
(46)
$${\varvec{A}}=\left[\begin{array}{cccc}-1.0728& -1.3210& -0.0660& -0.0424\\ 1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\end{array}\right], {\varvec{B}}=\left[\begin{array}{c}1\\ 0\\ 0\\ 0\end{array}\right],$$
$${\varvec{C}}=\left[\begin{array}{cccc}0& -0.4219& 38.2468& 17.2322\end{array}\right],D=0.$$
(47)

Angular joint variable transfer function and state-space of L5 link;

$$\frac{{\theta }_{5}\left(s\right)}{{\tau }_{5}(s)}=\frac{-9.8{s}^{3}+268{s}^{2}+13.28s-7.5427}{210{s}^{4}+204{s}^{3}+214.5{s}^{2}+9.5s+6.154},$$
(48)
$$ \begin{aligned} {\varvec{A}} & =\left[\begin{array}{cccc}-1.0728& -1.3210& -0.0660& -0.0317\\ 1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\end{array}\right],{\varvec{B}}=\left[\begin{array}{c}1\\ 0\\ 0\\ 0\end{array}\right],\\ {\varvec{C}} &=\left[\begin{array}{cccc}0& -0.4219& 38.2468& 17.1722\end{array}\right], \quad D=0. \end{aligned}$$
(49)

Angular joint variable transfer function and state-space of L6 link;

$$\frac{{\theta }_{6}\left(s\right)}{{\tau }_{6}(s)}=\frac{-273.5{s}^{2}+181s+9.337}{254{s}^{4}+298.2{s}^{3}+354.5{s}^{2}+11.5s+8.092},$$
(50)
$$ \begin{aligned} {\varvec{A}} &=\left[\begin{array}{cccc}-1.1728& -1.6188& -0.0260& -0.0224\\ 1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\end{array}\right], {\varvec{B}}=\left[\begin{array}{c}1\\ 0\\ 0\\ 0\end{array}\right], \\ {\varvec{C}} &=\left[\begin{array}{cccc}0& -0.6319& 52.9968& 24.9162\end{array}\right],D=0. \end{aligned}$$
(51)

The closed-loop control block diagram for the control of the angular joint variables of the landing gear is given in Fig. 2. The input value of the block diagram is the reference value of the angular joint variable. Ground reaction force and aerodynamic forces during landing are defined as disturbance magnitudes. With the input of the controller, the appropriate torque force is produced and given as an input to the dynamic model. The dynamic model calculates the available joint angles and uses them as feedback to the controller. The damping has been neglected while performing the analyses, and the maximum force that the aircraft can be exposed to at the moment of landing on the runway has been taken into account. In this study, analysis is performed for asphalt (µasphalt) and concrete (µconcrete) and pavement surfaces under the control of the angular joint variables of the landing gear mechanism. The friction coefficients for these runway pavements are given in Table 2 [19].

Fig. 2
figure 2

Closed-loop control block diagram

Full size image
Table 2 Friction coefficients of different runway pavement surfaces [19]
Full size table

Here θi(t)ref is the reference value of ith link angular joint variable, θi(t) is the output of the control system, τi is the torque of ith link, τT is the total torque, Fex is the external forces acting on the landing gear system and Faero is the aerodynamic force.

3.1 PID controller

PID controller comprises proportional P(e(t)), integral I(e(t)) and derivative D(e(t)) sections. It is a control effect that combines the superiorities of three main control effects under a single unit. The control signal u(t) produced by the controller is time-dependent and is given by:

$$u\left(t\right)={K}_{p}e\left(t\right)+{K}_{i}{\int }_{0}^{t}e(t)+{K}_{d}\frac{de(t)}{dt}.$$
(52)

The e(t) function, which is defined as the error function, is the difference between desired response and the actual response, and it changes depending on time. Kp is denoted proportional gain, Ki is the integral gain and Kd is the derivative gain. Also, Zeigler–Nichols methods are used to settle the optimum PID gain parameters. PID gain parameters are presented in Table 3.

Table 3 PID gain parameters
Full size table

3.2 Neural network controller

A neural network controller typically includes two stages: system definition and control designing. The feed-forward neural network structure is used to control the angular joint variables of the landing gear mechanism. The schematic view of the developed neural network model is given in Fig. 3.

Fig. 3
figure 3

Schematic representation of feed-forward neural network structure

Full size image

The output of the hidden layer;

$${Z}_{j}\left(t\right)=f\left[\sum_{i=1}^{10}{[\theta }_{i}\left(t\right){w}_{1j}\left(t\right)+{\theta }_{g}(t){w}_{2j}]+1\right].$$
(53)

The output of this layer is passed through the nonlinear activation function. The output of the hidden layer;

$$f\left(x\right)=\frac{2}{(1+{e}^{-2x})}-1,$$
(54)
$${Z}_{j}\left(t\right)=\frac{2}{\left(1+{e}^{-2\left[\sum_{i=1}^{10}{[\theta }_{i}\left(t\right){w}_{1j}\left(t\right)+{\theta }_{g}(t){w}_{2j}]+1\right]}\right)}-1.$$
(55)

The output signal of the output layer can be written as;

$${\theta }_{g}\left(t\right)=\sum_{j=1}^{10}{Z}_{j}\left(t\right){w}_{j1}\left(t\right)+1.$$
(56)

The output signal of neural network model;

$${\theta }_{g}\left(t\right)=\sum_{j=1}^{10}\left[\left[\frac{2}{\left(1+{e}^{-2\left[\sum_{i=1}^{10}{[\theta }_{i}\left(t\right){w}_{1j}\left(t\right)+{\theta }_{g}(t){w}_{2j}]+1\right]}\right)}-1\right]{w}_{j1}\left(t\right)+1\right].$$
(57)

Here w1j is the weight matrix between the input layer and the hidden layer, and w2j is the weight matrix between the hidden layer and the output layer [18]. In the neural network model, there is one linear neuron in the input layer, 10 nonlinear neurons in the hidden layer and one nonlinear neuron in the output layer. The number of iterations is determined as 1,000,000, and η (learning rate) is 0.1.

3.3 Levenberg–Marquardt (LM) algorithm

The Levenberg–Marquardt algorithm is used to randomly change the weights of the network. The Levenberg–Marquardt algorithm, like the Quasi-Newton methods, uses the approximate value of the Hessian matrix [18]. The approximate value of the Hessian matrix for the Levenberg–Marquardt algorithm can be found as follows:

$$H\left(t\right)={J}^{{\text{T}}}\left(t\right)J\left(t\right)+\mu {I}_{H}.$$
(58)

μ is the Marquardt parameter, and H is the unit matrix. J is called the Jacobian matrix and consists of the first derivatives of the network errors according to the weights.

$$J\left(t\right)=\frac{\partial e(t)}{\partial w(t-1)}.$$
(59)

e(t) is the vector of network errors. The Jacobian matrix is preferred as it is easier to compute than the Hessian matrix. The gradient of the network is calculated as follows,

$$g\left(t\right)={J}^{T}\left(t\right)e\left(t\right).$$
(60)

3.4 Model reference neural network control

The model reference neural network control organ is used as a mathematical model for comparison with the actual control system. In this neural network plant model, an error is generated based on the difference between the actual and model outputs. The control law of the model reference neural network controller is as follows;

$${\tau }_{NN}(t)= \sum_{j=1}^{10}\left[\left[\frac{2}{\left(1+{e}^{-2\left[\sum_{i=1}^{10}{[\theta }_{i}\left(t\right){w}_{1j}\left(t\right)+{\theta }_{g}(t){w}_{2j}]+1\right]}\right)}-1\right]{w}_{j1}\left(t\right)+1\right].$$
(61)

The Levenberg–Marquardt algorithm is used to adjust the weights in the feed-forward neural network. The block diagram of the model reference control system is schematically given in Fig. 4.

Fig. 4
figure 4

Block diagram of model reference controller

Full size image

where eRM is the reference model error, eNM is the error of the landing gear system model, θi(t) is the desired position input signal of the landing gear system, θg(t) is the actual position input signal of the landing gear system, θr(t) is the output signal of the reference model and θn(t) is the output signal of the neural network model. Here, a third-order system is chosen as the reference model transfer function of the system. The Laplace domain of this reference model can be given as follows;

$$G\left(s\right)=\frac{0.2s+2}{{s}^{3}+{71.5s}^{2}+113.05s+455.5}.$$
(62)

4 Simulation results

4.1 PID and ANN responses

The simulations are performed for two different runway coefficients and 200 km/h landing speed. At the first moment, the landing gear puts wheels on the runway, the suspension system acts rigid and the landing gear system is subjected to the greatest force. While performing the analyses, the damping effect in the wheel and suspension is neglected, and simulations are made for the maximum value of the reaction force. It is aimed to approximate the angular joint variables of the landing gear mechanism to the reference values by using the PID controller and the neural network controller. The simulation results for the control of angular joint variables with PID controller and neural network controller are given in Figs. 5, 6, 7, 8 and 9. In Fig. 5, the PID and ANN control responses of the θ2 angular joint variable of the lateral strut are presented. As shown in Fig. 5a and b, ANN shows better performance than PID in the analysis for different runway friction coefficients. In asphalt runway pavement, the system shows a stable state after 4 s and the response speed decreased to 2 s on the concrete pavement with a neural network controller.

Fig. 5
figure 5

PID and ANN response of θ2 angular joint variables, a µasphalt = 0.5 and b µconcrete = 0.3

Full size image
Fig. 6
figure 6

PID and ANN response of θ3 angular joint variables, a µasphalt = 0.5 and b µconcrete = 0.3

Full size image
Fig. 7
figure 7

PID and ANN response of θ4 angular joint variables, a µasphalt = 0.5 and b µconcrete = 0.3

Full size image
Fig. 8
figure 8

PID and ANN response of θ5 angular joint variables, a µasphalt = 0.5 and b µconcrete = 0.3

Full size image
Fig. 9
figure 9

PID and ANN response of θ6 angular joint variables, a µasphalt = 0.5 and b µconcrete = 0.3

Full size image

Figure 6a and b gives the result of the PID and ANN control system for θ3 angular joint variables. When the system responses under the PID control effect are examined, it is seen that the damping effect is obtained in the range of 2–4 s, and the system becomes stable. Besides, with the ANN controller, a stable behaviour was exhibited in approximately 2 s for all runway conditions.

The result of PID and ANN control for θ4 angular joint variables is given in Fig. 7a and b. As described in Fig. 7a and b, uncontrolled system outputs are unstable, and the neural network controller has a good performance at stability on both runway pavements. It is seen clearly, there are differences between PID and ANN controller. The results of the PID controller are weak to control compared to the neural network controller.

Response of PID and ANN controller for θ5 angular joint variables is given in Fig. 8a and b. As shown in Fig. 8a, the response of the system reached the desired value in the asphalt runway pavement in the 4th second with the PID controller. On the other hand, the damping effect with neural network control is observed in 2 s. Similarly, on concrete pavement, the neural network controller is suitable for controlling the angular displacement.

Lastly, Fig. 9a and b is demonstrated the response of the angular displacement of the landing gear main strut. When the graphs are examined, it is seen that uncontrolled system output magnitudes are raising. As shown in Fig. 9a, there is a stable behaviour in the 8th second with a neural network controller. Otherwise, the PID controller exhibits stable behaviour at 12th seconds. As seen in the relevant figure for concrete pavement, it is observed that the response times of both control organs are reduced. Reaction forces and moments act directly on the landing gear strut. Due to these reasons, both controllers have a late response time.

The simulation results show that the highest vibration occurred in the main strut of the landing gear system. This is because external forces act directly on the main strut. The least angular displacement values are observed in the unlock mechanism.

4.2 Sensitivity analysis

In the proposed ANN control model, a sensitivity analysis based on the algorithm called the Garson algorithm [20] was performed to analyse the effect of inputs on the output. Thus, the contribution of each input parameter in vibration control of the aircraft landing system was analysed. In this algorithm, the sensitivity coefficient can be calculated as follows:

$${Q}_{ik}\frac{{\sum }_{j=1}^{L}(\left|{w}_{ij}\left.{v}_{jk}\right|/\sum_{r=1}^{N}\left|{w}_{rj}{v}_{jk}\right|)\right.}{{\sum }_{i=1}^{N}\sum_{j=1}^{L}(\left|{w}_{ij}{v}_{jk}\right|/{\sum }_{r=1}^{N}\left|{w}_{rj}{v}_{jk}\right|)}.$$
(63)

where Qik represents the sensitivity coefficient of the input i to the output k, wij, and vjk represents the weights from input variable i to hidden neuron j and from hidden neuron j to the output k, respectively. L represents the number of neurons in the hidden layer, and N indicates input variables.

Sensitivity coefficients of all input parameters are presented in Fig. 10. As shown in Fig. 10, the most critical parameters affecting the control of the aircraft landing system are angular position variables and total torque values. The sensitivity coefficients of these values are 42.34% and 37.63%, respectively. External forces acting on the aircraft during landing are the next most important factor with a sensitivity coefficient of 13.59%. Aerodynamic force, on the other hand, has the lowest effect on landing gear vibration control with a sensitivity coefficient of 6.44%. The input parameters selected for an optimal model should reflect all factors affecting vibration control performance. However, choosing too many parameters may increase the complexity of the ANN model and negatively affect its accuracy and response time. With sensitivity analysis, the effect of each input parameter on the output parameter was revealed. Thus, the aerodynamic force parameter with the lowest effect on the output parameter was determined. The sensitivity analysis results provided the reference for developing a high accuracy and extensively feasible control model in controlling the aircraft landing system.

Fig. 10
figure 10

The sensitivity coefficients of each input parameter

Full size image

5 Conclusions and discussion

In this paper, neural networks and standard control systems are applied for aircraft landing gear vibration control. The landing gear mechanism is regarded as four degrees of freedom system. PID and ANN are compared for asphalt and concrete runway pavement. The proposed ANN control system is comprised of a feed-forward neural network predictive controller and model reference neural network controller. Standard control methods cannot adapt to disruptive factors because they have constant parameters and are insufficient in controlling complex systems. Therefore, it is more appropriate to use an adaptive ANN structure for the control and analysis of complex and nonlinear systems, and optimum control can be achieved. From the simulation results, it is seen that using ANN control system with a feedback controller and model reference neural network controller, high vibration control performance can be achieved for all runway conditions. In controlling the angular joint variables of the landing gear mechanism, the ANN control system is achieved superior performance than the standard PID control system because of its adaptive structure.