The minimum principle of hybrid optimal control theory

Abstract

The hybrid minimum principle (HMP) is established for the optimal control of deterministic hybrid systems with both autonomous and controlled switchings and jumps where state jumps at the switching instants are permitted to be accompanied by changes in the dimension of the state space and where the dynamics, the running and switching costs as well as the switching manifolds and the jump maps are permitted to be time varying. First-order variational analysis is performed via the needle variation methodology and the necessary optimality conditions are established in the form of the HMP. A feature of special interest in this work is the explicit presentations of boundary conditions on the Hamiltonians and the adjoint processes before and after switchings and jumps. Analytic and numerical examples are provided to illustrate the results.

Appendix A Proof of Lemma 1

Proof

Let us define

$$\begin{aligned} K_1=\sup \left\{ \left\| f_{q}\left( t,x,u\right) \right\| :\left( t,q,x,u\right) \in [t_{0},t_{f}] \times Q\times B_{r}\times U\right\} , \end{aligned}$$

(A1)

where $B_{r}:=\left\{ x \in {\mathbb {R}}^{n_{q}}: \left\| x\right\| ^2 <r^2\right\}$.

we first consider the stage where no remaining switching is available and hence $t\in \left( t_L,t_{L+1}\right) = \left( t_L,t_{f}\right)$. In this the case that

$$\begin{aligned} x\left( t_{f};t,x_{t}\right) =x_{t}+\int _{t}^{t_{f}}f_{q_{L}}\left( \tau , x_{\tau },u_{\tau }\right) \textrm{d}\tau , \end{aligned}$$

(A2)

which gives

$$\begin{aligned} \left\| x\left( t_{f};t,x_{t}\right) -x_{t}\right\| \le K_{1}\left| t_{f}-t\right| +\int _{t}^{t_{f}}L_{f}\left\| x\left( \tau ;t,x_{t}\right) -x_{t}\right\| \textrm{d}\tau , \end{aligned}$$

(A3)

where $L_{f}$ is defined in assumptions A0. By the Gronwall-Bellman inequality this results in

$$\begin{aligned} \left\| x\left( t_{f};t,x_{t}\right) -x_{t}\right\|\le & {} K_{1}\left| t_{f}-t\right| +\int _{t}^{t_{f}}L_{f}K_{1}\left( \tau -t\right) e^{L_{f}\left( t_{f}-\tau \right) }\textrm{d}\tau \nonumber \\\le & {} K_{2}\left| t_{f}-t\right| \le K_{2}\left| t_{f}-t_{L}\right| , \end{aligned}$$

(A4)

where $K_{2}=\max \left\{ K_{1},L_{f}K_{1}\left( t_{f}-t_{L}\right) e^{L_{f}\left( t_{f}-t_{L}\right) }\right\}$. Hence, by the semi-group properties of ODE solutions and by use of (A4), for $s \ge t$ and $x_s \in N_{r_{x}}\left( x_t\right)$ we have

$$\begin{aligned} \left\| x\left( t_{f};t,x_{t}\right) -x\left( t_{f};s,x_{s}\right) \right\|\le & {} \left\| x_{t}-x_{s}\right\| +\left\| x\left( s;t,x_{t}\right) -x_{t}\right\| \nonumber \\{} & {} +\int _{s}^{t_{f}}L_{f}\left\| x\left( \tau ;t,x_{t}\right) -x\left( \tau ;s,x_{s}\right) \right\| \textrm{d}\tau \nonumber \\\le & {} \left\| x_{t}-x_{s}\right\| +K_{2}\left| s-t\right| \nonumber \\{} & {} +\int _{s}^{t_{f}}L_{f}\left\| x\left( \tau ;t,x_{t}\right) -x\left( \tau ;s,x_{s}\right) \right\| \textrm{d}\tau , \end{aligned}$$

(A5)

and therefore, by the Gronwall inequality we have

$$\begin{aligned} \left\| x\left( t_{f};t,x_{t}\right) -x\left( t_{f};s,x_{s}\right) \right\|\le & {} \left( \left\| x_{t}-x_{s}\right\| +K_{2}\left| s-t\right| \right) e^{L_{f}\left( t_{f}-s\right) } \nonumber \\\le & {} \left( \left\| x_{t}-x_{s}\right\| +K_{2}\left| s-t\right| \right) e^{L_{f}\left( t_{f}-t_{L}\right) }\nonumber \\\le & {} K\left( \left\| x_{t}-x_{s}\right\| ^{2}+\left| s-t\right| ^{2}\right) ^{\frac{1}{2}}, \end{aligned}$$

(A6)

for some $K<\infty$ which depends only on $t_f - t_L$, $K_1$ and ${\tilde{K}}_f$ and not on the control input.

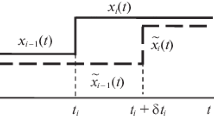
Now consider $t,s\in \left( t_j,t_{j+1}\right)$ where $t_{j+1}$ indicates a time of an autonomous switching for the trajectory $x\left( \tau ;t,x_{t}\right)$, and consider for definiteness the case where $x\left( \tau ;s,x_{s}\right)$ arrives on the switching manifold described locally by $m\left( x\right) = 0$ at a later time $t_{j+1}+\delta t$ (the case with an earlier arrival time can be handled similarly by considering $\delta t<0$). It directly follows by replacing $f_{q_L}$ and $t_{f}$ by $f_{q_j}$ and $t_{j+1}-$ in the above arguments, that

$$\begin{aligned} \left\| x\left( t_{j+1}-;t,x_{t}\right) -x\left( t_{j+1}-;s,x_{s}\right) \right\| \le K^{\prime }\left( \left\| x_{t}-x_{s}\right\| ^{2}+\left| s-t\right| ^{2}\right) ^{\frac{1}{2}}. \end{aligned}$$

(A7)

Now since

$$\begin{aligned} \left\| x\left( t_{j+1}+\delta t-;s,x_{s}\right) -x\left( t_{j+1}-;s,x_{s}\right) \right\| \le K_2 \left| t_{j+1}+\delta t - t_{j+1}\right| = K_2 \left| \delta t\right| ,\nonumber \\ \end{aligned}$$

(A8)

and

$$\begin{aligned}{} & {} \left\| x\left( t_{j+1}+\delta t-;s,x_{s}\right) -x\left( t_{j+1}-;t,x_{t}\right) \right\| ^2\nonumber \\{} & {} \le \left\| x\left( t_{j+1}+\delta t-;s,x_{s}\right) -x\left( t_{j+1}-;s,x_{s}\right) \right\| ^2 \nonumber \\{} & {} \quad + \left\| x\left( t_{j+1}-;t,x_{t}\right) -x\left( t_{j+1}-;s,x_{s}\right) \right\| ^2, \end{aligned}$$

(A9)

it is sufficient to show that the upper bound for $\left| \delta t\right|$ is proportional to $\big (\left\| x_{t}-x_{s}\right\| ^{2}+\left| s-t\right| ^{2}\big )^{\frac{1}{2}}$. This can be shown to hold by considering the fact that

$$\begin{aligned}{} & {} m\big (x(t_{j+1}+\delta t-;s,x_{s})\big ) =m\bigg (x(t_{j+1}-;s,x_{s})+\int _{t_{j}}^{t_{j}+\delta t}f_{q_{j}}\big (x(\tau ;s,x_{s}),u_{t_{j}-}\big )\textrm{d}\tau \bigg ) \nonumber \\{} & {} \quad =m\left( x(t_{j+1}-;t,x_{t})+\delta x(t_{j+1}-)+\int _{t_{j}}^{t_{j}+\delta t} f_{q_{j}}{\big (x(\tau ;s,x_{s}),u_{t_{j}-}\big )} \textrm{d}\tau \right) \nonumber \\{} & {} \quad =m\left( x\left( t_{j+1}-;t,x_{t}\right) \right) =0. \end{aligned}$$

(A10)

For $\left\| \delta x\left( t_{j+1}-\right) \right\| < \epsilon _{j+1}$ sufficiently small,

$$\begin{aligned} \nabla m^{\top }\left( \delta x_{t_{j+1}-}+\int _{t_{j}}^{t_{j}+\delta t}f_{q_{j}}{\left( x\left( \tau ;s,x_{s}\right) ,u_{t_{j}-}\right) }\textrm{d}\tau \right) +O\left( \epsilon _{j+1}^{2}\right) =0, \end{aligned}$$

(A11)

which is equivalent to

$$\begin{aligned} \nabla m^{\top }\delta x\left( t_{j+1}-\right) +\int _{t_{j}}^{t_{j}+\delta t}\nabla m^{\top }f_{q_{j}}{\left( x\left( \tau ;s,x_{s}\right) ,u_{t_{j}-}\right) }\textrm{d}\tau +O\left( \epsilon _{j+1}^{2}\right) =0.\nonumber \\ \end{aligned}$$

(A12)

Due to the transversal arrival of the trajectories with respect to the smooth switching manifold, $\left| \nabla m^{\top } f_{q_j}\right|$ is lower bounded by a strictly positive number $k_{m,f}$ (see (2)) and hence,

$$\begin{aligned}{} & {} \left| \nabla m^{\top }\delta x\left( t_{j+1}-\right) +O\left( \epsilon _{j+1}^{2}\right) \right| =\left| \int _{t_{j}}^{t_{j}+\delta t}\nabla m^{\top }f_{q_{j}}{\left( x\left( \tau ;s,x_{s}\right) ,u_{t_{j}-}\right) }\textrm{d}\tau \right| \nonumber \\{} & {} \quad \ge \int _{t_{j}}^{t_{j}+\delta t}\left| \nabla m^{\top }f_{q_{j}}{\left( x\left( \tau ;s,x_{s}\right) ,u_{t_{j}-}\right) }\right| \textrm{d}\tau \ge k_{m,f}\left| \delta t\right| , \end{aligned}$$

(A13)

which gives

$$\begin{aligned}{} & {} \left| \delta t\right| \le \frac{1}{k_{m,f}}\left( \left\| \nabla m\right\| \left\| \delta x\left( t_{j+1}-\right) \right\| +\left| O\left( \epsilon _{j+1}^{2}\right) \right| \right) \nonumber \\{} & {} \quad \le \frac{1}{k_{m,f}}\left\| \nabla m\right\| \epsilon _{j+1}+\epsilon _{j+1} \le \left( \frac{\left\| \nabla m\right\| }{k_{m,f}} +1\right) \epsilon _{j+1}=K_{j+1}\epsilon _{j+1}. \end{aligned}$$

(A14)

Hence, for $t\in \left( t_j,t_{j+1}\right)$ and $x_t\in B_r$ there exist a neighborhood $N_{r_x}\left( x_t\right)$ such that for $s\in \left( t_j,t_{j+1}\right)$ and $x_s \in \mathcal{N}_{r_x}\left( x_t\right)$ we have $\left\| \delta x\left( t_{j+1}-\right) \right\| \le K^{\prime }\left( \left\| x_{t}-x_{s}\right\| ^{2}+\left| s-t\right| ^{2}\right) ^{\frac{1}{2}} < \epsilon _{j+1}$ in order to ensure that $\delta t \le K_{j+1} \epsilon _{j+1}$ and consequently

$$\begin{aligned} \left\| x\left( t_{j+1}+\delta t-;s,x_{s}\right) -x\left( t_{j+1}-;t,x_{t}\right) \right\| \le K\left( \left\| x_{t}-x_{s}\right\| ^{2}+\left| s- t\right| ^{2}\right) ^{\frac{1}{2}},\nonumber \\ \end{aligned}$$

(A15)

for K independent of the control. Since $\xi$ is smooth and time invariant, it is therefore Lipschitz in x uniformly in time. $\square$