1 Introduction

Motivation

The investigation of microstructural mechanisms in materials science and associated phenomena is fundamental for developing and improving materials regarding their effective properties such as strength and ductility. Furthermore, the prediction of the material behavior under certain conditions is essential for various applications. Microstructural evolution involves a large diversity of often complex processes. In order to manipulate microstructural evolution and thereby tailor the effective material properties, a thorough understanding of the phenomena occurring on a microscopic scale is essential. Modeling and simulation of material behavior, help to gain insights into microstructural transformation processes. In contrast to experiments, specific phenomena can be modeled and investigated, separately. Regarding the simulation of microstructure evolution during recrystallization the modeling of migrating grain boundaries (GBs) is required. In this context, plastic deformation energy provides a driving force on GBs, amongst other sources of energy, cf., e.g., [1]. The plastic behavior of polycrystalline materials can be directly related to the evolution of lattice defects such as dislocations and experimental investigations are commonly based on the exploitation of dislocation density measurements. In the present work, the plastic deformation is considered in terms of classical crystal plasticity (CP) theory, cf., e.g., [2]. In this context, the plastic deformation is described by so-called plastic slips acting on specific slip systems characteristic for each crystal symmetry. Thus, the CP constitutes a phenomenological model that takes into account the underlying microstructure such as the characteristic slip systems. Based on Orowan’s law, cf., e.g., [3, Eq. (6.31b)], the plastic slips can be related to the dislocation densities in an approximative sense and the considered model is applied to describe the microstructural evolution during load as well as morphological changes of the microstructure after loading.

Multiphase-field method

The tracking of GBs in the sharp interface context is numerically challenging and costly. It can be circumvented by the use of a multiphase-field method (MPFM). Instead of modeling GBs as material singular surfaces, cf., e.g., [4], as commonly done in classical continuum mechanics, GBs are modeled as diffuse interfaces within the MPFM, cf., e.g., [5,6,7,8,9]. The position of interfaces is implicitly given by the contour of the field of order parameters, thus, no explicit tracking is needed, cf., e.g., Chen [9]. The MPFM is widely established for simulating microstructural evolution. Applications include solidification [10, 11], solid-solid phase transformations, cf., e.g., [12, 13], and more recently crack propagation [14,15,16]. In the work at hand, the MPFM is based on the work by Steinbach et al. [17], Steinbach and Pezzolla [18] and Nestler et al. [19].

Crystal plasticity in the context of the multiphase-field method

To implement CP in an MPFM, an approach is required to account for the mechanical fields in the diffuse interface. In literature, three approaches are discussed: the interpolation approach, the homogenization approach, cf., e.g., [20, 21], and, more recently, the jump condition approach, cf., e.g., [22,23,24,25]. Regarding the interpolation approach, all material points follow the same set of mechanical constitutive equations. The material parameters, however, may differ and are interpolated within the diffuse interface, cf., e.g., [20]. More possibilities are offered by homogenization approaches, where different constitutive equations may apply in different phases. The behavior of the diffuse interface is significantly influenced by the chosen homogenization scheme, cf., e.g., [20]. The inheritance of plastic strains during phase transitions is an important topic of an ongoing discussion. Within interpolation and homogenization approaches the transformation behavior is significantly different, as discussed, e.g., by Ammar et al. [26]. The jump condition approach can be seen as an addition to the homogenization approach. Schneider et al. [24] introduced a method for the calculation of stresses in a multiphase system, which satisfies the mechanical jump conditions in terms of the balance of linear momentum for a material singular surface and the Hadamard condition. Herrmann et al. [27] provided a comparison of the treatment of plastic fields with the interpolation approach and the jump condition approach, in the context of Mises plasticity. A novel model has been proposed by Prahs et al. [28], incorporating small strain CP theory that accounts for phase-specific fields and mechanical jump conditions into the MPFM, i.e., a coupling of CP theory and the MPFM is considered in each time step. The aforementioned model is used in the work at hand.

Recrystallization in the context of the multiphase-field method and crystal plasticity theory

The accurate representation of the deformation process is particularly important for the simulation of recrystallization, since the deformation and the associated energy significantly affect the properties of the recrystallization process, cf., e.g., [29]. The use of CP allows to account for the crystalline microstructure of a material. This motivates to incorporate CP into the study of recrystallization and, especially, grain boundary migration within the MPFM. In literature, several approaches are discussed on the subsequent simulation of a deformation accounting for crystal plasticity in the context of a finite element analysis and the recrystallization in the context of the phase-field method. Within the approach presented by Takaki et al. [30] and Takaki and Tomita [31] the dislocation density and crystal orientations are calculated using a strain gradient CP model, which function as an input for a subsequent phase-field simulation of recrystallization. The approach provided by Güvenç et al. [32, 33] employs a CP finite element method to compute the grain index, the mean grain orientation, and the mean stored energy in the grains, which are subsequently transferred to a multiphase-field simulation via an interpolation scheme. The development of more reliable orientation distributions is the main objective addressed by Vondrous et al. [29]. Within these approaches, the phase-field simulations account for the results of the deformation simulation, however, no coupling in each time step of the phase-field evolution and the balance of linear momentum is considered during the recrystallization process. Another approach is given by the coupling of a Cosserat crystal plasticity theory and an orientation phase-field method, e.g., by Ask et al. [34]. While this approach allows for the evolution of the orientation within a grain, no phase-specific strain fields are considered. As discussed by Prahs et al. [28], the interpolation of material parameters and crystallographic orientations across the diffuse interface leads to artificial results.

Objective of the current work

The incorporation of CP theory in an MPFM opens up new possibilities for the quantitative modeling of phase transformations that involve plasticity. The main objective of the work at hand is to gain insights in the possibilities of simulating microstructural evolution by combining a CP model with an MPFM following the recently presented approach by Prahs et al. [28]. Their approach is revisited and used for the simulation of evolving phases during load as well as for morphological changes of the microstructure after unloading. In this context, equilibrium shapes of an elastic inclusion subjected to transversely isotropic eigenstrains within an elasto-plastic matrix are evaluated. Additionally, GB migration during static recrystallization (SRX) is addressed. However, it should be emphasized that the present work does not attempt to quantitatively model or simulate SRX. Rather, the objective is to demonstrate the potential of the model to represent microstructure evolution and GB migration affected by anisotropic plastic deformation.

Originality

The advantage of implementing the CP theory within the MPFM, using phase-specific plastic fields that take into account jump conditions, is discussed by Prahs et al. [28]. So far, their discussion addresses non-evolving phases and their results show good agreement with the results from the sharp interface theory. In the work at hand, the application is extended to evolving phases and moving interfaces. Phase evolution is illustrated by an elastic inclusion within an elasto-plastic matrix. The phase evolution and, thus, the shape of the inclusion, depends on the anisotropic characteristics and heterogeneous distribution of plastic slip. Furthermore, a scheme including an approach to strain inheritance is developed for the simulation of microstructure evolution and GB migration driven by accumulated plastic slip. It is shown, how the approach by Prahs et al. [28] contributes to the development of a simulation of recrystallization on the basis of heterogeneous plastic slip fields. In the present work, microstructure evolution is modeled solving the phase-field evolution equation and the balance of linear momentum in each time step.

Outline

In Sect. 2, the preliminaries of CP theory and the MPFM are recapitulated and the implementation of the CP theory with respect to the bulk and the diffuse interface region is summarized. The considered boundary value problems are illustrated and their results discussed in Sect. 3. Concluding remarks are given in Sect. 4.

Notation

In the work at hand, a direct tensor notation is used. Scalars, vectors, 2nd-order, and 4th-order tensors are written as a, \({\varvec{a}}\), \({\varvec{A}}\), and \({\mathbb {A}}\), respectively. Tensor components refer to an orthonormal basis \(\{{\varvec{e}}_1,{\varvec{e}}_2,{\varvec{e}}_3\}\) and are written as \(A_{ij}\). The linear mapping of a vector by a 2nd-order tensor is denoted by \({\varvec{A}}{\varvec{b}}\), and the mapping of a 2nd-order tensor by a 4th-order tensor by \({\mathbb {A}}[{\varvec{B}}]\). A composition between two tensors of second order is written as \({\varvec{A}}{\varvec{B}}\). The dyadic product between two vectors and two 2nd-order tensors is given by \({\varvec{a}}\otimes {\varvec{b}}\) and \({\varvec{A}}\otimes {\varvec{B}}\), respectively. The scalar product between two vectors or tensors is written as \({\varvec{a}}\cdot {\varvec{b}}\), \({\varvec{A}}\cdot {\varvec{B}}\), and \({\mathbb {A}}\cdot {\mathbb {B}}\), respectively. Using the nabla operator \(\nabla \), the gradient of a scalar a is denoted by \(\nabla {a}\), and the divergence of a 2nd-order tensor \({\varvec{a}}\) is formulated as \(\nabla \cdot {{\varvec{a}}}\). The Frobenius norm of a tensor is written as \(\Vert {\varvec{A}} \Vert \) and is given by \({\Vert {\varvec{A}} \Vert =\sqrt{{\varvec{A}}\cdot {\varvec{A}}}}\). The material time derivative of field a is denoted by \(\dot{a}\) for all tensorial orders.

2 Method and theoretical preliminaries

2.1 Balance laws and constitutive equations of CP theory

Balance laws

In this work, a Cauchy-Boltzmann continuum \({{\mathcal {V}}}\) is considered. A material singular surface \({{\mathcal {S}}}\) divides the continuum into two subvolumes \({{\mathcal {V}}}^+\) and \({{\mathcal {V}}}^-\), which are bounded against the surroundings by \({{\mathcal {B}}}^+\) and \({{\mathcal {B}}}^-\). The normal vector on \({{\mathcal {S}}}\), pointing from  \({{\mathcal {V}}}^-\) to \({{\mathcal {V}}}^+\), and the outward normal vectors on \({{\mathcal {B}}}^+\) and \({{\mathcal {B}}}^-\) are denoted by \({\varvec{n}}_{{\mathcal {S}}}\), \({\varvec{n}}_{{{\mathcal {V}}}^+}\), and \({\varvec{n}}_{{{\mathcal {V}}}^-}\), respectively. The pill box theorem provides a relation between the normal vectors, which reads \( {\varvec{n}}_{{\mathcal {S}}}= {\varvec{n}}_{{{\mathcal {V}}}^+} = - {\varvec{n}}_{{{\mathcal {V}}}^-} \), cf., e.g., [35]. A jump across \({{\mathcal {S}}}\) of a quantity \(\psi \) with the corresponding limits \(\psi ^+\) and \(\psi ^-\) in \({{\mathcal {V}}}^+\) and \({{\mathcal {V}}}^-\) is written as . By exploitation of invariance considerations of the balance of total energy with respect to a change of observer balance equations at the singular surface and in regular points are derived. Svendsen [36] and Prahs and Böhlke [4] provided a detailed discussion on the derivation for regular points, and Prahs and Böhlke [37] for singular points. Furthermore, by means of invariance considerations the existence of the stress tensor \(\varvec{\sigma }\), the Cauchy stress, with \( \varvec{\sigma }{\varvec{n}}_{{\mathcal {V}}}= {\varvec{t}} \) is obtained. Herein, the traction force is denoted by \({\varvec{t}}\) and \({\varvec{n}}_{{\mathcal {V}}}\) describes the outer normal vector on \({{\mathcal {V}}}\). Subsequently, a quasi-static case is considered and body forces are neglected. Moreover, a small deformation framework, which implies a constant mass density, is considered. The balance of linear momentum regarding regular points, accounting for the above assumptions, is given by \( \nabla \cdot \varvec{\sigma }={\varvec{0}} \). At the singular surface \({{\mathcal {S}}}\) the balance of linear momentum reads , describing the continuity of the stress tensor in the normal direction of \({{\mathcal {S}}}\). The balance of angular momentum in regular points yields the symmetry of the Cauchy stress tensor \( \varvec{\sigma }= {\varvec{\sigma }}^{\textsf{T}} \).

Hadamard conditions

Additional conditions for a jump across a singular surface \({{\mathcal {S}}}\) are given by the Hadamard jump conditions, cf., e.g., [35, Eq. (2.26)]. Here, \({\varvec{a}}\) denotes an unknown jump vector. The Hadamard condition states the continuity of the deformation gradient \({\varvec{F}}\) tangential to \({{\mathcal {S}}}\). The Hadamard condition can be reformulated in terms of the displacement gradient \({\varvec{H}}={\varvec{F}}+ {\varvec{I}}\), where \({\varvec{I}}\) denotes the second-order identity tensor, as .

Constitutive equations of crystal plasticity

The considered framework was briefly discussed by Kannenberg et al. [38]. In the present work, the framework is explained in more detail and an extension to constant eigenstrains is provided. A phenomenological theory of plasticity is provided by classical CP theory, where plastic deformation is described by means of plastic slip, cf., e.g., [2]. The underlying microstructure is accounted for by its crystal lattice and corresponding slip systems, described by the slip directions \({\varvec{d}}_\xi \) and normal vectors to the slip planes \({\varvec{n}}_\xi \). Face-centered cubic (FCC) crystals exhibit twelve slip systems described by the {111}-planes and \(\langle 110\rangle \)-directions, cf., e.g., [39]. An additive composition of the infinitesimal total strain \(\varvec{\varepsilon }\) of an elastic contribution \(\varvec{\varepsilon }_{\textrm{e}}\), a plastic contribution \(\varvec{\varepsilon }_{\textrm{p}}\), and constant eigenstrains \(\varvec{\varepsilon }^*\), with \({\dot{\varvec{\varepsilon }}^*={\varvec{0}}}\), is assumed, i.e.,

$$\begin{aligned} \varvec{\varepsilon }= \varvec{\varepsilon }_{\textrm{e}}+ \varvec{\varepsilon }_{\textrm{p}}+ \varvec{\varepsilon }^*. \end{aligned}$$
(1)

The elastic strain \(\varvec{\varepsilon }_{\textrm{e}}\) is associated to the Cauchy stress \(\varvec{\sigma }\) through Hooke’s law

$$\begin{aligned} \varvec{\sigma }= {\mathbb {C}}[\varvec{\varepsilon }_{\textrm{e}}] = {\mathbb {C}}[\varvec{\varepsilon }-\varvec{\varepsilon }_{\textrm{p}}-\varvec{\varepsilon }^*]. \end{aligned}$$
(2)

Elastic deformation is associated with the distortion and rotation of the crystal lattice, while plastic deformation is associated with the movement of dislocations and occurs under conservation of the lattice, cf., e.g., [2, 40, Sect. 102]. Slip is defined as the glide of many dislocations and a reason for plastic deformation, cf., e.g., [41]. The plastic strain \(\varvec{\varepsilon }_{\textrm{p}}\) is expressed by the summation of the plastic slip \(\gamma _\xi \) over \( \xi = 1,\ldots ,N \) active slip systems, i.e.,

$$\begin{aligned} \varvec{\varepsilon }_{\textrm{p}}= \sum _{\xi =1}^N\gamma _\xi \dfrac{1}{2}({{\varvec{d}}_\xi \otimes {\varvec{n}}_\xi +{\varvec{n}}_\xi \otimes {\varvec{d}}_\xi }) = \sum _{\xi =1}^N\gamma _\xi {\varvec{M}}_\xi , \end{aligned}$$
(3)

cf., e.g., [42, Eq. (1)]. As a description of a slip system \(\xi \) the Schmid tensor \({\varvec{M}}_\xi \) is introduced. The accumulated plastic slip \(\gamma _{\textrm{ac}}\) is defined by its rate as \( \dot{\gamma }_\textrm{ac} = \sum _{\xi =1}^N |\dot{\gamma }_\xi | \), cf., e.g., [43, Eq. (25)]. The activation of slip in a particular slip system \(\xi \) is dependent on the resolved shear stress \(\tau _\xi \), given by the projection of the stress and the Schmid tensor, i.e., \( \tau _\xi = \varvec{\sigma }\cdot {\varvec{M}}_\xi \). Slip is activated if the resolved shear stress \(\tau _\xi \) reaches a certain threshold, known as the critical shear stress \(\tau _{\textrm{C}}\), which is represented in the flow rule for the individual plastic slips

$$\begin{aligned} \dot{\gamma }_\xi =\dot{\gamma }_0\textrm{sgn}\left( \tau _\xi \right) \bigg \langle \frac{|\tau _\xi |-\tau _\textrm{C}}{\tau _\textrm{D}}\bigg \rangle ^m, \end{aligned}$$
(4)

cf., e.g., [44, Eq. (1.16)]. The referential shear rate is written as \(\dot{\gamma }_0\) and \(\tau _\textrm{D}\) denotes a positive drag stress. The strain rate sensitivity is denoted by m. The Macauley brackets are defined as \( \langle a\rangle =\max {(a,0)} \) and ensure an argument of non-negativity. The critical shear stress is formulated as

$$\begin{aligned} \tau _\textrm{C}(\gamma _{\textrm{ac}}) = \tau _\infty - (\tau _\infty -\tau _0)\exp {\left( \frac{-\Theta _0}{\tau _\infty -\tau _0}\gamma _{\textrm{ac}}\right) } \end{aligned}$$
(5)

which describes an isotropic hardening of Voce type, cf., e.g., [45, Eq. (1.40)]. Herein, the initial yield stress and hardening modulus are written as \(\tau _0\) and \(\Theta _0\), respectively. The saturation yield stress is denoted by \(\tau _\infty \). As discussed by Prahs et al. [46], the framework presented constitutes a thermomechanically weakly coupled theory.

2.2 Multiphase-field method

Free energy functional

Based on a free energy functional \({{\mathcal {F}}}\), governing equations of the MPFM, cf., e.g., [17,18,19], are derived. The free energy functional \({{\mathcal {F}}}\), as used in the work at hand, reads

$$\begin{aligned} \begin{aligned}&{{\mathcal {F}}}= \int _{{\mathcal {V}}}f \,\textrm{d}v = \int _{{\mathcal {V}}}f_{\textrm{grad}}+ f_\textrm{pot}+ {\bar{f}}_\textrm{bulk} \,\textrm{d}v, \quad \\ {}&\text {with} \quad {\bar{f}}_\textrm{bulk} = {\bar{f}}_\textrm{e} + {\bar{f}}_\textrm{p}. \end{aligned} \end{aligned}$$
(6)

The free energy density f is composed of the interface contributions, i.e., the gradient and potential energy density \(f_{\textrm{grad}}\) and \(f_\textrm{pot}\), respectively, and the bulk contributions \({\bar{f}}_\textrm{bulk}\), i.e., the elastic and plastic energy density \({\bar{f_\textrm{e}}}\) and \({\bar{f_\textrm{p}}}\), respectively. The free energy density f depends among others on an \(N^*\)-tuple of order parameters \( \varvec{\phi }=\{\phi _1,\ldots ,\phi _{N^*}\} \) corresponding to \( \alpha =1,\ldots ,N^* \) phases, its gradients \( \nabla {\varvec{\phi }} = \{\nabla \phi _1,\ldots ,\nabla \phi _{N^*}\} \), and the displacement \({\varvec{u}}\). The order parameter \(\phi _\alpha \) can be interpreted as the volume fraction of phase \(\alpha \). Within its assigned region, the order parameter takes on a value of  \( \phi _\alpha ({\varvec{x}},t)=1 \) and outside it becomes \( \phi _\alpha ({\varvec{x}},t)=0 \). The transition between the phases is diffuse, i.e., within the diffuse interface region at least two order parameters coexist which vary continuously in the range of \( \,0<\phi _\alpha ({\varvec{x}},t)<1 \). The summation constraint

$$\begin{aligned} \sum _{\alpha =1}^{N^*} \phi _\alpha ({\varvec{x}},t) = 1, \quad \forall {\varvec{x}}\in {{\mathcal {V}}},t\ge 0, \end{aligned}$$
(7)

applies for the order parameters, cf., e.g., [19]. The gradient energy density \(f_{\textrm{grad}}\) is expressed by

$$\begin{aligned} f_{\textrm{grad}}(\nabla {\varvec{\phi }})&=-\epsilon \sum _{\alpha ,\beta >\alpha }^{N^*} \gamma _{\alpha \beta }\nabla \phi _\alpha \cdot \nabla \phi _\beta , \end{aligned}$$
(8)

cf., e.g., [18]. The potential term can be formulated in various ways. Here, the so called multi-obstacle potential is used, reading

$$\begin{aligned} f_\textrm{pot}(\varvec{\phi }) = \dfrac{16}{\epsilon \pi ^2}\sum _{\alpha ,\beta >\alpha }^{N^*} \gamma _{\alpha \beta }\phi _\alpha \phi _\beta , \end{aligned}$$
(9)

cf., e.g., [19]. Eq. (9) holds true, if the \(N^*\)-tuple \(\varvec{\phi }\) is within the Gibbs-simplex \( {{\mathcal {G}}}= [\varvec{\phi }\big \vert \sum _{\alpha =1}^{N^*}\phi _\alpha ({\varvec{x}},t)=1, \;\phi _\alpha \ge 0 \,\forall \alpha ] \), cf., e.g., [47, Eq. (7)], otherwise \( f_\textrm{pot}=\infty \) is enforced. The interfacial energy between phases \(\alpha \) and \(\beta \) is written as \(\gamma _{\alpha \beta }\) and is for simplicity assumed to be isotropic, i.e., not dependent on the crystal orientation, but can be easily extended, cf., e.g., [19]. The interface parameter \(\epsilon \) is computed based on the width of an interface \(l_\textrm{eq}\) in equilibrium, \( l_\textrm{eq}=\epsilon \pi ^2/4 \), cf., e.g., [48, Eq. (3.22)].

Crystal plasticity in the multiphase-field method

Employing the jump condition approach, the balance of linear momentum at a singular surface and the Hadamard jump condition are satisfied at each point within the diffuse interface. In context of crystalline microstructures, a specific grain orientation and specific constitutive equations can be assigned to each phase. The implementation of plasticity theory within the diffuse interface, referred to as phase-specific plastic fields approach by Prahs et al. [28], is based on the jump condition approach, cf., e.g., [27]. Thus, it is stressed that no interpolation of material parameters or orientations is carried out with respect to the diffuse interface. The phase-specific elastic energy density \(f_\textrm{e}^\alpha \) depends on the elastic strain and is given by

$$\begin{aligned}&f_\textrm{e}^\alpha \left( \varvec{\varepsilon }^\alpha (\varvec{\phi })-\varvec{\varepsilon }_\textrm{p}^\alpha -\varvec{\varepsilon }^{*,\alpha }\right) = \frac{1}{2}\left( \varvec{\varepsilon }^\alpha (\varvec{\phi })-\varvec{\varepsilon }_\textrm{p}^\alpha -\varvec{\varepsilon }^{*,\alpha }\right) \nonumber \\&\quad \cdot \left( {\mathbb {C}}^\alpha [\varvec{\varepsilon }^\alpha (\varvec{\phi })-\varvec{\varepsilon }_\textrm{p}^\alpha -\varvec{\varepsilon }^{*,\alpha }]\right) , \end{aligned}$$
(10)

cf., e.g., [27, p. 1402]. The phase-specific stiffness tensor is written as \({\mathbb {C}}^\alpha \). Within the equation above, the phase-specific plastic strains and the phase-specific eigenstrains, \( \varvec{\varepsilon }_\textrm{p}^\alpha \) and \( \varvec{\varepsilon }^{*,\alpha } \), respectively, are independent of the order parameters, only the phase-specific total strains \( \varvec{\varepsilon }^\alpha (\varvec{\phi }) \) depend on the order parameters, cf. [28, Eq. (11)]. By interpolation of the phase-specific elastic free energies \(f_\textrm{e}^\alpha \) the elastic energy density is obtained, reading \( {\bar{f}}_\textrm{e}= \sum _\alpha \phi _\alpha f_\textrm{e}^\alpha \), cf., e.g., [27, Eq. (13)]. Minimizing Eq. (6) with respect to the displacement \({\varvec{u}}\) yields the balance of linear momentum within the diffuse interface region

$$\begin{aligned} \nabla \cdot \bar{\varvec{\sigma }}= {\varvec{0}}, \quad \text {with} \quad \bar{\varvec{\sigma }}= \sum _{\alpha =1}^{N^*}\phi _\alpha \varvec{\sigma }^\alpha , \end{aligned}$$
(11)

cf., e.g., [28, Eq. (14)]. Analogous to the derivation of the elastic energy density, the plastic energy density \({\bar{f}}_\textrm{p}\) is obtained via interpolation, reading \( {\bar{f}}_\textrm{p} = \sum _{\alpha =1}^{N^*}\phi _\alpha f_\textrm{p}^\alpha (\gamma _{\textrm{ac}}^\alpha ) \), cf., e.g., [28, Eq. (17)]. The phase-specific plastic energy density \(f_\textrm{p}^\alpha \) is formulated as

$$\begin{aligned} f_\textrm{p}^\alpha (\gamma _{\textrm{ac}}^\alpha )=(\tau _\infty ^\alpha -\tau _0^\alpha )\gamma _{\textrm{ac}}^\alpha +\dfrac{(\tau _\infty ^\alpha -\tau _0^\alpha )^2}{\Theta _0^\alpha }\exp {\left( \dfrac{-\Theta _0^\alpha }{\tau _\infty ^\alpha -\tau _0^\alpha }\gamma _{\textrm{ac}}^\alpha \right) }, \end{aligned}$$
(12)

cf., e.g., [28, Eq. (18)], and is derived from the relation between the phase-specific critical shear stress \(\tau _{\textrm{C}}^\alpha \) and the plastic energy densities \(f_\textrm{p}^\alpha \), reading \( \tau _\textrm{C}^\alpha = \displaystyle {\partial f_\textrm{p}^\alpha }{/\partial \gamma _{\textrm{ac}}^\alpha }+\tau _0^\alpha \).

Evolution equation of order parameters

Striving to reduce the free energy of a system, the phases evolve. The phase evolution is described by the evolution equation of order parameters and derived by minimizing Eq. (6). Based on an approach by Steinbach[18], Steinbach and Pezzolla [6], the evolution of the order parameters is modelled as a superposition of pairwise interactions of \({\tilde{N}}\) locally active phases

$$\begin{aligned} \displaystyle \frac{\partial \phi _\alpha }{\partial t}&= -\frac{1}{{\tilde{N}}\epsilon }\sum _{\beta \ne \alpha }^{{\tilde{N}}}\left[ M_{{\alpha \beta }}\left( \dfrac{8\sqrt{\phi _\alpha \phi _\beta }}{\pi }\left( \displaystyle \frac{\delta \bar{f}_\textrm{bulk}}{\delta \phi _\alpha }-\displaystyle \frac{\delta {\bar{f}}_\textrm{bulk}}{\delta \phi _\beta }\right) \right. \right. \nonumber \\&\quad \left. \left. +\displaystyle \frac{\delta f_\textrm{intf}}{\delta \phi _\alpha }-\displaystyle \frac{\delta f_\textrm{intf}}{\delta \phi _\beta }+{\Delta }_\textrm{acurv}^{{\alpha \beta }}\right) \right] , \nonumber \\&= -\frac{1}{{\tilde{N}}\epsilon }\sum _{\beta \ne \alpha }^{{\tilde{N}}}\left[ M_{{\alpha \beta }}\left( \frac{8\sqrt{\phi _\alpha \phi _\beta }}{\pi }\Delta _\textrm{bulk}^{{\alpha \beta }}+ \Delta _\textrm{intf}^{{\alpha \beta }}+{\Delta }_\textrm{acurv}^{{\alpha \beta }}\right) \right] , \end{aligned}$$
(13)

cf., e.g., [49]. The mobility of an interface between phases \(\alpha \) and \(\beta \) is written as \(M_{\alpha \beta }\) and the variational derivative \(\displaystyle {\delta f}{/\delta \phi _\alpha }\) is defined as by Goldstein et al. [50, Eq. (13.63)] as

$$\begin{aligned} \displaystyle \frac{\delta f}{\delta \phi _\alpha } = \displaystyle \frac{\partial f}{\partial \phi _\alpha }-\nabla \cdot {\displaystyle \frac{\partial f}{\partial \nabla \phi _\alpha }}. \end{aligned}$$
(14)

Simplifications, described in detail by Prahs et al. [28, Sects. A.2.3-A.2.4], yield a compact form of the bulk driving force given as \( \Delta _\textrm{bulk}^{{\alpha \beta }}:= \displaystyle {\partial {\bar{f}}_\textrm{bulk}}{/\partial \phi _\alpha }-\displaystyle {\partial {\bar{f}}_\textrm{bulk}}{/\partial \phi _\beta } \), reading

(15)

cf., e.g., [28, Eq. (A34)]. In the context of the MPFM, it is common to express the jump of a quantity \(\psi \) in terms of the corresponding phases, reading . In order to ensure, that the phase evolution does not depend on an initially stored plastic energy, the jump of the plastic energy densities  should vanish for \( \gamma _{\textrm{ac}}^\alpha =\gamma _{\textrm{ac}}^\beta =0 \). For simplicity, since the plastic energy density \(f_\textrm{p}\) is accounted for only by its jump between phases, the condition \( f_\textrm{p}^\alpha (\gamma _{\textrm{ac}}^\alpha = 0) = 0 \;\forall \alpha \) is enforced. To this end, an integration constant \( C^\alpha = -{(\tau _\infty ^\alpha -\tau _0^\alpha )^2}/{\Theta _0^\alpha } \), which satisfies the latter condition, is added to Eq. (12). Thus, \( f_\textrm{p}^\alpha (\gamma _{\textrm{ac}}^\alpha =0) = f_\textrm{p}^\beta (\gamma _{\textrm{ac}}^\beta =0) \) holds true. It is pointed out, that with the introduction of the integration constant the Voce hardening resembles the linear hardening case at vanishing accumulated plastic slips \(\gamma _{\textrm{ac}}^\alpha \). For brevity, the three terms in Eq. (15) are, hereinafter, referred to as elastic energy density contribution \((\Delta _\textrm{bulk}^{{\alpha \beta }})_\textrm{e}\), plastic energy density contribution \((\Delta _\textrm{bulk}^{{\alpha \beta }})_\textrm{p}\) and stress interaction contribution \((\Delta _\textrm{bulk}^{{\alpha \beta }})_\textrm{inter}\), respectively. Thus, the abbreviated bulk driving force reads

$$\begin{aligned} \Delta _\textrm{bulk}^{{\alpha \beta }}= (\Delta _\textrm{bulk}^{{\alpha \beta }})_\textrm{p}+ (\Delta _\textrm{bulk}^{{\alpha \beta }})_\textrm{e}+ (\Delta _\textrm{bulk}^{{\alpha \beta }})_\textrm{inter}. \end{aligned}$$
(16)

The surface driving force \(\Delta _\textrm{intf}^{\alpha \beta }\) is formulated as

$$\begin{aligned}&\Delta _\textrm{intf}^{\alpha \beta }:= \displaystyle \frac{\partial f_{\textrm{grad}}+f_{\textrm{pot}}}{\partial \phi _\alpha }-\displaystyle \frac{\partial f_{\textrm{grad}}+f_\textrm{pot}}{\partial \phi _\beta }\nonumber \\ {}&- \left( \nabla \cdot {\displaystyle \frac{\partial f_{\textrm{grad}}}{\partial \nabla {\phi _\alpha }}}-\nabla \cdot {\displaystyle \frac{\partial f_{\textrm{grad}}}{\partial \nabla {\phi _\beta }}}\right) , \end{aligned}$$
(17)

cf. [28, Eqs. (A13-A14)]. The numerical stability of the interface depends on a balanced ratio between the terms building the interface \(\Delta _\textrm{intf}^{{\alpha \beta }}\), and the bulk driving forces \(\Delta _\textrm{bulk}^{{\alpha \beta }}\). However, the term \(\Delta _\textrm{intf}^{{\alpha \beta }}\) induces curvature minimization, which is used in the work at hand only to circumvent numerical artefacts within the interface. Thus, the interface term \(\Delta _\textrm{intf}^{{\alpha \beta }}\) cannot be increased without increasing the amount of curvature minimization. Therefore, as shown by Schoof et al. [49], an additional term \({\Delta }_\textrm{acurv}^{{\alpha \beta }}\) similar to the interface driving force \(\Delta _\textrm{intf}^{{\alpha \beta }}\) is introduced into the evolution equation, reading

$$\begin{aligned} {\Delta }_\textrm{acurv}^{{\alpha \beta }}=&-\gamma ^c\epsilon \left( \bigtriangleup \phi _\alpha -\Vert \nabla \phi _\alpha \Vert \nabla \cdot {\left( \dfrac{\nabla \phi _\alpha }{\Vert \nabla \phi _\alpha \Vert }\right) }\right. \nonumber \\&\left. - \bigtriangleup \phi _\beta + \Vert \nabla \phi _\beta \Vert \nabla \cdot {\left( \dfrac{\nabla \phi _\beta }{\Vert \nabla \phi _\beta \Vert }\right) }\right) \nonumber \\&- \gamma ^c \dfrac{16}{\epsilon \pi ^2} (\phi _\alpha -\phi _\beta ). \end{aligned}$$
(18)

It does not contribute to curvature minimization. The term \({\Delta }_\textrm{acurv}^{{\alpha \beta }}\) is not associated to the interfacial energy \(\gamma _{\alpha \beta }\) and instead depends on a numerical parameter \(\gamma ^c\), which can be considered to be a calibration factor for the strength of the artificially constructed interface. Herein, the curvature is subtracted from the gradient energy density contributions and to ensure a correct interaction of gradient and potential energy density a contribution from the potential energy density with \(\gamma ^c\) is included. It is stressed, that this addition to the evolution equation does not energetically influence the equilibrium state, cf., e.g., [49]. The superposition of the interface contributions \(\Delta _\textrm{intf}^{{\alpha \beta }}\) and \({\Delta }_\textrm{acurv}^{{\alpha \beta }}\), cf., e.g., [49, 51], allows to control the effect of curvature minimization by \(\gamma _{\alpha \beta }\), which is used in the present work as a numerical parameter to circumvent numerical artefacts within the interface, while balancing the ratio of interface and bulk terms with \(\gamma ^c\).

3 Numerical results

Fig. 1
figure 1

Schematic representation of the simulation domain with a cylindrical inclusion and the corresponding geometrical dimensions

Full size image

Remark

The Finite Element Method is used to solve the balance of linear momentum in the weak form. A linearization of the weak form of the balance of linear momentum is considered because of the high non-linearity of the material behavior. For further information, the reader is referred to the detailed derivation by Prahs et al. [28] regarding the numerical implementation of the model. The in-house code Pace3D is used for the computations, cf. [52].

Table 1 Material parameters are chosen corresponding to aluminium as an example for an FCC material, cf., e.g., [53]
Full size table

3.1 Equilibrium shapes

Table 2 Numerical and geometrical parameters are adjusted in a parameter study to minimize their impact on the phase evolution
Full size table
Fig. 2
figure 2

Temporal evolution of the circularity (a), and corresponding shape evolution (b) of an inclusion with transversely isotropic eigenstrains with \(\varepsilon ^* = {0.08}{\%}\) over time. The inclusion is displayed using the corresponding order parameter \(\phi _\textrm{I}\). The points in time \(t_0\) to \(t_4\) and the corresponding circularity are marked in (a). The location of the corresponding sharp interface, is illustrated by a black line

Full size image

Objective

The effects of the use of an anisotropic plasticity model within an MPFM and its impact on phase evolution are discussed in terms of the shape evolution of an elastic inclusion, subjected to transversely isotropic eigenstrains, within an elasto-plastic region. The objective of the subsequently discussed investigations is to identify equilibrium shapes of the inclusion, i.e., a state in which the bulk driving forces acting on the interface are balanced.

Domain, boundary, and load conditions

Subsequently, a quadratic and quasi-two dimensional domain is considered, cf. Fig. 1. A number of \( 400\times 400\times 1 \) cells is used for discretization on an equidistant Cartesian grid. The inclusion is subject to a volume constraint following the method by Nestler et al. [54]. Thus, the inclusion exhibits changes in shape but no volumetric changes. A plane strain set-up is implied employing Dirichlet boundary conditions

$$\begin{aligned} u_x(0,y,z)&= u_x(L,y,z) = 0, \nonumber \\ u_y(x,0,z)&= u_y(x,L,z) = 0, \nonumber \\ u_z(x,y,0)&= u_z(x,y,W)= 0. \end{aligned}$$
(19)

Here, L refers to the width and height of the domain and W to the thickness. Neumann boundary conditions apply regarding the field of order parameters, i.e., \( \displaystyle {\partial \phi _\alpha }{/\partial x_i}=0, \forall x_i \in \partial {{\mathcal {B}}}_i \). Here, \(\partial {{\mathcal {B}}}_i\) represents the boundary with its corresponding normal direction i. The inclusion with diameter D is subjected to transversely isotropic eigenstrains \(\varvec{\varepsilon }^{*,\textrm{I}}\), with

$$\begin{aligned} \varepsilon ^{*,\textrm{I}}_{xx} = \varepsilon ^{*,\textrm{I}}_{yy} = \varepsilon ^* \quad \text {and} \quad \varepsilon ^{*,\textrm{I}}_{zz} = \varepsilon ^{*,\textrm{I}}_{xy} =\varepsilon ^{*,\textrm{I}}_{xz} = \varepsilon ^{*,\textrm{I}}_{yz} = 0. \end{aligned}$$
(20)

The elastic properties of inclusion and matrix are identical. However, the matrix is considered to exhibit an elasto-plastic behavior and subject to isotropic hardening of Voce type, while the inclusion is solely elastic by increasing its flow stress \(\tau ^\textrm{I}_0\) sufficiently high.

Fig. 3
figure 3

The Mises stress \(\sigma _{\textrm{vM}}\) and accumulated plastic slip \(\gamma _{\textrm{ac}}\) fields of an inclusion with transversely isotropic eigenstrains with \( \varepsilon ^*={0.08}{\%} \) are displayed in a and b at time \(t_0\), respectively

Full size image
Fig. 4
figure 4

Comparison of the bulk driving forces \(\Delta _\textrm{bulk}^{{\alpha \beta }}\) of an inclusion with transversely isotropic eigenstrain with \({\varepsilon ^*_\textrm{I}={0.08}{\%}}\) at the beginning of phase evolution (\(t_0\)) in (a), and at equilibrium (\(t_4\)) in (b). In the first column the total bulk driving force \(\Delta _\textrm{bulk}^{{\alpha \beta }}\) acting on the interface is shown. In the second, third and fourth column the plastic \((\Delta _\textrm{bulk}^{{\alpha \beta }})_\textrm{p}\) and elastic energy density contribution \((\Delta _\textrm{bulk}^{{\alpha \beta }})_\textrm{e}\) and stress interaction contribution \((\Delta _\textrm{bulk}^{{\alpha \beta }})_\textrm{inter}\) are displayed, respectively. The grey area represents bulk

Full size image

Parameters

The material parameters, used for all subsequent simulations, are summarized in Table 1. The material is modeled mimicking aluminium as an example for an FCC material. If not otherwise mentioned, the crystallographic orientations within the matrix and inclusion are equal. Here, the \(\langle 100\rangle \)-directions correspond to the coordinate axes \(\{{\varvec{e}}_x,{\varvec{e}}_y,{\varvec{e}}_z\}\). A parameter study was conducted to minimize the impact of geometrical and numerical parameters on the phase evolution. The resulting parameters are summarized in Table 2. The interface parameter \( \epsilon \) is chosen with respect to a sufficient discretization of the diffuse interface and the width of an interface \(l_\textrm{eq}\) in equilibrium. The mobility \(M_{\alpha \beta }\) is computed via \( 1/M_{\alpha \beta }= (4\Delta t (\gamma _{\alpha \beta }+ \gamma ^c))/(\Delta x)^2 \) dependent on the spatial and time discretization, \(\Delta x\) and \(\Delta t\), respectively, as well as parameters related to the surface energy, \(\gamma _{\alpha \beta }\) and \(\gamma ^c\), in order to ensure a numerically stable interface, cf., e.g., [55, Eq. (3.39)]. Dimensionless parameters are used in the simulations. A stable interface is created in the normal direction of the interface by means of \({\Delta }_\textrm{acurv}^{{\alpha \beta }}\) associated to \(\gamma ^c\) without inducing curvature minimization. Nevertheless, to circumvent numerical artefacts in the interface a small amount of curvature minimization is introduced by \(\Delta _\textrm{intf}^{{\alpha \beta }}\) with the surface energy \(\gamma _{\alpha \beta }\).

Circularity

As the objective in this subsection is to investigate the equilibrium shape of an inclusion, a measurement and quantification for sphericity or in a quasi two-dimensional setting for circularity is needed, in order to compare different shapes. Wadell [56] uses a measure called sphericity to measure and quantify the shape and roundness of quartz and sand particles. Analogously, a measure for two-dimensional inclusions, subsequently referred to as circularity \(\Psi _\textrm{2D}\), is introduced in the work at hand. It is given by the ratio of the circumference of a circle with the same surface area as the investigated inclusion \( U(r) = 2\pi r \), where the radius \( r = \sqrt{A_\textrm{O}/\pi } \) is derived from the actual measured surface area \( A_\textrm{O} \), and the actual measured circumference \(U_\textrm{O}\),

$$\begin{aligned} \Psi _\textrm{2D}=\dfrac{U(r)}{U_\textrm{O}}=\dfrac{2\pi \sqrt{A_\textrm{O}/\pi }}{U_\textrm{O}} = \dfrac{\sqrt{4\pi A_\textrm{O}}}{U_\textrm{O}}. \end{aligned}$$
(21)

The surface area \(A_\textrm{O}\) and the circumference \(U_\textrm{O}\) of the inclusion are computed based on the corresponding phase-field order parameter \(\phi _\textrm{I}\) and its gradient \(\nabla \phi _\textrm{I}\), respectively.

Inclusion with transversely isotropic eigenstrains

Subsequently, \( \varepsilon ^*={0.08}{\%} \) is considered. In Fig. 2a, the circularity \(\Psi _\textrm{2D}\) of an inclusion is depicted over time. The shape of the inclusion reaches a steady state, i.e., an equilibrium, after about \({1250\,\mathrm{\text {s}}}\). Thus, the inclusion does not exhibit changes in the last \({3000\,\mathrm{\text {s}}}\) of the simulation. Nevertheless, the results are presented over a longer period, to emphasize the characteristics of the equilibrium. The resulting shapes at different time steps \(t_0\) to \(t_4\), which are marked in Fig. 2a, are illustrated in Fig. 2b. The initial circular inclusion loses its circularity and its shape evolves from a circle to one resembling a square with rounded corners. The inclusion at time \(t_4\) is subsequently referred to as equilibrium shape. The mechanical fields, which are involved in the phase evolution, are depicted in Fig. 3. The Mises stress \(\sigma _{\textrm{vM}}\) is shown in Fig. 3a. The Mises stress reaches a maximum in the matrix just outside of the inclusion and decreases to zero toward the boundary. Inside the inclusion the Mises stress is approximately constant. In Fig. 3b, the accumulated plastic slip \(\gamma _{\textrm{ac}}\) is displayed. Within the diffuse interface region, the accumulated plastic slip \(\gamma _{\textrm{ac}}\) is given by the interpolation of the phase-specific contributions of the accumulated plastic slip \(\gamma _{\textrm{ac}}^\alpha \) reading \( \gamma _{\textrm{ac}}= \sum _{\alpha =1}^{N^*}\phi _\alpha \gamma _{\textrm{ac}}^\alpha \). Within this first example, not all slip systems become active due to the small amplitude of eigenstrains. The distribution is heterogeneous around the inclusion, but equal in \({\varvec{e}}_x\)- and \({\varvec{e}}_y\)-direction. The driving force \(\Delta _\textrm{bulk}^{{\alpha \beta }}\), leading to the equilibrium shape, consists of three additive contributions, as described by Eq. (15) and by Eq. (16) in the abbreviated form. Herein, the elastic and plastic energy density contribution are denoted by \((\Delta _\textrm{bulk}^{{\alpha \beta }})_\textrm{e}\) and \((\Delta _\textrm{bulk}^{{\alpha \beta }})_\textrm{p}\), respectively. The stress interaction contribution is referred to as \((\Delta _\textrm{bulk}^{{\alpha \beta }})_\textrm{inter}\). The bulk driving force and its contributions, acting on the interface in normal direction, are compared at times \(t_0\) and \(t_4\), in Fig. 4a and b, respectively. The additive composition of the second, third and fourth column yields the total driving force in the first column. The sign determines the direction in which the force acts. Here, a negative sign indicates a force that is directed from the outside to the inside of the inclusion. However, volume changes are disabled. The equilibrium shape corresponds to the driving forces. At time \(t_0\), a strong fluctuation of the total bulk driving force along the circumferential direction is visible. The heterogeneous distribution is associated with the plastic deformation. At time \(t_4\), the distribution of the total bulk driving force \(\Delta _\textrm{bulk}^{{\alpha \beta }}\) is nearly homogeneous in tangential direction, i.e., the fluctuations of the driving force along the circumferential direction are nearly zero. Therefore, no further change of shape is invoked, i.e., the equilibrium shape of the inclusion is obtained. The plastic energy density contribution \((\Delta _\textrm{bulk}^{{\alpha \beta }})_\textrm{p}\) to the bulk driving force does not change over time by approximation. Thus, it can be assumed that the change in the other two contributions \((\Delta _\textrm{bulk}^{{\alpha \beta }})_\textrm{e}\) and \((\Delta _\textrm{bulk}^{{\alpha \beta }})_\textrm{inter}\) causes the equilibrium. The observation of the third and fourth column, i.e., of the elastic energy density \((\Delta _\textrm{bulk}^{{\alpha \beta }})_\textrm{e}\) and stress interaction contribution \((\Delta _\textrm{bulk}^{{\alpha \beta }})_\textrm{inter}\), coincide with the assumption. A change over time can be observed in these terms. In general, the total driving force on the interface equals zero in equilibrium, i.e., all forces inducing phase-field evolution are balanced. However, that is not the case here. With the use of a volume preserving method, an equilibrium is characterized by a homogeneous distribution of the driving force along the interface. The non-vanishing driving force \(\Delta _\textrm{bulk}^{{\alpha \beta }}\) in equilibrium leads without a volume constraint to a spherical growth or shrinkage only, and not to shape evolution, because of the homogeneous distribution of the driving force along the circumferential direction of the interface.

Fig. 5
figure 5

Comparison of equilibrium shapes with rotated and unrotated grain orientations. The inclusion is displayed using the corresponding order parameter \(\phi _\textrm{I}\) in subfigure a and b with rotated and unrotated grain orientation, respectively

Full size image

Crystallographic orientations

Subsequently, the crystallographic orientation of the elasto-plastic matrix is rotated. Rotations are described via the Bryant angles \({{\mathcal {O}}}= \{\psi _x,\psi _y',\psi _z''\}\), cf., e.g., [57, p. 351]. An initial coordinate system \(\{{\varvec{e}}_x,{\varvec{e}}_y,{\varvec{e}}_z\}\) is rotated via \(\psi _x\) around the \({\varvec{e}}_x\)-axis, yielding the primed coordinate system \( \{{\varvec{e}}_x',{\varvec{e}}_y',{\varvec{e}}_z'\} \). The rotation around the \({\varvec{e}}_y'\)-axis is described by \(\psi _y'\) and yields the double primed coordinate system \( \{{\varvec{e}}_x'',{\varvec{e}}_y'',{\varvec{e}}_z''\} \). Finally, rotations denoted by \(\psi _z''\) describe a rotation around the \({\varvec{e}}_z''\)-axis. In this chapter, rotations around the out-of-plane axis, i.e., \({\varvec{e}}_z\) are displayed, with \( {{\mathcal {O}}}= \{0,0,\psi _z''\} \). Thus, the \({\varvec{e}}_z''\)-axis equals the \({\varvec{e}}_z\)-axis, [28, Sect. (4.1.3)]. In this subsection, the crystallographic orientation, subsequently also referred to as grain orientation, of the elasto-plastic matrix is given by \( {{\mathcal {O}}}_\textrm{M} = \{0^\circ ,0^\circ ,13^\circ \} \). The equilibrium circularity of the inclusion within a matrix with a rotated crystallographic orientation equals the circularity of the inclusion in the unrotated case. Moreover, the orientation of the lattice vectors to the Cartesian grid, which is used to discretize the domain, has also been changed by rotating the grain orientation. However, the circularity is identical. Thus, no dominant direction of the grid, used for spatial discretization, can be observed. The influence of the rotated grain orientation is visible, nevertheless. The corresponding equilibrium shape is depicted in Fig. 5a and compared with the equilibrium shape of the inclusion within an unrotated matrix, cf. Fig. 5b. The resulting square-like shape of the inclusion in equilibrium, is rotated by \(13^\circ \) around the out-of-plane axis \({\varvec{e}}_z\), corresponding to the rotation of the grain orientation.

Fig. 6
figure 6

The impact of amplified eigenstrains \(\varepsilon ^*\) on the shape of the inclusion is illustrated by the temporal evolution of the circularity \(\Psi _\textrm{2D}\) of an inclusion with various transversely isotropic eigenstrains with \( \varepsilon ^{*,\textrm{I}}_{xx} = \varepsilon ^{*,\textrm{I}}_{yy}=\varepsilon ^* \) in (a). All other components of the eigenstrain equal zero. The shapes of the inclusion in equilibrium (b) are illustrated using the order parameter \(\phi _\textrm{I}\) of the inclusion and the corresponding fields of accumulated plastic slip \(\gamma _{\textrm{ac}}\) (c) are displayed at the beginning of phase evolution (\(t_0\))

Full size image

Increased eigenstrains

Subsequently, within the inclusion the transversely isotropic eigenstrain \( \varvec{\varepsilon }^{*} \) with \( \varepsilon ^{*,\textrm{I}}_{xx} = \varepsilon ^{*,\textrm{I}}_{yy} = \varepsilon ^* \) is increased to \({\varepsilon ^*={0.1}{\%}}\) and \(\varepsilon ^*={0.2}{\%}\) and the resulting equilibrium shapes are compared with the results of the inclusion with \(\varepsilon ^*={0.08}{\%}\). The parameter \(\gamma ^c\) is adjusted according to the increased bulk contributions. The resulting equilibrium shapes, their circularity and the elastic and plastic fields are compared in the following. As shown in Fig. 6a, the inclusion with the largest eigenstrain encounters the smallest decrease in circularity. Compared to the case of \( \varepsilon ^*={0.08}{\%} \), which is considered in the previous section, there is a significant difference in the circularity of the corresponding equilibrium shape. The resulting shapes in equilibrium are depicted in Fig. 6b. It is also clearly recognizable, that the shape of the inclusion for \(\varepsilon ^*={0.2}{\%}\) compared with the others is closest to a circle. The evaluation of the accumulated plastic slip \(\gamma _{\textrm{ac}}\) provides information about the reason for the different shape evolution. In contrast to the case of \( \varepsilon ^*={0.08}{\%} \), which is considered in the previous section, additional slip systems are activated for larger eigenstrains and, thus, the accumulated plastic slip is distributed more homogeneously in the diffuse interface region in case of larger eigenstrains, cf. Fig. 6c. The fluctuation of the distribution of the accumulated plastic slip along the circumferential direction of the inclusion decreases for larger eigenstrains. Contributions to the driving forces on the interface are, therefore, distributed more homogeneously. Thus, despite the increased accumulated plastic slip for increased eigenstrains, the resulting equilibrium exhibits a bigger circularity for larger eigenstrains.

3.2 Microstructure evolution—towards an application to static recrystallization

Objective and simulation setup

The evolution of an inclusion in a deformed material is examined for the application to the simulation of SRX. The aim is to develop an approach for modeling the evolution of an inclusion based on elastic and plastic fields, arising from a deformation simulated with CP in the context of the MPFM. For the comparison of different approaches a domain with periodically arranged honeycombs is used. The grain structure is visualized in Fig. 7 by black lines illustrating the corresponding sharp interfaces. The domain is composed of twelve phases. The grain orientation of the inner three grains is rotated using \({{\mathcal {O}}}= \{0,0,\psi _z''\}\), such that no adjacent phases have the same orientation. The grains are rotated by \(\psi _z''^\alpha \) around the out-of-plane axis \({\varvec{e}}_z\). For the study of the approaches, the angles \(\psi _z''\) are chosen in a way, that the three inner grains exhibit a higher degree of plastic deformation than the outer grains. The domain is discretized by \( 207\times 200\times 3 \) cubical cells with respect to the \({\varvec{e}}_x\)-, \({\varvec{e}}_y\)-, and \({\varvec{e}}_z\)-direction of an equidistant, Cartesian grid. During the simulation of the mechanical deformation, the phase-field order parameters are rigid, i.e., \( \displaystyle {\partial \phi _\alpha }{/\partial t} = 0 \). In order to create a deformed domain, Neumann boundary conditions

$$\begin{aligned} \bar{{\varvec{t}}}(0,y,z) = \bar{{\varvec{t}}}(L,y,z) = \bar{{\varvec{t}}}(x,y,0) = \bar{{\varvec{t}}}(x,y,W) = {\varvec{0}}\end{aligned}$$
(22)

describing a zero stress boundary and

$$\begin{aligned} \bar{{\varvec{t}}}(x,0,z) = -\bar{{\varvec{t}}}(x,L,z) = {\bar{t}}_0 {\varvec{e}}_y \end{aligned}$$
(23)

apply, i.e., the bottom and top of the domain are subject to a constant stress in normal direction. During the microstructure evolution, the phase-field order parameters are restricted by Neumann boundary conditions \( \displaystyle {\partial \phi _\alpha }{/\partial x_i} = 0 \; \forall x_i \in \partial {{\mathcal {B}}}_i \) on the top, bottom, back and front. As with Neumann boundary conditions the phase boundaries are perpendicular to the boundary. Thus, the left and right boundary are restricted with a constant phasefield, to ensure, that the honeycombs do not evolve. The elastic and plastic material parameters applied to the grains and nuclei are the same as considered for the matrix in the context of equilibrium shapes, cf. Table 1. The spatial discretization is given by \(\Delta x = \Delta y = \Delta z = {0.5}\,{\upmu }\hbox {m}\) and the time discretization by \(\Delta t = 1\,\hbox {s}\). A surface energy \(\gamma _{{\alpha \beta }}={0.25}\,\hbox {mJ}~\hbox {m}^{-2}\) is used and the parameter \(\gamma ^c\) is adjusted to ensure balanced ratio of interface and bulk driving forces. The simulation is divided into four parts:

  1. 1.

    Mechanical loading: The boundary stress \(\bar{t}_0\) is increased with a linear ramp from 0 to 50 MPa in 1000 time steps, performing a uniaxial compression.

  2. 2.

    Mechanical unloading: The normal stresses on the top and the bottom of the domain are relaxed with a linear ramp and a normal stress of zero is reinstated within another 1000 time steps.

  3. 3.

    Nucleation: In a separate simulation, nuclei are created. Without solving for mechanical fields, cylindrical phases, representing the nuclei, are placed into the domain and a diffuse interface is created within 100 time steps. Shrinkage of the nuclei is prevented by eliminating curvature minimization.

  4. 4.

    Microstructure evolution: As an initial state, the combination of the mechanical fields after unloading and the distribution of the order parameters, created in the nucleation step, is used. A mobility \(M_{\alpha \beta }=0\) applies if phase \(\alpha \) and \(\beta \) are both elements of the set of honeycombs or both of the set of nuclei.

Fig. 7
figure 7

The Mises stress \(\sigma _{\textrm{vM}}\) and the accumulated plastic slip \(\gamma _{\textrm{ac}}\) in the honeycomb structure upon loading are displayed in (a) and (b), respectively, and the Mises stress \(\sigma _{\textrm{vM}}\) upon unloading in (c). The black lines illustrate the sharp interfaces between grains

Full size image
Fig. 8
figure 8

Comparison of the approaches A, B, and C with the Mises stress \(\sigma _{\textrm{vM}}\) in (a) and the accumulated plastic slip \(\gamma _{\textrm{ac}}\) in (b). The grain boundaries between previously deformed grains are illustrated by grey lines. The region of the growing nucleus is enclosed by a white line. The first column \(t_0\) represents the start of the microstructure evolution simulation, the second \(t_1\) after 2000 simulation steps and the third column \(t_3\) after 10,000 simulation steps

Full size image

Approaches to strain inheritance

The Mises stress \(\sigma _{\textrm{vM}}\) after loading is illustrated in Fig. 7a. The inhomogeneous distribution of the stress is caused by the different crystallographic orientation in each grain. The inner three phases exhibit a smaller Mises stress \(\sigma _{\textrm{vM}}\). This is due to the larger plastic deformation in the inner phases than in the outer phases, as visible in Fig. 7b. Here, the accumulated plastic slip \(\gamma _{\textrm{ac}}\) is illustrated, which is larger in the inner grains. After unloading, the plastic deformation remains by definition, while the elastic deformation is relaxed. Due to the inhomogeneous structure and grain orientation, the elastic strain is not homogeneous and fluctuations of the stress are present. Thus, the Mises stress after unloading does not vanish everywhere, but exhibits small stress peaks, in particular at the GBs, as shown in Fig. 7c. The maximum Mises stress after unloading reaches just about 12 MPa. During unloading, no significant plastic slip occurs and the resulting field after unloading is equal to the field after loading, as displayed in Fig. 7b. In this section, the evolution of a nucleus is investigated. The simulation of the nucleation itself, however, is not part of this work. Following the simulation of the deformation, a nucleus is placed in the domain manually, as described above. The site of the nucleus is chosen to be a triple junction, as those sites are characterized by a highly inhomogeneous distribution of the accumulated plastic slip and, thus, likely to cause nucleation, cf. [1, Sect. 6.2.2]. Here, the triple junction in the middle of the domain is chosen, in order to be able to compare the approaches in a convenient way. In the following, the term nucleus or inclusion are used to describe the growing new grain. Since recrystallization occurs on a deformed structure, the inheritance of the strain fields has to be discussed. Inheritance describes how internal variables and fields associated with elastic and especially plastic deformation are passed on to the adjacent phase, when the corresponding interface crosses a plastified region. Stresses and migration kinetics are impacted by the model of inheritance. In general, inheritance of hardening structure is to be distinguished from inheritance of plastic deformation, cf., e.g., [26]. In the work at hand, the inheritance of hardening is not considered. The local hardening, i.e., the local accumulated plastic slip, is assumed to vanish as the area is consumed by a growing nucleus. A hardening evolution equation, cf., e.g., [34], is not considered within the present work. Nevertheless, the yield criterion is verified in each time step. Since no external load is applied to the domain during microstructure evolution, stresses do not exceed the initial flow stress. Three approaches to the inheritance of strain fields are defined and compared in the following:

  1. A

    No strain fields are inherited: The recrystallization is simulated on the reference configuration. The strain and displacement fields are neglected, while the phase-specific accumulated plastic slip \(\gamma _{\textrm{ac}}^\alpha \) is considered in the honeycombs. The migration of grain boundaries is driven by the accumulated plastic slip \(\gamma _{\textrm{ac}}^\alpha \), which is applied to the reference configuration, using the evolving field of order parameters.

  2. B

    Plastic strain fields are inherited: The information of the preceding plastic deformation is passed on to the next simulation step, the microstructure evolution. The phase-specific plastic strain fields \(\varvec{\varepsilon }_{\textrm{p}}^\alpha \) and the accumulated plastic slip \(\gamma _{\textrm{ac}}^\alpha \) are considered in the corresponding honeycombs. The nucleus inherits the preceding plastic deformation of the region it is placed onto and grows into. A phase-averaged plastic strain field \({\bar{\varvec{\varepsilon }}}_\textrm{p}\) is inherited to the nucleus, i.e., an inelastic strain which can be regarded as an eigenstrain, which carries the information of the preceding plastic deformation. In this context, the phase-averaged plastic strain is defined as \({\bar{\varvec{\varepsilon }}}_\textrm{p}:=\sum _{\alpha =1}^{N^*}\phi _\alpha \varvec{\varepsilon }_{\textrm{p}}^\alpha \). The displacement field of the preceding unloading step is applied to the domain during microstructure evolution.

  3. C

    Total strain fields are inherited: The total strain field \({\bar{\varvec{\varepsilon }}}\), i.e., the elastic and plastic contribution, is inherited to the nucleus. The phase-specific plastic strain \(\varvec{\varepsilon }_{\textrm{p}}^\alpha \) and the accumulated plastic slip \(\gamma _{\textrm{ac}}^\alpha \) are considered in the honeycombs. The total strain field \({\bar{\varvec{\varepsilon }}}\) is inherited to the nucleus as an inelastic strain, which can be regarded as an eigenstrain, containing the deformation. The displacement field of the preceding unloading step is applied to the domain during microstructure evolution.

Hereinafter, the approaches above are referred to as approach A, B and C, respectively. Using approach A, no unloading step is necessary, since the accumulated plastic slip is applied to the reference configuration. For all three approaches, the zero stress boundary conditions at the end of unloading are applied to the domain during microstructure evolution. No further external loads are applied, mimicking the conditions for SRX. In approach A, no strains are inherited and the simulation is performed on basis of the reference configuration. Hence, the resulting stresses are zero in each component, as is the Mises stress \(\sigma _{\textrm{vM}}\), which is illustrated at three different time steps in Fig. 8a (row A). The inclusion grows nevertheless, as highlighted by the white line. This is due to the accumulated plastic slip \(\gamma _{\textrm{ac}}\), which is distributed inhomogeneously throughout the honeycombs, resulting in a jump of the plastic energy density between honeycombs and nuclei, i.e., the bulk driving force acting on a grain boundary depends on the plastic energy density \(f_\textrm{p}^\alpha \) of the phases involved, more precisely on \(\gamma _{\textrm{ac}}^\alpha \). No further contributions to the bulk driving force, cf. Eq. (15), are present. Therefore, although the stresses and strains in the domain vanish, the interpolated accumulated plastic slip \(\gamma _{\textrm{ac}}\), can be predicted according to the microstructure evolution, i.e., the accumulated plastic slip in the newly built and growing inclusion equals zero, cf. Fig. 8b (row A), mimicking the evolution of a plastically undeformed grain. Regarding approach B, the stress field exhibits no change compared to the final unloading state. The displacement field is inherited to the domain according to the final state after unloading. All inhomogeneities arising from plastic deformation are inherited by the plastic strain fields \({\bar{\varvec{\varepsilon }}}_\mathrm{_p}\). In addition, elastic strains arise in the newly built and growing nucleus. Thus, the resulting stress field shows significant inhomogeneities in the inclusion, as illustrated by the Mises stress \(\sigma _{\textrm{vM}}\) in Fig. 8a (row B). As in approach A, the accumulated plastic slip of the nucleus equals zero, cf. Fig. 8b (row B). With approach C, a change in the Mises stress and the accumulated plastic slip is visible. The stress relaxes within the region of the expanding nucleus, cf. Fig. 8a (row C). The entire information of the displacement of the preceding deformation, i.e., the displacement originating from elastic and plastic deformation, respectively, is inherited as an eigenstrain. Thus, the newly built and growing inclusion can be considered “strain-free”, i.e., in this context free of elastic and plastic strain. As for the other approaches, the accumulated plastic strain equals zero in the growing inclusion, cf. Fig. 8b (row C). For all three approaches, the evolution of accumulated plastic slip \(\gamma _{\textrm{ac}}\), as illustrated in Fig. 8b, reflects the theory of recrystallization, which describes the elimination of the deformation structure through formation and migration of grain boundaries, cf. [1, Sect. 6.2]. In this context, the plastic deformation history is represented by the accumulated plastic slip \(\gamma _{\textrm{ac}}^\alpha \). The main difference of the approaches discussed above concerns the resulting stress fields, which are illustrated using the Mises stress in Fig. 8a. During SRX strain-free grains are formed, cf., e.g., [39]. Thus, with the chosen boundary conditions a vanishing stress field is expected within the growing nuclei. In addition, the newly formed grains exhibit a smaller dislocation density as the previously deformed grains. Moreover, no external load is applied to the domain. Therefore, no elastic or plastic strains are expected in the new grains. The evolution of the accumulated plastic slip can be simulated using all three approaches, i.e., the plastic slip within the nuclei equals zero. Since the dominating driving force \((\Delta _\textrm{bulk}^{{\alpha \beta }})_\textrm{p}\) depends on the accumulated plastic slip \(\gamma _{\textrm{ac}}^\alpha \), the evolution can be simulated using all of the approaches. Only with approach C, however, it is possible to simulate the relaxation of the stresses in the growing nucleus. Furthermore, the driving force obtained by approach C includes contributions arising from stress and strain fields. It follows, that with approach C the simulations of the microstructure evolution during the recrystallization are closer to experimental findings. Consequently, approach C is used in the following simulations.

Fig. 9
figure 9

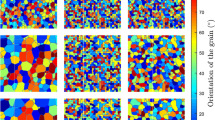
Schematic representation of a deformed grain structure with multiple growing nuclei in the top row (a). The colors refer to different grain orientations and allow an assignment in deformed grains and nuclei, respectively. In the bottom row, the Mises stress \(\sigma _{\textrm{vM}}\) (b), the superposition of the bulk driving force \(\Delta _\textrm{bulk}^\textrm{I}\) of two nuclei I (grey areas represent bulk) (d), and the accumulated plastic strain \(\gamma _{\textrm{ac}}\) (c) and (e) are depicted for selected areas at time \(t_1\)

Full size image

Grain boundary migration due to heterogeneous plastic fields

Recrystallization is characterized by nucleation and growth. Both processes occur consecutively for any particular grain. However, not only one nucleus is formed, but both processes occur simultaneously, cf., e.g., [39, sec. 7.1]. Thus, the domain size is increased to \( 300\times 300\times 3 \) cubical cells with 29 phases of five different grain orientations around the out-of-plane axis \({\varvec{e}}_z\). The number of nuclei is enhanced to 14. Furthermore, a structure with irregular grains is used, which is closer to experimentally observed crystalline microstructures than the honeycomb structure. The structure is generated using a Voronoi tessellation algorithm. The phase-field order parameters are constant at the lower, upper, left and right boundary. All other boundary conditions apply as described in the previous paragraph. The spatial discretization is \( \Delta x = {0.5\,\mathrm{\upmu \text {m}}} \) and a surface energy \( \gamma _{\alpha \beta }={0.25\,\mathrm{\text {m}\text {J}\square \text {m}^{-1}}} \) is considered. The parameter \(\gamma ^c\) is adjusted to ensure a balanced ratio of interface and bulk contributions. The initial structure used for the microstructure evolution is displayed on the left in Fig. 9a. Each color of the deformed grains corresponds to an arbitrary grain orientation around the out-of-plane axis \({\varvec{e}}_z\). The nuclei exhibit an unrotated grain orientation and are colored differently for better visibility. In Fig. 9, the evolution of multiple nuclei and their interaction is displayed. The previous structure is completely absorbed after \( t_3={3000} \) s. The different migration characteristics result from the heterogeneous stress and accumulated plastic slip distribution. In Fig. 9b and c, the Mises stress and the accumulated plastic slip are depicted at time \( t_1={500} \) s. As discussed for approach C, the stress relaxes within the growing nuclei and the accumulated plastic slip equals zero. Accounting for the above described boundary conditions, the newly formed grains are strain-free apart from the inherited eigenstrain and, thus, also stress-free. Further insights into the impact of a highly heterogeneous distribution of the accumulated plastic slip are obtained by the observation of the bulk driving forces acting on the interface between nucleus and previously deformed grains. For illustration, the plastic energy density contribution \((\Delta _\textrm{bulk}^\textrm{I})_\textrm{p}\) to the total bulk driving force \(\Delta _\textrm{bulk}^\textrm{I}\) acting on the interface of an inclusion is obtained by summation of the driving forces arising from each interaction of the inclusion \(\mathrm I\) and an adjacent grain, associated with \(\alpha \), i.e.,

$$\begin{aligned} (\Delta _\textrm{bulk}^\textrm{I})_\textrm{p}= & {} \sum _{\alpha =1}^A B(\phi _\alpha ,\phi _\textrm{I}) (\Delta _\textrm{bulk}^{\alpha \mathrm I})_\textrm{p}, \quad \text {with} \quad \nonumber \\ B(\phi _\alpha ,\phi _\textrm{I})= & {} {\left\{ \begin{array}{ll} 1, \;\forall \; \phi _\alpha \phi _\mathrm{_I}\ne 0, \\ 0, \;\text {else}. \end{array}\right. } \end{aligned}$$
(24)

Herein, A denotes the number of adjacent grains to the inclusion. The elastic energy density and stress interaction contribution \((\Delta _\textrm{bulk}^\textrm{I})_\textrm{e}\) and \((\Delta _\textrm{bulk}^\textrm{I})_\textrm{inter}\) are defined analogously. Consequently, the total bulk driving force \(\Delta _\textrm{bulk}^\textrm{I}\), acting on the interface between the inclusion and all adjacent grains, is given by

$$\begin{aligned} \Delta _\textrm{bulk}^\textrm{I} = (\Delta _\textrm{bulk}^\textrm{I})_\textrm{p} +(\Delta _\textrm{bulk}^\textrm{I})_\textrm{e} + (\Delta _\textrm{bulk}^\textrm{I})_\textrm{inter}. \end{aligned}$$
(25)

In Fig. 9d, the superposition of the driving force \(\Delta _\textrm{bulk}^\textrm{I}\) of two adjacent nuclei is displayed. The driving forces are obtained by means of Eq. (24) and Eq. (25). It is clearly visible, that no driving forces are present between the nuclei. This is explained by the fact, that the stresses and the elastic and plastic strains within the nuclei vanish and, moreover, there is no plastic deformation. Thus, all contributions to the driving force equal zero. Furthermore, it is clear to see that the driving force causing growth, depends on the plastic deformation of the adjacent grains. For example in Fig. 9d, the driving force causing growth is smaller at the bottom grain, where the accumulated plastic slip is smaller as visible in Fig. 9c. Thus, the dominating contribution to the driving force, the plastic energy density contribution \((\Delta _\textrm{bulk}^\textrm{I})_\textrm{p}\), is smaller resulting in a smaller grain boundary migration rate. By mechanical loading and unloading, a significantly heterogeneous distribution of \(\gamma _{\textrm{ac}}\), as visible in Fig. 9e, arises. The grain at the bottom of the considered domain, for example, exhibits a smaller amount of accumulated plastic slip as indicated by the darker coloring. It is noticeable, that the nucleus grows faster into the grains with larger accumulated plastic slip. It is pointed out, that for the order parameters constant boundary conditions apply. Thus, a nucleus cannot grow all the way to the boundary and the resulting phase evolution close to the boundary of the domain is not investigated. The last simulation step \(t_3\) is depicted on the far right in Fig. 9a. Here, the previously deformed Voronoi structure is completely absorbed by the growing nuclei. Consequently, a new grain structure is formed. The formation depends on the location of the nuclei and their migration characteristics, which are affected by the heterogeneous distribution of stress and accumulated plastic slip.

4 Conclusion

In the work at hand, the simulation of microstructural evolution of crystalline materials using crystal plasticity theory within a multiphase-field method is investigated. The use of crystal plasticity allows to capture the anisotropic plastic behavior of crystals, due to individually activated slip systems dependent on the crystal orientation. By coupling crystal plasticity with a multiphase-field method new possibilities regarding the simulation of microstructural behavior and evolution that involve plasticity arise.

Equilibrium shapes

The shape of an elastic inclusion subjected to transversely isotropic eigenstrains is significantly influenced by the distribution of plastic slip in the plastically deformed matrix. The grain orientation and the characteristics of the eigenstrain within the inclusion clearly affect the shape in equilibrium.

  • The anisotropic behavior of a crystalline material is captured using crystal plasticity. Thus, eigenstrains within the inclusion yield an inhomogeneous distribution of accumulated plastic slip within the surrounding elasto-plastic matrix. The inhomogeneous distribution leads to inhomogeneous evolution of the shape of the inclusion.

  • Contributions to the driving forces acting on the interface, which are responsible for the anisotropic shape evolution, are investigated separately and an equilibrium state is identified.

  • The phase-evolution is affected by the crystal orientation. A rotation of the grain orientation results in an identical rotation of the equilibrium shape of the inclusion.

Study of microstructure evolution towards a simulation of static recrystallization

A nucleus is constructed and placed into a matrix of regular grains, and subsequently irregular grains. The matrix is deformed beforehand with the use of crystal plasticity within a multiphase-field method, resulting in an inhomogeneous distribution of stresses and strains. The objective is to mimic and study the evolution of the nucleus in correspondence to the principles of static recrystallization. For this purpose, three approaches to strain inheritance are discussed.

  • The presented approaches on strain inheritance are compared regarding the resulting stress and strain fields on a honeycomb structure. Employing the proposed simulation sequence, the inheritance of the entire strain field \({\bar{\varvec{\varepsilon }}}\) to the nucleus allows a representation of the stress state within the new grain that is closer to experimental findings.

  • A Voronoi tessellation algorithm is used to create a microstructure that is closer to experimentally observed crystalline microstructures than the honeycomb structure.

  • The evolution and interaction of multiple nuclei is investigated and the formation of a new grain structure is observed. The migration characteristics of the nuclei depend on the anisotropic plastic deformation. The migration rate of a nucleus into grains with smaller accumulated plastic slip is smaller due to the smaller driving forces.