Numerical modeling of undersea acoustics using a partition of unity method with plane waves enrichment

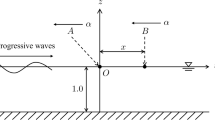
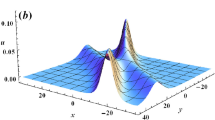
Abstract

A new 2D numerical model to predict the underwater acoustic propagation is obtained by exploring the potential of the Partition of Unity Method (PUM) enriched with plane waves. The aim of the work is to obtain sound pressure level distributions when multiple operational noise sources are present, in order to assess the acoustic impact over the marine fauna. The model takes advantage of the suitability of the PUM for solving the Helmholtz equation, especially for the practical case of large domains and medium frequencies. The seawater acoustic absorption and the acoustic reflectance of the sea surface and sea bottom are explicitly considered, and perfectly matched layers (PML) are placed at the lateral artificial boundaries to avoid spurious reflexions. The model includes semi-analytical integration rules which are adapted to highly oscillatory integrands with the aim of reducing the computational cost of the integration step. In addition, we develop a novel strategy to mitigate the ill-conditioning of the elemental and global system matrices. Specifically, we compute a low-rank approximation of the local space of solutions, which in turn reduces the number of degrees of freedom, the CPU time and the memory footprint. Numerical examples are presented to illustrate the capabilities of the model and to assess its accuracy.

Appendices

Appendix 1: Seawater absorption

In this appendix we deduce the relation between the absorption coefficient $\alpha$ and the imaginary part of the complex wavenumber $k_2$, see Eq. (7). The value of the seawater absorption coefficient $\alpha$ strongly depends on the frequency, but also on the temperature, the salinity, the hydrostatic pressure (depth) and the acidity. Our model estimates the coefficient by means of the Ainslie and McColm formula [40]:

$$\begin{aligned} \alpha= & {} 0.106 \exp \big ( (\text {pH}-8)/0.56 \big ) \frac{f_1 f^2}{f_1^2+f^2} \nonumber \\&+\,0.52 \left( 1 + \frac{T}{43} \right) \left( \frac{S}{35} \right) \exp (-d/6) \frac{f_2 f^2}{f_2^2+f^2} \nonumber \\&+\,0.00049 \exp \big (-\left( T/27 + d/17\right) \big ) f^2 , \end{aligned}$$

(26)

where

$$\begin{aligned} f_1 = 0.78 \left( \frac{S}{35} \right) ^{1/2} \exp \left( T/26 \right) \end{aligned}$$

is the boron acid relaxation frequency in kHz,

$$\begin{aligned} f_2 = 42 \exp \left( T/17 \right) \end{aligned}$$

is the magnesium sulfate relaxation frequency in kHz, $\alpha$ is the absorption coefficient in dB/km, f is the frequency in kHz, T is the seawater temperature in $^\circ$C, S is the salinity in ppt, d is the depth in km, and pH is the measure of the acidity.

If part of data is missing, Eq. (26) can be replaced by

$$\begin{aligned} \alpha = 0.159 \frac{f^2}{2.25+f^2} + 30.5 \frac{f^2}{1764+f^2} + 0.000261 f^2, \end{aligned}$$

(27)

that considers the average conditions at the ocean surface: T = 17 $^\circ$C, S = 35 ppt, and d = 0 km and pH = 8. Figure 13 shows the dependence of the absorption coefficient with the frequency according to Eq. (27). Note that the absorption is specially significant for frequencies above a few kHz, and that can be neglected for short and mid-range propagations at low frequency.

Fig. 13

Absorption coefficient $\alpha$ under the following conditions: S = 35 ppt, T = 17$^\circ$, d = 0 km, pH = 8

Once the absorption coefficient $\alpha$ is computed using Eqs. (26) or (27), it is included in our model via the the imaginary part of the complex wavenumber $k_2$. Given a plane wave with an arbitrary amplitude A, propagating in a free space following an arbitrary direction vector $\varvec{e}$, it suffers an exponential decay determined by $k_2$,

$$\begin{aligned} W(\varvec{x}) = A \exp (ik\,\varvec{e}\cdot \varvec{x}) = A \exp (-k_2\,\varvec{e}\cdot \varvec{x})\,\exp (ik_1\,\varvec{e}\cdot \varvec{x}) . \end{aligned}$$

(28)

Thus, and according to Eqs. (1) and (28), the transition loss between two points separated by a distance r (in km) produced exclusively by the physical absorption is:

$$\begin{aligned} \alpha r= & {} \text {SPL}_0-\text {SPL}_r = 20\log _{10}\frac{p_{\text {rms},0}}{p_{ref}}-20\log _{10}\frac{p_{\text {rms},r}}{p_{ref}} \\= & {} 20\log _{10}[\exp (k_2\cdot 1000 \, r)] \ , \end{aligned}$$

and Eq. (7) follows.

Appendix 2: Transmission coefficient

In this appendix we relate the transmission coefficient $\tau$ appearing in the Robin boundary condition (3) with several material properties of the surrounding media (air and sea bottom). The transmission coefficient can be written as [45]:

$$\begin{aligned} \tau = \tau _1+i\tau _2 , \end{aligned}$$

where $i=\sqrt{-1}$ is the imaginary unit,

$$\begin{aligned} \tau _1 = \frac{2K_r \sin \beta \cos \gamma }{1+K_r^2+2K_r \cos \beta } \end{aligned}$$

and

$$\begin{aligned} \tau _2 = \frac{(1-K_r^2)\cos \gamma }{1+K_r^2+2K_r \cos \beta } , \end{aligned}$$

being $K_r$ the reflection coefficient, which is the ratio between the reflected and the incident wave amplitudes $K_r = |p_r|/|p_i|$, $\beta$ the reflection phase angle, and $\gamma$ the incident wave direction relative to the normal at the boundary.

The reflection phase angle $\beta$ is set to zero, considering that the position of the numerical boundary agrees with its actual position. Thus, the complex transmission coefficient is purely imaginary. In addition, the incident wave direction $\gamma$ cannot be unambiguously specified since the full-wave approach implies multiple reflections with different wave incident directions angles. In our model we conservatively assume normal incidence ($\gamma =0$). This is conservative in the sense that the produced noise level is going to be larger than the actual one. Thus,

$$\begin{aligned} \tau = i \, \frac{1-K_r}{1+K_r}. \end{aligned}$$

(29)

The value of the transmission coefficient $K_r$ can be obtained either from the value of the transmission loss at the interface $\text {TL}_i$, measured in dB, or from the acoustic impedance $Z_b=\rho _b c_b$ of the boundary, being $\rho _b$ the density of the boundary material, depending on the availability of empirical measurements. In the first case, we have

$$\begin{aligned} K_r = 10^{-\text {TL}_i/20}. \end{aligned}$$

(30)

In the second case, assuming normal incidence, we have

$$\begin{aligned} K_r = \frac{Z_b/Z_{sw}-1}{Z_b/Z_{sw}+1} , \end{aligned}$$

(31)

where $Z_{sw} \approx 1.54 \times 10^6$ kg/(m$^2$s) is the acoustic impedance of the seawater. Substituting Eqs. (30) and (31) in (29) we obtain expression (8) and (9), respectively.