Fractal Tilings from Iterated Function Systems

Abstract

A simple, yet unifying method is provided for the construction of tilings by tiles obtained from the attractor of an iterated function system (IFS). Many examples appearing in the literature in ad hoc ways, as well as new examples, can be constructed by this method. These tilings can be used to extend a fractal transformation defined on the attractor of a contractive IFS to a fractal transformation on the entire space upon which the IFS acts.

1 Introduction

The subject of this paper is fractal tilings of ${\mathbb {R}}^{n}$ and, more generally, complete metric spaces. By “fractal”, we mean that each tile is the attractor of an iterated function system (IFS). Computer generated drawings of tilings of the plane by self-similar fractal figures appear in papers beginning in the 1980s and 1990s, for example the lattice tiling of the plane by copies of the twindragon. Tilings constructed from an IFS often possess global symmetry and self-replicating properties. Research on such tilings includes the work of numerous people including Akiyama, Bandt, Gelbrich, Gröchenig, Hass, Kenyon, Lagarias, Lau, Madych, Radin, Solomyak, Strichartz, Thurston, Vince, and Wang; see for example [1, 3, 12–14, 17, 19, 20, 22, 25, 27–30] and the references therein. Even aperiodic tilings can be put into the IFS context; see for example the fractal version of the Penrose tilings [4].

The use of the inverses of the IFS functions in the study of tilings is well-established, in particular in many of the references cited above. The main contribution of this paper is a simple, yet unifying, method for constructing tilings from an IFS. Many examples appearing in the literature in ad hoc ways, as well as new examples, can be constructed by this method. The usefulness of the method is demonstrated by applying it to the construction of fractal transformations between basins of attractors of pairs of IFSs.

Section 2 contains background on iterated function systems, their attractors, and addresses. Tiling are constructed for both non-overlapping and overlapping IFSs, concepts defined in Sect. 3. The tilings constructed in the non-overlapping case, in Sect. 3, include well known examples such as the digit tilings, crystallographic tilings, and non-periodic tilings by copies of a polygon, as well as new tilings in both the Euclidean and real projective planes. The tilings constructed in the overlapping case, in Sect. 4, depend on the choice of what is called a mask and are new. Theorems 3.8, 3.9, and 4.3 state that, in both of the above cases, when the attractor of a contractive IFS has nonempty interior, the resulting tiling almost always covers the entire space. Tilings associated with an attractor with empty interior are also of interest and include tilings of the graphs of fractal continuations of fractal functions, a relatively new development in fractal geometry [9]. The methods for obtaining tilings from an IFS can be extended to a graph iterated function system (GIFS); this is done in Sect. 5. The Penrose tilings, as well as new examples, can be obtained by this general construction. Section 6 describes how, using our tiling method, a fractal transformation, which is a special kind of mapping from the attractor of one IFS to the attractor of another, can be extended from the attractor to the entire space, for example, from ${\mathbb {R}}^{n}$ to ${\mathbb {R}}^{n}$ in the Euclidean case.

2 Iterated Function Systems, Attractors, and Addresses

Let $({\mathbb {X}},d_{{\mathbb {X}}})$ be a complete metric space and let $F$ be an IFS with attractor $A$; the definitions follow:

Definition 2.1

If $f_{n}:\mathbb {X}\rightarrow \mathbb {X}$, $n=1,2,\ldots ,N,$ are continuous functions, then $F=( \mathbb {X};f_{1},f_{2},\ldots ,f_{N})$ is called an iterated function system (IFS). If each of the maps $f\in F$ is a homeomorphism then $F$ is said to be invertible, and the notation $F^{*}:=( \mathbb {X};f_{1}^{-1},f_{2}^{-1},\ldots ,f_{N} ^{-1})$ is used.

Subsequently in this paper we refer to some special cases. An IFS is called affine if $\mathbb {X }= {\mathbb {R}}^{n}$ and the functions in the IFS are affine functions of the form $f(x) = Ax+a$, where $A$ is an $n\times n$ matrix and $a \in {\mathbb {R}}^{n}$. An IFS is called a projective IFS if $\mathbb {X }= \mathbb {RP}^{n}$, real projective space, and the functions in the IFS are projective functions of the form $f(x) = Ax$, where $A$ is an $(n+1)\times (n+1)$ matrix and $x$ is given by homogeneous coordinates.

By a slight abuse of terminology we use the same symbol $F$ for the IFS, the set of functions in the IFS, and for the following mapping. Letting $2^{\mathbb {X}}$ denote the collection of subsets of $\mathbb {X}$, define $F:2^{\mathbb {X}}\mathbb {\rightarrow }2^{\mathbb {X}}$ by

$$\begin{aligned} F(B)=\mathop {\bigcup }\limits _{f\in F}f(B) \end{aligned}$$

for all $B\in 2^{\mathbb {X}}$. Let $\mathbb {H=H(X)}$ be the set of nonempty compact subsets of $\mathbb {X}$. Since $F( \mathbb {H}) \subseteq \mathbb {H}$ we can also treat $F$ as a mapping $F:\mathbb {H\rightarrow H}$. Let $d_{\mathbb {H}}$ denote the Hausdorff metric on $\mathbb {H}$.

For $B\subset \mathbb {X}$ and $k\in \mathbb {N}:=\{1,2,\ldots \}$, let $F ^{k}(S)$ denote the $k$-fold composition of $F$, the union of $f_{i_{1}}\circ f_{i_{2} }\circ \cdots \circ f_{i_{k}}(S)$ over all finite words $i_{1}i_{2}\cdots i_{k}$ of length $k.$ Define $F^{0}(S)=S.$

Definition 2.2

A nonempty set $A\in \mathbb {H(X)}$ is said to be an attractor of the IFS $F$ if

• (i) $F(A)=A$ and

• (ii) there is an open set $U\subset \mathbb {X}$ such that $A\subset U$ and $\lim _{k\rightarrow \infty }F^{k}(S)=A$ for all $S\in \mathbb {H(}U)$, where the limit is with respect to the Hausdorff metric.

The largest open set $U$ such that (ii) is true, i.e. the union of all open sets $U$ such that (ii) is true, is called the basin of the attractor $A$ with respect to the IFS $F$ and is denoted by $B=B(A)$.

An IFS $F$ on a metric space $(\mathbb {X},d)$ is said to be contractive if there is a metric $\hat{d}$ inducing the same topology on $\mathbb {X}$ as the metric $d$ with respect to which the functions in $F$ are strict contractions, i.e., there exists $\lambda \in [0,1)$ such that $\hat{d}_{\mathbb {X}}(f(x),f(y))\le \lambda \hat{d}_{\mathbb {X}}(x,y)$ for all $x,y\in \mathbb {X}$ and for all $f\in F$. A classical result of Hutchinson [15] states that if $F$ is contractive on a complete metric space $\mathbb {X}$, then $F$ has a unique attractor with basin $\mathbb {X}$.

Let $[N]=\{1,2,\ldots ,N\}$, with $[N]^{k}$ denoting words of length $k$ in the alphabet $[N],$ and $[N]^{\infty }$ denoting infinite words of the form $\omega _{1}\omega _{2}\cdots$, where $\omega _{i}\in [N]$ for all $i$. “Word” will always refer to an infinite word unless otherwise specified. A subword (either finite or infinite) of a word $\omega$ is a string of consecutive elements of $\omega$. The length $k$ of $\omega \in [N]^{k}$ is denoted by $|\omega |=k$. For $\omega \in [N]^{k}$ we use the notation $\overline{\omega }=\omega \omega \omega \ldots$. For $\omega \in [N]^{\infty }$ and $k\in \mathbb {N}:=\{1,2,\ldots \}$ the notation

$$\begin{aligned} \omega |k:=\omega _{1}\omega _{2}\cdots \omega _{k} \end{aligned}$$

is introduced, and for an IFS $F=( \mathbb {X};f_{1} ,f_{2},\ldots ,f_{N})$ and $\omega \in [N]^{k}$, the following shorthand notation will be used for compositions of function:

$$\begin{aligned} f_{\omega }&:= f_{\omega _{1}}\circ f_{\omega _{2}} \circ \cdots \circ f_{\omega _{k}}, \\ ( f^{-1})_{\omega }&:= f^{-1} _{\omega _{1}}\circ f^{-1} _{\omega _{2}} \circ \cdots \circ f^{-1} _{\omega _{k}} \end{aligned}$$

Note that, in general, $(f^{-1})_{\omega } \ne (f_{\omega })^{-1}$.

In order to assign addresses to the points of an attractor of an IFS, it is convenient to introduce the point-fibred property. The following notions concerning point-fibred attractors [10] derive from results of Kieninger [18], adapted to the present setting. Let $A$ be an attractor of $F$ on a complete metric space ${\mathbb {X}}$, and let $B$ be the basin of $A$. The attractor $A$ is said to be point-fibred with respect to $F$ if (i) $\big \{ f_{\omega |k}(C)\big \} _{k=1}^{\infty }$ is a convergent sequence in $\mathbb {H(}{\mathbb {X)}}$ for all $C\in \mathbb {H(X)}$ with $C\subset B(A)$; (ii) the limit is a singleton whose value is independent of $C$. If $A$ is point-fibred (w.r.t. $F)$ then we denote the limit in (ii) by $\{ \pi (\omega )\} \subset A$.

Definition 2.3

If $A$ is a point-fibred attractor of $F$, then, with respect to $F$ and $A$, the coordinate map $\pi \,:\,[N]^{\infty }\rightarrow A$ is defined by

$$\begin{aligned} \pi (\omega )=\lim _{k\rightarrow \infty }f_{\omega |k}(x_{0}). \end{aligned}$$

(2.1)

The limit is independent of $x_{0} \in B(A)$. For $x\in A$, any word in $\pi ^{-1}(x)$ is called an address of $x$.

Equipping $[N]^{\infty }$ with the product topology, the map $\pi :[N]^{\infty }\rightarrow A$ is continuous and onto. If $F$ is contractive, then $A$ is point-fibred (w.r.t. $F$). A point belonging to the attractor of a point-fibred IFS has at least one address.

3 Fractal Tilings from a Non-overlapping IFS

Let $S^{\text {o}}$ denote the interior of a set $S$ in a complete metric space $\mathbb {X}$. Two sets $X$ and $Y$ are overlapping if $(X\cap Y)^{\text {o}} \ne \emptyset$.

Definition 3.1

In a metric space $\mathbb {X}$, a tile is a nonempty compact set. A tiling of a set $S$ is a set of non-overlapping tiles whose union is $S$.

Definition 3.2

An attractor $A$ of an IFS $F=({\mathbb {X}};f_{1},f_{2},\ldots ,f_{N})$ is called overlapping (w.r.t. $F$) if $f(A)$ and $g(A)$ are overlapping for some $f,g\in F$. Otherwise $A$ is called non-overlapping (w.r.t. $F$). A non-overlapping attractor $A$ is either totally disconnected, i.e, $f(A)\cap g(A)=\emptyset$ for all $f,g\in F$ or else$\ A$ is called just touching. Note that a non-overlapping attractor with nonempty interior must be just touching.

Starting with an attractor $A$ of an invertible IFS

$$\begin{aligned} F=\{X\,;\,f_{1},f_{2},\ldots ,f_{N}\}, \end{aligned}$$

potentially an infinite number of tilings can be constructed from $A$ and $F$—one tiling $T_{\theta }$ for each word $\theta \in [N]^{\infty }$. The basic construction is as follows. Given a word $\theta \in [N]^{\infty }$ and a positive integer $k$, for any $\omega \in [N]^{k}$, let

$$\begin{aligned} t_{\theta ,\omega }&= ((f^{-1})_{\theta |k}\circ f_{\omega })(A), \\ T_{\theta , k}&= \{ t_{\theta ,\omega } \, : \, \omega \in [N]^k\}. \end{aligned}$$

Since the IFS $F$ is non-overlapping, the sets in $T_{\theta , k}$ do not overlap. Since, for any $\omega \in [N]^{k}$, we have

$$\begin{aligned} (f^{-1})_{\theta |{k}}\circ f_{\omega }=(f^{-1})_{\theta |{k}}\circ (f_{\theta _{k+1}})^{-1}\circ f_{\theta _{k+1}}\circ f_{\omega }=(f^{-1} )_{\theta |{k+1}} \circ f_{\theta _{k+1}\omega }, \end{aligned}$$

the inclusion

$$\begin{aligned} T_{\theta ,k}\subset T_{\theta ,k+1} \end{aligned}$$

holds for all $k$. Therefore

$$\begin{aligned} T_{\theta }:=\mathop {\bigcup }\limits _{k=1}^{\infty }T_{\theta ,k} \end{aligned}$$

(3.1)

is a tiling of

$$\begin{aligned} \displaystyle B(\theta ):=\mathop {\bigcup }\limits _{k=1}^{\infty }(f^{-1})_{\theta |{k}}(A)\subseteq {X}, \end{aligned}$$

where the union is a nested union. Note that $B(\theta )$ is connected if $A$ is connected, and $B(\theta )$ has nonempty interior if $A$ has nonempty interior.

If $F$ is contractive and the unique attractor $A$ has nonempty interior, it is possible to tile the entire space ${\mathbb {X}}$ with non-overlapping copies of $A$. More specifically, if $F$ is contractive and $\theta$ satisfies a not too restrictive condition given below, then $T_{\theta }$ tiles the entire space ${\mathbb {X}}$. In the case that $T_{\theta }$ tiles ${\mathbb {X} }$, we call $T_{\theta }$ a full tiling.

Example 3.3

The IFS $F=\{{\mathbb {R}};\,f_{1},f_{2}\}$ where $f_{1}(x)=x/2$ and $f_{2}(x)=x/2+1/2$ has attractor $[0,1]$. In this case, the tiling $T_{\overline{1}}$ is the tiling of $[0,\infty )$ by unit intervals. The tiling $T_{\overline{2}}$ is the tiling of $(-\infty ,1]$ by unit intervals. If $\theta \ne {\overline{1}},{\overline{2}}$, then $T_{\theta }$ is the full tiling of ${\mathbb {R}}$ by unit intervals.

Definition 3.4

For an IFS $F$ with attractor $A$, call $\theta \in [N]^{\infty }$ full if there exists a nonempty compact set $A^{\prime } \subset A^o$ such that, for any positive integer $M$, there exist $n>m\ge M$ such that

$$\begin{aligned} f_{\theta _{n}}\circ f_{\theta _{n-1}} \circ \cdots \circ f_{\theta _{m+1}} (A) \subset A^{\prime }. \end{aligned}$$

By Proposition 3.7 and Theorem 3.9, nearly all words $\theta$ are full.

Definition 3.5

Call $\theta \in [N]^{\infty }$ reversible w.r.t. a point-fibred attractor $A$ and IFS $F$ if there exists an $\omega =\omega _{1}\omega _{2}\cdots \in [N]^{\infty }$ such that $\omega$ is the address of some point in $A^{\text {o}}$ and, for every pair of positive integer $M$ and $L$, there is an integer $m\ge M$ such that

$$\begin{aligned} \omega _{1}\omega _{2}\cdots \omega _{L} = \theta _{m+L}\theta _{m+L-1}\cdots \theta _{m+1}. \end{aligned}$$

(3.2)

Call $\theta \in [N]^{\infty }$ strongly reversible w.r.t. $A$ and $F$ if there exists $\omega =\omega _{1}\omega _{2}\cdots \in [N]^{\infty }$ such that $\omega$ is the address of some point in $A^{\text {o}}$ and, for every positive integer $M$, there is an integer $m\ge M$ such that

$$\begin{aligned} \omega _{1}\omega _{2}\cdots \omega _{m} = \theta _{m}\theta _{m-1}\cdots \theta _{1}. \end{aligned}$$

(3.3)

By statement (3) of Theorem 3.7 below, if $\theta$ is strongly reversible, then $\theta$ is reversible. The converse, however, is not true; for example, the string $\theta =3\overline{12}$ is reversible but not strongly reversible. To see that $3\overline{12}$ is reversible, choose $\omega =\overline{12}$.

Let $S:[N]^{\infty }\rightarrow [N]^{\infty }$ denote the usual shift map and introduce the notation $\overleftarrow{\omega |m}:=\omega _{m}\omega _{m-1}\cdots \omega _{2}\omega _{1}$. Equation 3.2 can be expressed $S^{m}\theta |L=\overleftarrow{\omega |L}$, while Eq. 3.3 can be expressed $\theta |m=\overleftarrow{\omega |m}$. Note that Definition 3.5 is equivalent to: there is a point $\omega$, whose image under $\pi _{F}$ lies in the interior of $A$, such that, if it is truncated to any given finite length and then reversed, then it occurs as a finite subword of $\theta$ infinitely many times.

Definition 3.6

A word $\theta \in [N]^{\infty }$ is disjunctive if every finite word is a subword of $\theta$. In fact, if $\theta$ is disjunctive, then every finite word (in the alphabet $[N]$) appears as a subword in $\theta$ infinitely many times.

Theorem 3.7

For an IFS $F$, let $A$ be a point-fibred attractor. With respect to $A$ and $F$:

• (1) There are infinitely many disjunctive words in $[N]^{\infty }$ for $N\ge 2$.

• (2) If $A^{\text {o}} \ne \emptyset$, then every disjunctive word is strongly reversible.

• (3) Every strongly reversible word is reversible.

• (4) A word is reversible if and only if it is full.

Proof

Not only are there infinitely many disjunctive words for $N\ge 2$, but the set of disjunctive sequences is a large subset of $[N]^{\infty }$ in a topological, in a measure theoretic, and in an information theoretic sense [26].

Concerning statement (2), assume that $\theta$ is disjunctive. Let $a\in A^{\text {o}}$ and let $\sigma$ be an address of $a$. There is a neighborhood $N(A)$ of $a$ that lies in $A$ and an integer $s$ such that any point whose address starts with $\sigma |s$ lies in $N(A)\subset A$. Statement (2) will now be proved by induction. We claim that there exists a word $\omega$ and an increasing sequence $t_{n}\ge n$ of integers and such that the following statements hold:

• (1) $\omega |{t_{n}}=\overleftarrow{\theta |{t_{n}}}$,

• (2) $\omega |{t_{n}}=\sigma |{s}\overleftarrow{\theta |{t_{n}-s}}$.

The two conditions guarantee that $\theta$ is stongly reversible. The case $n=1$ is shown as follows. Since $\theta$ is disjunctive, there is a $t_{1}>s$ such that $\sigma |s=\theta _{t_{1}}\theta _{t_{1}-1}\cdots \theta _{t_{1}-s+1}$. Define

$$\begin{aligned} \omega |{t_{1}}:=\overleftarrow{\theta |{t_{1}}}=\sigma |{s}\overleftarrow{\theta |{t_{1}-s}}. \end{aligned}$$

We next go from $n$ to $n+1$. Since $\theta$ is disjunctive, there is a $t_{n+1}>t_{n}$ such that

$$\begin{aligned} \omega |{t_{n}}=\theta _{t_{n+1}}\theta _{t_{n+1}-1}\cdots \theta _{t_{n+1} -t_{n}+1}. \end{aligned}$$

Now define

$$\begin{aligned} \omega |{t_{n+1}}:=\overleftarrow{\theta |{t_{n+1}}}=\omega |{t_{n} }\overleftarrow{\theta |{t_{n+1}-t_{n}}}=\sigma |{s}\,\overleftarrow{\theta |{t_{n+1}-s}}. \end{aligned}$$

The second equality guarantees that the initial $t_{n}$ elements of $\omega$ are unchanged; the third equality follows from condition (2) of the induction hypothesis.

Concerning statement (3), assume that $\theta$ is strongly reversible, and let positive integers $M$ and $L$ be given. If $\omega$, as required, has the strong reversal property with respect to $\theta$, then there exists an integer $n\ge M+L$ so that $\theta _{n}\theta _{n-1}\cdots \theta _{1} =\omega _{1}\omega _{2}\cdots \omega _{n}$, from which it follows that there is an integer $m \ge M$ such that $\theta _{m+L}\theta _{m+L-1}\cdots \theta _{1}=\omega _{1}\omega _{2}\cdots \omega _{m+L}$ and therefore $\theta _{m+L} \theta _{m+L-1}\cdots \theta _{m+1}=$ $\omega _{1}\omega _{2}\cdots \omega _{L}$. It follows that $\theta$ is reversible.

Concerning one direction of statement (4), assume that $\theta$ is reversible, and let $\omega$ have the required reversal property w.r.t. $\theta$. Since $\pi (\omega )\in A^{\circ }$ it follows that there is $L\in \mathbb {N}$ so that $f_{\omega |L}(A)\subset A^{\circ }$. Choose $A^{\prime }=f_{\omega |L}(A)$ in Definition 3.4 of full. Let $M$ be given. By the definition of $\theta$ reversible, there exists an $m\ge M$ such that

$$\begin{aligned} f_{\theta _{m+L}}\circ f_{\theta _{m+L-1}}\circ \cdots \circ f_{\theta _{m+1} }(A)=f_{\omega _{1}}\circ f_{\omega _{2}}\circ \cdots \circ f_{\omega _{L} }(A)=A^{\prime }. \end{aligned}$$

Taking $n = m+L$ in Definition 3.4, it follows that $\theta$ is full.

Concerning the other direction of statement (4), suppose that $\theta$ is full and let $A^{\prime }$ be the corresponding compact set. It follows that, for any positive integer $M$, there is $n>m\ge M$ so that $f_{\theta _{n}}\circ f_{\theta _{n-1}}\cdots \circ f_{\theta _{m+1}}(A)\subset A^{\prime }\subset A^{\circ }$, which implies that $f_{\theta _{n_{k}}}\circ f_{\theta _{n_{k}-1} }\cdots \circ f_{\theta _{1}}(A)\subset A^{\prime }\subset A^{\circ }$ for an infinite strictly increasing sequence $\{ n_{k}\} _{k=1}^{\infty }$ of positive integers. The set

$$\begin{aligned}{}[N]^{\infty }\cup \mathop {\bigcup }\limits _{k=1}^{\infty }[N]^{k} \end{aligned}$$

becomes a compact metric space when endowed with an appropriate metric (words with a long common prefix are close). Therefore the sequence of finite words $\{ \theta _{n_{k}}\theta _{n_{k}-1}...\theta _{1}\} _{k=1}^{\infty }$ has a convergent subsequence, which we continue to denote by the same notation $\{ \theta _{n_{k}}\theta _{n_{k}-1}...\theta _{1}\} _{k=1}^{\infty }$, with limit $\omega \in [N]^{\infty }.$ Hence, for any $L$ and $k$ sufficiently large, $\theta _{n_{k}}\theta _{n_{k}-1}...\theta _{n_{k}-L+1}=\omega _{1}\omega _{2}...\omega _{L}$. It follows that $\theta$ is reversible with reverse word $\omega$. $\square$

Theorem 3.8

For an invertible IFS $F=( \mathbb {X};f_{1} ,f_{2},\ldots ,f_{N}) ,$ let $A$ be a just-touching attractor with nonempty interior. If $\theta$ is a full word, then $T_{\theta }$ is a tiling of the set $B(\theta )$ which contains the basin of $A$. If $F$ is contractive, then $T_{\theta }$ is a full tiling of $\mathbb {X}$.

Proof

The proof is postponed because it is a special case of Theorem 4.3 in Sect. 4. $\square$

By the above theorem, if $F$ is contractive and $\theta$ is full, then $T_{\theta }$ tiles the entire space ${\mathbb {X}}$. According to Theorem 3.7, full words are plentyful. According to the next result, if $F$ is contractive, for any ransom infinite word $\theta$, $T_{\theta }$ tiles ${\mathbb {X}}$ with probability $1$. Define a word $\theta \in [N]^{\infty }$ to be a random word if there is a $p>0$ such that each $\theta _{k},\,k=1,2,\ldots$, is selected at random from $\{1,2,\ldots ,N\}$ where the probability that $\theta _{k}=n,\,n\in [N],$ is greater than or equal to $p,$ independent of the preceding outcomes.

Theorem 3.9

Let $F = \{{\mathbb {X}} ;\, f_{1}, f_{2}, \dots , f_{N}\}$, where ${\mathbb {X}}$ is compact, be a just touching invertible IFS with attractor $A$ with nonempty interior. If $\theta \in [N]^{\infty }$ is a random word, then, with probability $1$, the tiling $T_{\theta }$ covers the basin $B(A)$. If $F$ is contractive, then $T_{\theta }$ is a full tiling of ${\mathbb {X}}$.

Proof

Let $x$ lie in the basin $B$ of the attractor $A$ of $F$, and let $\theta$ be a random word. Then $x$ lies in the union of the tiles of $T_{\theta }$ if and only if $x \in f^{-1}_{\theta |n}(A)$ for some $n$ if and only if $f_{\theta _{n}}\circ f_{\theta _{n-1}} \circ \cdots \circ f_{\theta _{2}} \circ f_{\theta _{1}}(x) \in A$ for some $n$. Given a word $\omega$, consider a sequence $\big \{ x_{k}\big \} _{k=0}^{\infty }$ of points in $\mathbb {X}$ defined by $x_{k}=f_{\omega _{k}}(x_{k-1}), \, k\ge 1$. If $\omega$ is a random word, then $\big \{ x_{k}\big \} _{k=0}^{\infty }$ is called a random orbit of the point $x_{0}$. Since $\theta$ is assumed random, if$Q$ is an nonempty open subset of $A$, then, according to [7, Theorem 1], with probability $1$ there is a point in the random orbit of any point $x$ in the basin that lies in $Q \subset A$, i.e., with probability $1$, $f_{\theta _{n} }\circ f_{\theta _{n-1}} \circ \cdots \circ f_{\theta _{1}}(x) \in Q$ for some $n$. Therefore, with probability $1$, there is a ball $B_{x}$ centered at $x$ such that

$$\begin{aligned} f_{\theta _{n}}\circ f_{\theta _{n-1}} \circ \cdots \circ f_{\theta _{1}}(B_{x}) \subset Q \subset A. \end{aligned}$$

Next, for any $\varepsilon >0$ let $\overline{B}_{\varepsilon }$ be the open $\varepsilon$-neighborhood of the complement $\overline{B}$ of $B$, and let $B_{\varepsilon } = B\setminus \overline{B}_{\varepsilon }$. Since $B_{\varepsilon }$ is compact, $B_{\varepsilon }$ has a finite covering by balls $B_{x}$ and hence, with probability $1$, there is an $n$ such that

$$\begin{aligned} f_{\theta _{n}}\circ f_{\theta _{n-1}} \circ \cdots \circ f_{\theta _{1} }(B_{\varepsilon }) \subset A. \end{aligned}$$

Therefore, for any $\varepsilon >0$, with probability $1$, the tiling $T_{\theta }$ covers $B_{\varepsilon }$. Assume that $T_{\theta }$ does not cover $B$. Then there exists an $\varepsilon$ such that $T_{\theta }$ does not cover $B_{\varepsilon }$. But the probability of that is $0$. If $F$ is contractive, the basin $B$ is ${\mathbb {X}}$. $\square$

Example 3.10

(Digit tilings of ${\mathbb {R}}^{n}$) The terminology “digit tiling” comes from the data used to construct the tiling, which is analogous to the usual base and digits used to represent the integers. An expanding matrix is an $n\times n$ matrix such that the modulus of each eigenvalue is greater than 1. Let $L$ be an $n\times n$ expanding integer matrix. A set $D = \{d_{1}, d_{2}, \dots , d_{N}\}$ of coset representatives of the quotient $\mathbb {Z}^{n}/L(\mathbb {Z}^{n})$ is called a digit set. It is assumed that $0 \in D$. By standard algebra results, for $D$ to be a digit set it is necessary that

$$\begin{aligned} |D| = |\det L \,|. \end{aligned}$$

Consider an affine IFS $F := F(L,D) = ({\mathbb {R}}^{n} \, ; \,f_{1}, f_{2}, \dots , f_{N})$, where

$$\begin{aligned} f_{i}(x) = A^{-1}(x - d_{i}). \end{aligned}$$

Since $L$ is expanding, it is known that, with respect to a metric equivalent to the Euclidean metric, $L^{-1}$ is a contraction. Since $F$ is contractive, there is a unique attractor $A$ called a digit tile. The basin of $A$ is all of ${\mathbb {R}}^{n}$. Note that a digit tile is completely determined by the pair $(L,D)$ and will be denoted $T(L,D)$. It is known [30] that a digit tile $T$ is the closure of its interior and its boundary has Lebesque measure $0$. If $\theta \in [N]^{\infty }$ is full, then $T_{\theta }$ is a tiling of ${\mathbb {R}}^{n}$ called a digit tiling. Examples of digit tilings, for example by the twin dragon, appear in numerous books and papers on fractals. Under fairly mild assumptions [30, Theorem 4.3], a digit tiling is a tiling by translation by the integer lattice $\mathbb {Z}^{n}$ with the following self-replicating property: for any tile $t\in T_{L,D}$, its image $L(t)$ is the union of tiles in $T_{L,D}$. For this reason, such a tiling is often referred to as a reptiling of ${\mathbb {R}}^{n}$.

Example 3.11

(Crystallographic tilings of ${\mathbb {R}}^{n}$) Gelbrich [12] generalized digit tiling from the lattice group $\mathbb {Z}^{n}$ to any crystallographic group $\Gamma$. Let $L \, : \; {\mathbb {R}}^{n} \rightarrow {\mathbb {R}}^{n}$ be an expanding linear map such that $L\Gamma L^{-1} \subset \Gamma$. If $D = \{d_{1}, \dots , d_{N}\}$ is a set of right coset representatives of $\Gamma /L\Gamma L^{-1}$, then

$$\begin{aligned} F = \big \{{\mathbb {R}}^{n} ; \, L^{-1}( \cdot + d_{1}), \dots , L^{-1}(\cdot + d_{N})\big \} \end{aligned}$$

is a contractive IFS with attractor $T(\Gamma ,L,D)$ with nonempty interior, called a crystallographic tile. The Levy curve is an example of such a crystallographic tile (for the 2-dimensional crystallographic group $p4$). A tiling $T_{\theta }$ is called a crystallographic reptiling.

Example 3.12

(Chair tilings of ${\mathbb {R}}^{2}$) The IFS $F = \{{\mathbb {R}}^{2} ;\, f_{1}, f_{2}, f_{3}, f_{4}\}$ where

$$\begin{aligned} \begin{aligned} f_1(x,y)&= (x/2,y/2), \\ f_2(x,y)&= (x/2+1/4, y/2+1/4), \end{aligned} \qquad \qquad \begin{aligned} f_3(x,y)&= (-x/2 + 1,y/2), \\ f_4(x,y)&= (x/2,-y/2+1), \end{aligned} \end{aligned}$$

is an IFS whose attractor is a chair or ”L”-shaped polygon; see Figs. 1 and 2. The chair tilings are usually obtained by what is referred to as a “substitution method”. For the chair tile, there are uncountably many distinct (non-isometric) tilings $T_{\theta }$. There are numerous other such polygonal tiles that are the attractors of just touching IFSs.

Fig. 1

Three views of the tiling in Example 3.12 using $\theta = \overline{12301230}$. The L-shaped attractor is shown in white near the center. The viewing windows are centered at the origin, and are of width and height 20,40, and 60 from left to right

Fig. 2

Another tiling from the same IFS of Example 3.12, but using $\theta = \overline{12300312}$

Example 3.13

(Fold out tiling) Let $E$ denote a point in the interior of the filled square $[0,1]^{2}$ with vertices $ABCD$. Let $P,Q,R,S$ be the orthogonal projection of $E$ on $AB,BC,CD,DA$ respectively. Four affine maps are uniquely defined by $f_{1}(ABCD)=APES,$ $f_{2}(ABCD)=BPEQ,$ $f_{3}(ABCD)=CREQ,$ and $f_{4}(ABCD)=DRES$. The attractor of $F_{E} =\{\mathbb {R}^{2};f_{1},f_{2},f_{3},f_{4}\}$ is $[0,1]^{2}$. The IFS $F_{E}$ is of the type introduced in [6], pairs of which may be used to describe fractal homeomorphisms on $[0,1]^{2}$ (see Example 6.6 of Sect. 6). According to Theorem 3.8, for any full word $\theta \in \{1,2,3,4\}^{\infty }$, we obtain a tiling $T_{\theta }$ of ${\mathbb {R}}^{2}$, one of which is shown in Fig. 3, where $E=(2/3,1/3)$.

Since $a\in f_{i}([0,1]^{2})\cap f_{j}([0,1]^{2})\ne \emptyset$ implies that $f_{i}^{-1}(a)=f_{j}^{-1}(a)$, the mapping $T:$ $[0,1]^{2} \rightarrow$ $[0,1]^{2}$ given by $T(x) =f_{i}^{-1}(x)$ when $x\in f_{i}($ $[0,1]^{2})$ is well defined and continuous. It can be said that $f_{i}^{-1}$ applied to $[0,1]^{2}$ causes $[0,1]^{2}$ to be “continuously folded out from $[0,1]^{2}$”. The tilings $T_{\theta }$ can be thought of as repeated applications of such folding-outs.

Fig. 3

The tiling of Example 3.13

Example 3.14

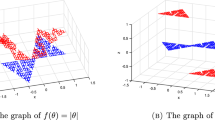
(Triangular affine and projective tilings) Fig. 5 shows two views of the same affine tiling of $\mathbb {R}^{2}$. As in Example 3.13, this tiling can be used to extend a fractal homeomorphism between two triangular attractors to a fractal homeomorphism of the Euclidean plane (see Sect. 6). Consider the IFS $F =\{{\mathbb {R}}^{2};f_{1},f_{2},f_{3},f_{4}\}$ where each $f_{n}$ is an affine transformations defined as follows. Let $A$, $B$, and $C$ denote three noncollinear points in $\mathbb {R}^{2}$. Let $c$ denote a point on the line segment $AB$, $a$ a point on the line segment $BC$, and $b$ a point on the line segment $CA$, such that $\{a,b,c\}\cap \{A,B,C\}=\emptyset$; see panel (i) of Fig. 4. Let $f_{1}:\mathbb {R}^{2}\rightarrow \mathbb {R}^{2}$ denote the unique affine transformation such that

$$\begin{aligned} f_{1}(ABC)=Abc\text {,} \end{aligned}$$

by which we mean that $f_{1}$ maps $A$ to $A$, $B$ to $b$, and $C$ to $c$. Using the same notation, let affine transformations $f_{2}$, $f_{3}$, and $f_{4}$ be the ones uniquely defined by

$$\begin{aligned} \begin{aligned} f_{2}(ABC)&=aBc, \\ f_{3}(ABC)&=abC, \\ f_{4}(ABC)&=abc. \end{aligned} \end{aligned}$$

Panel (ii) of Fig. 4 shows the images of the points $A,B,C$ under the four functions of the IFS, illustrating the special way that the four functions fit together. The attractor of $F$ is the filled triangle with vertices at $A$, $B$, and $C$, which we will denote by $\blacktriangle$, illustrated in (iii) in Fig. 4.

If $\theta =\theta _{1}\theta _{2}\theta _{3} \cdots \in \{1,2,3,4\}^{\infty }$ is full, then according to Theorem 3.8, $T_{\theta }$ is a tiling of ${\mathbb {R}}^{2}$ by triangles. One such affine tiling is illustrated in Fig. 5 at two resolutions. A related projective tiling is shown in Fig. 6. Note that, if $e$ is a common edge of two triangles $\Delta _{1},\Delta _{2}$ in $T_{\theta }$, then $e$ is the image of the same edge of the original triangle $ABC$ from $\Delta _{1}$ and $\Delta _{2}$, and if $v$ is a common vertex in $T_{\theta }$ of two triangles $\Delta _{2},\Delta _{2}$ in $T_{\theta }$, then $v$ is the image of the same vertex of the original triangle $ABC$ from $\Delta _{1}$ and $\Delta _{2}$.

Fig. 4

(i) The points used to define the affine transformations of the IFS $F=\{\mathbb {R}^{2};f_{1},f_{2},f_{3},f_{4}\}$; (ii) images of the the triangle $ABC$; (iii) the attractor of the IFS $\{\mathbb {R}^{2};\, f_{1},f_{2},f_{3}, f_{4}\}$

Fig. 5

The tiling of Example 3.14. Each image shows a portion of the same tiling of $\mathbb {R}^{2}$ generated by an affine IFS with a triangular attractor. All tiles are triangles (the black quadrilateral is the union of two black triangular tiles)

Fig. 6

This image illustrates a projective tiling in a fashion analogous to that of the tiling in Fig. 5. It is represented using the disk model for $\mathbb {R}P^{2}$

Although Theorems 3.8 and 3.9 hold for IFSs whose attractor has nonempty interior, the basic tiling construction of this section applies as well to IFSs with an attractor with empty interior.

Example 3.15

(Tilings from an attractor with empty interior) Fig. 7 shows a tiling by copies of the Sierpinski gasket.

Figures 8 and 9 show the tiling $T_{\theta }$, for a particular $\theta$, for the IFS $\big \{ \mathbb {R}^{2};f_{i} ,i=1,2,3\big \}$ where

$$\begin{aligned} f_{1}(x,y)&=(-0.7x+0.7,0.65y+0.35),\\ f_{2}(x,y)&=(-0.3y+1,-0.6x-0.3y+1.3),\\ f_{3}(x,y)&=( 0.375y+0.325,-0.6x+0.35y+0.65) . \end{aligned}$$

Fig. 7

The original attractor is the small black Sierpinski gasket near the middle bottom; $\theta =322222\cdots$

Fig. 8

The tiling of Example 3.15

Fig. 9

Zoom of the tiling in Figure 8

Example 3.16

(A tiling of a fractal continuation of a fractal function) A fractal function, defined say on the unit interval, is a function, often everywhere non-differentiable, whose graph is the attractor of an IFS. Figure 10 shows a tiling, obtained by the method of this section, by copies of the graph of such a function. Such extensions of fractal functions are essential to the notion of a fractal continuation, a generalization of analytic continuation of an analytic function; see [9].

Fig. 10

A tiling of the graph of a continuation [9] of a fractal function by copies of the graph of the fractal function

4 Fractal Tilings from an Overlapping IFS

In this section the concept of a mask is used to generalize the tilings of the previous section from the non-overlapping to the overlapping case.

Definition 4.1

For an IFS $F =\big ( \mathbb {X};f_{1},f_{2},\ldots ,f_{N} \big )$ with attractor $A$, a mask ${\mathcal {M}} = \{M_{i}, 1\le i \le N\}$ is a tiling of $A$ such that $M_{i} \subseteq f_{i}(A)$ for all $f_{i}\in F$.

Let $F$ be an invertible IFS with attractor $A$, and let $\theta \in [N]^{\infty }$. Let ${\mathcal {M}}=\{M_{1},M_{2},\ldots ,M_{N}\}$ be any mask of $A$ with the property that $M_{\theta _{1}}=f_{\theta _{1}}(A)$. Define recursively a sequence of masked IFSs $F_{n}=\{{\mathbb {X}};\,f_{n,1} ,f_{n,2},\ldots ,f_{n,N}\}$ with respective masks ${\mathcal {M}}_{n}$ and attractors $A_{n}$ and associated tilings $T_{n}$, for $n=1,2,\ldots$, as follows: $F_{1}=F,\,A_{1}=A,\,T_{1}=\{A\},\,{\mathcal {M}}_{1}={\mathcal {M}}$, and

$$\begin{aligned} \begin{aligned} T_{n+1}&:= \big \{ f_{n,\theta _n}^{-1} ( f_{n,i} (t) \cap M_{n,i}) \,:\, i=1,2,\ldots , N,\, t\in T_n\big \}, \\ F_{n+1}&:= \big \{ {\mathbb X}; \ f_{n,\theta _n}^{-1}\circ f_{n,i}\circ f_{n,\theta _n} \, : \, i=1,\ldots ,N \big \}, \\ A_{n+1}&:= f^{-1}_{n,\theta _n}(A_n),\\ {\mathcal M}_{n+1}&:= \{ M_{n+1,1}, \dots , M_{n+1,N}\}, \quad \text {where} \\&\left\{ \begin{array}{llll} M_{n+1,\theta _{n+1}} = f_{n+1,\theta _{n+1}}(A_{n+1}), \\ M_{n+1,j} = f_{n,\theta _n}^{-1}(M_{n,j}) \setminus f_{n+1,\theta _{n+1}}(A_{n+1}) \quad \text {if}\; j \ne \theta _{n+1} \end{array}\right. \end{aligned} \end{aligned}$$

(4.1)

The following proposition is not hard to verify.

Proposition 4.2

For all $n=1,2,\ldots ,$ we have

• (1) $A_{n}$ is the attractor of $F_{n}$;

• (2) ${\mathcal {M}}_{n}$ is a mask for $A_{n}$;

• (3) $T_{n}\subset T_{n+1}$.

In light of statement (3), define, with respect to $F$ and $A$:

$$\begin{aligned} T_{\theta } := T_{{\mathcal {M}},\theta } = \mathop {\bigcup }\limits _{n=1}^{\infty }T_{n}. \end{aligned}$$

If an attractor $A$ of an IFS $F$ is non-overlapping, then

$$\begin{aligned} {\mathcal {M}} := \{ f_{i}(A) \, : \, i = 1,2, \dots , N \} \end{aligned}$$

is a mask for $A$. It is not hard to verify that, in this case, the tiling $T_{{\mathcal {M}},\theta }$ is exactly the tiling $T_{\theta }$ defined by Eq. (3.1) in Sect. 3.

Theorem 4.3

Let $F=\big ( \mathbb {X}\, ; \, f_{1},f_{2},\ldots ,f_{N} \big )$ be an invertible IFS with attractor $A$ with nonempty interior and mask $\mathcal {M}$. If $\theta$ is a full word, then the tiling $T_{{\mathcal {M}, \theta }}$ covers the basin $B(A)$. If $F$ is contractrive, then $T_{{\mathcal {M}, \theta }}$ is a full tiling of ${\mathbb {X}}$.

Proof

It is sufficient to show that the basin $B:=B(A)$ is covered by the tiling, so let $x\in B$. According to the third line of Eq. (4.1), the tiling $T_{{\mathcal {M}, \theta }}$ covers

$$\begin{aligned}&\cdots [ ( f_{\theta _1}^{-1} f_{\theta _2}^{-1} f_{\theta _1} )( f_{\theta _1}^{-1} f_{\theta _3}^{-1} f_{\theta _1} ) ( f_{\theta _1}^{-1} f_{\theta _2} f_{\theta _1}) ]( f_{\theta _1}^{-1} f_{\theta _2}^{-1} f_{\theta _1}) f_{\theta _1}^{-1} (A) \nonumber \\&= f_{\theta _1}^{-1} f_{\theta _2}^{-1} f_{\theta _3}^{-1} \cdots f_{\theta _n}^{-1} (A) \end{aligned}$$

for any $n$. So it sufices to show that $x \in f_{\theta _{1}}^{-1} f_{\theta _{2}}^{-1} f_{\theta _{3}}^{-1} \cdots f_{\theta _{n}}^{-1} (A)$ for some $n$, or equivalently

$$\begin{aligned} f_{\theta _{n}} f_{\theta _{n-1}} \cdots f_{\theta _{1}} (x) \in A. \end{aligned}$$

By the definition of attractor, for any $\varepsilon > 0$ there is an $M_{\varepsilon }$ such that if $m \ge M_{\varepsilon }$, then

$$\begin{aligned} F^{m}(x) \subset A_{\varepsilon }, \end{aligned}$$

where $A_{\varepsilon }$ is the open $\varepsilon$-neighborhood of $A$. Because $\theta$ is assumed to be full, there exists a compact $A^{\prime }$ with $A' \subset A^o$ with the property that, for any $M$ there exist $n>m\ge M$ such that

$$\begin{aligned} f_{\theta _{n}}\circ \cdots \circ f_{\theta _{m+1}}(A) \subset A' \subset A^o. \end{aligned}$$

This implies that there exists an $\varepsilon _{0}$-neighborhood $A_{\varepsilon _{0}}$ of $A$ such that

$$\begin{aligned} f_{\theta _{n}}\circ \cdots \circ f_{\theta _{m+1}}(A_{\varepsilon _{0}}) \subset A^{\text {o}} \end{aligned}$$

for some $\varepsilon _{0}>0$. If $M \ge M_{\varepsilon _{0}}$, then

$$\begin{aligned} f_{\theta _{n}}\circ \cdots \circ f_{\theta _{m+1}}\circ f_{\theta _{m}} \circ \cdots \circ f_{\theta _{1}}(x) \in f_{\theta _{n}}\circ \cdots \circ f_{\theta _{m+1}}(A_{\varepsilon _{0}}) \subset A, \end{aligned}$$

as required.$\square$

Example 4.4

A portion of a one-dimensional masked tiling, illustrated in Fig. 11, is generated by the overlapping IFS

$$\begin{aligned} F=\big \{ \mathbb {R}:f_{1}(x)=bx,f_{2}(x)=bx+(1-b)\big \} \end{aligned}$$

with $b=0.65$. The unique attractor of $F$ is $A=[0,1]$. The mask for $A$ (w.r.t. $F$) is $\{M_{1}=[0,b],M_{2}=[b,1]\}$. The left-most tile is black and corresponds to the interval $A$.

In this and other pictures, different colors represent different tiles. Some colors may be close together. The images are approximate.

Fig. 11

Part of a tiling of $\mathbb {R}$ generated by a masked IFS

Example 4.5

Figures 12 ($b=0.65$) and 13 ($b=0.9$) illustrate masked tilings of $\mathbb {[}0,\infty )^{2}\subset \mathbb {R}^{2}$ associated with the family of IFSs $F=\big \{ \mathbb {[}0,\infty )^{2} :f_{1},f_{2},f_{3},f_{4}\big \}$ where

$$\begin{aligned} \begin{aligned} f_{1}(x,y)&= (bx,by), \\ f_{3}(x,y)&= (bx,by+l), \end{aligned} \qquad \begin{aligned} f_{2}(x,y)&=(bx+l,by), \\ f_{4}(x,y)&= (bx+l,by+l), \end{aligned} \end{aligned}$$

with  $l=(1-b)$. The attractor is the filled unit square $A=[0,1]^{2} =[0,1]^{2}$ represented by the black tile in the upper left corner of both images. The mask is

$$\begin{aligned} \begin{aligned} M_{1}&=f_{1}([0,1]^{2}), \\ M_{k+1}&=f_{k+1}([0,1]^{2})\backslash \mathop {\bigcup }\limits _{i=1}^{k}M_{i}\text { }\quad (k=1,2,3), \end{aligned} \end{aligned}$$

which is referred to as the tops mask. In both cases the tiling is generated by the string $\theta =\overline{1}$.

Fig. 12

Part of a two-dimensional masked tiling. The top row shows the same one-dimensional masked tiling illustrated in Fig. 11

Fig. 13

A masked tiling of a quadrant of the Euclidean plane, similar to Fig. 12, but with scaling factor $b=0.9$

5 Tilings from a Graph IFS

The construction of tilings from an IFS can be generalized to the construction of tilings from a graph IFS. There is considerable current interest in graph IFS and tilings corresponding to Rauzy fractals [16, 23, 24]. Hausdorff dimension of attractors associated with graph IFSs has been considered in [21]. Graph IFSs arise in connection with substitution tilings and number theory; see for example [2, 11].

Let ${\mathbb {H}}^{M}$ denote the $N$-fold cartesian product of $M$ copies of ${\mathbb {H}}(\mathbb {X })$. A graph iterated function system (GIFS) is a directed graph $G$, possibly with loops and multiple edges in which the vertices of $G$ are labeled by $\{ 1,2, \dots , M\}$ and each directed edge $e$ is labeled with a continuous function $f_{e}: \mathbb {X }\rightarrow \mathbb {X}$. It is also assumed that $G$ is strongly connected, i.e., that there is a directed path from any vertex to any other. Let $E_{ij}$ denote the set of edges from vertex $i$ to vertex $j$. Define the function

$$\begin{aligned} F \; : \;{\mathbb {H}}^{M} \rightarrow {\mathbb {H}}^{M} \end{aligned}$$

as follows. If $\mathbf {X} = (X_{1},X_{2}, \dots , X_{M}) \in {\mathbb {H}}^{M}$, then

$$\begin{aligned} F(\mathbf {X}) = (F_{1}(\mathbf {X}), F_{2}(\mathbf {X}), \dots , F_{M} (\mathbf {X})), \end{aligned}$$

where

$$\begin{aligned} F_{i}(\mathbf {X}) = \mathop {\bigcup }\limits _{j=1}^{M} \;\mathop {\bigcup }\limits _{e\in E_{ij}} f_{e}(X_{j}) \end{aligned}$$

for $i=1,2,\ldots , M$. It can be shown that, if each $f_{e}$ is a contraction, then $F$ is a contraction on ${\mathbb {H}} ^{M}$, and consequently has a unique fixed point or attractor $\mathbf {A} = (A_{1}, A_{2}, \dots , A_{M})$. The concepts of non-overlapping and invertible are defined exactly as for an IFS. In fact, an ordinary IFS is the special case of a graph IFS where $G$ has exactly one vertex and all the edges are loops.

Assume that the graph IFS is a non-overlapping and invertible with attractor $\mathbf {A} = (A_{1}, A_{2}, \dots , A_{M})$. Let $G^{\prime }$ denote the graph obtained from $G$ by reversing the directions on all of the edges. For any directed (infinite) path $\theta =e_{1}e_{2}\cdots$ in $G^{\prime }$, a tiling is constructed as follows. First extend previous notation so that $\theta _{k}=e_{k},\;\theta |k=e_{1}e_{2}\cdots e_{k}$ and $f_{\theta |k}=f_{e_{1}}\circ f_{e_{2}}\circ \cdots \circ f_{e_{k}},\; (f^{-1})_{\theta |k} :=f_{e_{1}} ^{-1}\circ f_{e_{2}}^{-1}\circ \cdots \circ f_{e_{k}}^{-1}$. Given any directed path $\omega$ of length $k$ in $G$ that starts at the vertex at which $\theta |k$ terminates, let

$$\begin{aligned} \begin{aligned} t_{\theta ,\omega }&= ((f^{-1})_{\theta |k}\circ f_{\omega })(A_j), \\ T_{\theta ,k}&= \{ t_{\theta ,\omega } \, : \, \omega \in W_{k} \}, \end{aligned} \end{aligned}$$

where $j$ is the terminal vertex of the path $\omega$, and $W_{k}$ is the set of directed paths of length $k$ in $G$ that start at the vertex at which $\theta |k$ terminates. Since, for any $\omega \in W_{k}$, we have

$$\begin{aligned} (f^{-1})_{\theta |k}\circ f_{\omega }=(f^{-1})_{\theta |k}\circ (f_{\theta _{k+1} })^{-1}\circ f_{\theta _{k+1}}\circ f_{\omega }=(f^{-1})_{\theta |k+1}\circ f_{\theta _{k+1}\omega }, \end{aligned}$$

the inclusion

$$\begin{aligned} T_{\theta ,k}\subset T_{\theta ,k+1} \end{aligned}$$

holds for all $k$. Therefore

$$\begin{aligned} T_{\theta } :=\mathop {\bigcup }\limits _{k=1}^{\infty }T_{\theta ,k} \end{aligned}$$

is a tiling.

Example 5.1

(Penrose tilings of ${\mathbb {R}}^{2}$) In this example the graph $G$ is given in Fig. 14 where, using the complex representation of ${\mathbb {R}}^{2}$, the functions are

$$\begin{aligned} f_{1}(z)=( \tau - \frac{z}{\tau } ) \,\omega _{1},\quad f_{2} (z)=\frac{z}{\tau } \omega _4+\tau ^{2},\quad f_{3}(z)=\frac{z}{\tau }\,\omega _{3} +\tau ^{2}, \end{aligned}$$

where $\tau =(1+\sqrt{5})/2$ is the golden ratio and $\omega _{k}=\cos (k\pi /5)+i\,\sin (k\pi /5),\,0\le k\le 9$, are the tenth roots of unity. (The origin is at the leftmost vertex of each triangle.) The acute isosceles triangle $A$ and obtuse isosceles triangle $B$ in the figure have long and short sides in the ratio $\tau :1$, and the angles are $\pi /5,2\pi /5,2\pi /5$ and $\pi /5,\pi /5,3\pi /5$, respectively. The attractor of the graph IFS is the pair $(A,B)$:

$$\begin{aligned} \begin{aligned} A&= f_1(B)\cup f_2(A) \cup f_3(A), \\ B&= f_1(B) \cup f_2(A). \end{aligned} \end{aligned}$$

Clearly, there are periodic tilings of the plane using copies of these tiles. However, if $\theta$ is a directed path in $G$ and $T_{\theta }$ tiles ${\mathbb {R}}^{2}$, then this is a non-periodic tiling. Although a Penrose tiling is usually given in terms of kites and darts or thin and fat rhombs, these are equivalent to tiling by the acute and obtuse triangles described in this example.

Fig. 14

Graph IFS for the Penrose tiles

Example 5.2

(Another GIFS tiling) In Fig. 15 the graph has two vertices corresponding to the two components of the attractor, the isosceles right triangle $T$ and square $S$ shown at the top. The eight edges of the graph, corresponding to the eight functions are shown graphically by their images, the eight colored triangles and rectangles shown at the top. Four of the functions map the triangle $T$ onto the four smaller triangles, and the other four functions map the square $S$ to the two smaller squares and two rectangles. One of the infinitely many possible tilings that can be constructed, using the method described of this section, is shown in the bottom panel.

Fig. 15

Another GIFS tiling; see Example 5.2

6 Fractal Transformations from Tilings

The goal of this section is, given a fractal transformation, to extend its domain from the attractor of the IFS to the basin of the IFS, for example in the contractive IFS case, from the attractor to all of ${\mathbb {X}}$.

6.1 Fractal Transformation

In Sect. 2, each point of a point-fibred attractor an IFS was assigned a set of addresses. To choose a particular address for each point of the attractor, the following notion is introduced.

Definition 6.1

Let $A$ be a point-fibred attractor of an invertible IFS $F$. A section of the coordinate map $\pi \, : \, [N]^{\infty } \rightarrow A$ is a map $\tau \,:\,A\rightarrow [N]^{\infty }$ such that $\pi \circ \tau$ is the identity. For $x\in A$, the word $\tau (x)$ is referred to as the address of $x$ with respect to the section $\tau$.

If $A$ is a point-fibred attractor of $F$, then the following diagram commutes for all $n\in [N]$:

where the inverse shift map $S_{n}\,:\, [N]^{\infty } \rightarrow [N]^{\infty }$ is defined by $S_{n}(\omega )=n\omega$ for $n\in [N]$.

The notion of fractal transformation was introduced in [5]; see also [6, 8]. A fractal transformation is a mapping from the attractor of one IFS to the attractor of another IFS of the following type.

Definition 6.2

Given two IFSs $F$ and $G$ with an equal number of functions, with point-fibred attractors $A_{F}$ and $A_{G}$, with coordinate maps $\pi _{F}$ and $\pi _{G}$ and with shift invariant sections $\tau _{F}$ and $\tau _{G}$, each of the maps $\pi _{F} \circ \tau _{G} \, : A_{G} \rightarrow A_{F}$ and $\pi _{G} \circ \tau _{F} \, : A_{F} \rightarrow A_{G}$ is called a fractal transformation. If a fractal transformation $h$ is a homeomorphism, then $h$ is called a fractal homeomorphism.

A homeomorphism $h \,: A_{F} \rightarrow A_{G}$ is a fractal homeomorphism with respect to shift invariant sections $\tau _{F}$ and $\tau _{G}$ if and only if $h$ satisfies the commuting diagram

$$\begin{aligned} \begin{array} [c]{ccc} A_{F} &{} \underset{h}{\rightarrow } &{} A_{G}\\ \tau _{F} \searrow &{} &{} \swarrow \tau _{G}\\ &{} [N]^{\infty } &{} \end{array} \end{aligned}$$

(6.1)

i.e., the function $h$ takes each point $x\in A_{F}$ with address $\omega = \tau _{F}(x)$ to the point $y \in A_{G}$ with the same address $\omega =\tau _{G}(y)$. See [8].

6.2 Extending the Domain of a Fractal Transformation

To extend the domain of a fractal transformation, we introduce a “decimal” notation $\theta \cdot \omega$, where $\theta$ is a finite word and $\omega$ is an infinite word in the alphabet $[N]$. Let

$$\begin{aligned} \Omega := \{\theta _{1} \theta _{2} \cdots \theta _{k} \cdot \omega _{1} \omega _{2} \cdots \, | \, k\in \{0\}\cup \mathbb {N}, \, \theta _{i}, \omega _{i} \in [N] \; \text {for all} \; i, \, \theta _{k} \ne \omega _{1}\}. \end{aligned}$$

For an IFS $F$ the coordinate map $\pi \, : \, [N]^{\infty } \rightarrow A$ can be extended as follows.

Definition 6.3

For an invertible IFS on a complete metric space ${\mathbb {X}}$ with point-fibred attractor $A$ and $\theta \cdot \omega \in \Omega$, define the extended coordinate map $\widehat{\pi } \, : \, \Omega \rightarrow {\mathbb {X}}$ of $\pi \, : \, [N]^{\infty } \rightarrow A$ by

$$\begin{aligned} \widehat{\pi } (\theta \cdot \omega ) := (f^{-1})_{\theta }(\pi (\omega )). \end{aligned}$$

Recall the notation $F^{*}:=\big ( \mathbb {X};f_{1}^{-1},f_{2}^{-1},\ldots ,f_{N}^{-1}\big )$, so that $F^*(X) = \cup _{f\in F} f^{-1}(X)$. The range of $\widehat{\pi }$, called the fast basin of the attractor $A$ and denoted ${\widehat{B}} = {\widehat{B}}(A)$, is equal to

$$\begin{aligned} {\widehat{B}}(A) = \cup _{k=0}^{\infty } (F^*)^{k} (A) =\Big \{ x \in {\mathbb {X}} \, : \, f_{\theta }(x) \in A \;\text { for some}\; \theta \in \cup _{k=1}^{\infty } [N]^{k}\Big \} . \end{aligned}$$

Proposition 6.4

The fast basin $\widehat{B}$ of a point-fibred attractor $A$ of an invertible IFS $F$ on ${\mathbb {X}}$ is the smallest subset of ${\mathbb {X}}$ invariant under $F^*$ and containing $A$, i.e., $F^*({\widehat{B}}) = {\widehat{B}}$ and

$$\begin{aligned} {\widehat{B}} = \mathop {\bigcap }\limits _{F^*(D) = D} D. \end{aligned}$$

Moreover, if $B$ is the basin and $\widehat{B}$ the fast basin of $A$, then

• (1) $B \subseteq {\widehat{B}}$ if $A^{\text {o}}\ne \emptyset$,

• (2) ${\widehat{B}}^{\text {o}} = \emptyset$ if $A^{\text {o}} =\emptyset$.

Proof

Concerning the first statement, that $\widehat{B}$ is invariant follows from the definition. Concerning the minimality statement, if $C$ is invariant under $F^*$ and $A \subseteq C$, then

$$\begin{aligned} {\widehat{B}} =\mathop {\bigcup }\limits _{k=0}^{\infty } (F^*)^{k} (A) \subseteq \mathop {\bigcup }\limits _{k=0}^{\infty } C = C. \end{aligned}$$

Concerning the second statement, in the case that $A^{\text {o}} \ne \emptyset$, there is a $\omega \in [N]^{\infty }$ such that $\pi (\omega ) \in A^{\text {o}}$. If $x \in B$, then $\lim _{k\rightarrow \infty } f_{\omega |k}(x) = \pi (\omega ) \in A^{\text {o}}$. Therefore $f_{\omega |K} \in A^{\text {o}}$ for some $K$. In the case that $A^{\text {o}} =\emptyset$, since ${\widehat{B}} =\cup _{k=0}^{\infty } (F^*)^{k} (A)$ is a countable union of nowhere dense sets, then so is $\widehat{B}$ by the Baire catgegory theorem.$\square$

Definition 6.5

Let $F$ be an invertible IFS with point-fibred attractor $A$. Let $\theta \in [N]^{\infty }$, and recall the notation $B(\theta ) :=\cup _{k=1}^{\infty }(f^{-1})_{\theta |{k}}(A)$. For a section $\tau \, : \, A \rightarrow [N]^{\infty }$ define the extended section

$$\begin{aligned} {\widehat{\tau } _{\theta }}\, : B(\theta ) \rightarrow \Omega \end{aligned}$$

as follows. For $x \in B(\theta )$, let $k$ be the least integer such that $x \in (f^{-1})_{\theta |k}(A)$. Therefore there is a $y\in A$ such that $x = (f^{-1})_{\theta |k}(y)$. Define

$$\begin{aligned} {\widehat{\tau }_{\theta }}(x) := \theta |k\cdot \tau (y). \end{aligned}$$

Then clearly $\widehat{\pi }\circ \widehat{\tau }_{\theta }$ is the identity.

Now consider two IFSs $F$ and $G$ on the same complete metric space, with an equal number of functions, with point-fibred attractors $A_{F}$ and $A_{G}$, with coordinate maps $\pi _{F}$ and $\pi _{G}$, and with sections $\tau _{F}$ and $\tau _{G}$. Each word $\theta \in [N]^{\infty }$ induces two extended sections $\widehat{\tau _{F}} := \widehat{\tau _{F,\theta }}$ and $\widehat{\tau _{G}} :=\widehat{\tau _{G,\theta }}$. The maps

$$\begin{aligned} \widehat{\pi }_{F} \circ \widehat{\tau _{G}} \, : B_{G}(\theta ) \rightarrow B_{F}(\theta ) \quad \text {and} \quad \widehat{\pi }_{G} \circ \widehat{\tau _{F}} \, : B_{F}(\theta ) \rightarrow B_{G}(\theta ) \end{aligned}$$

are called extended fractal transformations of the fractal transformations

$$\begin{aligned} \pi _{F} \circ \tau _{G} \, : \, A_{G} \rightarrow A_{F} \quad \text {and} \quad \pi _{G} \circ \tau _{F} \, : \, A_{F} \rightarrow A_{G}, \end{aligned}$$

respectively. In particular, if $\theta$ is full for both $F$ and $G$, then an extended fractal transformation is defined on the basin of an attractor. If, in addition, $F$ and $G$ are contractive, then the extended fractal transformations take the whole space ${\mathbb {X}}$ to itself.

A transformation that takes, for example, the unit square $[0,1]^{2}$ to itself, can be visualized by its action on an image. Define an image as a function $c \, : \, [0,1]^{2} \rightarrow {\mathcal C}$, where $\mathcal C$ denotes the color palate, for example ${\mathcal C} = \{ 0,1,2,\ldots , 255\}^3$. If $h$ is any transformation from $[0,1]^{2}$ onto $[0,1]^{2}$, define the transformed image $h(c) \, : \, [0,1]^{2} \rightarrow {\mathcal C}$ by $h(c) := c \circ h.$

Example 6.6

Consider two “fold-out” affine IFSs, $F$ and $G$, which, up to conjugation by an affine transformation, are of the form in Example 3.13 for two different values of the parameter $E$. The IFS $F$ corresponds to $E=(0.5,0.5)$ and the IFS $G$ corresponds to $E=(0.4,0.45)$. The attractor of $F$ is a small rectangle $L$ located in the bottom left corner of the left hand image of Fig. 16. The attractor of $G$ is a small rectangle R situated in the bottom left corner of the right hand image. The fractal homeomorphism generated by $F$ and $G$ maps the portion of the left hand image lying over $L$ to the portion of the right hand image that lies over $R$. The word $\theta =\overline{1}$ extends the fractal homeomorphism to the upper left quadrant of the plane; the right hand image illustrates the result of applying this extended homeomorphism to the left hand image.

Fig. 16

Example of an extended fractal homeomorphism, generated by a pair of affine IFSs each with a rectangular just-touching attractor