Abstract
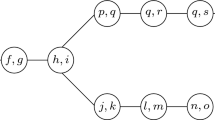
Let G=(VG,AG) be a digraph and let S ⊔ T be a bipartition of VG. A bibranching is a subset B⊆AG such that for each node s∈S there exists a directed s–T path in B and, vice versa, for each node t∈T there exists a directed S–t path in B.
Bibranchings generalize both branchings and bipartite edge covers. Keijsper and Pendavingh proposed a strongly polynomial primal-dual algorithm that finds a minimum weight bibranching in O(n′(m+nlog n)) time (where n:=|VG|, m:=|AG|, n′:=min (|S|,|T|)).
Assuming that arc weights are integers we develop a weight-scaling algorithm of time complexity \(O(m\sqrt{n}\;\log n\log(nW))\) for the minimum weight bibranching problem (where W denotes the maximum magnitude of arc weights).
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Babenko, M.: An efficient scaling algorithm for the minimum weight bibranching problem. Lect. Notes Comput. Sci. 5369, 232–245 (2008)
Cormen, T., Stein, C., Rivest, R., Leiserson, C.: Introduction to Algorithms. McGraw-Hill Higher Education, New York (2001)
Dinic, E.: Algorithm for solution of a problem of maximum flow in networks with power estimation. Sov. Math. Dokl. 11, 1277–1280 (1980)
Edmonds, J.: Optimum branchings. J. Res. Natl. Bur. Stand. 71B, 233–240 (1967)
Frank, A.: How to make a digraph strongly connected. Combinatorica 1(2), 145–153 (1981)
Fredman, M., Tarjan, R.: Fibonacci heaps and their uses in improved network optimization algorithms. J. ACM 34(3), 596–615 (1987)
Gabow, H.: A representation for crossing set families with applications to submodular flow problems. In: Proceedings of the Fourth Annual ACM-SIAM Symposium on Discrete Algorithms, pp. 202–211 (1993)
Gabow, H.: A framework for cost-scaling algorithms for submodular flow problems. In: SFCS ’93: Proceedings of the 1993 IEEE 34th Annual Foundations of Computer Science, pp. 449–458 (1993)
Gabow, H., Galil, Z., Spencer, T., Tarjan, R.: Efficient algorithms for finding minimum spanning trees in undirected and directed graphs. Combinatorica 6(2), 109–122 (1986)
Goldberg, A., Tarjan, R.: Solving minimum-cost flow problems by successive approximation. In: STOC ’87: Proceedings of the Nineteenth Annual ACM Conference on Theory of Computing, pp. 7–18 (1987)
Gabow, H., Tarjan, R.: Faster scaling algorithms for network problems. SIAM J. Comput. 18(5), 1013–1036 (1989)
Gabow, H., Tarjan, R.: Faster scaling algorithms for general graph matching problems. J. ACM 38(4), 815–853 (1991)
Keijsper, J., Pendavingh, R.: An efficient algorithm for minimum-weight bibranching. J. Comb. Theory, Ser. B 73(2), 130–145 (1998)
Schrijver, A.: Min-max relations for directed graphs. Ann. Discrete Math. 16, 261–280 (1982)
Schrijver, A.: Combinatorial Optimization. Springer, Berlin (2003)
Sleator, D., Tarjan, R.: A data structure for dynamic trees. J. Comput. Syst. Sci. 26(3), 362–391 (1983)
Tarjan, R.: Data Structures and Network Algorithms. Society for Industrial and Applied Mathematics, Philadelphia (1983)
Author information
Authors and Affiliations
Corresponding author
Additional information
Supported by RFBR grant 06-01-00122.
Rights and permissions
About this article
Cite this article
Babenko, M.A. An Efficient Scaling Algorithm for the Minimum Weight Bibranching Problem. Algorithmica 61, 898–922 (2011). https://doi.org/10.1007/s00453-009-9377-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00453-009-9377-1